Dimensional Synthesis Approach for Planar Open Path Based on Chord Angle Descriptor
-
摘要:
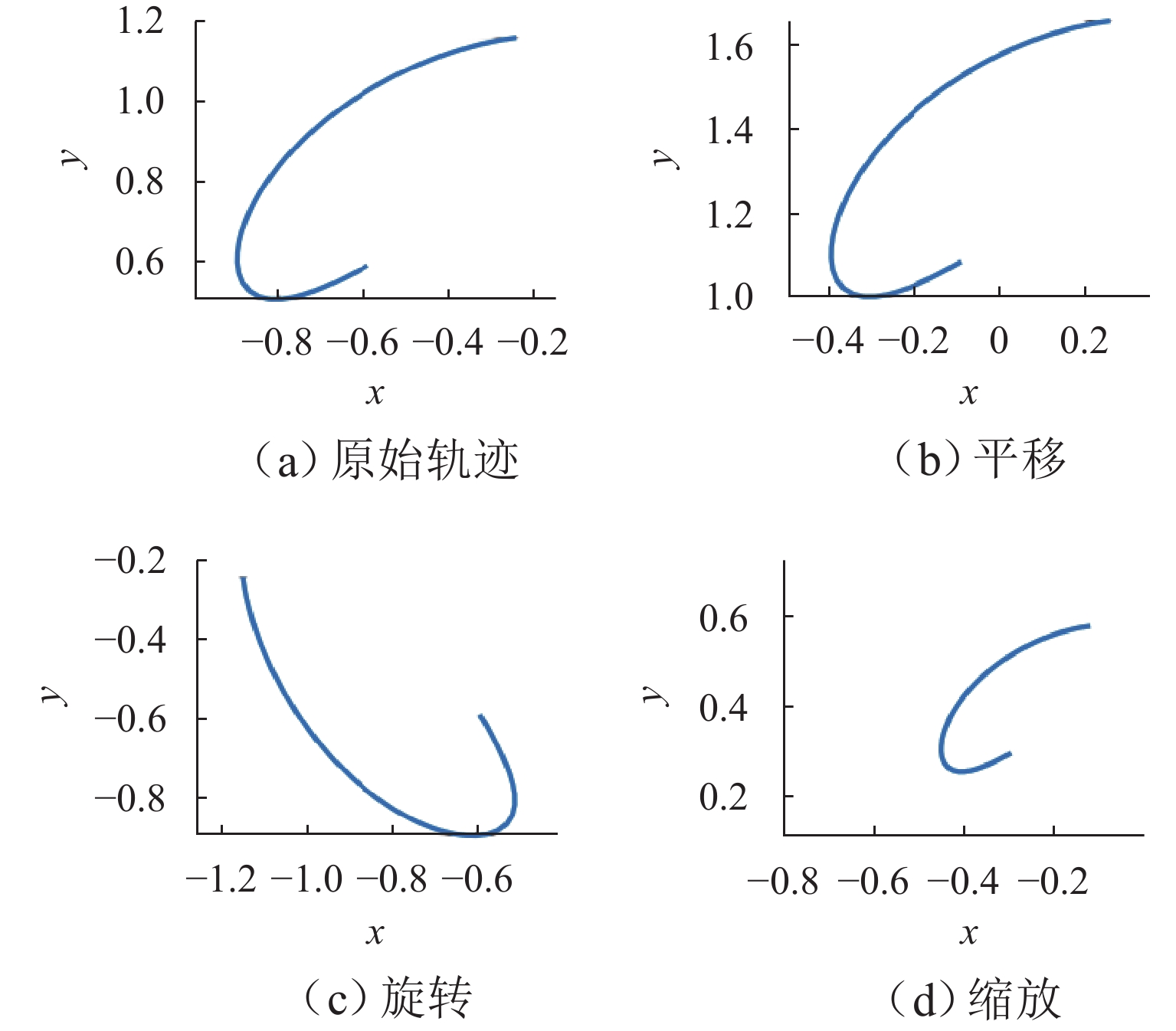
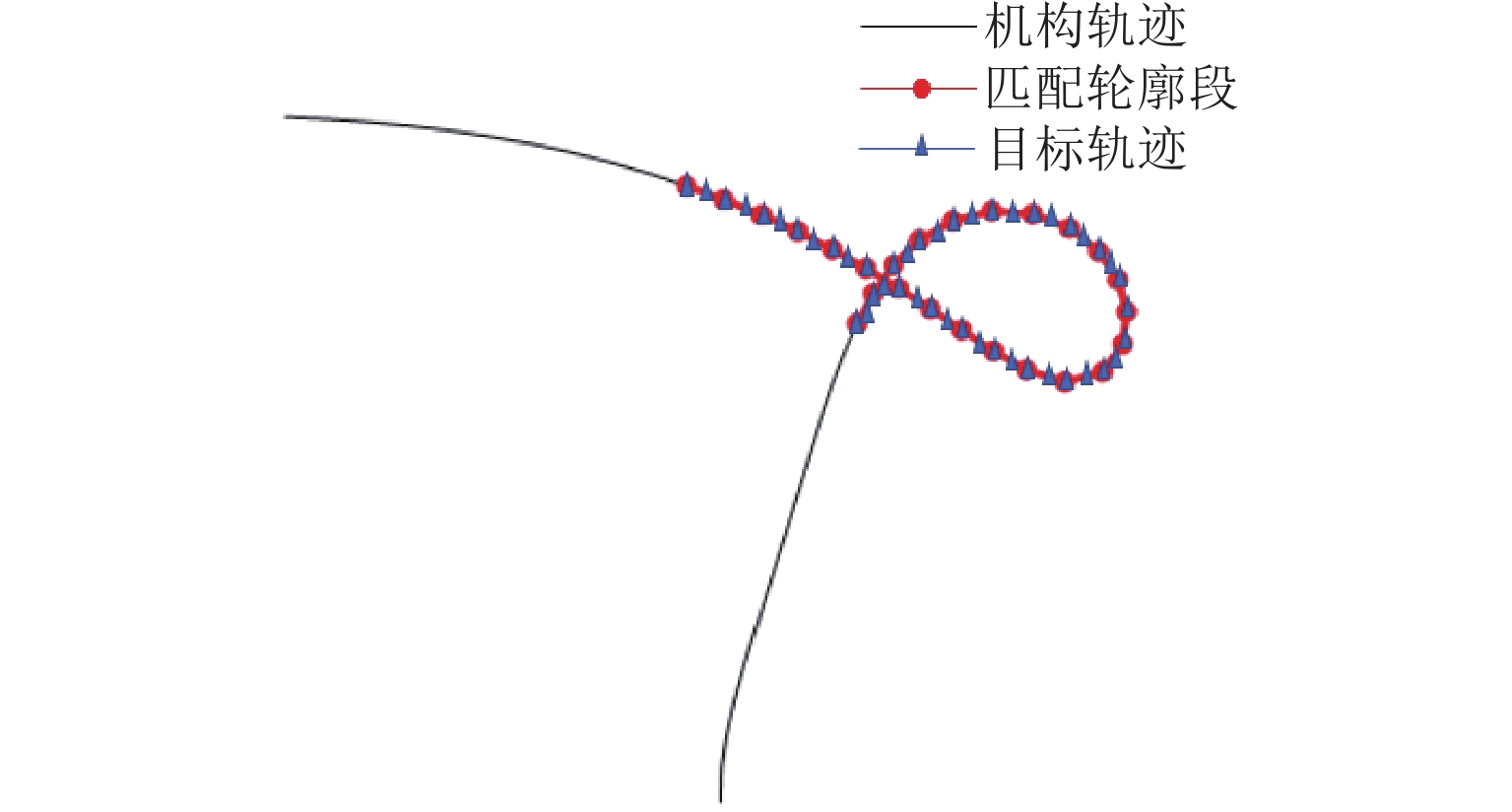
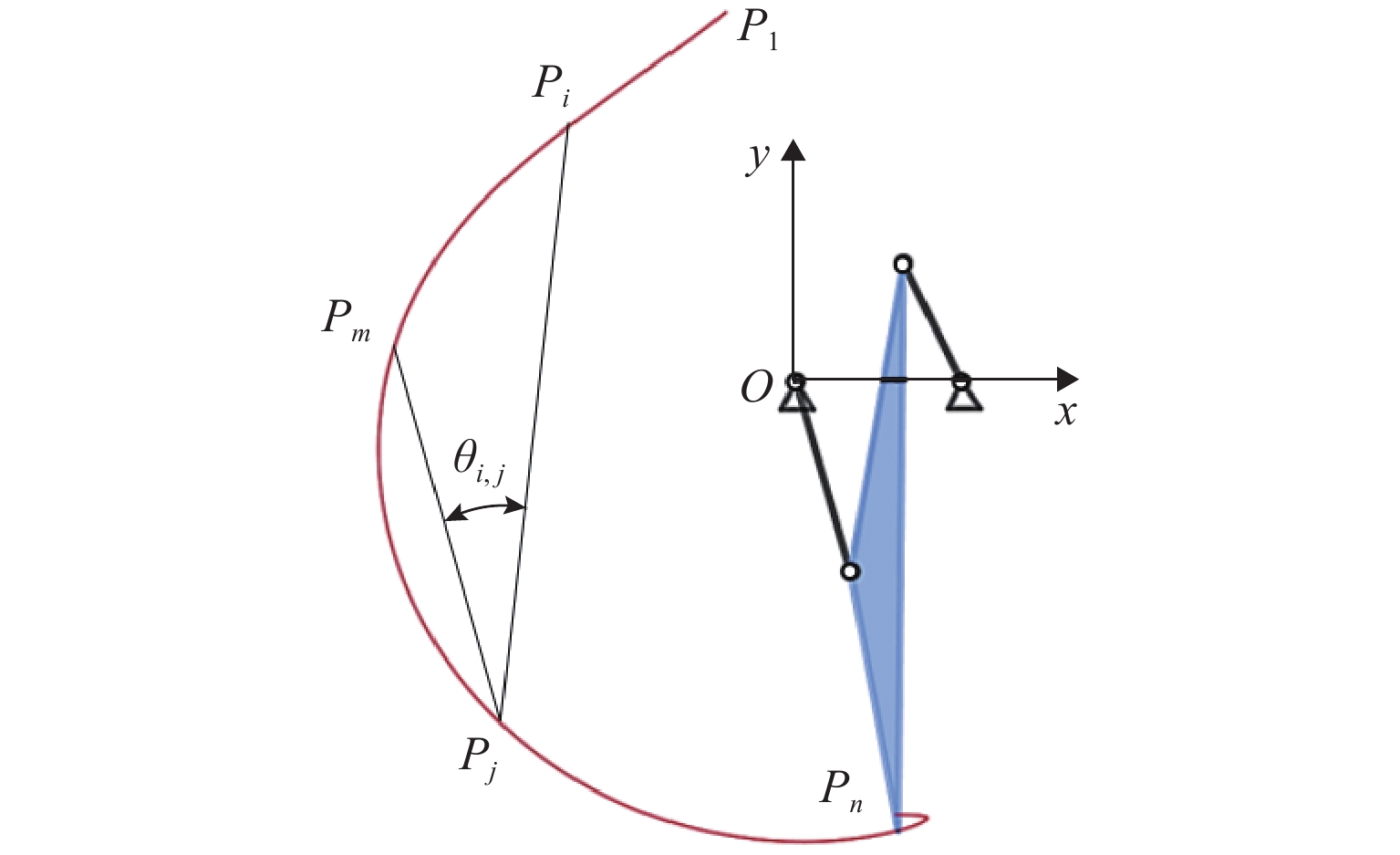
针对数值图谱法提取平面开环轨迹特征计算量大、检索效率低的问题，提出一种基于弦角描述符的平面开环轨迹尺寸综合方法. 首先，利用弦角描述符的平移、旋转、缩放不变性，得到与机构机架位置、机架偏转角度和整体缩放均无关的开环轨迹形状特征；其次，基于弦角描述符自包含属性提出不受采样分辨率影响的开环轨迹部分匹配算法；然后，通过多维尺度缩放法将弦角描述符压缩为2维特征，并结合层次聚类算法，建立16 000组平面四杆机构的数值图谱库；在此基础上，根据弦角描述符与图谱库中弦角描述符的相似程度，检索出满足设计要求的机构尺寸型；最后，通过2个平面开环轨迹尺寸综合算例，验证该方法的有效性. 研究结果表明：所提尺寸综合方法能够得到满足设计要求的平面开环轨迹尺寸综合结果，且无需对轨迹进行归一化处理；与B样条曲线描述符、曲率描述符、傅里叶描述符相比，弦角描述符的开环轨迹匹配总时间分别减少了43%、35%、38%.
Abstract:To deal with huge computation and low retrieval efficiency in extracting planar open path features by a numerical atlas method, a dimensional synthesis approach was proposed for planar open paths based on chord angle descriptors. Firstly, by using the invariance of translation, rotation, and scaling of chord angle descriptors, the open path shape features independent of the frame position, orientation, and overall scaling of linkages were obtained. Secondly, based on the self-contained properties of chord angle descriptors, a partial matching algorithm not affected by the sampling resolution was proposed for open paths. Furthermore, the chord angle descriptors were compressed into two-dimensional features by multi-dimensional scaling. The numerical atlases of 16 000 groups of planar four-bar linkages were established by combining the hierarchical clustering algorithm. On this basis, the linkage dimension type suitable for design requirements was retrieved according to the similarity between the chord angle descriptors and those in the atlases. Finally, this method was validated by two-dimensional synthesis examples of planar open paths. The research findings show that overall dimensional results of planar open paths satisfying the design requirements can be achieved through the dimensional synthesis approach, and normalization is not required for paths. Compared with that of the curve descriptor, the curvature descriptor, and the Fourier descriptor of the B sample, the total open path matching time of the chord angle descriptors decreases by 43%, 35%, and 38%, respectively.
-
图 12 表3机构的运动轨迹及其匹配轮廓段
Figure 12. Motion paths of linkages in Tab.3 and their matching segments
图 13 肩关节运动轨迹及坐标
Figure 13. Motion path of shoulder joint coordinate graphalong with coordinate
图 14 表4机构的运动轨迹及其匹配轮廓段
Figure 14. Motion paths of linkages in Tab.4 and their matching segments
表 1 轨迹匹配过程所用时间
Table 1. Time consumption of path matching process
描述符 归一化
时间/ms相似度
计算时间/ms总时
间/ms减少时间
百分比/%弦角描述符 13 13 B 样条曲线描述符 12 11 23 43 曲率描述符 12 8 20 35 傅里叶描述符 12 9 21 38 
下载: 导出CSV
表 2 ${\boldsymbol{\varLambda }}$中最大的前10个特征值
Table 2. Top 10 largest eigenvalues in ${\boldsymbol{\varLambda }}$
编号 1 2 3 4 5 6 7 8 9 10 特征值 127984 34480 27102 19090 7166 4120 3694 3068 2586 1847
下载: 导出CSV
表 3 算例1的尺寸综合结果
Table 3. Dimensional synthesis results of example 1
编号 ${r_1}$ ${r_2}$ ${r_3}$ ${r_4}$ $\phi $ ${\rho _{\max }}$ 1 1.3587 3.2236 3.8587 1.2522 − 2.2294 0.9981 2 1.0514 1.1401 2.2410 2.9365 − 0.7038 0.9980 3 0.6868 1.1227 0.7865 0.4678 0.4194 0.9974 4 0.5852 0.8668 0.9214 0.1351 − 0.7159 0.9974 5 0.3917 0.6009 1.5018 1.1475 − 0.2561 0.9973 6 0.7365 1.8271 1.6517 0.3828 0.8777 0.9973
下载: 导出CSV
表 4 算例2的尺寸综合结果
Table 4. Dimensional synthesis results of example 2
编号 ${r_1}$ ${r_2}$ ${r_3}$ ${r_4}$ $\phi $ ${\rho _{\max }}$ 1 0.6485 0.7565 0.7875 2.7891 1.1536 0.9974 2 0.2227 0.7548 0.3097 0.8841 1.2532 0.9969 3 0.6797 0.3256 0.2244 0.3311 − 1.2038 0.9968 4 1.2501 0.6843 0.4309 0.7100 − 1.7501 0.9968 5 0.6241 1.0639 1.1351 1.9733 − 0.6183 0.9967 6 1.3592 1.2685 0.5040 1.8007 − 1.4115 0.9967
下载: 导出CSV
-
[1] LEE W T, RUSSELL K. Developments in quantitative dimensional synthesis (1970–present): four-bar path and function generation[J]. Inverse Problems in Science and Engineering, 2018, 26(9): 1280-1304. doi: 10.1080/17415977.2017.1396328 [2] LI X G, WEI S M, LIAO Q Z, et al. A novel analytical method for four-bar path generation synthesis based on Fourier series[J]. Mechanism and Machine Theory, 2020, 144: 103671.1-103671.7. [3] 刘武芃. 平面连杆机构系统分析与解域综合的理论与方法研究[D]. 北京:北京科技大学,2022. [4] 曹阳. 基于解域的空间连杆机构综合理论与方法研究[D]. 北京:北京科技大学,2020. [5] 张瑶,孔建益,孙亮波,等. 平面含复铰杆组拓扑结构的同构判定方法[J]. 组合机床与自动化加工技术,2019(5): 47-50.ZHANG Yao, KONG Jianyi, SUN Liangbo, et al. Isomorphism identification method for topological structure of planar assur groups with multiple jionts[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2019(5): 47-50. [6] EQRA N, ABIRI A H, VATANKHAH R. Optimal synthesis of a four-bar linkage for path generation using adaptive PSO[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40(9): 469.1-469.11. doi: 10.1007/s40430-018-1392-1 [7] 冯卓. 仿生四足机器人机构设计与动力学尺寸综合[D]. 马鞍山:安徽工业大学,2019. [8] 孙园喜. 基于齿轮-五杆机构的假肢膝关节设计优化与驱动控制研究[D]. 西安:西北工业大学,2018. [9] 郑鹏程. 空间连杆机构轨迹综合理论与方法的研究[D]. 大连:大连理工大学,2000. [10] CHU J K, SUN J W. Numerical atlas method for path generation of spherical four-bar mechanism[J]. Mechanism and Machine Theory, 2010, 45(6): 867-879. doi: 10.1016/j.mechmachtheory.2009.12.005 [11] 韩建友,袁玉芹,吕翔宇,等. 平面多杆机构杆组自动生成方法[J]. 机械工程学报,2015,51(19): 1-10. doi: 10.3901/JME.2015.19.001HAN Jianyou, YUAN Yuqin, LU Xiangyu, et al. Methodology for the automatic generation of assur groups from planar multi-bar linkages[J]. Journal of Mechanical Engineering, 2015, 51(19): 1-10. doi: 10.3901/JME.2015.19.001 [12] 路懿,TATU Leinonen. 用计算机辅助几何技术对Stephenson六杆机构近似位姿的综合[J]. 计算机辅助设计与图形学学报,2003,15(6): 685-691.LU Yi, TATU Leinonen. Computer-aided AD geometry approach of approximate dimensional synthesis for Stephenson six-bar linkage[J]. Journal of Computer-Aided Design & Computer Graphics, 2003, 15(6): 685-691. [13] DESHPANDE S, PURWAR A. An image-based approach to variational path synthesis of linkages[J]. Journal of Computing and Information Science in Engineering, 2021, 21(2): 021005.1-021005.13. [14] DESHPANDE S, PURWAR A. Computational creativity via assisted variational synthesis of mechanisms using deep generative models[J]. Journal of Mechanical Design, 2019, 141(12): 121402.1-121402.10. [15] SUN J W, XUE N, LIU W R, et al. A synthesis method for path generation of a planar five-bar mechanism based on dynamic self-adaptive atlas database[J]. Inverse Problems in Science and Engineering, 2020, 28(5): 1745792.1-1745792.24. [16] 于红英,赵彦微,许栋铭. 平面铰链四杆机构的轨迹综合方法[J]. 哈尔滨工业大学学报,2015,47(1): 40-47.YU Hongying, ZHAO Yanwei, XU Dongming. A path synthesis method of planar hinge four-bar linkage[J]. Journal of Harbin Institute of Technology, 2015, 47(1): 40-47. [17] ZHANG W, LIU Z, SUN J W, et al. Path synthesis of a spherical five-bar mechanism based on a numerical atlas method[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(11): 554. doi: 10.1007/s40430-022-03860-w [18] 丁健生,刘文瑞,孙建伟. 平面四杆机构少位置设计要求特征提取方法[J]. 机械传动,2018,42(12): 59-63.DING Jiansheng, LIU Wenrui, SUN Jianwei. Feature extraction method for planar four-bar mechanism with design requirement of finitely separated position[J]. Journal of Mechanical Transmission, 2018, 42(12): 59-63. [19] GALÁN-MARÍN G, ALONSO F J, DEL CASTILLO J M. Shape optimization for path synthesis of crank-rocker mechanisms using a wavelet-based neural network[J]. Mechanism and Machine Theory, 2009, 44(6): 1132-1143. doi: 10.1016/j.mechmachtheory.2008.09.006 [20] WEI W, SHU X, CHEN P, et al. A chord-angle-based approach with expandable solution space to 1-degree-of-freedom (DOF) rehabilitation mechanism synthesis[J]. Mechanical Sciences, 2022, 13(1): 341-352. doi: 10.5194/ms-13-341-2022 [21] BUŚKIEWICZ J, STAROSTA R, WALCZAK T. On the application of the curve curvature in path synthesis[J]. Mechanism and Machine Theory, 2009, 44(6): 1223-1239. doi: 10.1016/j.mechmachtheory.2008.08.001 [22] BUŚKIEWICZ J. Design of a feeder with the use of the path synthesis method[M]//Mechanisms and Machine Science. Dordrecht: Springer Netherlands, 2014: 251-259. [23] 韩远飞. 基于傅里叶描述符的单自由度辅助站立机构构型尺度融合设计[D]. 成都:西南交通大学,2019. [24] WU J, GE Q J, GAO F, et al. On the extension of a Fourier descriptor based method for planar four-bar linkage synthesis for generation of open and closed paths[J]. Journal of Mechanisms and Robotics, 2011, 3(3): 031002.1-031002.8. [25] 李晓东,李磊. 基于数值图谱的空间RRSS机构开区间轨迹综合方法[J]. 机械传动,2021,45(12): 28-33.LI Xiaodong, LI Lei. Open Interval path synthesis method of spatial RRSS mechanism based on numerical atlas[J]. Journal of Mechanical Transmission, 2021, 45(12): 28-33. [26] YUE C, SU H J, GE Q J. A hybrid computer-aided linkage design system for tracing open and closed planar curves[J]. Computer-Aided Design, 2012, 44(11): 1141-1150. doi: 10.1016/j.cad.2012.06.004 [27] SUN J W, LIU W R, CHU J K. Dimensional synthesis of open path generator of four-bar mechanisms using the haar wavelet[J]. Journal of Mechanical Design, 2015, 137(8): 082303.1-082303.8. [28] LIU W R, SUN J W, ZHANG B C, et al. Wavelet feature parameters representations of open planar curves[J]. Applied Mathematical Modelling, 2018, 57: 614-624. doi: 10.1016/j.apm.2017.05.035 [29] 刘文瑞,孙建伟,褚金奎. 基于小波特征参数的平面四杆机构轨迹综合方法[J]. 机械工程学报,2019,55(9): 18-28. doi: 10.3901/JME.2019.09.018LIU Wenrui, SUN Jianwei, CHU Jinkui. Synthesis method for path generation of a planar four-bar mechanism based on the wavelet feature parameters[J]. Journal of Mechanical Engineering, 2019, 55(9): 18-28. doi: 10.3901/JME.2019.09.018 [30] DESHPANDE S, PURWAR A. A machine learning approach to kinematic synthesis of defect-free planar four-bar linkages[J]. Journal of Computing and Information Science in Engineering, 2019, 19(2): 021004.1-021004.10. [31] DONOSER M, RIEMENSCHNEIDER H, BISCHOF H. Efficient partial shape matching of outer contours[C]//Asian Conference on Computer Vision. Berlin:Springer, 2010: 281-292. [32] 黄伟国,胡大盟,杨剑宇,等. 用于遮挡形状匹配的弦角特征描述[J]. 光学 精密工程,2015,23(6): 1758-1767. doi: 10.3788/OPE.20152306.1758HUANG Weiguo, HU Dameng, YANG Jianyu, et al. Chord angle representation for shape matching under occlusion[J]. Optics and Precision Engineering, 2015, 23(6): 1758-1767. doi: 10.3788/OPE.20152306.1758 [33] 杨世明,马庆国. 双摇杆机构运动分析及设计研究[J]. 机械设计与研究,2018,34(2): 71-75.YANG Shiming, MA Qingguo. Motion analysis and design of double-rocker mechanism[J]. Machine Design & Research, 2018, 34(2): 71-75. [34] ALTMAN N, KRZYWINSKI M. The curse(s) of dimensionality[J]. Nature Methods, 2018, 15: 399-400. doi: 10.1038/s41592-018-0019-x [35] WANG J Z. Geometric structure of high-dimensional data and dimensionality reduction[M]. Berlin: Springer Berlin Heidelberg, 2011. [36] JOHNSON S C. Hierarchical clustering schemes[J]. Psychometrika, 1967, 32(3): 241-254. doi: 10.1007/BF02289588 -
下载:
点击查看大图
计量
- 文章访问数: 100
- HTML全文浏览量: 33
- PDF下载量: 10
- 被引次数: 0