Calculation Method for Reinforcement Stress in Ultra-High Performance Concrete Beams Considering Bond-Slip Effect
-
摘要:
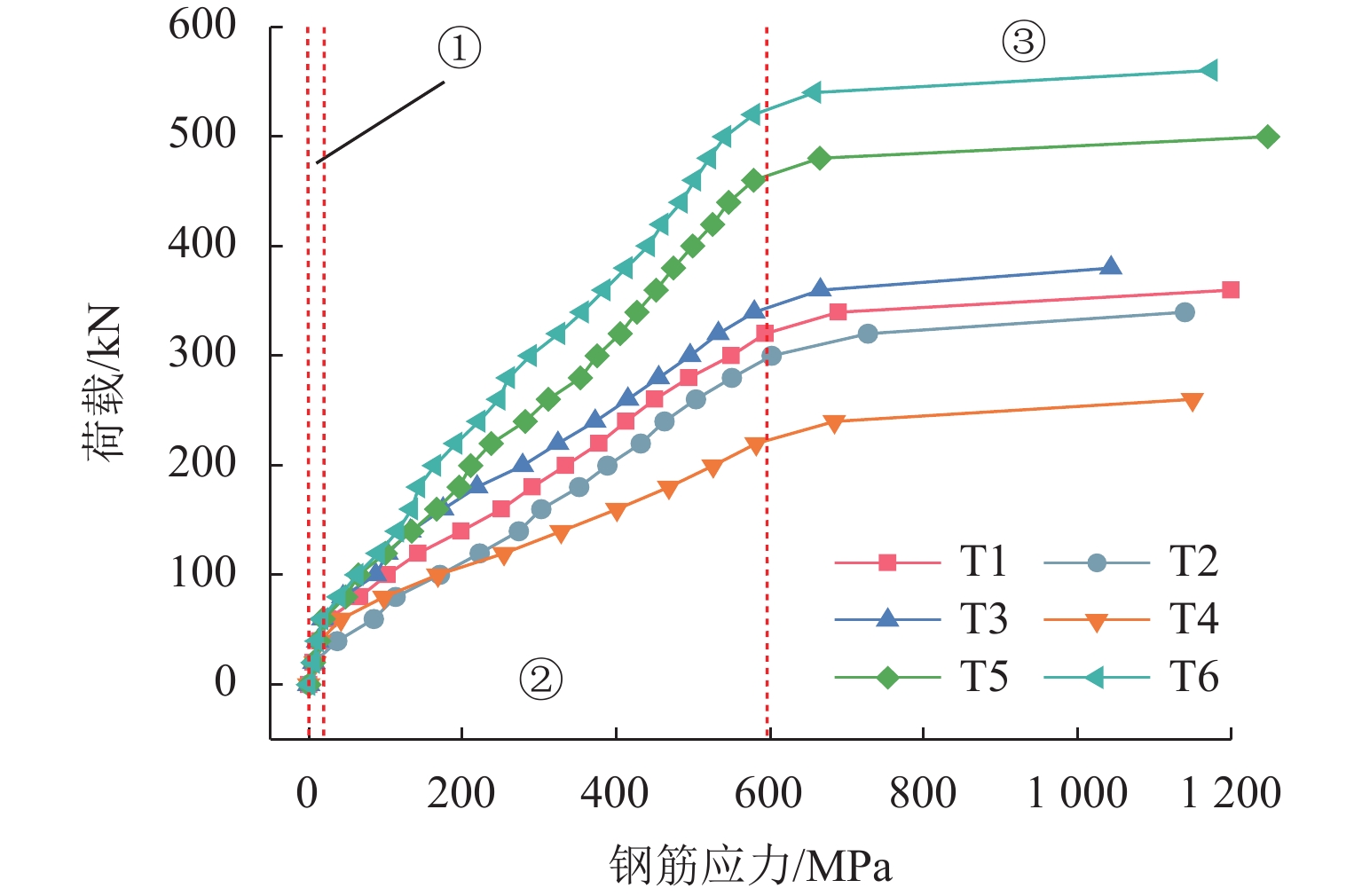
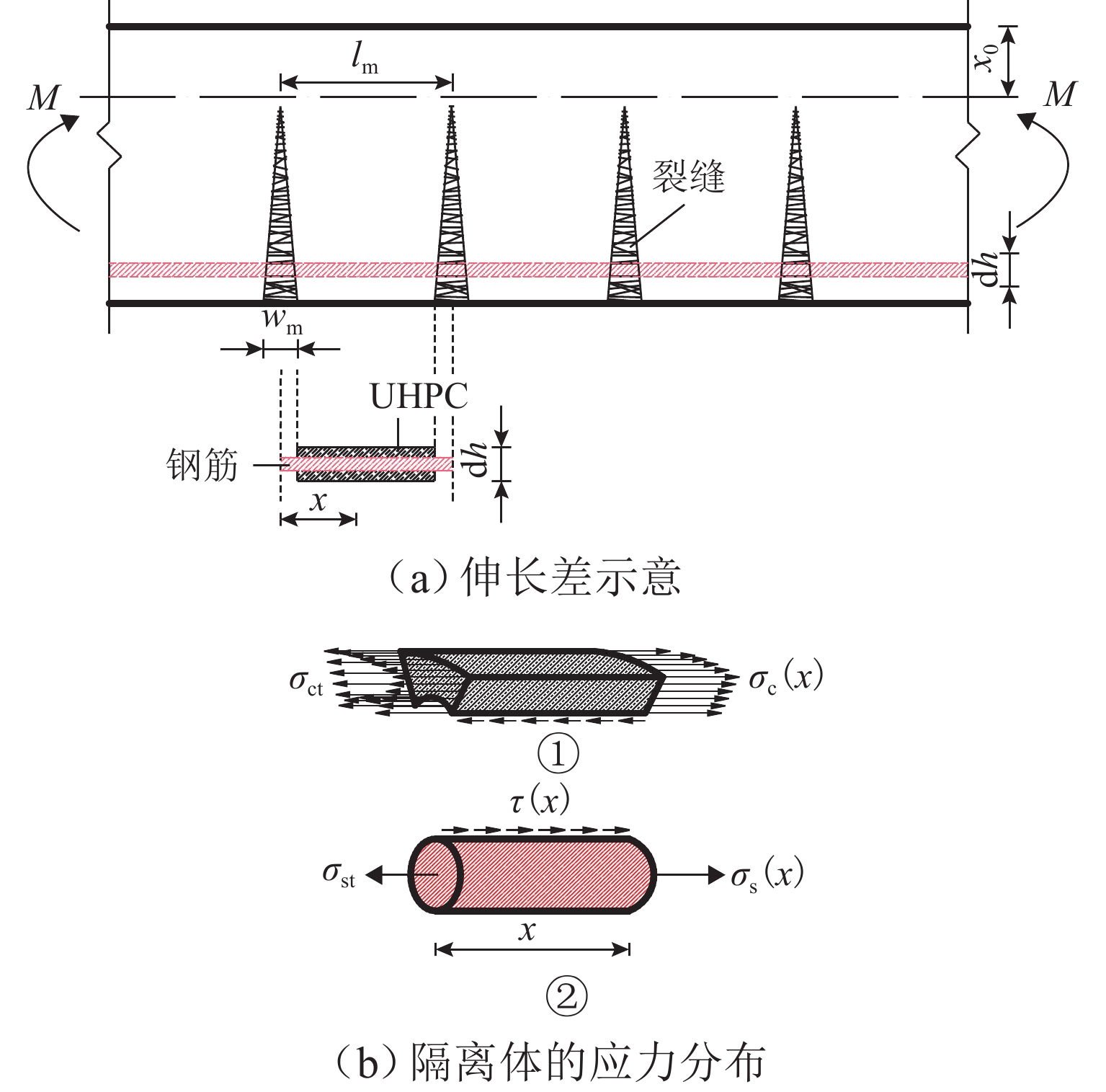
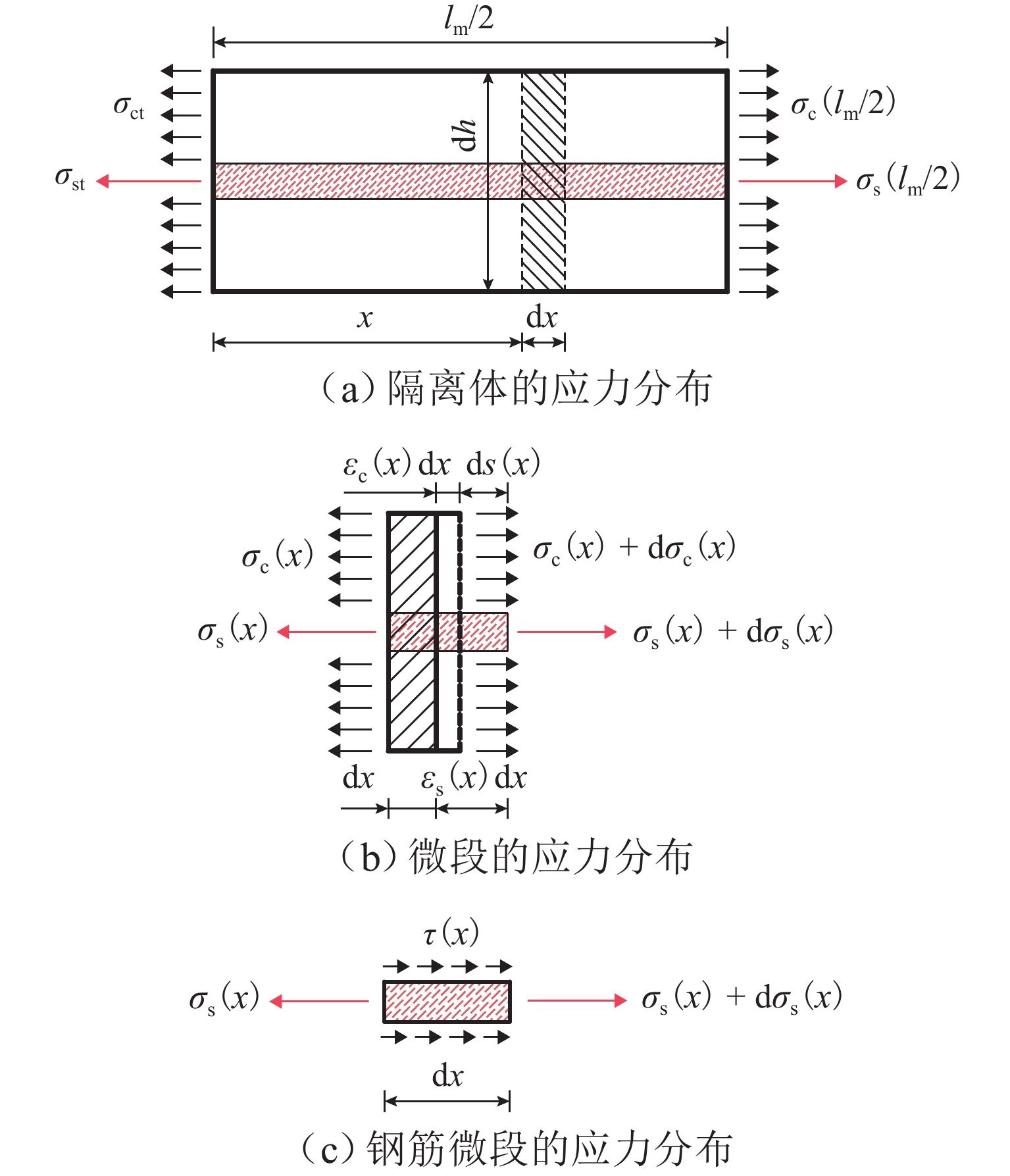
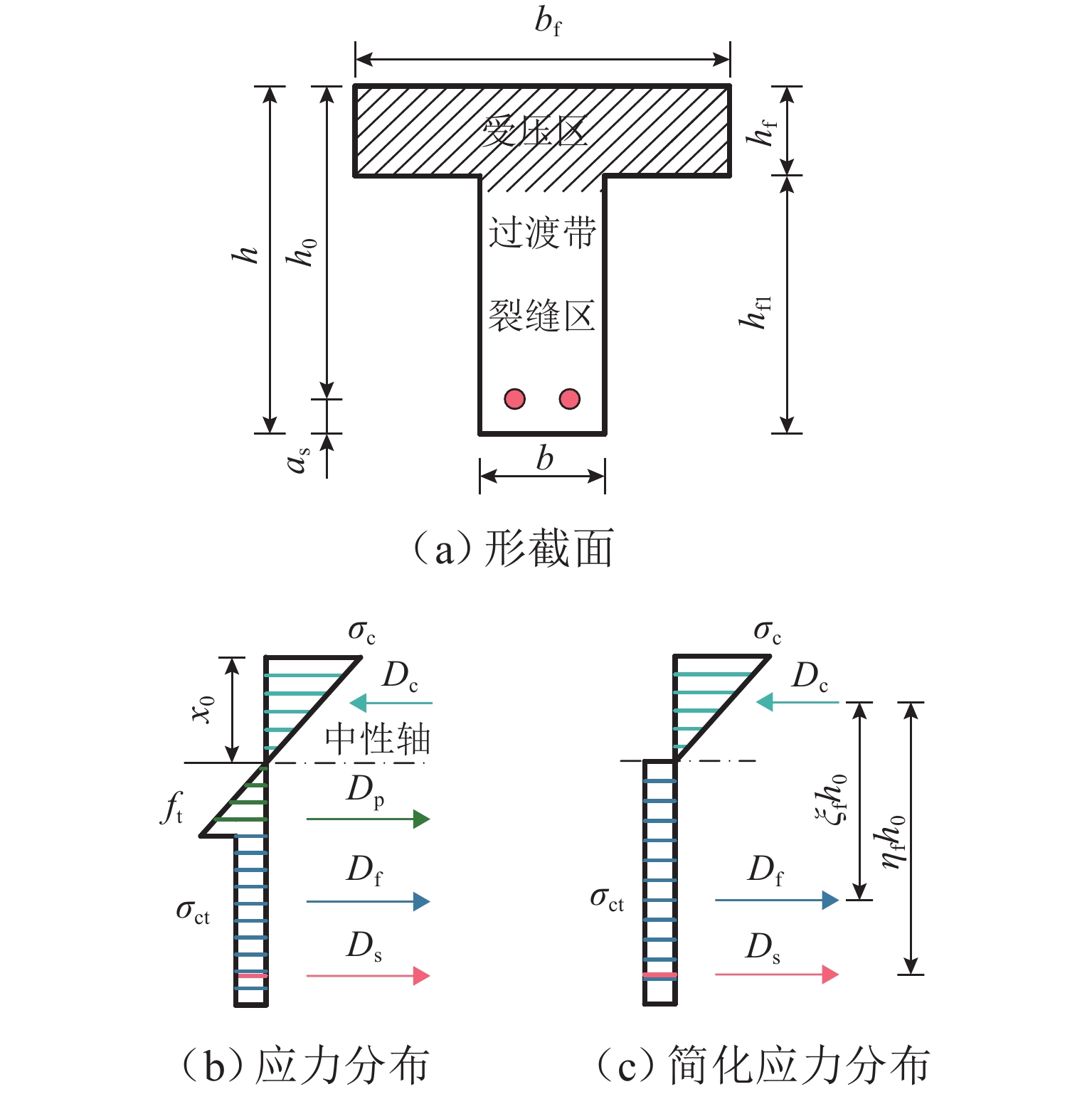
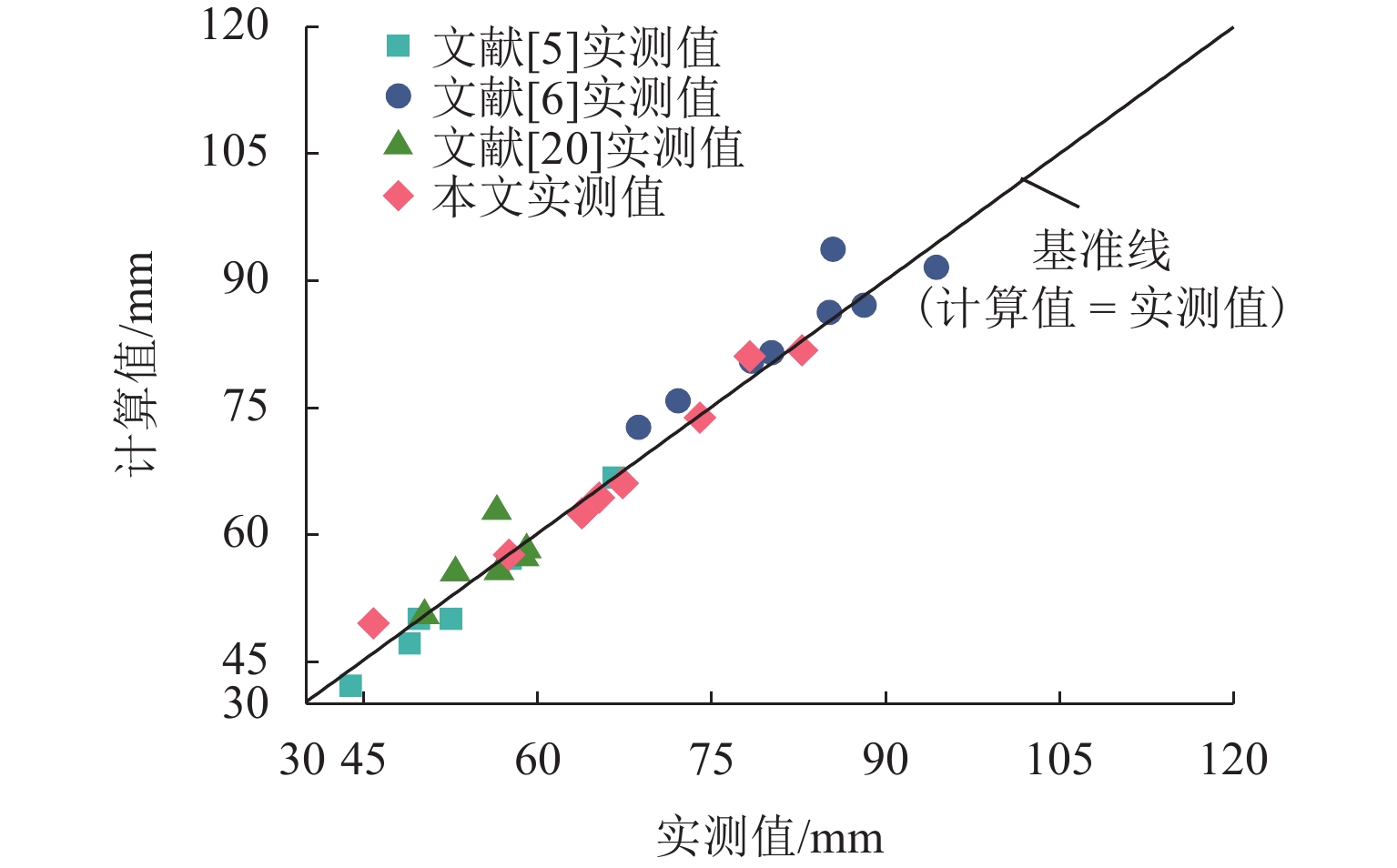
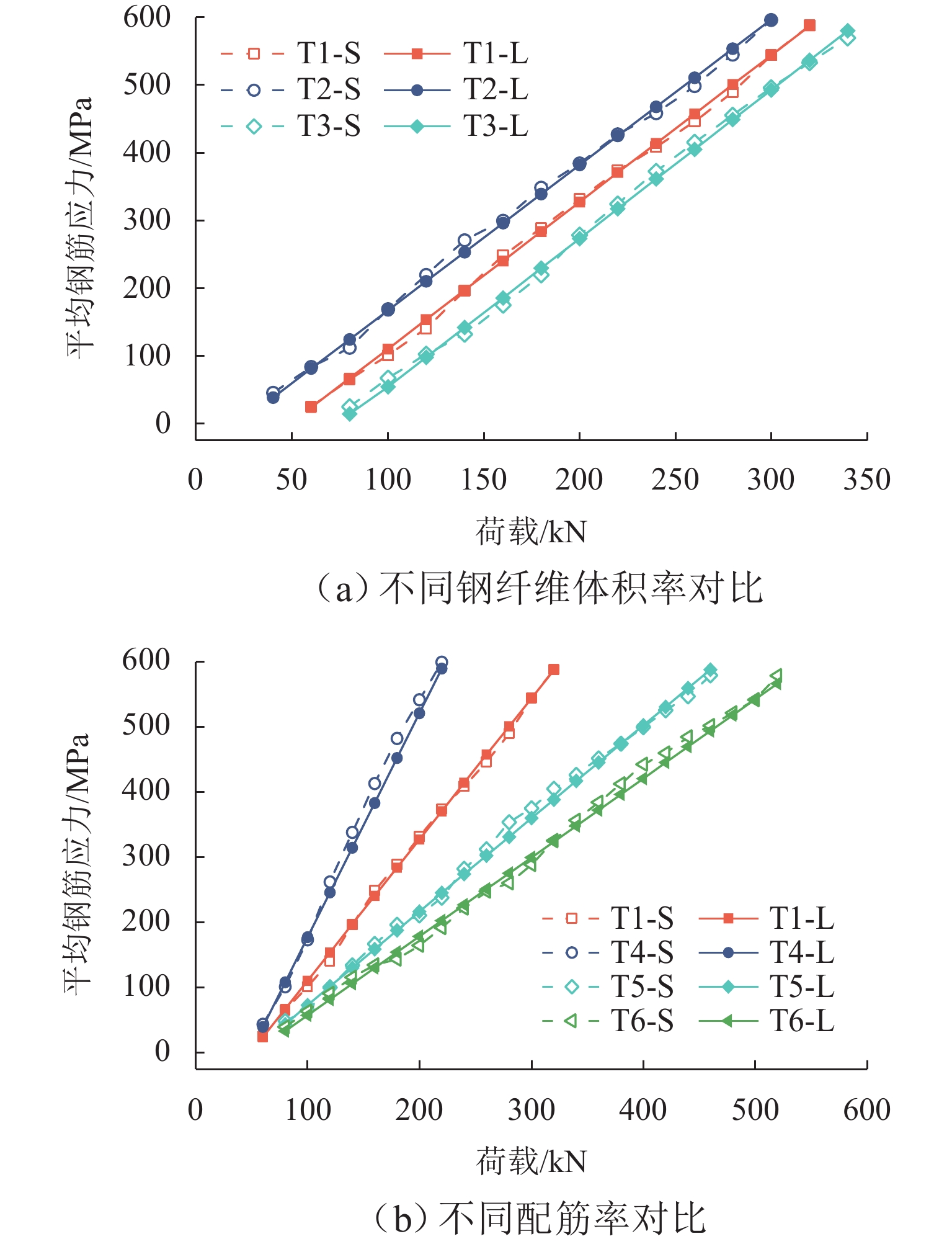
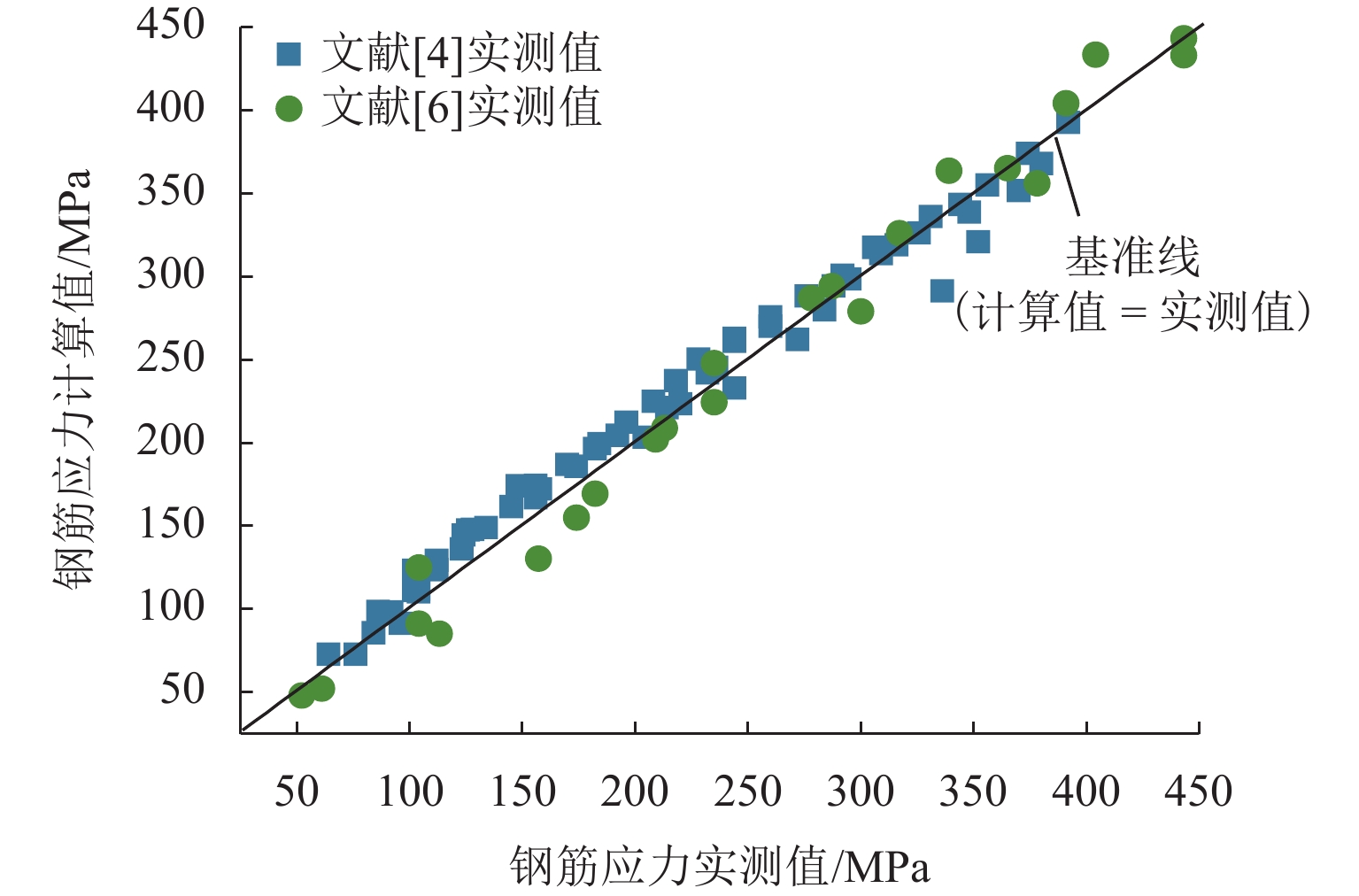
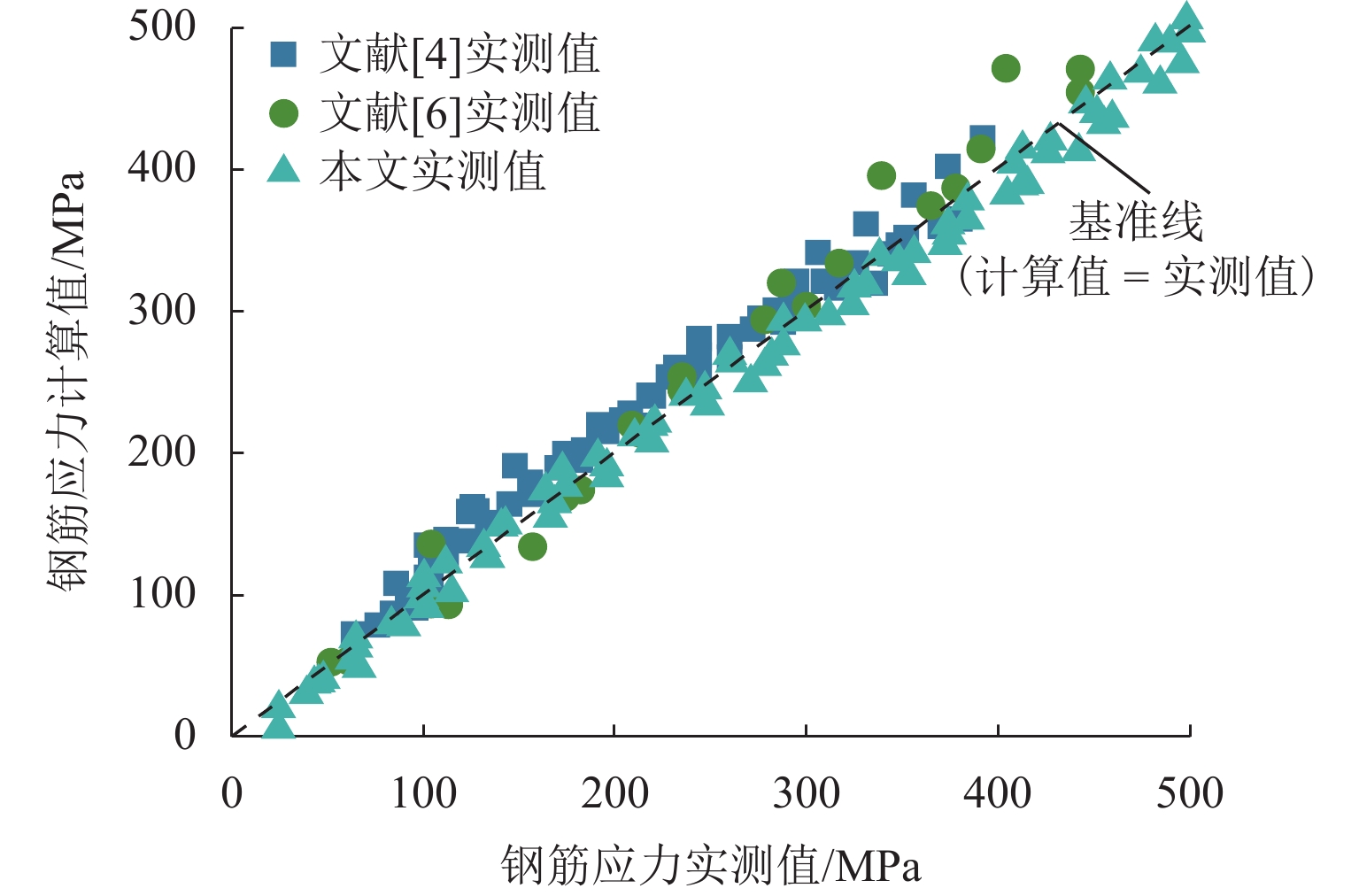
为建立适用于配筋超高性能混凝土（UHPC）梁的钢筋应力计算方法，对6片UHPC-T形截面梁开展四点弯曲试验，研究钢筋应力的变化规律. 从钢筋-UHPC受力平衡与变形协调机理出发，应用微元体建立平衡、变形以及黏结-滑移微分方程，导出能综合反映钢筋与UHPC界面黏结-滑移影响及钢纤维抗拉贡献的钢筋应力计算公式，并通过简化应变不均匀系数与裂缝截面钢筋应力计算，提出便于工程应用的钢筋应力简化公式. 研究表明：单位荷载下钢筋应力的增幅随配筋率的提高而减小，而与钢纤维体积率的变化无关；与普通混凝土梁相比，UHPC梁的钢筋应力在开裂截面处偏小，但其分布在相邻裂缝间的不均匀程度更高；钢筋应力建议公式计算值与本文、既有文献的试验值均吻合良好；钢筋应力简化公式计算值与试验值之比的均值为1.03，变异系数为0.06，表明该简化式可用于UHPC梁的钢筋应力计算.
-
关键词:
- 超高性能混凝土（UHPC） /
- 钢筋应力 /
- 黏结-滑移 /
- 应变不均匀系数 /
- 微元体
Abstract:Four-point bending tests were conducted on six ultra-high performance concrete T-shaped (UHPC-T) section beams to establish a reinforcement stress calculation method for reinforced UHPC beams and study the variation law of reinforcement stress. Based on the mechanism of force balance and deformation coordination between reinforcement and UHPC, a reinforcement stress calculation formula was derived using the differential equations of equilibrium, deformation, and bond-slip established by micro elements, which could comprehensively reflect the influence of bond-slip between reinforcement and UHPC interfaces and the contribution of steel fibers to tensile strength. By simplifying the calculation of the strain non-uniformity coefficient and the reinforcement stress in cracked sections, a simplified formula for reinforcement stress suitable for engineering applications was proposed. The results show that the increase in reinforcement stress under unit load decreases with the increase in reinforcement ratio, but it is not related to the change in steel fiber volume fraction. Compared with ordinary concrete beams, the reinforcement stress in UHPC beams is relatively small in the cracked section, but the uneven distribution of reinforcement stress between adjacent cracks is intensified. The calculation value of the suggested formula for reinforcement stress is in good agreement with the experimental values in this article and existing literature. The average ratio of the calculated value of the simplified formula for reinforcement stress to the experimental value is 1.03, and the coefficient of variation is 0.06, indicating that this simplified formula can be used for calculating reinforcement stress in UHPC beams.
-
近年来，飞轮电池（飞轮储能系统）作为一种物理储能方式，突破了化学电池的局限，凭借绿色环保、储能密度高、瞬时功率大、使用寿命长等优点备受关注，已广泛应用于航空航天、舰船、新能源汽车、UPS后备铅酸电池替代、电网储能调频等重要科技领域[1-4]. 随着磁悬浮轴承（简称磁轴承）技术的发展及日益成熟，采用绿色无摩擦的新型磁悬浮支承-飞轮系统代替原有大规模机械轴承支承技术，已成为解决旋转机械设备支承问题行之有效的方案之一. 一般地，按照磁力来源可将磁轴承划分为主动磁轴承、被动磁轴承和混合磁轴承[1]. 主动磁轴承依靠线圈及电磁铁提供磁力，通过控制电流调节自身支承特性；被动磁轴承的磁力来源于永磁体或超导体产生的相互作用支承转子悬浮；混合磁轴承结合了主动和被动磁轴承的各自特点，采用永磁体等磁性材料提供偏置磁场，叠加控制电流产生的控制磁场实现转子的稳定悬浮. 以主动磁轴承构成的磁悬浮支承系统为例，其具体工作原理为：径向/轴向位移传感器测量转子距中心位置的相对偏移量，将其作为反馈量输入至控制器中，控制器经过计算发出控制指令传输至功率放大器，功率放大器输出驱动信号，调节磁轴承的控制电流进而改变其产生的电磁力，实现转子在中心位置的稳定悬浮[1-2].
因此，磁悬浮支承系统的稳定性至关重要，对于利用其支承的飞轮电池系统而言，其运行品质更是受到磁轴承系统的直接影响. 特别是基于非基础（基础是指各种领域背景下的应用载体）静止场合或受外界扰动较大的场合，如航天用飞轮电池、车载飞轮电池及舰船用飞轮电池等，给磁悬浮支承-飞轮系统的安全运转带来双重考验. 因此，探究影响磁悬浮支承-飞轮系统稳定性的原因，并寻求相关的应对策略，是飞轮电池研究领域中亟须完善的重要技术难点.
本文首先对影响飞轮系统的不稳定行为进行阐述与分析；其次，围绕这些不稳定因素，从磁悬浮支承-飞轮系统的拓扑结构、动力学建模、控制策略和辅助保护四大关键技术展开综述；最后，以如何进一步实现飞轮系统的稳定运行为主要探究点，从多个技术方面进行延伸展望，为我国加快推进“碳达峰、碳中和”目标，抢占储能技术、新能源汽车、航天及国防科技等关键战略制高点奠定研究基础.
1. 不稳定因素来源分析
1.1 飞轮储能系统工作原理
飞轮储能装置工作时，通过高速旋转的飞轮转子完成机械动能与电能间的相互转化，整个系统实现了电能的输入、存储和输出过程，具体的工作方式可分为充电、待机及放电3个阶段[1]：
1） 充电储能阶段. 电能通过电力转换器变换后驱动双向电机（此时用作电动机）运行，电机带动飞轮加速转动，飞轮以动能的形式将能量存储在高速旋转的飞轮体中，完成“电能—机械动能”转换的储能过程.
2） 待机恒速阶段. 能量存储后，电机维持一个恒定转速，直至接收到一个能量释放的控制信号，此过程不进行能量转换，飞轮恒速运行.
3） 放电释能阶段. 高速旋转的飞轮输出能量，拖动双向电机（此时用作发电机）发电，经电力转换器输出适用于负载的电能，完成“机械动能-电能”转换的释能过程.
1.2 不稳定行为分析
理想状态下飞轮电池装置实现稳定充放电过程的必要条件为系统所受的干扰要在磁轴承支承调节能力范围内，然而，现实中飞轮系统所受的扰动偏差常会大于可预期的程度，进而导致系统失稳. 这些不稳定因素主要来源于飞轮运行时受多方面振动的干扰，其典型的振动形式包括飞轮自身的模态自激振动和环境因素引起的强迫响应振动.
1） 模态自激振动. 典型表现为飞轮转轴受陀螺力矩作用时的强陀螺效应. 从飞轮自身角度看，高速转子的强陀螺效应会在冲击力矩的干扰下产生陀螺力矩，在陀螺力矩的作用下，飞轮的典型固有振动表现为章动和进动. 从磁轴承控制系统角度分析，陀螺效应仅仅是作为影响多输入多输出系统的部分参数摄动项，那么在不同转速区间内设计的控制器并不能保障全转速范围内的磁轴承系统稳定[5-6]. 因此，当系统转速越高，陀螺效应引发的章动和进动频率越大，进而在高转速下会加剧系统的不稳定特性，引发系统不平衡响应.
此外，耦合振动同样会引起系统的模态失稳，且这些振动模态不是独立的，而是受到一个模态到其他模态的能量传递影响的复杂振动过程. 造成耦合振动的原因除了陀螺效应外，主要还包括磁轴承拓扑结构不合理产生的电磁耦合及各自由度间的耦合效应、控制系统的电学微分方程、传感器与磁轴承间的非共点安装等[7-8].
2） 强迫响应振动. 典型表现为磁轴承力学模型的非线性、功放饱和、传感器波动引起的谐波电流和动力学特性引起的超临界转速及磁轴承位移输出有界，当外扰较大时，这些问题的存在会使系统趋于不稳定状态[9-10]. 同时，类似基座、车辆等外界基础运动以及飞轮质量不均衡产生的离心力引起的偏心同步振动，也会造成系统的不平衡响应. 据统计，旋转机械高速运行中，约三分之一故障来自材料和机加工等客观原因造成的转子不均衡，微小残余不均衡量都会对系统产生严重影响[11].
2. 关键技术分析
2.1 磁悬浮支承-飞轮系统拓扑结构
传统飞轮电池的磁悬浮支承-飞轮系统拓扑结构多围绕“长惯性主轴”进行排布，如图1所示. 但该类拓扑使得飞轮电池系统的轴向体积增大，且稳定工作转速区间小，不适用大储能量要求且受空间限制等应用场合[12]. 进一步地，“短轴”甚至“无轴”式拓扑结构被设计出来，如图2所示. 该类拓扑结构实质是通过改变转子的转动惯量比获得系统的稳定性能[13]，可以解决现有长轴式飞轮电池系统的不足，但同时也存在陀螺效应严重、控制难度高等弊端[14]. 然而，仅仅依赖于飞轮电池轴系拓扑结构的改进远远不够，磁轴承部件是实现飞轮系统稳定性的关键保障，设计新型拓扑的高性能磁轴承来实现飞轮的稳定运行十分必要.
图 1 长轴式飞轮电池悬浮支承-转子系统拓扑结构Figure 1. Topological structure of suspension support-rotor system for a flywheel battery with long shaft
图 2 短轴/无轴飞轮电池悬浮支承-转子系统拓扑结构Figure 2. Topological structure of suspension support-rotor system for a flywheel battery with short shaft/no shaft目前，典型的磁轴承拓扑结构多为柱面磁轴承支承系统，然而，当飞轮受到自激振动或强迫振动发生偏转或偏移时，会导致其较大的干扰力矩，此时柱面磁轴承产生的电磁力不能始终指向转子质心位置，这种情况下需要依赖精确的数学模型以实现系统的稳定控制. 为进一步提高磁轴承拓扑上的自稳定优势，保障各类振动中飞轮系统的稳定性，近年来相继突破柱面的制约，出现了球面、阻尼式等新型磁悬浮支承-飞轮系统拓扑结构.
2.1.1 柱面磁悬浮支承-飞轮系统
从拓扑上可简单将柱面磁悬浮支承-飞轮系统定义为磁轴承的定子、转子都呈圆柱面设计（即两者之间形成柱面气隙），此种设计不复杂，且柱面因素使磁路经过柱面气隙时不易在轴向/径向上产生分解，从而可以避免一系列的耦合性问题，因此，对其进行实时控制较容易. 一种结合柱面磁悬浮支承技术的产品级动能回收系统如图3所示，该系统由沈阳微控新能源技术公司联合美国VYCON公司联合开发，已广泛应用于数据中心、轨道交通、新能源工业等自动化领域.
图 3 产品级动能回收系统用柱面磁悬浮支承技术Figure 3. Support technology of cylindrical magnetic levitation for product kinetic energy recovery system进一步地，文献[15]研究了飞轮转子系统的柱面轴向永磁轴承径向干扰力问题，通过仿真和控制算法对磁轴承模型作了相应测试，满足了系统抗干扰性的要求. 文献[16]提出并测试了一种舰船背景下用柱面同极性径向磁轴承支承的飞轮电池，采用可修改的比例谐振控制器，改善全速范围内转子系统稳定性，图4为其应用测试平台. 此外，相关学者研究了不同导体材料性质及导磁体的摆放位置对磁悬浮支承-飞轮系统的影响，诸如高温超导磁轴承以导体材料作为切入点、永磁体采用环形哈尔巴赫阵列等，为磁悬浮技术发展提供了不同维度的思路[17-18].
研究侧重于整体磁悬浮技术的发掘，而鲜有探寻气隙规律对磁路及电磁力的影响. 因而，现有应用于飞轮系统中的磁悬浮支承拓扑结构大多呈现柱面形式，研究深度较广，一定程度上已实现产品普及应用化.
2.1.2 球面磁悬浮支承-飞轮系统
尽管柱面支承系统应用普及，但其在转子受不平衡响应时，柱面气隙的单一导磁方向会使磁路间的相互干扰不可控，从而影响整个飞轮系统的稳定性能. 因此，突破柱面拓扑的制约，球面磁悬浮支承-飞轮系统应运而生，其球面拓扑的定、转子间形成的球面气隙能够使电磁力始终指向球心，实现实时调心，进而削弱陀螺效应引起的转子不平衡响应；同时，球面拓扑能够减小因外界附加干扰导致的强迫响应振动. 综上，球面拓扑抗干扰能力强，其在多个领域具有广阔的工程化应用前景. 然而，也正是球面气隙的制约，此种拓扑会造成轴径向磁路间不同程度的耦合，因此，其面临的建模和控制难度也更为严苛.
文献[19-20]研究了一种卫星姿态机动用磁悬浮万向飞轮装置，由球形磁轴承、球面偏转电动机和球面旋转电动机三大核心组件构成，采用双磁悬浮万向飞轮反向安装的构型，更加快速地实现整星零动量的稳定控制. 文献[21-22]提出了一种配合飞轮电池用于航空姿态执行机构中的径向球面纯电磁轴承，具有低干扰力矩，其球面设计使得电磁力能够始终指向转子球心，从而降低定子磁极对转子产生的干扰力矩. 文献[23]提出了一种可用于电动汽车上的球形磁悬浮飞轮电池，能够在旋转时实现飞轮的自动悬浮与调心，其球形悬浮飞轮设计为围绕电动机定子球心旋转的结构，实现飞轮绕球形定子的球心任意角度旋转，从而显著减弱飞轮由于车辆复杂路况所产生的陀螺效应. 文献[24-26]提出了一种车载飞轮电池用向心力式球面磁轴承，图5为其球面拓扑结构原理，该磁轴承可使不同工况下的飞轮转子具有较强的抗干扰性.
因此，在具体应用背景下，在车载、航空姿态控制器、船舶动力装置等基础运动场合，当基础受到诸如车辆行驶工况、路况颠簸，或是船舶航行状态、海面浪击、冲礁等复杂运动时，飞轮转子更适宜采用球面磁悬浮支承拓扑，可以从磁轴承自身改善其拓扑，从而降低后续控制难度. 相反地，若采用柱面拓扑形式，飞轮转子在模态自激振动的基础上还要叠加不确定性环境因素的影响（导致强迫响应振动），无疑对控制方法提出更严苛的要求.
2.1.3 阻尼式磁悬浮支承-飞轮系统
随着飞轮转子系统转速或振动频率的增加，陀螺效应加剧，导致磁轴承所能提供的阻尼快速下降，进而影响系统的稳定性[27]. 为解决这一问题，研究者提出了一种将电磁阻尼器应用到磁悬浮系统的设计思路，即相当于将一种电磁质量弹簧阻尼系统用作减震器[28]，结合悬浮物以抑制磁悬浮系统的振动.
文献[29]研究一种电磁分流阻尼器（类似实验装置如图6所示）用于抑制超导磁轴承支承-转子系统的非线性振动，通过线性分析和数值计算，得出阻尼磁轴承支承-转子系统不仅能抑制主共振的涡动，而且能抑制次谐波的涡动，有效提高了系统的稳定性. 图中：Fd、Id分别为外扰力和控制电流；vx为导体相对于磁场 x 方向的速度；Ve、Re、Le分别为独立电压源、电阻和电感；Fe为作用在线圈上的力；Vz、Iz分别为阻抗的电压和电流. 文献[30-31]在原有磁轴承支承-转子系统的基础上增加磁悬浮阻尼器，构成阻尼磁悬浮组合式支承系统，通过模态理论分析和高速旋转实验，研究了不同阻尼控制参数下磁轴承支承-转子系统的不平衡响应，结果表明附加阻尼后的支承系统能够改善转子的动态性能，降低振动幅值范围，实现系统在高速下的稳定运行.
结合以上研究的阻尼磁轴承支承特征，常规的阻尼器和磁轴承安装方式表现为“异位”安装，这会造成阻尼执行器和磁轴承振动位移量的不一致，从而增加了控制系统的复杂度. 进一步地，为解决阻尼器与磁轴承检测位移不一致的问题，文献[32]提出了一种新型同位电磁阻尼，用于抑制磁轴承支承-转子系统的振动，将阻尼器与磁轴承安装在转子的同一位置，同位阻尼结构示意图如图7所示，实验结果表明，加入同位阻尼后的磁轴承支承-转子系统的抑制振动能力更强.
此外，还有直接采用粘弹性阻尼支座抑制系统的共振效应，将阻尼材料特性纳入磁轴承动力学建模中[33]. 利用外部阻尼增强稳定性固然可靠，但从整体层面而言，目前针对阻尼式磁悬浮支承-飞轮系统的研究仍不够深入，其主要原因在于：1） 拓扑上将阻尼因素融入磁轴承系统中的难度较大，存在同时考虑磁轴承磁路布置、阻尼器位置以及涡流传感器位移检测等综合问题的复杂性，增加了投入成本；2） 控制上对抑制转子的不平衡响应需同时考虑磁轴承及阻尼两类控制参数，加大了控制难度.
从综合角度看，若仅仅通过改进飞轮电池自身的拓扑结构，难以解决飞轮转子的绝大部分减振问题. 因此，依据不同应用背景，对磁悬浮支承-飞轮系统进行合理的动力学建模及稳定性控制，是决定整个系统能否稳定运行的另两大关键技术.
2.2 磁悬浮支承-飞轮系统动力学建模
处于基础运动环境下的磁悬浮支承-飞轮系统，诸如车载飞轮电池，往往会由于车辆不确定的行驶状态及复杂路面等级影响飞轮电池充放电等行为. 因此，结合运动特征的磁悬浮支承-飞轮系统动力学建模是实现磁轴承优化控制和分析其稳定性的重要基础. 为解决不同振动问题的动力学建模方法主要有理论推导、有限元分析及系统辨识等[34-36].
2.2.1 抑制强陀螺效应等模态自激振动问题
动力学建模对于实现磁轴承的优化控制至关重要，是解决电磁耦合、强陀螺效应等自激振动问题的基础. 此外，在解决模态自激振动问题时，不同研究者看待此类问题的角度也有所区别.
其一，将磁悬浮支承-飞轮系统视为一种耦合系统. 文献[37]为解决陀螺效应给高速转子带来的不稳定悬浮问题，建立了磁轴承支承-转子系统的动力学模型，并考虑转子的径向平动模态和倾斜模态的耦合特性，引入解耦控制，实现了抑制转子高速振动的目的；文献[38]对磁轴承支承-转子系统构建了机电耦合动力学模型，考虑了陀螺效应和多自由度波动引起的耦合效应，但缺乏实验验证. 其二，将磁悬浮支承-飞轮系统视为一种多输入多输出系统. 文献[39]将磁轴承支承-转子系统看作为多输入多输出系统，并将随转速变化的陀螺效应项看作是系统的参数摄动，建立了状态空间动力学模型，有效提高了磁悬浮控制力矩陀螺的章动和进动稳定性. 其三，将磁悬浮支承-飞轮系统视为一种时变系统. 从这一角度看，高度非线性和时变特征往往作为此类磁轴承支承-转子系统控制优化的重要目标，不单纯依赖转子动力学模型，高精度控制策略显得更为重要；文献[40]将磁轴承支承-转子系统看作为时变非线性，建立解耦动力学模型，提出一种分散积分滑膜控制方法，有效改善了系统的动态控制性能；文献[分滑膜控制方法，有效改善了系统的动态控制性能；文献[41]定义一种具有恒定时滞性的磁轴承支承-刚性飞轮储能系统，利用Pade近似方法进行建模，通过分析系统极点确定稳定性效果.
2.2.2 抑制不平衡振动等强迫响应振动问题
除了考虑磁轴承自身产生的自激振动因素，另一方面，动力学建模仍须考虑飞轮因加工误差引起的质量不均衡或实验用传感器波动等不可避免的实际振动因素，造成的系统强迫响应振动是影响磁轴承动态不平衡的诱因之一. 虽然目前可以采取相关方法评估并矫正根源，如飞轮质量不均衡/不对中经过定量估计能够及时进行返加工[42]，但最终衡量飞轮系统稳定性仍须结合动力学特性及后续的控制策略实现. 进一步地，从基础载体角度看，与基础静止等常规应用环境不同，动力学建模还要考虑外界基础运动的影响，不同运行工况作为磁悬浮支承-飞轮系统的典型特征，同样对磁轴承的动态性能影响显著.
基础静止等常规应用环境下，文献[43]提出了一种动力学理论模型用以预测磁悬浮飞轮的微振动特性，通过对模型的仿真测试，显示系统中存在大量由飞轮转子质量不均衡引起的同步振动分量以及传感器波动干扰引起的多频谐波分量，所提动力学模型为研究微振动抑制方法提供了参考价值. 文献[44]建立了一种高温超导磁轴承的电磁-热力学模型，分析了在有热效应和无热效应两种状态下受地震、轨道不规则、侧风等不同外界激励作用时系统的动态稳定性影响. 然而，鉴于实际的磁悬浮支承-飞轮系统多应用于如电动汽车等基础工况频发的环境场合，因此，外界基础运动对飞轮转子系统造成的强迫响应振动影响显得尤为突出.
考虑基础运动时的应用背景，文献[45]针对车载飞轮电池，利用ADAMS软件建立了飞轮转子与等效基础间的动力学模型，通过与MATLAB的联合仿真，分析了加速、减速、转弯、爬坡以及路面不平整引起的颠簸等不同基础运动状态对高速飞轮转子系统产生的动态响应规律，所设计的磁轴承能够承受外界冲击力及转子的不平衡力. 文献[46]通过机械动力学软件构建了车载磁轴承支承-转子系统的动力学模型，研究了不同路面等级的随机激励对系统振动特性的影响. 文献[47]建立了一种考虑基座不同激励现象的车载磁轴承支承-转子系统的有限元模型，在地基上施加脉冲激励，通过所预测和实测的响应效果对比，验证后续控制器保持系统稳定性的能力.
相比于基础静止，基础运动研究更倾向于利用动力学软件进行等效动力学建模，其弊端在于模型精度不够，影响后续的稳定控制. 为了追求更高精度的动力学模型，基于数学推导建立理论模型是必要的，即使其推导过程复杂性较高，融合基础运动产生的附加因素会增加模型思维计算量. 文献[48]建立了一种磁轴承支承-转子-基础系统的机电耦合动力学模型，除了考虑陀螺效应和多种因素引起的耦合影响，还将基础的横向振动纳入动态建模中. 文献[49]以船用复杂环境下的磁轴承支承-转子系统为研究对象，将平台的大幅度运动纳入动力学建模中，利用Lagrange方程对转子任意倾斜角度下的动力学模型进行了理论推导，并用摇摆台模拟了复合工况下的船舶动态环境实验. 文献[50]基于推导飞轮转子系统的振动数学模型，提出了一种简便的飞轮转子等效动力学模型的建模方法，然而其只进行了稳定悬浮验证，缺乏多工况动态特性分析.
综合而言，考虑飞轮转子自激振动因素及不同支承基础影响引起的系统振动差异，如何获取精确的动力学模型实现对磁悬浮支承-飞轮系统的优化稳定控制，依旧是磁轴承应用于高速旋转机械中的难点之一.
2.3 磁悬浮支承-飞轮系统控制策略
在确保磁轴承正常工作的条件下，实现振动抑制、提高系统稳定性及安全可靠性是控制算法设计的核心思想. 如表1所示，从飞轮转子系统振动类型来看，目前磁轴承的主要控制手段包含解耦控制、不平衡控制和抗干扰控制.
表 1 抑制飞轮转子振动的控制策略Table 1. Control strategy to suppress flywheel vibration控制目标 控制策略 主要方法 抑制模态自激振动（强陀螺效应等） 解耦控制 反馈、特征结构配置、奇异摄动、
智能自适应、逆系统解耦抑制强迫响应振动（不平衡振动等） 不平衡控制 陷波、开环不平衡控制、前馈控制、
最小均方根（least mean square，
LMS）控制、自适应补偿等抗干扰控制 自适应控制、前馈控制、
卡尔曼滤波、重复控制等2.3.1 抑制强陀螺效应等模态自激振动方面
解耦控制作为抑制模态自激振动的有效控制手段，主要目标是采用某种结构寻找合适的控制律，将多变量系统解耦为单输入单输出的子系统[51]. 目前主流的解耦控制策略有反馈解耦、特征结构配置解耦、奇异摄动解耦、智能自适应解耦和逆系统解耦等.
文献[52]针对磁悬浮控制力矩陀螺中的高速转子系统提出一种基于交叉反馈控制的章动模式跟踪补偿方法，控制电流在磁轴承支承-转子控制系统中的复频域形式如式（1）所示.
I(s)=−ksGc(s)Ga(s)Q(s), (1) 式中：I(s)为控制电流；ks为传感器的增益；Gc(s)为控制器的传递函数；Ga(s)为功率放大器的传递函数；Q(s)为转子偏移量的传递函数.
根据式（1）可得到具体的电磁力方程，进而实现后续控制的求解结果，即通过为章动模式提供足够的阻尼，实现章动分量相位裕度降低 −31.3 ~ −56.2 dB，显著改善陀螺效应对航天器的影响. 文献[39]利用参数摄动鲁棒控制和区域极点配置的方法设计了鲁棒控制器，并与PID控制器进行了试验对比，对比结果反映了在系统初始状态采用鲁棒控制器时，5%调节时间由0.246 s降低至0.045 s，超调量由95.4%降低至18.7%，且能够有效抑制系统章动与进动，保证系统稳定性.
文献[53]提出一种自适应积分三阶滑膜控制器以抑制主动磁轴承支承-转子系统的位移偏差，引入自适应控制律评估控制器增益，实现系统不确定性扰动带来的耦合抖振效应，通过数值分析法证明了策略的稳定性. 文献[54]基于逆系统解耦结合扩展二自由度PID控制策略，通过准确控制磁悬浮飞轮储能系统径向位置，能够使其稳定悬浮至24000 r/min，整定后的系统稳定性能、跟踪性能及鲁棒性能都得到了有效提高，也为后续控制器的设计提供了便利.
2.3.2 抑制不平衡响应等强迫响应振动方面
除了模态自激振动，转子的强迫振动也是导致系统不稳定的重要组成因素，对其进行有效抑制十分必要，在推动磁悬浮稳定控制方面意义重大. 按控制功能来看，不平衡控制和抗干扰控制是抑制强迫振动的主要控制类型.
不平衡控制主要以抑制同频位移、抑制同频电流和超临界转速引起的共振为实现目标. 文献[55]基于自适应陷波器提出了一种开环轴承力补偿的控制方法应用于磁悬浮支承-飞轮系统中，以抑制轴承力中的同频量为目标，轴承力FX为
FX=(Kh+KiiX)(x+ΘX), (2) 式中：Kh、Ki分别为位移刚度系数和电流刚度系数；x为转子质心与几何中心的位移量；iX为控制电流；
ΘX 为不平衡量对磁轴承对位移的干扰.对上述轴承力施加控制后可取得的同频分量为未控制时的5.2%，实现了0~5000 r/min全速范围内的飞轮转子不平衡振动抑制. 同样地，文献[56]针对应用于航天器中的主被动高速磁轴承支承-转子系统，提出了一种基于位移陷波结合前馈补偿的自平衡控制方法，其同频分量幅值最大可达未采用算法时的23.3%，显著降低了同频振动对航天器载体的影响. 此外，文献[57]通过LMS算法和开环前馈控制两种处理方式抑制磁轴承支承-转子系统的同频振动. 文献[58]基于沉浸和不变性控制理论，采用一种自适应补偿方案评估实际应用中磁轴承系统未知且可变的不均衡质量，实现了消除不平衡力的目的. 文献[59]针对磁悬浮控制力矩陀螺设计了一种自适应陷波滤波器，并进行了相关实验测试，结果表明：在广域运行速度范围内也能始终使同频电流产生的噪声幅值基本维持在 −50 dB以下，有效提高系统的控制稳定性.
抗干扰控制主要是针对力学模型非线性、外界基础运动/基座振动、传感器噪声及其波动产生的谐波电流振动等干扰因素. 文献[60]设计一种基于Lur’e系统方法的控制器评估磁轴承的非线性磁化行为，实验结果能够使传感器位置的峰值位移降低60%，验证了控制器的有效性. 文献[61]以基础加速度信号作为自适应滤波器的参考输入，可有效抑制基础激励响应对移动载体磁轴承振动轨迹幅值（降幅可达0.1 mm）的影响. 文献[62]将PD反馈和最优前馈控制相结合，显著抑制基座简谐运动对磁轴承支承-转子系统振幅的影响，使其小于整个扰动频率范围内的扰动幅度. 文献[63]提出一种基于扩展卡尔曼滤波的改进控制策略，相比经典PID算法，能够将转子位移精度提高3倍 ~ 4倍，明显改善系统的动态性能，且有效抑制高频噪声干扰，使系统具备较好的稳态精度和鲁棒性. 文献[64-65]研究了分数阶重复控制方案用于磁轴承支承-转子系统，在控制电流中考虑质量不平衡力和传感器跳动引起的谐波分量，最终消除不同频率下的谐波电流对转子的扰动影响，优化了系统的动态性能，控制电流复频域形式为
I(s)=W[R(s)−ksGp(s)kiFi(s)−ksXs(s)], (3) 式中：R(s)为系统的参考输入；Gp (s)为转子的传递函数；ks为传感器增益；ki 为电流刚度系数；Fi (s)、Xs (s)分别为质量不平衡力和传感器跳动引起的谐波分量；系数W为
W=Gc(s)Ga(s)1+ksGc(s)Ga(s)Gp(s). (4) 整体而言，当前针对磁悬浮支承-飞轮系统的振动抑制算法研究有一定的进展，但是拓展面依旧不深，仍存在较大的发展空间. 限制控制算法广度和深度的主要原因在于：1） 在复杂多变的环境背景和干扰因素下，同时满足多重目标（稳定性、安全性可靠性、实时性等）的飞轮转子系统会给其建模和控制策略提出更高的要求；2） 磁悬浮支承-飞轮系统控制性能的效果依赖于模型的匹配度，解决不同问题时由于看待系统的角度不同，如何选择控制策略需根据具体系统模型进行相应匹配.
然而，现有适用于控制系统设计的被控对象模型往往难以准确计算，涉及一些如涡流、磁滞、非线性、时变及外扰引起的耦合等无法估量的非理想因素，增加了控制器设计难度和精度，对此研究者进行了无模型相关控制方法研究，但抑制振动效果并不显著[66]. 因此，为规避传统基于“有模型”控制策略的弊端，从飞轮转子系统的物理机理、动力学特性和环境特征出发，结合控制目标与性能要求，建立基于“无模型”的特征预测模型及其控制策略将是未来磁悬浮支承-飞轮系统控制的主流方向[67].
2.4 磁悬浮支承-飞轮系统辅助保护技术
实际应用中，当飞轮转子系统受强迫响应振动或其导致的模态自激振动加剧，磁轴承或许会产生电磁吸力不稳定或承载能力不足等故障问题，因此，从安全可靠性角度出发，磁轴承的传统设计方法中均需考虑配合辅助轴承（保护轴承/备用轴承）使用. 当磁轴承失效后，辅助轴承将临时承担起支撑转子的作用，以维持转子正常运行，避免转子系统出现灾难性后果，达到保护磁轴承和转子的目的[68]，辅助轴承作为配备磁悬浮支承-飞轮系统的重要组件或是关键技术，对其进行分析和设计尤为重要.
以目前的研究现状，对磁悬浮支承-飞轮系统而言，辅助轴承的分析主体大多围绕转子失稳后与保护轴承发生碰撞时的碰摩动力学建模，以及引起的热力学计算展开[69-71]. 其中，碰摩动力学建模有助于了解转子发生碰撞后的动态运行规律，提升转子恢复稳定的控制效率. 文献[72]提出了一种径-轴向一体化辅助轴承，从理论上建立了转子跌落后与安全轴承间的接触动力学模型，通过如图8所示的实验装置对转子进行了5自由度的跌落测试，使得所设计的辅助轴承能够维持转子紧急状态下的正常运行. 文献[73]利用数值分析法，从理论上计算了磁轴承故障时转子跌落至辅助轴承上摩擦产生的热量.
图 8 径-轴向一体化辅助轴承实验装置Figure 8. Experimental device of a radial-axial integration auxiliary bearing事实上，由于碰撞特性的复杂程度，从数学层面建立准确模型，对辅助轴承进行理论分析十分冗余且繁琐，目前辅助轴承的性能研究大都仍以实验和有限元分析为主[74-76]. 实验分析法固然可以较准确地判断辅助轴承的性能是否满足所需应用要求，但是这一方法效率不佳，尤其对于飞轮电池中的磁轴承，其特殊的应用场合和多因素特征很难通过仿真去模拟复杂环境下辅助轴承的碰摩特性，因此，亟需寻找建立有效模型的方法，使之准确地预判和分析辅助轴承的性能.
此外，对磁悬浮支承-飞轮系统而言，材料和结构的选取更有助于辅助轴承的设计优化，为适应高速飞轮电池这一应用对象，尽可能地减小摩擦损耗和碰撞接触产生的过热现象，辅助轴承的材料应满足高疲劳强度、高耐磨耗性及优良耐热性. 同时，受限于辅助轴承的使用寿命，生命周期、可维护性和可更替性等要求应纳入结构设计考量中.
3. 未来展望
1） 向优化更佳性能的轴系方向发展. 飞轮转子系统的稳定性能及磁轴承的排布方式都紧密围绕轴系进行，不合理的轴系设计会直接影响飞轮转子的动态性能，甚至会造成飞轮转子失效，发生不可逆事故. 未来应在飞轮转子轴系设计及优化方面综合其长短板优势，努力提高系统集成度的同时也要协调储能量与稳定性之间的矛盾.
2） 向改进更加优质的材料方向拓展. 随着新型导电、导磁和绝缘材料的发展，有助于进一步提高磁轴承的刚度和阻尼特性，保障系统的稳定运行；同时，具有优良机械参数的材料能够保证飞轮转子的动力学结构，间接维持系统的稳定性能. 未来应结合不同应用场合，选取合理的材料或寻求最佳的材料配比方式，以提高飞轮转子系统的环境适应性和安全可靠性.
3） 向实现更高稳定的辅助控制策略方向趋近. 良好的控制系统是维持磁悬浮-支承飞轮系统高稳定运行的强有力保障. 未来应基于现有的控制手段，融合系统诸多不确定性因素，设计更高安全保障的辅助控制系统，尽可能地提高系统容错能力，实现恶劣情况下的动态稳定性.
4） 向保障更高极限稳定的辅助轴承方向靠拢. 备用轴承作为保障飞轮转子系统极限情况下稳定性的辅助设备，未来应着重设计更高疲劳强度、高耐磨耗性及优良耐热性的辅助轴承，最大限度实现系统二次稳定运行、延长其寿命周期.
4. 总 结
本文围绕磁悬浮支承-飞轮系统所表现的模态自激振动和强迫响应振动两类影响系统稳定性的行为，从拓扑结构、动力学建模、控制策略及辅助保护四大关键技术层面展开综述.
拓扑结构方面，以柱面、球面、阻尼支承为分类点阐述了其拓扑结构影响系统稳定性的特点；动力学建模方面，结合磁悬浮支承系统的不同建模性质及各类应用背景下的建模特征，以抑制两类不稳定振动为支点，总结归纳了当前飞轮转子领域的建模技术；控制策略方面，针对飞轮转子系统的不平衡振动因素，以主要控制策略为分类点，阐述了解决此类问题所采取的控制技术方案. 辅助保护方面，基于不稳定行为对磁悬浮支承系统可能造成的危害，综述了当前辅助轴承技术的主要研究重点. 最后展望了磁悬浮支承-飞轮系统如何进一步实现稳定运行的发展方向，对我国构建清洁低碳、安全高效的新能源体系提供参考.
-
图 7 平均裂缝间距计算值与实测值的对比
Figure 7. Comparison between calculated and measured values of average crack spacing
图 9 计算值与文献实测值的对比
Figure 9. Comparison between calculated values and measured values in literature
图 10 简化计算值与文献实测值的对比
Figure 10. Comparison between calculated values of simplified formula and measured values in literature
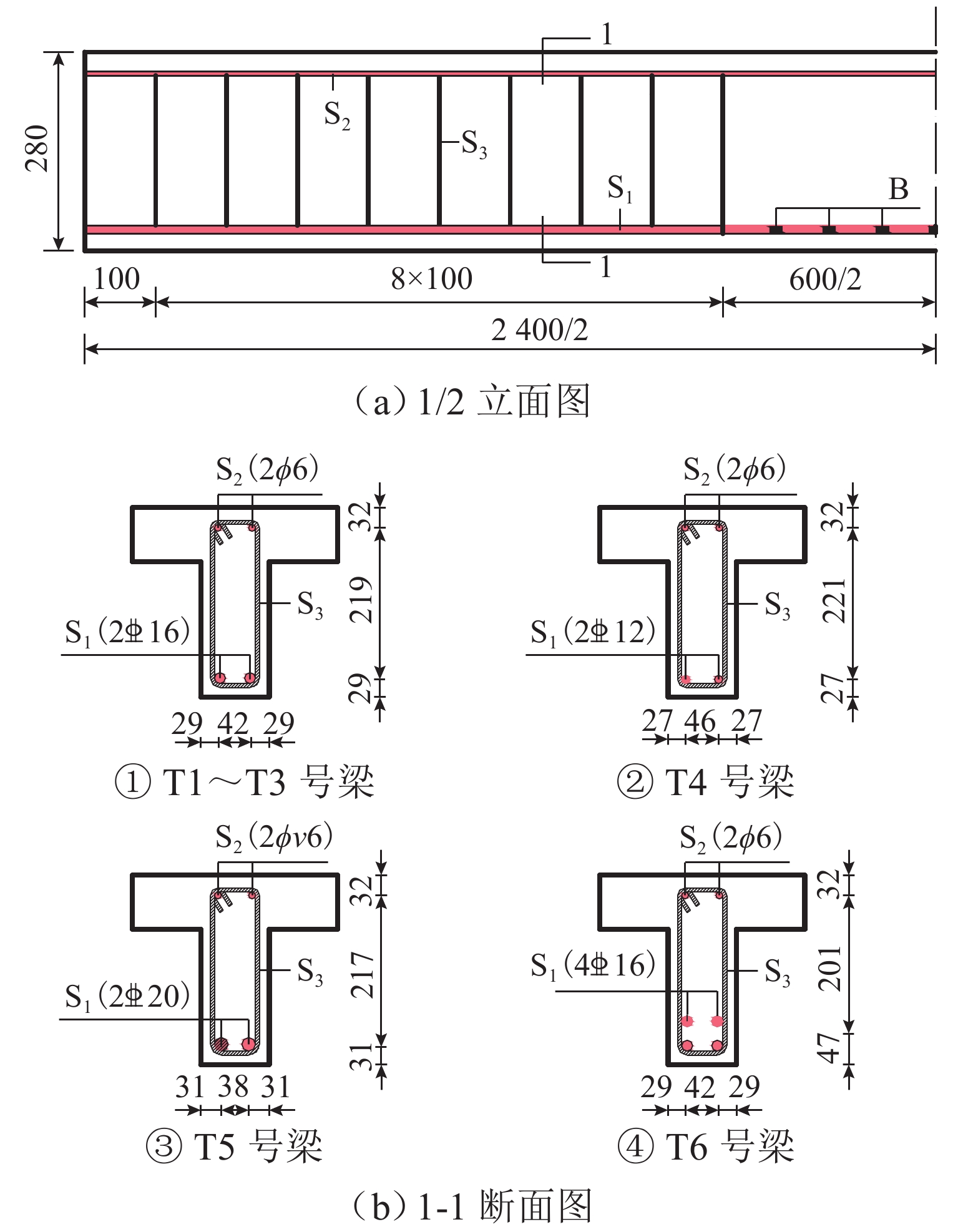
表 1 试件的编号与参数
Table 1. Number and parameters of specimens
变量 梁号 Vf/% 纵筋配置 ρs/% c/mm 标准梁 T1 2 2 
1.60 15 钢纤维
体积率T2 1 2 1.60 T3 3 配筋率 T4 2 2 0.89 T5 2 2.51 T6 4 3.20 
下载: 导出CSV
表 2 基本力学指标
Table 2. Basic mechanical indicators
Vf/% fcu/MPa fc/MPa ft/MPa Ec/GPa 1 121.22 83.72 6.35 41 2 133.71 89.14 7.84 42 3 141.53 97.82 9.32 44
下载: 导出CSV
表 3 钢筋应力的实测结果
Table 3. Measured results of reinforcement stress
梁号 Fcr/kN Ft/kN σcr/MPa σt/MPa Vm/（MPa•kN−1） T1 55.24 321.42 37.77 593.75 2.09 T2 37.27 311.31 32.23 602.22 2.08 T3 69.72 334.27 44.53 579.63 2.02 T4 43.43 218.51 41.82 581.70 3.08 T5 60.67 454.88 48.34 579.06 1.35 T6 61.14 529.20 39.25 578.51 1.15
下载: 导出CSV
表 4 系数n与S1的取值
Table 4. Values of coefficients n and S1
梁号 n S1 T1 0.64 1.10 T2 0.66 0.90 T3 0.60 0.99 T4 0.62 1.17 T5 0.64 0.95 T6 0.71 0.87
下载: 导出CSV
-
[1] SHIRAI K, YIN H, TEO W. Flexural capacity prediction of composite RC members strengthened with UHPC based on existing design models[J]. Structures, 2020, 23: 44-55. doi: 10.1016/j.istruc.2019.09.017 [2] ELSAYED M, BADAWY S, TAYEH B A, et al. Shear behaviour of ultra-high performance concrete beams with openings[J]. Structures, 2022, 43(6): 546-558. [3] WANG J Q, QI J N, TONG T, et al. Static behavior of large stud shear connectors in steel-UHPC composite structures[J]. Engineering Structures, 2019, 178: 534-542. doi: 10.1016/j.engstruct.2018.07.058 [4] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范:GB 50010—2010[S]. 北京:中国建筑工业出版社,2010. [5] 邱明红,邵旭东,胡伟业,等. 钢筋UHPC受弯构件裂缝宽度计算方法研究[J]. 土木工程学报,2020,53(10): 89-98,119.QIU Minghong, SHAO Xudong, HU Weiye, et al. Calculation method for crack width of reinforced UHPC flexural components[J]. China Civil Engineering Journal, 2020, 53(10): 89-98,119. [6] 邱明红,邵旭东,胡伟业,等. 钢筋UHPC矩形截面受弯构件的钢筋应力简化计算[J]. 中国公路学报,2021,34(8): 106-117.QIU Minghong, SHAO Xudong, HU Weiye, et al. Simplified calculation of reinforcement stress in reinforced UHPC bending members with rectangular sections[J]. China Journal of Highway and Transport, 2021, 34(8): 106-117. [7] 郑文忠,李莉,卢姗姗. 钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J]. 建筑结构学报,2011,32(6): 125-134.ZHENG Wenzhong, LI Li, LU Shanshan. Experimental research on mechanical performance of normal section of reinforced reactive powder concrete beam[J]. Journal of Building Structures, 2011, 32(6): 125-134. [8] 赵国藩,王清湘. 钢筋混凝土构件裂缝宽度分析的应力图形和计算模式[J]. 大连工学院学报,1984,24(4): 87-94.ZHAO Guofan, WANG Qingxiang. Stress distribution and calculation formula for crack width analysis of reinforced concrete members[J]. Journal of Dalian University of Technology, 1984, 24(4): 87-94. [9] 朱虹,董志强,吴刚,等. FRP筋混凝土梁的刚度试验研究和理论计算[J]. 土木工程学报,2015,48(11): 44-53.ZHU Hong, DONG Zhiqiang, WU Gang, et al. Experimental study and theoretical calculation on the flexural stiffness of concrete beams reinforced with FRP bars[J]. China Civil Engineering Journal, 2015, 48(11): 44-53. [10] 贾方方. 钢筋与活性粉末混凝土粘结性能的试验研究[D]. 北京:北京交通大学,2013. [11] 徐海宾,邓宗才. UHPC梁开裂弯矩和裂缝试验[J]. 哈尔滨工业大学学报,2014,46(4): 87-92.XU Haibin, DENG Zongcai. Cracking moment and crack width of ultra-high performance concrete beams[J]. Journal of Harbin Institute of Technology, 2014, 46(4): 87-92. [12] YOO D Y, YOON Y S. A review on structural behavior, design, and application of ultra-high-performance fier-reinforced concrete[J]. International Journal of Concrete Structures and Materials, 2016, 10(2): 125-142. doi: 10.1007/s40069-016-0143-x [13] HASGUL U, TURKER K, BIROL T, et al. Flexural behavior of ultra-high-performance fiber reinforced concrete beams with low and high reinforcement ratios[J]. Structural Concrete, 2018, 19(6): 1577-1590. doi: 10.1002/suco.201700089 [14] AHMED K S, HABIB M A, ASEF M F. Flexural response of stainless steel reinforced concrete beam[J]. Structures, 2021, 34: 589-603. doi: 10.1016/j.istruc.2021.08.019 [15] 中华人民共和国住房和城乡建设部. 活性粉末混凝土:GB/T 31387—2015 [S]. 北京:中国标准出版社,2015. [16] 中国建筑科学研究院. 混凝土结构试验方法标准:GB/T 50152—2012[S]. 北京:中国建筑工业出版社,2012. [17] 高丹盈,张明,赵军. 疲劳荷载下钢纤维高强混凝土梁裂缝宽度的计算方法[J]. 土木工程学报,2013,46(3): 40-48.GAO Danying, ZHANG Ming, ZHAO Jun. Calculating method for crack width of steel fiber reinforced high-strength concrete beams under fatigue loads[J]. China Civil Engineering Journal, 2013, 46(3): 40-48. [18] 宁喜亮,丁一宁. 钢筋钢纤维自密实混凝土梁裂缝宽度试验研究[J]. 工程力学,2017,34(4): 116-124.NING Xiliang, DING Yining. Experimental research on crack width of steel fibers reinforced self-consolidating concrete beams[J]. Engineering Mechanics, 2017, 34(4): 116-124. [19] 高丹盈,刘建秀. 钢纤维混凝土基本理论[M]. 北京:科学技术文献出版社,1994. [20] 贾方方,安明喆,余自若,等. 钢筋与活性粉末混凝土黏结性能的梁式试验研究[J]. 铁道学报,2012,34(6): 83-87.JIA Fangfang, AN Mingzhe, YU Ziruo, et al. Beam test of bond behavior between steel bars and reactive powder concrete[J]. Journal of the China Railway Society, 2012, 34(6): 83-87. [21] BABY F, MARCHAND P, ATRACH M, et al. Analysis of flexure-shear behavior of UHPFRC beams based on stress field approach[J]. Engineering Structures, 2013, 56: 194-206. doi: 10.1016/j.engstruct.2013.04.024 [22] 徐明雪,梁兴文,汪萍,等. 超高性能混凝土梁正截面受弯承载力理论研究[J]. 工程力学,2019,36(8): 70-78.XU Mingxue, LIANG Xingwen, WANG Ping, et al. Theoretical investigation on normal section flexural capacity of uhpc beams[J]. Engineering Mechanics, 2019, 36(8): 70-78. [23] BAE B I, CHOI H K, CHOI C S. Flexural strength evaluation of reinforced concrete members with ultra high performance concrete[J]. Advances in Materials Science and Engineering, 2016, 2016: 2815247.1-2815247.11. [24] 王景全,戚家南,刘加平. 基于细观本构模型的UHPC梁受弯全过程分析[J]. 建筑结构学报,2020,41(9): 137-144.WANG Jingquan, QI Jianan, LIU Jiaping. Flexural analysis of UHPC beams based on a mesoscale constitutive model[J]. Journal of Building Structures, 2020, 41(9): 137-144. [25] 周建民,王眺,赵勇,等. 高强钢筋混凝土受弯构件裂缝宽度计算方法的研究[J]. 土木工程学报,2010,43(9): 69-76.ZHOU Jianmin, WANG Tiao, ZHAO Yong, et al. Research on the calculation of crack width for RC flexural member using high-strength bars[J]. China Civil Engineering Journal, 2010, 43(9): 69-76. [26] 程东辉,范永萱,王彦松. RC类活性粉末混凝土钢筋粘结-滑移本构模型[J]. 吉林大学学报(工学版),2021,51(4): 1317-1330.CHENG Donghui, FAN Yongxuan, WANG Yansong. Bond-slip constitutive model of steel bars and reactive powder concrete under standard curing[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(4): 1317-1330. [27] 张哲,李帅帅,朱平,等. 钢筋-超高性能混凝土界面黏结性能试验[J]. 湖南大学学报(自然科学版),2022,49(11): 105-115.ZHANG Zhe, LI Shuaishuai, ZHU Ping, et al. Test on interface bonding behavior between steel rebar and ultra-high performance concrete[J]. Journal of Hunan University (Natural Sciences), 2022, 49(11): 105-115. [28] 梁芮,黄远. 高强钢筋与超高性能混凝土黏结性能试验研究[J]. 建筑结构学报,2022,43(9): 294-302.LIANG Rui, HUANG Yuan. Experimental study on bond performance between high strength steel rebar and ultra-high performance concrete[J]. Journal of Building Structures, 2022, 43(9): 294-302. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 278
- HTML全文浏览量: 114
- PDF下载量: 50
- 被引次数: 0