Vibration Reduction of Bearing-Rotor with Electromagnetic Damper Considering Dynamic Stiffness
-
摘要:
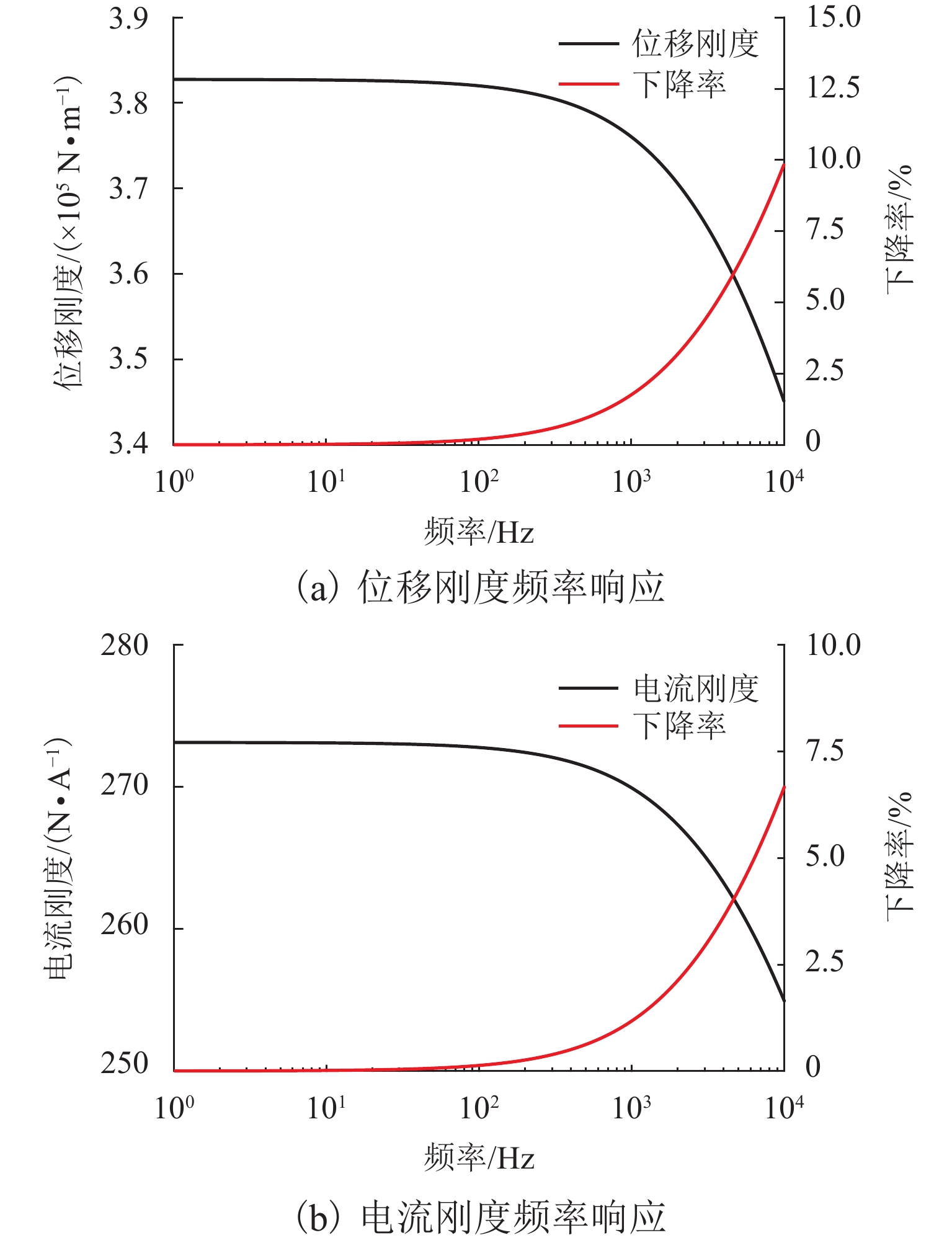
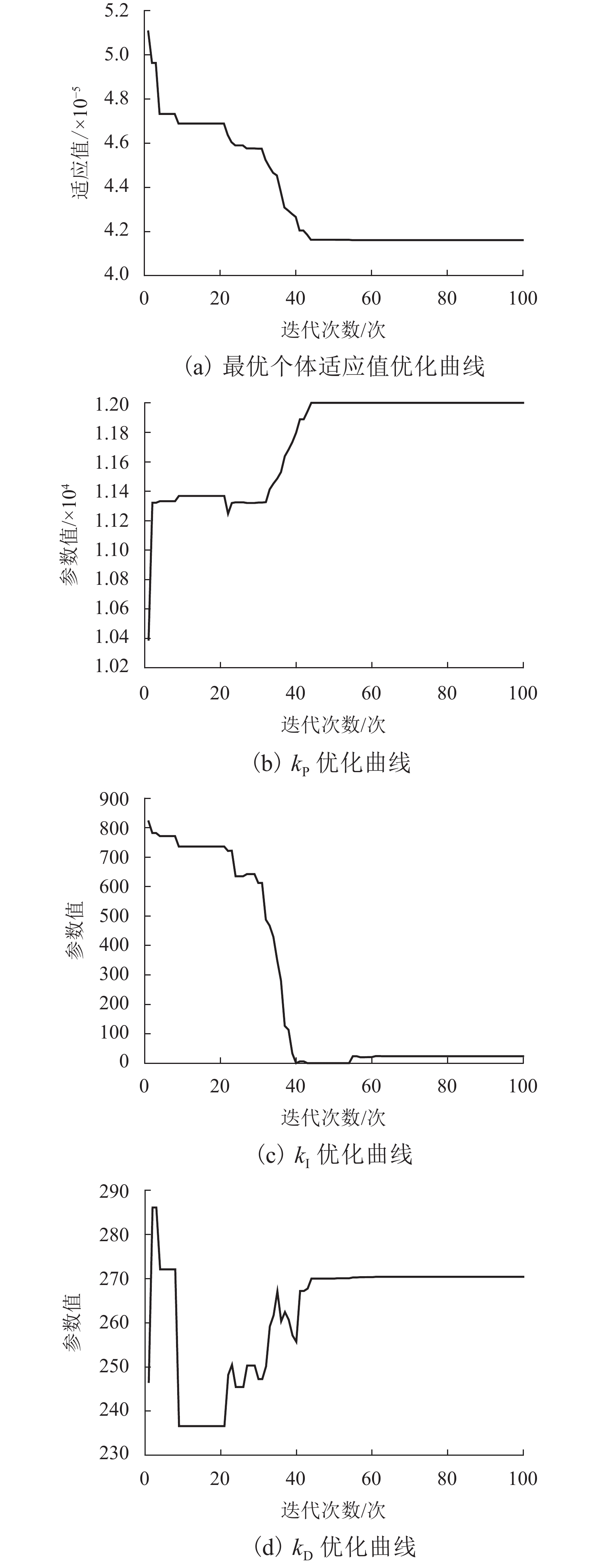
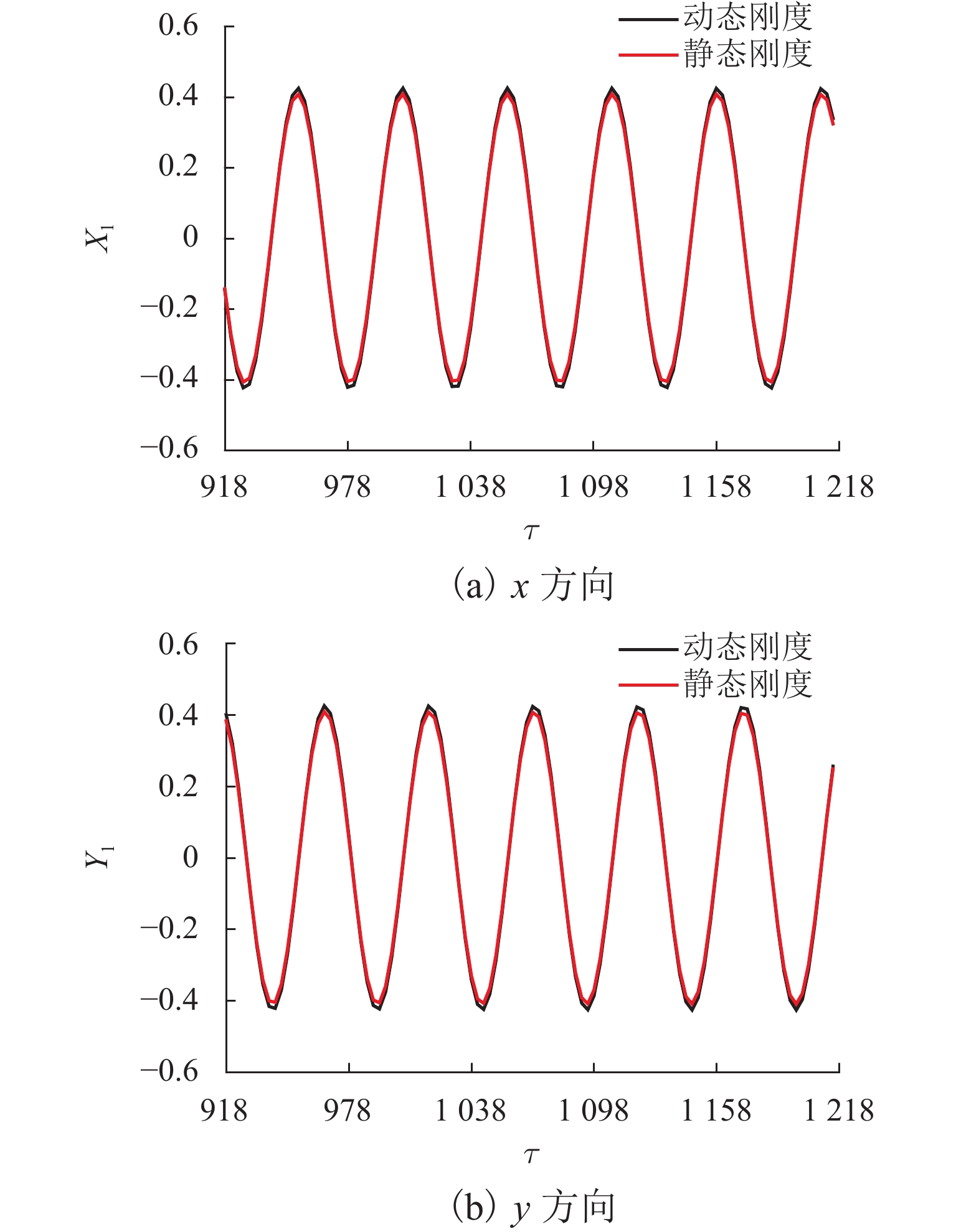
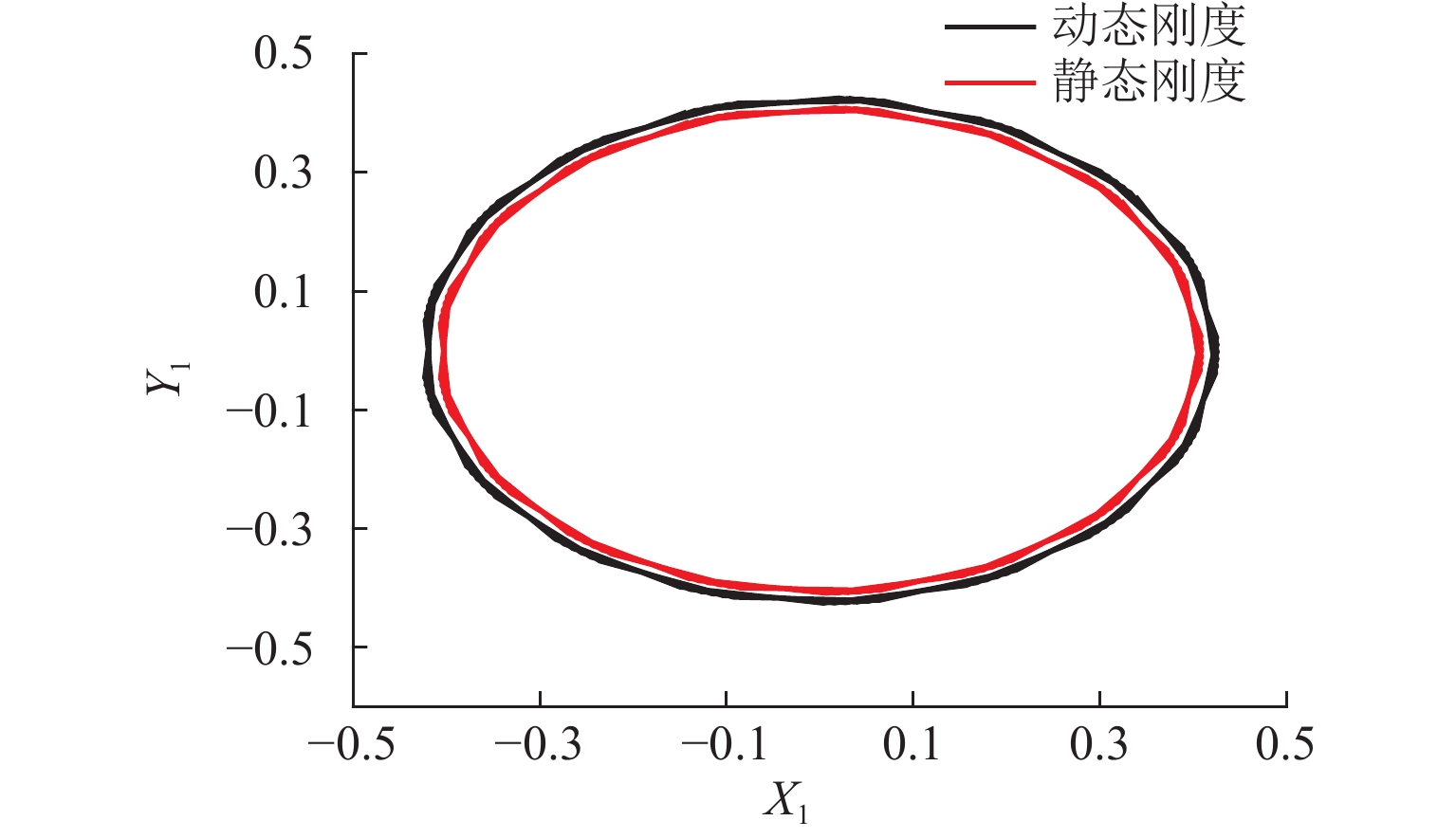
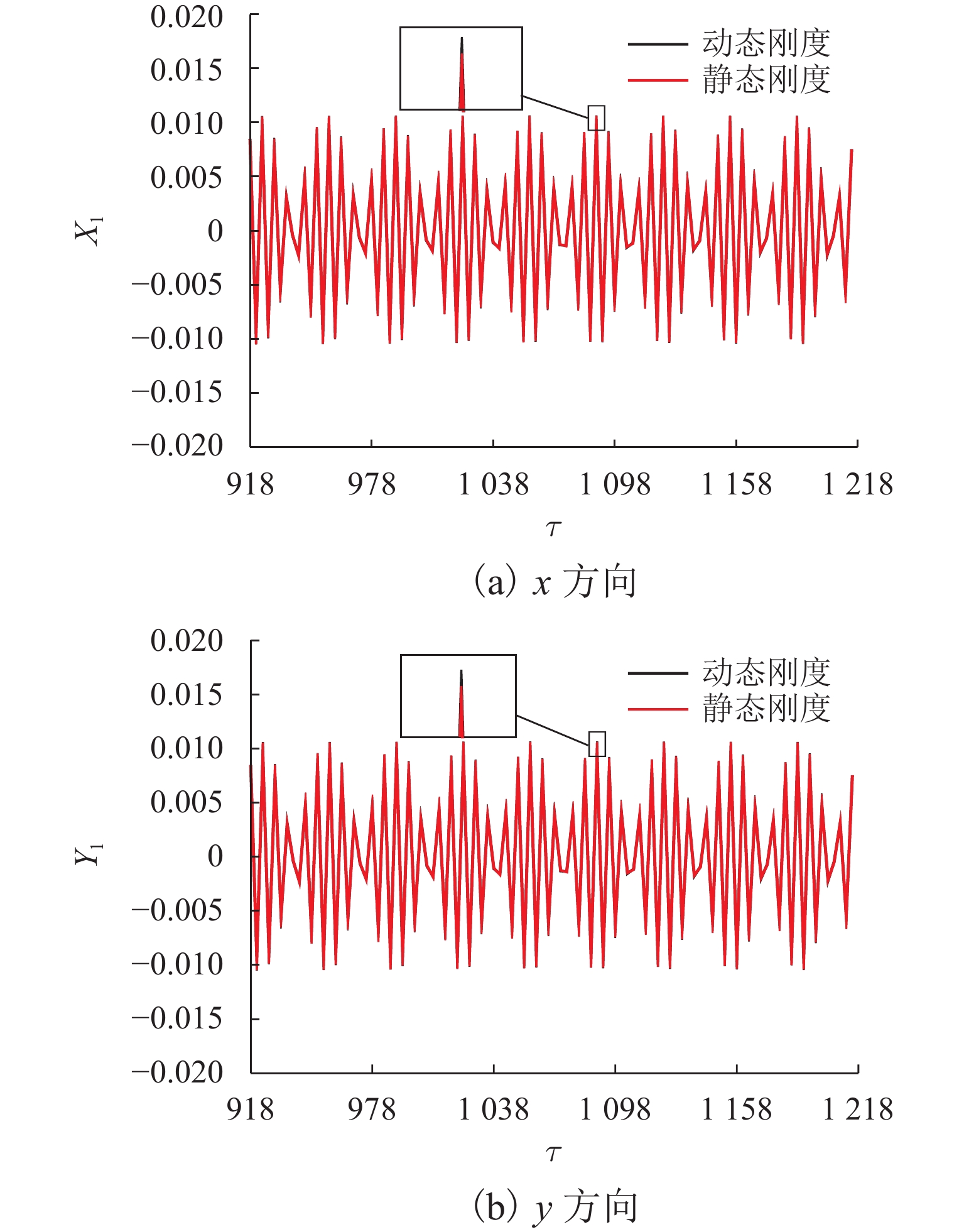
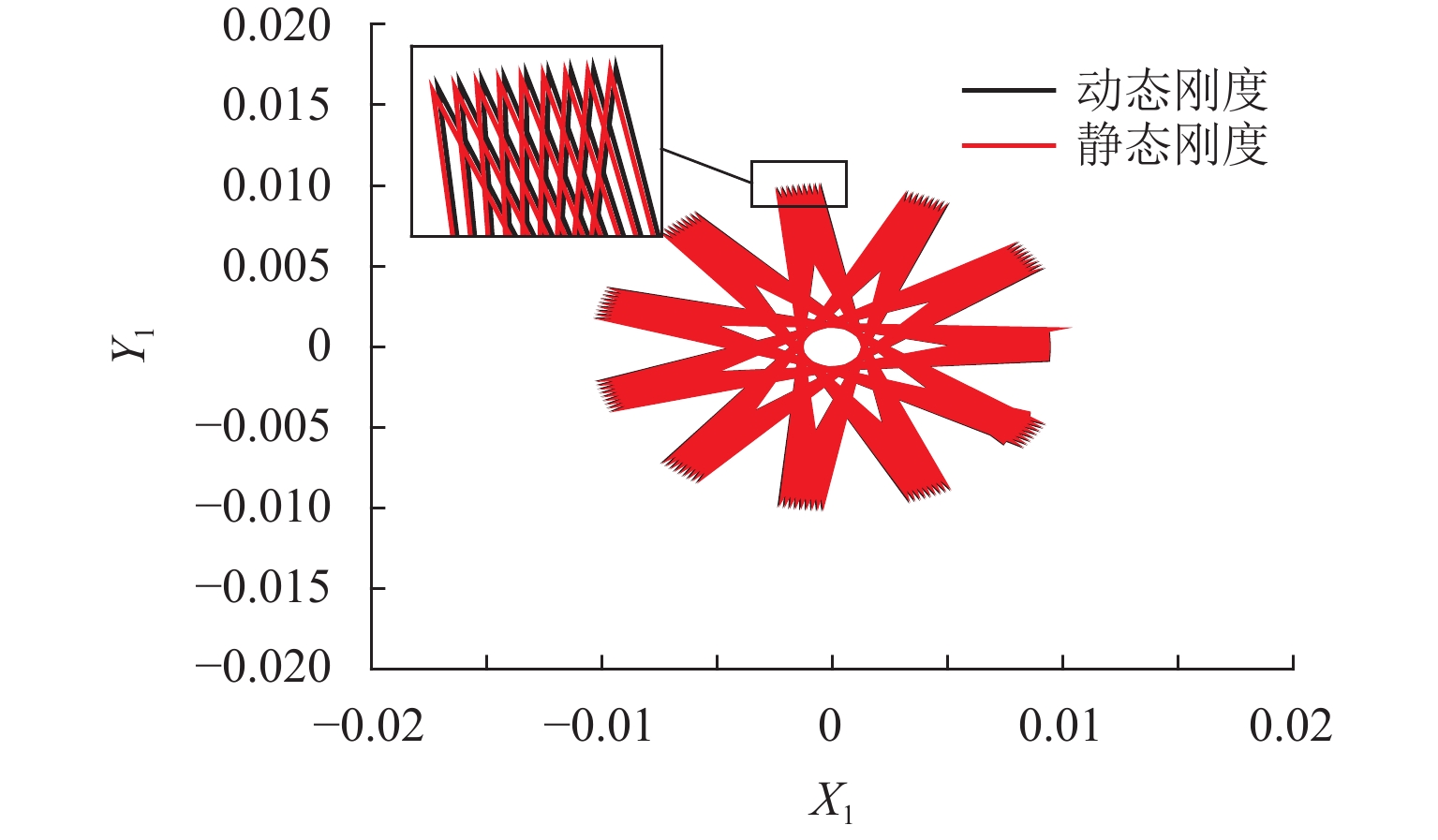
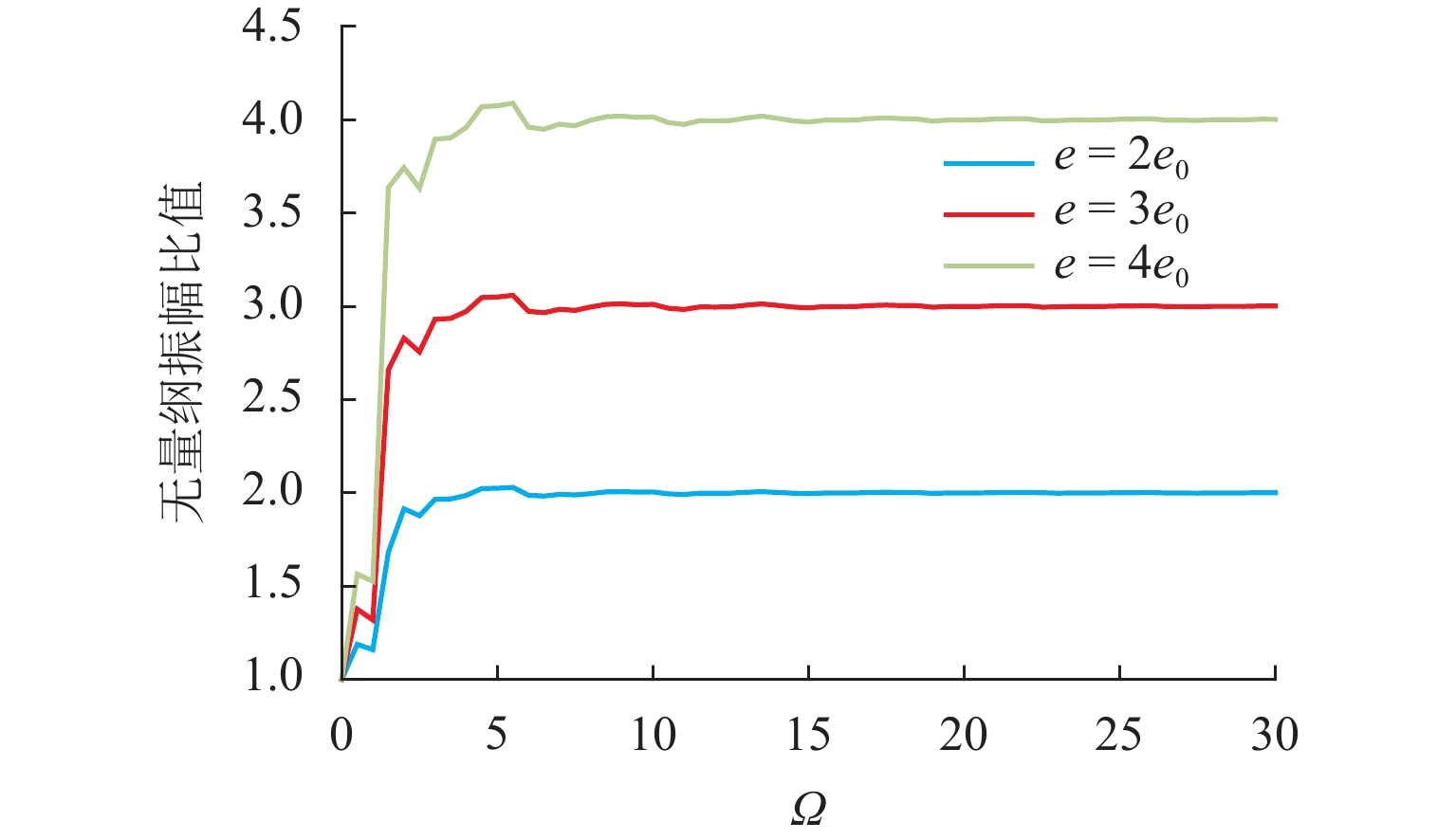
为了有效抑制转子系统的不平衡振动，本文提出将考虑动态刚度的电磁阻尼器应用于转子系统中. 首先，建立转子系统运动方程并对其进行无量纲化；其次，基于等效磁路法，建立了考虑涡流效应的电磁阻尼器模型，分析了涡流效应对电磁阻尼器刚度的影响，并采用非线性动态自适应惯性权重的PSO算法对电磁阻尼器的PID （比例、积分、微分）3个控制参数进行优化；最后，对转子的动力学特性进行了分析. 研究结果表明：在涡流效应的影响下，电磁阻尼器的刚度是动态变化的，当转速为100 kHz时，理论上位移刚度和电流刚度分别下降了10.0%、6.6%；通过非线性动态自适应惯性权重的PSO算法优化得到的PID参数响应快，超调量小，能够在0.1 s内迅速地将圆盘的偏离量调至0，具有良好的控制效果；相比于静态刚度，考虑动态刚度后，圆盘的振幅有所增大，当转速为4782 Hz时，圆盘的振幅增大了5.33%；偏心距增大会导致圆盘的振幅增大，当转速超过242 Hz时，圆盘振幅增大的幅度与圆盘偏心距增大的幅度几乎成正比.
Abstract:In order to suppress the unbalance vibration of the rotor system effectively, the electromagnetic damper considering dynamic stiffness was applied to the rotor system in this paper. Firstly, the motion equations of the rotor system were established and nondimensionalized; secondly, based on the equivalent magnetic circuit method, the electromagnetic damper model considering the eddy-current effect was established, and the influence of the eddy-current effect on the stiffness of the electromagnetic damper was analyzed. The particle swarm optimization (PSO) algorithm with nonlinear dynamic adaptive inertia weight was used to optimize the three control parameters of the proportion integration differentiation (PID) of the electromagnetic damper; finally, the dynamic characteristics of the rotor were analyzed. The results indicate that under the influence of the eddy-current effect, the stiffness of the electromagnetic damper dynamically changes. When the speed is 100 kHz, the displacement stiffness and current stiffness decrease by 10.0% and 6.6% respectively; the PID parameters optimized by the PSO algorithm with nonlinear dynamic adaptive inertia weight have great control effects, such as fast response and small overshoot, and they can quickly adjust the deviation of the disk to 0 within 0.1 seconds; compared with static stiffness, the amplitude of the disk increases slightly after considering dynamic stiffness. When the speed is 4 782 Hz, the amplitude of the disk increases by 5.33%; the increase in eccentricity will lead to an increase in the amplitude of the disk. When the speed exceeds 242 Hz, the amplitude of the disk increases almost proportionally to that of the disk eccentricity.
-
Key words:
- electromagnetic damper /
- magnetic circuit /
- eddy-current /
- dynamic stiffness
-
图 1 带电磁阻尼器的电磁轴承-转子系统的模型
Figure 1. Model of electromagnetic bearing-rotor system with electromagnetic damper
图 7 两种刚度下无量纲振幅的变化曲线
Figure 7. Variation curves of dimensionless amplitude under two kinds of stiffness
图 9 两种刚度下圆盘的时域图（Ω=70.0）
Figure 9. Time domain of disk under two kinds of stiffness (Ω=70.0)
图 10 两种刚度下圆盘的轴心轨迹图（Ω=70.0）
Figure 10. Axis center track of disk under two kinds of stiffness （Ω = 70.0）
图 11 两种刚度下圆盘的时域图（Ω=71.0）
Figure 11. Time domain of disk under two kinds of stiffness （Ω = 71.0）
图 12 两种刚度下圆盘的轴心轨迹图（Ω=71.0）
Figure 12. Axis center track of disk under two kinds of stiffness （Ω = 71.0）
图 13 不同偏心距时无量纲振幅的变化曲线
Figure 13. Variation curve of dimensionless amplitude with different eccentricity
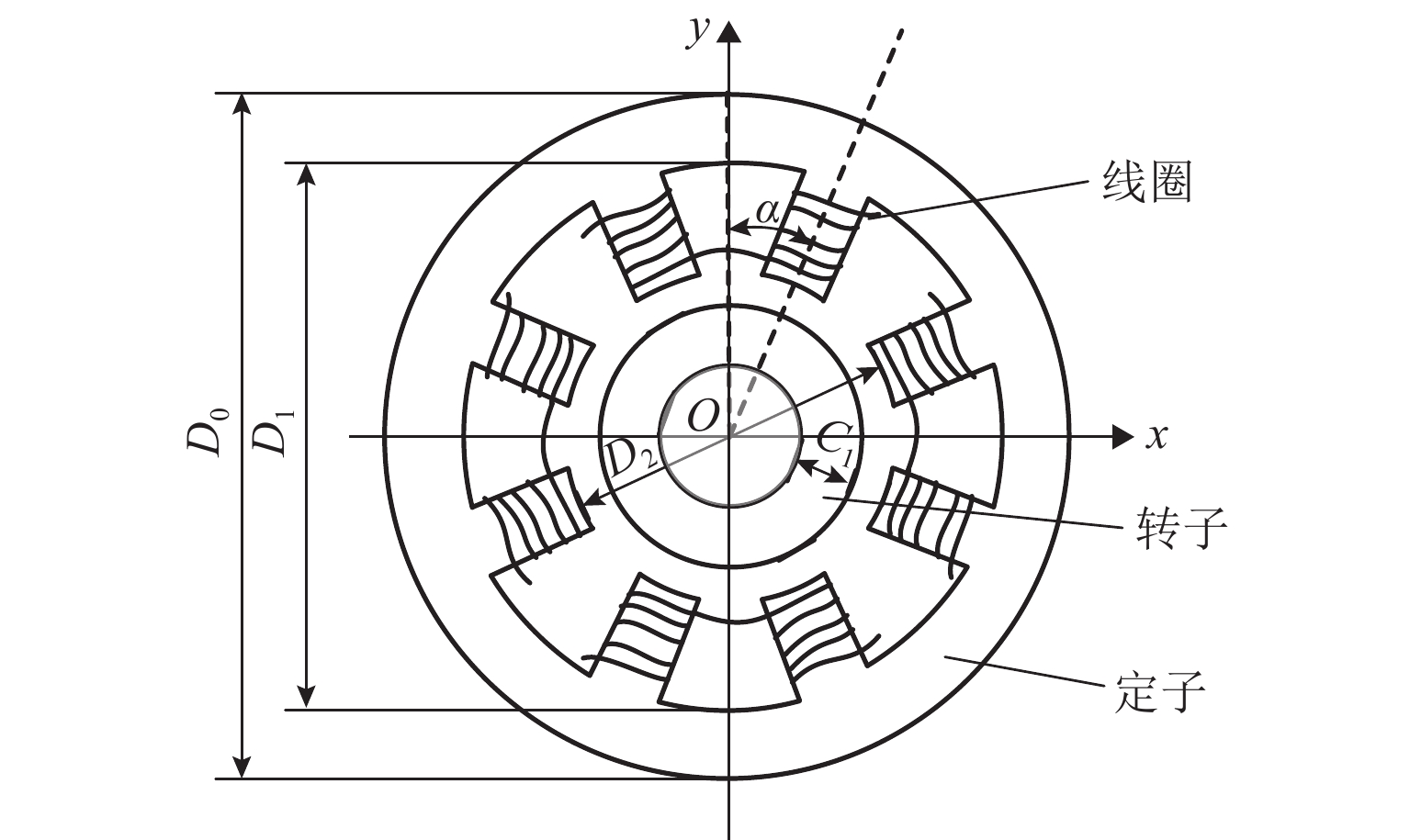
表 1 电磁阻尼器结构参数
Table 1. Structure parameters for electromagnetic damper
结构参数 取值 圆盘直径 D/mm 150 转子直径 d/mm 35 阻尼器外径 D0/mm 340.6 阻尼器内径 D2/mm 153.0 定子厚度 b/mm 50 磁极面积 A/mm2 1500 线圈匝数 N/匝 280 静态电流 I0/A 2.3 磁极角 α/(°) 22.5 气隙长度 C1/mm 1.5 
下载: 导出CSV
表 2 仿真参数
Table 2. Parameters of simulation
系统参数 取值 圆盘质量 m1/kg 6.39 轴颈质量 m2/kg 2.15 转轴刚度 k/(N·m−1) 106 初始相位角 φ/(°) 45 原始偏心距 e0/mm 0.5 固有频率 ωn/(rad·s−1) 305 电磁轴承气隙长度 C2/mm 0.4 电磁轴承位移刚度 K2/(N·m−1) 3.657 × 105 电磁轴承电流刚度 G2/(N·A−1) 73.14 比例增益 kP2/(A·m−1) 5500 积分增益 kI2/(A·（m·s）−1) 8000 微分增益 kD2/(A·s·m−1) 3
下载: 导出CSV
-
[1] 张凤阁,杜光辉,王天煜,等. 高速电机发展与设计综述[J]. 电工技术学报,2016,31(7): 1-18. doi: 10.3969/j.issn.1000-6753.2016.07.001ZHANG Fengge, DU Guanghui, WANG Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18. doi: 10.3969/j.issn.1000-6753.2016.07.001 [2] ZHANG Y P, HE L D, YANG J J, et al. Vibration control of Tie rod rotors with optimization of unbalanced force and unbalanced moment[J]. IEEE Access, 2020, 8: 66578-66587. doi: 10.1109/ACCESS.2020.2985847 [3] HEINDEL S, MÜLLER P C, RINDERKNECHT S. Unbalance and resonance elimination with active bearings on general rotors[J]. Journal of Sound and Vibration, 2018, 431: 422-440. doi: 10.1016/j.jsv.2017.07.048 [4] 吴华春,涂星,周建,等. 磁悬浮转子不平衡振动控制研究综述[J]. 轴承,2022(3): 1-9. doi: 10.19533/j.issn1000-3762.2022.03.001WU Huachun, TU Xing, ZHOU Jian, et al. Review on unbalanced vibration control for magnetic suspension rotor[J]. Bearing, 2022(3): 1-9. doi: 10.19533/j.issn1000-3762.2022.03.001 [5] 黄威,邓智泉,李克翔,等. 一种磁悬浮轴承支承刚性转子现场动平衡方法[J]. 电工技术学报,2020,35(22): 4636-4646. doi: 10.19595/j.cnki.1000-6753.tces.191289HUANG Wei, DENG Zhiquan, LI Kexiang, et al. A filed dynamic balancing method for rigid rotor supported by magnetic bearings[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4636-4646. doi: 10.19595/j.cnki.1000-6753.tces.191289 [6] SHE C F, ZHANG M, GE Y B, et al. Design and simulation analysis of an electromagnetic damper for reducing shimmy in electrically actuated nose wheel steering systems[J]. Aerospace, 2022, 9(2): 1-21. doi: 10.3390/aerospace9020113 [7] 黄翠翠,李晓龙,杨洋,等. 基于自抗扰技术的机械-电磁悬浮复合隔振控制[J]. 西南交通大学学报,2022,57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850HUANG Cuicui, LI Xiaolong, YANG Yang, et al. Mechanical-electromagnetic suspension compound vibration isolation control based on active disturbance rejection technology[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850 [8] CAI Q L, HUA Y Y, ZHU S Y. Energy-harvesting adaptive vibration damping in high-speed train suspension using electromagnetic dampers[J]. International Journal of Structural Stability and Dynamics, 2021, 21(14): 2140002.1-2140002.28. [9] XIA X J, ZHENG M Y, LIU P F, et al. Friction observer-based hybrid controller for a seat suspension with semi-active electromagnetic damper[J]. Mechatronics, 2021, 76: 102568.1-102568.11. [10] KAVIANIPOUR O. Effects of the passive electromagnetic damper on the behavior of a fluid-conveying pipeline[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(7): 2329-2339. doi: 10.1177/0954406218784627 [11] 祝长生,钟志贤. 带主动电磁阻尼器的裂纹转子系统动力学[J]. 振动工程学报,2010,23(3): 298-304. doi: 10.3969/j.issn.1004-4523.2010.03.010ZHU Changsheng, ZHONG Zhixian. The dynamics of a cracked rotor with active magnetic dampers[J]. Journal of Vibration Engineering, 2010, 23(3): 298-304. doi: 10.3969/j.issn.1004-4523.2010.03.010 [12] ZACCARDO V M, BUCKNER G D. Active magnetic dampers for controlling lateral rotor vibration in high-speed rotating shafts[J]. Mechanical Systems and Signal Processing, 2021, 152: 107445.1-107445.16. [13] XIANG B, WONG W. Electromagnetic vibration absorber for torsional vibration in high speed rotational machine[J]. Mechanical Systems and Signal Processing, 2020, 140: 106639.1-106639.18. [14] SUN J J, ZHOU H, JU Z Y. Dynamic stiffness analysis and measurement of radial active magnetic bearing in magnetically suspended molecular pump[J]. Scientific Reports, 2020, 10: 1401.1-1401.16. doi: 10.1038/s41598-020-70784-7 [15] SUN J J, ZHOU H, MA X, et al. Study on PID tuning strategy based on dynamic stiffness for radial active magnetic bearing[J]. ISA Transactions, 2018, 80: 458-474. doi: 10.1016/j.isatra.2018.07.036 [16] LE Y, FANG J C, HAN B C, et al. Dynamic circuit model of a radial magnetic bearing with permanent magnet bias and laminated cores[J]. International Journal of Applied Electromagnetics and Mechanics, 2014, 46(1): 43-60. doi: 10.3233/JAE-141746 [17] 肖玲,赵晨曦,窦经纬,等. 轴-径向混合磁轴承动态特性及控制研究[J]. 西南交通大学学报,2022,57(3): 640-647,656. doi: 10.3969/j.issn.0258-2724.20210883XIAO Ling, ZHAO Chenxi, DOU Jingwei, et al. Research on dynamic characteristics and control of axial-radial hybrid magnetic bearing[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 640-647,656. doi: 10.3969/j.issn.0258-2724.20210883 [18] XIAO L, HE X W, CHENG W J, et al. Structural optimization and dynamic characteristics of the new type 3-degrees of freedom axial and radial hybrid magnetic bearing[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(9): 5097-5110. doi: 10.1177/09544062211052826 [19] 王生亮,刘根友. 一种非线性动态自适应惯性权重PSO算法[J]. 计算机仿真,2021,38(4): 249-253,451. doi: 10.3969/j.issn.1006-9348.2021.04.050WANG Shengliang, LIU Genyou. A nonlinear dynamic adaptive inertial weight particle swarm optimization[J]. Computer Simulation, 2021, 38(4): 249-253,451. doi: 10.3969/j.issn.1006-9348.2021.04.050 [20] KUMAR P, TIWARI R. Dynamic analysis and identification of unbalance and misalignment in a rigid rotor with two offset discs levitated by active magnetic bearings: a novel trial misalignment approach[J]. Propulsion and Power Research, 2021, 10(1): 58-82. doi: 10.1016/j.jppr.2020.06.003 -
下载:
点击查看大图
计量
- 文章访问数: 1160
- HTML全文浏览量: 143
- PDF下载量: 31
- 被引次数: 0