Simulation of Dynamic Coupling of Metro-Earth-Grid for DC Interference in Rail Transit
-
摘要:
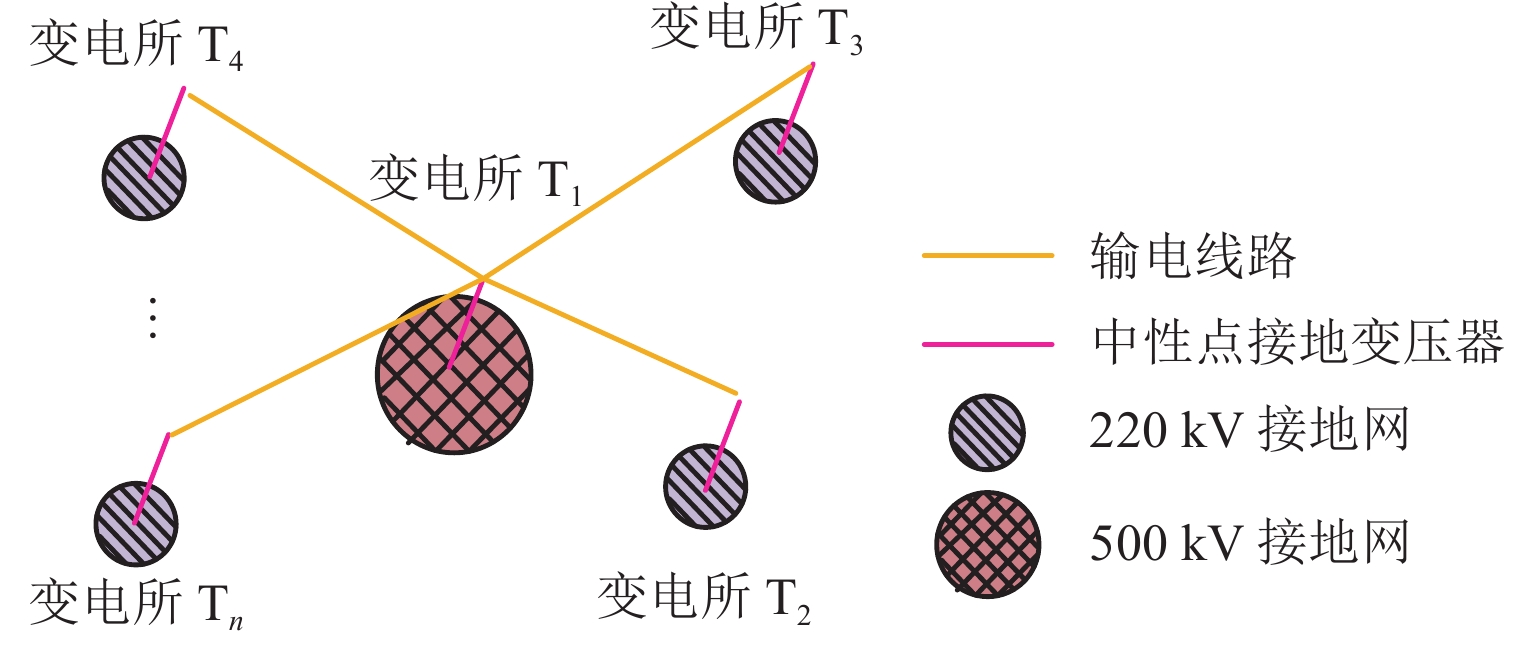
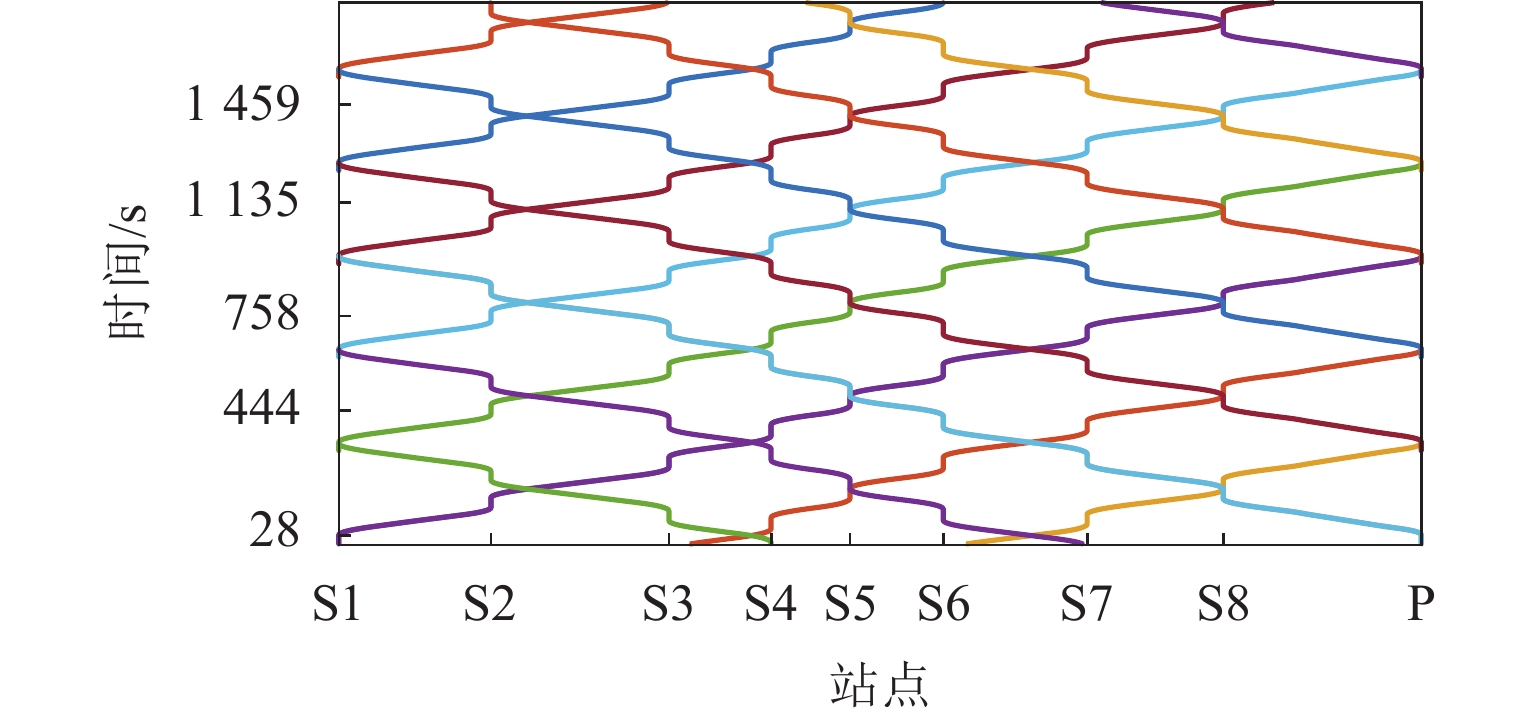
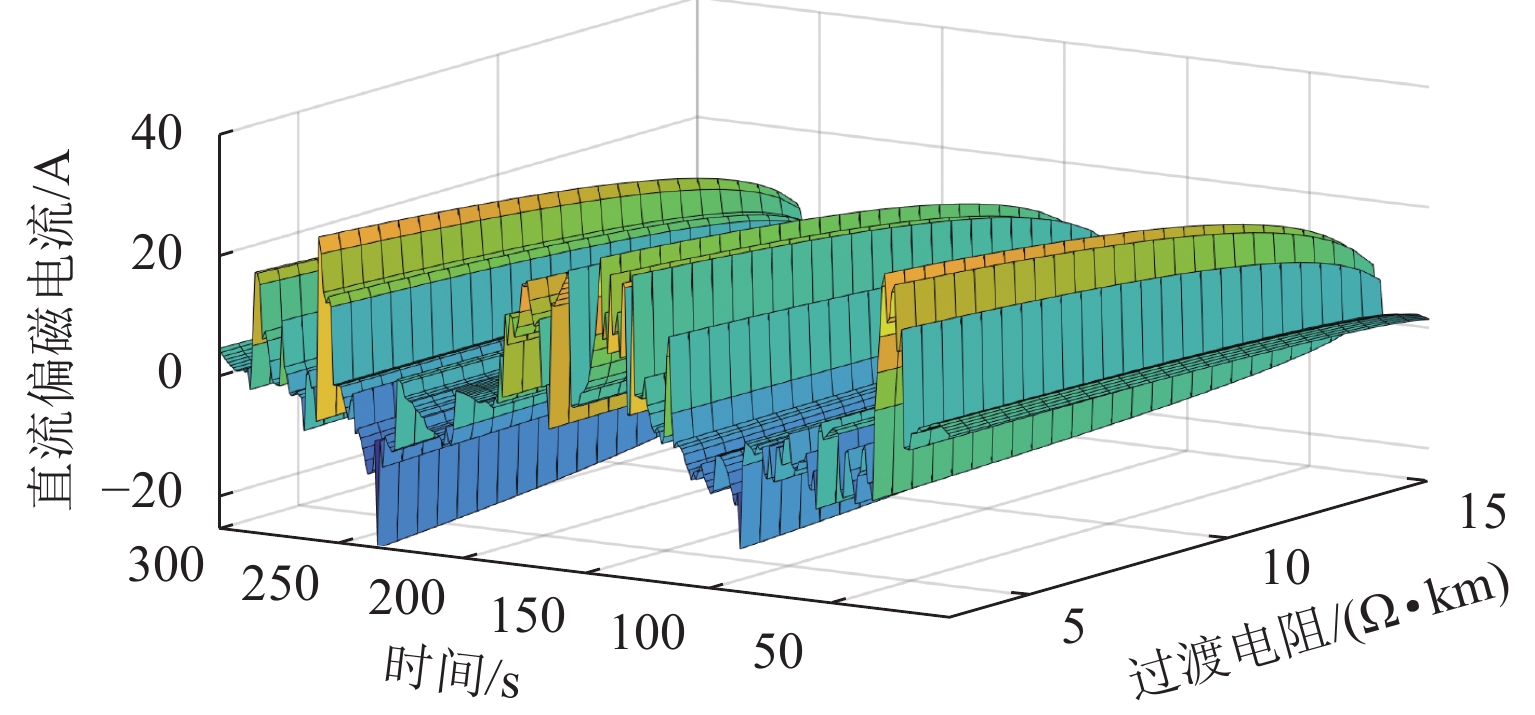
针对中性点接地变压器直流偏磁电流受轨道交通动态杂散电流泄漏和段场接地影响的问题，综合考虑多列车运行工况，建立杂散电流分布扩散的车-地-网耦合模型，并采用复镜像法计算大地电位；定义接地网的自电阻系数和互电阻系数，建立直流偏磁电流与大地电位的耦合关系，根据杂散电流侵入路径的拓扑结构，构建大地电位和直流偏磁电流的场路耦合模型；设计轨道交通杂散电流侵入电网的缩比模拟试验，并通过试验与模型计算进行验证. 研究结果表明：试验结果和模型计算之间的最大误差为8.41%；钢轨对地过渡电阻从3.00 Ω·km增大到15.00 Ω·km，直流偏磁电流的绝对平均值减小82.4%；在车辆段和正线之间采用阻断式连接装置比采用单向导通装置减小23.45%的直流偏磁电流.
Abstract:In response to the problem that direct current (DC) bias current of neutral grounded transformer is affected by dynamic stray current leakage and depot grounding of rail transit, a metro-earth-grid coupling model of stray current distribution and diffusion under multi-train operation was proposed, and the complex image method was used to calculate the earth potential. The self and mutual resistance coefficients of grounding grids were defined, and the coupling relationship between DC bias current and earth potential was proposed. The field-circuit coupling model of earth potential and DC bias current was built according to the topology of stray current intrusion path. A scaled-down simulation test of stray current intrusion into the grid for rail transit was designed, and tests and model calculation were conducted for verification. The results show that the maximum error between the experimental data and the model calculation data is 8.41%. The rail-to-earth transition resistance increases from 3.00 Ω·km to 15.00 Ω·km, and the absolute average of DC bias current decreases by 82.4%. Using a blocking connection device between the car depot and the main line can reduce DC bias current by 23.45% compared with using a unidirectional conduction device.
-
Key words:
- DC traction power supply system /
- stray current /
- DC magnetic bias
-
我国高速铁路事业近年来发展迅猛，在高速列车的长期高频冲击下，铁路基础设施的服役性能在不断发生变化[1-4]. 因此，需要对铁路系统的主要结构组件（包括钢轨、扣件、轨枕、无砟道床等）的结构健康状态进行长期持续监测[5]. 轨枕作为将车轮荷载从钢轨传递到道床的关键结构，若能嵌入传感功能，则可提供列车荷载作用下的枕上压力等关键信息，其在一定程度上反映了高速列车载荷下的轮轨力状态.
目前，对轨道结构的监测主要分为车载监测和地面监测[6]. 金鑫等[7]分析了轮轨作用力对轮轴结构受力特性的影响，提出了在车辆轮轴上粘贴传感器的轮轨力测试方法. 宫雪[8]结合轮辐测力与车轴测力的特点，提出了辐轴结合法，并在模拟滚动台上进行了验证. 上述车载测试方法，尽管能够达到较高的测量精度，但均需制备特殊的测力轮对，测试成本较高，且只能用于周期性的轮轨作用关系检测，难以满足全天候安全服役状态监测的需要. 因此，进行地面监测也十分必要.
Zhang等[9]在轨下胶垫中植入了压电压力传感器，在实验室内完成标定后，将其布置到运营线路中进行现场测试，并获取了列车通过时轨枕承受的压力大小. Sadeghi[10]利用压电压力传感器研究了钢轨和轨枕、轨枕和道床之间的相互作用力及其线性关系. 宋颖等[11]提出了基于压电薄膜的轮轨力测试方法，并通过有限元法计算验证了监测原理的可行性. 由于电信号传感元件在防水、抗电磁干扰、耐高温、耐腐蚀等方面性能的不足，在长期监测过程中会不可避免地产生损坏，其监测稳定性和可靠性大大降低.
光纤光栅传感器是以光波为载体，光纤为媒介，通过捕捉反射光波的变化特征，实现对其相关物理量的测试[12]. 近年来，光纤光栅在大型工程安全监测领域得到了迅速发展和广泛应用[13-16]. 孟汇[17]研究了光纤光栅传感器在复杂环境中的使用年限，预测寿命在20年左右. 在高速铁路运营线路的复杂工况下，光纤光栅传感器监测的稳定性以及耐久性具有较大优势. 除此之外，光纤光栅传感器尺寸较小、有良好的动态特性，其测试精度与测试量程满足高速铁路监测需求.
国内外学者对光纤光栅传感器在铁路领域的应用展开了大量研究. Wei等[18]在钢轨垂向、纵向安装布拉格光栅（FBG）光纤传感器，根据实验列车以不同速度经过时钢轨的应变响应，找到了最适合的布置位置，然后在运营线路钢轨上安装光纤传感器测量了钢轨的应变变化. 张兆亭等[19]使用光纤光栅传感器进行了动态载荷下的钢轨应变监测实验，结果表明，光纤光栅应变传感器适用于钢轨应变的监测需要，具有良好的工作性能. 高亮等[20]提出了一种基于光纤光栅的轮轨力长期监测方法，通过在钢轨跨中断面的3处不同部位粘贴光纤光栅传感器，采集列车通过时的钢轨修正应变，结合现场标定的轮轨力-钢轨应变线性关系，可长期实时获取轮轨相互作用力. 但上述研究均基于表面接触式监测，由于传感器及其导线外露，在长期监测中有脱落的风险.
因此，可通过在轨道结构的混凝土部件内植入传感器作为监测方法的补充手段，Butler等 [21-23]研究了有砟铁路道床、轨枕状态的监测方法，在预应力混凝土轨枕的制造阶段将光纤光栅准分布式传感系统埋入其中，并初步讨论了自感知轨枕用于铁路道床荷载传递监测的可行性. 上述研究是基于有砟轨道的预应力轨枕，目前对高速铁路无砟轨道轨枕、承轨台位置荷载的传递监测还处于空白.
鉴于现有研究的不足，本文以CRTS Ⅰ型双块式轨枕为研究对象，首次提出了一种双块式无砟轨道枕上压力监测标定方法. 将光纤光栅传感器埋入双块式轨枕中，通过反力架静载试验对传感器进行标定，并通过有限元仿真进行修正. 采用该技术可实现对轨枕枕上压力的长期监测，为轮轨力监测提供一种间接监测方法，也可为研究高速铁路轮轨荷载传递、完善无砟轨道结构的强度计算理论和方法提供重要依据.
1. 双块式轨枕及其传感器布置
1.1 光纤光栅传感器及其测试原理
本文试验选取如图1所示的埋入式光纤光栅FRP-OF （fiber reinforced polymer-optical fiber）应变传感器，其尺寸小，埋入混凝土后不影响结构的应力状态与应力分布.
该传感器采用无胶封装，克服了传统胶封光纤光栅传感器的耐久性问题，并且在实际工程中布设简单，量程大、精度高，动态特性良好. 具体参数见表1.
表 1 FRP-OF应变传感器技术参数Table 1. Technical parameters of FRP-OF strain sensor传感器技术参数 数值 量程/με −1500～3 000 分辨率/με ±0.1 测量精度/% 0.5 应变系数/ （pm·με） 0.8～1.2 线性度/% 99.9 重复性误差/% ≤0.5 中心波长/nm 1528～1568 反射率/% ≥90 标距尺寸/mm 60 工作温度范围/℃ −30～80 FRP-OF应变传感器的结构示意及其工作原理如图2所示. 传感器端部采用锚头限位，使其与被测混凝土协同变形，布拉格光栅（FBG）被封装在纤维增强复合材料（FRP）中，通过光纤（OF）传导光信号. 当入射光经过布拉格光栅时，满足相位匹配条件的光会被反射回来，不满足布拉格相位匹配的则会被透射出去. 利用光纤光栅对压力的敏感特性，制成了FRP-OF应变传感器.
图 2 FRP-OF应变传感器结构及其工作原理Figure 2. Structure of FRP-OF strain sensor and its working principle当满足相位匹配条件时，光纤的谐波长如式（1）所示，其中任何一个参数发生变化都会引起光纤谐振波长发生偏移，由此可得布拉格光栅谐振波长偏移量如式（2）所示，当外界应变或者温度发生变化时，引起光纤光栅传播有效折射率ne和光栅周期T的变化，通过光纤光栅解调仪可以检测出谐振波长的偏移量，得到输出波长，如式（3）所示，通过计算波长变化量与出厂时传感器的应变标定系数Kb的比值可以计算出相应的应变变化.
λB = 2neT， (1) ΔλB = 2ΔneT + 2neΔT， (2) ε = λ−λ0Kb， (3) 式中：ε为测试应变值；λ为输出波长；λ0为初始波长；$\Delta {{{n}}_{\rm{e}}} $为光纤光栅受到外界应力时的有效折射率变化；$\Delta T $为光纤光栅受到外界应力时的光栅周期变化.
1.2 传感器埋设
本文试验所用的双块式轨枕由某轨枕厂制造. 图3为传感器植入位置示意，其中传感器中心距离承轨台表面约为80 mm，距离螺栓孔116.5 mm，位于承轨台正下方.
图 3 双块式轨枕结构以及传感器埋设位置示意Figure 3. Bi-block sleeper structure and sensor embedment position如图4所示，在轨枕模具中通过轧带垂向固定FRP-OF应变传感器，用于感知当轨枕表面受到压力时轨枕内部的垂向应变，传感器导线沿着桁架筋从轨枕底部边缘引出.
图 4 双块式轨枕生产阶段安装传感器示意Figure 4. Schematic diagram of installing sensor in production stage of bi-block sleeper在传感器安装完毕后向模具中浇筑C60混凝土，在振捣台上将混凝土振捣均匀后送入养护室进行蒸汽养护，待其蒸养24 h完毕后进行脱模，将制作好的4根双块式轨枕的8块轨枕块编号为1#～8#，随后进行标定试验.
2. 标定试验
2.1 试验方法
由于SK-Ⅱ型双块式轨枕下部有桁架筋结构，无法将其直接放在压力试验机上进行静载标定. 为测试轨枕内传感器的感知能力以及找到枕上压力-枕内应变的线性关系，本文设计了一套反力架工装，如图5所示. 安装轨下胶垫、铁垫板、侧向挡块以及反力架，将千斤顶放置于铁垫板和反力架钢板之间，并且在千斤顶上安装一个压电压力传感器用于记录加载数值，构成了一套自反力加载系统. 通过千斤顶对轨枕进行加载，而反力架钢板作为反力点，铁垫板和轨下胶垫均匀地将荷载均匀传递到轨枕表面.
如图6所示，使用DH5983便携式动态信号分析仪采集枕上压力数据，使用光纤光栅解调仪采集埋入轨枕的FRP-OF应变传感器的波长变化，采样频率均为3 Hz. 进行预加载，使结构进入正常的工作状态，使反力架和轨枕之间贴合紧密，预加载为10 kN. 加载过程中观察光纤光栅应变计波长变化情况以及卸载后波长是否恢复到加载前的状态，并且观察放置于轨枕上方的压电传感器数值是否稳定，准备工作完成后开始正式加载.
在正式加载中使用千斤顶将载荷缓慢增加到20 kN，待其稳定约30 s后卸载至0，每个轨枕块经过3次加载-卸载循环. 高速列车轴重一般为150 kN，轮载为75 kN，根据文献[24]轮对正下方轨枕的轮载分配率约为33%，枕上压力约为24.75 kN. 混凝土单轴受压时的本构模型在前1000 με的应力-应变曲线为线性[25]，故轨枕在服役过程中实际受力超过20 kN时的应力应变也为线性变化的.
2.2 试验结果
通过千斤顶对轨枕施加荷载，如图7（a）所示，轨枕内的FRP-OF应变传感器对枕上压力具有良好的感知性能，所测得的应变与载荷同步变化. 当载荷增加到20 kN时，轨枕在3个加载周期的应变分别达到了3.8、3.5 με和3.7 με，由于载荷迅速减小到0，轨枕内应变传感器的应变也急剧减小到0. 图7（b）为3次加载试验枕内应变-枕上压力的曲线，3次加载周期的曲线重合程度较高，线性度良好. 图7（c）为第1次加载时1#～8# 号轨枕块的枕内应变-枕上压力曲线，不同轨枕块之间的线性变化趋势一致，但斜率略有不同. 如图7（d）所示，为了得到枕上压力和枕内应变的线性关系斜率，对采样点进行线性拟合，得到线性回归曲线方程，如式（4）所示. 线性回归曲线的损失函数J（K, b）如式（5）所示（K为斜率，b为标定截距），用损失函数来衡量回归模型的误差，这个损失函数的值越小，直线能更好地拟合实际数据. 因此，对J（K, b）的K求导，使其导数为0即可得到K的最优解. 线性回归曲线的斜率K可由式（6）计算. 1#～8# 号轨枕块在反力架加载时的枕内应变-枕上压力斜率约为4.90～5.28，如表2所示.
基于反力架的静载试验初步表明，植入FRP-OF应变传感器在轨枕中具有良好的传感性能，并初步得到每块轨枕的标定曲线及标定系数，通过标定系数($\bar K $)，为斜率的平均值和截距可以得到轨枕枕上压力的计算如式（7）.
Fi=Kεi+b， (4) J(K,b) = n∑i=1(Fi−(Kεi+b))2， (5) b=ˉF−Kˉε， (6) K = n∑i=1Fi(εi−ˉε)n∑i=1ε2i−1n(n∑i=1εi)2， (7) F=ˉKε11+b， (8) 式中：F为枕上压力；ε11为标定试验枕内传感器测试应变；n为采样点数量；Fi为枕上压力的第i个数据样本点；ɛi为枕内应变的第i个数据样本点；$ \bar{F} $为所有样本的平均枕上压力；$ \bar{\mathrm{\varepsilon }} $为所有样本的平均枕内应变.
表 2 标定试验的荷载值为20 kN时的数据Table 2. Data obtained at load of 20 kN in calibration test轨枕块
编号枕内应变
平均值/με枕内应变-枕
上压力斜率
平均值/
（kN·με−1）枕内应变-枕
上压力截距
平均值/kN1# 3.7 5.03 0.61 2# 3.6 4.98 1.11 3# 3.9 4.90 0.73 4# 3.9 4.93 0.76 5# 3.9 4.78 0.50 6# 3.7 5.10 0.69 7# 3.6 5.28 0.10 8# 3.7 5.21 1.14 3. 自感知性能测试试验仿真分析
通过标定试验初步验证了枕内应变-枕上压力具有良好的线性关系. 为进一步验证试验数据的正确性，通过有限元仿真模拟双块式轨枕在实际工况受力时的枕内应变，并对标定试验的枕上压力计算公式进行修正.
3.1 模型建立
如图8所示，采用有限元软件建立双块式轨枕、道床板的有限元模型，在轨枕的内部预留一个和光纤光栅传感器尺寸相当的孔，随后将传感器装配进预留的孔里与轨枕块进行约束.
轨枕、道床板和传感器的模型材料参数如表3所示.
表 3 有限元模型材料参数Table 3. Material parameters of finite element model部件 材料 弹性
模量/GPa泊松比 密度/
(kg·m−3)轨枕块 C60 混凝土 36.5 0.20 2640 道床板 C40 混凝土 32.5 0.24 2440 传感器 FRP 72.0 0.20 反力架静力加载标定试验的边界条件如图9（a）所示，将轨枕底部的反力架约束区域进行完全固定，并且对其轨枕表面施加分布荷载；轨枕在道床板中实际的边界条件如图9（b）所示，将轨枕与道床板进行绑定约束，并且将道床板固定在底座板上，对轨枕块表面施加均布荷载.
3.2 仿真计算分析
如图10所示，标定试验中1# 轨枕块的实际测量枕内应变-枕上压力线性拟合斜率为5.03，仿真模拟的斜率为4.99，误差为0.80%，且1#～8# 轨枕块与仿真数据的误差均在5.00%以内. 仿真数据和实测数据基本一致，由此说明模型建立正确并且现场试验所得数据可靠.
图 10 反力架标定试验数据与仿真数据对比Figure 10. Comparison of reaction frame calibration test data and simulation data图11为轨枕在不同工况下施加20 kN枕上压力时的应变云图，其中，图11（a）为反力架加载工况下内部传感器埋入点应变大小约为3.77 με；图11（b）为轨枕在道床板实际工况下，内部传感器埋入点的应变大小约为3.40 με.
由于利用反力架进行标定时的边界条件与轨枕在道床板中的实际边界条件不同，通过有限元仿真模拟两种工况的传力区别，找到在两种工况下枕内应变的线性拟合曲线方程，如式（9）. 得到了两种工况下枕内应变的换算关系如图12所示.
图 12 反力架约束工况和实际工况枕内应变数值线性拟合Figure 12. Linear fitting of strain values under reaction frame constraint condition and actual condition根据式（9）对反力架约束工况的标定试验进行修正，修正后的枕上压力换算公式如式（10）所示.
ε11=αε22+β， (9) F=Kαε22 + Kβ+b， (10) 式中：ɛ22为实际工况下的轨枕应变；α为标定工况与实际工况的修正系数，取1.35；b取0.1；$\beta $为标定工况与实际工况线性拟合曲线截距.
4. 现场测试分析
将埋入FRP-OF应变传感器的轨枕安装在我国某设计速度为350 km/h的高速铁路运营线路上，设置光纤光栅解调仪的采集频率为1 000 Hz，使用低通滤波器过滤高频干扰信号后得到如图13（a）所示的应变曲线，该数据来源于图4中的1# 号轨枕块的传感器. 当8车厢编组的CRH380AJ列车以350 km/h速度通过，枕内应变约为4～6 με. 如图13（b）所示，根据式（9）的标定系数将枕内应变换算为枕上压力，幅值约为30～42 kN，根据文献[24]所使用的测力垫板进行枕上压力测试，幅值范围为32～38 kN，说明本文提出的枕上压力测试方法是可信的，证明了该监测标定方法的使用价值.
图 13 高速铁路运营线路现场测试数据时程Figure 13. Time history diagram of field test data from high-speed railway operating line5. 结 论
本文提出了一种利用埋入式应变传感器监测双块式轨枕枕上压力的新方法. 首次将FRP-OF应变传感器植入双块式轨枕中，进行了轨枕块反力架静力加载标定试验，通过有限元仿真计算进行验证，并修正了枕上压力计算公式，最后在现场试验证明了其可行性，具体得出了以下结论.
1） 提出了一种双块式轨枕枕上压力的监测新方法，并通过现场试验和理论计算验证了此方法的可行性. 为实现轨枕支点反力的长期监测、高速铁路轮轨荷载传递研究、无砟轨道结构的强度计算理论和方法完善、列车轮对状态监测提供了试验基础.
2） 通过将反力架安装在轨枕上进行静力加载试验，枕上压力和枕内应变之间的线性关系良好，其标定系数在4.90～5.28，说明了FRP-OF光纤光栅传感器植入轨枕内部具有较好的感知能力且重复性良好.
3） 通过仿真计算验证了反力架静力加载试验的测试数据误差在5.00%以内. 轨枕在道床板中实际工况的应变值略低于反力架加载工况，最后通过仿真模拟对反力架静载试验的标定试验进行修正，得出了枕上压力的计算方法.
4） 在350 km/h高速列车动载作用下测试到轨枕应变约为4～6 με，根据本文的标定方法计算出枕上压力幅值为30～42 kN，证明了该方法具有较高的使用价值.
-
图 1 杂散电流分布和扩散的车-地-网耦合模型
Figure 1. Metro-earth-grid coupling model of stray current distribution and diffusion
图 4 直流偏磁电流模拟试验示意（单位：cm）
Figure 4. Schematic diagram of DC bias current simulation test (unit: cm)
图 7 变电站和地铁线路之间的位置关系
Figure 7. Location relationship between substation and subway line
图 10 钢轨对地过渡电阻和直流偏磁电流的关系
Figure 10. Relationship between rail-to-earth transition resistance and DC bias current
图 11 车辆段CD连接方式和直流偏磁电流的关系
Figure 11. Relationship between the connection mode of car depot CD and DC bias current
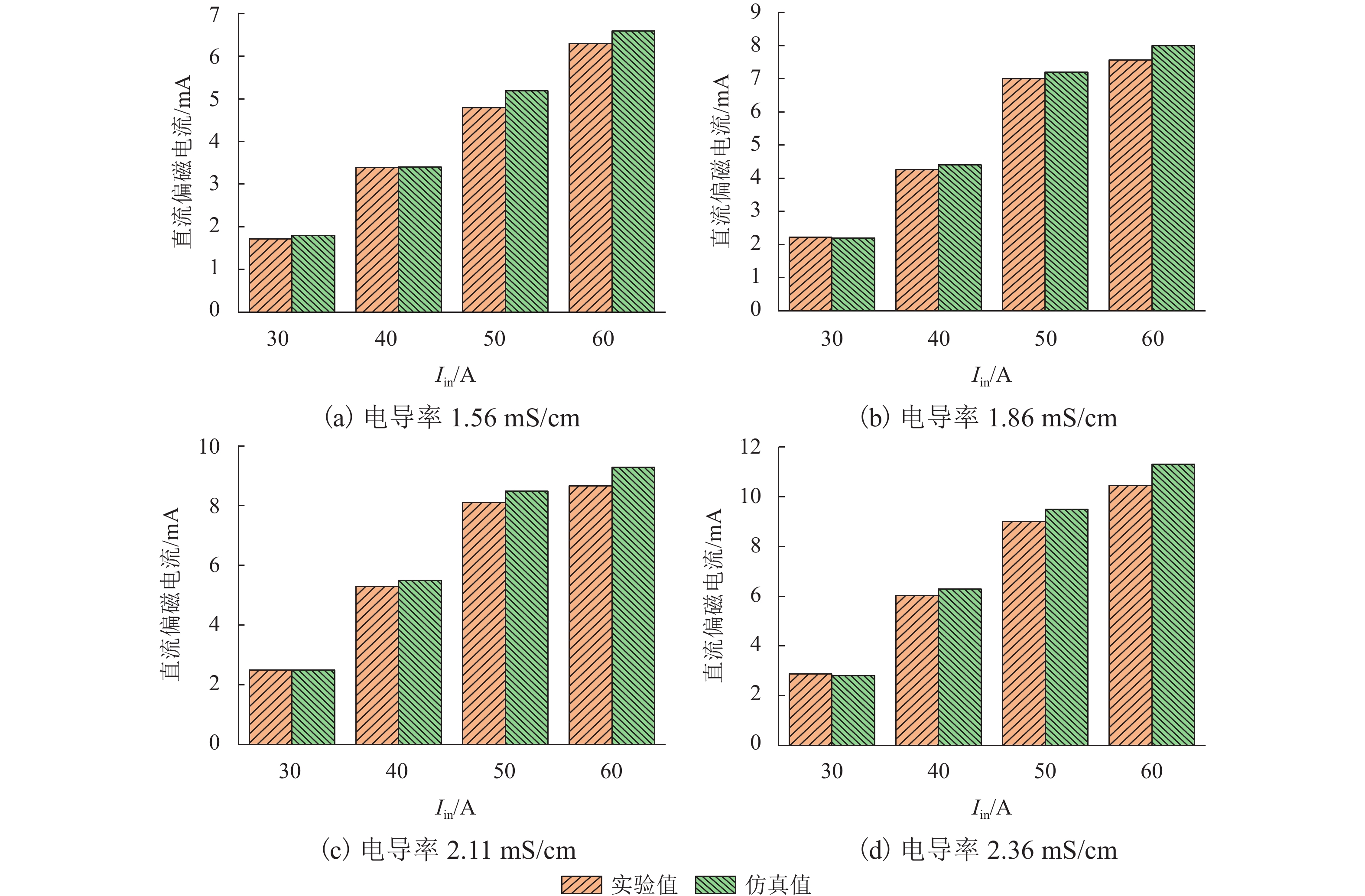
表 1 直流偏磁电流模拟试验主要参数
Table 1. Main parameters of DC bias current simulation test
参数 数值 铜网深度/mm 10 石墨棒深度/mm 10 接地模块线路电阻/Ω 0.018 盐溶液电导率/（mS·cm−1） 1.56，1.86，2.11，2.36 石墨棒载流/A 30，40，50，60 
下载: 导出CSV
表 2 变电所的位置坐标
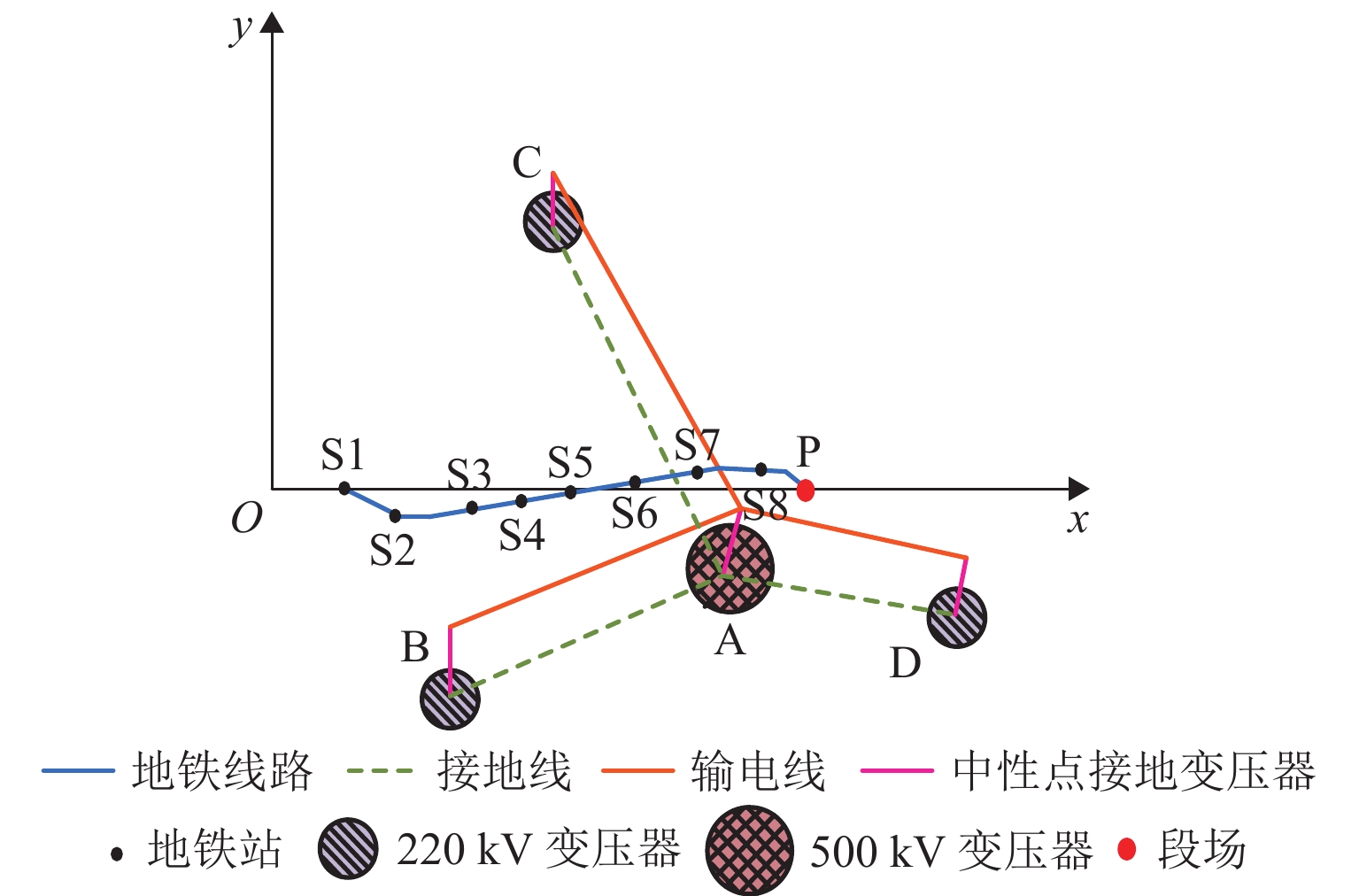
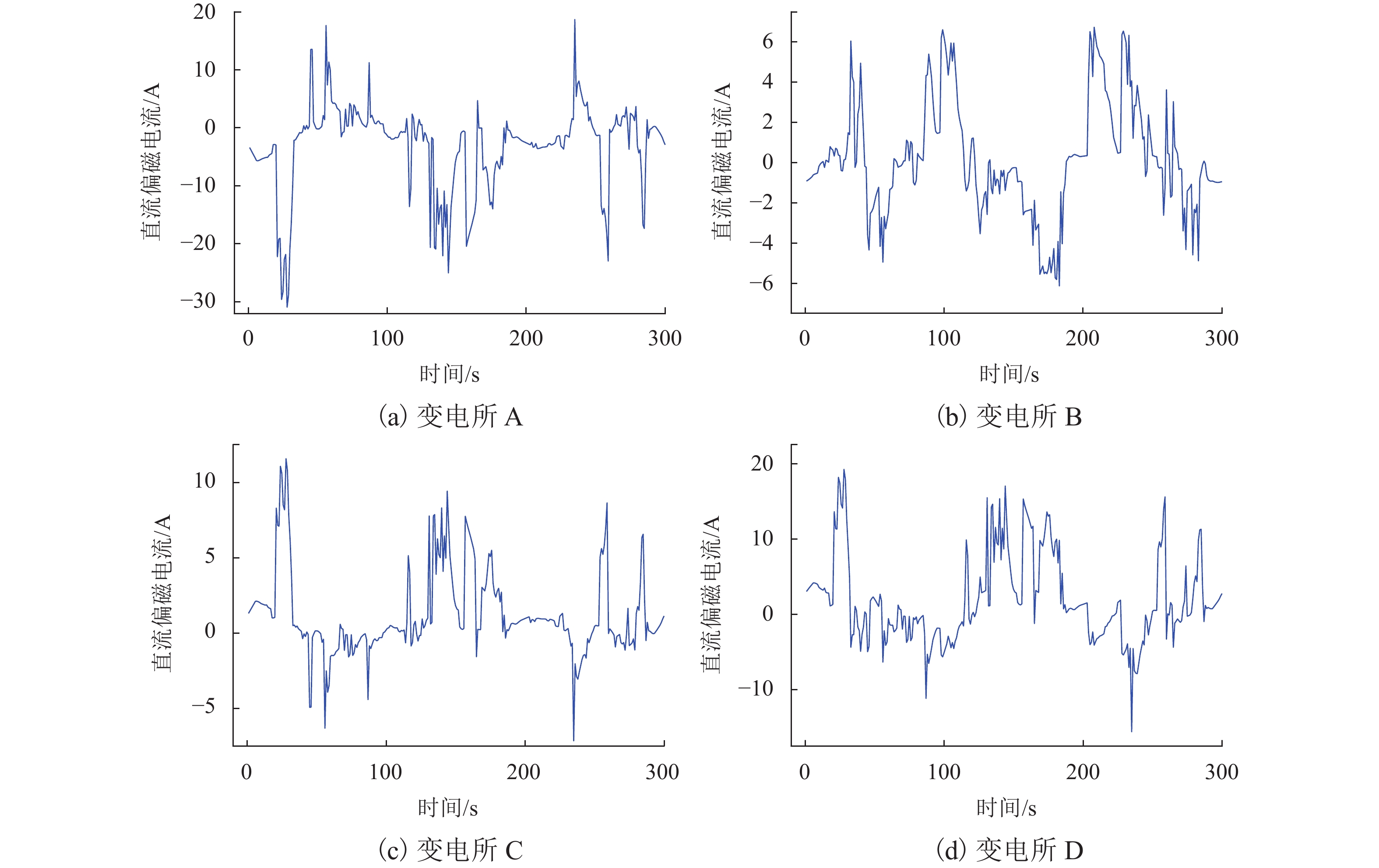
Table 2. Location coordinates of substations
变电所 A B C D 坐标 （10，−2） （4，−5） （6，7） （15，−4）
下载: 导出CSV
表 3 模型的主要参数
Table 3. Main parameters of the model
模型 参数 数值 直流地铁线路 一行钢轨电阻/（Ω·km−1） 0.018 SCCN 电阻/（Ω·km−1） 0.066 SCCN 埋地深度/m 0.6 钢轨对地过渡电阻/（Ω·km） 5.5 钢轨电位限制器接地电阻/Ω 0.04 发车间隔/s 300 停站时间/s 30 交流电网系统 接地网接地电阻/Ω 2 接地网埋地深度/m 0.8 避雷线/（Ω·km−1） 0.5 500 kV 变压器阻抗/Ω 1 220 kV 变压器阻抗/Ω 2 500 kV 变压器额定容量/（MV·A） 750 220 kV 变压器额定容量/（MV·A） 240 500 kV 变压器直流偏磁电流允许值/A 18.2 220 kV 变压器直流偏磁电流允许值/A 13.2 输电线路阻抗/（Ω·km−1） 0.01 土壤模型 混凝土/（Ω·m） 180 土壤/（Ω·m） 100 混凝土厚度/m 1
下载: 导出CSV
表 4 直流偏磁电流峰值的仿真值与计算值对比
Table 4. Comparison of simulation data and calculation data of peak DC bias current
时间/s 变电所 计算数据/A 仿真数据/A 误差/% 28 A 30.94 31.30 1.16 B 0.14 0.15 7.14 C 11.57 10.94 5.45 D 19.23 18.37 4.47 144 A 25.04 23.95 4.35 B 1.39 1.27 8.63 C 9.42 8.84 6.16 D 17.02 16.22 4.70 158 A 19.36 20.44 5.58 B 2.44 2.21 9.43 C 7.34 7.16 2.45 D 14.47 15.25 5.39 235 A 18.67 17.69 5.25 B 4.07 3.81 6.39 C 7.15 7.26 1.54 D 15.60 15.27 2.12 259 A 22.99 22.63 1.57 B 1.23 1.12 8.94 C 8.64 8.03 7.06 D 15.59 16.56 5.86
下载: 导出CSV
表 5 不同发车间隔下直流偏磁电流的特征值
Table 5. Characteristic values of DC bias current at different departure intervals
A 发车间隔/s 变电所 绝对平均值 最大绝对值 120 A 9.30 33.84 B 3.69 7.42 C 3.50 12.65 D 7.78 21.78 180 A 7.16 27.64 B 2.24 7.33 C 2.68 10.47 D 5.85 19.99 240 A 5.81 26.28 B 2.28 7.83 C 2.07 9.87 D 3.48 16.07 300 A 5.16 30.94 B 2.02 6.05 C 1.91 11.57 D 4.31 19.23
下载: 导出CSV
表 6 不同治理方式下直流偏磁电流的特征值
Table 6. Characteristic values of DC bias current under different management modes
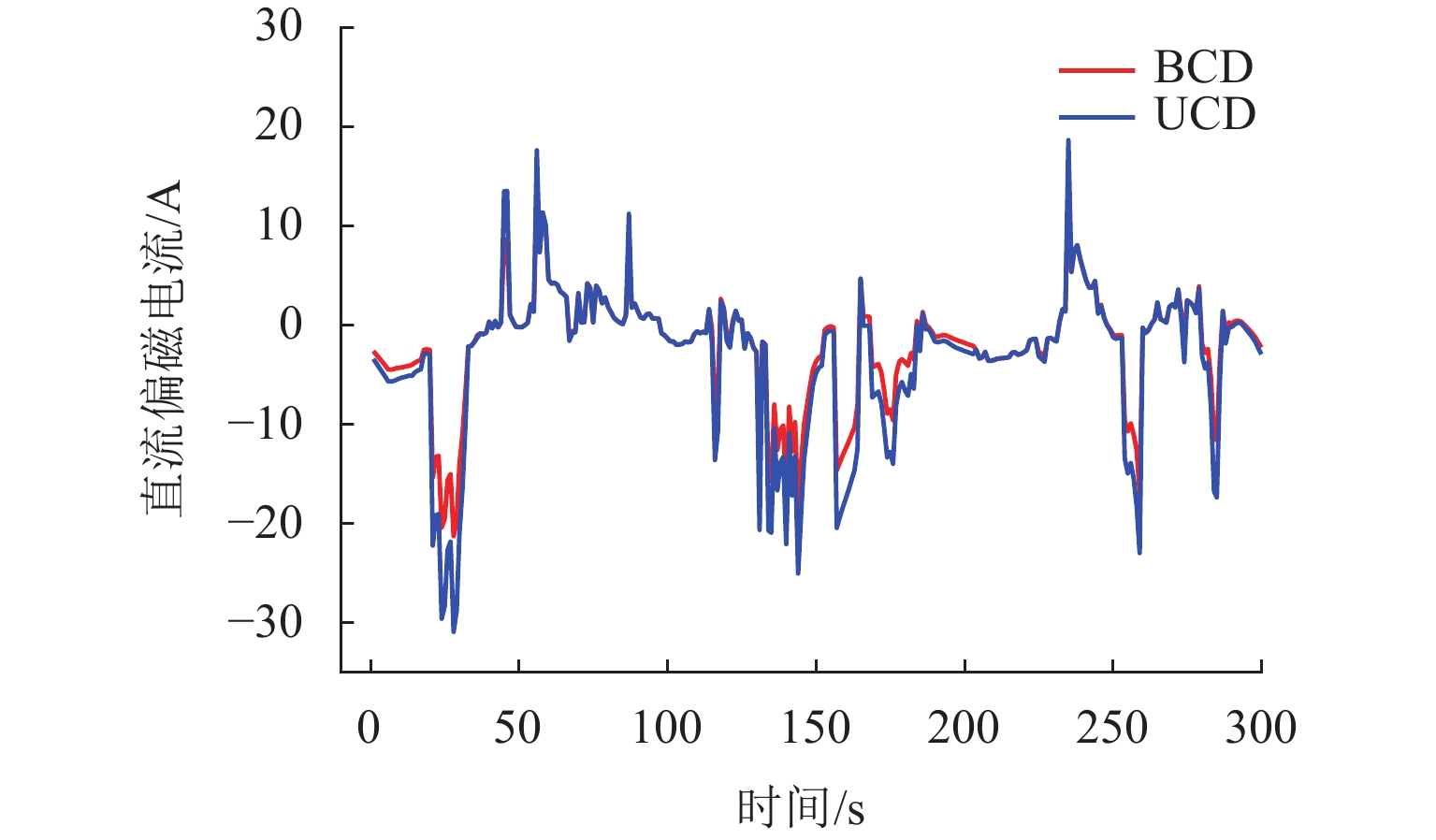
A 治理方式 变电所 绝对平均值 最大绝对值 隔直电容 A 0 0 B 5.67 31.09 C 7.07 42.52 D 8.86 50.19 限流电阻 A 4.82 18.31 B 1.58 3.19 C 1.35 6.49 D 4.03 11.28
下载: 导出CSV
表 7 BCD和UCD的直流偏磁电流特征值
Table 7. Characteristic values of DC bias current in BCD and UCD
A CD 连接方式 变电所 绝对平均值 最大绝对值 BCD A 3.95 21.28 B 1.97 7.21 C 1.45 7.93 D 3.98 16.72 UCD A 5.16 30.94 B 2.02 6.74 C 1.91 11.57 D 4.31 19.23
下载: 导出CSV
-
[1] 施仲衡,丁树奎. 城市轨道交通绿色低碳发展策略[J]. 都市快轨交通,2022,35(1): 1-4,11. doi: 10.3969/j.issn.1672-6073.2020.01.001SHI Zhongheng, DING Shukui. Strategies for green and low-carbon development of urban rail transit[J]. Urban Rapid Rail Transit, 2022, 35(1): 1-4,11. doi: 10.3969/j.issn.1672-6073.2020.01.001 [2] 解绍锋,李卫兰,黄大锐,等. 市域铁路对埋地管道感性耦合干扰建模及仿真[J]. 西南交通大学学报,2024,59(6):1256-1266.XIE Shaofeng, LI Weilan, HUANG Darui, et al. Modelling and simulation of inductive coupled interference from suburban railways to buried pipelines[J]. Journal of Southwest Jiaotong University, 2024, 59(6):1256-1266. [3] 全江涛,谢志成,陈科基,等. 特/超高压直流输电系统单极运行下变压器中性点直流电流分布规律仿真分析[J]. 高电压技术,2015,41(3): 787-793.QUAN Jiangtao, XIE Zhicheng, CHEN Keji, et al. Mechanism analysis and simulation of DC current distribution along transformer neutral point under the condition of UHVDC/HVDC single-pole operation[J]. High Voltage Engineering, 2015, 41(3): 787-793. [4] 张冰,刘连光,肖湘宁. 地磁感应电流对变压器振动、噪声的影响[J]. 高电压技术,2009,35(4): 900-904.ZHANG Bing, LIU Lianguang, XIAO Xiangning. Effects of geomagnetically induced current on the vibration and noise of transformers[J]. High Voltage Engineering, 2009, 35(4): 900-904. [5] 李晓华,褚福源,时胜寒. 轨道交通对沿线220 kV变电站中性点电流及振动影响[J]. 电工技术学报,2021,36(增2): 423-429,437.LI Xiaohua, CHU Fuyuan, SHI Shenghan. Influence of rail transit on neutral current and vibration of 220 kV substation along the line[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 423-429,437. [6] 黄华,陈璐,吴天逸,等. 城市轨道交通动态运行对交流电网变压器偏磁直流的影响[J]. 电网技术,2022,46(11): 4524-4533.HUANG Hua, CHEN Lu , WU Tianyi, et al. Influence of dynamic operation of urban rail transit on DC magnetic bias of AC power grid transformer[J]. Power System Technology, 2022, 46(11): 4524-4533. [7] WANG A M, LIN S, HU Z H, et al. Evaluation model of DC current distribution in AC power systems caused by stray current of DC metro systems[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 114-123. doi: 10.1109/TPWRD.2020.2975367 [8] CHENG X X, NI Y R, YU K, et al. Analysis on harmonic characteristic of transformer DC bias caused by metro stray current[J]. Journal of Physics: Conference Series, 2022, 2196(1): 012014.1-012014.10. [9] 倪砚茹,曾祥君,喻锟,等. 地铁杂散电流引起动态地电位分布建模及影响因素分析[J]. 中国电机工程学报,2023,43(23): 9059-9072.NI Yanru, ZENG Xiangjun, YU Kun, et al. Modeling and influencing factors analysis of dynamic potential distribution caused by metro stray current[J]. Proceedings of the CSEE, 2023, 43(23): 9059-9072. [10] 孙结中,刘力. 运用等值复数镜像法求解复合分层土壤结构的格林函数[J]. 中国电机工程学报,2003,23(9): 146-151. doi: 10.3321/j.issn:0258-8013.2003.09.030SUN Jiezhong, LIU Li. Derivation of green’s function by equivalent complex image method in a horizontal and vertical combined-layer soil structure[J]. Proceeding of the CSEE, 2003, 23(9): 146-151. doi: 10.3321/j.issn:0258-8013.2003.09.030 [11] 李中新,袁建生,张丽萍. 变电站接地网模拟计算[J]. 中国电机工程学报,1999,19(5): 76-79. doi: 10.3321/j.issn:0258-8013.1999.05.018LI Zhongxin, YUAN Jiansheng, ZHANG Liping. Numerical calculation of substation grounding systems[J]. Proceedings of the CSEE, 1999, 19(5): 76-79. doi: 10.3321/j.issn:0258-8013.1999.05.018 [12] 郭剑,邹军,何金良,等. 水平分层土壤中点电流源格林函数的递推算法[J]. 中国电机工程学报,2004,24(7): 101-105. doi: 10.3321/j.issn:0258-8013.2004.07.019GUO Jian, ZOU Jun, HE Jinliang, et al. Recursive method to obtain analytic expressions of Green’s functions in multi-layer soil by computer[J]. Proceedings of the CSEE, 2004, 24(7): 101-105. doi: 10.3321/j.issn:0258-8013.2004.07.019 [13] 史云涛,赵丽平,林圣,等. 城市电网中地铁杂散电流分布规律及影响因素分析[J]. 电网技术,2021,45(5): 1951-1957.SHI Yuntao, ZHAO Liping, LIN Sheng, et al. Analysis of distribution of metro stray current in urban power grid and its influencing factors[J]. Power System Technology, 2021, 45(5): 1951-1957. [14] 刘炜,杨龙,李国玉,等. 计及回流系统设备行为过程的钢轨电位动态仿真[J]. 电工技术学报,2022,37(4): 1000-1009.LIU Wei, YANG Long, LI Guoyu, et al. Dynamic simulation of rail potential considering the equipment behavior process of recirculation system[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1000-1009. [15] 国家能源局. 高压直流接地极技术导则:DL/T 437—2012[S]. 北京:中国电力出版社,2012. [16] Sahil Bhagat,杨晓峰,王淼,等. 城市轨道交通杂散电流治理的综述与评估[J]. 电工技术学报,2021,36(23): 4851-4863.SAHIL Bhagat, YANG Xiaofeng, WANG Miao, et al. Review and evaluation of stray current mitigation for urban rail transit[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4851-4863. [17] 何金良,曾嵘. 电力系统接地技术[M]. 北京:科学出版社,2007:359. [18] 刘炜,尹乙臣,潘卫国,等. 直流动态杂散电流在分层介质中的扩散模型[J]. 电工技术学报,2021,36(23): 4864-4873.LIU Wei, YIN Yichen, PAN Weiguo, et al. Diffusion model of DC dynamic stray current in layered soil[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4864-4873. [19] 许军,蓝磊,文习山,等. 三峡电站模型地网接地电阻小比例模型试验研究[J]. 电网技术,2003,27(1): 38-40.XU Jun, LAN Lei, WEN Xishan, et al. Small-scale model test for grounding resistance of grounding mesh model for Three Gorges hydroelectric power station[J]. Power System Technology, 2003, 27(1): 38-40. [20] 刘炜,刘童童,王辉,等. 运行图驱动的城轨供电系统负荷过程动态仿真[J]. 西南交通大学学报,2022,57(5): 967-975.LIU Wei, LIU Tongtong, WANG Hui, et al. Dynamic simulation of load process for urban rail power supply system driven by operation diagram[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 967-975. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 262
- HTML全文浏览量: 102
- PDF下载量: 60
- 被引次数: 0