Identification of Wheel-Rail Vertical Forces of Rail Vehicles Based on Square Root Cubature Kalman Filter Algorithm
-
摘要:
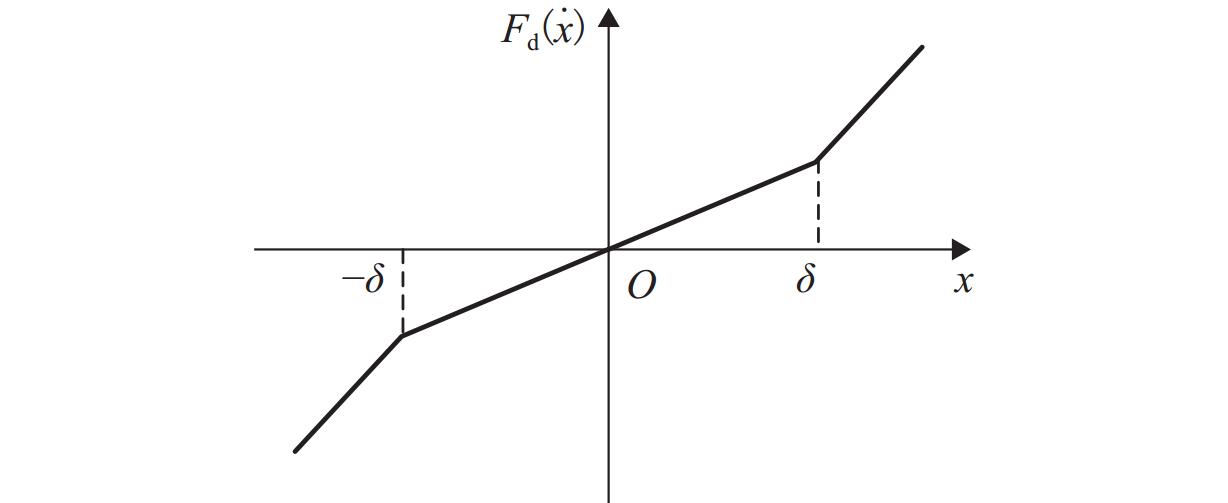
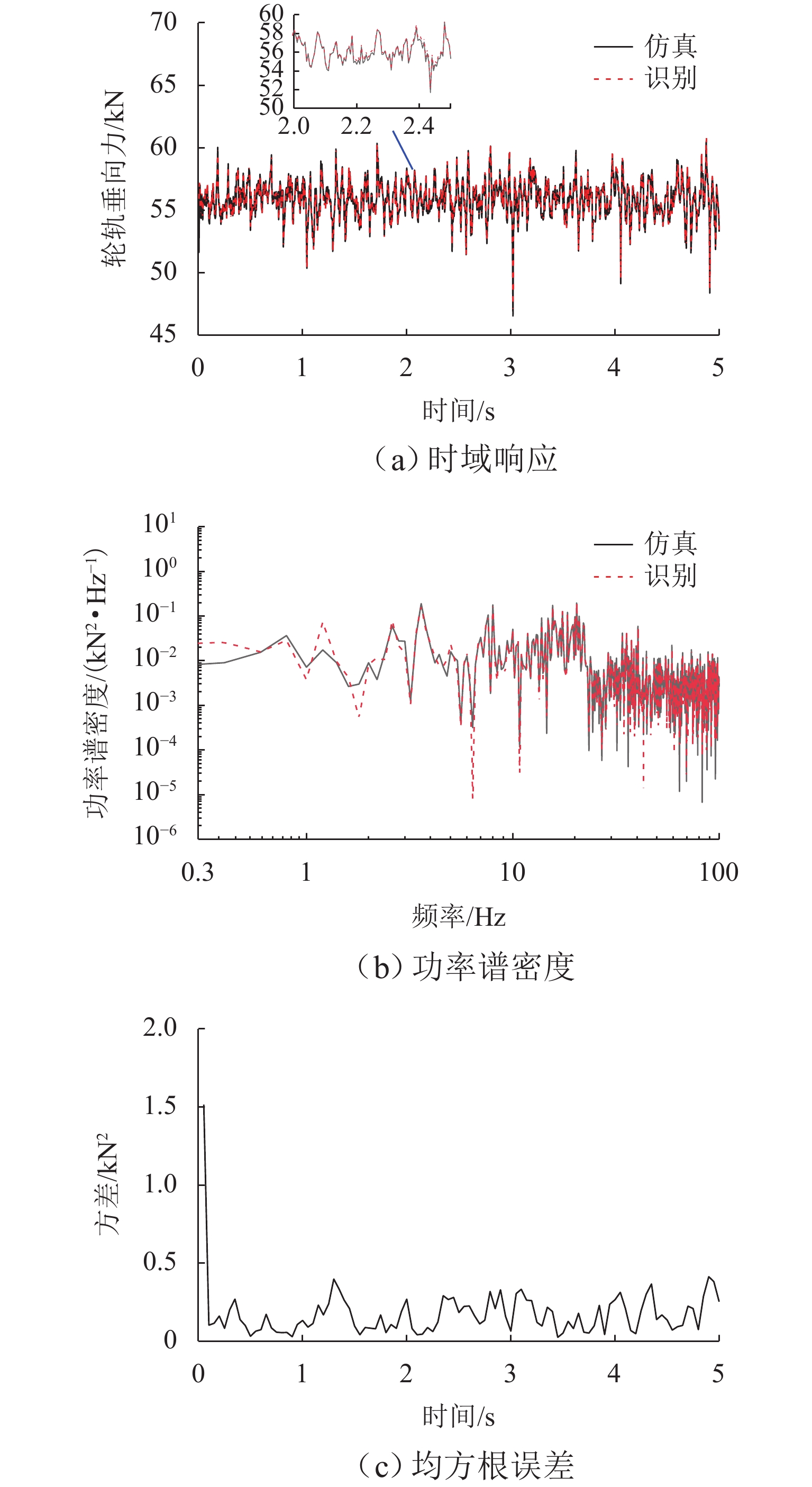
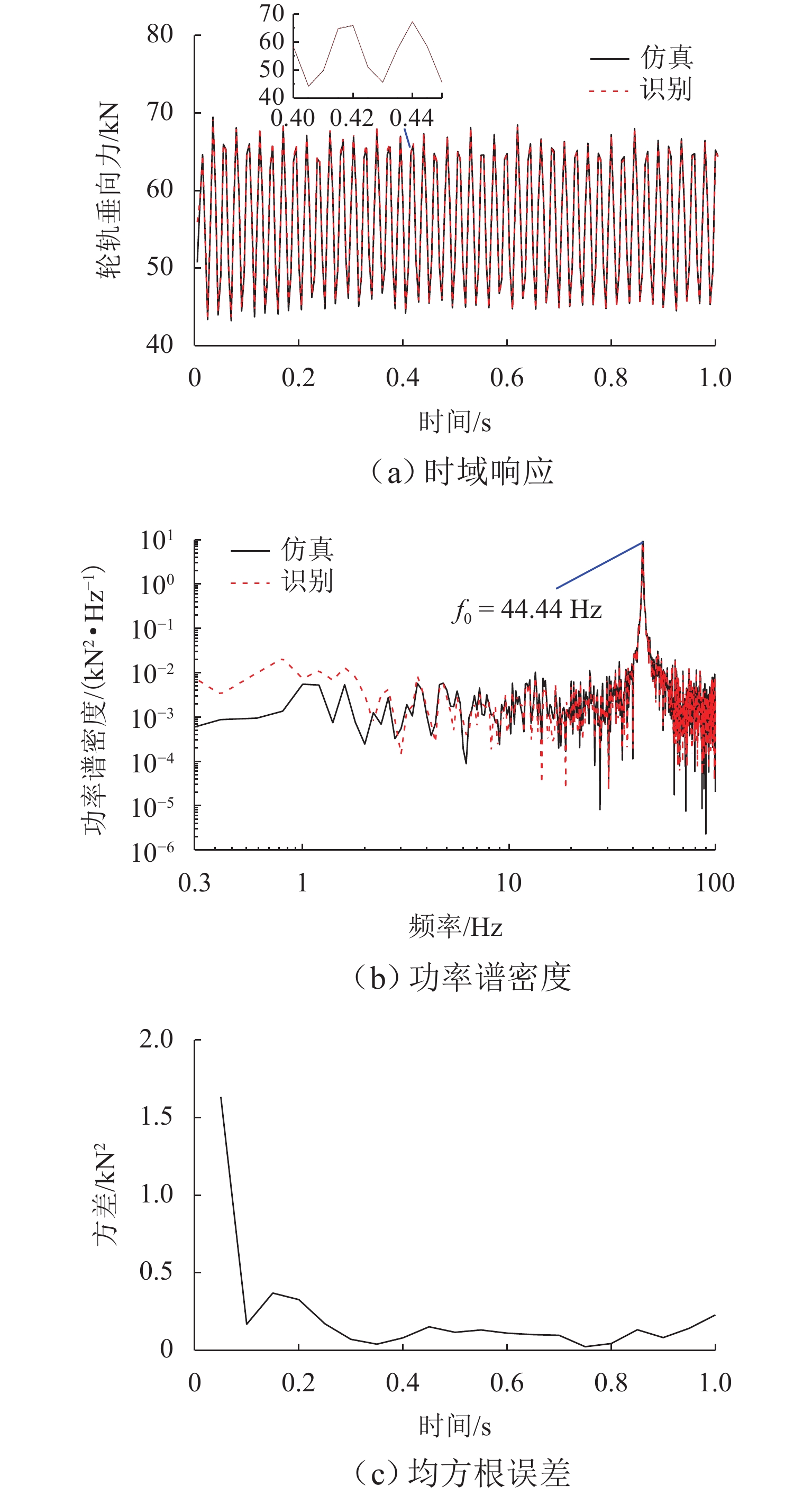
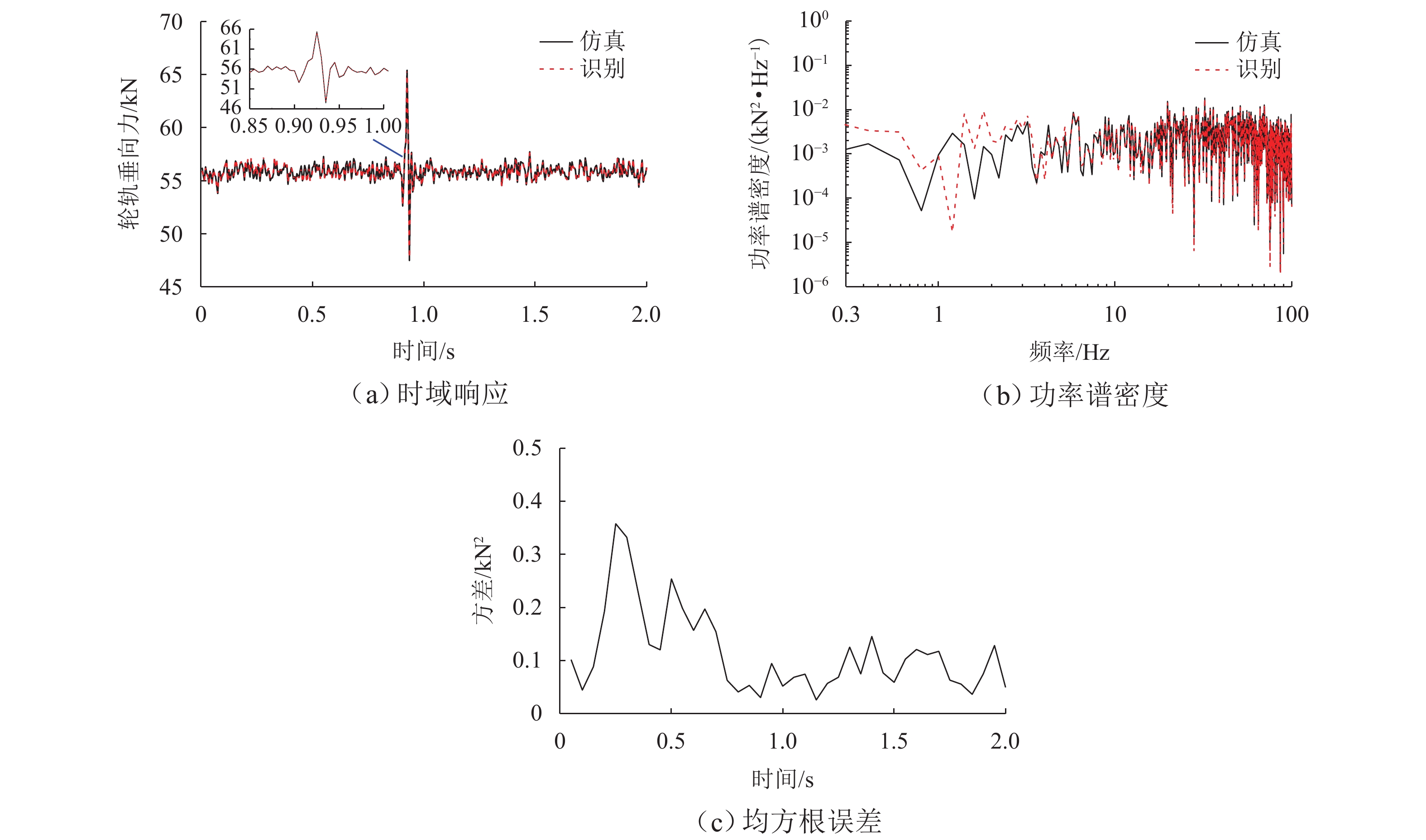
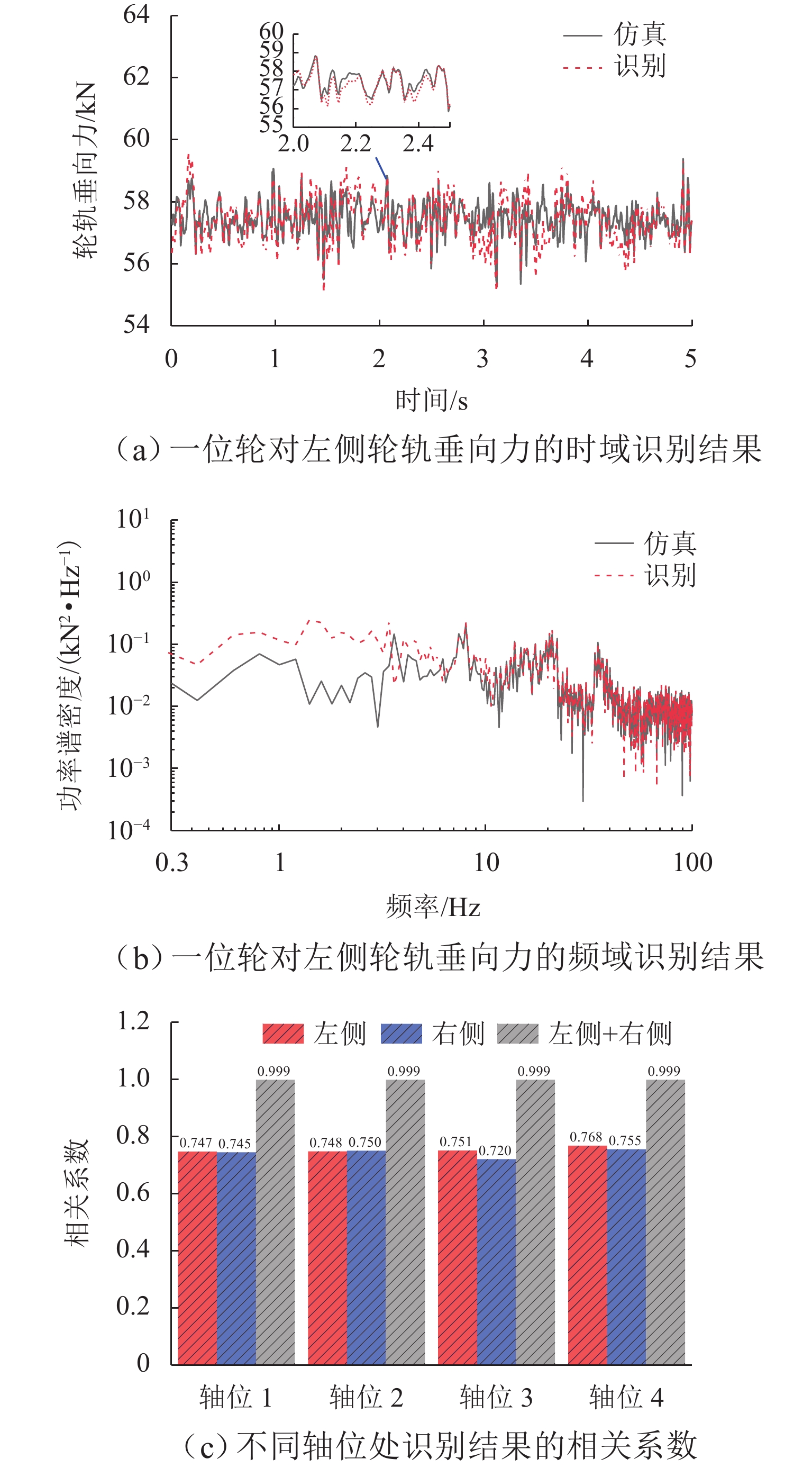
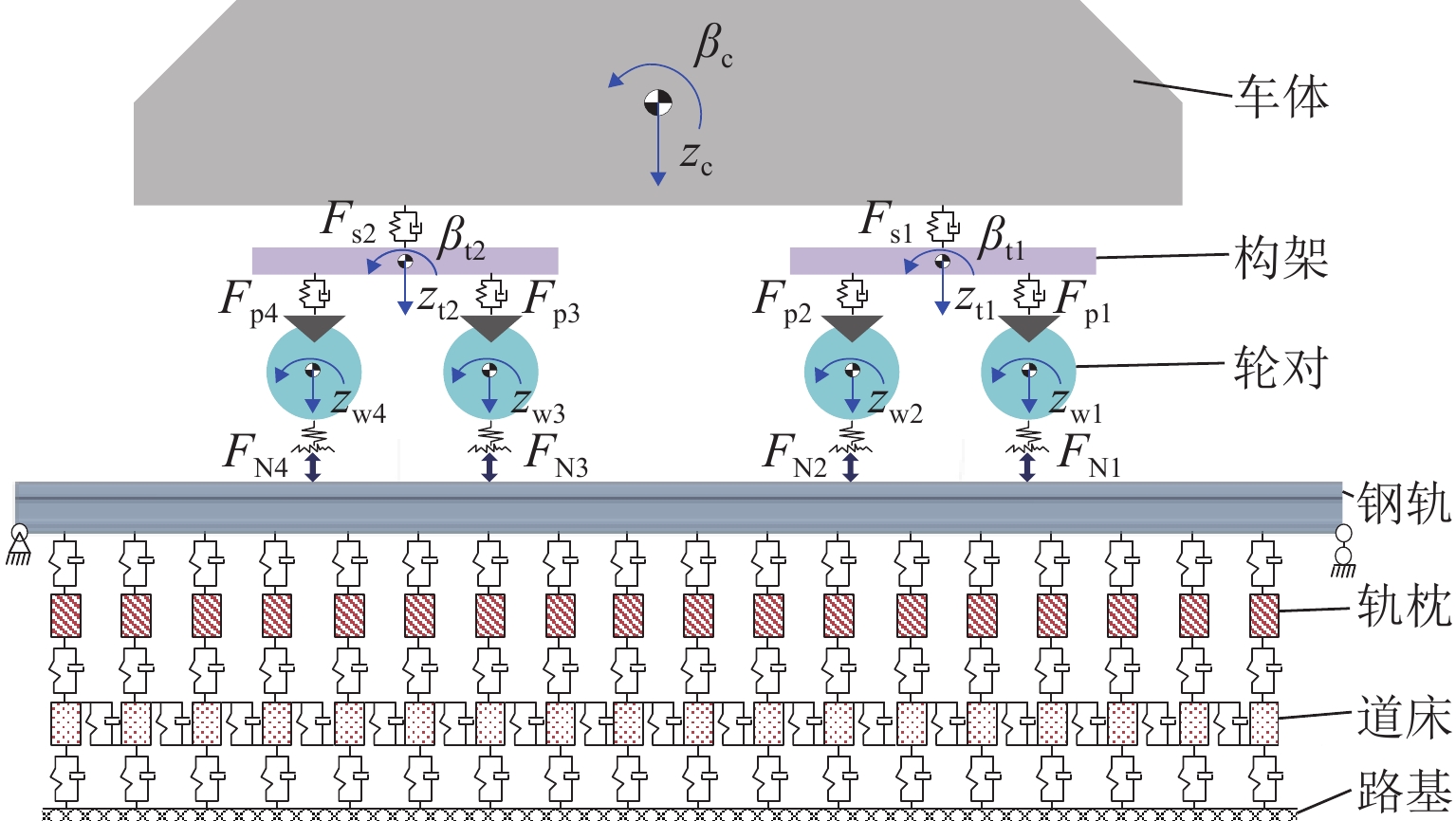
轮轨作用力是评估轨道车辆运行品质的关键指标,为实现对轨道车辆轮轨垂向力的在线监测,提出一种基于平方根容积卡尔曼滤波(SRCKF)算法的识别方法. 以考虑悬挂元件非线性的车辆-轨道垂向耦合动力学模型为例,建立包含轮轨垂向力和车辆部件状态变量的非线性过程函数,将车体、构架和轮对垂向加速度作为观测量,基于SRCKF算法递推识别轮轨垂向力;在此基础上,建立整车动力学模型及其对应的17自由度轮轨垂向力估计模型,对车辆在实际不平顺激扰下的左右侧轮轨垂向力进行识别. 仿真结果表明:所提方法识别垂向车辆模型在随机不平顺、钢轨波磨不平顺和钢轨焊缝不平顺作用下的轮轨垂向力时,轮轨垂向力识别值在时域和频域同仿真值均有较高的吻合度,相关系数分别为0.988、0.999和0.969;在识别整车模型的轮轨垂向力时,左、右侧轮轨垂向力的相关系数最低分别为0.747和0.720,左、右侧轮轨垂向力之和的相关系数为0.999.
Abstract:The wheel-rail interaction force is the key index to evaluate the operation quality of rail vehicles. An identification method based on the square root cubature Kalman filter (SRCKF) algorithm was proposed for online monitoring of the wheel-rail vertical force of rail vehicles. By taking the vehicle-track vertical coupled dynamics model considering the nonlinearity of suspension elements as an example, a nonlinear process function of wheel-rail vertical forces and state variables of vehicle components was established. The vertical accelerations of the vehicle body, frame, and wheelset were adopted as observations, and the SRCKF algorithm was employed for the recursive estimation of wheel-rail vertical forces. Furthermore, a vehicle dynamics model and its corresponding wheel-rail vertical force estimation model of 17 degrees of freedom were established to identify the vehicle’s left and right wheel-rail vertical forces under actual irregularity excitation. Simulation results indicate that the proposed method can precisely identify wheel-rail vertical forces of vehicles excited by the random irregularity, rail corrugation irregularity, and rail weld irregularity, with the identified value of wheel-rail vertical forces is in good agreement with the simulation value in both time domain and frequency domain. The correlation coefficients are 0.988, 0.999, and 0.969, respectively. When the proposed method is used to identify the vehicle’s wheel-rail vertical force, the lowest correlation coefficients of the left and right wheel-rail vertical forces are 0.747 and 0.720, respectively, and the correlation coefficient of the sum of the left and right wheel-rail vertical forces is 0.999.
-
-
[1] 刘永锋,赵旭峰,栗杨等. 轮轨界面低黏着对大功率电力机车车轮滚动接触疲劳的影响[J]. 铁道学报,2022,44(12): 22-29.LIU Yongfeng, ZHAO Xufeng, LI Yang, et al. Effect of adhesion between wheel and rail on wheel rolling contact fatigue of high-power AC locomotives[J]. Journal of the China Railway Society, 2022, 44(12): 22-29. [2] 杨飞,吴细水,孙宪夫,等. 钢轨轧制不平顺激扰下的动车组动力响应特性[J]. 西南交通大学学报,2022,57(2): 267-276,294.YANG Fei, WU Xishui, SUN Xianfu, et al. Dynamic response characteristics of EMU under excitation of rail straightening irregularity[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 267-276,294. [3] 施以旋,戴焕云,毛庆洲等. 基于车轨耦合的地铁车轮多边形形成机理研究[J]. 西南交通大学学报,2024,59(6): 1357-1367,1388.SHI Yixuan, DAI Huanyun, MAO Qingzhou, et al. Study on formation mechanism of metro wheel polygonal based on vehicle-track coupling[J]. Journal of Southwest Jiaotong University, 2024,59(6): 1357-1367,1388. [4] XIA F J, COLE C, WOLFS P. Grey box-based inverse wagon model to predict wheel-rail contact forces from measured wagon body responses[J]. Vehicle System Dynamics, 2008, 46(S1): 469-479. [5] WEI L, ZENG J, WU P B, et al. Indirect method for wheel–rail force measurement and derailment evaluation[J]. Vehicle System Dynamics, 2014, 52(12): 1622-1641. doi: 10.1080/00423114.2014.953180 [6] ZHU T, WANG X R, FAN Y W, et al. A time domain method for wheel-rail force identification of rail vehicles[J]. Vehicle System Dynamics, 2022, 60(3): 790-809. doi: 10.1080/00423114.2020.1838562 [7] SUN Y Q, COLE C, SPIRYAGIN M. Monitoring vertical wheel-rail contact forces based on freight wagon inverse modelling[J]. Advances in Mechanical Engineering, 2015, 7(5): 1-11. [8] 王明猛,朱涛,王小瑞,等. 一种逆结构滤波法的轨道车辆轮轨力识别[J]. 振动工程学报,2019,32(4): 602-608.WANG Mingmeng, ZHU Tao, WANG Xiaorui, et al. An inverse structural filter method for wheel-rail contact forces identification of railway vehicles[J]. Journal of Vibration Engineering, 2019, 32(4): 602-608. [9] WARD C P, GOODALL R M, DIXON R, et al. Adhesion estimation at the wheel–rail interface using advanced model-based filtering[J]. Vehicle System Dynamics, 2012, 50(12): 1797-1816. doi: 10.1080/00423114.2012.707782 [10] 苏义鑫,赵俊,张华军. 带有UKBF的船舶动力定位预测控制器设计[J]. 西南交通大学学报,2018,53(3): 589-595.SU Yixin, ZHAO Jun, ZHANG Huajun. Predictive controller with UKBF for marine dynamic positioning system[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 589-595. [11] 宋义彤,舒红宇,陈仙宝等. 分布式驱动电动汽车双无迹卡尔曼滤波状态参数联合观测[J]. 机械工程学报,2019,55(22): 93-102. doi: 10.3901/JME.2019.22.093SONG Yitong, SHU Hongyu, CHEN Xianbao, et al. State and parameters estimation for distributed drive electric vehicle based on unscented Kalman filter[J]. Jouranl of Mechanical Engineering, 2019, 55(22): 93-102. doi: 10.3901/JME.2019.22.093 [12] 肖业方,郭蕴华,高海波,等. 基于多传感器鲁棒容积卡尔曼融合的半潜式起重平台立柱快速压载舱液位估计[J]. 船舶力学,2023,27(1): 70-80.XIAO Yefang, GUO Yun Hua, GAO Haibo, et al. Level estimation of column side ballast tank of semi-submersible crane vessel based on multi-sensor robust cubature Kalman fusion[J]. Journal of Ship Mechanics, 2023, 27(1): 70-80. [13] 杜常清,吴中意,武冬梅等. 基于KF-EKF算法的动力电池SOC估计[J]. 武汉理工大学学报,2022,44(4): 84-92.DU Changqing, WU Zhongyi, WU Dongmei, et al. State of charge estimation of power battery based on KF-EKF algorithm[J]. Jouranl of Wuhan University of Technology, 2022, 44(4): 84-92. [14] 肖仁鑫,李斌,黄志强,等. 基于SRCKF的电动汽车锂离子电池荷电状态估计[J]. 电源技术,2021,45(11): 1443-1447.XIAO Renxin, LI Bin, HUANG Zhiqiang, et al. State of charge estimation of electric vehicle lithium ion battery based on SRCKF[J]. Chinese Journal of Power Sources, 2021, 45(11): 1443-1447. [15] 乔美英,高翼飞,李宛妮,等. 基于模糊鲁棒自适应CKF算法的MEMS-IMU姿态估计[J]. 中国惯性技术学报,2022,30(3): 296-303.QIAO Meiying, GAO Yifei, LI Wanni, et al. Attitude estimation of MEMS-IMU based on fuzzy robust adaptive CKF algorithm[J]. Journal of Chinese Inertial Technology, 2022, 30(3): 296-303. [16] 章司怡,陈熙源. 运动约束辅助的基于SVD-CKF的组合导航方法[J]. 电子测量与仪器学报,2022,36(4): 82-89.ZHANG Siyi, CHEN Xiyuan. Motion constraint aided integrated navigation method based on SVD-CKF[J]. Journal of Electronic Measurement and Instrumentation, 2022, 36(4): 82-89. [17] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. doi: 10.1109/TAC.2009.2019800 [18] 穆静,蔡远利. 平方根容积卡尔曼滤波算法及其应用[J]. 兵工自动化,2011,30(6): 11-13,26.MU Jing, CAI Yuanli. Square root cubature Kalman filter algorithm and application[J]. Ordnance Industry Automation, 2011, 30(6): 11-13,26. [19] 翟婉明. 车辆-轨道耦合动力学理论的发展与工程实践[J]. 科学通报,2022,67(32): 3793-3807.ZHAI Wanming. Development of vehicle-track coupled dynamics theory and engineering practice[J]. Chinese Science Bulletin, 2022, 67(32): 3793-3807. [20] 翟婉明. 车辆-轨道耦合动力学下册[M]. 4版. 北京: 科学出版社,2015: 41-42. [21] 陈光雄. 钢轨波磨预测模型验证工况的研究[J]. 西南交通大学学报,2022,57(5): 1017-1023,1054. doi: 10.3969/j.issn.0258-2724.20200842CHEN Guangxiong. Study on validation conditions of rail corrugation prediction models[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 1017-1023,1054. doi: 10.3969/j.issn.0258-2724.20200842 [22] 陈美,翟婉明,閤鑫,等. 高速铁路多边形车轮通过钢轨焊接区的轮轨动力特性分析[J]. 科学通报,2019,64(25): 2573-2582. doi: 10.1360/N972018-01288CHEN Mei, ZHAI Wanming, GE Xin, et al. Analysis of wheel-rail dynamic characteristics due to polygonal wheel passing through rail weld zone in high-speed railways[J]. Chinese Science Bulletin, 2019, 64(25): 2573-2582. doi: 10.1360/N972018-01288 -




 下载:
下载: