竖向荷载作用下加筋埋地管道力学与变形行为细观分析

王志杰; 成彪; 杨广庆; 高古顺; 王贺

doi:10.3969/j.issn.0258-2724.20230046

竖向荷载作用下加筋埋地管道力学与变形行为细观分析

doi: 10.3969/j.issn.0258-2724.20230046

王志杰^{1, 2, 3,},
成彪³,
杨广庆^{1, 2, 3, ,},
高古顺³,
王贺^{1, 2, 3}

1.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043
2.
石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，河北石家庄 050043
3.
石家庄铁道大学土木工程学院，河北石家庄 050043

基金项目: 国家自然科学基金项目（51709175）；河北省高等学校科学技术研究项目（BJ2020045）

详细信息

作者简介:
王志杰（1985—），男，副教授，博士，研究方向为土工合成材料加筋土技术，E-mail：zwang@stdu.edu.cn

通讯作者:
杨广庆（1971—），男，教授，博士，研究方向为土工合成材料加筋土技术，E-mail：yanggq@stdu.edu.cn

中图分类号: TU990.3
计量
- 文章访问数: 248
- HTML全文浏览量: 105
- PDF下载量: 36
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-10
- 修回日期: 2023-04-30
- 网络出版日期: 2024-07-09
- 刊出日期: 2023-07-07

Mesoscopic Study on Mechanical and Deformation Behaviors of Reinforced Buried Pipelines Under Vertical Loads

WANG Zhijie^{1, 2, 3
,},
CHENG Biao³,
YANG Guangqing^{1, 2, 3
, ,},
GAO Gushun³,
WANG He^{1, 2, 3}

1.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
Key Laboratory of Roads and Railway Engineering Safety Control, Shijiazhuang Tiedao University, Ministry of Education, Shijiazhuang 050043, China
3.
School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

摘要

摘要:
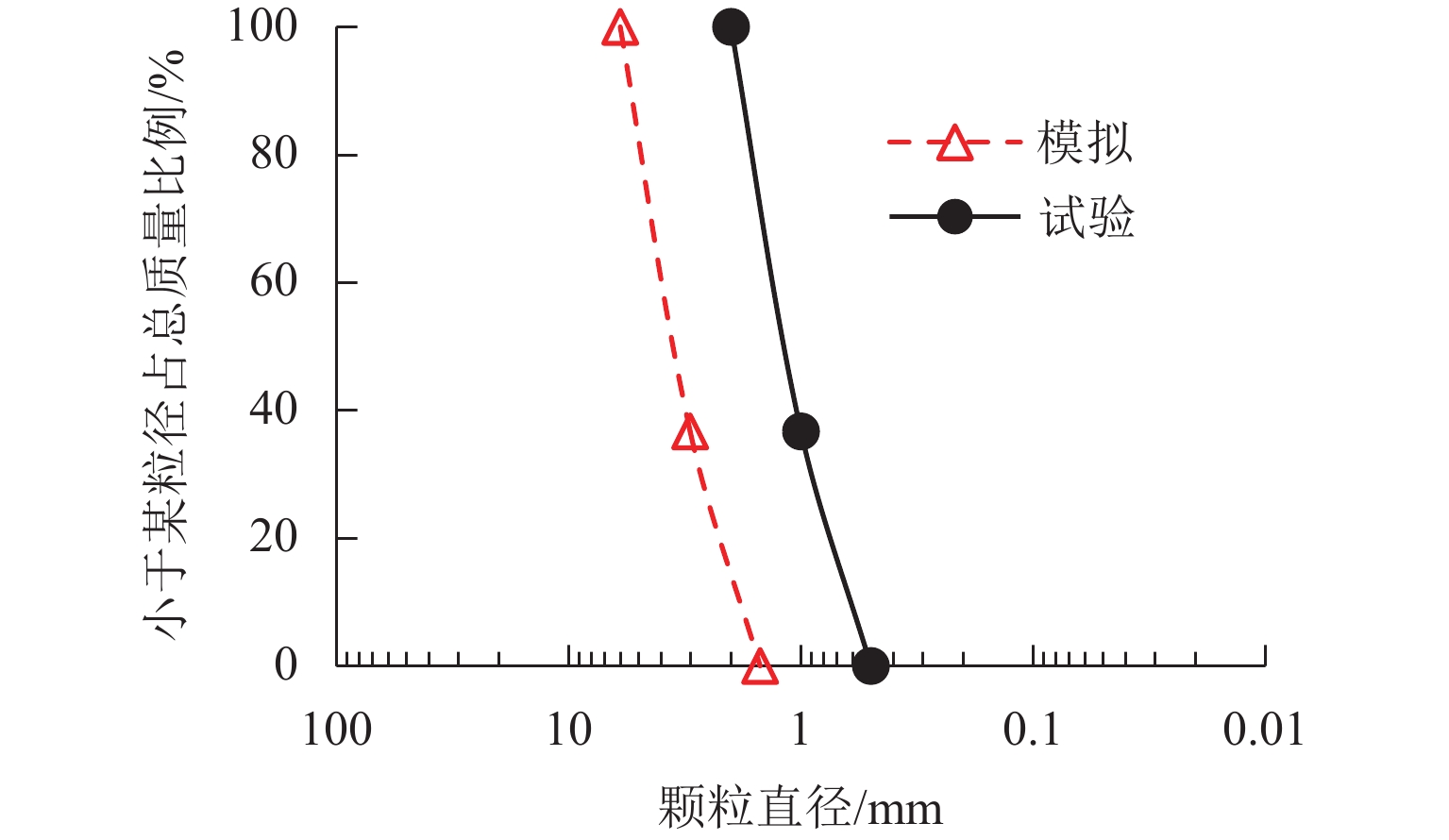
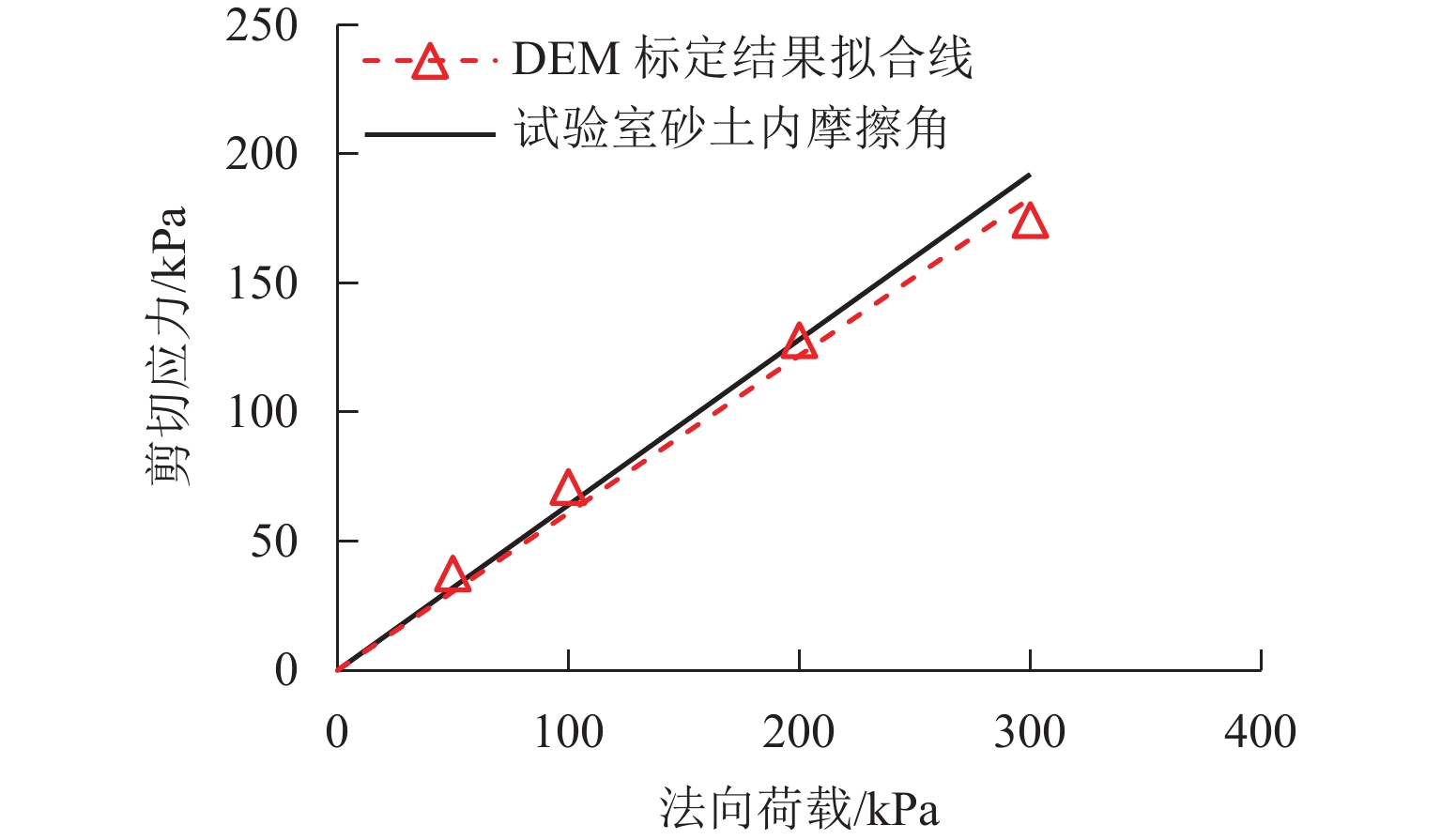
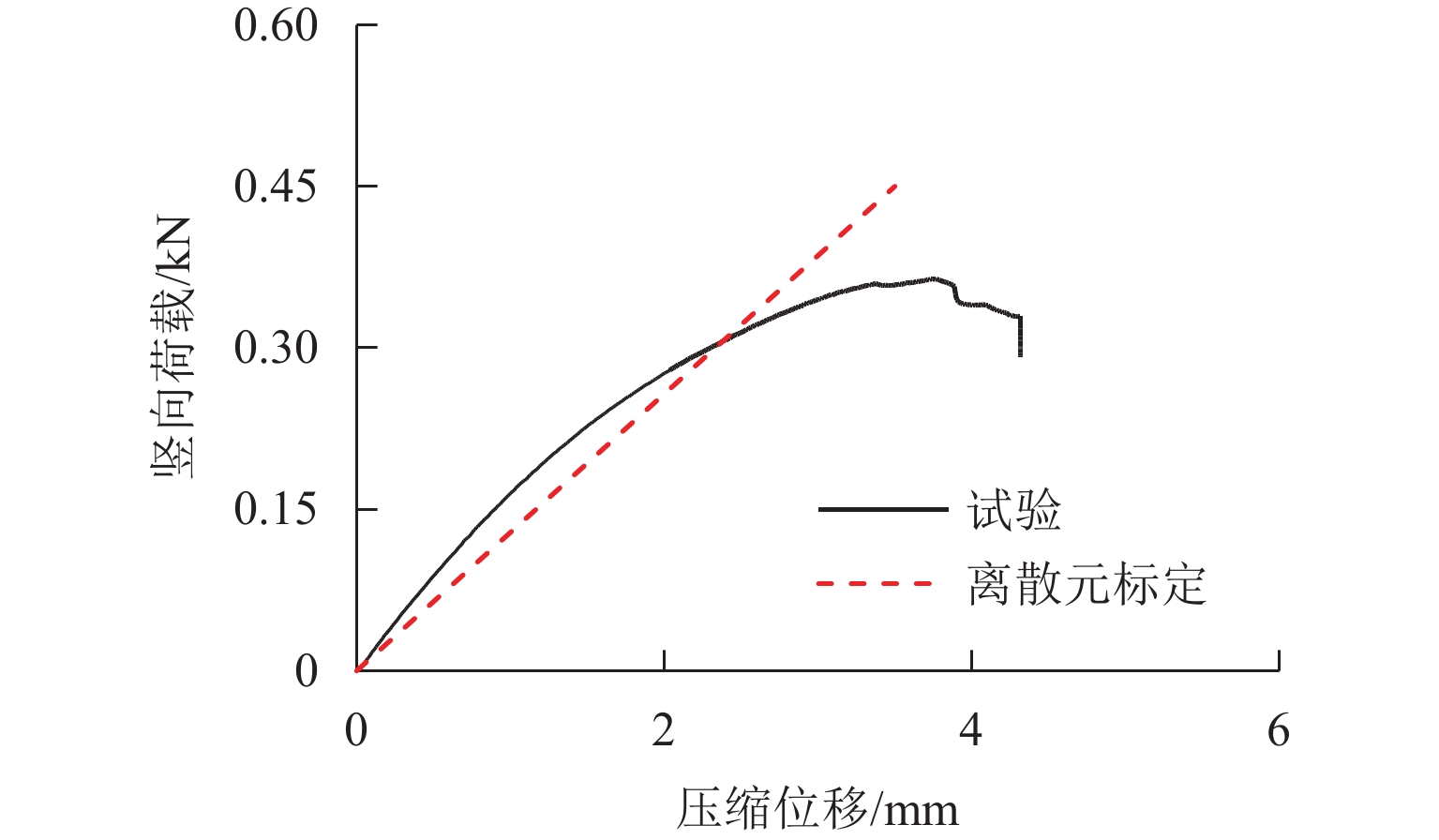
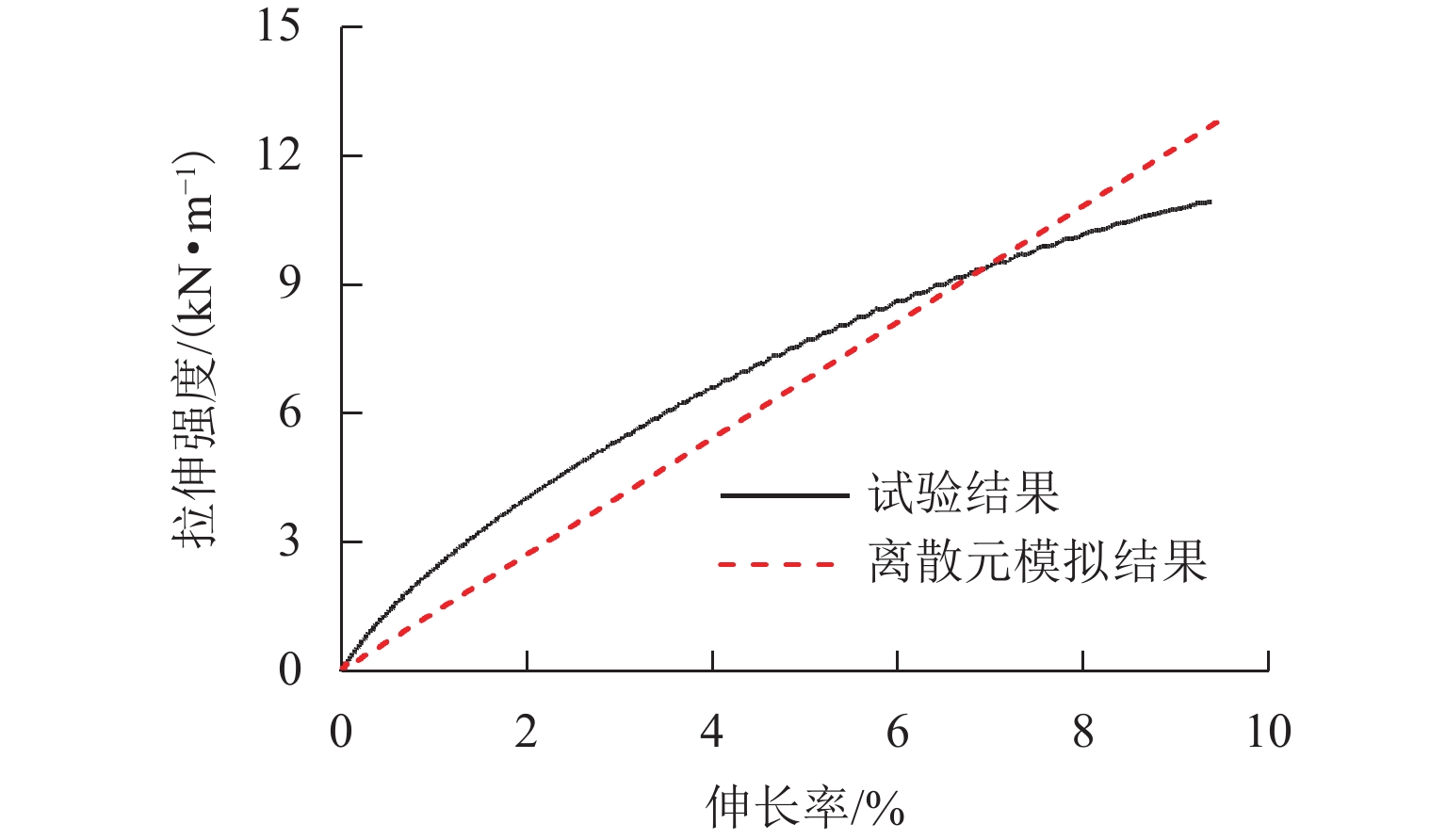
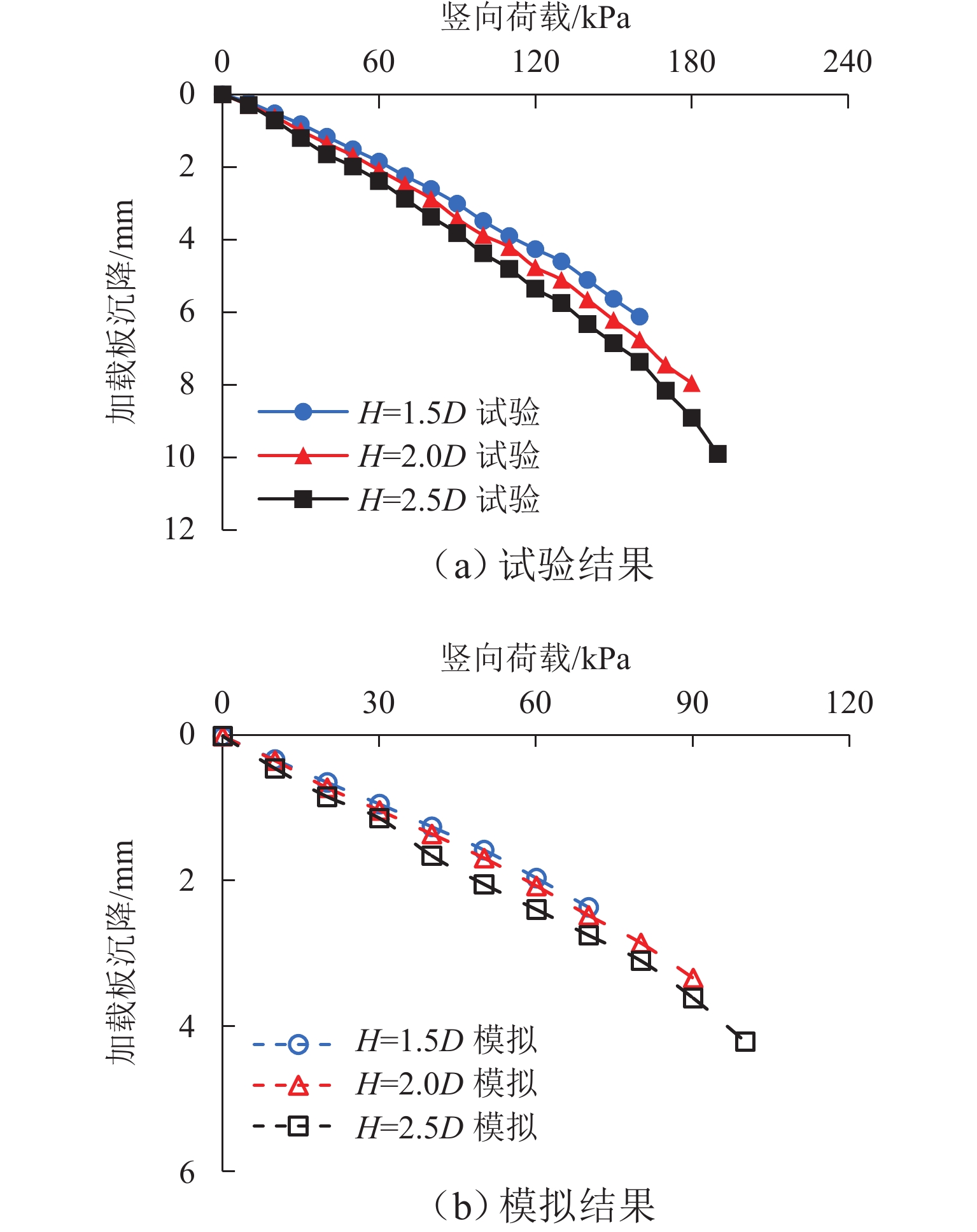
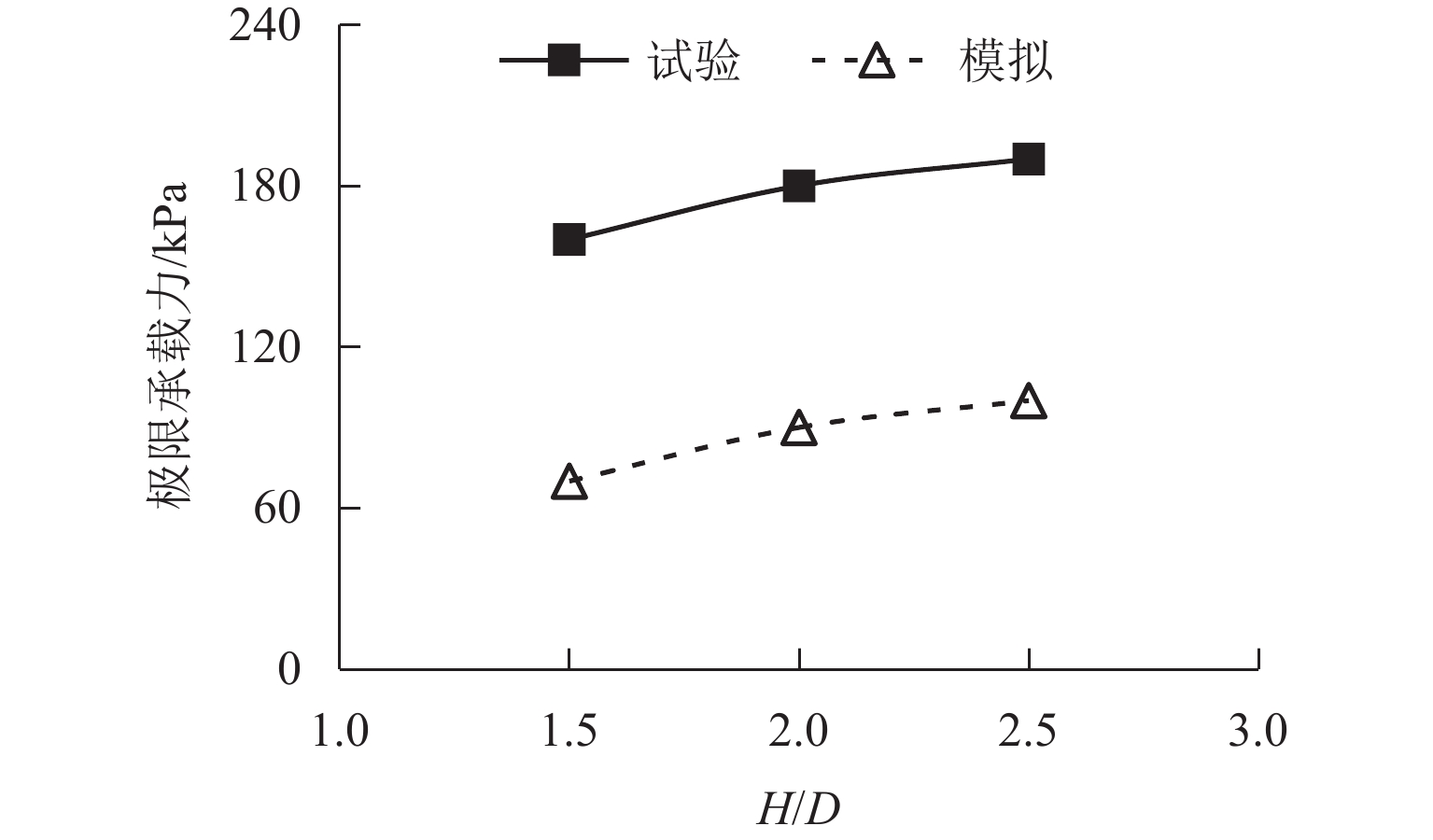
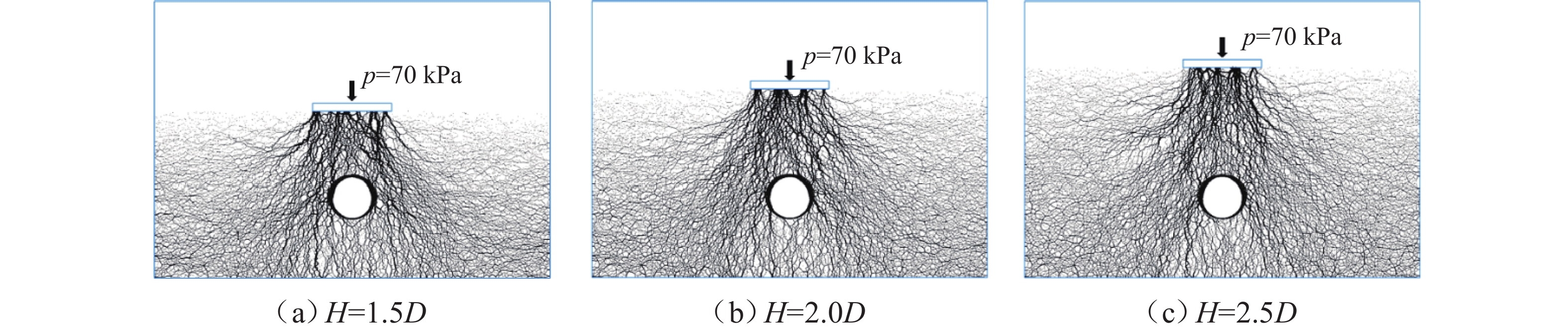
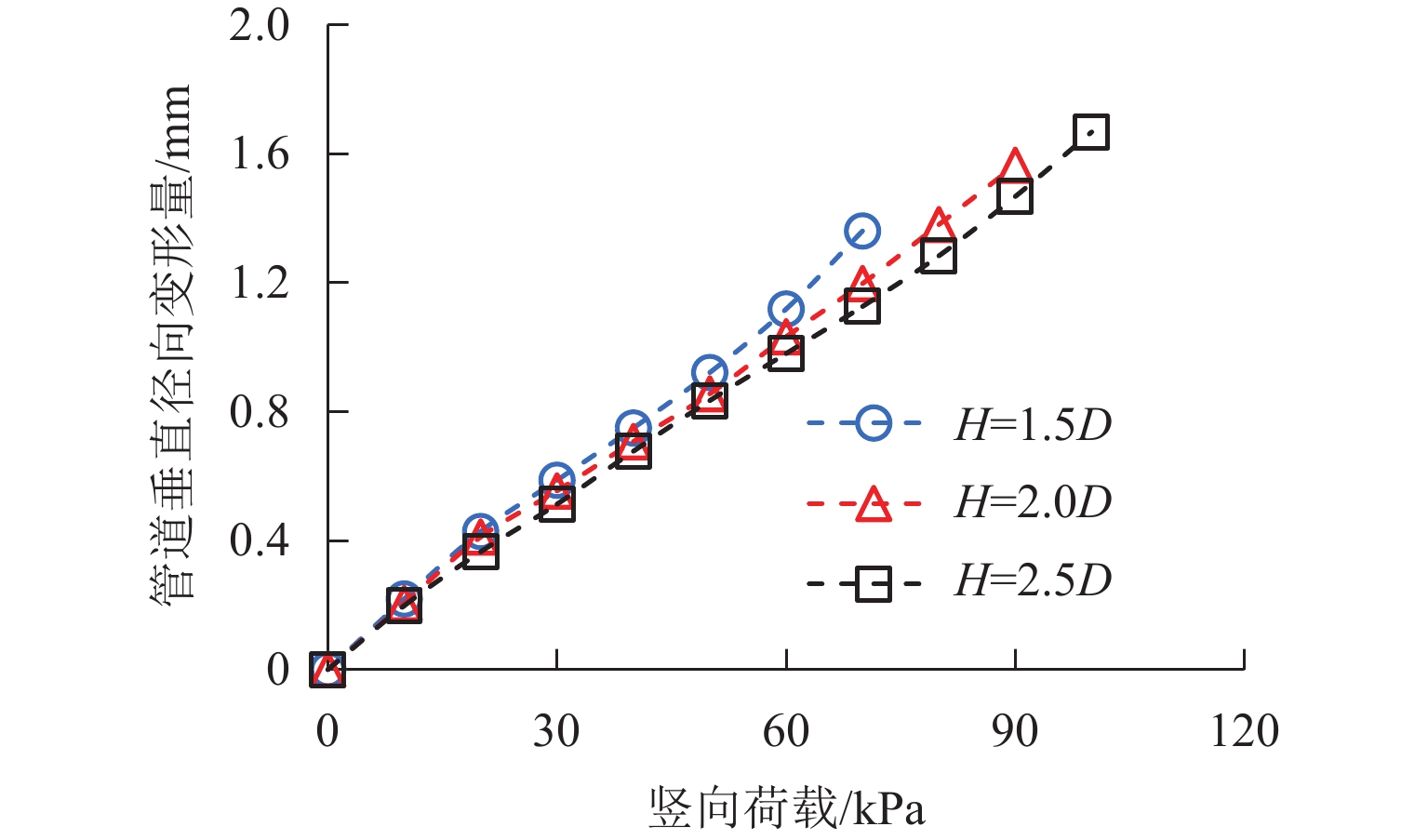
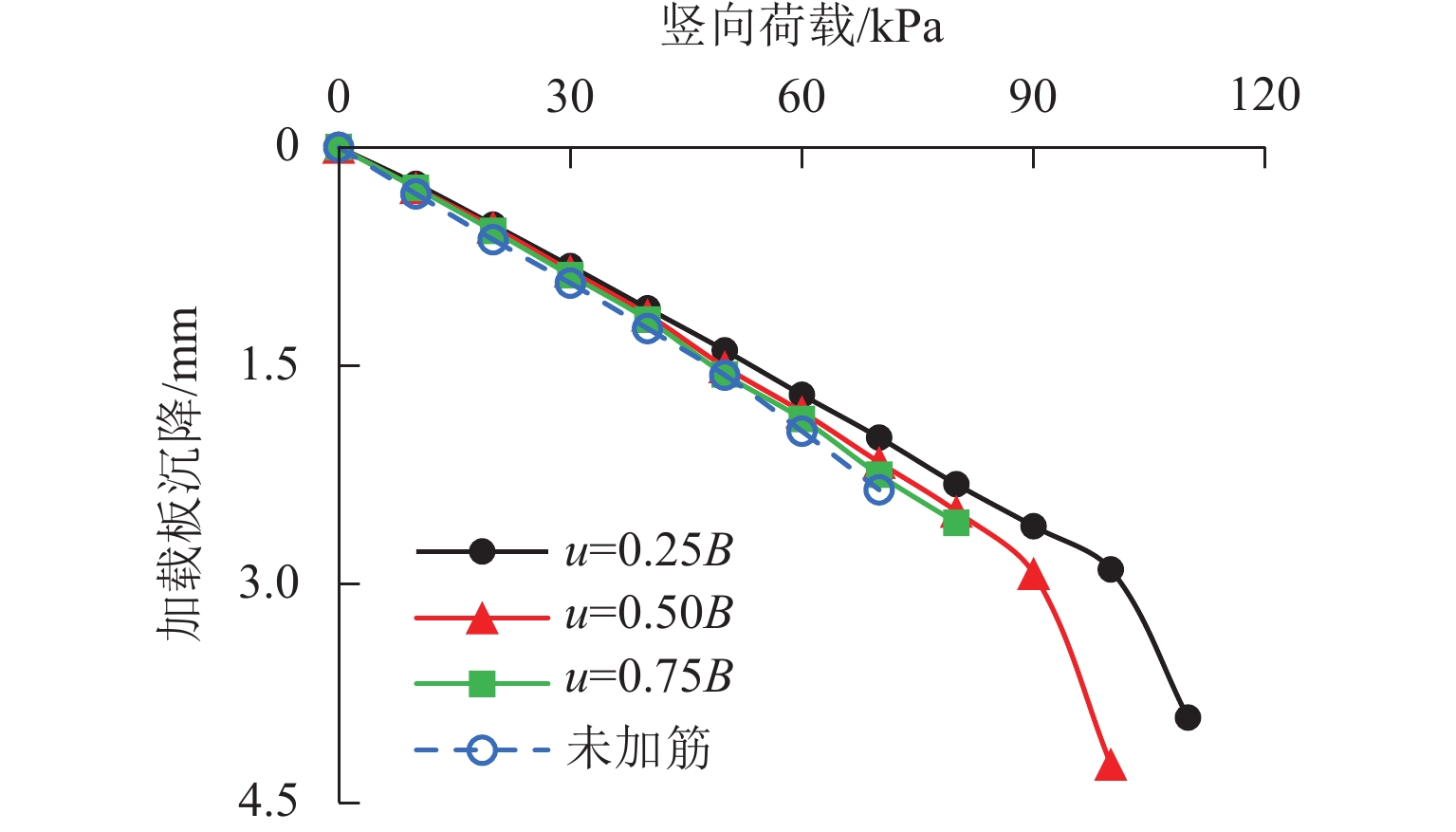
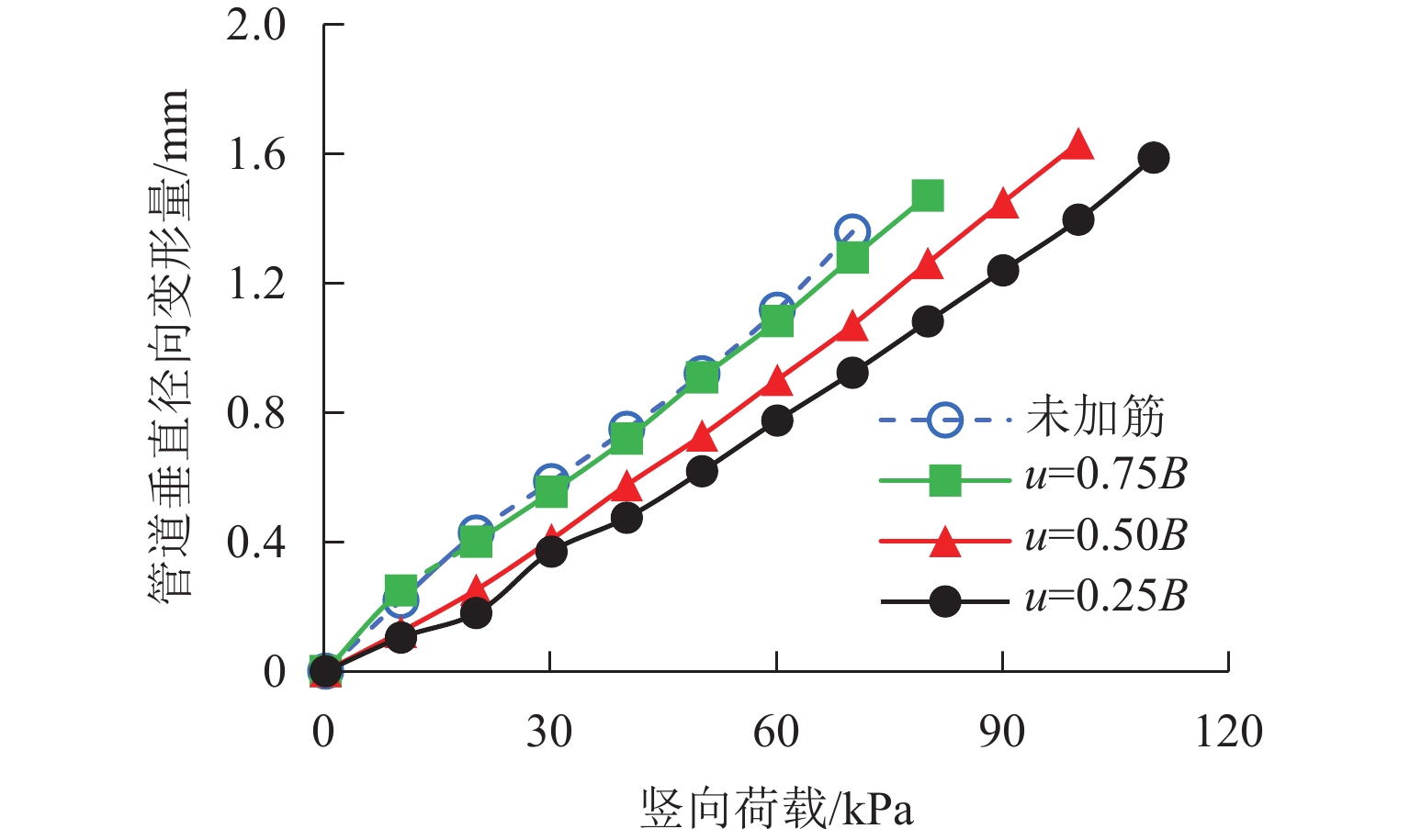
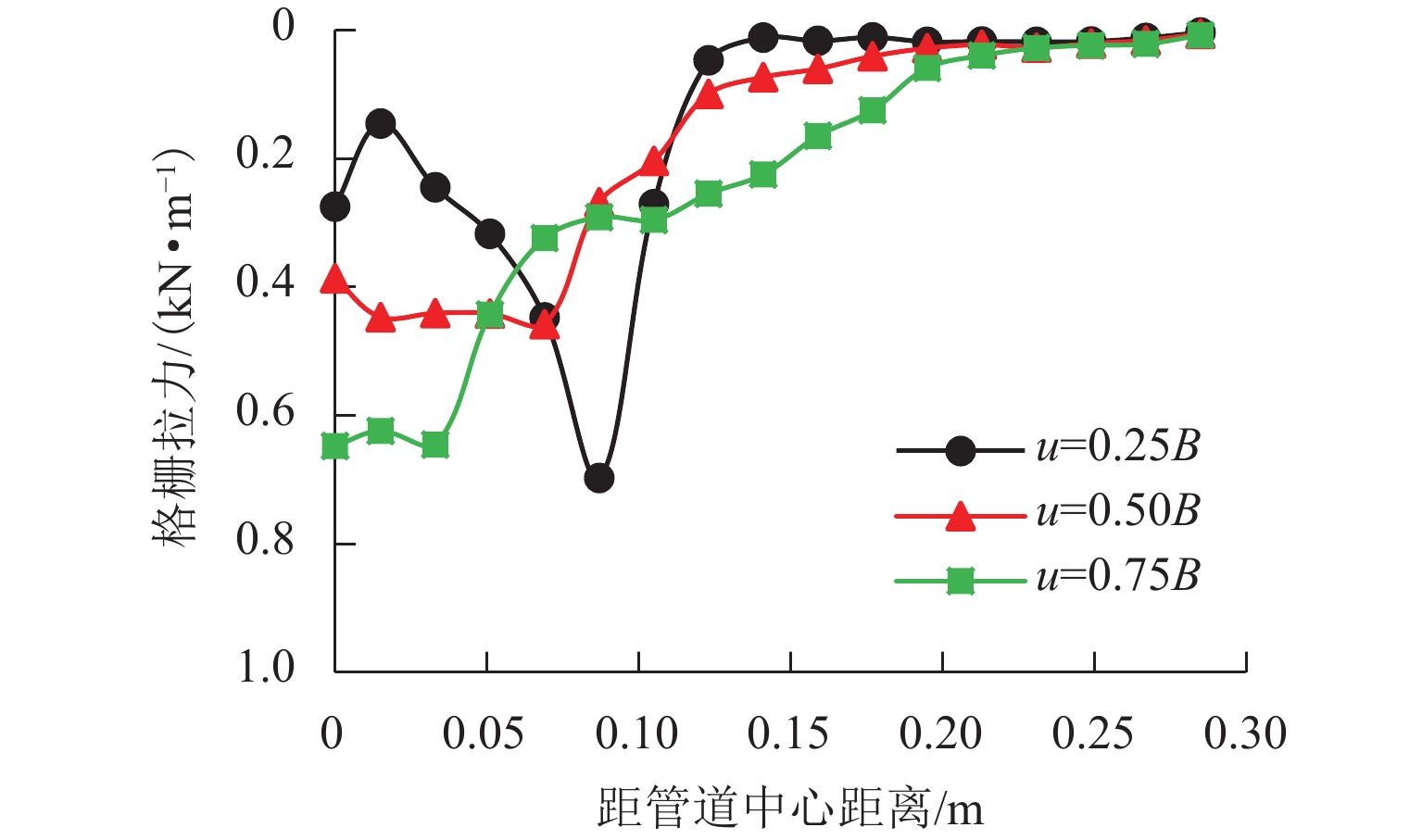
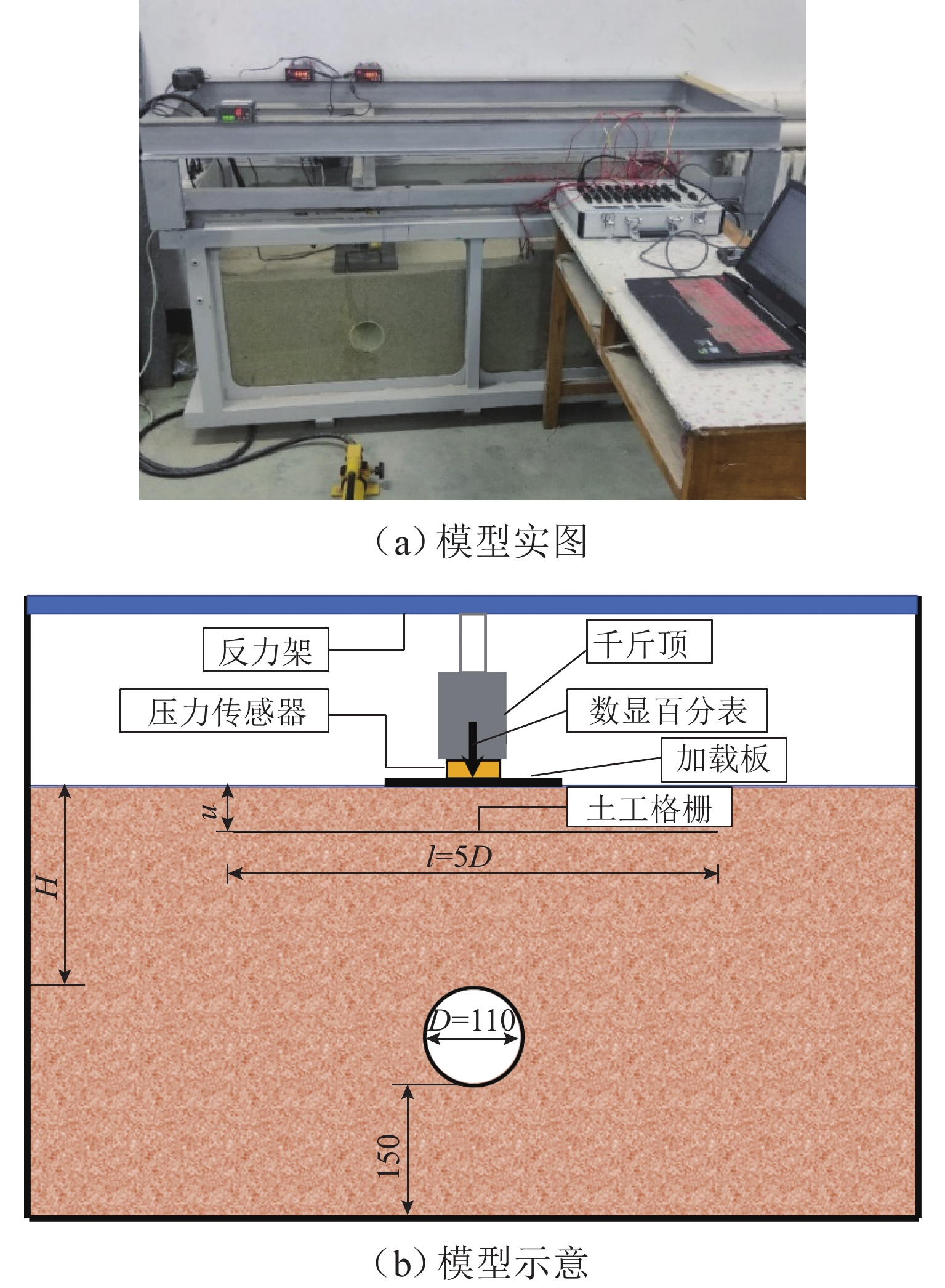
为深入研究竖向荷载作用下土工格栅加筋埋地管道的防护效果，基于室内模型试验，建立离散元仿真分析模型，从细观层面探究竖向荷载作用下土工格栅加筋埋地管道与周围土体系统的力学响应与变形行为，揭示不同管道埋深与不同筋材埋深条件下，加载板荷载-沉降关系曲线、模型内部颗粒间接触力、颗粒位移与管道垂直径向变形等发展演化规律. 研究结果表明：当管道埋深H较浅时（H=1.5D，D为管道模型外径），其极限承载力小于管道埋深较大的工况，虽然相同荷载作用下加载板沉降较小，但管道垂直径向变形较大；对管道上方进行土工格栅加筋后，模型系统承载力显著提高，管道垂直径向变形减小；土工格栅埋深越浅，加筋效果越显著，当土工格栅埋深从0.75B减小至0.25B时，极限承载力提高约57.2%，管道径向变形减小约27.9%. 本研究从细观层面揭示了管道、土体与土工格栅之间的相互作用机理，实现土工格栅加筋防护埋地管道力学与变形行为的可视化.
- 埋地管道 /
- 土工格栅 /
- 力学行为 /
- 变形特征 /
- 离散元 /
- 细观研究
Abstract:
In order to deeply study the protective effect of geogrid-reinforced buried pipelines under vertical load, indoor model tests were carried out, and a discrete element simulation analysis model was established. The mechanical response and deformation behavior of geogrid-reinforced buried pipelines and surrounding soil systems under vertical load were explored from the mesoscopic level, and the development and evolution laws of the load-settlement curve of loading plate, contact force between particles inside the model, particle displacement, and vertical radial deformation of pipelines were revealed under different buried depths of pipelines and reinforcements. The results show that when the buried depth of the pipeline H is shallow (H = 1.5D, D is the outer diameter of the pipeline model), the ultimate bearing capacity is smaller than that of the pipeline with a large buried depth. Although the settlement of the loading plate is smaller under the same load, the vertical radial deformation of the pipeline is large. After the geogrid above the pipeline is reinforced, the ultimate bearing capacity of the model system is significantly increased, and the vertical radial deformation of the pipeline is reduced. A shallower buried depth of the geogrid indicates a more obvious reinforcement effect. When the buried depth of the geogrid u is reduced from 0.75B to 0.25B, the ultimate bearing capacity is increased by about 57.2%, and the radial deformation of the pipeline is reduced by about 27.9%. In this study, the interaction mechanism among pipelines, soil, and geogrid is revealed from the mesoscopic level, and the mechanical and deformation behavior of geogrid-reinforced protected buried pipelines were visualized.
- buried pipelines /
- geogrid /
- mechanical behavior /
- deformation characteristics /
- discrete element /
- mesoscopic study

HTML全文

随着交通强国战略的实施，我国地铁线路的建设发展迅猛. 但随着地铁建设规模的急剧扩大，其运营成本尤其是基础设施维护成本与日俱增. 作为地铁线路典型轨道损伤问题，钢轨波磨是一种钢轨表面出现波浪形的周期性磨耗问题^[1]. 钢轨波磨加剧了轮轨冲击，加速了车辆设备和线路设施服役性能的劣化和失效进程^[2-3]，特别是在钢轨波磨高发区段伴随着大量的扣件弹条断裂，严重影响列车运营安全^[4-6].

为探究扣件弹条的断裂机理，国内外学者主要从共振响应、疲劳失效角度开展研究. 共振响应角度：Ling等^[7]结合线路检测、列车-轨道动力学模型与局部扣件有限元模型，发现特定的线路半径和钢轨波磨会引发弹条的断裂；Wang等^[8-9]则认为弹条固有频率与波磨区段轮轨间振动主频的一致引发了弹条共振，进而导致弹条的断裂. 疲劳失效的角度：刘玉涛等^[10]结合疲劳分析方法与数学统计方法，评价扣件弹条的服役可靠性；辛涛等^[11-12]采用疲劳分析方法，探究了不同扣件和波磨参数对弹条疲劳寿命的影响；还有学者结合疲劳试验，探究安装状态^[13-14]、弹条的加工工艺^[15]等因素对弹条疲劳寿命的影响. 现有关于扣件弹条断裂机理的研究，一方面仅从扣件弹条系统共振响应或疲劳失效的单一角度开展分析，缺乏对两者共同作用的综合考虑；另一方面，大多数研究都没有建立能够还原系统中轮轨摩擦耦合振动关系的数值模型. 如Ling等^[7]建立了弹条及部分相邻接触部位的数值模型，辛涛等^[11]建立了完整的扣件数值模型，潘兵等^[9]建立了钢轨、轮对和由弹簧单元代替扣件系统的数值模型，但这些学者都忽略了钢轨波磨区段特殊的轮轨耦合关系和复杂线路特性对于扣件弹条共振响应的影响. 因此，综合考虑共振响应和疲劳失效的相互作用，建立一个完整包括轮轨系统和扣件系统的数值模型，有助于更加准确地揭示钢轨波磨区段扣件弹条的断裂机理.

本文从共振响应和疲劳失效角度探究钢轨波磨高发区段科隆蛋扣件弹条的断裂机理. 首先，基于现场调研数据，建立包含钢轨波磨不平顺的科隆蛋扣件的轮对-钢轨-扣件有限元模型. 然后，通过共振响应分析和疲劳失效分析，探究钢轨波磨区段轮轨摩擦耦合振动激励下科隆蛋扣件弹条的共振响应及其共振状态下的疲劳寿命，进而揭示钢轨波磨高发区段科隆蛋扣件弹条的断裂机理.

1. 现场调研和数值模型

1.1 科隆蛋扣件支撑区段现场调研

科隆蛋扣件区段作为钢轨波磨的高发区段，其钢轨波磨在小半径曲线轨道上尤为严重，并伴随扣件断裂问题，如图1所示. 本文对重庆地铁一号线的小什字—较场口区段进行了现场调研. 该区段采用Ⅲ型科隆蛋减震扣件支撑，主要由DI型弹条、减振器、轨距垫、螺旋道钉、轨下垫板和调高垫板组成. 其中，DI型弹条是一种典型的“e”型弹条，可以划分为中肢、后拱、跟端、前拱和趾端5个具体部位. 在科隆蛋扣件支撑的直线和小半径曲线段均有波磨发生，在小半径曲线段尤为严重. 本文着重调研了K1.261—K2.050区段曲线半径为350 m处的钢轨波磨. 该区段列车运营速度在60 km/h左右，此处钢轨波磨主要发生在该小半径曲线轨道的低轨处，波长为40～50 mm，波深为0.1～0.5 mm. 调研发现，在该钢轨波磨高发区段出现了部分扣件弹条断裂，断裂位置主要集中在后拱附近.

图 1 科隆蛋扣件区段钢轨波磨及扣件断裂特征

Figure 1. Rail corrugation and fastener fracture characteristics of Cologne-egg fastener section

下载: 全尺寸图片幻灯片

1.2 轮对-钢轨-扣件系统的有限元模型

为还原包含完整科隆蛋扣件的轮对-钢轨-扣件系统模型当中复杂的轮轨摩擦耦合振动关系，以及科隆蛋扣件弹条在该复杂系统当中的共振响应，本文结合现场调研，构建包含完整科隆蛋扣件的轮对-钢轨-扣件系统的有限元模型，如图2所示，其材料属性如表1所示. 该模型主要由轮轨子系统和扣件子系统组成. 在轮轨子系统中，包含轮对和钢轨，轮对的车轮滚动圆直径为840 mm，车轮踏面为LM型踏面，轮对运行速度设为60 km/h. 在外侧和内侧车轴两端分别采用耦合方式加载40.87 kN和28.23 kN的垂向悬挂力^[16]. 钢轨设为16跨长度，两端采用固定约束. 为模拟轮对通过钢轨波磨的振动响应，需将钢轨划分为松弛区和波磨区，松弛区为1250 mm，波磨区为3125 mm. 其中，对波磨区进行网格细化，采用谐波函数模拟钢轨波磨，波长设为45 mm，波深设为0.3 mm. 此外，轮轨接触采用面-面接触，摩擦系数设为0.4. 根据车辆-轨道系统动力学分析结果，确定科隆蛋扣件小半径曲线区段的轮轨接触位置，此时轮对外轮轮缘与高轨轨头侧面接触，轮对内轮踏面与低轨轨头顶面接触^[17].

图 2 轮对-钢轨-扣件系统的有限元模型

Figure 2. Finite element model of wheel set-rail-fastener system

下载: 全尺寸图片幻灯片

表 1 轮对-钢轨-扣件系统有限元模型的材料属性^[9,18-19]

Table 1. Material properties of finite element model of wheel set-rail-fastener system^[9,18-19]

部件	弹性模量/Pa	泊松比	密度/ （kg•m⁻³）
轮对	210.00×10⁹	0.30	7800
钢轨	206.00×10⁹	0.30	7800
DI 弹条	206.00×10⁹	0.30	7800
轨距垫	6.20×10⁹	0.35	1400
调高垫板	6.00×10⁶	0.45	1190
承轨座/底座	170.00×10⁹	0.30	7900
减振橡胶	5.58×10⁶	0.49	1190

下载: 导出CSV

| 显示表格

在扣件子系统中，本文较为完整地构建了科隆蛋扣件的有限元模型. 其中，减振器由承轨座、减振橡胶和底座构成，减振橡胶底面与底座间留有3 mm竖直间距，扣件间距为625 mm^[18]. 各部件之间的接触属性如表2所示.

表 2 轮对-钢轨-扣件系统有限元的主要接触属性^[18-19]

Table 2. Main contact properties of finite element of wheel set-rail-fastener system^[18-19]

接触对	接触方式	主面	从面	摩擦系数
轮对-轨道	摩擦	轮面	轨面	0.4
弹条-减振器板	摩擦	弹条	减振器板	0.3
弹条-轨距块	摩擦	弹条	轨距块	0.7
轨道-轨距块	绑定	轨距块	轨道
轨下垫板- 钢轨	绑定	轨下垫板	钢轨
轨下垫板- 承轨座	绑定	轨下垫板	承轨座

下载: 导出CSV

| 显示表格

需要特别说明的是，科隆蛋扣件的扣压力是由弹条形变提供的，故需要在轮对-钢轨-扣件系统的有限元模型中还原科隆蛋扣件弹条的扣压过程. 如图3所示，本文采取的扣压模拟方式如下：首先，在弹条趾端施加随时间线性增加的竖直拉力F，直至扣件弹条趾端平面略高于轨距块接触表面，期间需要暂时约束承轨座，以保证扣压过程平稳；然后，使得弹条与轨距块的接触生效，并使施加在弹条趾端的力逐步减小至0，期间弹条会与轨距块直接接触，并产生相应的弹条扣压力以完成安装.

图 3 科隆蛋扣件弹条扣压过程模拟

Figure 3. Simulation of Cologne-egg fastener clip compression process

下载: 全尺寸图片幻灯片

2. 分析理论

2.1 轮轨摩擦耦合振动分析理论

为探究钢轨波磨高发区段的科隆蛋扣件弹条断裂的振动诱因，需研究轮对通过钢轨波磨高发区段的轮轨摩擦耦合振动特性. 显式瞬时动态分析是一种从时域研究轮轨摩擦耦合振动的常用方法^[20]. 显式瞬时动态分析过程中，将在初始分析步建立总系统平衡方程，如式（1）所示.

${\boldsymbol{M}}{{\boldsymbol{\ddot x}}_t} = {{\boldsymbol{P}}_{t}} - {{\boldsymbol{I}}_{t}} ，$

(1)

式中：M为系统的对角集中质量矩阵，$ {{\boldsymbol{ x}}_t} $为系统的位移向量，P_t为系统所受外力向量，I_t为系统的内力向量，t为时间.

系统加速度向量为

${{\boldsymbol{\ddot x}}_t} = \frac{{{{\boldsymbol{P}}_t} - {{\boldsymbol{I}}_t}}}{{\boldsymbol{M}}} .$

(2)

利用中心差分法进行积分，便可得出该系统在t +Δt时的系统速度以及t+2Δt时的系统位移， Δt为单个时间增量步，定义中间增量t+Δt和t−Δt，于是有

$\boldsymbol{\dot{x}}_{t+\Delta t}=\boldsymbol{\dot{x}}_{t-\Delta t}+\frac{\Delta T_{t+2\Delta t}+\Delta T_t}{2}\boldsymbol{\ddot{x}}_t，$

(3)

$\boldsymbol{x}_{t+2\Delta t}=\boldsymbol{x}_t+\Delta T_{t+2\Delta t}\boldsymbol{\dot{x}}_{t+\Delta t},$

(4)

式中：$\Delta T_t $为t时的增量步时长.

由于中间增量的存在，需要系统在t=0时刻的速度与加速度被完全定义，才能计算下一增量步. 本文中所有节点的初始速度和位移都被定义为0，通过该显式瞬时动态分析方法，还原系统的摩擦耦合振动下弹条的共振响应，进而从共振响应的角度探究弹条的断裂机理.

2.2 扣件弹条疲劳分析理论——疲劳失效的研究

为探究科隆蛋扣件支撑钢轨波磨高发区段扣件弹条断裂的疲劳特性，需计算钢轨波磨高发区段处科隆蛋扣件弹条的疲劳寿命. 线性累积损伤理论是一种用于扣件弹条疲劳寿命分析的常用方法^[21]. 首先，提取瞬时动态分析中弹条最大应力节点的应力时程曲线；接着，利用雨流计数法统计应力时程曲线，将其转换为相应的应力循环均值、应力循环幅值以及循环次数^[22]；然后，通过Goodman曲线公式（式（5））修正循环幅值，使应力均值为0，以消除应力均值对疲劳分析计算的影响.

$S=\frac{{S} _{{\mathrm{a}}}{S} _{{\mathrm{u}}}}{{S} _{{\mathrm{u}}}-{S} _{{\mathrm{m}}}} ，$

(5)

式中：S为等效应力均值为0的应力循环均值；S_a为原始应力幅值；S_m为原始应力循环均值；S_u为材料的抗拉强度，本文弹条材料抗拉强度为1600 MPa^[19].

将修正应力循环带入弹条材料（60Si2Mn弹簧钢）存活率为95%的 S-N 曲线^[13]，如式（6）所示.

$\lg \;N = 39.595\;3 - 11.843\;6\lg \;S,$

(6)

式中：N为材料失效所需的最大循环次数.

在求解出N后，将其带入Palmgren-Miner公式，如式（7）所示.

$D = \sum\limits_{i = 1}^k {{D_i}} = \sum\limits_{i = 1}^k {\frac{{{n_i}}}{N}，}$

(7)

式中：D为所有应力循环造成的总损伤，D_i为第i个应力循环造成的累积损伤，k为应力循环次数，n_i为雨流计数得到的应力循环次数.

对D取倒数，可以得到弹条的疲劳寿命为

${N_{{\mathrm{life}}}} = \frac{1}{D} .$

(8)

通过计算弹条寿命，可以将弹条的疲劳损伤量化，探究轮轨摩擦耦合振动对于弹条的疲劳损伤，进而结合共振响应和疲劳损伤揭示科隆蛋扣件弹条断裂的机理.

3. 结果与讨论

3.1 科隆蛋扣件弹条安装状态验证

弹条的安装状态对扣件的服役性能和扣件弹条的使用寿命都有着极大的影响，其中，“e”型弹条的安装状态主要通过改变弹条的中肢插入深度和弹程实现^[13]. 本文取弹条的中肢插入深度为9 mm，弹程为10.5 mm，此时对应的扣压力为8.475 kN，满足标准扣压力为8.25 kN的需求^[23]，如图4（a）所示. 安装状态下弹条应力主要集中于后拱端内侧，与现场调研中科隆蛋扣件弹条的断裂位置一致，弹条上的最大应力值为1430 MPa，大于标准GB/T 1222—2016^[24]中弹簧钢材料的屈服极限1400 MPa，此时应力集中部位存在微小的塑形变形，如图4（b）所示. 以上研究表明，本文所采取的上拉弹条趾端的模拟扣压方式能够有效还原弹条的真实安装状态，并且在已选定的安装状态下能够满足弹条扣压力大于8.25 kN的扣压要求.

图 4 科隆蛋扣件弹条安装状态

Figure 4. Installation status of Cologne-egg fastener clip

下载: 全尺寸图片幻灯片

3.2 科隆蛋扣件弹条共振响应分析

通过对已建立的科隆蛋扣件小半径曲线波磨区段轮对-钢轨-扣件系统有限元模型进行瞬时动态分析，求解得到轮轨在松弛区和波磨区的轮轨摩擦耦合振动响应. 由于小半径区段钢轨波磨主要发生在低轨处，这里通过内轮与低轨间的轮轨法向接触力体现科隆蛋扣件小半径曲线区段轮轨系统的摩擦耦合振动特性^[1]，如图5（a）所示. 在松弛区的轮轨接触法向力变化较为柔和；在进入波磨区后，该接触力变化显著加剧，说明钢轨波磨会显著加剧轮轨系统的振动响应. 为进一步分析轮轨接触特性，通过对轮轨接触法向力进行短时傅里叶变换，求解得出轮轨接触法向力在200～1000 Hz的时频信息^[25]，如图5（b）所示. 在松弛区中，轮轨接触法向力具有370 Hz左右的主频，与后续钢轨波磨的主频一致^[26]；在进入波磨区后，轮轨接触法向力的主频基本不发生变化；轮轨接触的振动能量显著增大，已存在的钢轨波磨的反馈振动会加剧轮轨摩擦耦合振动响应.

图 5 轮对-钢轨-扣件系统的瞬时动态分析结果

Figure 5. Instantaneous dynamic analysis results of wheel set-rail-fastener system

下载: 全尺寸图片幻灯片

另外，科隆蛋扣件弹条的约束模态能够体现弹条在装配状态下的振动特性，当外部激励与约束模态一致时，弹条会发生共振强迫振动，进而使得弹条的疲劳寿命急剧减小^[27-28]. 本文通过子空间法，提取科隆蛋扣件弹条在10～1000 Hz内安装状态下的约束模态特性^[19]，如图6所示.

图 6 科隆蛋扣件弹条10～2000 Hz约束模态频率及振型

Figure 6. Constraint modal frequency and vibration mode of Cologne-egg fastener clip at 10–2000 Hz

下载: 全尺寸图片幻灯片

科隆蛋扣件弹条的一阶模态频率为368.54 Hz，与轮轨摩擦耦合振动主频接近，该频率的模态振型表现为弹条后拱端振动. 结合图5的分析结果发现，钢轨波磨加剧的轮轨摩擦耦合振动可能会引发该区段科隆蛋扣件弹条的共振响应，且对应振型下该科隆蛋扣件弹条主要振动位置在弹条后拱端，这与现场调研中科隆蛋扣件弹条的断裂位置一致^[29]. 可以初步推断，钢轨波磨区段科隆蛋扣件弹条在轮轨摩擦耦合振动下的共振响应是该扣件弹条断裂的主要原因^[30].

进一步验证科隆蛋扣件弹条的共振状态，本文分别提取图7（a）中1号位弹条趾端端面标记的受测节点在有、无波磨工况下的加速度，以模拟弹条在平滑区段和波磨区段行驶，如图7（b ）所示. 无波磨工况下，在轮轨驶过的过程中其加速度未发生显著改变；在有波磨工况下，随着轮对驶过提取弹条所属扣件，同一位置扣件弹条受测节点的加速度显著增加，在轮轨驶过提取弹条所属扣件时，其加速度约为无波磨工况下的10倍，钢轨波磨加剧了轮轨摩擦耦合振动激励下科隆蛋扣件的共振响应. 结合前文瞬时动态分析和模态分析结果，进一步确认了钢轨波磨区段科隆蛋扣件弹条在轮轨摩擦耦合振动下的共振响应是其扣件弹条断裂的主要原因^[31].

图 7 科隆蛋扣件弹条节点加速度

Figure 7. Node acceleration of Cologne-egg fastener clip

下载: 全尺寸图片幻灯片

3.3 科隆蛋扣件弹条疲劳损伤分析

本文结合线性累积损伤理论，研究科隆蛋扣件弹条在轮轨摩擦耦合振动下的疲劳特性. 同时，结合前文共振响应分析结果，将疲劳寿命作为量化指标，对比不同振动响应下科隆蛋扣件弹条的疲劳损伤情况. 如图8（a）、（b）分别为轮轨摩擦耦合振动下瞬时动态计算中提取图7（a）中1号和2号弹条的最大应力时程图，当轮对驶过受测弹条时，由于弹条此时发生共振响应，导致其最大应力产生显著变化，并且位于工作边一侧的1号弹条变化更为明显. 通过雨流计数法统计弹条最大应力时程曲线，分别得到1、2号弹条的雨流计数分布，如图9（a）、（b）所示，其中，柱体颜色由紫到红表示应力循环次数少到多. 接着，利用Goodman公式修正应力均值，再带入弹条材料的S-N曲线，最终计算得出两者的疲劳寿命分别是15.56万次和45.26万次，仅为弹条500.00万次设计疲劳寿命^[8]的3.11%和9.05%，不能满足弹条的疲劳寿命要求. 图8（c）为无波磨工况下中图7（a）中1号位扣件弹条的最大应力时程图，其最大应力变化幅值显著小于有波磨工况下同一位置弹条的应力幅值. 通过图9（c）中无波磨工况下的雨流计数分布图，计算得出无波磨工况下1号位弹条疲劳寿命为1678.26万次，远远大于500.00万次的设计寿命，基本不会发生疲劳断裂. 综上所述，小半径区段中的科隆蛋扣件工作边一侧的弹条更容易发生疲劳失效^[32]；钢轨波磨加剧了轮轨摩擦耦合振动，使得科隆蛋扣件弹条的共振响应加剧，降低了波磨区段中科隆蛋扣件弹条寿命的99.07%，导致弹条在设计寿命内的疲劳失效.

图 8 科隆蛋扣件弹条最大应力时程图

Figure 8. Maximum stress time history diagram of Cologne-egg fastener clips

下载: 全尺寸图片幻灯片

图 9 科隆蛋扣件弹条雨流计数分布

Figure 9. Rain flow count distribution of Cologne-egg fastener clips

下载: 全尺寸图片幻灯片

4. 结　论

本文建立小半径波磨区段下包含完整科隆蛋扣件的轮对-钢轨-扣件系统有限元模型，还原了科隆蛋扣件弹条在列车行驶过程中轮轨的摩擦耦合振动特性下的共振响应，并基于该振动特性计算扣件弹条的疲劳损伤情况，进而结合共振响应和疲劳损伤，揭示弹条的断裂机理，最终得出以下结论：

1）钢轨波磨高发区段中，轮轨摩擦耦合振动主频与科隆蛋扣件弹条的一阶约束模态频率接近，一阶模态振型下在后拱端的受力复杂区域与现场调研弹条断裂位置一致，轮轨摩擦耦合振动引起的弹条共振是科隆蛋扣件弹条断裂的主要原因.

2）钢轨波磨高发区段中，钢轨波磨会加剧系统中的轮轨摩擦耦合振动，使得科隆蛋扣件弹条寿命对比无波磨工况下降了99.07%，仅为设计寿命的3.11%，进而引发科隆蛋扣件弹条在设计寿命内的提前疲劳失效.

3）钢轨波磨高发区段中，靠近小半径工作边一侧的科隆蛋扣件弹条更容易发生疲劳失效，其疲劳失效位于扣件弹条后拱端内侧，与调研现场情况一致.

致谢：轨道交通基础设施性能检测与保障国家重点实验室开放课题（HJGZ2021115）资助.

图 1 模型试验示意

Figure 1. Model test

下载: 全尺寸图片幻灯片

图 2 砂土颗粒粒径级配曲线

Figure 2. Particle size distribution curves of sands

下载: 全尺寸图片幻灯片

图 3 砂土直剪试验结果

Figure 3. Direct shear test results of sands

下载: 全尺寸图片幻灯片

图 4 管道压缩荷载-位移关系曲线

Figure 4. Compression load-displacement curves of pipelines

下载: 全尺寸图片幻灯片

图 5 土工格栅数值模拟与试验结果对比

Figure 5. Comparison between numerical simulation and test results of geogrid

下载: 全尺寸图片幻灯片

图 6 加筋埋地管道离散元数值模型示意

Figure 6. Numerical discrete element model of reinforced buried pipelines

下载: 全尺寸图片幻灯片

图 7 不同管道埋深时加载板荷载-沉降关系曲线

Figure 7. Load-settlement curves of loading plate under different buried depths of pipelines

下载: 全尺寸图片幻灯片

图 8 不同管道埋深时模型系统极限承载力结果对比

Figure 8. Comparison of ultimate bearing capacity results of model system under different buried depths of pipelines

下载: 全尺寸图片幻灯片

图 9 不同管道埋深时模型内部接触力链分布

Figure 9. Distribution of contact force chain in model under different buried depths of pipelines

下载: 全尺寸图片幻灯片

图 10 不同管道埋深时模型内部颗粒位移云图

Figure 10. Particle displacement cloud diagram in model under different buried depths of pipelines

下载: 全尺寸图片幻灯片

图 11 不同管道埋深时管道垂直径向变形量随荷载变化

Figure 11. Variation of vertical radial deformation of pipelines with load under different buried depths of pipelines

下载: 全尺寸图片幻灯片

图 12 不同土工格栅埋深时加载板荷载-沉降关系曲线

Figure 12. Load-settlement curves of loading plate under different buried depths of geogrid

下载: 全尺寸图片幻灯片

图 13 不同土工格栅埋深时管道垂直径向变形随荷载变化

Figure 13. Variation of vertical radial deformation of pipelines with load under different buried depths of geogrid

下载: 全尺寸图片幻灯片

图 14 不同土工格栅埋深时模型内部颗粒位移云图

Figure 14. Particle displacement cloud diagram in model under different buried depths of geogrid

下载: 全尺寸图片幻灯片

图 15 不同土工格栅埋深时模型内部接触力链分布

Figure 15. Distribution of contact force chain in model under different buried depths of geogrid

下载: 全尺寸图片幻灯片

图 16 管道上方土工格栅拉力定量分布对比

Figure 16. Quantitative distribution comparison of geogrid tension above pipelines

下载: 全尺寸图片幻灯片

表 1 离散元模型参数取值

Table 1. Parameter used in discrete element model

名称	接触模型	孔隙率	ρ₁/ （kg·m⁻³）	颗粒直径/mm	摩擦系数	有效模量/MPa	刚度比	E₁/MPa	平行黏结刚度比	黏结激活间隙	S₁/ （MPa·m⁻¹）	S₂/ （MPa·m⁻¹）
砂土	线性	0.151	2650	1.5～6.0	4.00	20	1
管道	平行黏结		1500	3.2	0.25	8	2	1900.0	2	10⁻⁵	400.0	400.0
土工格栅	平行黏结		905	3.0	0.30	8	1	64.5	1	10⁻⁵	24.5	24.5

下载: 导出CSV

表 2 离散元数值模拟方案

Table 2. Numerical simulation scheme of discrete element

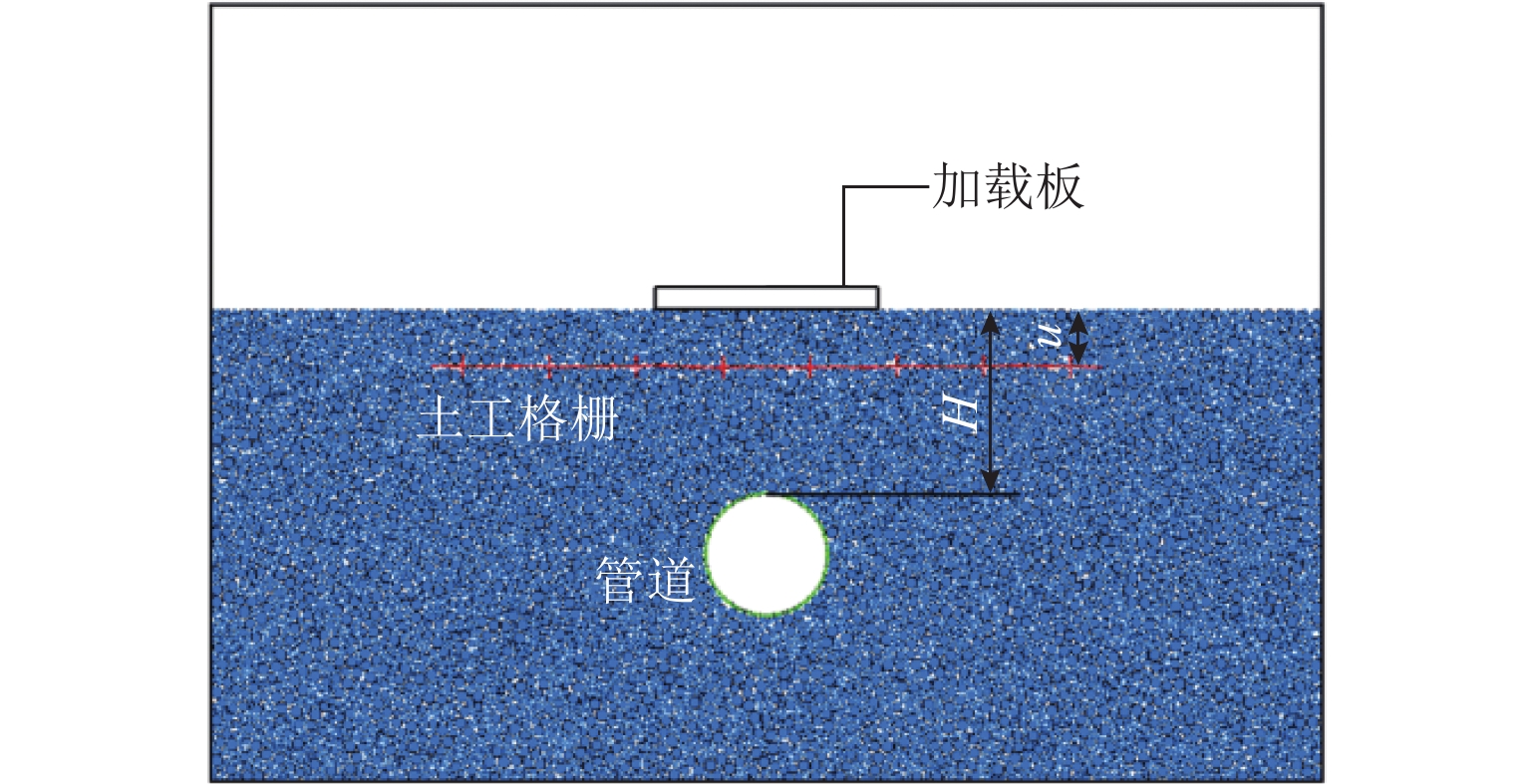
名称	H	l	u
未加筋	1.5D/2.0D/2.5D
土工格栅加筋	1.5D	5.0D	0.25B/0.50B/0.75B

下载: 导出CSV

参考文献(17)

[1]	李玉芹,郭恩栋,于天洋,等. 基于VB6.0的供水管网震害预测方法和软件[J]. 自然灾害学报,2020,29(1): 72-78. LI Yuqin, GUO Endong, YU Tianyang, et al. Earthquake damage prediction method and software for water supply pipeline network based on VB6.0[J]. Journal of Natural Disasters, 2020, 29(1): 72-78.
[2]	周恩全,宗之鑫,王琼,等. 橡胶-粉土轻质混合土中管道动力响应特性[J]. 岩土力学,2020,41(4): 1388-1395. ZHOU Enquan, ZONG Zhixin, WANG Qiong, et al. Dynamic characteristics of pipe buried in rubber-silt lightweight mixtures[J]. Rock and Soil Mechanics, 2020, 41(4): 1388-1395.
[3]	张虎,邵磊,余成,等. 冲击荷载对埋地管道影响的试验与数值模拟研究[J]. 地震工程与工程振动,2022,42(3): 243-252. ZHANG Hu, SHAO Lei, YU Cheng, et al. Experimental and numerical simulation study of impact loading on buried pipeline[J]. Earthquake Engineering and Engineering, 2022, 42(3): 243-252.
[4]	钟紫蓝,韩春堂,李锦强,等. 浅埋管道水平横向作用下砂土极限承载力研究[J]. 岩土力学,2022,43(增2): 95-103. ZHONG Zilan, HAN Chuntang, LI Jinqiang, et al. Ultimate bearing capacity of sand under lateral horizontal movement of shallowly buried pipelines[J]. Rock and Soil Mechanics, 2022, 43(S2): 95-103.
[5]	肖成志,王嘉勇,杨爱克. 静载作用下埋地管道数值模拟及其力学性能分析[J]. 防灾减灾工程学报,2018,38(1): 22-29,167. XIAO Chengzhi, WANG Jiayong, YANG Aike. Numerical simulation and mechanical performance analysis of buried pipes subjected to static load[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(1): 22-29,167.
[6]	罗滔,陈鹏,邱焕峰,等. 土工格栅与填料相互作用研究进展[J]. 武汉大学学报(工学版),2020,53(增1): 111-115. LUO Tao, CHEN Peng, QIU Huanfeng, et al. A review on the interaction between geogrid and backfill[J]. Engineering Journal of Wuhan University, 2020, 53(S1): 111-115.
[7]	MOGHADDAS TAFRESHI S N, KHALAJ O. Laboratory tests of small-diameter HDPE pipes buried in reinforced sand under repeated-load[J]. Geotextiles and Geomembranes, 2008, 26(2): 145-163. doi: 10.1016/j.geotexmem.2007.06.002
[8]	肖成志,王嘉勇,杨亚欣,等. 土工格栅防护埋地HDPE管道的变形与力学性能[J]. 西南交通大学学报,2017,52(1): 38-44,68. doi: 10.3969/j.issn.0258-2724.2017.01.006 XIAO Chengzhi, WANG Jiayong, YANG Yaxin, et al. Deformation and mechanical performance of buried HDPE pipes reinforced by geogrids[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 38-44,68. doi: 10.3969/j.issn.0258-2724.2017.01.006
[9]	刘宽,肖成志,王子寒. 格栅防护埋地管道的承载特性及设计参数分析[J]. 深圳大学学报(理工版),2019,36(1): 52-60. doi: 10.3724/SP.J.1249.2019.01052 LIU Kuan, XIAO Chengzhi, WANG Zihan. Performance of bearing capacity and analysis of design parameters of buried pipelines with geogrid protection[J]. Journal of Shenzhen University (Science and Engineering), 2019, 36(1): 52-60. doi: 10.3724/SP.J.1249.2019.01052
[10]	肖成志,何晨曦,王嘉勇. 循环荷载作用下格栅防护柔性埋地管道的性能分析[J]. 岩土工程学报,2018,40(10): 1852-1861. doi: 10.11779/CJGE201810012 XIAO Chengzhi, HE Chenxi, WANG Jiayong. Performance of flexible buried pipes reinforced by geogrids under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(10): 1852-1861. doi: 10.11779/CJGE201810012
[11]	王卫华,李夕兵. 离散元法及其在岩土工程中的应用综述[J]. 岩土工程技术,2005,19(4): 177-181. doi: 10.3969/j.issn.1007-2993.2005.04.005 WANG Weihua, LI Xibing. A review on fundamentals of distinct element method and its applications in geotechnical engineering[J]. Geotechnical Engineering Technique, 2005, 19(4): 177-181. doi: 10.3969/j.issn.1007-2993.2005.04.005
[12]	崔晓艳,庄妍,张希栋,等. 循环荷载下桩承式路堤中土拱效应动力折减系数离散元研究[J]. 湖南大学学报(自然科学版),2022,49(9): 164-172. CUI Xiaoyan, ZHUANG Yan, ZHANG Xidong, et al. Discrete element analysis on dynamic reduction coefficient of soil arching effect in pile supported embankment under cyclic load[J]. Journal of Hunan University (Natural Sciences), 2022, 49(9): 164-172.
[13]	WANG Z J, RUIKEN A, JACOBS F, et al. A new suggestion for determining 2D porosities in DEM studies[J]. Geomechanics and Engineering, 2014, 7(6): 665-678. doi: 10.12989/gae.2014.7.6.665
[14]	WANG Z J, JACOBS F, ZIEGLER M. Experimental and DEM investigation of geogrid–soil interaction under pullout loads[J]. Geotextiles and Geomembranes, 2016, 44(3): 230-246. doi: 10.1016/j.geotexmem.2015.11.001
[15]	胡雄玉,晏启祥,何川,等. 土压平衡盾构掘进对散粒体地层扰动和开挖面破坏特性研究[J]. 岩石力学与工程学报,2016,35(8): 1618-1627. HU Xiongyu, YAN Qixiang, HE Chuan, et al. Study on the disturbance and excavation face failure feature of granular mixtures stratum due to EPB shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(8): 1618-1627.
[16]	刘勇,朱俊樸,闫斌. 基于离散元理论的粗粒土三轴试验细观模拟[J]. 铁道科学与工程学报,2014,11(4): 58-62. doi: 10.3969/j.issn.1672-7029.2014.04.010 LIU Yong, ZHU Junpu, YAN Bin. Meso-mechanical simulation study on triaxial test of coarse-grained soil based on DEM[J]. Journal of Railway Science and Engineering, 2014, 11(4): 58-62. doi: 10.3969/j.issn.1672-7029.2014.04.010
[17]	肖成志,杨亚欣,杨爱克,等. 静载作用下土工格栅加筋防护埋地管道力学性能实验研究[J]. 岩石力学与工程学报,2015,34(9): 1928-1937. XIAO Chengzhi, YANG Yaxin, YANG Aike, et al. Mechanical performance of buried pipes protected by geogrids under static load[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1928-1937.