Theoretical Method for Calculating Rail Deformation of Ballastless Railway Caused by Tunnel Undercrossing Based on Dual Beam Model
-
摘要:
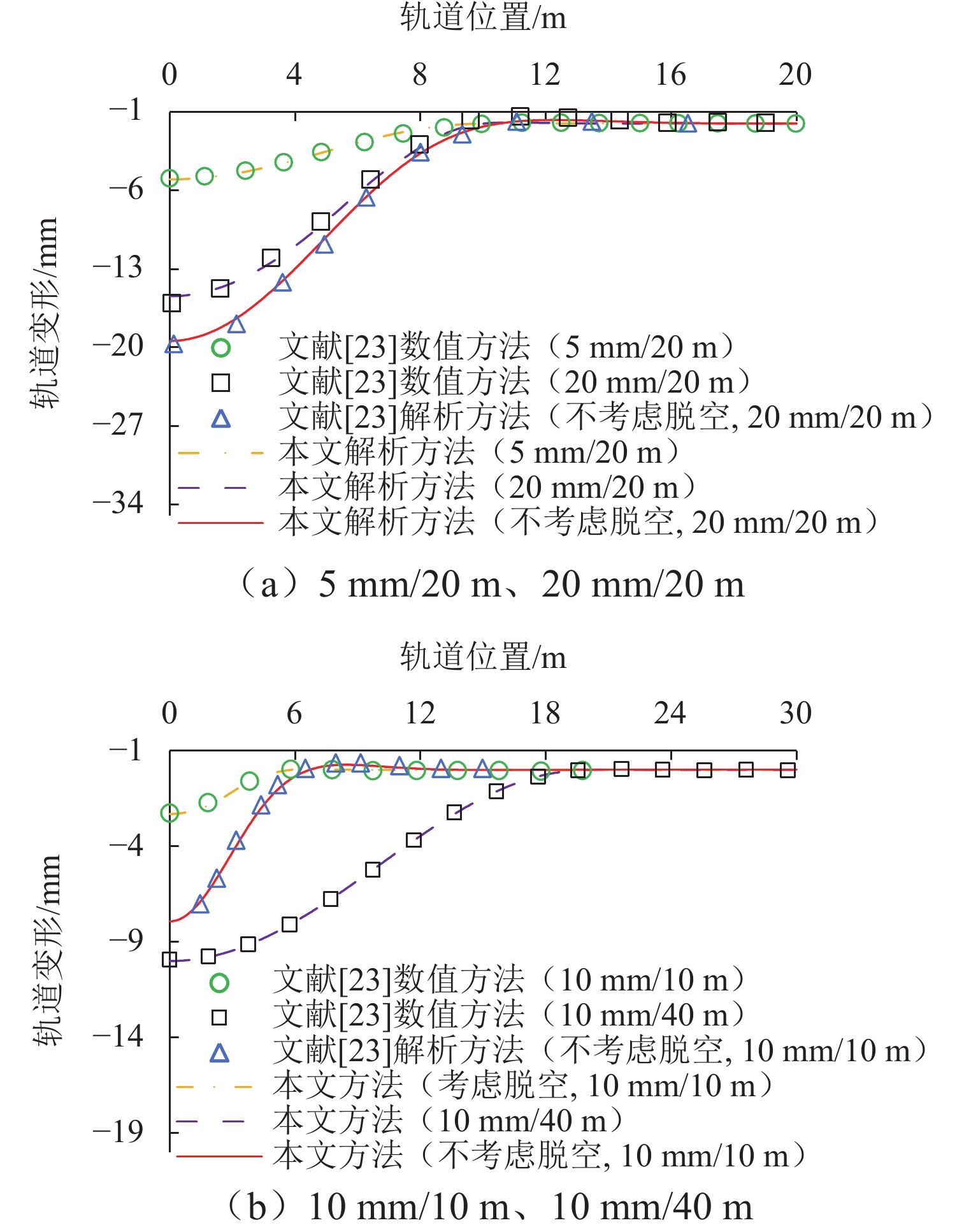
为研究隧道下穿无砟铁路轨道时板底部脱空对轨道变形的影响，提出一种改进的隧道下穿引起无砟铁路变形的计算方法. 首先，将无砟铁路轨道结构简化为双层地基梁模型，建立隧道下穿施工引起无砟铁路变形的控制方程；然后，将无砟铁路分为中间脱空段和两端接地段共三部分，推导隧道下穿施工诱发无砟铁路变形的计算式，对比路基不均匀沉降引起无砟轨道变形的理论计算值与数值模拟结果，验证了理论计算方法的正确性；最后，探讨了新建隧道埋深、隧道下穿施工引起周围地层的损失率，以及既有铁路与隧道间的水平夹角对无砟铁路轨道变形的影响. 研究结果表明：当隧道从铁路下方6 m处垂直穿越既有铁路时，轨道中点变形将达到最大值；隧道施工引起周围地层损失率从0.25%增大到2.50%时，轨道中点变形和轨道板底部脱空区宽度将分别增大4.0倍和2.2倍.
Abstract:To analyze the effect of a void under the track slab on the rail deformation of a ballastless railway caused by tunnel undercrossing, an improved calculation method was proposed to predicate the tunnel undercrossing-induced rail deformation of the ballastless railway. Firstly, the rail of the ballastless railway was simplified as a dual subgrade beam model, and the governing equation was established for the rail deformation of ballastless railway caused by tunnel undercrossing. Then, the ballastless railway was divided into three parts including the middle section above a void and the two sections connecting with the subgrade, and the formulas for the rail deformation of the ballastless railway caused by tunnel undercrossing were derived. The proposed theoretical calculation method was verified by comparing the theoretically calculated and numerically simulated results of rail deformation of the ballastless railway caused by uneven settlement of the subgrade. Finally, the influences of parameters on the rail deformation of the ballastless railway were discussed, including the burial depth of the new tunnel, the ground loss rate caused by tunnel undercrossing construction, and the intersection angle between the railway and the tunnel. The results show that when the undercrossing tunnel is 6 m below the railway, the deformation at the midpoint of the rail reaches the maximum. When the ground loss rate caused by tunnel undercrossing construction increases from 0.25% to 2.50%, the deformation at the midpoint of the rail and the width of the void under the track slab increase by 4.0 and 2.2 times, respectively.
-
Key words:
- rail deformation /
- tunnel undercrossing /
- dual beam model /
- Winkle foundation /
- theoretical method
-
图 1 隧道下穿既有铁路力学分析示意
Figure 1. Mechanical analysis of existing railway caused by tunnel undercrossing
图 4 隧道施工引起地层损失率的影响
Figure 4. Influence of ground loss rate caused by tunnel undercrossing construction
图 5 地铁线路与隧道水平夹角的影响
Figure 5. Influence of intersection angle between between railway and tunnel
表 1 无砟轨道材料参数
Table 1. Parameters of ballastless rail material
结构 弹性模量/Pa 泊松比 说明 钢轨 2.10 × 1011 0.30 T60 轨 道床板 3.25 × 1010 0.17 C40 混凝土 支承层 2.55 × 1010 0.17 C20 混凝土 路基 180 0.25 密度 300 kg/m3 
下载: 导出CSV
-
[1] 刘建友,赵勇,吕刚,等. 隧道下穿高速铁路路基风险分级及风险评价方法研究[J]. 现代隧道技术,2020,57(6): 8-16,54.LIU Jianyou, ZHAO Yong, LV Gang, et al. Research on risk classification and assessment method for tunnels crossing under high-speed railway subgrade[J]. Modern Tunnelling Technology, 2020, 57(6): 8-16,54. [2] 仇文革,万世付,高刚刚,等. 砂卵石地层盾构隧道下穿铁路咽喉区地表沉降控制研究[J]. 现代隧道技术,2021,58(5): 37-45.QIU Wenge, WAN Shifu, GAO Ganggang, et al. Study on the control measures against ground settlement induced by shield tunnel construction underneath railway throat in sandy cobble stratum[J]. Modern Tunnelling Technology, 2021, 58(5): 37-45. [3] 吕培林,周顺华. 软土地区盾构隧道下穿铁路干线引起的线路沉降规律分析[J]. 中国铁道科学,2007,28(2): 12-16. doi: 10.3321/j.issn:1001-4632.2007.02.003LV Peilin, ZHOU Shunhua. Analysis on upper rail settlement in soft ground resulting from shield tunnelling across main railway line[J]. China Railway Science, 2007, 28(2): 12-16. doi: 10.3321/j.issn:1001-4632.2007.02.003 [4] 孙连勇,黄永亮,王启民,等. 地铁盾构隧道下穿既有铁路变形控制研究[J]. 现代隧道技术,2018,55(5): 140-145,173.SUN Lianyong, HUANG Yongliang, WANG Qimin, et al. Study of controlling measures for existing railway deformation caused by metro shield tunnel under-passing construction[J]. Modern Tunnelling Technology, 2018, 55(5): 140-145,173. [5] 张乾,蔡小培,钟阳龙,等. 无砟轨道路基不均匀沉降区高速列车动力特性[J]. 西南交通大学学报,2023,58(1): 133-140.ZHANG Qian, CAI Xiaopei, ZHONG Yanglong, et al. Dynamic characteristics of high-speed trains in differential subgrade settlement zone of ballastless track[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 133-140. [6] 唐钱龙,李永恒,彭立敏,等. 盾构下穿施工变形条件下既有铁路行车限速标准研究[J]. 铁道科学与工程学报,2022,19(9): 2700-2708.TANG Qianlong, LI Yongheng, PENG Limin, et al. Study on speed limit standard of existing railway traffic under the deformation condition of shield tunneling construction[J]. Journal of Railway Science and Engineering, 2022, 19(9): 2700-2708. [7] KLAR A, VORSTER T E, SOGA K, et al. Elastoplastic solution for soil-pipe-tunnel interaction[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 782-792. doi: 10.1061/(ASCE)1090-0241(2007)133:7(782) [8] ZHANG Z G, HUANG M S, ZHANG M X. Deformation analysis of tunnel excavation below existing pipelines in multi-layered soils based on displacement controlled coupling numerical method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(11): 1440-1460. doi: 10.1002/nag.2098 [9] 杨成永,马文辉,费腾,等. 考虑轴力和剪切效应的盾构隧道纵向变形分析[J]. 西南交通大学学报,2022,57(1): 139-147.YANG Chengyong, MA Wenhui, FEI Teng, et al. Analysis of longitudinal deformation of shield tunnel structures with consideration of axial force and shear effect[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 139-147. [10] LI P, DU S J, WANG Y H, et al. Timoshenko beam solution for the response of existing tunnels because of tunneling underneath[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(5): 766-784. doi: 10.1002/nag.2426 [11] KLAR A, VORSTER T E B, SOGA K, et al. Soil-pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions[J]. Géotechnique, 2005, 55(6): 461-466. [12] LIU X, FANG Q, ZHANG D L, et al. Behaviour of existing tunnel due to new tunnel construction below[J]. Computers and Geotechnics, 2019, 110: 71-81. doi: 10.1016/j.compgeo.2019.02.013 [13] LIN C G, HUANG M S, NADIM F, et al. Tunnelling-induced response of buried pipelines and their effects on ground settlements[J]. Tunnelling and Underground Space Technology, 2020, 96: 103193.1-103193.17. doi: 10.1016/j.tust.2019.103193 [14] LIU X, JIANG A N, HAI L, et al. Study on soil gap formation beneath existing underground structures due to new excavation below[J]. Computers and Geotechnics, 2021, 139: 104379.1-104379.12. doi: 10.1016/j.compgeo.2021.104379 [15] 可文海,管凌霄,刘东海,等. 盾构隧道下穿管道施工引起的管-土相互作用研究[J]. 岩土力学,2020,41(1): 221-228,234.KE Wenhai, GUAN Lingxiao, LIU Donghai, et al. Research on upper pipeline-soil interaction induced by shield tunnelling[J]. Rock and Soil Mechanics, 2020, 41(1): 221-228,234. [16] 冯国辉,徐长节,郑茗旺,等. 新建隧道下穿既有隧道引起的隧-土相互作用研究[J]. 工程力学,2023,40(5): 59-68.FENG Guohui, XU Changjie, TEY Mingwang, et al. Study of tunnel-soil interaction induced by tunneling underlying[J]. Engineering Mechanics, 2023, 40(5): 59-68. [17] 黄晓林,周志刚,刘齐建. 浅埋隧道开挖引起的高铁轨道变形与内力分析[J]. 湖南科技大学学报(自然科学版),2019,34(1): 42-48.HUANG Xiaolin, ZHOU Zhigang, LIU Qijian. Study on internal forces and deformation of the high-speed rail by the excavation of the shallow tunnel[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2019, 34(1): 42-48. [18] DECK O, SINGH A. Analytical model for the prediction of building deflections induced by ground movements[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(1): 62-84. doi: 10.1002/nag.993 [19] 邹春华,周顺华,王炳龙,等. 路基不均匀沉降对有砟轨道沉降影响的模型试验[J]. 同济大学学报(自然科学版),2011,39(6): 862-869. doi: 10.3969/j.issn.0253-374x.2011.06.014ZOU Chunhua, ZHOU Shunhua, WANG Binglong, et al. Model test study of influence of differential subgrade settlement on ballasted track settlement[J]. Journal of Tongji University (Natural Science), 2011, 39(6): 862-869. doi: 10.3969/j.issn.0253-374x.2011.06.014 [20] 付龙龙,宫全美,周顺华,等. 列车荷载作用下有砟轨道轨面沉降与路基不均匀沉降间的相关关系[J]. 振动与冲击,2013,32(14): 23-28,39.FU Longlong, GONG Quanmei, ZHOU Shunhua, et al. Relationships between ballasted track settlement and differential subgrade settlement under train load[J]. Journal of Vibration and Shock, 2013, 32(14): 23-28,39. [21] 邹春华,周顺华,王长丹,等. 路基不均匀沉降引起有砟轨道沉降的计算方法[J]. 同济大学学报(自然科学版),2013,41(8): 1237-1242.ZOU Chunhua, ZHOU Shunhua, WANG Changdan, et al. Calculation method of ballasted track settlement caused by subgrade differential settlement[J]. Journal of Tongji University (Natural Science), 2013, 41(8): 1237-1242. [22] 张乾,蔡小培,钟阳龙,等. 路基沉降区双块式无砟轨道损伤行为与轨面不平顺分析[J]. 中南大学学报(自然科学版),2022,53(7): 2573-2581.ZHANG Qian, CAI Xiaopei, ZHONG Yanglong, et al. Analysis of damage and rail irregularity of double-block ballastless track in subgrade settlement area[J]. Journal of Central South University (Science and Technology), 2022, 53(7): 2573-2581. [23] 郭宇,高建敏,孙宇,等. 路基沉降与双块式无砟轨道轨面几何变形的映射关系[J]. 铁道学报,2016,38(9): 92-100.GUO Yu, GAO Jianmin, SUN Yu, et al. Mapping relationship between subgrade settlement and rail deflection of the double-block ballastless track[J]. Journal of the China Railway Society, 2016, 38(9): 92-100. [24] JIANG H G, LI X L, XIN G F, et al. Geometry mapping and additional stresses of ballastless track structure caused by subgrade differential settlement under self-weight loads in high-speed railways[J]. Transportation Geotechnics, 2019, 18: 103-110. doi: 10.1016/j.trgeo.2018.10.007 -
下载:
点击查看大图
计量
- 文章访问数: 220
- HTML全文浏览量: 138
- PDF下载量: 87
- 被引次数: 0