一种压缩感知测量矩阵的联合优化算法

杨柳; 白朝元; 范平志

doi:10.3969/j.issn.0258-2724.20230032

一种压缩感知测量矩阵的联合优化算法

doi: 10.3969/j.issn.0258-2724.20230032

杨柳^{1, 2, 3,},
白朝元^{1, 2,},
范平志^{1, 2, ,}

1.
西南交通大学信息科学与技术学院，四川成都 611756
2.
西南交通大学四川省信息编码与传输重点实验室，四川成都 611756
3.
西南交通大学综合交通大数据应用技术国家工程实验室，四川成都 611756

基金项目: 国家自然科学基金项目（62020106001，U2468201）

详细信息

作者简介:
杨柳（1978—），女，副教授，博士，研究方向为大规模物联网多址接入技术，E-mail：yangliu@swjtu.edu.cn

通讯作者:
范平志（1955—），男，教授，研究方向为信息与通信工程，E-mail：pzfan@swjtu.edu.cn

中图分类号: TN929.5
计量
- 文章访问数: 119
- HTML全文浏览量: 50
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-08
- 修回日期: 2023-04-25
- 网络出版日期: 2024-12-07

Co-optimization Algorithm for Measurement Matrix of Compressive Sensing

YANG Liu^{1, 2, 3
,},
BAI Chaoyuan^{1, 2
,},
FAN Pingzhi^{1, 2
, ,}

1.
School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756, China
2.
Information Coding & Transmission Key Lab of Sichuan Province, Southwest Jiaotong University, Chengdu 611756, China
3.
National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
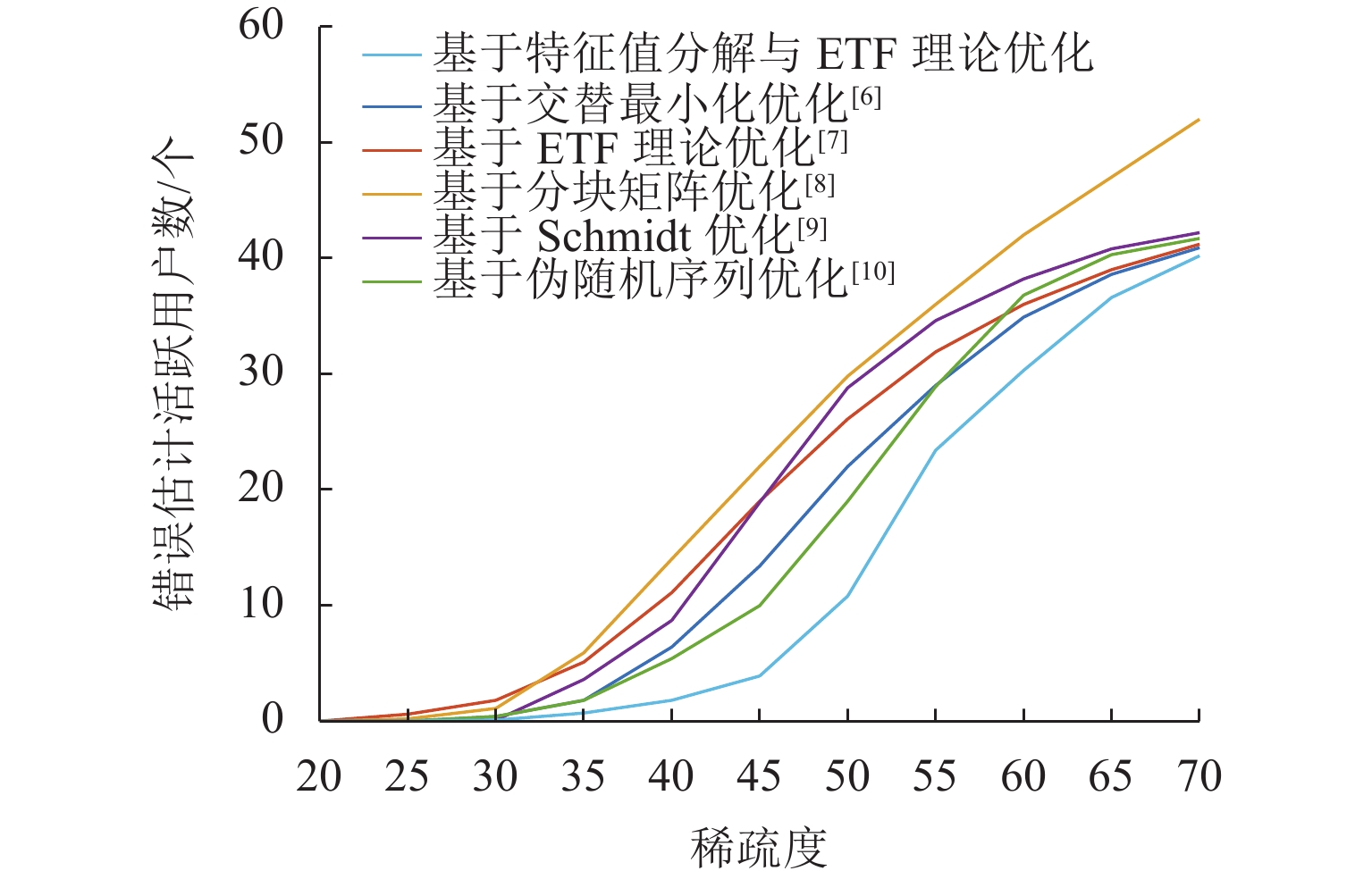
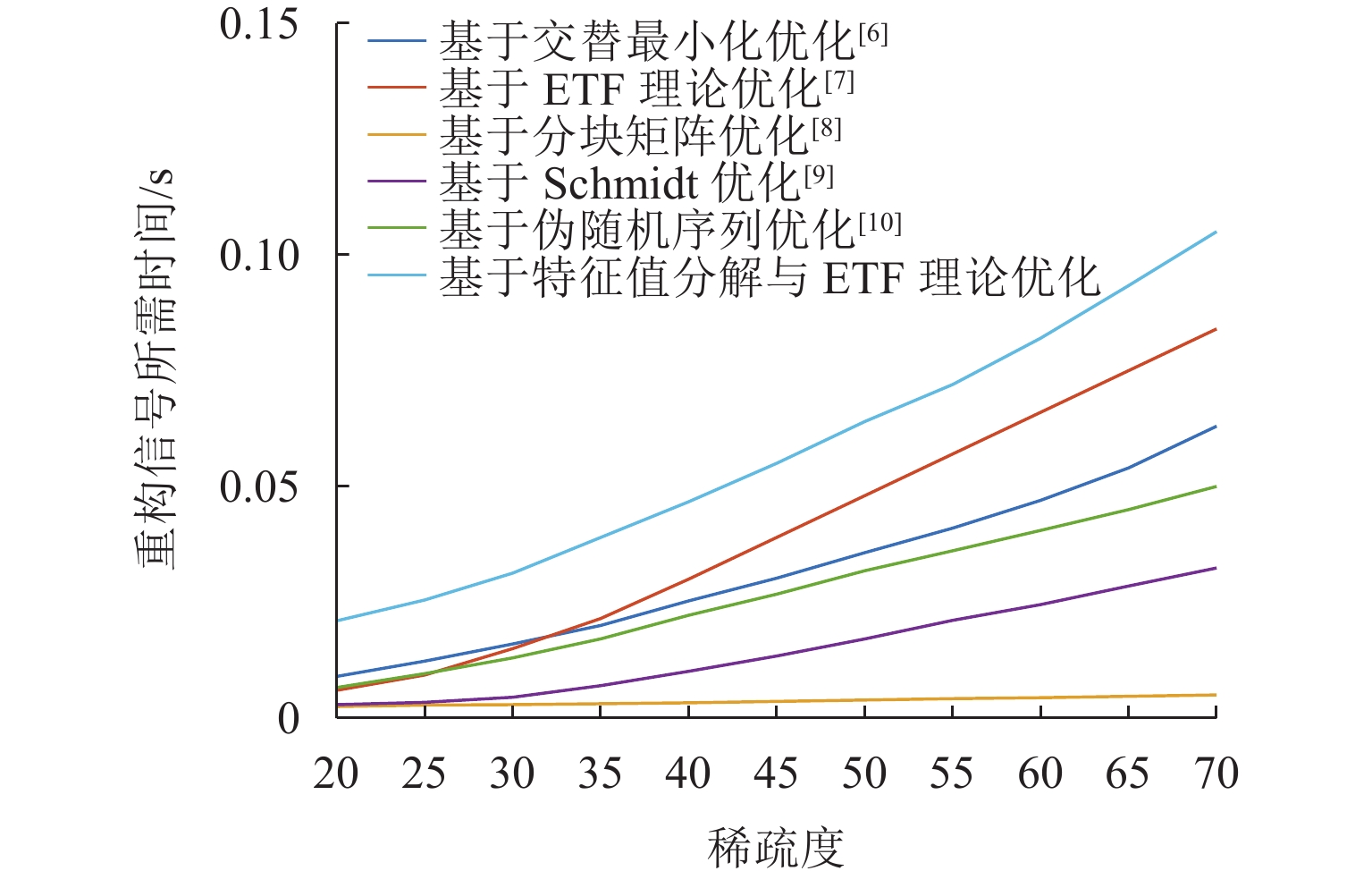
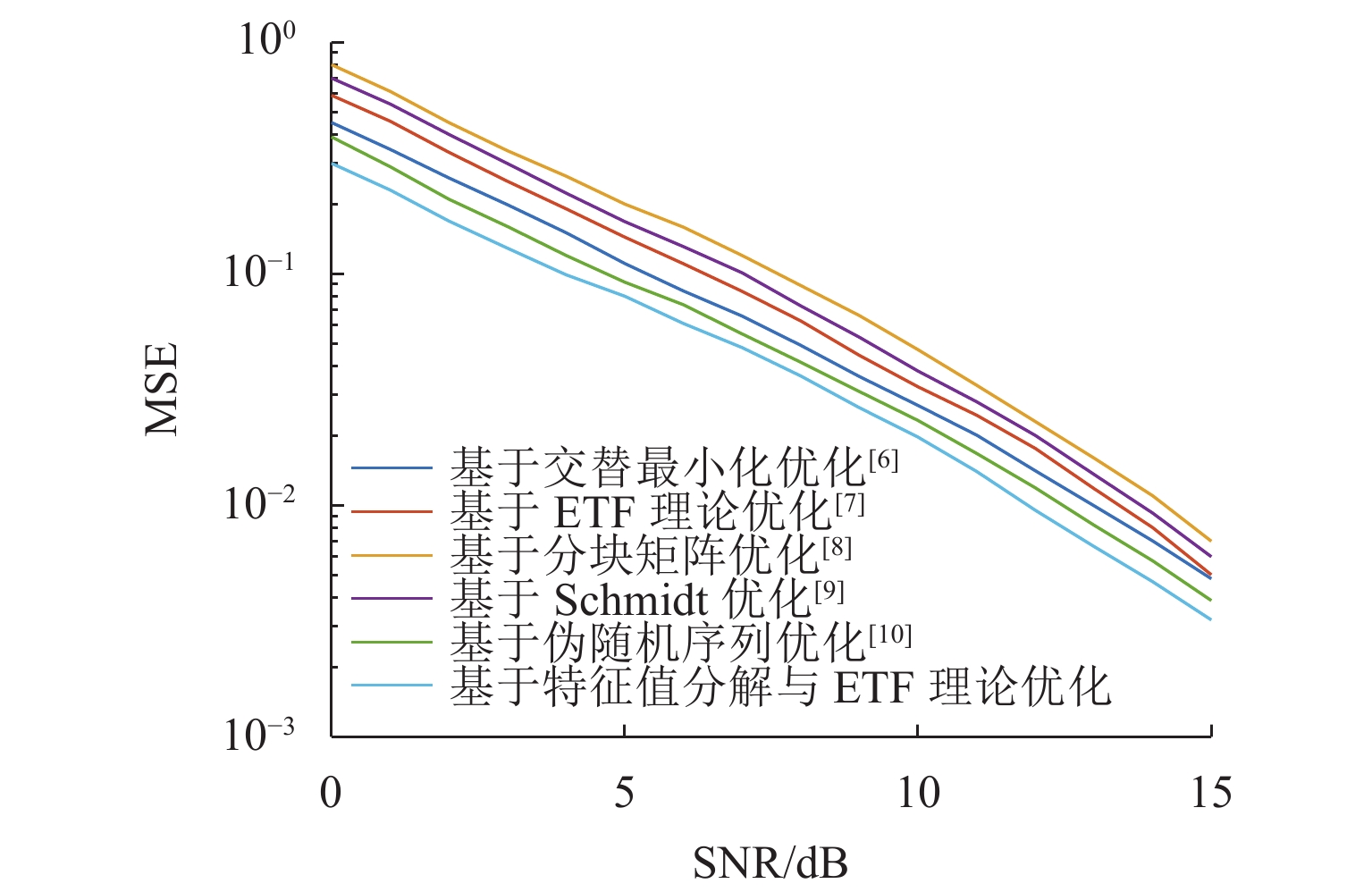
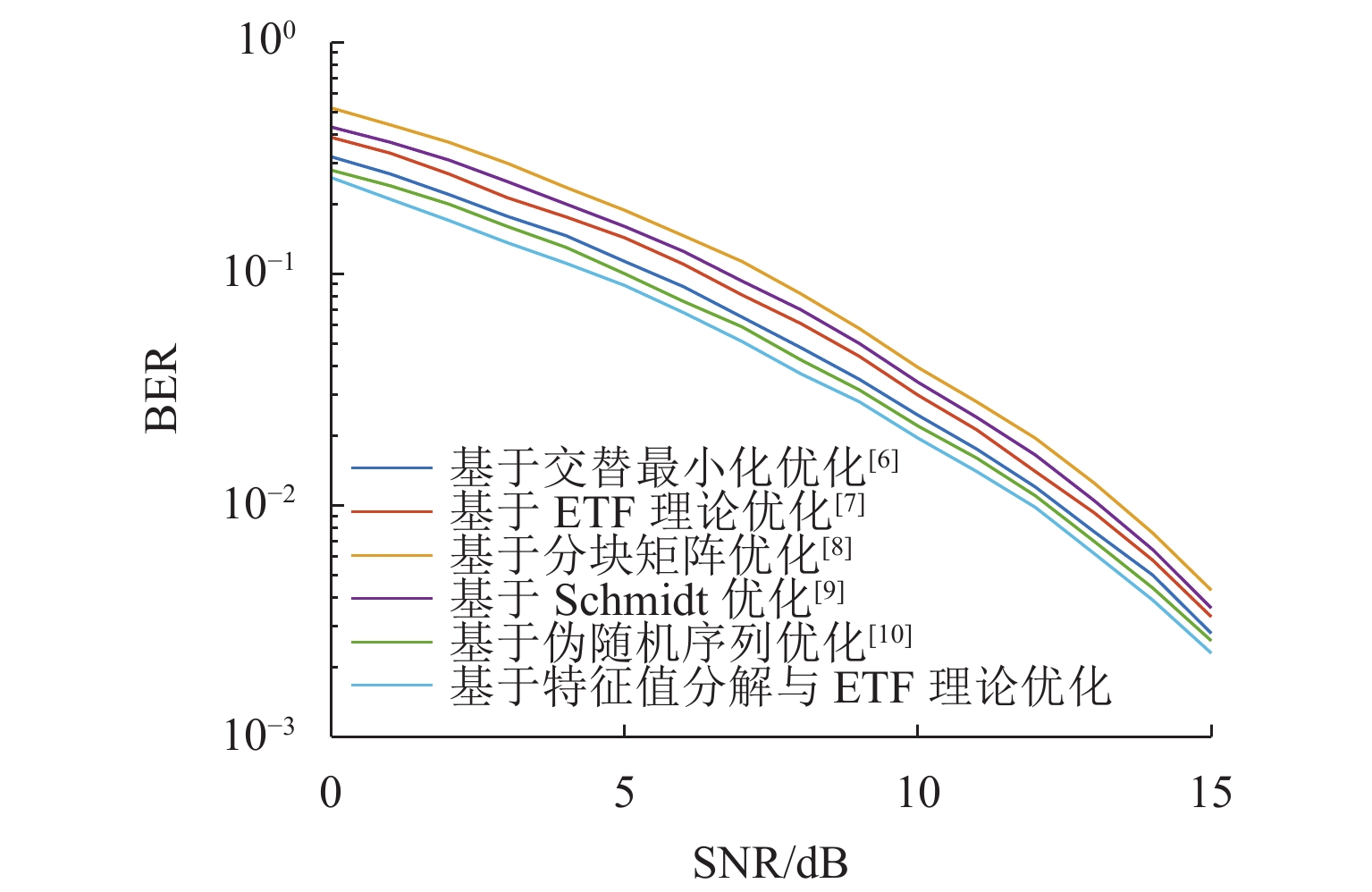
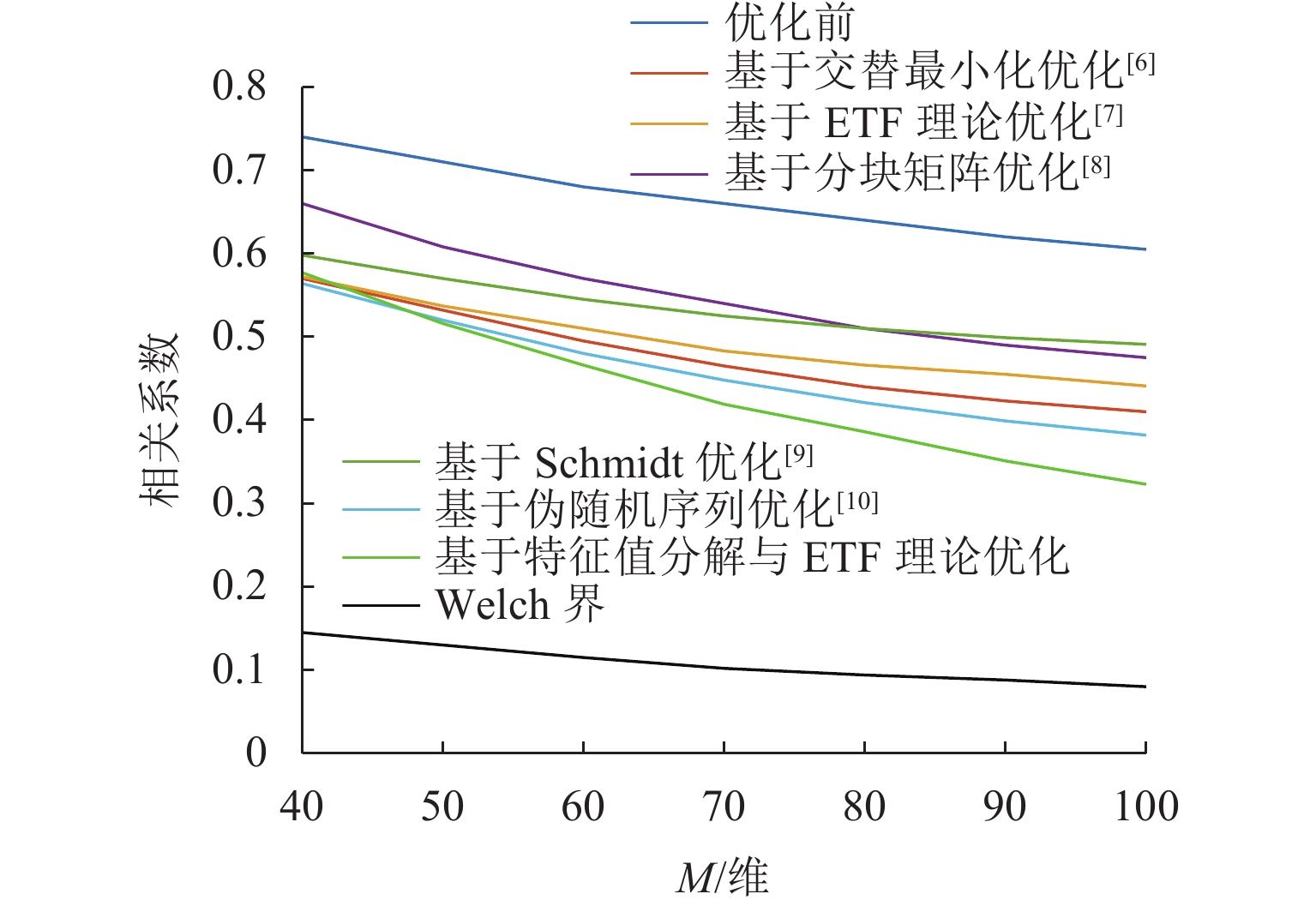
对于压缩感知算法，其测量矩阵与稀疏基之间的相关性往往决定了信号恢复精度. 为提升大规模通信场景下压缩感知算法重构信号的性能，基于矩阵分解与等角紧框架理论对测量矩阵进行改进. 首先，基于测量矩阵和稀疏基构造字典矩阵，并进一步构造Gram矩阵，利用特征值分解降低Gram矩阵的平均相关性；然后，基于等角紧框架理论与梯度缩减理论，通过使Gram矩阵逼近等角紧框架矩阵来减小Gram矩阵非主对角线元素的最大值，从而降低测量矩阵与稀疏基之间的最大相关性；最后，以正交匹配追踪（orthogonal matching pursuit， OMP）为重构算法进行仿真验证. 仿真结果表明：相比于优化前，矩阵相关系数降低40%～50%；在信道估计与活跃用户检测中，本文在较高稀疏度下的算法错误估计数比其他优化算法降低50%以上，信道估计的均方误差相比其他矩阵提升3 dB，误码率性能提升2 dB.
- 压缩感知 /
- 矩阵分解 /
- 等角紧框架理论 /
- 信道估计 /
- 活跃用户检测
Abstract:
For the compressive sensing algorithm, the correlation between measurement matrix and sparse base always determines the accuracy of signal recovery. In order to improve the performance of the compressive sensing algorithm in signal reconstruction in large-scale communication scenarios, the measurement matrix was improved based on matrix decomposition and equiangular tight frame (ETF) theory. Firstly, a dictionary matrix was constructed based on the measurement matrix and sparse base, and a Gram matrix was constructed. Eigenvalue decomposition was used to reduce the average correlation of the Gram matrix. Then, based on the ETF theory and gradient reduction theory, the Gram matrix was pushed to approach the ETF matrix to reduce the maximum value of the non-principal diagonal elements of the Gram matrix and the maximum correlation between the measurement matrix and the sparse basis. The orthogonal matching pursuit (OMP) algorithm was used as the reconstruction algorithm for simulation and verification, and the simulation results show that after optimization, the correlation coefficient of the matrix is reduced by 40%–50%. In channel estimation and active user detection, the estimation error of active user number by the proposed algorithm is more than 50% lower than that by other optimization algorithms under high sparsity; compared with other matrices, the mean square error of channel estimation is improved by 3 dB, and the bit error rate performance is improved by 2 dB.
- compressed sensing /
- matrix decomposition /
- equiangular tight frame theory /
- channel estimation /
- active user detection

HTML全文

图 1 相关系数随观测维度M的变化

Figure 1. Variation of correlation coefficient with observed dimension M

下载: 全尺寸图片幻灯片

图 2 不同稀疏度下错误估计用户数比较

Figure 2. Comparison of estimation errors of user number under different sparsity

下载: 全尺寸图片幻灯片

图 3 不同稀疏度下单次重构时间比较

Figure 3. Comparison of single reconstruction time under different sparsity

下载: 全尺寸图片幻灯片

图 4 不同SNR下的MSE比较

Figure 4. Comparison of MSEs under different SNRs

下载: 全尺寸图片幻灯片

图 5 不同SNR下的BER比较

Figure 5. Comparison of BERs under different SNRs

下载: 全尺寸图片幻灯片

表 1 参数表

Table 1. Parameters

参数名称	参数值
$ \boldsymbol{\varPhi } $	随机导频矩阵
$ {\boldsymbol{\varPsi }}$	单位矩阵
t/次	1000
$ \beta $	0.01
信道类型	随机瑞利衰落
导频长度	100
信号长度	256
潜在用户数/人	30

下载: 导出CSV

参考文献(23)

[1]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582
[2]	SENEL K, LARSSON E G. Grant-free massive MTC-enabled massive MIMO: a compressive sensing approach[J]. IEEE Transactions on Communications, 2018, 66(12): 6164-6175. doi: 10.1109/TCOMM.2018.2866559
[3]	ROBAEI M, AKL R, CHATAUT R, et al. Adaptive millimeter-wave channel estimation and tracking[C]//2022 24th International Conference on Advanced Communication Technology (ICACT). PyeongChang: IEEE, 2022: 23-28.
[4]	DUAN L G, YANG X Y, LI A P. WSN data compression model based on K-SVD dictionary and compressed sensing[C]//International Conference of Pioneering Computer Scientists, Engineers and Educators. Singapore: Springer, 2021: 429-442.
[5]	JIANG R K, WANG X T, CAO S, et al. Joint compressed sensing and enhanced whale optimization algorithm for pilot allocation in underwater acoustic OFDM systems[J]. IEEE Access, 2019, 7: 95779-95796. doi: 10.1109/ACCESS.2019.2929305
[6]	曾祥洲. 基于压缩感知块结构信号的稀疏表示与重构算法研究[D]. 广州: 华南理工大学,2016.
[7]	XU Q R, SHENG Z C, FANG Y, et al. Measurement matrix optimization for compressed sensing system with constructed dictionary via Takenaka-Malmquist functions[J]. Sensors, 2021, 21(4): 1229.1-1229.14.
[8]	宋儒瑛,张朝阳. 基于分块矩阵法优化测量矩阵的研究[J]. 太原师范学院学报(自然科学版),2022,21(2): 1-7.
[9]	魏从静. 压缩感知中测量矩阵的构造与优化研究[D]. 南京: 南京邮电大学,2016.
[10]	HE J A, WANG T, WANG C F, et al. Improved measurement matrix construction with pseudo-random sequence in compressed sensing[J]. Wireless Personal Communications, 2022, 123(4): 3003-3024. doi: 10.1007/s11277-021-09274-6
[11]	BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. doi: 10.1109/MSP.2007.4286571
[12]	DONOHO D L, ELAD M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ¹ minimization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2003, 100(5): 2197-2202.
[13]	TROPP J A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. doi: 10.1109/TIT.2004.834793
[14]	郭桂祥. 基于非凸优化方法的压缩感知SAR成像研究[D]. 南京: 南京信息工程大学,2022.
[15]	WU Q S, FU Y, ZHANG Y D, et al. Structured Bayesian compressive sensing exploiting dirichlet process priors[J]. Signal Processing, 2022, 201: 108680.1-108680.15.
[16]	WANG B C, MIR T, JIAO R C, et al. Dynamic multi-user detection based on structured compressive sensing for IoT-oriented 5G systems[C]//2016 URSI Asia-Pacific Radio Science Conference (URSI AP-RASC). Seoul: IEEE, 2016: 431-434.
[17]	JIANG X H, LI N, GUO Y, et al. Sensing matrix optimization for multi-target localization using compressed sensing in wireless sensor network[J]. China Communications, 2022, 19(3): 230-244. doi: 10.23919/JCC.2022.03.017
[18]	TSILIGIANNI E, KONDI L P, KATSAGGELOS A K. Approximate equiangular tight frames for compressed sensing and CDMA applications[J]. EURASIP Journal on Applied Signal Processing, 2017, 2017(1): 66.1-66.14.
[19]	ELAD M. Optimized projections for compressed sensing[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5695-5702. doi: 10.1109/TSP.2007.900760
[20]	SARDY S, BRUCE A G, TSENG P. Block coordinate relaxation methods for nonparametric wavelet denoising[J]. Journal of Computational and Graphical Statistics, 2000, 9(2): 361-379. doi: 10.1080/10618600.2000.10474885
[21]	WANG G, NIU M Y, FU F W. Deterministic constructions of compressed sensing matrices based on codes[J]. Cryptography and Communications, 2019, 11(4): 759-775. doi: 10.1007/s12095-018-0328-z
[22]	YI R J, CUI C, WU B, et al. A new method of measurement matrix optimization for compressed sensing based on alternating minimization[J]. Mathematics, 2021, 9(4): 329.1-329.19.
[23]	YU L F, LI G, CHANG L P. Optimizing projection matrix for compressed sensing systems[C]//2011 8th International Conference on Information, Communications & Signal Processing. Singapore: IEEE, 2011: 1-5.