Fracture Mechanism of Cologne-Egg Fastener Clips in Rail Corrugation Sections
-
摘要:
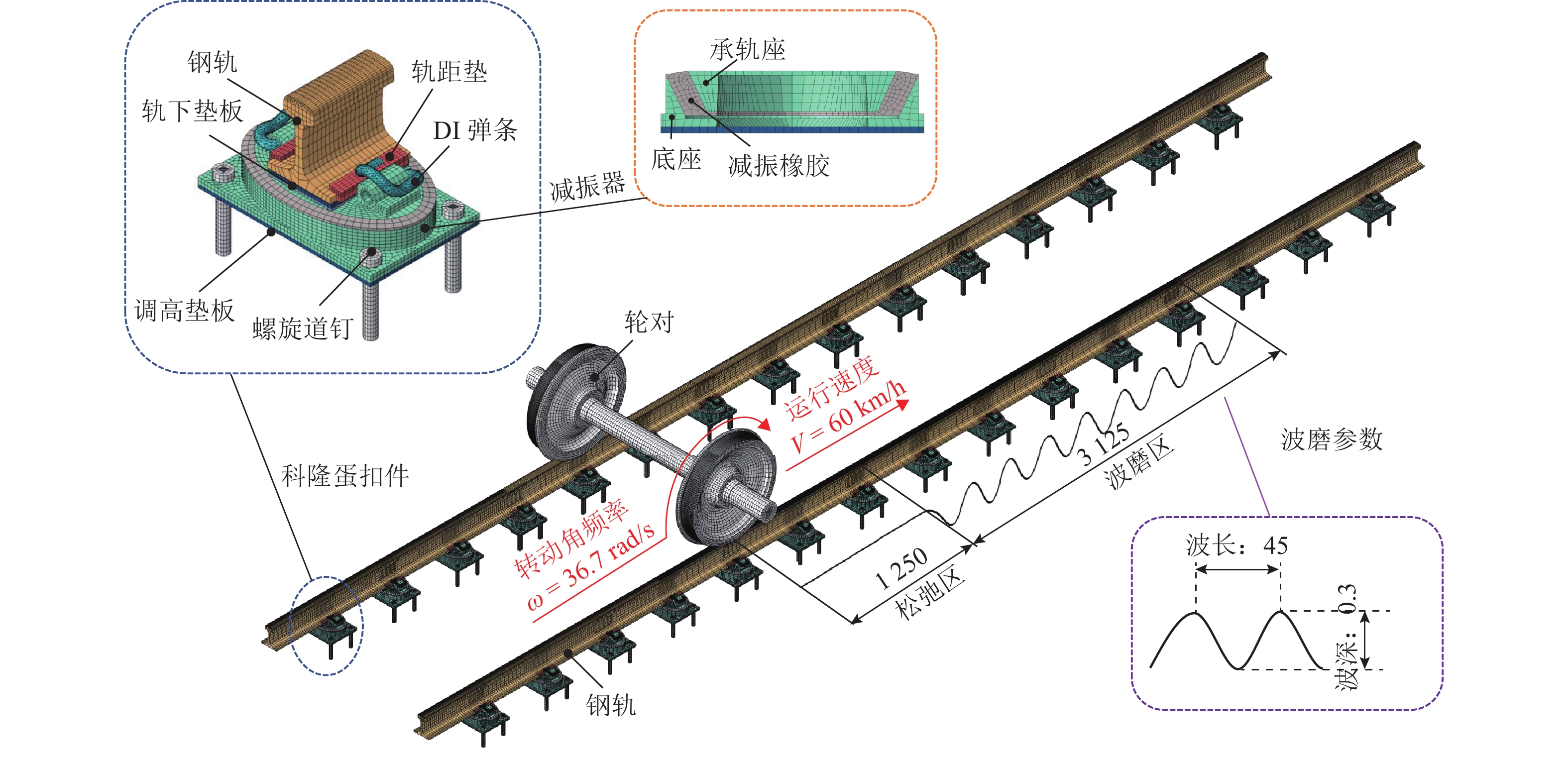
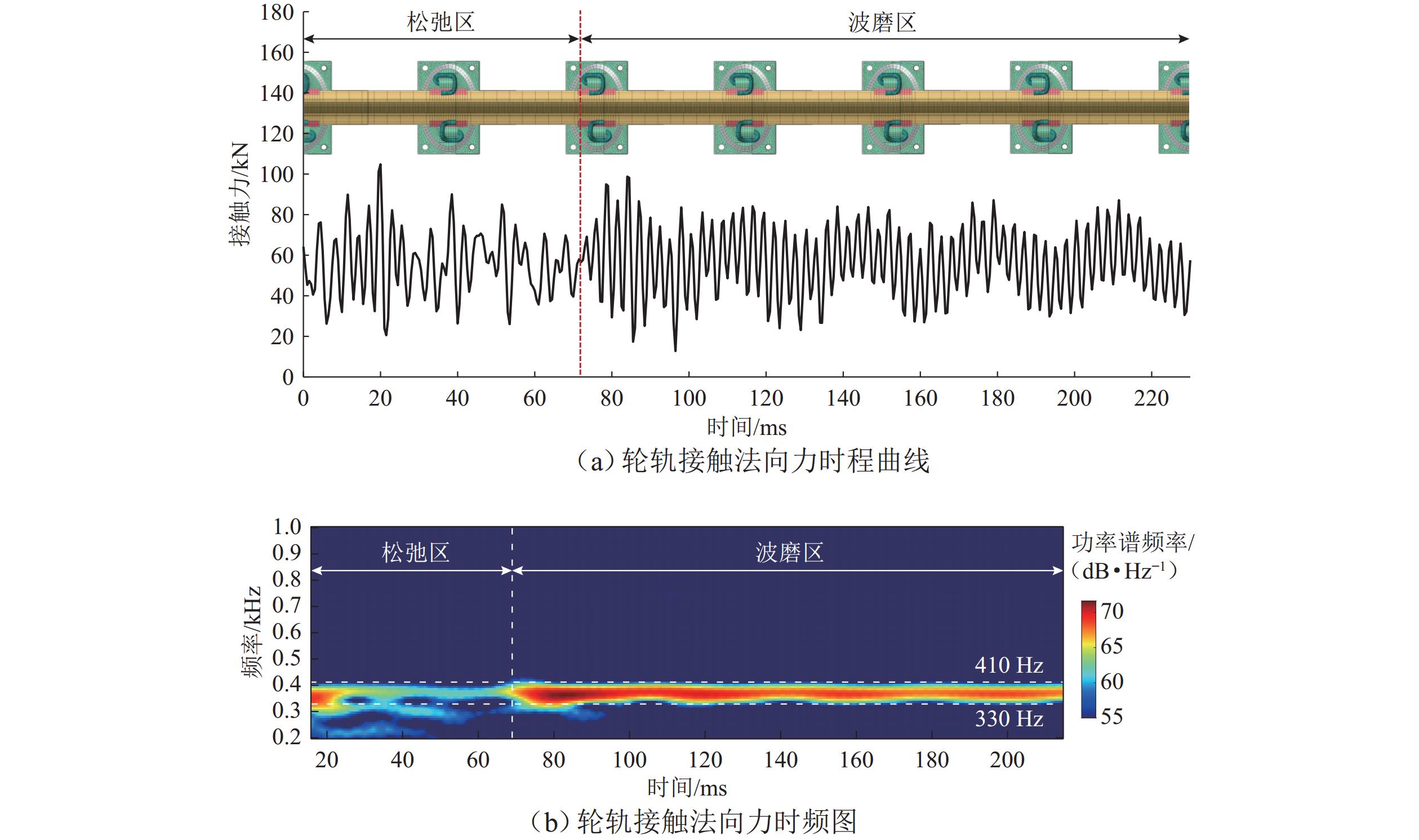
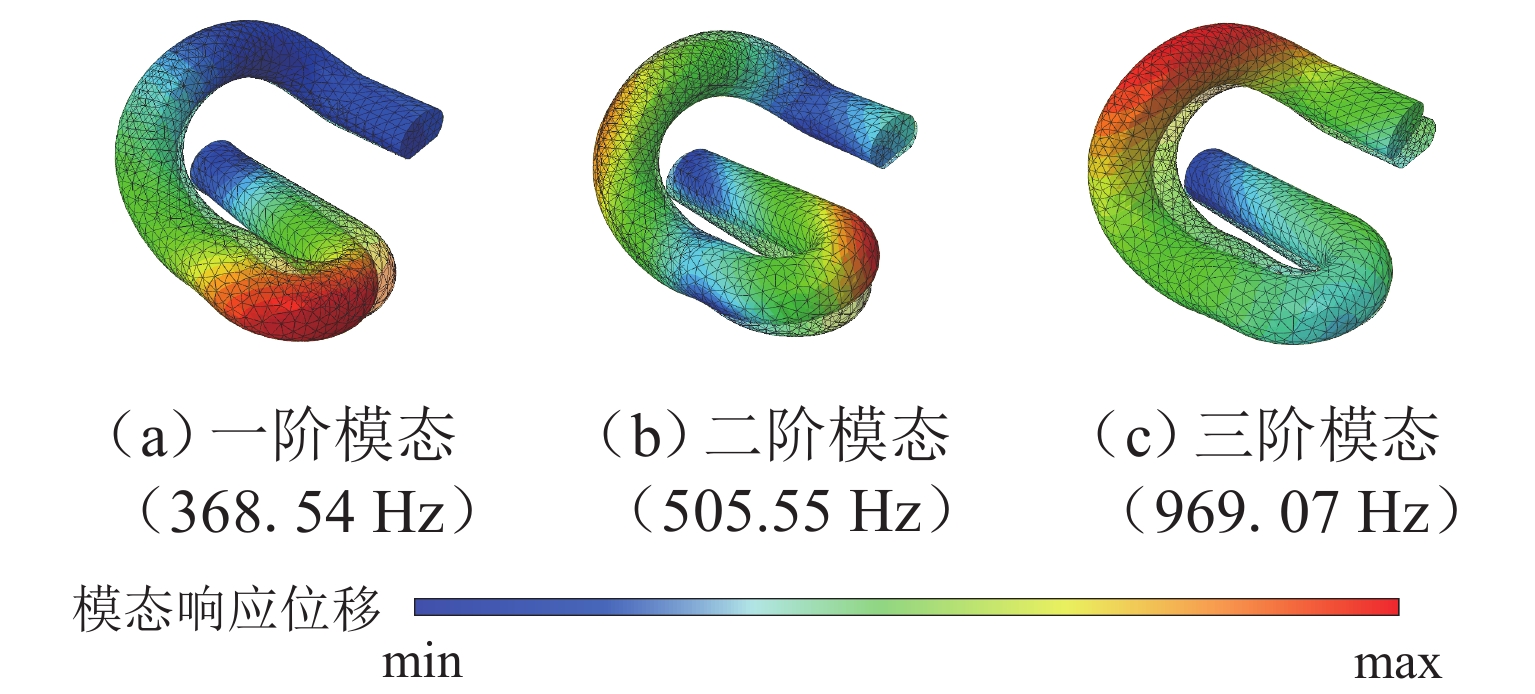
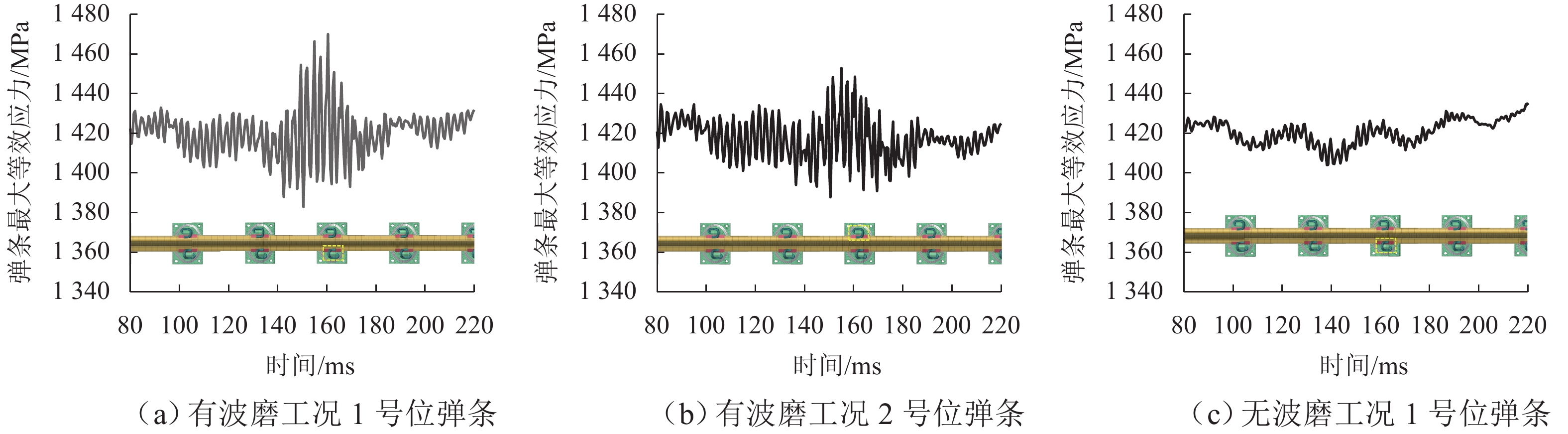
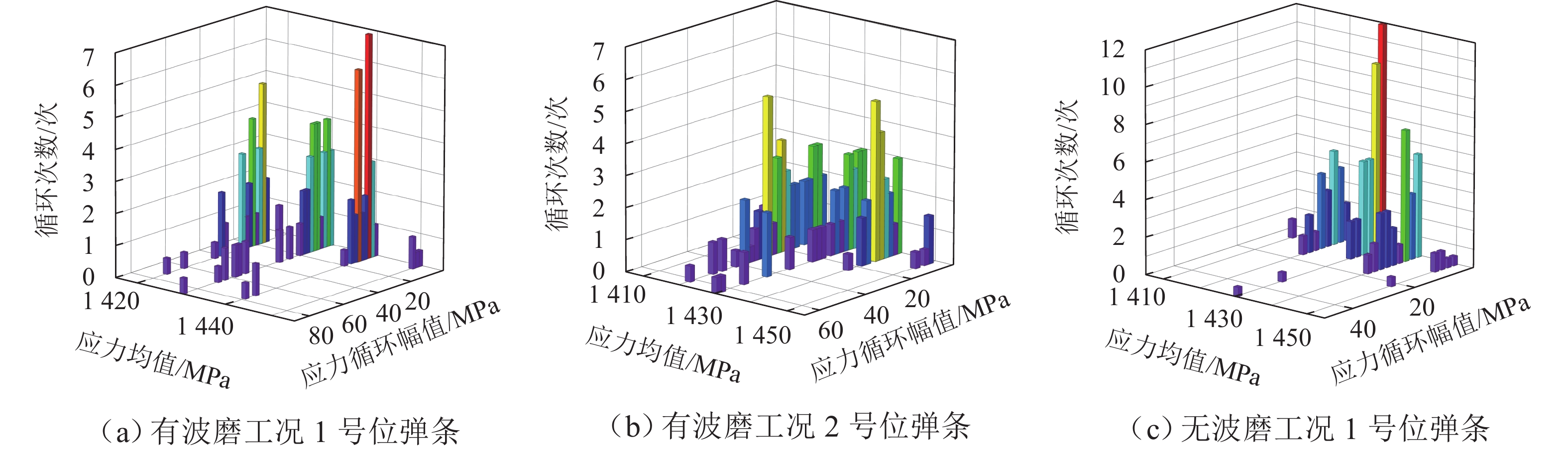
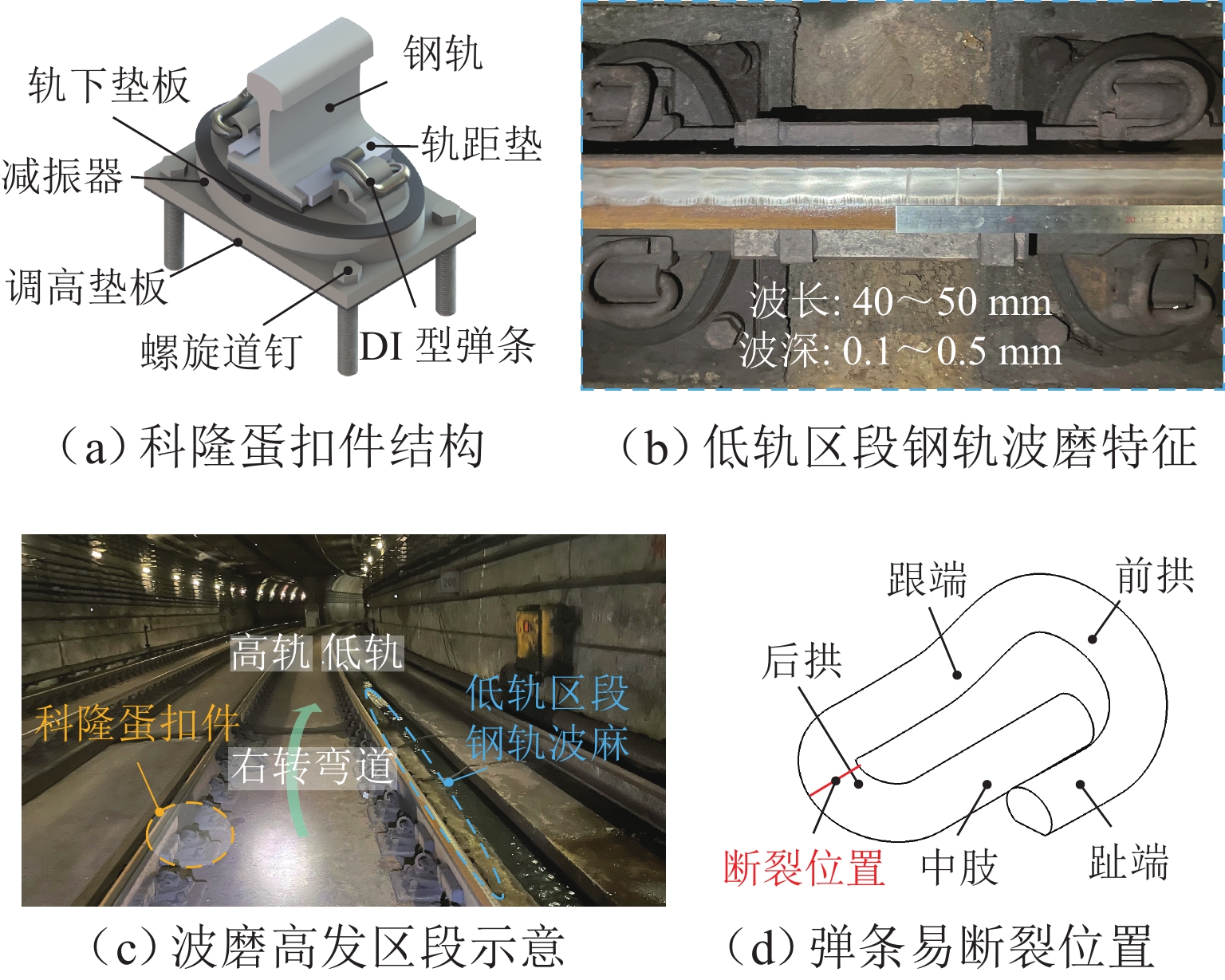
钢轨波磨作为地铁线路的典型钢轨损伤形式，其高发区段常伴随着扣件弹条断裂问题，严重影响列车的运营安全. 其中，科隆蛋扣件小半径区段是钢轨波磨的高发区段. 为探究科隆蛋扣件弹条的断裂机理，首先结合现场调研，构建包含完整科隆蛋扣件的轮对-钢轨-扣件系统有限元模型；然后，从共振响应的角度探究轮轨摩擦耦合振动激励下科隆蛋扣件弹条的共振响应；最后，从疲劳寿命角度，对比有无波磨区段科隆蛋扣件弹条的疲劳寿命情况，并以此量化不同弹条的疲劳损伤情况. 研究结果表明：在钢轨波磨高发区段，轮轨摩擦耦合振动主频与科隆蛋扣件弹条一阶约束模态一致，轮轨摩擦耦合振动引起的弹条共振是科隆蛋扣件断裂的主要原因；钢轨波磨加剧了轮轨摩擦耦合振动，使得科隆蛋扣件弹条寿命相较无波磨区段下降99.04%，仅为设计寿命的3.11%；此外，科隆蛋扣件小半径曲线区段低轨工作边一侧的弹条更容易发生疲劳失效，失效位置位于其弹条后拱端内侧.
Abstract:As typical rail damage of the railway, rail corrugation is often accompanied by the fastener clip fracture, which seriously affects the operation safety of the train. Moreover, the small-radius section of the Cologne-egg fastener experiences frequent rail corrugation. To explre the fracture mechanism of Cologne-egg fastener clips, firstly, the finite element model of the wheel set-rail-fastener system, including the complete Cologne-egg fastener model, was established baesd on the field investigation. Then, the resonant response of the Cologne-egg fastener clip was explored, considering the frictional coupling vibration of the wheel-rail system. Finally, the fatigue life of the Cologne-egg fastener clip was compared in the cases of with and without rail corrugation sections, and the fatigue damage of different clips was quantified. The results show that the dominant frequency of the frictional coupling vibration of the wheel-rail system is consistent with the first-mode constraint mode of the Cologne-egg fastener clip in the frequent rail corrugation sections, which indicates that the clip resonance induced by the frictional coupling vibration of the wheel-rail system is the main reason for the Cologne-egg fastener fracture. The frictional coupling vibration of the wheel-rail system is aggravated by the rail corrugation, which makes the clip life of the Cologne-egg fastener in the rail corrugation section decrease by 99.04% compared with that in the absence of rail corrugation section. The clip life is thus only 3.11% of the design clip life. Besides, the Cologne-egg fastener clip on the low gauge side is more prone to fatigue failure in the small-radius curved section, and the failure position is located on the inner side of the rear arch end of the clip.
-
随着交通强国战略的实施，我国地铁线路的建设发展迅猛. 但随着地铁建设规模的急剧扩大，其运营成本尤其是基础设施维护成本与日俱增. 作为地铁线路典型轨道损伤问题，钢轨波磨是一种钢轨表面出现波浪形的周期性磨耗问题[1]. 钢轨波磨加剧了轮轨冲击，加速了车辆设备和线路设施服役性能的劣化和失效进程[2-3]，特别是在钢轨波磨高发区段伴随着大量的扣件弹条断裂，严重影响列车运营安全[4-6].
为探究扣件弹条的断裂机理，国内外学者主要从共振响应、疲劳失效角度开展研究. 共振响应角度：Ling等[7]结合线路检测、列车-轨道动力学模型与局部扣件有限元模型，发现特定的线路半径和钢轨波磨会引发弹条的断裂；Wang等[8-9]则认为弹条固有频率与波磨区段轮轨间振动主频的一致引发了弹条共振，进而导致弹条的断裂. 疲劳失效的角度：刘玉涛等[10]结合疲劳分析方法与数学统计方法，评价扣件弹条的服役可靠性；辛涛等[11-12]采用疲劳分析方法，探究了不同扣件和波磨参数对弹条疲劳寿命的影响；还有学者结合疲劳试验，探究安装状态[13-14]、弹条的加工工艺[15]等因素对弹条疲劳寿命的影响. 现有关于扣件弹条断裂机理的研究，一方面仅从扣件弹条系统共振响应或疲劳失效的单一角度开展分析，缺乏对两者共同作用的综合考虑；另一方面，大多数研究都没有建立能够还原系统中轮轨摩擦耦合振动关系的数值模型. 如Ling等[7]建立了弹条及部分相邻接触部位的数值模型，辛涛等[11]建立了完整的扣件数值模型，潘兵等[9]建立了钢轨、轮对和由弹簧单元代替扣件系统的数值模型，但这些学者都忽略了钢轨波磨区段特殊的轮轨耦合关系和复杂线路特性对于扣件弹条共振响应的影响. 因此，综合考虑共振响应和疲劳失效的相互作用，建立一个完整包括轮轨系统和扣件系统的数值模型，有助于更加准确地揭示钢轨波磨区段扣件弹条的断裂机理.
本文从共振响应和疲劳失效角度探究钢轨波磨高发区段科隆蛋扣件弹条的断裂机理. 首先，基于现场调研数据，建立包含钢轨波磨不平顺的科隆蛋扣件的轮对-钢轨-扣件有限元模型. 然后，通过共振响应分析和疲劳失效分析，探究钢轨波磨区段轮轨摩擦耦合振动激励下科隆蛋扣件弹条的共振响应及其共振状态下的疲劳寿命，进而揭示钢轨波磨高发区段科隆蛋扣件弹条的断裂机理.
1. 现场调研和数值模型
1.1 科隆蛋扣件支撑区段现场调研
科隆蛋扣件区段作为钢轨波磨的高发区段，其钢轨波磨在小半径曲线轨道上尤为严重，并伴随扣件断裂问题，如图1所示. 本文对重庆地铁一号线的小什字—较场口区段进行了现场调研. 该区段采用Ⅲ型科隆蛋减震扣件支撑，主要由DI型弹条、减振器、轨距垫、螺旋道钉、轨下垫板和调高垫板组成. 其中，DI型弹条是一种典型的“e”型弹条，可以划分为中肢、后拱、跟端、前拱和趾端5个具体部位. 在科隆蛋扣件支撑的直线和小半径曲线段均有波磨发生，在小半径曲线段尤为严重. 本文着重调研了K1.261—K2.050区段曲线半径为350 m处的钢轨波磨. 该区段列车运营速度在60 km/h左右，此处钢轨波磨主要发生在该小半径曲线轨道的低轨处，波长为40～50 mm，波深为0.1～0.5 mm. 调研发现，在该钢轨波磨高发区段出现了部分扣件弹条断裂，断裂位置主要集中在后拱附近.
图 1 科隆蛋扣件区段钢轨波磨及扣件断裂特征Figure 1. Rail corrugation and fastener fracture characteristics of Cologne-egg fastener section1.2 轮对-钢轨-扣件系统的有限元模型
为还原包含完整科隆蛋扣件的轮对-钢轨-扣件系统模型当中复杂的轮轨摩擦耦合振动关系，以及科隆蛋扣件弹条在该复杂系统当中的共振响应，本文结合现场调研，构建包含完整科隆蛋扣件的轮对-钢轨-扣件系统的有限元模型，如图2所示，其材料属性如表1所示. 该模型主要由轮轨子系统和扣件子系统组成. 在轮轨子系统中，包含轮对和钢轨，轮对的车轮滚动圆直径为840 mm，车轮踏面为LM型踏面，轮对运行速度设为60 km/h. 在外侧和内侧车轴两端分别采用耦合方式加载40.87 kN和28.23 kN的垂向悬挂力[16]. 钢轨设为16跨长度，两端采用固定约束. 为模拟轮对通过钢轨波磨的振动响应，需将钢轨划分为松弛区和波磨区，松弛区为
1250 mm，波磨区为3125 mm. 其中，对波磨区进行网格细化，采用谐波函数模拟钢轨波磨，波长设为45 mm，波深设为0.3 mm. 此外，轮轨接触采用面-面接触，摩擦系数设为0.4. 根据车辆-轨道系统动力学分析结果，确定科隆蛋扣件小半径曲线区段的轮轨接触位置，此时轮对外轮轮缘与高轨轨头侧面接触，轮对内轮踏面与低轨轨头顶面接触[17].部件 弹性模量/Pa 泊松比 密度/
（kg•m−3）轮对 210.00×109 0.30 7800 钢轨 206.00×109 0.30 7800 DI 弹条 206.00×109 0.30 7800 轨距垫 6.20×109 0.35 1400 调高垫板 6.00×106 0.45 1190 承轨座/底座 170.00×109 0.30 7900 减振橡胶 5.58×106 0.49 1190 在扣件子系统中，本文较为完整地构建了科隆蛋扣件的有限元模型. 其中，减振器由承轨座、减振橡胶和底座构成，减振橡胶底面与底座间留有3 mm竖直间距，扣件间距为625 mm[18]. 各部件之间的接触属性如表2所示.
接触对 接触方式 主面 从面 摩擦系数 轮对-轨道 摩擦 轮面 轨面 0.4 弹条-减振器板 摩擦 弹条 减振器板 0.3 弹条-轨距块 摩擦 弹条 轨距块 0.7 轨道-轨距块 绑定 轨距块 轨道 轨下垫板-
钢轨绑定 轨下垫板 钢轨 轨下垫板-
承轨座绑定 轨下垫板 承轨座 需要特别说明的是，科隆蛋扣件的扣压力是由弹条形变提供的，故需要在轮对-钢轨-扣件系统的有限元模型中还原科隆蛋扣件弹条的扣压过程. 如图3所示，本文采取的扣压模拟方式如下：首先，在弹条趾端施加随时间线性增加的竖直拉力F，直至扣件弹条趾端平面略高于轨距块接触表面，期间需要暂时约束承轨座，以保证扣压过程平稳；然后，使得弹条与轨距块的接触生效，并使施加在弹条趾端的力逐步减小至0，期间弹条会与轨距块直接接触，并产生相应的弹条扣压力以完成安装.
图 3 科隆蛋扣件弹条扣压过程模拟Figure 3. Simulation of Cologne-egg fastener clip compression process2. 分析理论
2.1 轮轨摩擦耦合振动分析理论
为探究钢轨波磨高发区段的科隆蛋扣件弹条断裂的振动诱因，需研究轮对通过钢轨波磨高发区段的轮轨摩擦耦合振动特性. 显式瞬时动态分析是一种从时域研究轮轨摩擦耦合振动的常用方法[20]. 显式瞬时动态分析过程中，将在初始分析步建立总系统平衡方程，如式（1）所示.
$$ {\boldsymbol{M}}{{\boldsymbol{\ddot x}}_t} = {{\boldsymbol{P}}_{t}} - {{\boldsymbol{I}}_{t}} ，$$ (1) 式中：M为系统的对角集中质量矩阵，$ {{\boldsymbol{ x}}_t} $为系统的位移向量，Pt为系统所受外力向量，It为系统的内力向量，t为时间.
系统加速度向量为
$$ {{\boldsymbol{\ddot x}}_t} = \frac{{{{\boldsymbol{P}}_t} - {{\boldsymbol{I}}_t}}}{{\boldsymbol{M}}} .$$ (2) 利用中心差分法进行积分，便可得出该系统在t +Δt时的系统速度以及t+2Δt时的系统位移， Δt为单个时间增量步，定义中间增量t+Δt和t−Δt，于是有
$$ \boldsymbol{\dot{x}}_{t+\Delta t}=\boldsymbol{\dot{x}}_{t-\Delta t}+\frac{\Delta T_{t+2\Delta t}+\Delta T_t}{2}\boldsymbol{\ddot{x}}_t， $$ (3) $$ \boldsymbol{x}_{t+2\Delta t}=\boldsymbol{x}_t+\Delta T_{t+2\Delta t}\boldsymbol{\dot{x}}_{t+\Delta t}, $$ (4) 式中：$\Delta T_t $为t时的增量步时长.
由于中间增量的存在，需要系统在t=0时刻的速度与加速度被完全定义，才能计算下一增量步. 本文中所有节点的初始速度和位移都被定义为0，通过该显式瞬时动态分析方法，还原系统的摩擦耦合振动下弹条的共振响应，进而从共振响应的角度探究弹条的断裂机理.
2.2 扣件弹条疲劳分析理论——疲劳失效的研究
为探究科隆蛋扣件支撑钢轨波磨高发区段扣件弹条断裂的疲劳特性，需计算钢轨波磨高发区段处科隆蛋扣件弹条的疲劳寿命. 线性累积损伤理论是一种用于扣件弹条疲劳寿命分析的常用方法[21]. 首先，提取瞬时动态分析中弹条最大应力节点的应力时程曲线；接着，利用雨流计数法统计应力时程曲线，将其转换为相应的应力循环均值、应力循环幅值以及循环次数[22]；然后，通过Goodman曲线公式（式（5））修正循环幅值，使应力均值为0，以消除应力均值对疲劳分析计算的影响.
$$ S=\frac{{S} _{{\mathrm{a}}}{S} _{{\mathrm{u}}}}{{S} _{{\mathrm{u}}}-{S} _{{\mathrm{m}}}} ，$$ (5) 式中：S为等效应力均值为0的应力循环均值；Sa为原始应力幅值；Sm为原始应力循环均值；Su为材料的抗拉强度，本文弹条材料抗拉强度为
1600 MPa[19].将修正应力循环带入弹条材料（60Si2Mn弹簧钢） 存活率为95%的 S-N 曲线[13]，如式（6）所示.
$$ \lg \;N = 39.595\;3 - 11.843\;6\lg \;S, $$ (6) 式中：N为材料失效所需的最大循环次数.
在求解出N后，将其带入Palmgren-Miner公式，如式（7）所示.
$$ D = \sum\limits_{i = 1}^k {{D_i}} = \sum\limits_{i = 1}^k {\frac{{{n_i}}}{N}，} $$ (7) 式中：D为所有应力循环造成的总损伤，Di为第i个应力循环造成的累积损伤，k为应力循环次数，ni为雨流计数得到的应力循环次数.
对D取倒数，可以得到弹条的疲劳寿命为
$$ {N_{{\mathrm{life}}}} = \frac{1}{D} .$$ (8) 通过计算弹条寿命，可以将弹条的疲劳损伤量化，探究轮轨摩擦耦合振动对于弹条的疲劳损伤，进而结合共振响应和疲劳损伤揭示科隆蛋扣件弹条断裂的机理.
3. 结果与讨论
3.1 科隆蛋扣件弹条安装状态验证
弹条的安装状态对扣件的服役性能和扣件弹条的使用寿命都有着极大的影响，其中，“e”型弹条的安装状态主要通过改变弹条的中肢插入深度和弹程实现[13]. 本文取弹条的中肢插入深度为9 mm，弹程为10.5 mm，此时对应的扣压力为8.475 kN，满足标准扣压力为8.25 kN的需求[23]，如图4（a）所示. 安装状态下弹条应力主要集中于后拱端内侧，与现场调研中科隆蛋扣件弹条的断裂位置一致，弹条上的最大应力值为
1430 MPa，大于标准GB/T 1222—2016[24]中弹簧钢材料的屈服极限1400 MPa，此时应力集中部位存在微小的塑形变形，如图4（b） 所示. 以上研究表明，本文所采取的上拉弹条趾端的模拟扣压方式能够有效还原弹条的真实安装状态，并且在已选定的安装状态下能够满足弹条扣压力大于8.25 kN的扣压要求.3.2 科隆蛋扣件弹条共振响应分析
通过对已建立的科隆蛋扣件小半径曲线波磨区段轮对-钢轨-扣件系统有限元模型进行瞬时动态分析，求解得到轮轨在松弛区和波磨区的轮轨摩擦耦合振动响应. 由于小半径区段钢轨波磨主要发生在低轨处，这里通过内轮与低轨间的轮轨法向接触力体现科隆蛋扣件小半径曲线区段轮轨系统的摩擦耦合振动特性[1]，如图5（a） 所示. 在松弛区的轮轨接触法向力变化较为柔和；在进入波磨区后，该接触力变化显著加剧，说明钢轨波磨会显著加剧轮轨系统的振动响应. 为进一步分析轮轨接触特性，通过对轮轨接触法向力进行短时傅里叶变换，求解得出轮轨接触法向力在200～
1000 Hz的时频信息[25]，如图5（b） 所示. 在松弛区中，轮轨接触法向力具有370 Hz左右的主频，与后续钢轨波磨的主频一致[26]；在进入波磨区后，轮轨接触法向力的主频基本不发生变化；轮轨接触的振动能量显著增大，已存在的钢轨波磨的反馈振动会加剧轮轨摩擦耦合振动响应.
图 5 轮对-钢轨-扣件系统的瞬时动态分析结果Figure 5. Instantaneous dynamic analysis results of wheel set-rail-fastener system另外，科隆蛋扣件弹条的约束模态能够体现弹条在装配状态下的振动特性，当外部激励与约束模态一致时，弹条会发生共振强迫振动，进而使得弹条的疲劳寿命急剧减小[27-28]. 本文通过子空间法，提取科隆蛋扣件弹条在10～
1000 Hz内安装状态下的约束模态特性[19]，如图6所示.
图 6 科隆蛋扣件弹条10～2000 Hz约束模态频率及振型Figure 6. Constraint modal frequency and vibration mode of Cologne-egg fastener clip at 10–2000 Hz科隆蛋扣件弹条的一阶模态频率为368.54 Hz，与轮轨摩擦耦合振动主频接近，该频率的模态振型表现为弹条后拱端振动. 结合图5的分析结果发现，钢轨波磨加剧的轮轨摩擦耦合振动可能会引发该区段科隆蛋扣件弹条的共振响应，且对应振型下该科隆蛋扣件弹条主要振动位置在弹条后拱端，这与现场调研中科隆蛋扣件弹条的断裂位置一致[29]. 可以初步推断，钢轨波磨区段科隆蛋扣件弹条在轮轨摩擦耦合振动下的共振响应是该扣件弹条断裂的主要原因[30].
进一步验证科隆蛋扣件弹条的共振状态，本文分别提取图7（a） 中1号位弹条趾端端面标记的受测节点在有、无波磨工况下的加速度，以模拟弹条在平滑区段和波磨区段行驶，如图7（b ）所示. 无波磨工况下，在轮轨驶过的过程中其加速度未发生显著改变；在有波磨工况下，随着轮对驶过提取弹条所属扣件，同一位置扣件弹条受测节点的加速度显著增加，在轮轨驶过提取弹条所属扣件时，其加速度约为无波磨工况下的10倍，钢轨波磨加剧了轮轨摩擦耦合振动激励下科隆蛋扣件的共振响应. 结合前文瞬时动态分析和模态分析结果，进一步确认了钢轨波磨区段科隆蛋扣件弹条在轮轨摩擦耦合振动下的共振响应是其扣件弹条断裂的主要原因[31].
3.3 科隆蛋扣件弹条疲劳损伤分析
本文结合线性累积损伤理论，研究科隆蛋扣件弹条在轮轨摩擦耦合振动下的疲劳特性. 同时，结合前文共振响应分析结果，将疲劳寿命作为量化指标，对比不同振动响应下科隆蛋扣件弹条的疲劳损伤情况. 如图8（a）、（b） 分别为轮轨摩擦耦合振动下瞬时动态计算中提取图7（a） 中1号和2号弹条的最大应力时程图，当轮对驶过受测弹条时，由于弹条此时发生共振响应，导致其最大应力产生显著变化，并且位于工作边一侧的1号弹条变化更为明显. 通过雨流计数法统计弹条最大应力时程曲线，分别得到1、2号弹条的雨流计数分布，如图9（a）、（b） 所示，其中，柱体颜色由紫到红表示应力循环次数少到多. 接着，利用Goodman公式修正应力均值，再带入弹条材料的S-N曲线，最终计算得出两者的疲劳寿命分别是15.56万次和45.26万次，仅为弹条500.00万次设计疲劳寿命[8]的3.11%和9.05%，不能满足弹条的疲劳寿命要求. 图8（c）为无波磨工况下中图7（a） 中1号位扣件弹条的最大应力时程图，其最大应力变化幅值显著小于有波磨工况下同一位置弹条的应力幅值. 通过图9（c）中无波磨工况下的雨流计数分布图，计算得出无波磨工况下1号位弹条疲劳寿命为
1678.26 万次，远远大于500.00万次的设计寿命，基本不会发生疲劳断裂. 综上所述，小半径区段中的科隆蛋扣件工作边一侧的弹条更容易发生疲劳失效[32]；钢轨波磨加剧了轮轨摩擦耦合振动，使得科隆蛋扣件弹条的共振响应加剧，降低了波磨区段中科隆蛋扣件弹条寿命的99.07%，导致弹条在设计寿命内的疲劳失效.
图 8 科隆蛋扣件弹条最大应力时程图Figure 8. Maximum stress time history diagram of Cologne-egg fastener clips
图 9 科隆蛋扣件弹条雨流计数分布Figure 9. Rain flow count distribution of Cologne-egg fastener clips4. 结 论
本文建立小半径波磨区段下包含完整科隆蛋扣件的轮对-钢轨-扣件系统有限元模型，还原了科隆蛋扣件弹条在列车行驶过程中轮轨的摩擦耦合振动特性下的共振响应，并基于该振动特性计算扣件弹条的疲劳损伤情况，进而结合共振响应和疲劳损伤，揭示弹条的断裂机理，最终得出以下结论：
1） 钢轨波磨高发区段中，轮轨摩擦耦合振动主频与科隆蛋扣件弹条的一阶约束模态频率接近，一阶模态振型下在后拱端的受力复杂区域与现场调研弹条断裂位置一致，轮轨摩擦耦合振动引起的弹条共振是科隆蛋扣件弹条断裂的主要原因.
2） 钢轨波磨高发区段中，钢轨波磨会加剧系统中的轮轨摩擦耦合振动，使得科隆蛋扣件弹条寿命对比无波磨工况下降了99.07%，仅为设计寿命的3.11%，进而引发科隆蛋扣件弹条在设计寿命内的提前疲劳失效.
3） 钢轨波磨高发区段中，靠近小半径工作边一侧的科隆蛋扣件弹条更容易发生疲劳失效，其疲劳失效位于扣件弹条后拱端内侧，与调研现场情况一致.
致谢：轨道交通基础设施性能检测与保障国家重点实验室开放课题（HJGZ2021115）资助.
-
图 1 科隆蛋扣件区段钢轨波磨及扣件断裂特征
Figure 1. Rail corrugation and fastener fracture characteristics of Cologne-egg fastener section
图 3 科隆蛋扣件弹条扣压过程模拟
Figure 3. Simulation of Cologne-egg fastener clip compression process
图 5 轮对-钢轨-扣件系统的瞬时动态分析结果
Figure 5. Instantaneous dynamic analysis results of wheel set-rail-fastener system
图 6 科隆蛋扣件弹条10～
2000 Hz约束模态频率及振型Figure 6. Constraint modal frequency and vibration mode of Cologne-egg fastener clip at 10–
2000 Hz
图 8 科隆蛋扣件弹条最大应力时程图
Figure 8. Maximum stress time history diagram of Cologne-egg fastener clips
图 9 科隆蛋扣件弹条雨流计数分布
Figure 9. Rain flow count distribution of Cologne-egg fastener clips
表 1 轮对-钢轨-扣件系统有限元模型的材料属性[9,18-19]
Table 1. Material properties of finite element model of wheel set-rail-fastener system[9,18-19]
部件 弹性模量/Pa 泊松比 密度/
（kg•m−3）轮对 210.00×109 0.30 7800 钢轨 206.00×109 0.30 7800 DI 弹条 206.00×109 0.30 7800 轨距垫 6.20×109 0.35 1400 调高垫板 6.00×106 0.45 1190 承轨座/底座 170.00×109 0.30 7900 减振橡胶 5.58×106 0.49 1190 
下载: 导出CSV
-
[1] 陈光雄,钱韦吉,莫继良,等. 轮轨摩擦自激振动引起小半径曲线钢轨波磨的瞬态动力学[J]. 机械工程学报,2014,50(9): 71-76. doi: 10.3901/JME.2014.09.071CHEN Guangxiong, QIAN Weiji, MO Jiliang, et al. A transient dynamics study on wear-type rail corrugation on a tight curve due to the friction-induced self-excited vibration of a wheelset-track system[J]. Journal of Mechanical Engineering, 2014, 50(9): 71-76. doi: 10.3901/JME.2014.09.071 [2] BAO P Y, CUI X L, DING H H, et al. Influences of friction self-excited vibration characteristics of various types of high-speed trains on rail corrugations in braking sections[J]. Engineering Failure Analysis, 2022, 134: 106087.1-106087.10. [3] 崔晓璐,唐传平,包鹏羽,等. 高速列车制动区段钢轨波磨抑制方法[J]. 西南交通大学学报,2023,58(3):656-664.CUI Xiaolu, TANG Chuanping, BAO Pengyu, et al. Rail corrugation suppression method on braking sections of high-speed trains[J]. Journal of Southwest Jiaotong University, 2023, 58(3):656-664. [4] 吴浩,韦凯,郭恭兵,等. 地铁扣件e型弹条受载特征分析[J]. 铁道科学与工程学报,2022,19(3): 665-673.WU Hao, WEI Kai, GUO Gongbing, et al. Analysis on loading characteristics of e-type clip of rail fastener[J]. Journal of Railway Science and Engineering, 2022, 19(3): 665-673. [5] 杨程亮,李承亮. Ⅲ型弹条断裂原因分析[J]. 铁道建筑,2019,59(4): 135-138. doi: 10.3969/j.issn.1003-1995.2019.04.30YANG Chengliang, LI Chengliang. Cause analysis of fracture of Ⅲ-type elastic rod[J]. Railway Engineering, 2019, 59(4): 135-138. doi: 10.3969/j.issn.1003-1995.2019.04.30 [6] HOLDER D E, CSENGE M V, QIAN Y, et al. Laboratory investigation of the Skl-style fastening system’s lateral load performance under heavy haul freight railroad loads[J]. Engineering Structures, 2017, 139: 71-80. doi: 10.1016/j.engstruct.2017.02.039 [7] LING L, LI W, SHANG H X, et al. Experimental and numerical investigation of the effect of rail corrugation on the behaviour of rail fastenings[J]. Vehicle System Dynamics, 2014, 52(9): 1211-1231. doi: 10.1080/00423114.2014.934844 [8] WANG P, LU J, ZHAO C Y, et al. Numerical investigation of the fatigue performance of elastic rail clips considering rail corrugation and dynamic axle load[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2021, 235(3): 339-352. doi: 10.1177/0954409720926016 [9] 潘兵,王安斌,高晓刚. 高速轮轨瞬态响应特性对弹条伤损的影响[J]. 噪声与振动控制,2020,40(2): 174-179. doi: 10.3969/j.issn.1006-1355.2020.02.031PAN Bing, WANG Anbin, GAO Xiaogang. Influences of the characteristics of high-speed wheel-rail transient responses on clip damage[J]. Noise and Vibration Control, 2020, 40(2): 174-179. doi: 10.3969/j.issn.1006-1355.2020.02.031 [10] 刘玉涛,段玉振,王豪,等. 高速铁路无砟轨道扣件弹条疲劳损伤统计分析[J]. 铁道标准设计,2021,65(2): 42-46,53.LIU Yutao, DUAN Yuzhen, WANG Hao, et al. Statistical analysis of fatigue damage of fasteners clips for ballastless track of high speed railway[J]. Railway Standard Design, 2021, 65(2): 42-46,53. [11] 辛涛,杨学敏,肖宏,等. 基于车轨耦合和扣件精细模型的弹条疲劳分析[J]. 中南大学学报(自然科学版),2016,47(12): 4269-4275.XIN Tao, YANG Xuemin, XIAO Hong, et al. Fatigue analysis of spring clip based on vehicle-track coupled model and detailed fastener model[J]. Journal of Central South University (Science and Technology), 2016, 47(12): 4269-4275. [12] 亓伟,刘玉涛,陈江,等. 客货混运线路扣件弹条疲劳特性准静态分析[J]. 机械工程学报,2018,54(12): 1-7. doi: 10.3901/JME.2018.12.001QI Wei, LIU Yutao, CHEN Jiang, et al. Quasi-static analysis of fatigue characteristic of rail fastening clip for railways with passenger and freight traffic[J]. Journal of Mechanical Engineering, 2018, 54(12): 1-7. doi: 10.3901/JME.2018.12.001 [13] HASAP A, NORAPHAIPHIPAKSA N, KANCHANOMAI C. Influence of malposition on the performance of elastic rail clip: toe load, stress, and friction[J]. Structures, 2020, 28: 2661-2670. doi: 10.1016/j.istruc.2020.10.073 [14] 刘艳,姜秀杰,李秋彤,等. W300-1型扣件弹条疲劳寿命的预测和评估[J]. 同济大学学报(自然科学版),2021,49(8): 1152-1161.LIU Yan, JIANG Xiujie, LI Qiutong, et al. Fatigue life prediction and evaluation of the W300-1 fastening clip[J]. Journal of Tongji University (Natural Science), 2021, 49(8): 1152-1161. [15] 陈明明,卢俊,余鸿,等. 地铁扣件DI弹条安装受力分析及工艺优化改进研究[J]. 铁道标准设计,2019,63(4): 52-57.CHEN Mingming, LU Jun, YU Hong, et al. Force analysis of installation state and optimization of type DI fastening clip in subway[J]. Railway Standard Design, 2019, 63(4): 52-57. [16] XU J, CUI X L, DING H H, et al. Optimization of vibration absorbers for the suppression of rail corrugation in the sharp curved section with Cologne-egg fasteners[J]. Vehicle System Dynamics, 2024, 62(2): 395-410. doi: 10.1080/00423114.2023.2170255 [17] CUI X L, CHEN G X, YANG H G, et al. Effect of the wheel/rail contact angle and the direction of the saturated creep force on rail corrugation[J]. Wear, 2015, 330/331: 554-562. doi: 10.1016/j.wear.2014.12.046 [18] 吴建忠. Ⅲ型轨道减振器扣件的设计与研究[D]. 北京: 北京交通大学,2009. [19] 宋子洋,卢俊,胡世斌,等. DT-Ⅲ型扣件系统弹条疲劳特性及优化研究[J]. 中南大学学报(自然科学版),2021,52(10): 3623-3635. doi: 10.11817/j.issn.1672-7207.2021.10.025SONG Ziyang, LU Jun, HU Shibin, et al. Study on fatigue characteristics and optimization of fastener clips of DT-Ⅲ fastener system[J]. Journal of Central South University (Science and Technology), 2021, 52(10): 3623-3635. doi: 10.11817/j.issn.1672-7207.2021.10.025 [20] 杨宏光,崔晓璐,陈光雄. 科隆蛋扣件与普通短轨枕过渡段钢轨波磨的瞬态动力学研究[J]. 润滑与密封,2016,41(11): 26-30,70. doi: 10.3969/j.issn.0254-0150.2016.11.006YANG Hongguang, CUI Xiaolu, CHEN Guangxiong. A transient dynamics study on rail corrugation in the transitional section from cologne-egg fasteners section to fix-dual short sleepers in a sharp curved track[J]. Lubrication Engineering, 2016, 41(11): 26-30,70. doi: 10.3969/j.issn.0254-0150.2016.11.006 [21] FERREÑO D, CASADO J A, CARRASCAL I A, et al. Experimental and finite element fatigue assessment of the spring clip of the SKL-1 railway fastening system[J]. Engineering Structures, 2019, 188: 553-563. doi: 10.1016/j.engstruct.2019.03.053 [22] 毕继红,陈花丽,任洪鹏. 基于雨流计数法的接触线疲劳寿命分析[J]. 铁道学报,2012,34(6): 34-39. doi: 10.3969/j.issn.1001-8360.2012.06.007BI Jihong, CHEN Huali, REN Hongpeng. Analysis on fatigue life of contact wire based on rain-flow counting method[J]. Journal of the China Railway Society, 2012, 34(6): 34-39. doi: 10.3969/j.issn.1001-8360.2012.06.007 [23] 郭骁. 地铁e型弹条扣件系统疲劳伤损机理研究[D]. 北京: 北京交通大学,2016. [24] 国家质量监督检验检疫总局,中国国家标准化管理委员会. 弹簧钢:GB/T 1222—2016[S]. 北京:中国标准出版社,2016. [25] XIAO H, GUO X, WANG H Y, et al. Fatigue damage analysis and life prediction of e-clip in railway fasteners based on ABAQUS and FE-SAFE[J]. Advances in Mechanical Engineering, 2018, 10(3): 168781401876724.1-168781401876724.12. [26] 崔晓璐. 地铁线路钢轨波磨现象发生机理研究[D]. 成都: 西南交通大学,2017. [27] 刘文光,陈国平. 含裂纹悬臂梁的振动与疲劳耦合分析[J]. 振动与冲击,2011,30(5): 140-144. doi: 10.3969/j.issn.1000-3835.2011.05.029LIU Wenguang, CHEN Guoping. Coupling analysis for vibration and fatigue of a cracked cantilever beam[J]. Journal of Vibration and Shock, 2011, 30(5): 140-144. doi: 10.3969/j.issn.1000-3835.2011.05.029 [28] 蔡力钢,马仕明,赵永胜,等. 多约束状态下重载机械式主轴有限元建模及模态分析[J]. 机械工程学报,2012,48(3): 165-173. doi: 10.3901/JME.2012.03.165CAI Ligang, MA Shiming, ZHAO Yongsheng, et al. Finite element modeling and modal analysis of heavy-duty mechanical spindle under multiple constraints[J]. Journal of Mechanical Engineering, 2012, 48(3): 165-173. doi: 10.3901/JME.2012.03.165 [29] DAMIR A, ELKHATIB A, NASSEF G. Prediction of fatigue life using modal analysis for grey and ductile cast iron[J]. International Journal of Fatigue, 2007, 29(3): 499-507. doi: 10.1016/j.ijfatigue.2006.05.004 [30] CUI X L, CHEN G X, YANG H J, et al. A case study of rail corrugation phenomenon based on the viewpoint of friction-induced oscillation of a wheelset-track system[J]. Journal of Vibroengineering, 2017, 19(6): 4516-4530. doi: 10.21595/jve.2017.17867 [31] SMUTNY J. Measurement and analysis of dynamic and acoustic parameters of rail fastening[J]. NDT & E International, 2004, 37(2): 119-129. [32] 肖宏,马春生,郭骁,等. e型扣件弹条断裂原因频谱分析[J]. 同济大学学报(自然科学版),2017,45(7): 1000-1008.XIAO Hong, MA Chunsheng, GUO Xiao, et al. Fractures of e-type fastening clip by spectral analysis method[J]. Journal of Tongji University (Natural Science), 2017, 45(7): 1000-1008. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 279
- HTML全文浏览量: 97
- PDF下载量: 50
- 被引次数: 0