基于多属性决策的一阶逻辑子句选择方法

曾国艳; 徐扬; 陈树伟; 姜世攀

doi:10.3969/j.issn.0258-2724.20230023

基于多属性决策的一阶逻辑子句选择方法

doi: 10.3969/j.issn.0258-2724.20230023

曾国艳^{1, 2,},
徐扬^{1, 2, ,},
陈树伟^{1, 2},
姜世攀^{1, 2}

1.
西南交通大学数学学院，四川成都 611756
2.
西南交通大学系统可信性自动验证国家地方联合工程实验室，四川成都 611756

基金项目: 国家自然科学基金项目（61976130）

详细信息

作者简介:
曾国艳（1997—），女，博士研究生，研究方向为自动推理、定理机器证明，E-mail：guoyanzeng_math@163.com

通讯作者:
徐扬（1956—），男，教授，博士，研究方向为智能信息处理、自动推理、定理机器证明，E-mail：xuyang@home.swjtu.edu.cn

中图分类号: TP311；O14
计量
- 文章访问数: 75
- HTML全文浏览量: 42
- PDF下载量: 7
- 被引次数: 0
出版历程
- 收稿日期: 2023-01-17
- 修回日期: 2023-06-20
- 网络出版日期: 2024-09-25

First-Order Logic Clause Selection Method Based on Multi-criteria Decision Making

ZENG Guoyan^{1, 2
,},
XU Yang^{1, 2
, ,},
CHEN Shuwei^{1, 2},
JIANG Shipan^{1, 2}

1.
School of Mathematics, Southwest Jiaotong University, Chengdu 611756, China
2.
National-Local Joint Engineering Laboratory of System Credibility Automatic Verification, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
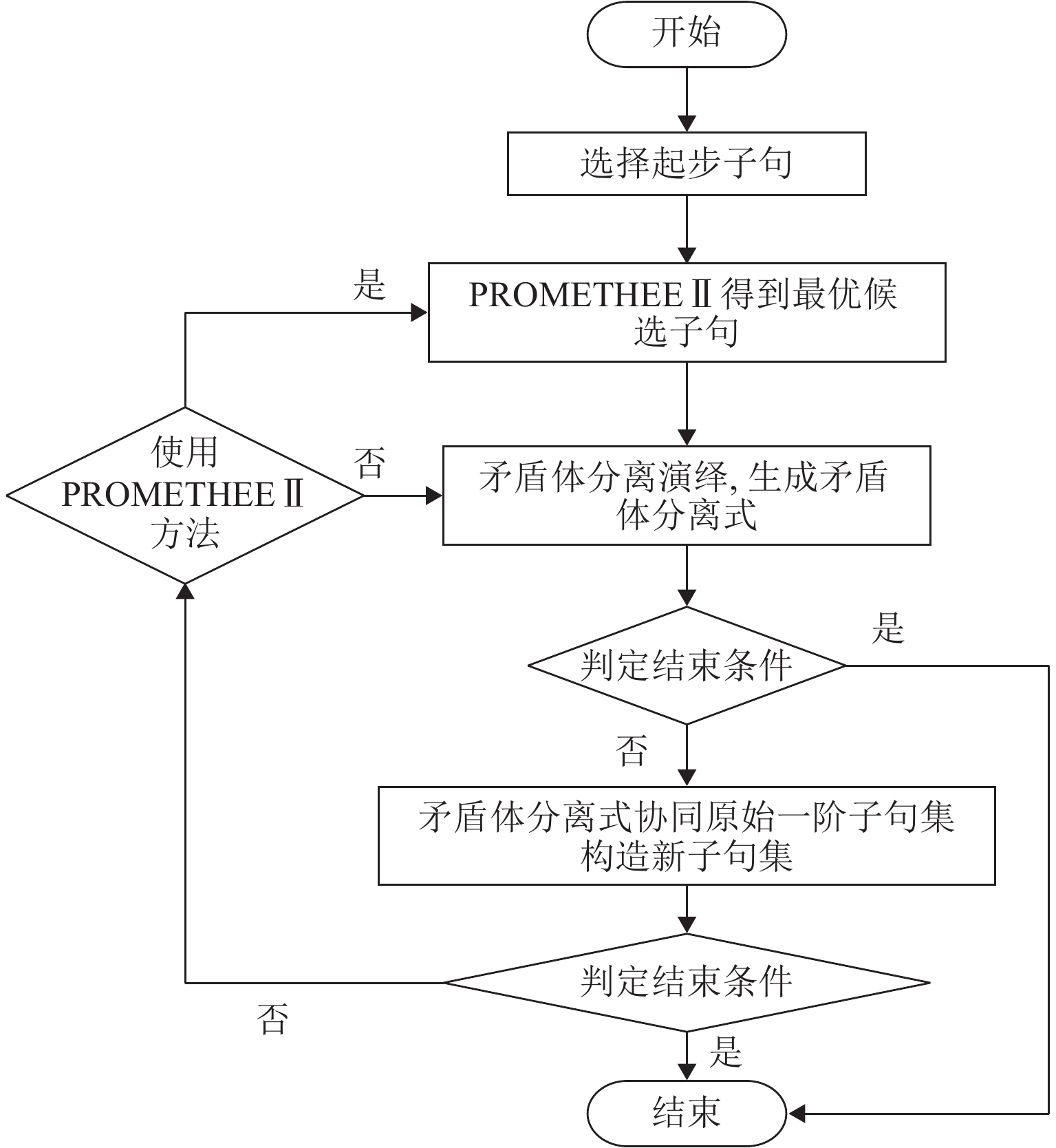
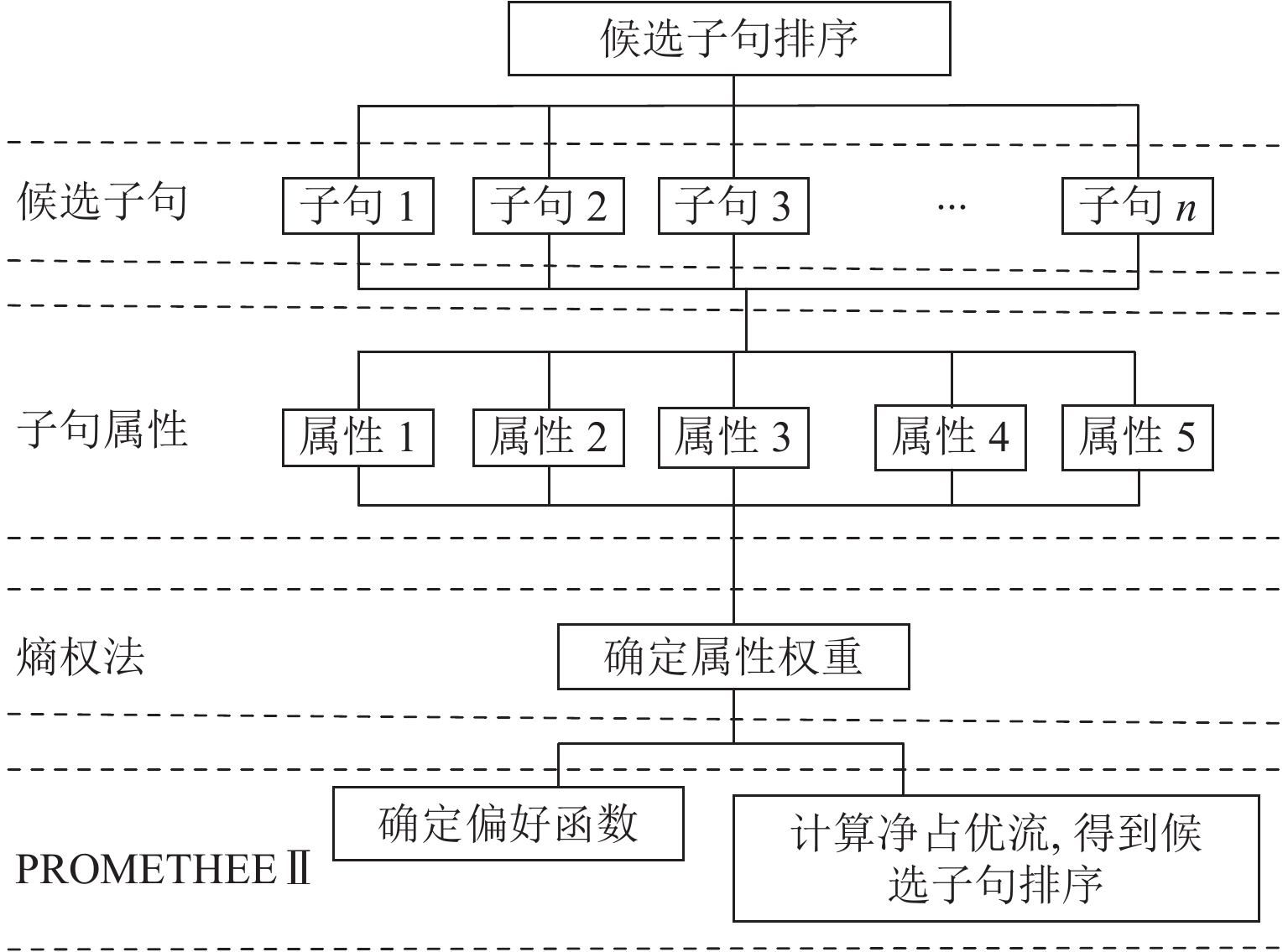
基于一阶逻辑的自动定理证明器（ATP）在知识表达和自动推理研究中占据重要地位，而启发式策略则是提升ATP性能的关键研究方向. 主流的启发式策略通常通过描述子句属性来确定属性优先级，从而选择子句，但属性优先级受人为因素影响，且评估子句耗时较长. 为此，本文基于矛盾体分离（S-CS）规则，提出一种新的多属性决策（MCDM）子句评估方法. 首先，利用熵权法对子句属性进行客观赋权；其次，结合偏好顺序结构评估法（PROMETHEE Ⅱ）对子句进行评估，得到子句的完全排序；最后，将提出的MCDM方法加入自动定理证明器CSE 1.5 （contradiction separation extension 1.5）、Vampire 4.7和Eprover （E 2.6）中，分别形成新的证明器MCDM_CSE、 MCDM_V和MCDM_E. 对MCDM_CSE测试了国际定理证明器问题库TPTP （Thousands of Problems for Theorem Provers）中一阶逻辑格式的定理，并对MCDM_V和MCDM_E测试了2022年CADE （Conference on Automated Deduction）竞赛例（一阶逻辑组）. 实验表明：MCDM_CSE比CSE 1.5多证明了151个定理（来自TPTP），并且能够证明Vampire 4.7无法证明的5个定理、E 2.6无法证明的41个定理以及Prover9无法证明的293个定理；在更短的平均时间内，MCDM_V比Vampire 4.7多证明了6个定理（来自CADE 2022），MCDM_E比E 2.6多证明了8个定理.
- 一阶逻辑 /
- 矛盾体分离规则 /
- 启发式策略 /
- 多属性决策 /
- 熵权法
Abstract:
First-order logic-based automatic theorem provers (ATPs) are important for the research on knowledge representation and automatic reasoning, and heuristic strategies are a critical research topic to enhance the performance of ATPs. Mainstream heuristic strategies select clauses by describing clause properties and then determining the priority of the properties. However, the priority of properties is subject to human factors, and it takes a long time to evaluate clauses. A new multi-criteria decision making (MCDM) clause evaluation method was proposed based on the standard contradiction separation (S-CS) rule. Firstly, the entropy weight method was used to objectively assign weights to clause properties. Secondly, preference ranking organization method for enrichment evaluations (PROMETHEE Ⅱ) was combined to evaluate the clauses and obtain the complete order of the clauses. Finally, the proposed MCDM method was applied to ATPs CSE 1.5 (contradiction separation extension 1.5), Vampire 4.7, and Eprover (E 2.6) to form new ATPs MCDM_CSE, MCDM_V, and MCDM_E. The theorems in first-order form (FOF) from the international theorem provers problem library Thousands of Problems for Theorem Provers (TPTP) were tested on MCDM_CSE, and the Conference on Automated Deduction (CADE) 2022 competition (FOF division) was tested on MCDM_V and MCDM_E. The experiments show that MCDM_CSE proves 151 more theorems (from TPTP) than CSE 1.5 and proves 5 theorems unproved by Vampire 4.7, 41 theorems unproved by E 2.6, and 293 theorems unproved by Prover9. In a shorter average time, MCDM_V proves 6 more theorems (from CADE 2022) than Vampire 4.7, and MCDM_E proves 8 more theorems than E 2.6.
- first-order logic /
- contradiction separation rule /
- heuristic strategy /
- multi-criteria decision making /
- entropy weight method

HTML全文

图 1 基于 PROMETHEE Ⅱ的候选子句选择框架

Figure 1. Framework diagram for candidate clause selection based on PROMETHEE Ⅱ

下载: 全尺寸图片幻灯片

图 2 基于 PROMETHEE Ⅱ的 S-CS 算法流程

Figure 2. Flowchart of S-CS algorithm based on PROMETHEE Ⅱ

下载: 全尺寸图片幻灯片

图 3 不同ATP在2022年CADE竞赛的CPU时间比较

Figure 3. Comparison of CPU time of different ATPs for the CADE 2022 competition

下载: 全尺寸图片幻灯片

表 1 MCDM_CSE和CSE 1.5在不同难度等级下证明的定理数量对比

Table 1. Comparison of the number of theorems proved by MCDM_CSE and CSE 1.5 at different difficulty levels 个

难度等级	MCDM_CSE	CSE 1.5
[0, 0.10）	1061	1073
[0.10,0.50）	1338	1212
[0.50,0.60）	98	79
[0.60,0.70）	43	39
[0.70,0.80）	22	16
[0.80,0.90）	13	11
[0.90,1.00）	8	5
1.00	3	0

下载: 导出CSV

表 2 MCDM_CSE证明难度大于0.90的定理所需的证明时长

Table 2. Time consumed by MCDM_CSE to prove theorems with difficulty greater than 0.90

定理名称	难度等级	证明时间/s
SEU413 + 2	0.92	26.81
SWB088 + 1	0.97	137.78
SWB090 + 1	0.97	126.04
NUM736 + 4	1.00	65.49
SYO625-1	1.00	219.51
SYO587 + 1	1.00	218.41

下载: 导出CSV

表 3 对已证明定理（按难度等级）在国际知名自动定理证明器中证明数量的比较

Table 3. Comparison of the number of theorems (by difficulty level) proved by internationally known ATPs 个

自动定理证明器	难度等级
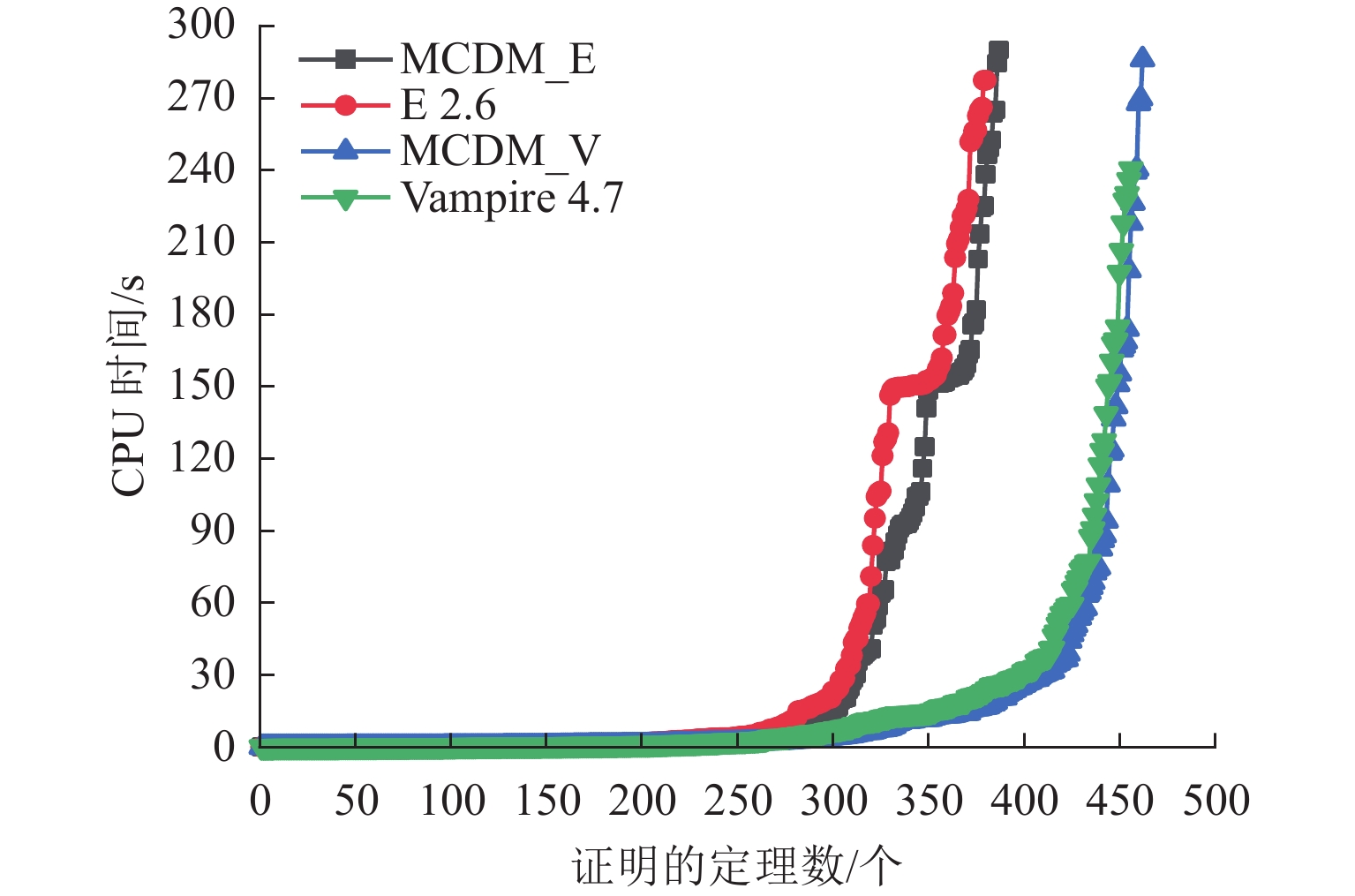
自动定理证明器	[0,0.70）	[0.70,0.80）	[0.80,0.90）	[0.90,1.00]
MCDM_CSE	2540	22	13	11
Vampire 4.7	2539	21	13	8
E 2.6	2532	12	1	0
Prover9	2264	13	8	8

下载: 导出CSV

表 4 2022年CADE竞赛的比较结果

Table 4. Comparative results on the CADE 2022 competition

自动定理证明器	平均时间/s	证明个数/个
MCDM_V	15.3	462
Vampire 4.7	16.1	456
MCDM_E	27.4	387
E 2.6	31.7	380

下载: 导出CSV

参考文献(30)

[1]	ROBINSON J A. A machine-oriented logic based on the resolution principle[J]. Journal of the ACM, 1965, 12(1): 23-41. doi: 10.1145/321250.321253
[2]	BECKERT B, HÄHNLE R. Reasoning and verification: state of the art and current trends[J]. IEEE Intelligent Systems, 2014, 29(1): 20-29. doi: 10.1109/MIS.2014.3
[3]	HALES T, ADAMS M, BAUER G, et al. A formal proof of the Kepler conjecture[J/OL]. Forum of Mathematics, Pi, 2017, 5: 1-21. [2023-01-02]. https://arxiv.org/pdf/1501.02155.
[4]	PAVLOV V, SCHUKIN A, CHERKASOVA T. Exploring automated reasoning in first-order logic: tools, techniques and application areas[M]//Communications in Computer and Information Science. Berlin: Springer, 2013: 102-116.
[5]	XU Y, LIU J, CHEN S W, et al. Contradiction separation based dynamic multi-clause synergized automated deduction[J]. Information Sciences, 2018, 462: 93-113. doi: 10.1016/j.ins.2018.04.086
[6]	XU Y, CHEN S W, LIU J, et al. Distinctive features of the contradiction separation based dynamic automated deduction[C]//Data Science and Knowledge Engineering for Sensing Decision Support. Belfast: World Scientific, 2018: 725-732.
[7]	JAKUBŮV J, KALISZYK C. Relaxed weighted path order in theorem proving[J]. Mathematics in Computer Science, 2020, 14(3): 657-670 doi: 10.1007/s11786-020-00474-0
[8]	RAWSON M, REGER G. Old or heavy? decaying gracefully with age/weight shapes[M]//Lecture Notes in Computer Science. Cham: Springer, 2019: 462-476.
[9]	曹锋,徐扬,陈树伟,等. 多元协同演绎在一阶逻辑ATP中的应用[J]. 西南交通大学学报,2020,55(2): 401-408,427. doi: 10.3969/j.issn.0258-2724.20180800 CAO Feng, XU Yang, CHEN Shuwei, et al. Application of multi-clause synergized deduction in first-order logic automated theorem proving[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 401-408,427. doi: 10.3969/j.issn.0258-2724.20180800
[10]	CHEN S W, XU Y, JIANG Y, et al. Some synergized clause selection strategies for contradiction separation based automated deduction[C]//2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE). Nanjing: IEEE, 2017: 1-6.
[11]	HWANG C L, YOON K. Methods for multiple attribute decision making[M]//Lecture Notes in Economics and Mathematical Systems. Berlin: Springer, 1981: 58-191.
[12]	PARK J H, CHO H J, KWUN Y C. Extension of the VIKOR method for group decision making with interval-valued intuitionistic fuzzy information[J]. Fuzzy Optimization and Decision Making, 2011, 10(3): 233-253. doi: 10.1007/s10700-011-9102-9
[13]	BRANS J P, VINCKE P. Note—a preference ranking organization method[J]. Management Science, 1985, 31(6): 647-656. doi: 10.1287/mnsc.31.6.647
[14]	BRANS J P, DE SMET Y. PROMETHEE methods[M]//HAMID F. International Series in Operations Research & Management Science. New York: Springer, 2016: 187-219.
[15]	ROBINSON J A, VORONKOV A. Handbook of automated reasoning[M]. Amsterdam: Elsevier, 2001.
[16]	LÖCHNER B. Things to know when implementing KBO[J]. Journal of Automated Reasoning, 2006, 36(4): 289-310.
[17]	TAMMET T. GKC: A reasoning system for large knowledge bases[C]//International Conference on Automated Deduction. Switzerland: Springer, 2019: 538-549.
[18]	RAWSON M, REGER G. Dynamic strategy priority: empower the strong and abandon the weak[C]// Proceedings of the 6th Workshop on Practical Aspects of Automated Reasoning. Oxford: PAAR, 2018: 58-71.
[19]	LIU P Y, XU Y, LIU J, et al. Fully reusing clause deduction algorithm based on standard contradiction separation rule[J]. Information Sciences, 2023, 622: 337-356. doi: 10.1016/j.ins.2022.11.128
[20]	杨梦,雷博,史露娜,等. 基于标准离差法的模糊散度多阈值图像分割[J]. 计算机应用与软件,2020,37(5): 219-225. doi: 10.3969/j.issn.1000-386x.2020.05.038 YANG Meng, LEI Bo, SHI Luna, et al. Fuzzy divergence multi-threshold image segmentation based on standard deviation method[J]. Computer Applications and Software, 2020, 37(5): 219-225. doi: 10.3969/j.issn.1000-386x.2020.05.038
[21]	刘照德,詹秋泉,田国梁. 因子分析综合评价研究综述[J]. 统计与决策,2019,35(19): 68-73. LIU Zhaode, ZHAN Qiuquan, TIAN Guoliang. Research review on comprehensive evaluation of factor analysis[J]. Statistics & Decision, 2019, 35(19): 68-73.
[22]	ZHU Y X, TIAN D Z, YAN F. Effectiveness of entropy weight method in decision-making[J]. Mathematical Problems in Engineering, 2020, 2020: 3564835.1-3564835.5.
[23]	JIANG L L, WANG H, TONG A H, et al. The measurement of green finance development index and its poverty reduction effect: dynamic panel analysis based on improved entropy method[J]. Discrete Dynamics in Nature and Society, 2020, 2020: 8851684.1-8851684.13.
[24]	ZHONG J, CAO F, WU G F, et al. Multi-clause synergized contradiction separation based first-order theorem prover—MC-SCS[C]//2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE). Nanjing: IEEE, 2017: 1-6.
[25]	SUTCLIFFE G, DESHARNAIS M. The CADE-28 automated theorem proving system competition–CASC-28[J]. AI Communications, 2022, 34(4): 259-276. doi: 10.3233/AIC-210235
[26]	SUTCLIFFE G. The TPTP problem library and associated infrastructure[J]. Journal of Automated Reasoning, 2017, 59(4): 483-502. doi: 10.1007/s10817-017-9407-7
[27]	KOVÁCS L, VORONKOV A. First-order theorem proving and vampire[M]//Lecture Notes in Computer Science. Berlin: Springer, 2013: 1-35.
[28]	SCHULZ S. System description: E 1.8[C]//International Conference on Logic for Programming Artificial Intelligence and Reasoning. Berlin: Springer, 2013: 735-743.
[29]	MCCUNE W. Release of Prover9[R]//Denver: Mathematics and Computer Science Division, Argonne National Laboratory, 2005.
[30]	MCCUNE W. OTTER 3.3 reference manual[J]. Office of Scientific & Technical Information Technical Reports, 2007, 11(4): 217-220.