Theoretical Study on Uplift Calculation of Embedded Twelve Ground Screws of Transmission Angle Steel Tower
-
摘要:
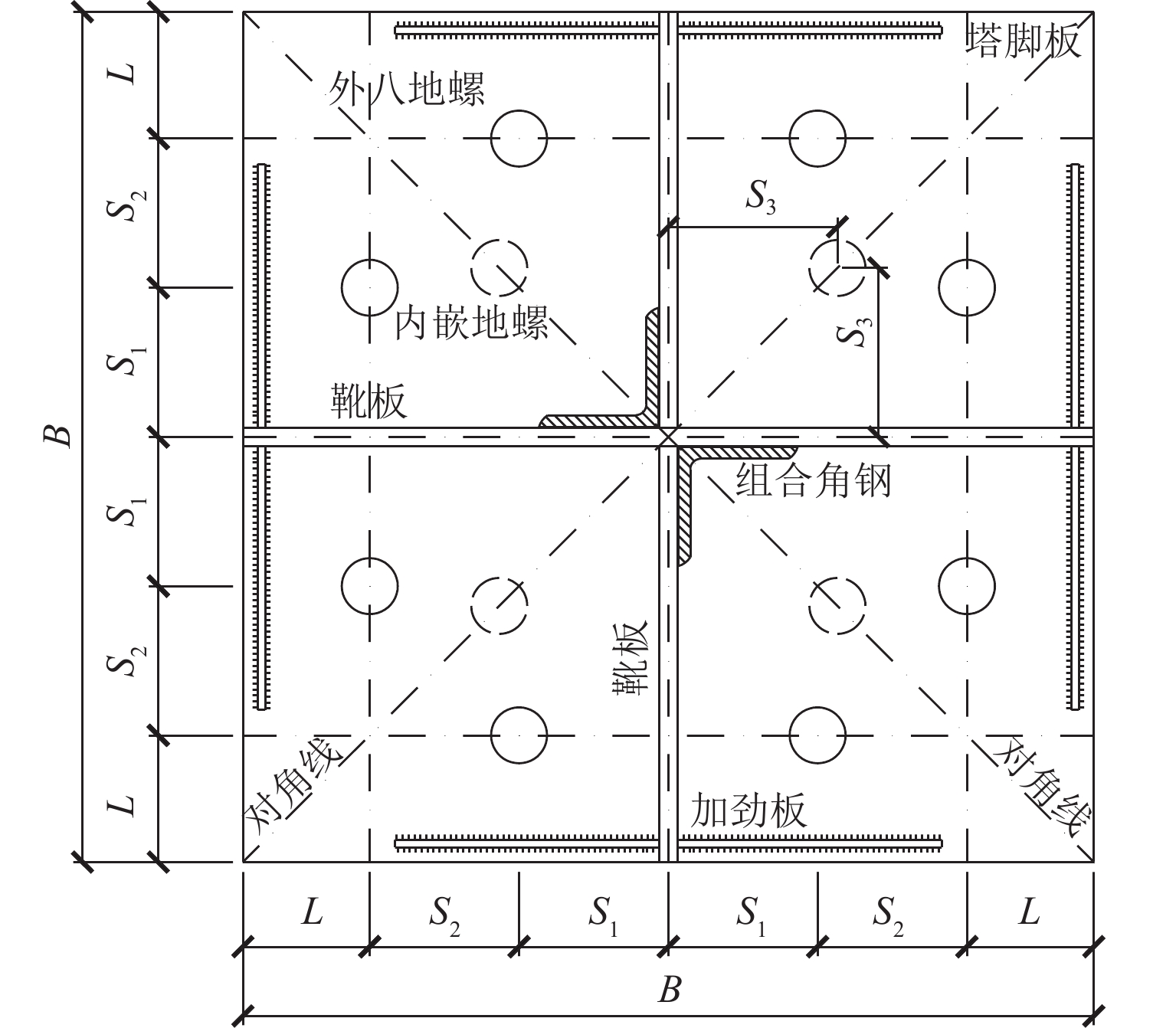
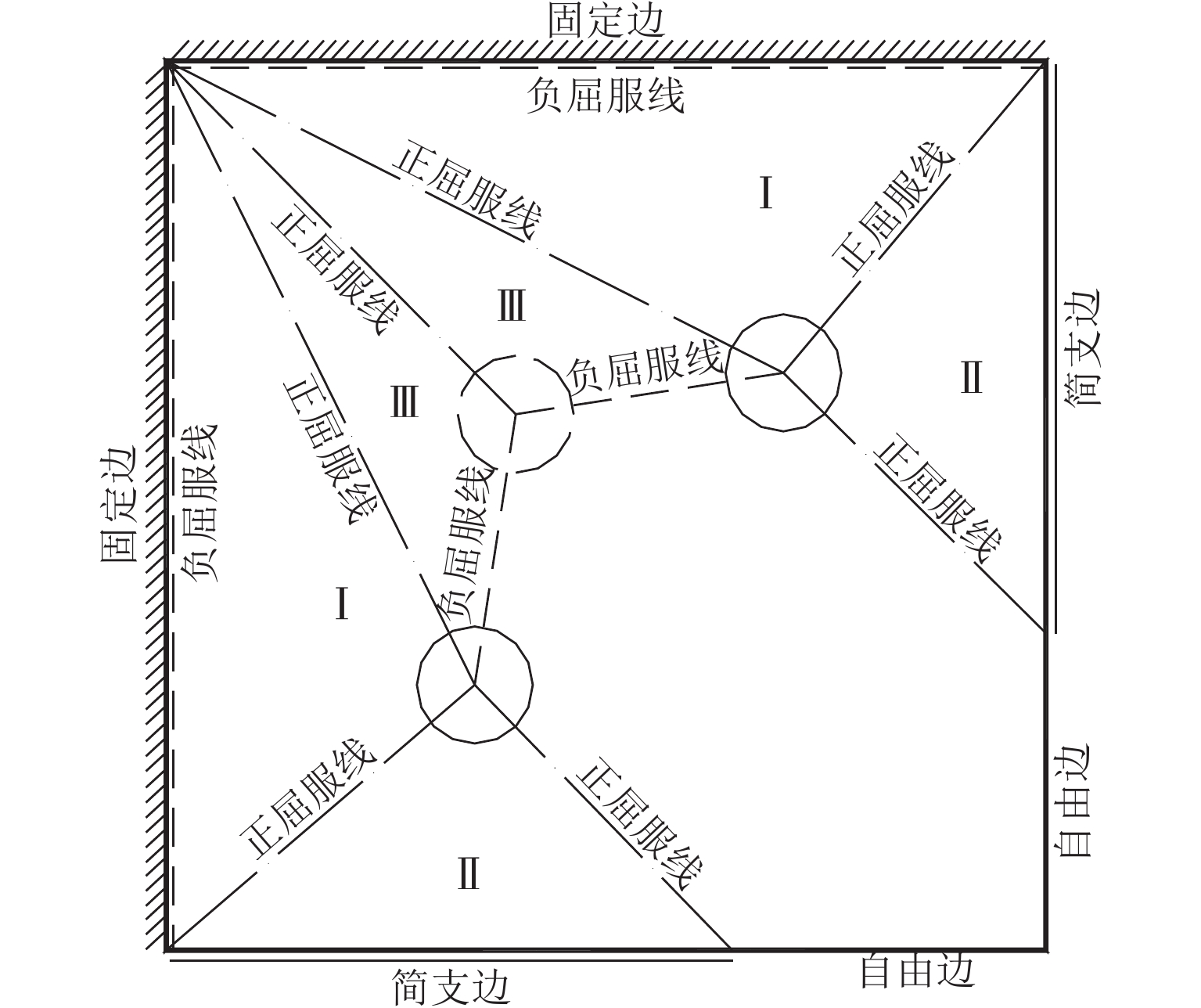
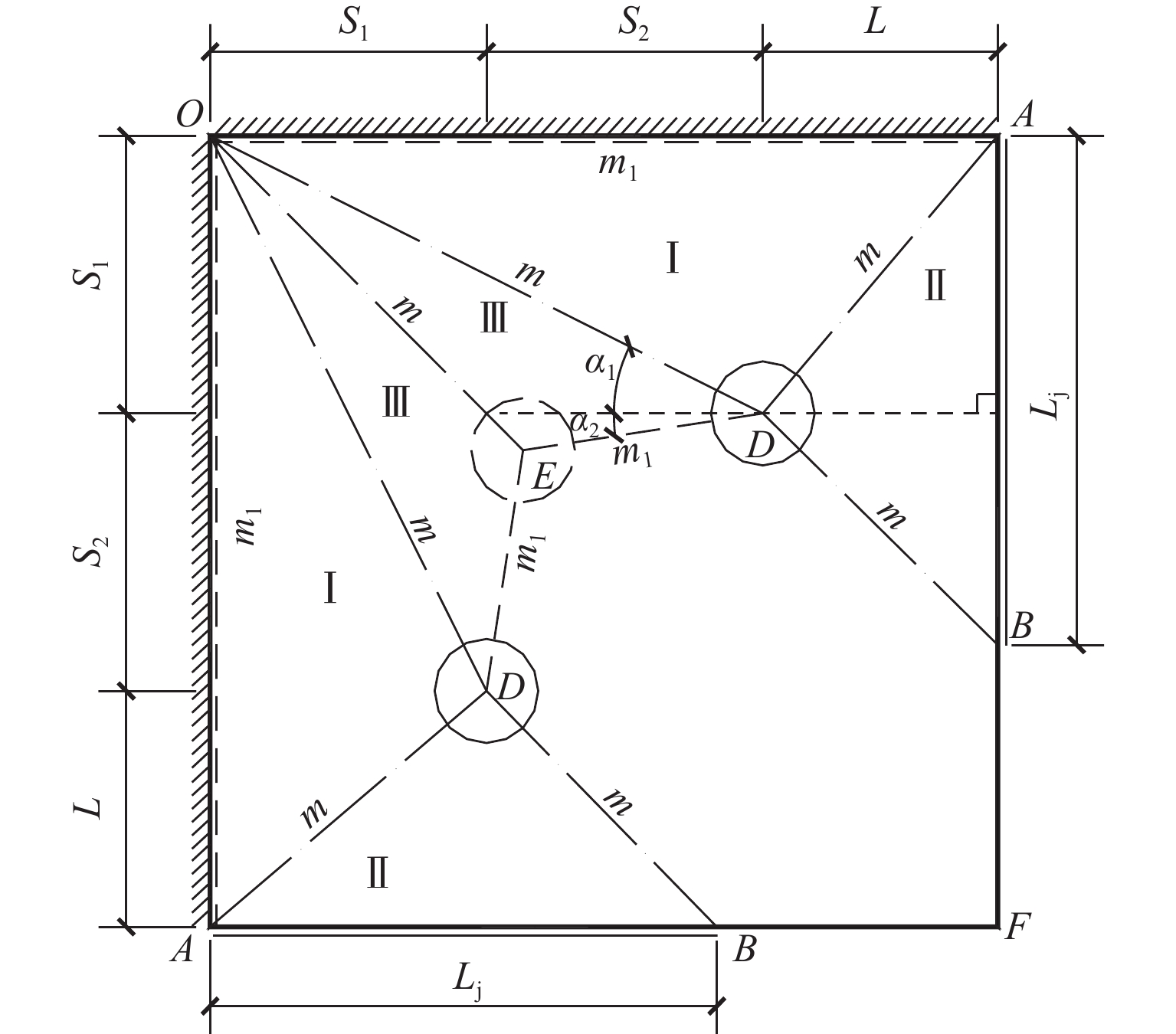
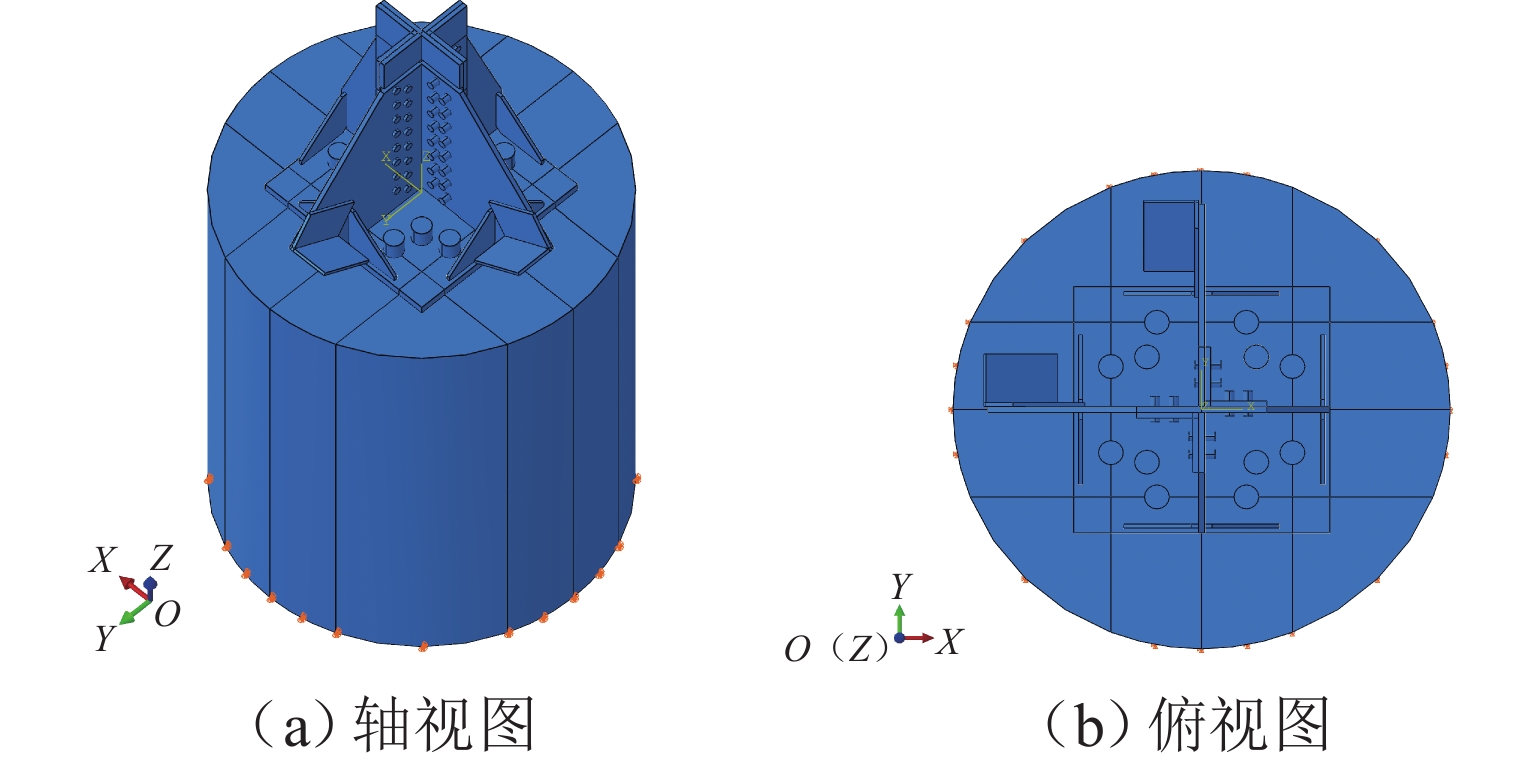
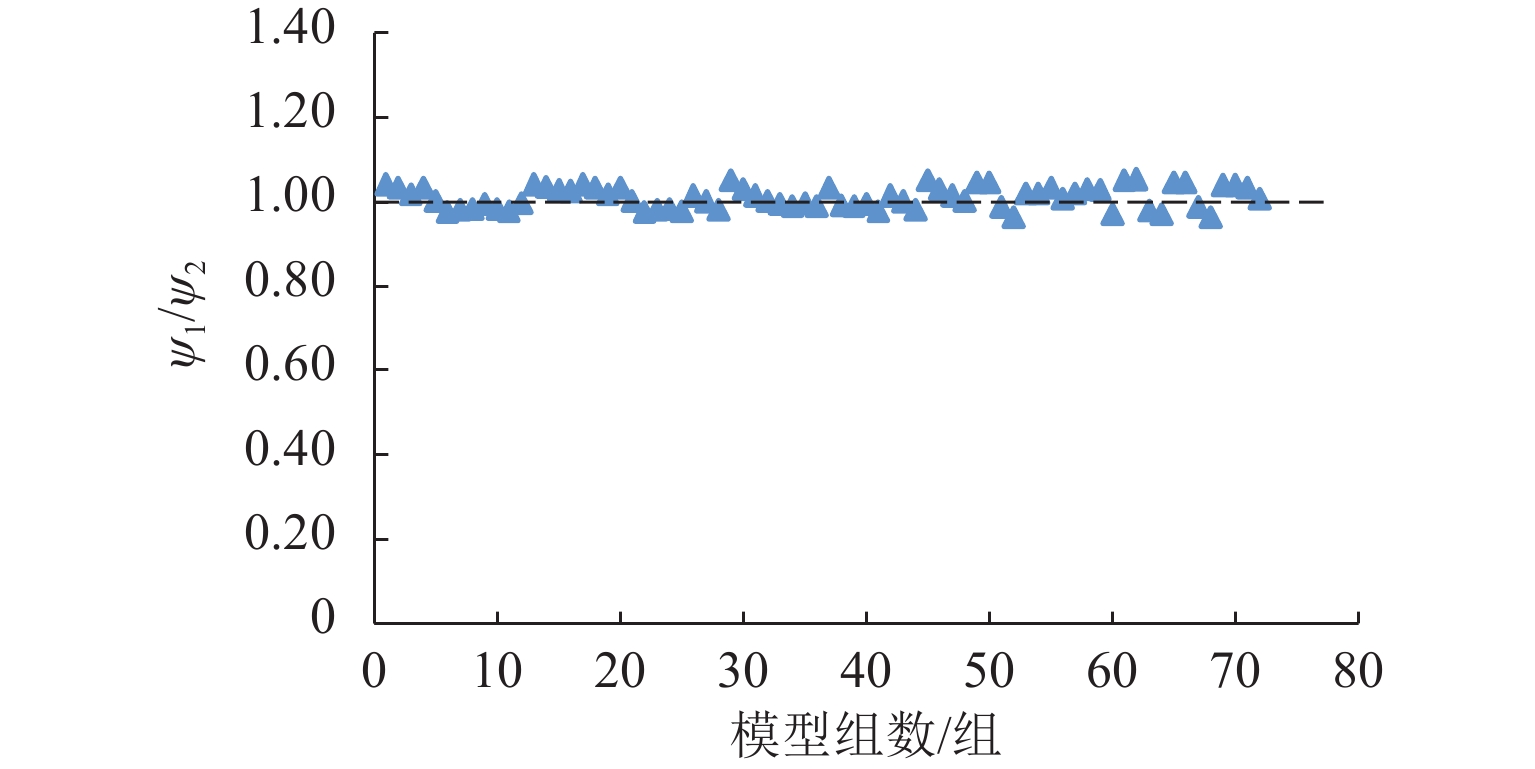
为解决输电角钢塔大荷载作用下的地螺连接问题，提出一种内嵌式十二地螺节点结构. 基于刚度差异演化的塑性屈服线理论，考虑地螺位置、地螺与塔脚板刚度差异的影响，推导出上拔荷载作用下内嵌地螺与外地螺内力不均匀计算的理论公式；然后，结合24组精细化数值分析，研究不同地螺直径、地螺间距和塔脚板厚度对内、外地螺上拔内力差异的影响，并对其刚度差异修正系数进行标定；最后，通过72组数值试验验证理论公式的合理性. 研究结论表明：内嵌式十二地螺结构较传统八地螺结构可以提高节点上拔承载力40%～50%；当内地螺布置在外地螺正交线上时，内、外地螺在上拔荷载作用下的内力不均匀分布系数约为1.1，且不随地螺直径和塔脚板厚度变化；当内地螺沿着对角线靠近外地螺时，内地螺内力的不均匀分布系数减小，但当塔脚板厚度增大时，不均匀分布系数会增大；考虑刚度差异演化的塔脚板塑性屈服线理论的计算结果与数值模拟结果相比，理论不均匀分布系数与数值不均匀分布系数比值的均值为1.01，变异系数为0.03.
Abstract:In order to solve the problem of ground screw connection under large load of transmission angle steel tower, an embedded twelve ground screw joint structure was proposed. Based on the plastic yield line theory of stiffness difference evolution, the influence of the position of ground screws and the stiffness difference between ground screws and tower foot plates was considered, and the theoretical formula of uneven internal force between embedded ground screws and external ground screws under uplift load was derived. Then, combined with 24 sets of refined numerical analysis, the influence of different ground screw diameters, ground screw spacings, and tower foot plate thicknesses on the differences in uplift forces of internal and external ground screws was studied, and the correction coefficient of stiffness difference was calibrated. Finally, the theoretical formula was verified by 72 sets of numerical experiments. The research results show that the embedded twelve ground screw structure can improve the uplift bearing capacity of the joint by 40%–50% compared with the traditional eight ground screw structure; when the internal ground screw is arranged on the orthogonal line of the external ground screw, the uneven distribution coefficient of internal force of the internal and external ground screws under the uplift load is about 1.1, and it does not change with the diameter of the ground screw and the thickness of the tower foot plate. When the internal screw is close to the external screw along the diagonal, the uneven distribution coefficient of the internal force of the internal screw will decrease, but when the thickness of the tower foot plate increases, the uneven distribution coefficient will increase. The calculation results based on the plastic yield line theory of stiffness difference evolution of the tower foot plate are compared with the numerical simulation results. The average value of the ratio of the theoretical uneven distribution coefficient to the numerical uneven distribution coefficient is 1.01, and the coefficient of variation is 0.03.
-
图 10 理论计算不均匀分布系数与数值模拟不均匀分布系数的比值
Figure 10. Ratio of theoretical uneven distribution coefficient to numerical uneven distribution coefficient
表 1 尺寸参数
Table 1. Dimension parameters
mm 地螺
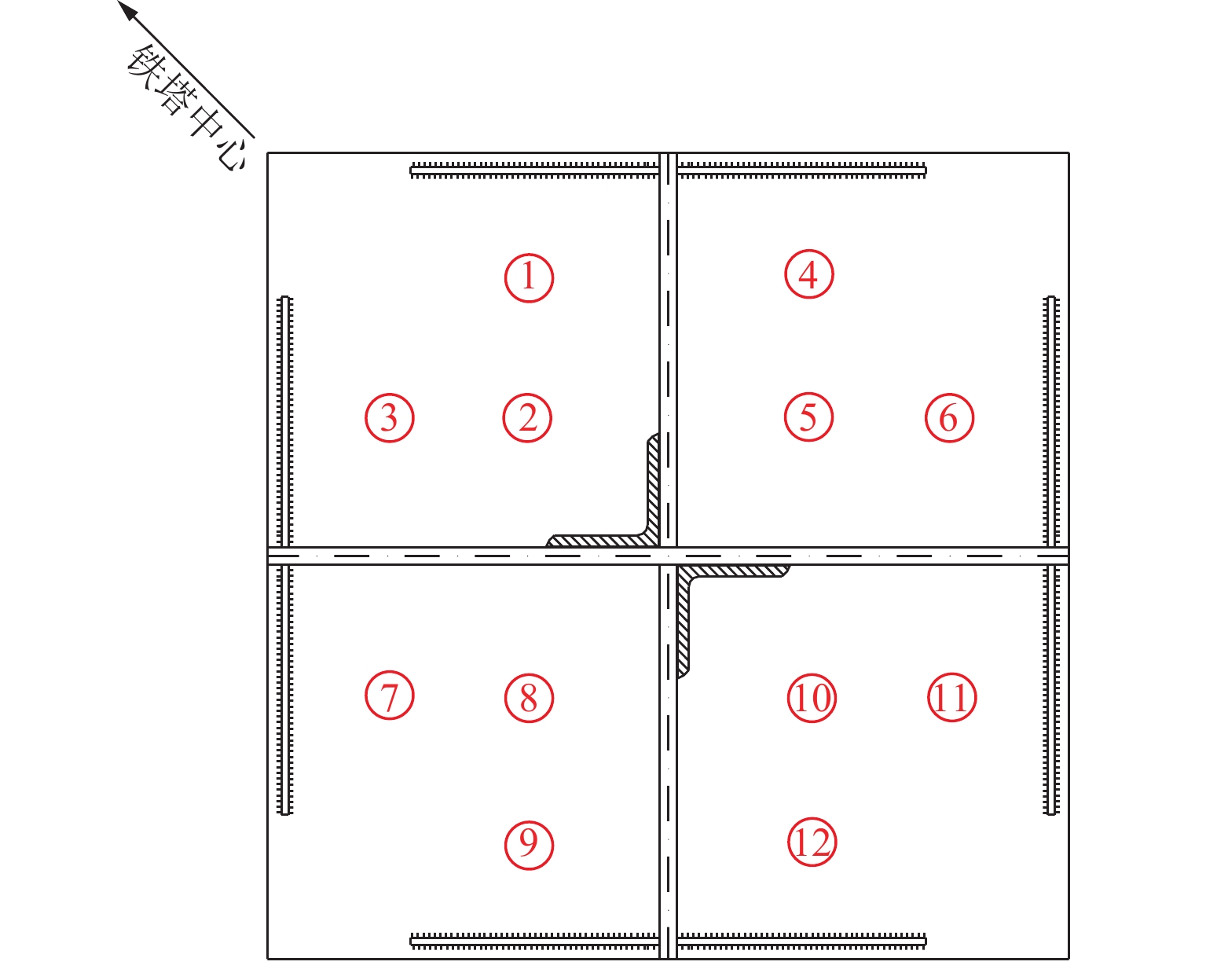
模型S1 S2 S3 L t 12M64 180 185 180.0，202.5，220.0 150 45，55，65，75 12M72 200 205 200.0，225.0，250.0 170 45，55，65，75 
下载: 导出CSV
表 2 规格及荷载
Table 2. Specifications and loads
地螺模型 主材规格 地螺承载
力/kN施加荷载/
kN应力比 12M64 2L250 × 28 9954.7 8500 0.85 12M72 2L280 × 35 12871.2 11000 0.85
下载: 导出CSV
表 3 12M64地螺内力对比分析（S3 = 180.0 mm）
Table 3. Comparative analysis of internal force of 12M64 ground screw （S3 = 180.0 mm）
地螺
编号t = 45 mm t = 55 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 716 1.08 695 1.11 677 1.10 694 1.06 2 745 755 740 724 3 669 662 674 668 4 741 1.04 759 1.03 741 1.06 735 1.05 5 730 738 753 747 6 668 667 674 683 7 765 1.02 755 1.02 751 1.03 753 1.03 8 726 733 740 740 9 656 678 682 681 10 756 1.14 744 1.13 765 1.17 758 1.15 11 648 641 654 648 12 681 672 649 670 $\overline \psi $ 1.07 1.08 1.09 1.08
下载: 导出CSV
表 4 12M64地螺内力对比分析（S3 = 202.5 mm）
Table 4. Comparative analysis of internal force of 12M64 ground screw （S3 = 202.5 mm）
地螺
编号t = 45 mm t = 45 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 727 1.00 720 0.96 694 1.01 684 1.03 2 708 685 698 709 3 694 702 691 686 4 790 0.91 798 0.91 782 0.97 767 1.00 5 677 675 704 722 6 698 694 672 681 7 791 0.87 791 0.90 775 0.92 752 0.99 8 653 674 690 717 9 703 699 720 699 10 678 0.98 697 1.02 709 1.04 717 1.05 11 690 681 695 682 12 690 682 671 684 $\overline \psi $ 0.94 0.95 0.98 1.02
下载: 导出CSV
表 5 12M64地螺内力对比分析（S3 = 220.0 mm）
Table 5. Comparative analysis of internal force of 12M64 ground screw (S3 = 220.0 mm)
地螺
编号t = 45 mm t = 55 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 762 0.76 762 0.81 720 0.90 710 0.93 2 583 602 642 654 3 777 731 706 702 4 826 0.72 813 0.80 797 0.85 759 0.93 5 569 617 646 687 6 746 739 725 722 7 848 0.73 830 0.80 807 0.87 785 0.92 8 576 619 662 690 9 740 719 716 712 10 594 0.80 623 0.86 678 0.97 684 0.98 11 752 713 710 710 12 728 731 690 685 $\overline \psi $ 0.75 0.82 0.90 0.94
下载: 导出CSV
表 6 12M72地螺内力对比分析（S3 = 200.0 mm）
Table 6. Comparative analysis of internal force of 12M72 ground screw （S3 = 200.0 mm）
地螺
编号t = 45 mm t = 55 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 903 1.15 877 1.17 873 1.17 875 1.15 2 1024 1010 1009 1002 3 877 857 854 860 4 960 1.05 975 1.05 952 1.06 948 1.06 5 947 959 960 957 6 849 847 858 864 7 923 1.01 907 1.07 912 1.07 915 1.08 8 937 953 965 970 9 876 874 890 878 10 964 1.07 972 1.10 979 1.12 989 1.13 11 855 882 877 863 12 903 889 874 881 $\overline \psi $ 1.09 1.10 1.10 1.11
下载: 导出CSV
表 7 12M72地螺内力对比分析（S3 = 225.0 mm）
Table 7. Comparative analysis of internal force of 12M72 ground screw （S3 = 225.0 mm）
地螺编号 t = 65 mm t = 75 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 950 0.88 924 0.99 903 1.01 910 1.04 2 836 900 905 932 3 943 900 892 888 4 1004 0.86 975 0.95 956 0.99 959 1.02 5 837 892 906 934 6 954 904 882 881 7 981 0.87 966 0.97 949 0.96 956 0.98 8 834 905 890 908 9 935 905 910 900 10 846 0.90 911 1.00 990 1.09 946 1.06 11 925 903 912 887 12 951 914 904 899 $\overline \psi $ 0.88 0.98 1.01 1.02
下载: 导出CSV
表 8 12M72地螺内力对比分析（S3 = 250.0 mm）
Table 8. Comparative analysis of internal force of 12M72 ground screw （S3 = 250.0 mm）
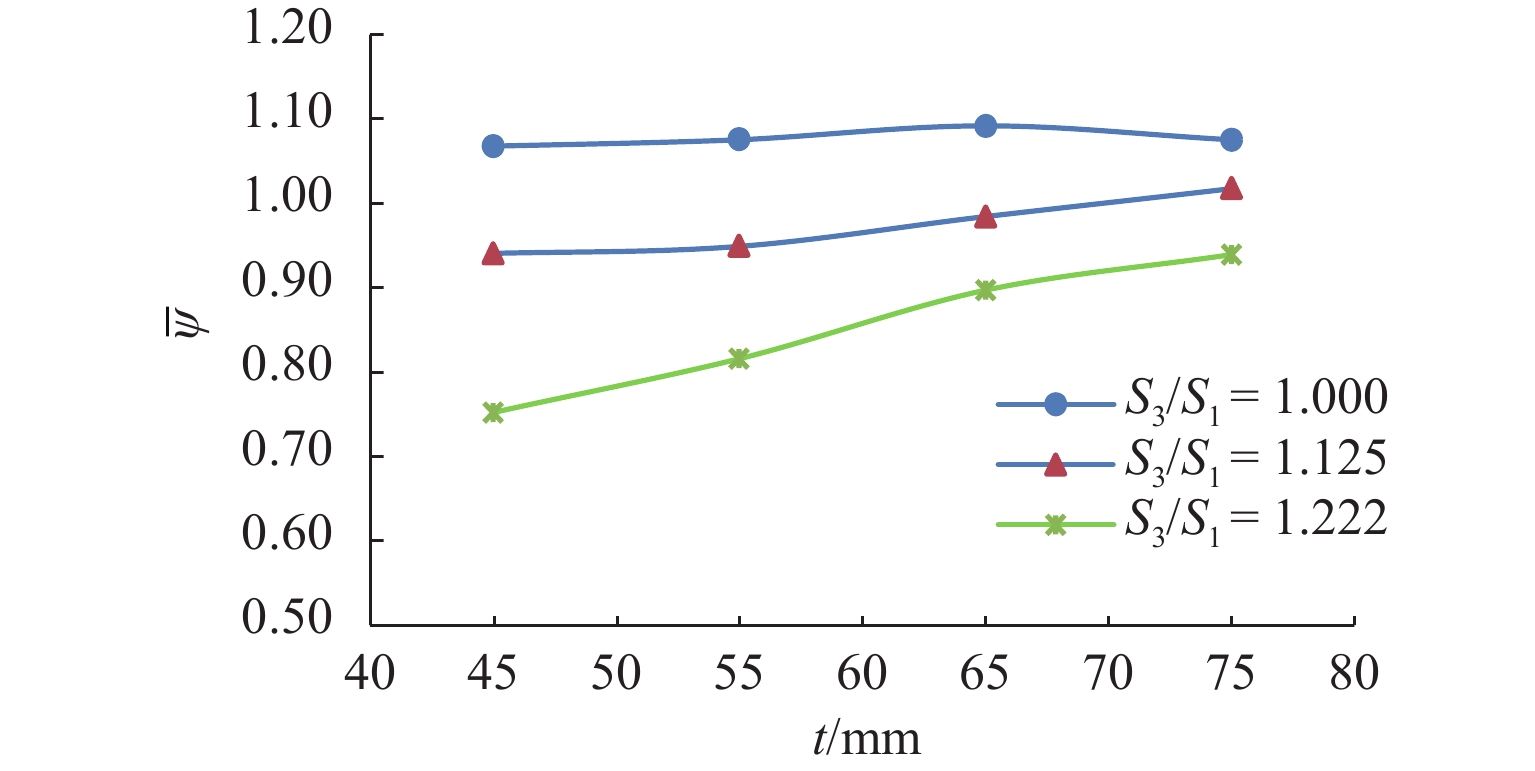
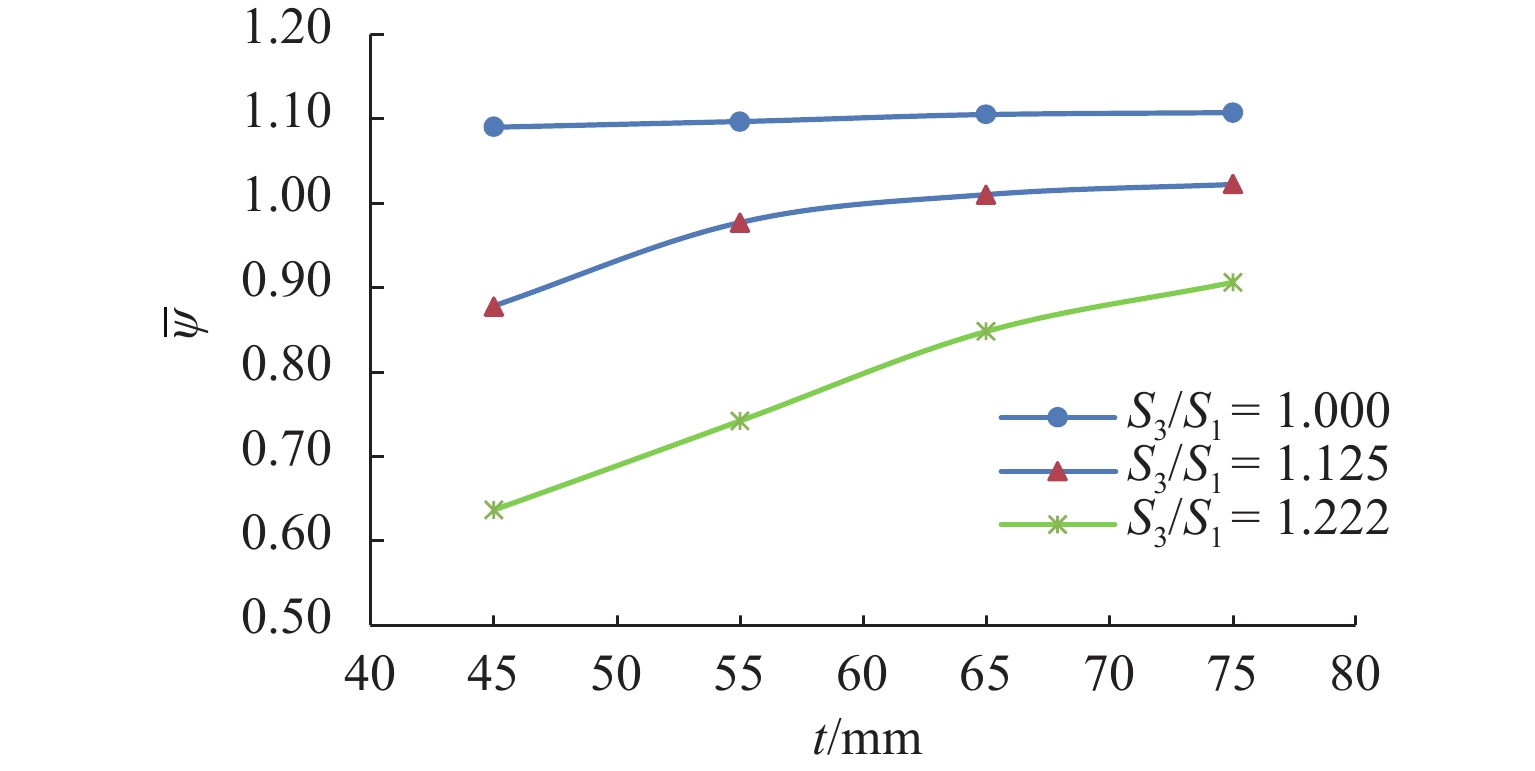
地螺编号 t = 45 mm t = 55 mm t = 65 mm t = 75 mm N/kN ψo N/kN ψo N/kN ψo N/kN ψo 1 1026 0.68 996 0.77 950 0.87 943 0.92 2 692 755 823 855 3 1014 979 942 918 4 1105 0.60 1054 0.70 1038 0.82 1012 0.87 5 637 721 806 844 6 1034 996 926 919 7 1093 0.62 1057 0.72 999 0.85 985 0.91 8 669 726 828 868 9 1048 972 952 924 10 656 0.65 772 0.78 819 0.85 861 0.92 11 1010 984 970 937 12 1023 990 954 937 $\overline \psi $ 0.64 0.74 0.85 0.91
下载: 导出CSV
表 9 不均匀分布系数均值$\overline \psi $
Table 9. Mean value of uneven distribution coefficient $\overline \psi $
地螺模型 t/mm S3/S1 1.000 1.125 1.222 12M64 45 1.07 0.94 0.75 55 1.08 0.95 0.82 65 1.09 0.98 0.90 75 1.08 1.02 0.94 12M72 45 1.09 0.88 0.64 55 1.10 0.98 0.74 65 1.10 1.01 0.85 75 1.11 1.02 0.91
下载: 导出CSV
表 10 数值试验参数
Table 10. Numerical test parameters
地螺模型 S1/mm S2/mm S3/mm L/mm t/mm 模型组数/组 12M64 180.0 195.0≥3.0d 180.0，202.5，220.0 150 45，55，65，75 12 225.0≥3.5d 260.0≥4.0d 12M72 200.0 195.0≥3.0d 200.0，225.0，250.0 170 45，55，65，75 12 225.0≥3.5d 260.0≥4.0d
下载: 导出CSV
表 11 上拔力计算结果对比
Table 11. Comparison of calculation results of uplift force
地螺型式 $\psi $ 最不利地螺内力/T 内嵌式十二地螺 1.0～1.1 0.083～0.089 八地螺 1.0 0.125
下载: 导出CSV
-
[1] 国家能源局. 架空输电线路杆塔结构设计技术规程:DL/T 5486—2020[S]. 北京: 中国电力出版社,2020. [2] 国家能源局. 输电线路杆塔制图和构造规定:DL/T 5442—2020[S]. 北京: 中国电力出版社,2020. [3] 王学明,薛晓敏,文凡,等. 八地脚塔脚板受拉承载力及其设计参数影响分析[J]. 西安交通大学学报,2020,54(3): 169-178.WANG Xueming, XUE Xiaomin, WEN Fan, et al. Research on tensile capacity of eight-bolted baseplate of electricity pylon and the influence parameters[J]. Journal of Xi’an Jiaotong University, 2020, 54(3): 169-178. [4] 杨攀,张雷,孟宪乔,等. 单角钢八地脚螺栓的受力分析及其塔脚板厚度设计[J]. 南昌大学学报(工科版),2016,38(3): 240-244. doi: 10.3969/j.issn.1006-0456.2016.03.007YANG Pan, ZHANG Lei, MENG Xianqiao, et al. Stress analysis of single angle eight foundation bolts and its design of bottom plate thickness[J]. Journal of Nanchang University (Engineering & Technology), 2016, 38(3): 240-244. doi: 10.3969/j.issn.1006-0456.2016.03.007 [5] 袁红丽. 特高压输电塔塔座板承载力研究及地震响应分析[D]. 西安: 西安建筑科技大学,2019. [6] 何松洋,韩大刚,蒋锐,等. 输电塔塔脚板式靴板连接计算方法[J]. 土木工程与管理学报,2021,38(4): 127-132,146. doi: 10.3969/j.issn.2095-0985.2021.04.019HE Songyang, HAN Dagang, JIANG Rui, et al. Calculation method on shoe plate connection of transmission tower[J]. Journal of Civil Engineering and Management, 2021, 38(4): 127-132,146. doi: 10.3969/j.issn.2095-0985.2021.04.019 [7] 付庭聪,肖奉英,孟凯,等. 塔脚板劲板尺寸对底板传递力分配比的影响[J]. 南昌大学学报(工科版),2022,44(3): 246-253. doi: 10.3969/j.issn.1006-0456.2022.03.007FU Tingcong, XIAO Fengying, MENG Kai, et al. Distribution ratio of tower foot stiffener plate size to bottom plate transfer force[J]. Journal of Nanchang University (Engineering & Technology), 2022, 44(3): 246-253. doi: 10.3969/j.issn.1006-0456.2022.03.007 [8] 蒋童,徐海潮,张树林,等. 塔脚板结构强度与底板接触应力分析[J]. 南昌大学学报(工科版),2021,43(4): 347-353. doi: 10.3969/j.issn.1006-0456.2021.04.007JIANG Tong, XU Haichao, ZHANG Shulin, et al. Analysis of tower foot structure strength and bottom plate contact stress[J]. Journal of Nanchang University (Engineering & Technology), 2021, 43(4): 347-353. doi: 10.3969/j.issn.1006-0456.2021.04.007 [9] 周文杰. 输电线路塔脚板的受力分析及其结构优化研究[D]. 南昌: 南昌大学,2019. [10] 俞登科,任吉华,段松涛,等. 基于区格法的输电塔有加劲塔脚板强度分析[J]. 电力勘测设计,2017(2): 42-45.YU Dengke, REN Jihua, DUAN Songtao, et al. Strength analysis of tower footing plate with stiffening in transmission tower based on lattice method[J]. Electric Power Survey & Design, 2017(2): 42-45. [11] 蒋童. 输电铁塔塔脚板结构强度与底板接触应力分布的研究[D]. 南昌: 南昌大学,2022. [12] 马瑞君,吴森坤,吕健,等. 输电铁塔十二颗地脚螺栓塔脚节点设计方法研究[J]. 工业建筑,2019,49(4): 44-51.MA Ruijun, WU Senkun, LYU Jian, et al. Research on design method of twelve-bolted leg joint of transmission tower[J]. Industrial Construction, 2019, 49(4): 44-51. [13] 向越,马海云,刘洪昌,等. 一种组合角钢塔圆形塔脚板布置结构:CN215717694U[P]. 2022-02-01. [14] KENNEDY G GOODCHILD C. Practical yield line design[M]. London: British Cement Association, 2003. [15] 沈聚敏,王传志,江见鲸. 钢筋混凝土有限元与板壳极限分析[M]. 北京: 清华大学出版社,1993. [16] 王稳,郝鑫,曹岳,等. 基于屈服线理论的塔脚板上拔承载力计算方法[C]//2021年工业建筑学术交流会论文集(上册). 北京: 国核电力规划设计研究院有限公司,2021:254-258,367. [17] 中华人民共和国住房和城乡建设部. 钢结构设计标准:GB 50017—2017[S]. 北京: 中国建筑工业出版社,2017. [18] 何松洋,蒋锐,辜良雨,等. 输电塔挂线角钢节点理论计算方法研究[J]. 建筑钢结构进展,2022,24(4): 82-91.HE Songyang, JIANG Rui, GU Liangyu, et al. Theoretical calculation method of angle steel joint of transmission tower[J]. Progress in Steel Building Structures, 2022, 24(4): 82-91. [19] 杨昌. 输电铁塔连接节点螺栓群力分配与螺栓布置形式和预拉力的关系研究[D]. 南昌: 南昌大学,2017. [20] 国家能源局. 输电线路杆塔及电力金具用热浸镀锌螺栓与螺母:DL/T 284—2021[S]. 北京: 中国电力出版社,2021. -
下载:
点击查看大图
计量
- 文章访问数: 64
- HTML全文浏览量: 31
- PDF下载量: 7
- 被引次数: 0