Design and Implementation of Magnetic Suspension Vibration Isolation Platform with Quasi-Zero Stiffness Based on Fuzzy PID Control
-
摘要:
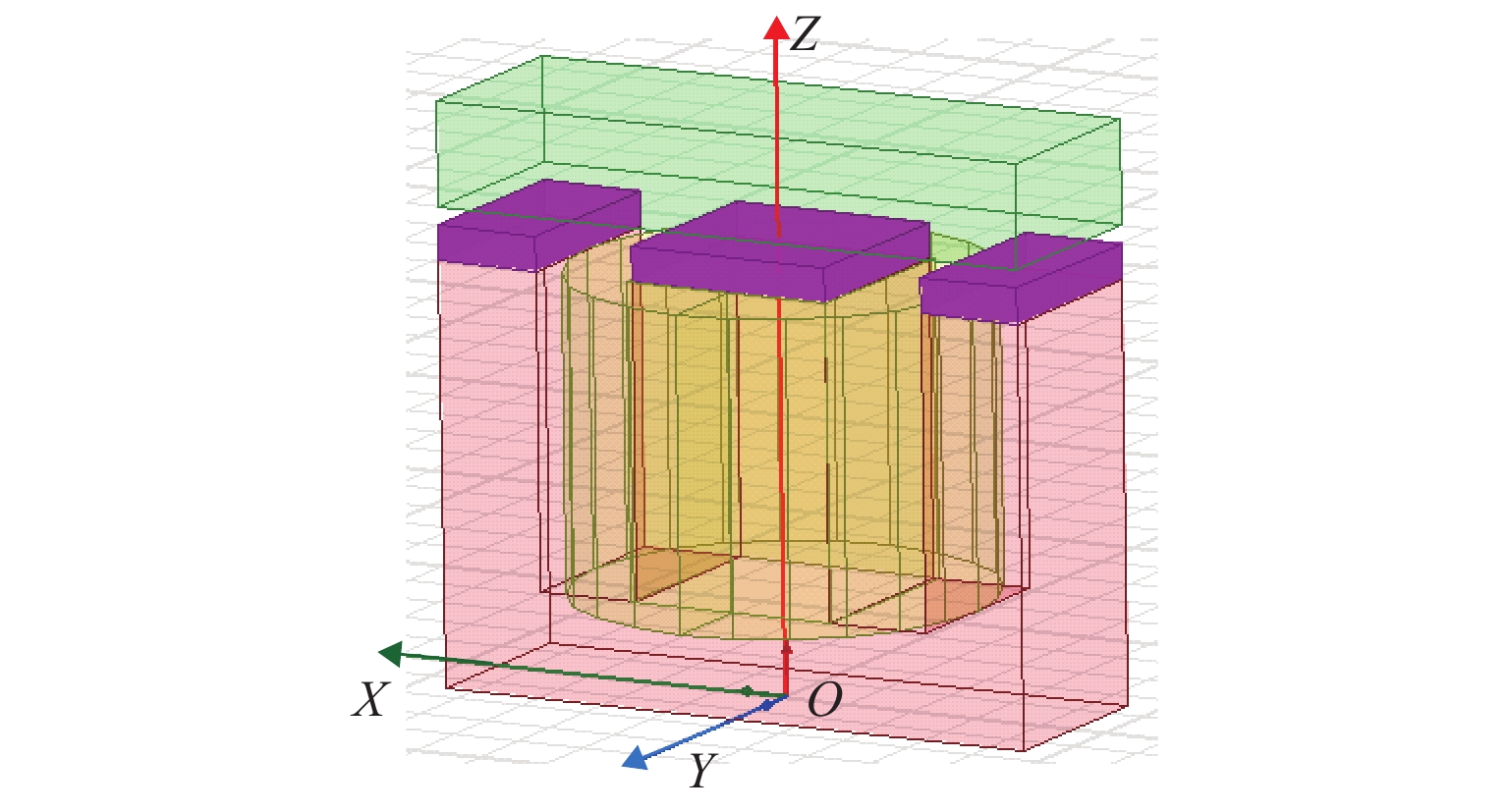
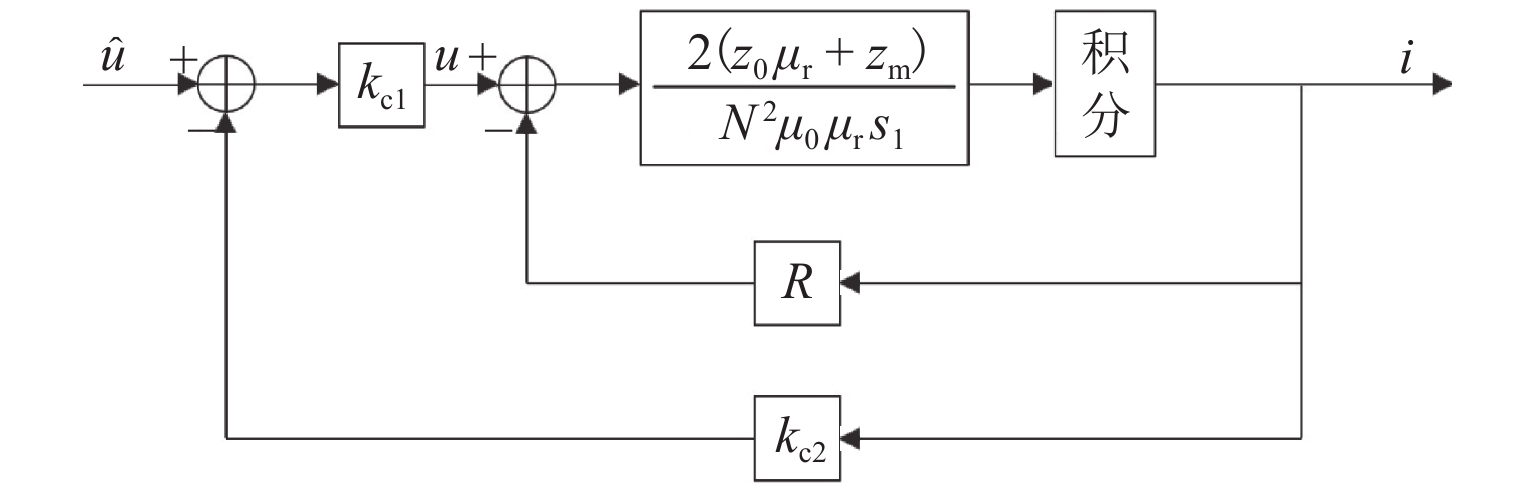
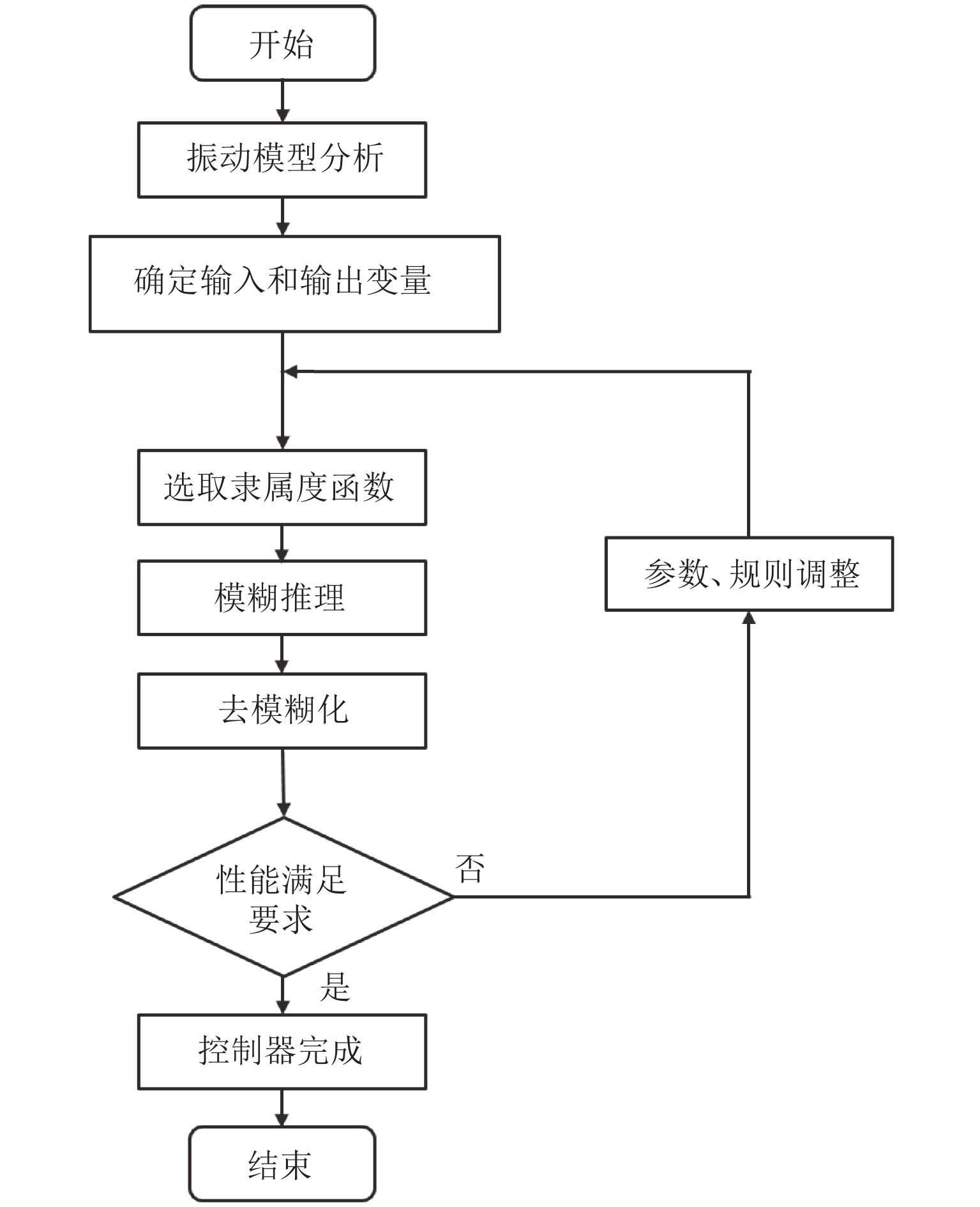
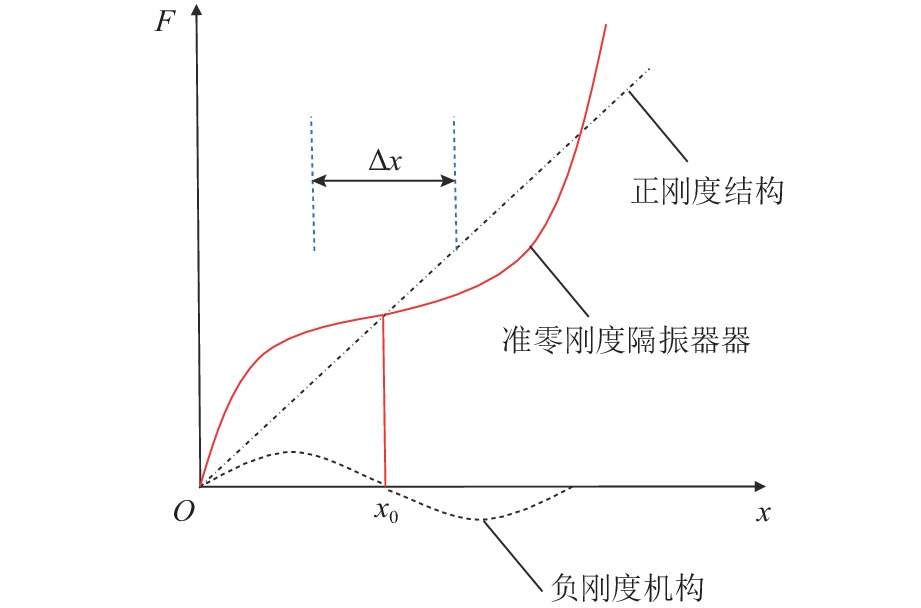
为有效降低系统固有频率，获得外部振动在多频段的强衰减，以永磁电磁混合作动器为负刚度结构提出并设计了一种准零刚度的磁悬浮隔振平台，实现了基于模糊PID (proportional integral differential)算法的振动主动控制系统. 首先，通过特性分析与参数计算，基于准零刚度理论完成了准零刚度磁悬浮隔振平台的方案设计；其次，建立磁悬浮隔振系统模型，提出基于模糊PID算法的振动主动控制策略，可主动调节系统的等效刚度和阻尼；最后，基于Speedgoat实时目标机开发振动主动控制系统，搭建隔振测试平台，并开展了隔振性能测试. 研究结果表明：本文设计的准零刚度磁悬浮隔振平台通过采用模糊PID的控制策略能够主动调节PID参数，动态调整系统的等效刚度和阻尼；外部振动频率在20～100 Hz频率段内，振动衰减率大于80%；外部振动频率在100～500 Hz频率段内，振动衰减率大于90%.
Abstract:In order to effectively reduce the natural frequency of systems and realize the strong attenuation of external vibrations in multiple frequency bands, a magnetic suspension vibration isolation platform with quasi-zero stiffness was designed, in which the permanent-magnet and electromagnetic hybrid actuator was the negative stiffness structure, and an active vibration control system based on fuzzy PID (proportional integral differential) algorithm was implemented. Firstly, based on the theory of quasi-zero stiffness, the scheme of the magnetic suspension vibration isolation platform with quasi-zero stiffness was designed through characteristic analysis and parameter calculation; secondly, the model of the magnetic suspension vibration isolation system was established, and the active vibration control strategy based on fuzzy PID algorithm was designed to actively adjust the equivalent stiffness and damping of the system; finally, an active vibration control system was developed based on the Speedgoat real-time target machine. A vibration isolation test platform was built, and a series of vibration isolation performance tests were carried out. The results show that the magnetic suspension vibration isolation platform with quasi-zero stiffness can actively adjust PID parameters by adopting a fuzzy PID control strategy and dynamically adjust the equivalent stiffness and damping of the system. When the external vibration frequency is 20–100 Hz, the vibration attenuation rate is greater than 80%; when the external vibration frequency is 100–500 Hz, the vibration attenuation rate is greater than 90%.
-
数字式仪表具有读数准确方便、测量速度快、能提供数字信号输出、方便进行目视观察和数字记录等优点，已被广泛应用到变电站、工业、军事、航空等领域. 然而，在实际应用中，由于技术限制和各类其他原因，变电站中一些数字仪表的数据读取和记录始终依靠人工观察. 但是，人工观察在整个工作过程中存在手动工作量大、实时性差、效率低等问题.
对变电站数字仪表数据进行智能化监测和管理能有效增强实时性，减少安全隐患. 随着变电站智能化发展，人工采集已不能满足变电站对数据实时性的需求，对变电站数字仪表数据的实时处理已成为当前重要研究问题之一. 近年来，相关研究人员提出使用计算机视觉处理技术实现变电站数字仪表数据读取，这类方法大多先使用相机获取图像，再运用数字图像处理相关技术获取数字仪表读数，进而完成识别任务.
数字仪表读数识别采用的方法有支持向量机、神经网络、模板匹配、穿针引线法等. Cui等[1]提出一种数字仪表数字识别方法，采用基于方向梯度直方图的线性支持向量机，其拥有较好的精确度以及鲁棒性，但不适用于大样本数据的处理；卜令正等[2]提出一种改进的卷积神经网络（CNN）实现手写数字与数码管数字的识别，具有较快的检测速度，但是有一定精度损失；郭兰英等[3]提出一种基于可变形CNN的数显仪表示数分割与识别方法，准确率高，但是检测速率相对较慢；陈刚等[4]提出一种基于特征提取的数字仪表数码快速直接识别算法，能够快速识别字符，但其在复杂环境中鲁棒性较差；郭爽[5]采用穿线法对数字仪表进行识别，有较好的识别效果，但是依赖简单的识别环境；高菊等[6]在模板匹配的基础上，通过增加对字符特征的匹配，减少对相近字符的误判，适用于某一种类型仪表的数字识别，但对不同字体、不同倾斜程度的数字字符识别效果不佳，且模板匹配法容易遭受噪声影响.
近年来，随着计算机视觉技术发展迅速，深度学习的方法在图像目标检测领域中应用愈加广泛. 2014年提出的基于区域的CNN （RCNN）[7]、2015年提出的全卷积网络 （FCN）[8-9]以及2015年提出的Faster RCNN[10-11]等标志着计算机视觉领域目标检测的巨大进步. 与此同时，You Only Look Once （YOLO）系列算法也相继被提出，包括2015年YOLO-v1[12]、2016年YOLO-v2[13]、2017年YOLO-9000[14]、2018年YOLO-v3[15]、2019年YOLO-v4[16]以及YOLO-v5[17]. YOLO-v4作为检测速率与精确度并肩的检测算法，已经在各个行业被广泛应用，如煤矸石检测[18]、人体检测[19]、安全帽检测[20]等. 相比于其他深度学习目标检测模型，YOLO-v4模型可兼顾检测性能和预测速度，能满足大部分实际检测任务的实时性需求.
尽管YOLO-v4模型的计算效率已大大提高，但对于变电站数字仪表的智能监测这一实际应用而言，其实时性和存储复杂度仍有待进一步改进. 针对深度学习模型的轻量化问题，常用的轻量级网络为MobileNet系列模型，包括2017年Howard提出的MobileNet-v1[21]、2018年MobileNet-v2[22]、2019年MobileNet-v3[23]等. 该系列模型中构建的深度可分离卷积模块能在低参数量的情况下有效提取特征，但也存在非线性能力不足、模型压缩程度有限等问题.
针对上述问题，面向变电站数字仪表检测识别的实际应用需求，本文提出一种基于轻量级YOLO-v4模型的数字仪表检测识别方法，在几乎不损失模型准确度的同时，有效降低整个模型的计算和存储复杂度. 主要工作包括以下3个部分：
1） 考虑到传统深度可分离卷积模块存在的非线性能力不足、压缩程度有限等问题，本文结合非线性拟合能力更强的Mish函数，提出轻量级网络模块bneck-m. 进一步，结合有效通道注意力（ECA）模块，构建ECA改进的bneck-m （ECA-bneck-m）模块，有效提高其非线性处理能力和计算效率.
2） 考虑到传统YOLO-v4模型无法满足实际场景中变电站数字仪表检测识别的实时性和低存储复杂度需求，基于ECA-bneck-m模块，本文提出一种轻量级YOLO-v4模型，在几乎不损失模型检测准确度的前提下，提升模型的推理速度.
3） 从鄂尔多斯变电站实际场景中采集数字仪表图像，并使用Albumentations框架对图像进行弹性变化、旋转、色彩空间变换等方式的数据增强，构建一个数据量充足、能较为全面反映变电站数字仪表可能情况的数字仪表检测识别数据集.
1. 深度学习数字仪表检测识别方法
1.1 总体研究思路
面向变电站实际场景中对数字仪表检测识别实时性和准确性的应用要求，以鄂尔多斯变电站采集的数字仪表图像作为研究对象，基于由特征提取网络以及路径聚合网络（PANet）组成的轻量级YOLO-v4网络，提出深度学习数字仪表检测识别方法，其总体框架如图1所示，主要包括数字仪表预处理、数字仪表数据集构建、用于数字仪表目标检测以及数字字符识别的轻量级YOLO-v4模型、数字仪表检测识别等部分.
图 1 深度学习数字仪表检测识别方法总体框架Figure 1. General framework of deep learning-based method for detection and recognition of digital instruments1.2 基于轻量级YOLO-v4的数字仪表检测算法
类似于传统自然图像目标检测，最简单的变电站数字仪表检测方法为模板匹配.
1.2.1 模板匹配
模板匹配是在一幅图像中寻找与另一幅模板图像相似部分的技术[24]. 该方法通过目标图像在待匹配图像中进行遍历，选择一定的匹配方式得到每个起始像素点的匹配度，匹配度最高的位置就是候选匹配位置，达到匹配查找的效果，如图2所示. 图中，T(m,n)为模板图像，A(u,v)为待识别图像，(m,n)为模板图像像素点坐标，u、v分别为待识别图像的宽、高.
通过将模板图像在待识别图像上进行平移，被模板覆盖的搜索区域为子图Aij(m,n)，i、j为子图左上角坐标，i∈[1, u−M]，j∈[1, v−N]，M、N分别为模板图像的宽、高. T(m,n)和Aij(m,n)间的误差值为D(i, j)，如式（1）所示. 误差值越小，则匹配度越高，相似性越高.
尽管这种方法计算量小，且检测速度快，但其鲁棒性较差，在复杂环境下并不适用.
D(i,j)=M∑m=1N∑n=1[Aij(m,n)−T(m,n)]2. (1) 1.2.2 轻量级YOLO-v4模型
YOLO-v4的算法框架由主干特征提取网络（CSPDarknet-53）、空间金字塔池化（SPP）和PANet构成，如图3所示.
面向变电站数字仪表检测识别，本文结合Mish函数和注意力机制，提出一种轻量级 YOLO-v4 模型，包含 4 个改进思路：
1） bneck是一种特殊的深度可分离卷积模块，能有效提取目标的特征信息，且拥有较少的参数量. 如图4所示，bneck由3 × 3深度可分离卷积（Dwise）、SE （squeeze-and-excitation）通道注意力机制和残差连接结构构成. 图中：NL代表非线性激活函数，Pool为池化处理，FC为全连接层，ReLU与Hard-σ （σ为Sigmoid函数）为激活函数，+ 表示残差连接，Dwise用于提取图像特征，SE通道注意力用于提高特征的表达能力，残差连接结构用于解决由于网络层数过深而产生过拟合的问题.
bneck模块采用H-Swish函数作为模型的激活函数，使用光滑的激活函数的模型拥有较好的性能[25]. H-Swish、Mish函数曲线如图5所示，图中，x为函数自变量. 可以看出，H-Swish函数存在拐点，Mish函数呈现为光滑曲线. 因此，选用Mish函数作为激活函数，提出改进的深度可分离卷积模块bneck-m，提高整个模块的特征提取能力.
基于上述分析，所提出bneck-m模块结构与图4相同，由逆残差结构、深度可分离卷积结构和SE注意力模块构成，在提高模块非线性能力的同时，自适应地从特征的通道维度学习有用特征信息，同时抑制干扰信息.
2） 在1）基础上，为进一步降低bneck-m模块参数量，且提高其计算效率，结合ECA模块，将SE模块（图6）替换为ECA模块（图7），提出如图8所示的ECA-bneck-m模块. 图6中：e为输入特征，H × W × C为通道维度. SE模块对每个特征通道单独使用全局平均池化（GAP），然后使用2个FC层，最后，使用Hard-σ函数生成通道权值，将通道权重与原特征相乘，获得输出特征˜e. 其中，FC层的设计是为了捕捉非线性的跨通道交互，并通过降维控制其复杂性. 如图7所示，ECA模块先对每个通道单独全局平均池化，然后，通过考虑每个通道及其s个邻居来捕获局部跨通道交互信息，即使用s个1维卷积捕获局部跨通道交互信息，最后，用Sigmoid函数来生成通道权值. 相较SE模块，ECA模块的s个1维卷积结构复杂度低，且推理速度快. 因此，ECA模块的整体性能更佳.
相比于bneck-m模块，ECA-bneck-m模块具有参数量小和特征提取能力强的特点，能有效降低模型参数量和存储大小.
3） 传统YOLO-v4主干网络CSPDarkNet-53的参数量大，导致推理时间较长，无法满足变电站数字仪表检测识别要求，本文基于Mish函数提出ECA-bneck-m模块，构建轻量级特征提取网络，并将其作为YOLO-v4模型新的主干网络.
4） 空间金字塔池化（SPP）层能提取多尺度空间特征，提升模型对于空间布局和物体变形的鲁棒性，如图9所示. SPP对特征分别采用4种最大池化操作处理并使用kl表示，池化得到图像特征ql，如式（2） 所示. 最后，通过级联得到输出特征q （式（3））.
ql=klo,l=1,2,3,4, (2) q=4∑l=1ql, (3) 式中：o为主干网络提取的图像特征.
由于变电站数字仪表目标不同于常规目标，本文结合实际采集的仪表图像，对SPP层进行优化，通过对不同池化组合的研究，获取最优尺度，使改进后的模型更好地适用于数字仪表的检测识别，提高模型精度.
轻量级YOLO-v4模型结构如图10所示，将其应用于变电站数字仪表的智能检测识别，从实际拍摄的图像中定位数字仪表的位置，为数字仪表读数提供更为精确的数字仪表数显区域，降低计算复杂度，同时提高整个模型的识别准确度.
1.3 数字仪表检测数据集构建
由于鄂尔多斯变电站日常摄像机所拍摄的数字仪表图像受到实际环境因素的影响，图像会出现亮度较暗等情况. 因此，需要对实际采集的数字仪表图像进行预处理，本文采用伽马变换，提高原始数字仪表图像的质量.
考虑到深度学习模型需要大量的标签数据，而变电站中实际能够采集到的数字仪表图像数据有限，无法满足深度学习模型的训练需求. 因此，本文使用基于Albumentations框架的数据增强方式，实现数字仪表图像数据量级的有效提升. 该框架包括多种图像扩充的方式，例如弹性变化、旋转、高斯噪声以及色相和饱和度值偏移（HSV）等. 基于上述4种处理方法，对采集到的变电站数字仪表图像进行数据增强，并构建得到变电站数字仪表检测识别数据集，用于轻量级YOLO-v4模型的训练和学习.
1.4 基于轻量级YOLO-v4的数字仪表数显区域定位和读数识别算法
尽管1.2节已完成对变电站数字仪表的精确定位，但还需对数字仪表的数显区域和读数进行定位与识别，为工作人员智能监测变电站运行情况与异常情况提供及时的参考和辅助.
如图1所示，本文采用轻量级YOLO-v4模型，先对数字仪表的数显区域进行定位，然后定位与识别其中的数字字符，根据数字字符坐标顺序依次输出分类结果，得到最终的数字仪表读数识别结果.
2. 实验结果以及分析
2.1 数据集构建
考虑到深度学习模型需要大量标签样本，本文使用Albumentations框架对实际采集的数字仪表图像进行扩充，进而构建变电站数字仪表检测识别数据集（见表1）. 原始数字仪表图像数据集从1571幅扩充到5000幅，原始数字字符图像数据集从1201幅扩充到5000幅. 数据扩充效果如图11所示.
表 1 图像数据扩充结果Table 1. Image data expansion results幅 数据集 数字仪表 数字字符 总计 原数据集 1571 1201 2772 扩充数据集 5000 5000 10000 参考文献[26-29]，基于扩充数据集，按照9∶1的比例制作训练集及测试集. 其中，用于仪表检测的数据集总数为5000幅，4500幅为训练集，500幅为测试集；用于字符检测的数据集总数为5000幅，4500幅为训练集，500幅为测试集.
2.2 实验环境与参数设置
实验环境配置为：操作系统Windows 10，CPU AMD Ryzen 5 3600，内存16 GB，显卡NVIDIA Geforce RTX 2060 （6 GB）. 模型的训练平台为深度学习开发工具Pytorch 1.2.0，编程语言为Python.
轻量级YOLO-v4模型相关训练参数为：学习率为0.001，Batch_size为4，Epoch设置为180次.
2.3 性能评价指标
采用目标检测常用的性能评价指标衡量模型性能，包括平均精度（average precision, AP）、平均精确度均值（mean average precision, mAP）、精确率（P）、召回率（R）以及F1值.
P是模型对某类正确预测为正样本的数量TP与该类所有预测为正样本总数（即TP与预测为正样本的负样本数量FP之和）的比值，如式（4）所示.
P=TPTP+FP. (4) R是TP与实际为该类正样本总数（TP与预测错误的正样本数量FN之和）的比值，如式（5）所示.
R=TPTP+FN. (5) F1值（式（6））为精确率和召回率的加权调和平均，是分类问题中对性能综合评估的常用评价指标.
F1=2RPR+P. (6) AP即精确率召回曲线的面积，AP值越高，则检测效果越好. mAP是所有类别AP的均值，作为综合评价指标.
2.4 实验结果与对比分析
2.4.1 伽马变换效果
对数字仪表图像采用1.3节基于伽马变换的预处理操作，当变换参数γ=0.7时，图像效果如图12所示. 数字仪表图像的亮度值得到有效提升，图像特征信息更加明显.
2.4.2 预选框的选取与设置
由于数字仪表和字符目标较为固定，使用YOLO-v4原有的预选框尺寸效果较差，需重新设定预选框尺寸. 数字仪表数据集类型和目标尺寸均较为单一，直接通过k-means聚类算法得到的聚类中心往往较为集中，进而影响整个模型训练效果.
本文采用改进的预选框尺寸聚类方法. 首先，使用k-means方法对人工标注的数字仪表数据集重新进行聚类，获取初始预选框尺寸. 在此基础上，通过线性尺度的缩放操作，对预选框尺寸进行调整，进而获得满足变电站数字仪表检测识别所需的预选框尺寸，如式（7）所示.
{(˜α1,˜β1)=0.5(α1,β1),(˜α9,˜β9)=3(α9,β9),(˜αδ,˜βδ)=(αδ−α1α9−α1(˜α9−˜α1),˜αδβδαδ),2⩽δ⩽8, (9) 式中：αδ和βδ分别为k-means聚类预选框尺寸的宽和高；˜αδ和˜βδ分别为线性尺寸缩放后的预选框尺寸的宽和高； δ为聚类预选框的编号，1⩽δ⩽9.
因此，通过上述计算得到的变电站数字仪表检测识别对应的预选框尺寸如表2所示.
表 2 k-means预选框聚类结果Table 2. k-means clustering results of prior box模型 特征层 13 × 13 26 × 26 52 × 52 仪表检测
模型（204, 149） （84, 174） （5, 16） （221, 448） （128, 227） （21, 36） （288, 144） （174, 479） （71, 131） 字符识别
模型（159, 191） （94, 127） （14, 24） （163, 270） （127, 167） （42, 62） （297, 876） （131, 633） （70, 308） 2.4.3 SPP层的尺度优化
输入图像通过轻量级YOLO-v4模型的主干特征提取网络后，需经过SPP层，对空间尺度为13 × 13的特征进行不同尺寸的最大池化，进一步学习输入图像的多尺度属性. 先根据经验固定2组核大小为1 × 1和13 × 13，再从常用池化尺寸{3 × 3，5 × 5，7 × 7，9 × 9，11 × 11}中选取经典组合{3 × 3，5 × 5 }、{5 × 5，7 × 7}、{7 × 7，9 × 9 }、{7 × 7，11 × 11}、{5 × 5，9 × 9}. 通过5组池化尺度进行实验对比，结果如表3所示. 当尺度组合设置为{7 × 7, 9 × 9}时，整个模型的mAP值最高. 因此，用于数字仪表图像识别的轻量级YOLO-v4模型中剩余2个最大池化尺度组合设置为{7 × 7, 9 × 9}.
表 3 SPP层不同池化尺度性能对比结果Table 3. Performance comparison of SPP layer at different pooling scales池化尺度 mAP/% {3 × 3, 5 × 5} 99.75 {5 × 5, 7 × 7} 99.69 {7 × 7, 9 × 9} 99.78 {7 × 7, 11 × 11} 99.74 {5 × 5, 9 × 9} 99.68 2.4.4 模型训练参数设置
为直观展示轻量级YOLO-v4模型的训练过程，图13给出了模型的学习曲线. 当迭代次数超过180次后，整个模型趋于稳定收敛. 因此，实验中迭代次数Epoch设置为180次.
2.4.5 不同深度学习模型性能对比分析
为突出YOLO-v4模型在改进过程中的轻量化变化程度，表4给出上述4种模型大小的对比结果. 由于激活函数不会影响模型大小及参数量，基于bneck和bneck-m模块的轻量级YOLO-v4模型相比原始模型（基于DarkNet-53模块），大小均从244.0 MB减少到53.8 MB，参数从63986151个缩减到14018719个. 而基于ECA-bneck-m模块轻量级YOLO-v4网络的模型大小仅为48.0 MB，参数量为12506463个，均小于原始模型，上述实验结果表明，所提出的模型在模型存储大小和参数量上更有优势.
表 4 不同网络模型大小对比结果Table 4. Comparison results of different model sizes网络模型 参数量/个 模型大小/MB YOLO-v4 （DarkNet-53） 63986151 244.0 YOLO-v4 （bneck） 14018719 53.8 YOLO-v4 （bneck-m） 14018719 53.8 YOLO-v4 （ECA-bneck-m） 12506463 48.0 基于2.1节训练集与测试集，为验证轻量级YOLO-v4 （ECA-bneck-m）模型在检测准确度和实时性上的优势，表5给出不同识别模型性能对比结果，选择Faster-RCNN、YOLO-v3、YOLO-v4、轻量级YOLO-v4 （bneck）和YOLO-v4 （bneck-m）5种模型与本文模型作对比分析. 表6给出轻量级YOLO-v4 （ECA-bneck-m）模型的每类字符识别、仪表检测与数显区域定位结果. 而图14给出数字仪表检测与读数识别结果.
表 5 不同深度学习目标检测模型对比结果Table 5. Comparison of different deep learning detection models网络 mAP/% FPS/（帧·s−1） Faster-RCNN 83.88 6.0 YOLO-v3 99.64 30.0 YOLO-v4 99.80 24.0 轻量级YOLO-v4 （bneck） 99.58 33.7 轻量级YOLO-v4 （bneck-m） 99.75 35.6 轻量级YOLO-v4 （ECA-bneck-m） 99.78 36.9 表 6 轻量级YOLO-v4（ECA-bneck-m）测试结果Table 6. Lightweight YOLO-v4 （ECA-bneck-m） test results类别 P/% R/% F1 字符 0 识别 99.83 99.65 1.00 字符 1 识别 99.43 98.87 0.99 字符 2 识别 98.58 100.00 0.99 字符 3 识别 100.00 100.00 1.00 字符 4 识别 98.56 100.00 0.99 字符 5 识别 96.58 99.30 0.98 字符 6 识别 95.27 98.60 0.97 字符 7 识别 99.05 100.00 1.00 字符 8 识别 97.54 100.00 0.99 字符 9 识别 100.00 99.25 1.00 仪表检测 97.22 100.00 0.99 数显区域定位 98.25 100.00 0.99 
图 14 数字仪表检测与读数识别结果示意Figure 14. Recognition results of digital instrument detection and reading根据表5、6所示的实验结果，YOLO-v4模型的mAP值比Faster-RCNN高15.92%，比YOLO-v3高0.16%. 从实时性角度，YOLO-v4的每秒处理帧数（frames per second，FPS）比Faster-RCNN高18.0帧/s，但略低于YOLO-v3模型（仅降低6.0帧/s）. 可以看出，相比于YOLO-v3与Faster-RCNN模型，YOLO-v4模型可以在获得较高检测准确度的同时，保证较快的推理速度.
与YOLO-v4模型相比，改进的轻量级YOLO-v4 （ECA-bneck-m）模型在仅降低0.02% mAP值的前提下，推理速度FPS从原始的24.0帧/s提升到36.9帧/s. 相比YOLO-v4 （bneck）和YOLO-v4 （bneck-m）这2种模型，轻量级YOLO-v4 （ECA-bneck-m）模型的mAP值分别提高0.20%和0.03%，同时推理速度FPS也分别提高3.2 帧/s和1.3 帧/s. 实验结果说明了ECA-bneck-m模块的有效性，同时也证明了轻量级YOLO-v4 （ECA-bneck-m）模型更符合变电站数字仪表检测识别的实际应用需求. 此外，从类别识别结果上看，使用改进ECA-bneck-m模块设计的轻量级YOLO-v4模型在每个类别的精确率均达到95%以上，而且在测试图像中存在噪声或其他复杂情况下，仍然拥有较好的准确度和鲁棒性.
3. 结 论
面向变电站数据仪表智能检测识别的实际应用需求，本文提出一种基于轻量级YOLO-v4模型的数字仪表检测识别方法. 该方法以YOLO-v4模型为基础，通过设计改进的ECA-bneck-m模块，对YOLO-v4主干特征提取网络进行轻量化设计，进而得到轻量级YOLO-v4 （ECA-bneck-m）模型，在几乎不损失准确度的前提下，有效降低模型的计算和存储复杂度. 此外，本文从鄂尔多斯变电站实际场景下采集了数字仪表图像数据，并使用Albumentations框架进行数据增强，构建了变电站数字仪表检测识别数据集. 实验结果表明，基于轻量级YOLO-v4模型的数字仪表检测识别方法能够实时、准确地实现数字仪表检测与读数识别，进而推动变电站数字仪表检测识别的智能化发展.
-
图 1 准零刚度隔振器工作原理
Figure 1. Working principle of quasi-zero stiffness vibration isolator
图 2 准零刚度磁悬浮隔振平台
Figure 2. Magnetic suspension vibration isolation platform with quasi-zero stiffness
图 3 永磁电磁混合作动器的结构
Figure 3. Structure of permanent-magnet and electromagnetic hybrid actuator
图 4 永磁电磁混合作动器三维有限元模型
Figure 4. Three-dimensional finite element model of permanent-magnet and electromagnetic hybrid actuator
图 8 PID与模糊PID控制算法隔振效果对比
Figure 8. Comparison of vibration isolation effects of PID and fuzzy PID control algorithms
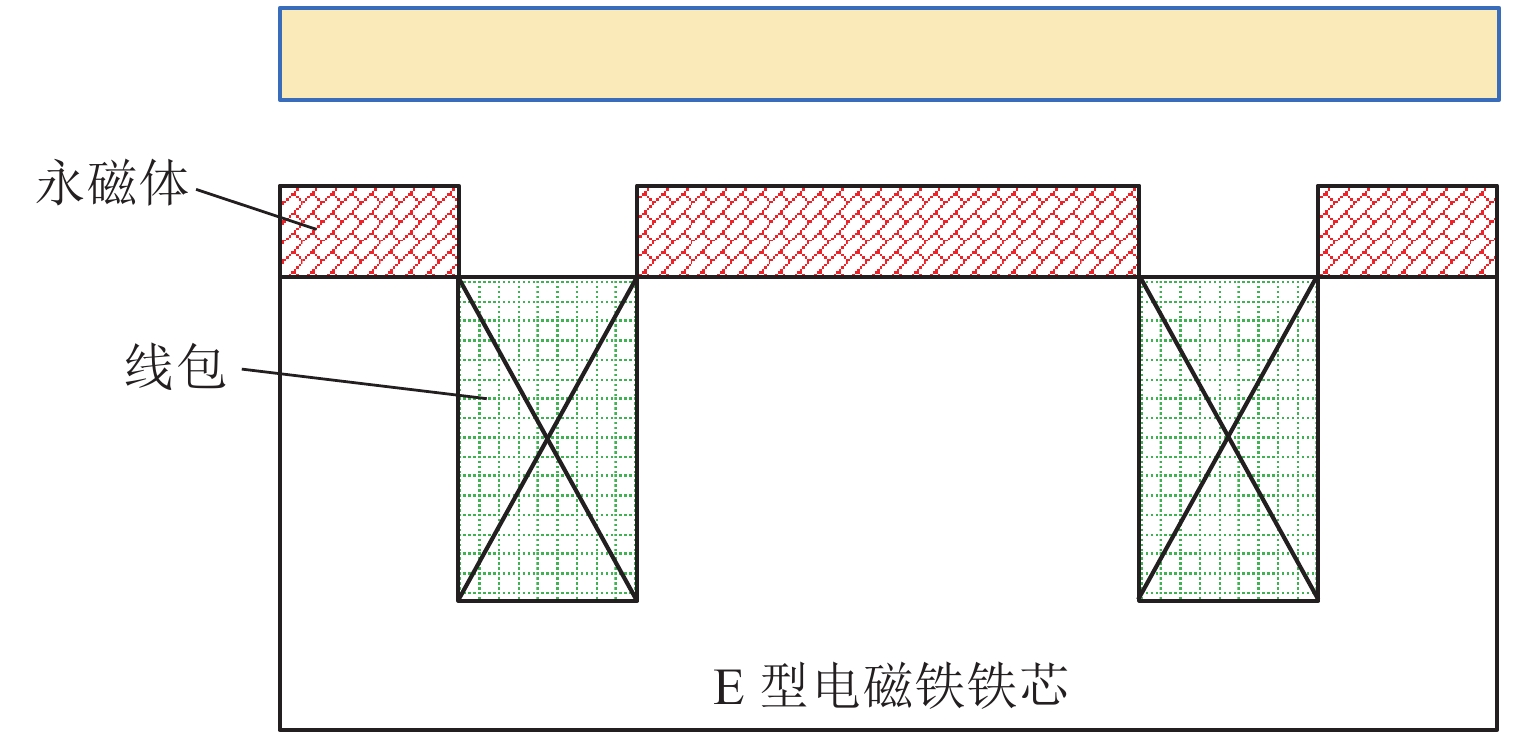
表 1 永磁体具体参数
Table 1. Detailed parameters of permanent magnet
参数名称 参数符号 参数值 剩余磁感应强度/T Br 1.2 矫顽力/（kA•m−1） Hc 896 相对磁导率 μr 1.05 
下载: 导出CSV
表 2 永磁体在工作点附近产生的电磁吸力
Table 2. Electromagnetic attraction generated by permanent magnet near working point
N 永磁体
厚度/mm悬浮间隙/mm 9.5 10.0 10.5 7 465.1 430.4 399.0 8 532.5 493.9 459.3 9 595.4 553.1 515.6 10 652.2 608.9 567.8 11 705.5 658.7 615.3 12 753.2 704.2 659.3 13 797.1 747.0 699.9
下载: 导出CSV
表 3 模糊控制器参数
Table 3. Parameters of fuzzy controller
模糊变量 基本论域 模糊论域 映射系数 e [−0.0025，0.0025] [−1，1] 400 δ [−0.05，0.05] [−1，1] 20 ΔKP [−5000，5000] [−1，1] 0.0002 ΔKI [−10，10] [−1，1] 0.1 ΔKD [−50，50] [−1，1] 0.02
下载: 导出CSV
表 4 ΔKP整定规则
Table 4. Setting rules of ΔKP
e δ NB NM NS ZE PS PM PB NB NB NB NM NM NM ZE ZE NM NB NM NM NM NS ZE PS NS NM NM NS NS ZE PS PS ZE NM NS NS ZE PS PS PM PS NS NS ZE PS PS PM PM PM NS ZE PS PM PM PM PB PB ZE ZE PM PM PM PB PB
下载: 导出CSV
表 5 ΔKI整定规则
Table 5. Setting rules of ΔKI
e δ NB NM NS ZE PS PM PB NB ZE ZE ZE ZE ZE ZE ZE NM ZE ZE ZE ZE ZE ZE ZE NS PS PS PS PS PS PS PS ZE PS PS PS PS PS PS PS PS PS PS PS PS PS PS PS PM ZE ZE ZE ZE ZE ZE ZE PB ZE ZE ZE ZE ZE ZE ZE
下载: 导出CSV
表 6 ΔKD整定规则
Table 6. Setting rules of ΔKD
e δ NB NM NS ZE PS PM PB NB NB NB PM PM PS ZE ZE NM NB NB PM PS PS ZE ZE NS NB NM PS PS ZE NS NS ZE NM NS PS ZE NS NS NM PS NS NS ZE NS NS NM NB PM ZE ZE NS NS NM NB NB PB ZE ZE NS NM NM NB NB
下载: 导出CSV
表 7 振动衰减率和振动传递率
Table 7. Vibration attenuation rate and vibration transmission rate
振动频率/Hz 振动衰减率/% 振动传递率/dB 20 83.64 −15.72 50 90.55 −19.83 100 91.91 −21.84 200 92.60 −22.61 300 93.52 −23.77 500 95.35 −26.66
下载: 导出CSV
-
[1] ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001 [2] REN C, YANG D, QIN H. Mechanical performance of multidirectional buckling-based negative stiffness metamaterials: an analytical and numerical study[J]. Materials, 2018, 11(7): 1078.1-1078.19. [3] 张磊. 电磁主动隔振系统建模与控制方法研究[D]. 武汉: 武汉大学, 2020. [4] YAN B, YU N, WU C Y. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms[J]. Applied Mathematics and Mechanics, 2022, 43(7): 1045-1062. doi: 10.1007/s10483-022-2868-5 [5] ZHANG F, SHAO S B, TIAN Z, et al. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress[J]. Mechanical Systems and Signal Processing, 2019, 123: 244-263. doi: 10.1016/j.ymssp.2019.01.022 [6] 沈铖武. 车载光电瞄准平台主被动隔振关键技术研究[D]. 北京: 中国科学院大学, 2021. [7] 黄翠翠,李晓龙,杨洋,等. 基于自抗扰技术的机械-电磁悬浮复合隔振控制[J]. 西南交通大学学报,2022,57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850HUANG Cuicui, LI Xiaolong, YANG Yang, et al. Mechanical-electromagnetic suspension compound vibration isolation control based on active disturbance rejection technology[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 582-587,617. doi: 10.3969/j.issn.0258-2724.20210850 [8] CARRELLA A, BRENNAN M, KOVACIC I, et al. On the force transmissibility of a vibration isolator with quasi-zero stiffness[J]. Journal of Sound and Vibration, 2009, 322(4): 707-717. [9] 苏攀,吴杰长,刘树勇,等. 弹簧-电磁力准零刚度隔振器研究[J]. 海军工程大学学报,2018,30(5): 36-41.SU Pan, WU Jiechang, LIU Shuyong, et al. Spring-electromagnetic force vibration isolator with quasi-zero-stiffness[J]. Journal of Naval University of Engineering, 2018, 30(5): 36-41. [10] 江友亮. 磁气混合准零刚度隔振系统设计与控制研究[D]. 武汉: 武汉理工大学, 2019. [11] XU J W, YANG X F, LI W, et al. Research on semi-active vibration isolation system based on electromagnetic spring[J]. Mechanics & Industry, 2020, 21(1): 101.1-101.12. [12] ZHANG L, ZHUAN X T. An experimental study of an electromagnetic isolator system with active control[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 61(3): 329-340. doi: 10.3233/JAE-180112 [13] 邹圣楠,刘畅,邓舒同,等. 基于混合式磁浮平台的解耦及控制分析[J]. 西南交通大学学报,2022,57(3): 40-548.ZOU Shengnan, LIU Chang, DENG Shutong, et al. Decoupling and control stability analysis based on hybrid repulsion maglev platform[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 40-548. [14] HU Y F, CHEN C H, WU H C, et al. Study on structural optimization design and cascade PID control of maglev actuator for active vibration isolation system[J]. Journal of Vibration and Control, 2018, 24(10): 1829-1847. doi: 10.1177/1077546317714939 [15] SUN Y G, XU J Q, WU H, et al. Deep learning based semi-supervised control for vertical security of maglev vehicle with guaranteed bounded airgap[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(7): 4431-4442. doi: 10.1109/TITS.2020.3045319 [16] MITRA P, DEY C, MUDI R K. Fuzzy rule-based set point weighting for fuzzy PID controller[J]. SN Applied Sciences, 2021, 3(6): 1-34. [17] YANG T, SUN N, FANG Y C. Adaptive fuzzy control for a class of MIMO underactuated systems with plant uncertainties and actuator deadzones: design and experiments[J]. IEEE Transactions on Cybernetics, 2022, 52(8): 8213-8226. doi: 10.1109/TCYB.2021.3050475 [18] WANG H Q, LIU P X, ZHAO X D, et al. Adaptive fuzzy finite-time control of nonlinear systems with actuator faults[J]. IEEE Transactions on Cybernetics, 2019, 50(5): 1786-1797. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 1343
- HTML全文浏览量: 172
- PDF下载量: 60
- 被引次数: 0