高寒动车组温变特性对运行性能的影响分析

祁亚运; 李龙; 石怀龙; 宋烨; 戴焕云

doi:10.3969/j.issn.0258-2724.20220876

高寒动车组温变特性对运行性能的影响分析

doi: 10.3969/j.issn.0258-2724.20220876

祁亚运^{1, 2,},
李龙^3, ,,
石怀龙²,
宋烨²,
戴焕云²

1.
重庆交通大学机电与车辆工程学院，重庆 400074
2.
西南交通大学轨道交通运载系统全国重点实验室，四川成都 610031
3.
包头北方创业有限责任公司，内蒙古包头 014030

基金项目: 国家自然基金项目（U2268211，52302467，52002341）；四川省自然科学基金项目（2022NSFSC1887）；牵引动力国家重点实验室开放课题（TPL2309）

详细信息

作者简介:
祁亚运（1990—），男，副教授，研究方向为车辆动力学与轮轨磨耗，E-mail：yayun_qi@163.com

通讯作者:
李龙（1985—），男，高级工程师，研究方向为轨道车辆结构与设计，E-mail：Lil1919@126.com

中图分类号: U270.1
计量
- 文章访问数: 264
- HTML全文浏览量: 118
- PDF下载量: 52
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-20
- 修回日期: 2023-03-20
- 网络出版日期: 2024-06-17
- 刊出日期: 2023-05-11

Influence of Temperature-Varying Characteristics on Operating Performance of Alpine Electric Multiple Units

QI Yayun^{1, 2
,},
LI Long^{3
, ,},
SHI Huailong²,
SONG Ye²,
DAI Huanyun²

1.
School of Mechatronics and Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China
2.
State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China
3.
Baotou Beifang Chuangye Co., Ltd., Baotou 014030, China

摘要

摘要:
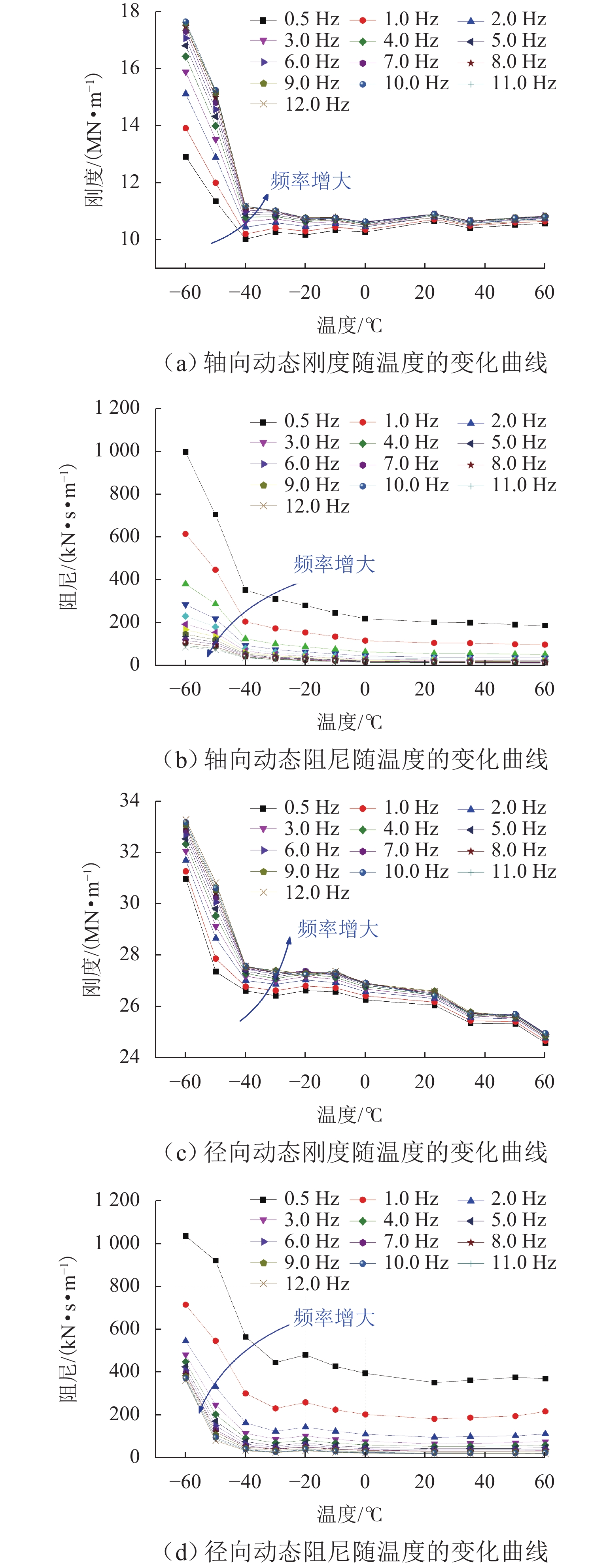
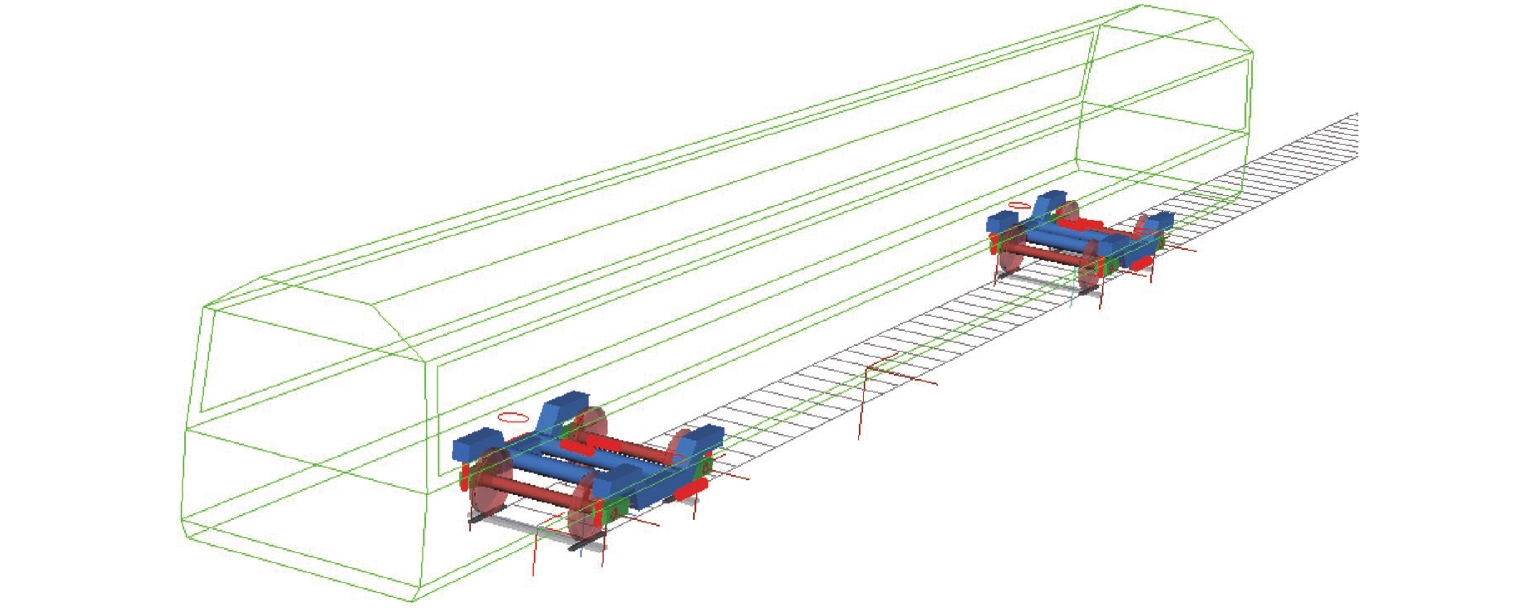
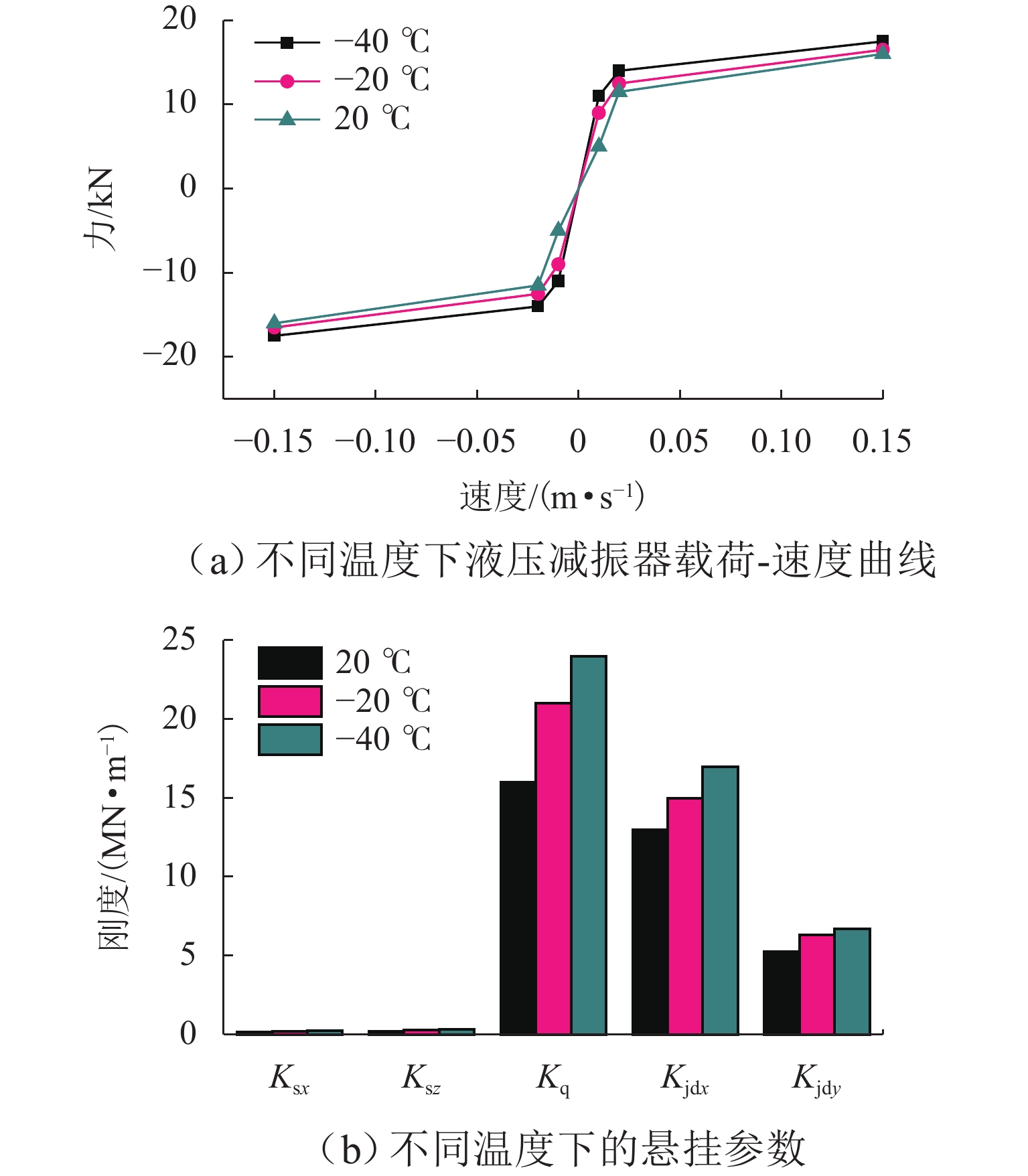
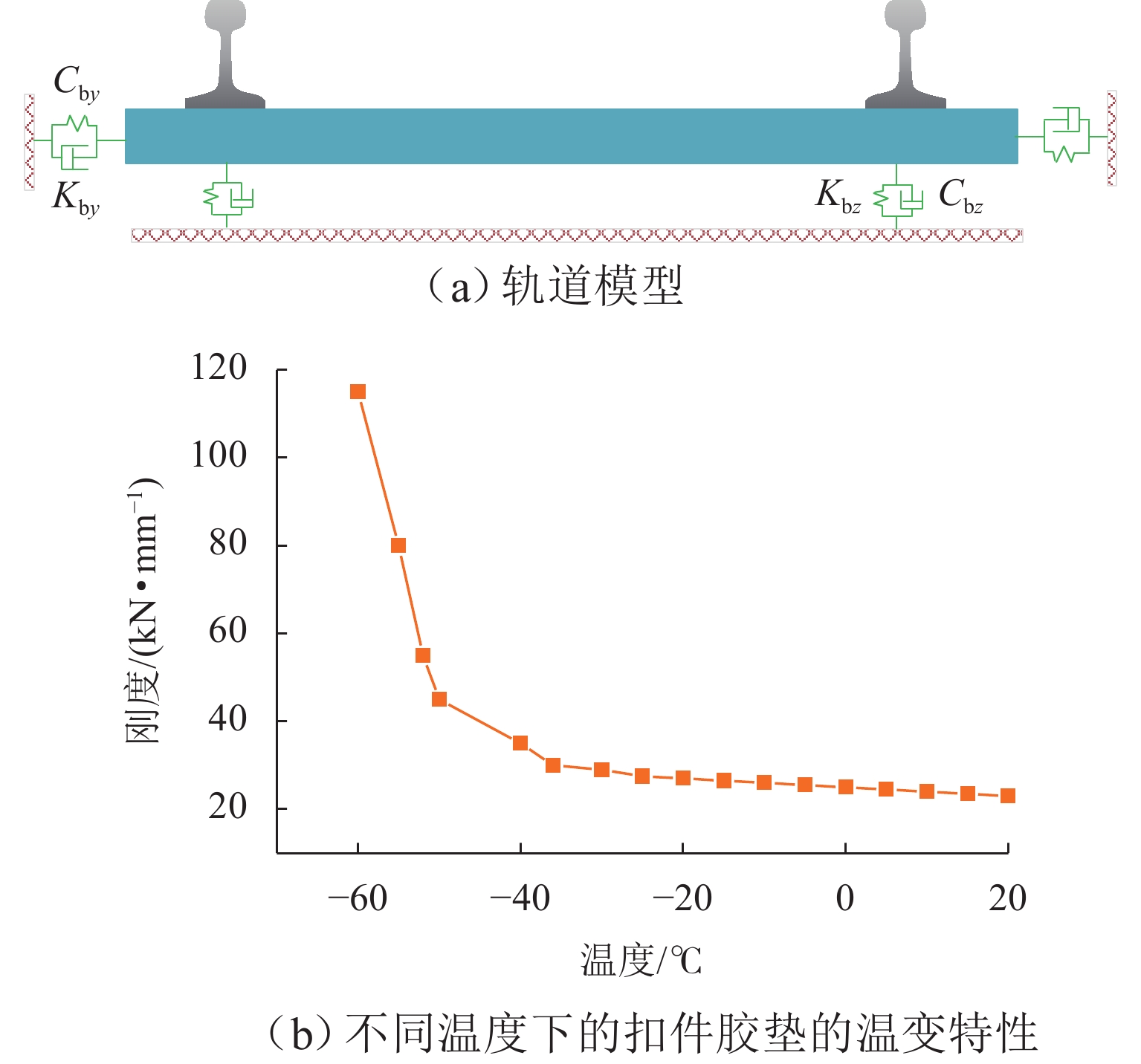
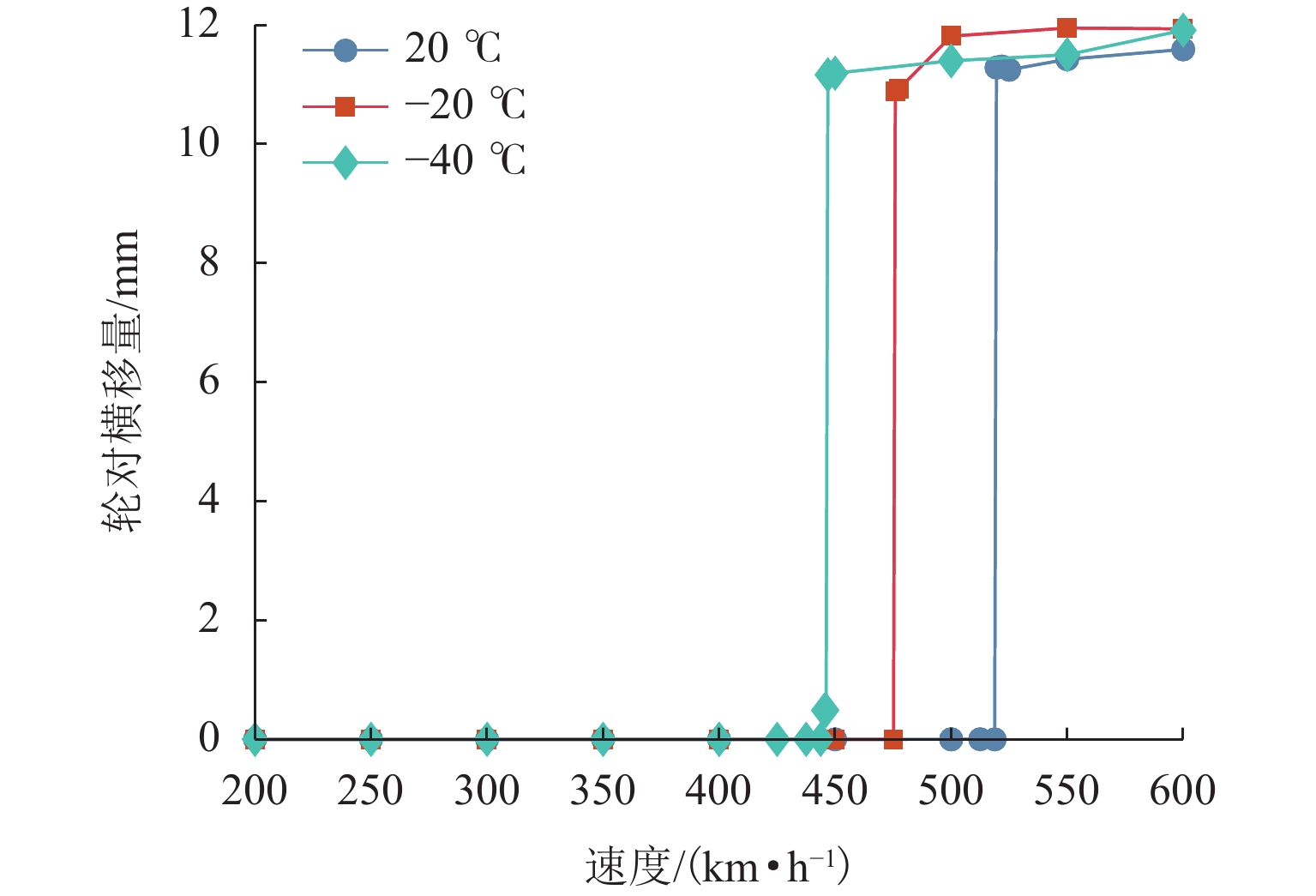
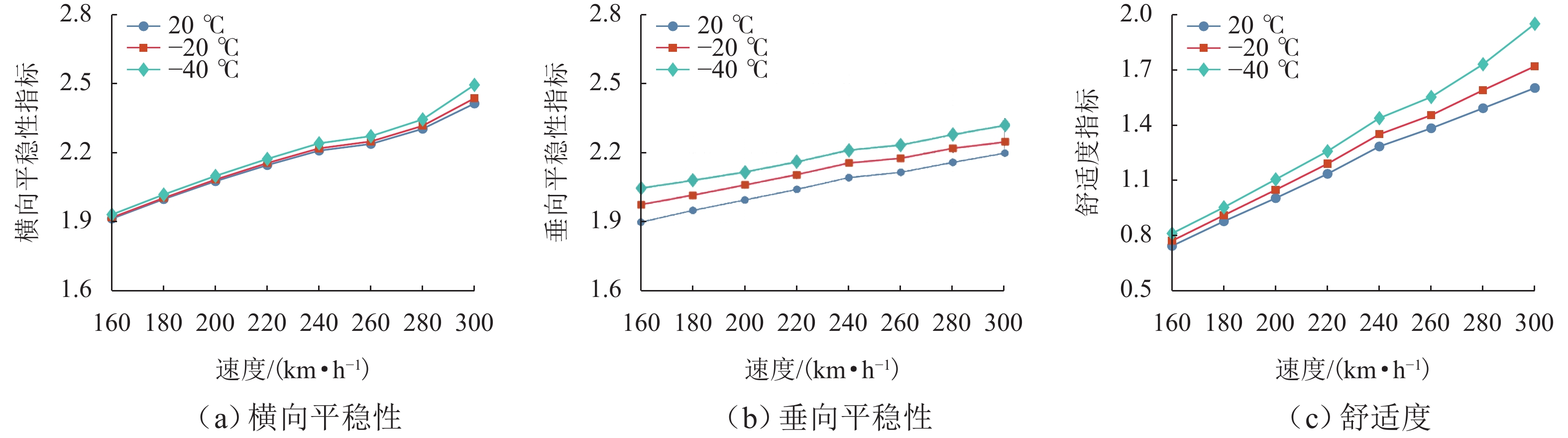
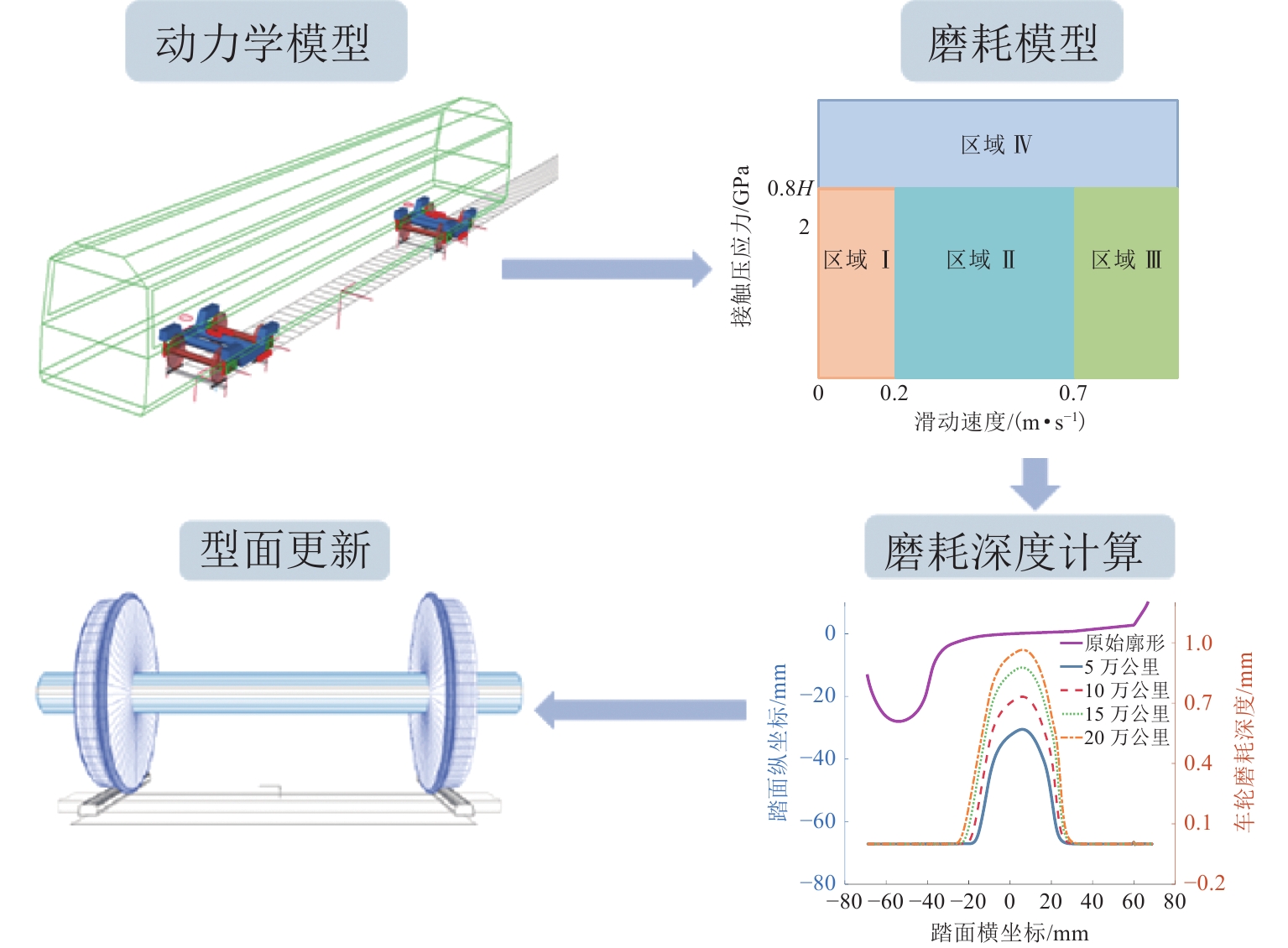
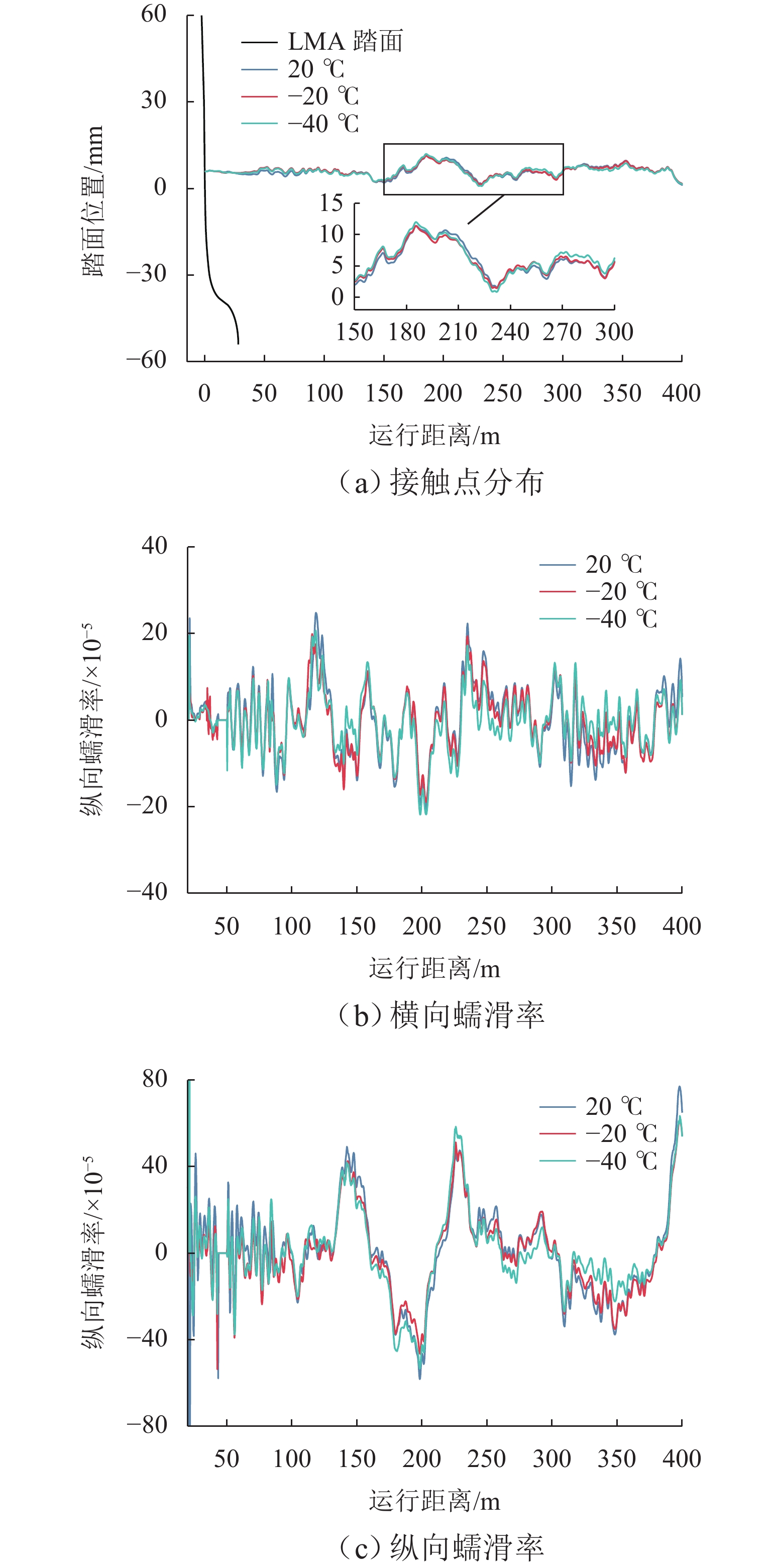
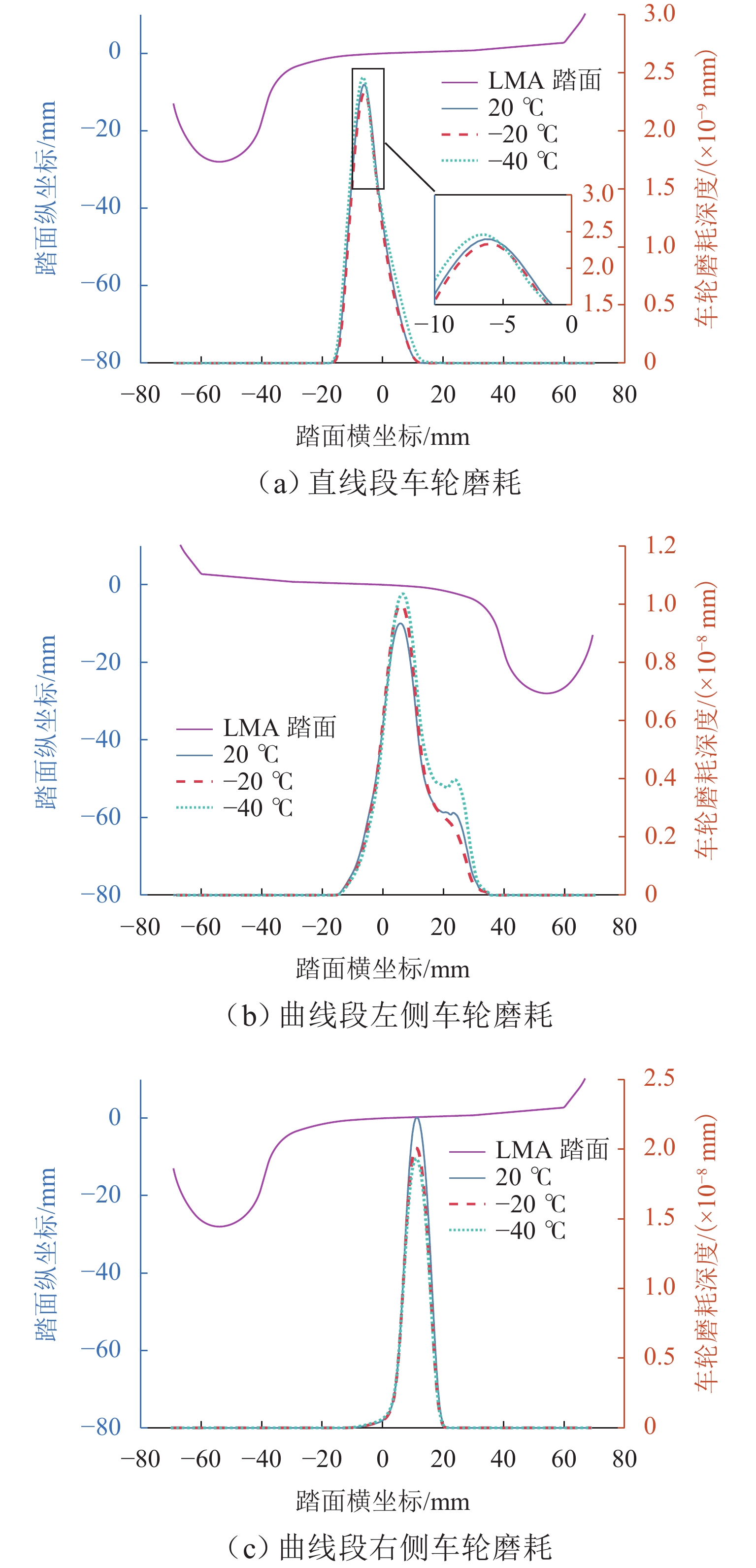
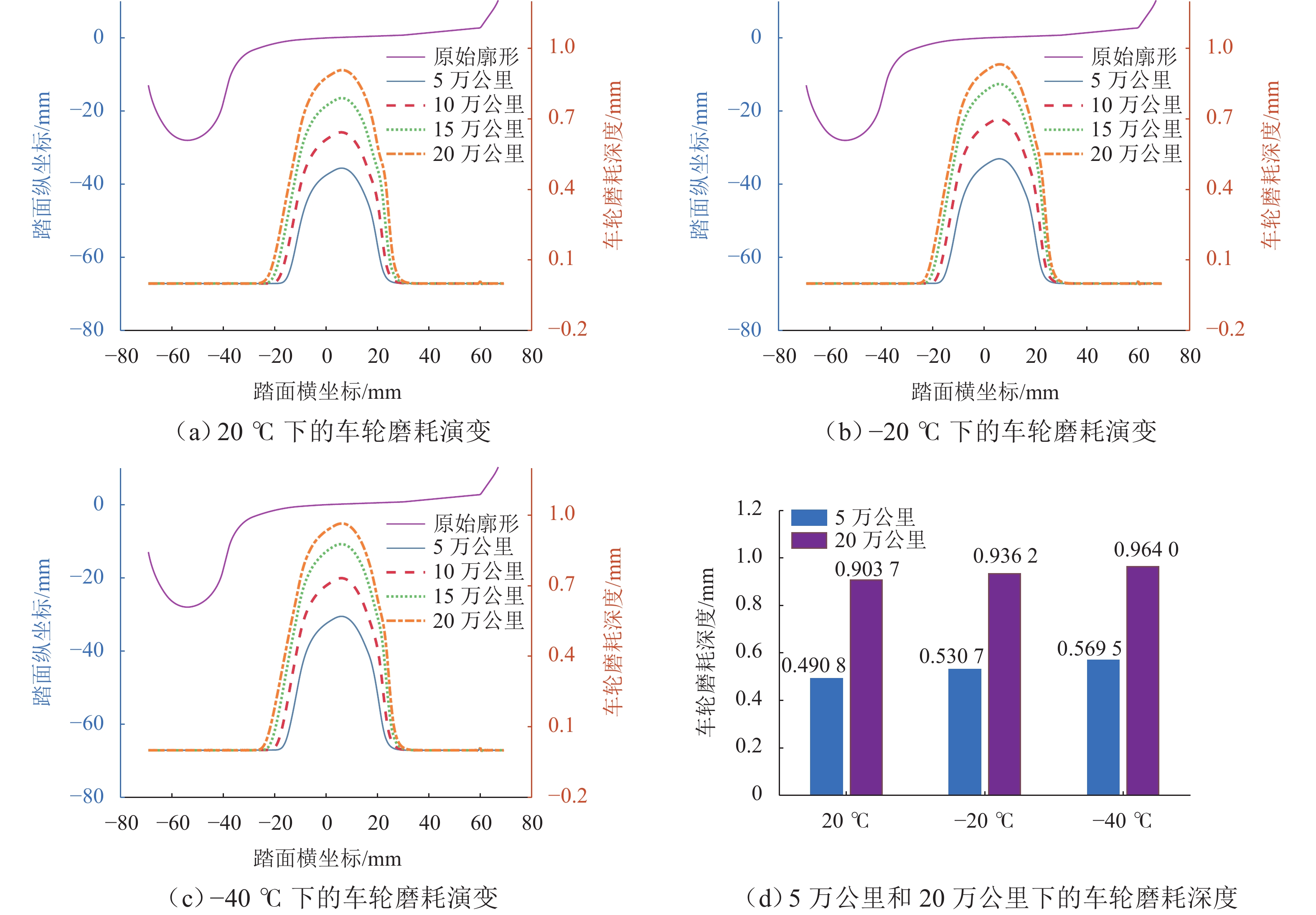
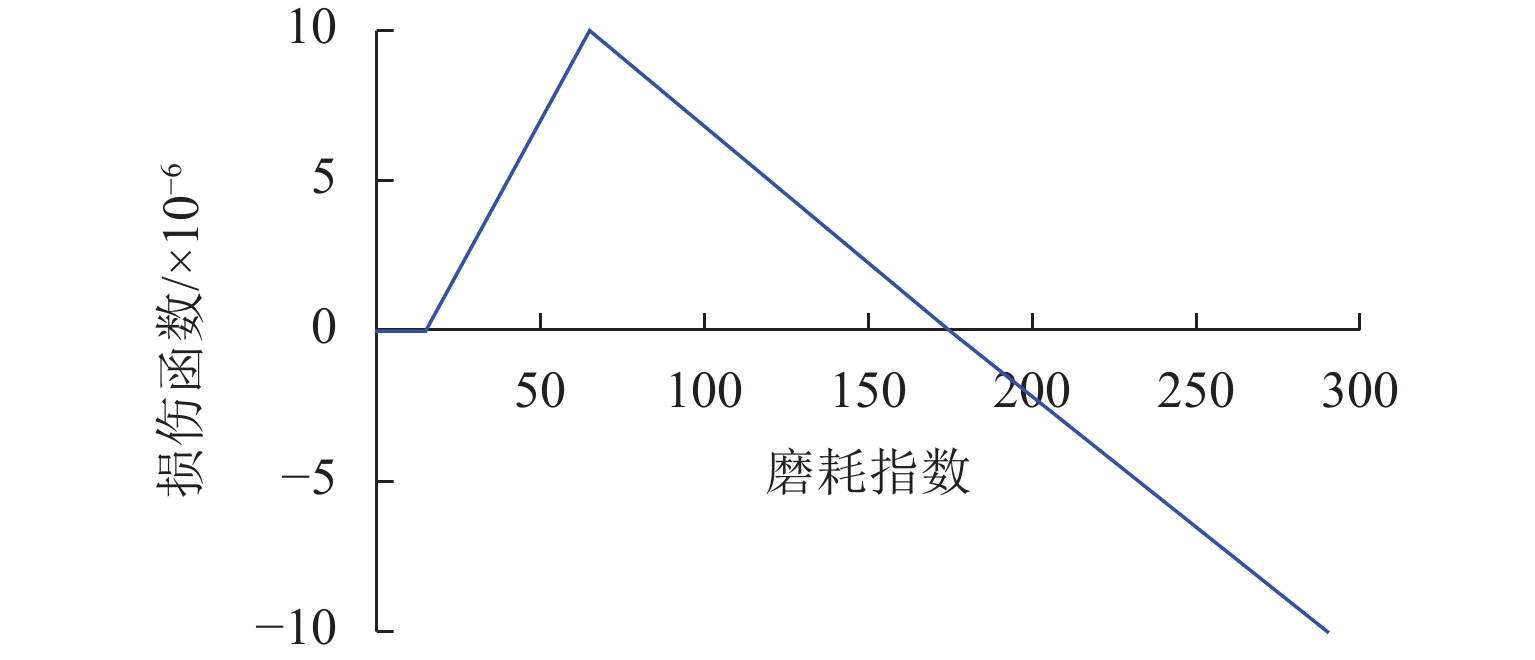
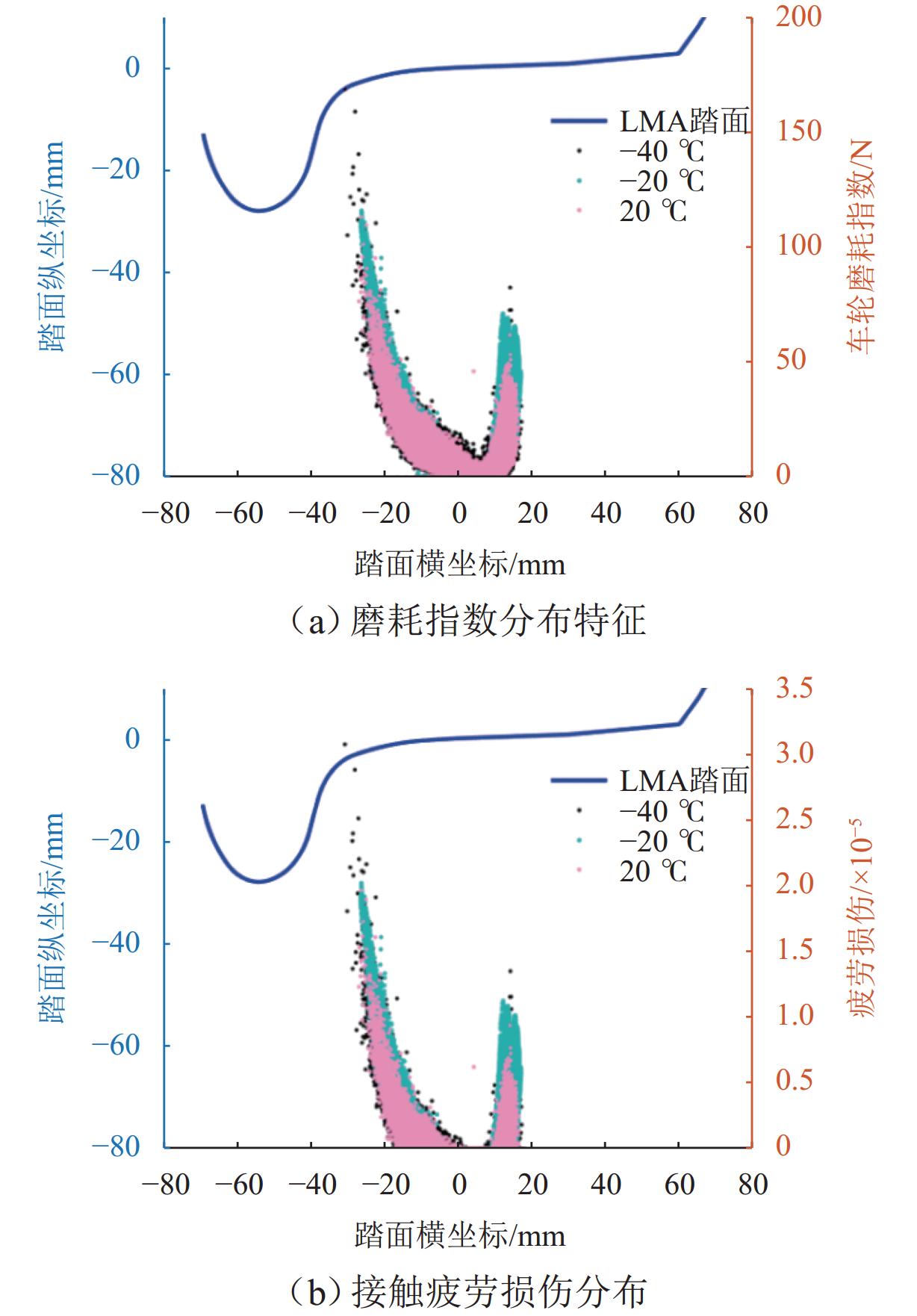
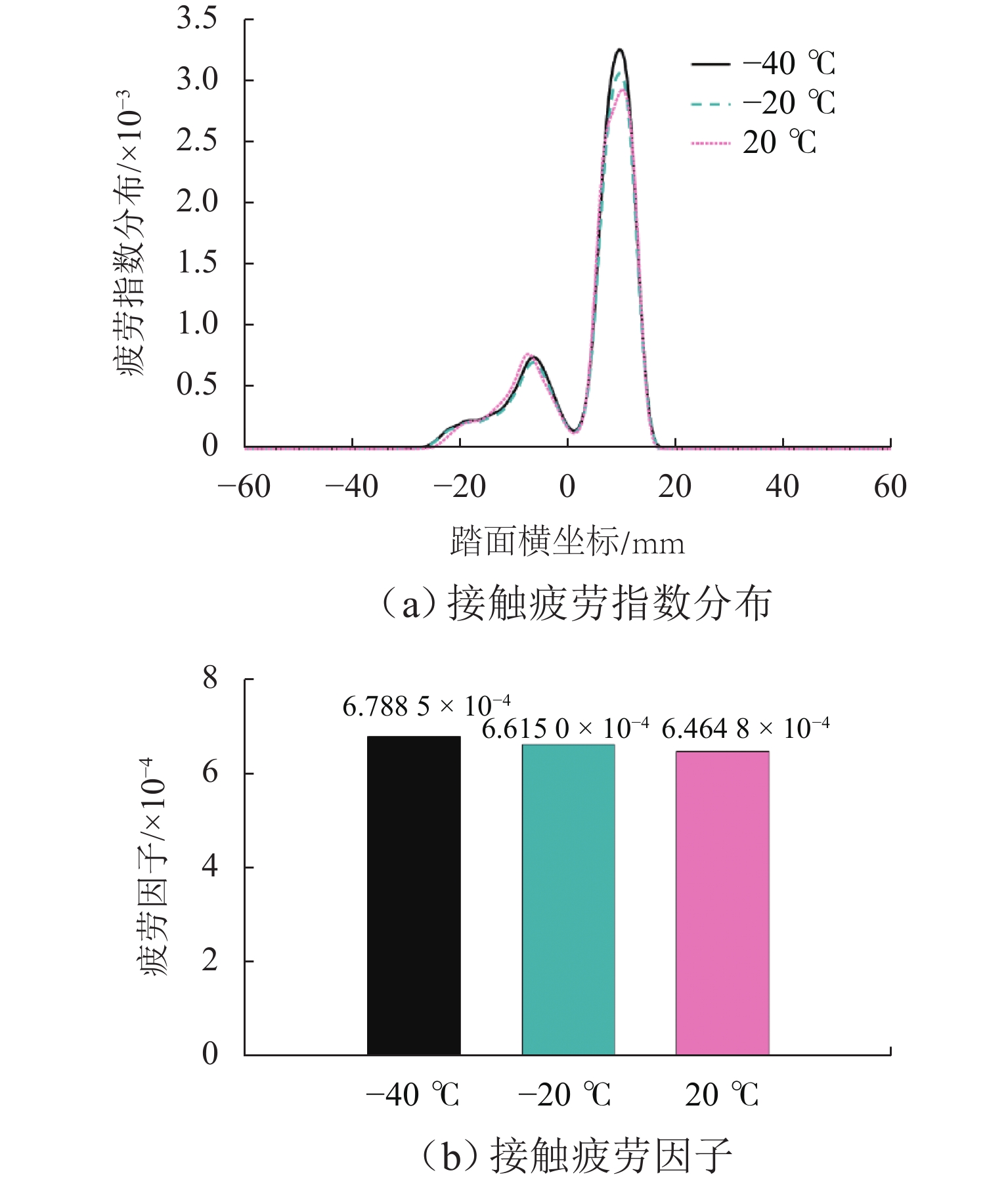
高寒动车组服役环境长期受温度的影响，车辆悬挂元件参数和轨下参数具有很强的季节变化特性，为了探究高寒动车组中橡胶元件温变特性对运行性能的影响，本文建立高寒动车组多体动力学模型，分析不同温度下的车辆动力学特性；利用Jendel磨耗模型探究不同温度下的车轮磨耗特性；基于疲劳预测模型提出车轮表面疲劳因子. 结果表明：温度变化会改变悬挂参数的刚度和阻尼值，随着温度降低，悬挂参数刚度增大；低温状态下，动车组动力学性能整体下降，随着温度降低车辆磨耗都会增大，当运行20万里程后，−40 ℃下车轮的磨耗深度最大，较20 ℃ 时增大6.2%；随着温度降低，表面接触疲劳指数也逐渐增大，温度分别为20、−20、−40 ℃时，车轮表面疲劳因子分别为6.4648×10⁻⁴，6.6150×10⁻⁴，6.7885×10⁻⁴；温变特性对高寒动车组悬挂参数有较大影响，低温下整体动力学性能下降，磨耗增大，车轮表面疲劳增大.
- 高寒动车组 /
- 温变特性 /
- 轮轨接触 /
- 车轮磨耗 /
- 接触疲劳因子
Abstract:
The service environment of alpine electric multiple units (EMUs) is affected by temperature for a long time, and the vehicle suspension element parameters and under-rail parameters have strong seasonal variation characteristics. To investigate the influence of temperature-varying characteristics of rubber elements on the operating performance of alpine EMUs, a multi-body dynamics model of alpine EMUs was established to analyze the vehicle dynamics characteristics under different temperatures. Then, the wheel wear characteristics at different temperatures were analyzed by the Jendel wear model. Finally, the wheel surface fatigue index was proposed based on the fatigue prediction model. The results show that the temperature variation will change the stiffness and damping value of suspension parameters, and the stiffness of suspension parameters increases as the temperature decreases. The dynamic performance of the EMUs decreases at low temperatures. The wear of the vehicle increases as the temperature decreases. After 200 000 miles of operation, the largest depth of wheel wear is found at a temperature of −40 ℃, which is 6.2% greater than the depth of wheel wear at a temperature of 20 ℃. The surface contact fatigue index gradually increases as the temperature decreases, with wheel surface fatigue indexes being 6.4648×10⁻⁴, 6.6150×10⁻⁴, and 6.7885×10⁻⁴ at temperatures of 20 ℃, −20 ℃, and −40 ℃, respectively. Temperature-varying characteristics have a large effect on the suspension parameters of alpine EMUs, with dynamic performance deteriorating at low temperatures, wear intensifying, and wheel surface fatigue increasing.
- alpine EMUs /
- temperature-varying characteristics /
- wheel-rail contact /
- wheel wear /
- contact fatigue index

HTML全文

磁悬浮轴承是通过磁场产生的电磁力将转子悬浮在空中的一种无摩擦的高性能轴承^[1]，具有无接触、损耗低、运行速度高及寿命长等优点，因此被广泛应用在航空航天、飞轮储能、人工心脏等领域^[2-9]. 从工作原理的角度，磁悬浮轴承分为主动型、被动型和混合型. 主动型磁悬浮轴承通过传感器和功率放大器等单元，主动控制通电线圈的电流，以此调控电磁力，从而实现转子的主动悬浮；被动型磁悬浮轴承则利用永磁体间、永磁体和软磁材料间的斥力或电磁吸力，产生不可控的电磁力以实现转子悬浮^[10]；混合磁悬浮轴承综合两者特点，通过永磁体生成偏置磁场和电磁线圈生成控制磁场，减少功率放大器的数量，并降低其功耗^[11-12].

混合磁悬浮轴承按其结构型式可分为同极性结构和异极性结构. 同极性磁轴承的偏置磁场和控制磁场在不同的平面，工作产生的损耗较低但轴向尺寸较长^[13]，限制了其转子的最高临界转速. 异极性磁轴承磁极的极性相反，极性交替排列，偏置磁通与控制磁通在同一平面，相比于同极性轴承，其轴向长度短，对提升转子最高转速有利^[14-17]. Okada等^[18]将传统磁轴承永磁体在两径向轴承间形成磁通回路的方式改变为将永磁体置于径向磁轴承内部，使得磁路在内部闭合，减小了磁轴承漏磁，提高了轴承效率. 孙津济等^[19]提出一种外转子式的新型磁轴承结构，在定子内部引入第二气隙，使得电磁磁路与永磁磁路共面，且不经过永磁体，同时，将定子铁心磁极数由8个减为4个，大大降低了磁轴承损耗. 朱润泽等^[20]提出一种4极型磁轴承，将传统的8极结构变为4极，并引入辅助气隙以防止永磁体发生短路，使得轴承在减少损耗的同时降低径向两自由度间的电磁耦合，有效提高轴承性能. 钟志贤等^[21]提出一种新型4极径向磁轴承，将外定子在轴向上进行拓展，形成具有6条独立磁路的结构，使其电磁磁路与永磁磁路相互独立，实现径向两自由度的电磁力解耦，但由于轴向较长，在一定程度上会影响转子的临界转速.

本文提出一种新型异极径向混合磁轴承（heteropolar radial hybrid magnetic bearing，HRHMB），可以控制径向2个自由度，具有轴向长度短、空间利用率高、永磁磁路与电磁磁路耦合距离短等优点. 首先，介绍新型HRHMB的结构原理，采用等效磁路法解析得到该磁轴承的电磁力、位移刚度和电流刚度，并与仿真结果进行分析对比；为验证该磁悬浮轴承的静态性能，在同悬浮力约束条件下与传统偏置磁轴承^[22]进行对比；最后，通过有限元分析验证该新型磁轴承在径向两自由度间的电磁力耦合较小.

1. 新型HRHMB结构及原理

1.1 新型HRHMB结构

新型HRHMB和传统八极偏置磁轴承的结构及磁路如图1所示. 新型HRHMB主要由定子铁心、转子铁心、控制绕组及永磁体组成. 定子铁心上包含主动控制磁1、3、5、7和辅磁极2、4、6、8，4组控制绕组分别在4个主动控制磁极上，产生控制磁场；4个辅磁极交错分布在主动控制磁极之间. 8个永磁体采用平行充磁的方式两两分布在主动控制磁极两侧，与转子形成工作气隙，用以产生偏置磁场. 定子铁心上的主辅磁极沿圆周形成NS相间的异极极性分布，为异极型磁悬浮轴承的结构形式. 同时，在定子铁心的横向处引入辅助气隙，起到减少X方向的永磁体在定子极间的漏磁及加强偏置磁场的作用. 由于异极型磁轴承损耗较大，其定转子铁心采用硅钢片叠压而成以降低转子高速运转下的铁耗. 永磁体采用钕铁硼烧结而成，嵌装在主辅磁极之间.

图 1 两种混合型磁悬浮轴承结构

Figure 1. Two kinds of hybrid magnetic bearing structures

下载: 全尺寸图片幻灯片

1.2 新型HRHMB工作原理

由于新型HRHMB具有对称性，以Y向磁极为例，控制绕组产生的控制磁通路径如图1（a）虚线所示，主动控制磁极上的控制绕组通入电流产生Y向的磁通，经过气隙、转子铁心及磁轭形成回路. 当转子处于平衡位置时，由于定子结构对称，Y方向上永磁体产生的气隙磁密相同，此时线圈中未通入电流，没有控制磁通. 假设转子受到向下的扰动力时， + Y方向气隙长度变大，−Y方向气隙长度变小. 在差动控制方式下，线圈通入电流，控制绕组产生的控制磁通和永磁体产生的偏置磁通在 + Y方向气隙处叠加，−Y方向气隙处抵消，使 + Y方向气隙磁通大于−Y方向气隙磁通，导致转子产生一个 + Y方向的电磁力，将转子拉回平衡位置. 线圈通电产生不同方向的力以使转子受到其它方向的干扰时保持平衡位置.

新型HRHMB的优点在于磁通路径和轴向长度短，且由于偏置磁通由永磁体产生，因此，功耗较低. 另外，其永磁磁路和电励磁磁路耦合距离较短，利于降低径向二自由度之间的磁场力耦合. 与传统八极径向偏置磁悬浮轴承相比，磁极数量同为八极，但新型HRHMB磁极区域大，在飞轮储能系统和磁悬浮电机等透平机械中有潜在的应用前景.

2. HRHMB磁路分析

2.1 等效磁路模型

单独考虑永磁体产生的偏置磁场和通电线圈产生的控制磁场，对HRHMB磁场进行仿真，结果如图2所示.

图 2 新型异极径向混合磁轴承磁场仿真

Figure 2. Magnetic field simulation of novel HRHMB

下载: 全尺寸图片幻灯片

由磁场仿真结果可以看出：偏置磁通经过永磁体、主动控制磁极、气隙、转子铁心和定子辅磁极，漏磁通经过永磁体、定子主磁极、定子磁轭、定子极间空隙和定子辅磁极；Y方向偏置磁通漏磁主要分布在定子的极间，由于X方向第二气隙的引入，X方向永磁体产生的偏置磁通漏磁大为减小；控制磁通经过主动控制磁极、气隙、转子铁心和定子磁轭.

假设该新型磁轴承定转子铁心磁阻及涡流损耗为零，建立其等效磁路模型，如图3所示. 在偏置磁场等效磁路（图3（a））中，R_gb1 ～ R_gb8为永磁体下偏置磁路气隙磁阻，转子处在平衡位置时，其结构对称，此时R_gb1=R_gb2，R_gb3=R_gb4；R_k1 ～ R_k8为永磁体漏磁磁阻；F_p为永磁体磁动势；R_p为永磁体磁阻.

图 3 新型异极径向混合磁轴承等效磁路

Figure 3. Equivalent magnetic circuit of novel HRHMB

下载: 全尺寸图片幻灯片

${F_{\text{p}}} = {H_{\text{c}}}{l_{\text{m}}},$

(1)

${R_{\text{p}}} = {l_{\text{m}}}/\left( {{\mu _{\text{p}}}{S_{\text{p}}}} \right),$

(2)

式中：H_c为永磁体矫顽力，l_m为永磁体宽度，$ {\mu _{\text{p}}} $为永磁体磁导率，S_p为永磁体中性面面积.

在控制磁场等效磁路（图3（b））中，R_c1、R_c2、R_c3、R_c4分别为4个控制磁极气隙的磁阻，R_a为辅助气隙磁阻，N_x、N_y分别为水平、垂直方向的线圈匝数，i_x、i_y分别为水平、垂直方向上的电流.

$\left\{ \begin{array}{l}\left[{R}_{\text{c}1}\;{R}_{\text{c}2}\;{R}_{\text{c}3}\;{R}_{\text{c}4}\right]=\left[\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0} + x}{{\mu }_{0}{A}_{\text{r}}}\;\dfrac{{g}_{0}-x}{{\mu }_{0}{A}_{\text{r}}}\right]\\ {R}_{\text{a}}={g}_{\text{a}}/\left({\mu }_{0}{A}_{\text{r}}\right),\end{array},\right.$

(3)

式中：μ₀为空气磁导率，g₀为转子铁心在平衡位置时的气隙长度，g_a为辅助气隙长度，x、y分别为转子在X、Y轴方向的位移量，A_r为主动控制磁极气隙的面积.

2.2 新型异极径向混合磁轴承磁通计算

在高速电机和飞轮储能系统中转子最大允许的偏心位移为气隙长度的1/10，此时可认为4个径向方向偏置磁通彼此解耦^[23-24]. 将图3（a）偏置磁路图简化为Y + 、Y−、X + 、X− 4条磁路，分别计算其气隙处磁通，由于该磁轴承结构对称，由磁网络法计算Y + 、X−处可得到其他气隙处磁通.

2.2.1 Y + 方向偏置磁路磁通

偏置磁通在Y + 方向的等效磁路如图4（a）所示，φ_pmk1、φ_pmk2为漏磁磁通，φ_pmy1、φ_pmy2为永磁体下的偏置磁通；R_gb1、R_gb2为偏置磁通气隙磁阻，R_k2为漏磁磁阻，R_k1漏磁阻可以看作是端部漏磁磁阻R_k11和极间磁阻R_k12的并联磁阻，且R_k1//R_p//R_gb1.

图 4 Y + 方向等效磁路

Figure 4. Equivalent magnetic circuit along Y + direction

下载: 全尺寸图片幻灯片

漏磁磁阻和气隙磁阻分别为

$\left\{ \begin{array}{l}{R}_{\text{k}1}={R}_{\text{k2}}={R}_{\text{k}12}{R}_{\text{k}11}/({R}_{\text{k}12} + {R}_{\text{k}11}),\\ \left[{R}_{\text{gb}1}\;{R}_{\text{gb}2}\;{R}_{\text{gb}3}\;{R}_{\text{gb}4}\right]=\left[\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0} + y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-y}{{\mu }_{0}{A}_{\text{ra}}}\right],\end{array}\right.$

(4)

式中：$ {R_{{\text{k11}}}} = \ln ({r_{{\text{a}}2}}/{r_{{\text{a1}}}})/\left( {2{\mu _0}{\text{π}} {L_{\text{z}}}} \right) $^[25]，r_a1和r_a2为两极间半径，$ {R}_{\text{k12}}=(2/{m}_{\text{y}} + 0.5)/\left(0.64{\mu }_{0}{L}_{\text{z}}\right) $，L_z为磁轴承轴向长度，m_y为端部漏磁路半径，A_ra为辅磁极截面积.

根据磁路基尔霍夫定律可求出Y + 方向2个永磁体产生的偏置磁通和漏磁磁通，对应图4（a）的磁网络矩阵如式（5）所示. 各磁阻由图4磁阻模型得出，可得偏置磁场的磁通${\phi} _{\text{pmy1}}$、${\phi}_{\text{pmy2}} $如式（6）所示.

$\quad\quad\quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{R_{{\text{k}}1}}}&0&{ - {R_{\text{p}}}}&0 \\ 0&{{R_{{\text{k}}2}} + {R_{\text{p}}}}&0&{ - {R_{\text{p}}}} \\ { - {R_{\text{p}}}}&0&{{R_{{\text{gb}}1}} + {R_{{\text{c}}1}} + {R_{\text{p}}}}&{ - {R_{{\text{c}}1}}} \\ 0&{ - {R_{\text{p}}}}&{ - {R_{{\text{c}}1}}}&{{R_{{\text{gb2}}}} + {R_{{\text{c}}1}} + {R_{\text{p}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\phi _{{\text{pmk}}1}}} \\ {{\phi _{{\text{pmk2}}}}} \\ {{\phi _{{\text{pmy}}1}}} \\ {{\phi _{{\text{pmy2}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ {{F_{\text{p}}}/\sigma } \end{array}} \right],$

(5)

$\quad\quad\quad\quad\quad\quad\quad\quad \left\{\begin{array}{l}{\phi }_{\text{pmy}1}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}1}-{R}_{\text{k1}})}{\sigma [{R}_{\text{p}}({R}_{\text{k1}} + {R}_{\text{gb1}} + {R}_{\text{c1}}) + {R}_{\text{k2}}({R}_{\text{gb1}} + {R}_{\text{c1}})]({R}_{\text{p}} + {R}_{\text{gb2}} + {R}_{\text{c1}})},\\ {\phi }_{\text{pmy2}}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}1}-{R}_{\text{k2}})}{\sigma [{R}_{\text{p}}({R}_{\text{k2}} + {R}_{\text{gb2}} + {R}_{\text{c1}}) + {R}_{\text{k1}}({R}_{\text{gb2}} + {R}_{\text{c1}})]({R}_{\text{p}} + {R}_{\text{gb1}} + {R}_{\text{c1}})},\end{array}\right.$

(6)

式中：σ为永磁体漏磁系数.

2.2.2 X-方向偏置磁路磁通

偏置磁通X−方向的等效磁路如图5所示，φ_pmk5、φ_pmk6为漏磁磁通，φ_pmx1、φ_pmx2为永磁磁极下的偏置磁通；R_gb5、R_gb6为偏置磁通气隙磁阻，R_k5、R_k6为漏磁磁阻. 气隙磁阻及漏磁磁阻分别为

图 5 X−方向等效磁路

Figure 5. Equivalent magnetic circuit along X− direction

下载: 全尺寸图片幻灯片

$\left\{ \begin{array}{l}{R}_{\text{k5}}={R}_{\text{k}6}=\left(2/{m}_{x} + 0.5\right)/\left(0.64{\mu }_{0}{L}_{{\textit{z}}}\right),\\ \left[{R}_{\text{gb}5}\;{R}_{\text{gb}6}\;{R}_{\text{gb}7}\;{R}_{\text{gb}8}\right]=\left[\dfrac{{g}_{0} + x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0} + x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-x}{{{\mu }_{0}}{A}_{\text{ra}}}\;\dfrac{{g}_{0}-x}{{{\mu }_{0}}{A}_{\text{ra}}}\right],\end{array}\right.$

(7)

式中:$ {m_x} $为永磁体端部漏磁半径.

对应图5的磁网络矩阵如式（8）所示，式中各磁阻由图5磁阻模型得出，进而可得偏置磁通如式（9）所示.

$\quad\quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{R_{{\text{gb}}5}} + {R_{\text{p}}} + {R_{{\text{c}}3}}}&{ - {R_{{\text{c}}3}}}&{ - {R_{\text{p}}}}&0 \\ { - {R_{{\text{c}}3}}}&{{R_{{\text{gb6}}}} + {R_{\text{p}}} + {R_{{\text{c}}3}}}&0&{ - {R_{\text{p}}}} \\ { - {R_{\text{p}}}}&0&{{R_{{\text{k5}}}} + {R_{\text{p}}}}&0 \\ 0&{ - {R_{\text{p}}}}&0&{{R_{{\text{gb6}}}} + {R_{\text{p}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\phi _{{\text{pmx1}}}}} \\ {{\phi _{{\text{pmx2}}}}} \\ {{\phi _{{\text{pmk5}}}}} \\ {{\phi _{{\text{pmk6}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ { - {F_{\text{p}}}/\sigma } \\ {{F_{\text{p}}}/\sigma } \end{array}} \right],$

(8)

$\quad\quad\quad\quad\quad\quad\quad\quad \left\{\begin{array}{l}{\phi }_{\text{pmx}1}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{\text{c}3}-{R}_{\text{k5}})}{\sigma [{R}_{\text{p}}({R}_{\text{k5}} + {R}_{\text{gb5}} + {R}_{\text{c3}}) + {R}_{\text{k6}}({R}_{\text{gb5}} + {R}_{\text{c3}})]({R}_{\text{p}} + {R}_{\text{gb6}} + {R}_{\text{c3}})},\\ {\phi }_{\text{pmx2}}=\dfrac{{F}_{\text{p}}{R}_{\text{p}}({R}_{c3}-{R}_{\text{k5}})}{\sigma [{R}_{\text{p}}({R}_{\text{k6}} + {R}_{\text{gb6}} + {R}_{\text{c3}}) + {R}_{\text{k5}}({R}_{\text{gb6}} + {R}_{\text{c3}})]({R}_{\text{p}} + {R}_{\text{gb5}} + {R}_{\text{c3}})}.\end{array}\right.$

(9)

2.2.3 电磁磁路磁通

在图3（b）中，径向X、Y方向的控制磁路总磁阻分别为R_rx、R_ry，如式（19）所示.

$\left\{ \begin{array}{l} {R_{{\text{rx}}}} = {R_{{\text{c}}3}} + {R_{{\text{c}}4}} + 2{R_{\text{a}}} , \\ {R_{{\text{ry}}}} = {R_{{\text{c}}1}} + {R_{{\text{c}}2}}. \end{array} \right.$

(10)

径向X、Y方向的控制磁路磁通φ_cx、φ_cy分别为

$\left\{ \begin{array}{l} {\phi _{{\text{cx}}}} = 2{N_x}{i_x}/{R_{{\text{rx}}}}, \\ {\phi _{{\text{cy}}}} = 2{N_y}{i_y}/{R_{{\text{ry}}}}. \end{array} \right.$

(11)

2.3 悬浮力与刚度计算

由磁网络分析法求解该磁轴承的各磁路磁通，从而可得该磁轴承的刚度和承载力. 将笛卡尔坐标系的正方向作为力的正方向，根据麦克斯韦方程组可推导出径向两自由度的悬浮力分别为

$\left\{ \begin{array}{l} {F_y} = \dfrac{{{{({\phi _{{\text{pmy}}1}} + {\phi _{{\text{cy}}}})}^2} - {{({\phi _{{\text{pmy}}2}} - {\phi ^2_{{\text{cy}}}})}}}}{{2{\mu _0}{A_{\text{r}}}}} + \dfrac{{{\phi ^2_{{\text{pmy}}1}} - {\phi ^2_{{\text{pmy}}3}}}}{{2{\mu _0}{A_{{\text{ra}}}}}}, \\ {F_x} = \dfrac{{{{({\phi _{{\text{pmx}}1}} + {\phi _{{\text{cx}}}})}^2} - {{({\phi _{{\text{pmx}}2}} - {\phi ^2_{{\text{cx}}}})}}}}{{2{\mu _0}{A_{\text{r}}}}} + \dfrac{{{\phi ^2_{{\text{pmx}}1}} - {\phi ^2_{{\text{pmx3}}}}}}{{2{\mu _0}{A_{{\text{ra}}}}}} . \end{array} \right.$

(12)

联立式（9）～（12），求出该磁轴承在Y、X方向两自由度的电流刚度$k_{i_y} $、$k_{i_x} $和位移刚度$k_{d_y} $、$k_{d_x} $分别为

$\left\{ \begin{array}{l} k_{i_y}=\left.\dfrac{\partial F_y}{\partial i_y}\right|_{\substack{x=y=0,\\ i_x=i_y=0}}=\dfrac{2 \phi_{\mathrm{cy}} N}{\sigma \mu_0 g_0\left(R_{\mathrm{c} 2}+R_{\mathrm{c} 1} / R_{\mathrm{ry}}\right)}, \\ k_{i_x}=\left.\dfrac{\partial F_x}{\partial i_x}\right|_{\substack{x=y=0, \\ i_x=i_y=0}}=\dfrac{2 \phi_{\mathrm{cx}} N}{\sigma \mu_0 g_0\left(R_{\mathrm{rx}}+R_{\mathrm{a} 1}\right)}, \\ k_{d_y}=\left.\dfrac{\partial F_y}{\partial y}\right|_{\substack{x=y=0, \\ i_x=i_y=0}}=\dfrac{32\left(\dfrac{A_{\mathrm{ra}} g_0}{\mu_0}-\dfrac{R_{\mathrm{k} 12} R_{\mathrm{k} 11}}{R_{\mathrm{k} 12}+R_{k 11}}\right) S_{\mathrm{p}}^2 l_{\mathrm{m}}}{\sigma \mu_{\mathrm{p}}^2 A_{\mathrm{r}}^2\left(R_{\mathrm{p}} R_{\mathrm{k} 1}+6 R_{\mathrm{k} 2}+R_{\mathrm{p}}\right)^3}, \\ k_{d_x}=\left.\dfrac{\partial F_x}{\partial x}\right|_{\substack{x=y=0,\\ i_x=i_y=0}}=\dfrac{32\left(A_{\mathrm{ra}} g_0 / \mu_0-2 R_{\mathrm{c} 1}\right) S_{\mathrm{p}}^2 l_{\mathrm{m}}}{\sigma \mu_{\mathrm{p}}^2 A_{\mathrm{r}}^2\left(4 R_{\mathrm{c} 2}+2 R_{\mathrm{k} 3} R_{\mathrm{p}}+R_{\mathrm{p}}\right)^3}, \end{array}\right.$

(13)

式中：N为控制绕组的匝数.

3. 仿真分析

为验证磁路计算及悬浮力式的正确性，对新型磁轴承进行有限元仿真. 图1中2种磁轴承结构的主要模型参数如表1所示.

表 1 磁轴承主要参数

Table 1. Main parameters of magnetic bearing

参数	传统	新型
定子外直径/mm	130	139
转子外直径/mm	50	50
轴向长度/mm	45	45
主气隙长度/mm	0.5	0.5
辅助气隙长度/mm		1
永磁体厚度/mm	2	3
永磁体宽度/mm	15	8
磁极截面积/mm²	920	1560
最大控制电流/A	3.6	12/3

下载: 导出CSV

| 显示表格

3.1 磁场分布

新型磁悬浮轴承转子处于平衡位置时，给Y方向线圈通入不同电流时的磁密如图6所示，图中，序号1 ～ 8为图1（a）中对应的磁极位置. 当电流为0 A时，磁通仅由永磁体产生，磁极1、5处的磁密幅值高于磁极3、7处，这是由于引入辅助气隙导致减少了磁极1、5处的永磁体漏磁；随着控制电流的增大，永磁体和控制电流产生的磁通会在磁极1气隙处叠加，使得气隙磁密增大，在磁极5气隙处抵消，使得气隙磁密减小，其他磁极处的磁密基本不变.

图 6 气隙磁密随电流变化

Figure 6. Variation of magnetic density in air gap with current

下载: 全尺寸图片幻灯片

控制线圈未接入电流时，转子在Y方向上不同位置的气隙磁密如图7所示. 图中箭头为气隙增加趋势. 当转子向上偏转时，磁极3气隙处的磁通密度增强，而定子另一侧磁极7气隙处的磁通密度会减弱. 当转子不在平衡位置发生偏离时，此时转子和定子磁极的圆弧面不再平行，使得相同磁极不同位置上的气隙长度有所不同，出现磁极1、2、4、5、6、8处气隙磁通密度不均匀现象.

图 7 气隙磁密随位移变化

Figure 7. Variation of magnetic density in air gap with displacement

下载: 全尺寸图片幻灯片

3.2 电磁力仿真分析

悬浮力和位移刚度、电流刚度为磁悬浮轴承的基本特性，是衡量磁轴承性能的重要指标. 为验证磁路法分析的正确性，由式（13）对HRHMB的刚度特性进行计算并仿真，位移刚度和电流刚度如图8所示.

图 8 径向电流刚度与位移刚度

Figure 8. Radial current stiffness and displacement stiffness

下载: 全尺寸图片幻灯片

从图8（a）中可以看出，铁心材料处于不饱和状态时，转子所受到的悬浮力与绕组电流几乎成正比，同时也与转子在平衡位置附近的位移成正比. 当控制电流在−3 ～ 3 A时，通过磁路法计算出的最大电磁力为472.8 N，仿真得到的电磁力为447.7 N，等效磁路与仿真结果有所偏差，误差为5.6%，这是由于忽略了部分漏磁和定转子铁心中的磁阻造成的，在误差允许范围内.

在图8（b）中，转子位移在（−0.1 ～ + 0.1）mm时，等效磁路法和仿真结果的平均偏差为5.6%. 转子位置在 + 0.1 mm时，磁路法得到的电磁力为134.2 N，仿真的电磁力为123.2 N，偏差为8.9%，这是因为铁心磁通达到饱和引起的，而在高速电机等设备中转子最大允许的偏心位移为气隙长度的1/10，小于达到铁心饱和时的区间，故可忽略铁心饱和的影响. 另外，由于增加了第二气隙，该新型磁轴承X方向的位移刚度和电流刚度小于Y方向. 在应用中可以将Y轴放置于重力方向上，用以增强转子浮动的动态性能，同时，可以通过适当增加X轴方向上的控制线圈的匝数来提高其X方向上的电流刚度.

3.3 两种磁轴承对比

为比较新型和传统偏置磁轴承的悬浮性能及空间利用率，建立相同最大承载力和偏置磁通、转子尺寸等约束条件的仿真模型，传统磁轴承和新型HRHMB的永磁磁密分布如图9所示. 通过有限元仿真计算，在相同承载力下，新型磁轴承为传统偏置磁轴承体积的0.87倍，这表明新型磁轴承结构有着更高的空间利用率.

图 9 2种磁轴承的永磁磁通密度分布

Figure 9. Permanent magnetic flux density distribution of two types of magnetic bearings

下载: 全尺寸图片幻灯片

2种磁悬浮轴承的电流刚度和位移刚度如图10所示. 由图10（a）可以看出，新型HRHMB在X和Y方向上的位移刚度都相对较小，这表明当转子发生偏移时，通过控制系统回到平衡位置较为容易^[20]；图10（b）可以看出，新型HRHMB Y方向上的电流刚度大于传统结构磁轴承的电流刚度，这表明在相同的电流下，新型HRHMB能产生更大的悬浮力. 此外，由于引入辅助气隙，其X方向上的电流刚度会小于Y方向上的电流刚度，因此，新型HRHMB适用于卧式系统等应用场合.

图 10 2种磁轴承的位移刚度和电流刚度对比

Figure 10. Comparison of displacement stiffness and current stiffness of two types of magnetic bearings

下载: 全尺寸图片幻灯片

3.4 电磁力耦合分析

为分析新型异极径向混合磁轴承X、Y方向2个自由度间的电磁力耦合，对转子位移和控制电流对电磁力的影响进行仿真分析，并与图1（b）中的传统八极偏置磁轴承进行对比.

首先，定义转子处于坐标$ (x,y) $时，Y方向电磁力的相对误差为

$\delta (x,y) = \left| {\frac{{{f_Y}(x,y) - {f_Y}(0,y)}}{{{f_Y}(0,y)}}} \right| \times 100{\text{%}}$

(14)

式中：$ {f_Y}(x,y) $为转子在坐标（x，y）时Y方向上的电磁力.

在X轴、Y轴绕组不通电情况下，X和Y方向转子不同位移对Y方向电磁力的影响和电磁力相对误差如图11所示. 由图11（a）可以看出，在x位移量的影响下，新型磁轴承转子在Y方向上受到的电磁力随Y轴位移量仍成正比，变化不明显，最大相对误差为2.76%. 而从图11（b）可以看出，传统偏置磁轴承转子在Y方向上受到的电磁力最大相对误差达到了3.87%.

图 11 转子偏心时的耦合特性

Figure 11. Coupling characteristics with eccentric rotor

下载: 全尺寸图片幻灯片

定义转子位置在（0，y）时，电磁力的相对误差为

$\kappa ({I_X},y) = \left| {\frac{{{f_Y}({I_X},y) - {f_Y}(0,y)}}{{{f_Y}(0,y)}}} \right| \times 100{\text{%}}$

(15)

式中：$ {f_Y}({I_X},y) $和$ {f_Y}(0,y) $分别为转子在（0，y）处通入X方向电流I_X和不通电时Y方向的电磁力.

磁轴承x位移量和Y方向电流为0，通入X方向不同电流时，Y方向电磁力随y的关系曲线和电磁力相对误差如图12所示，由图12（a）可以看出，新型磁轴承Y方向的电磁力与Y轴位移量基本成正比关系，最大误差为3.52%，表明该新型磁轴承X方向电流对Y方向位移刚度影响较小；由图12（b）可以看出，传统偏置磁轴承X方向电流会增加转子在Y方向受的电磁力，其最大相对误差为7.6%.

图 12 转子不偏心时控制电流的耦合特性

Figure 12. Coupling characteristics of control current when rotor is not eccentric

下载: 全尺寸图片幻灯片

当转子在X方向偏心0.1 mm时，图13为磁轴承Y方向电磁力随Y轴位移量和X方向控制电流的关系和电磁力相对误差. 由图13（a）可以看出，在转子偏心条件下通入不同的X方向电流时，Y方向的电磁力仍然正比于Y轴位移量，相对误差最大值为6.5%，这表明转子在X方向发生偏移时，通入X方向电流对Y方向电磁力随Y方向位移的线性特性影响较小，有利于该新型磁悬浮轴承的控制系统设计. 由图13（b）可以看出，通入X方向电流对传统偏置磁轴承转子在Y方向上受的电磁力有较大的影响，最大相对误差为13.6%，其径向两自由度之间的运动存在一定耦合.

图 13 转子偏移0.1mm时控制电流的耦合特性

Figure 13. Coupling characteristics of control current when rotor offsets 0.1 mm

下载: 全尺寸图片幻灯片

综上可知，新型HRHMB在X方向的转子位移基本不影响Y方向的电磁力. 无论转子是否在X方向上发生偏移，X方向上的控制电流对Y方向上的电磁力基本没有影响. 其两自由度之间的电磁力耦合明显小于传统偏置磁轴承，这是由于该新型HRHMB永磁体排列组合方式使其永磁磁路与电磁磁路耦合距离短，且两磁场的相互影响效果较弱，有利于获得良好的解耦特性.

4. 结　论

对于飞轮储能系统等空间利用率要求较高的场合，本文提出了一种新型异极径向混合磁悬浮轴承，该磁轴承电磁磁路和永磁磁路耦合距离短，具有解耦性高的优点. 由等效磁路法建立了该新型轴承的磁路模型，通过解析和仿真研究得出以下结论：

1）由等效磁路法得到的新型HRHMB的承载力、位移刚度和电流刚度的理论结果，与有限元仿真结果相吻合，验证了解析结果的正确性.

2）在相同承载力、偏置磁通、转子尺寸等约束条件下，新型HRHMB结构更为紧凑，空间利用率较高，同时有着较大的电流刚度.

3）新型HRHMB在不同自由度的转子位移和控制电流变化影响下，电磁力相对误差最大值较传统偏置磁轴承小，表明该结构特殊的永磁体排列方式使得电磁磁路与永磁磁路间耦合小，径向二自由度之间电磁力解耦效果较好.

图 1 转臂节点三维图

Figure 1. Three-dimensional drawing of rotary arm node

下载: 全尺寸图片幻灯片

图 2 橡胶节点动态特性

Figure 2. Dynamic characteristics of rubber node

下载: 全尺寸图片幻灯片

图 3 高寒动车组车辆动力学模型

Figure 3. Vehicle dynamics model of alpine EMUs

下载: 全尺寸图片幻灯片

图 4 悬挂参数温变特性

Figure 4. Temperature-varying characteristics of suspension parameters

下载: 全尺寸图片幻灯片

图 5 轨道模型和扣件胶垫温变特性

Figure 5. Temperature-varying characteristics of track model and fastener pad

下载: 全尺寸图片幻灯片

图 6 临界速度

Figure 6. Critical speed

下载: 全尺寸图片幻灯片

图 7 平稳性和舒适度指标

Figure 7. Smoothness and comfort indexes

下载: 全尺寸图片幻灯片

图 8 车轮磨耗计算流程

Figure 8. Calculation process of wheel wear

下载: 全尺寸图片幻灯片

图 9 轮轨接触参数分析

Figure 9. Analysis of wheel-rail contact parameters

下载: 全尺寸图片幻灯片

图 10 短距离车轮磨耗

Figure 10. Short-distance wheel wear

下载: 全尺寸图片幻灯片

图 11 不同温度下的磨耗预测演变

Figure 11. Evolution of wear prediction at different temperatures

下载: 全尺寸图片幻灯片

图 12 轮轨滚动接触疲劳损伤曲线

Figure 12. Fatigue damage curve of wheel-rail rolling contact

下载: 全尺寸图片幻灯片

图 13 磨耗指数和接触疲劳损伤分布

Figure 13. Wear index and contact fatigue damage distribution

下载: 全尺寸图片幻灯片

图 14 不同温度下的疲劳指数分布和接触疲劳因子

Figure 14. Distribution of fatigue index and contact fatigue factor at different temperatures

下载: 全尺寸图片幻灯片

表 1 高速客运专线典型计算工况

Table 1. Typical calculation working conditions for high-speed passenger special lines

曲线半径/m	超高/ mm	缓和曲线长/m	圆曲线长/m	运行速度/ (km•h⁻¹)	所占比例/ %
直线				300	60
12000	80	220	480	300	1
9000	100	300	320	300	7
8000	120	340	250	300	8
7000	145	360	210	300	10
5500	165	360	210	300	7
5000	120	360	210	300	7

下载: 导出CSV

参考文献(26)

[1]	金学松,赵国堂,梁树林,等. 高速铁路轮轨磨损特征、机理、影响和对策:车轮踏面横向磨耗[J]. 机械工程学报,2018,54(4): 3-13. doi: 10.3901/JME.2018.04.003 JIN Xuesong, ZHAO Guotang, LIANG Shulin, et al. Characteristics, mechanisms, influences and counter measures of high speed wheel/rail wear: transverse wear of wheel tread[J]. Journal of Mechanical Engineering, 2018, 54(4): 3-13. doi: 10.3901/JME.2018.04.003
[2]	谢清林,陶功权,王鹏,等. 高寒动车组车轮磨耗演变特性及其影响分析[J]. 工程力学,2019,36(10): 229-237. XIE Qinglin, TAO Gongquan, WANG Peng, et al. Wheel wear evolution characteristics of alpine high-speed emu and analysis of its influence[J]. Engineering Mechanics, 2019, 36(10): 229-237.
[3]	徐腾养,池茂儒,田向阳,等. 抗蛇行减振器内部油液温度对其动态特性的影响[J]. 机车电传动,2016(6): 43-46. XU Tengyang, CHI Maoru, TIAN Xiangyang, et al. Infl uence of oil temperature of yaw damper on dynamic performance[J]. Electric Drive for Locomotives, 2016(6): 43-46.
[4]	谭富星,石怀龙,王玮,等. 转向架橡胶件动态参数的高低温特性[J]. 交通运输工程学报,2019,19(4): 104-114. TAN Fuxing, SHI Huailong, WANG Wei, et al. High and low temperature characteristics of rubber component dynamic parameters of a bogie[J]. Journal of Traffic and Transportation Engineering, 2019, 19(4): 104-114.
[5]	侯茂锐,胡晓依,郭涛,等. 高速动车组轴箱转臂节点性能对轮轨耦合振动的影响[J]. 交通运输工程学报,2021,21(6): 170-180. HOU Maorui, HU Xiaoyi, GUO Tao, et al. Effect of axle box rotary arm node performance on wheel-rail coupling vibration for high-speed EMUs[J]. Journal of Traffic and Transportation Engineering, 2021, 21(6): 170-180.
[6]	侯茂锐,胡晓依,宗仁莉,等. 高速动车组转臂定位橡胶节点刚度对车辆动力学性能影响[J]. 中国铁道科学,2021,42(4): 120-128. HOU Maorui, HU Xiaoyi, ZONG Renli, et al. Influence of stiffness of arm positioning rubber node on vehicle dynamic performance of high-speed EMU[J]. China Railway Science, 2021, 42(4): 120-128.
[7]	滕万秀,罗仁,石怀龙,等. 高寒动车组−40 ℃环境下动力学性能[J]. 机械工程学报,2019,55(4): 148-153. doi: 10.3901/JME.2019.04.148 TENG Wanxiu, LUO Ren, SHI Huailong, et al. Dynamics behaviour of high-speed train at the low temperature of −40 ℃[J]. Journal of Mechanical Engineering, 2019, 55(4): 148-153. doi: 10.3901/JME.2019.04.148
[8]	罗仁,李然,胡俊波,等. 考虑随机参数的高速列车动力学分析[J]. 机械工程学报,2015,51(24): 90-96. doi: 10.3901/JME.2015.24.090 LUO Ren, LI Ran, HU Junbo, et al. Dynamic analysis of high-speed train with stochastic parameters[J]. Journal of Mechanical Engineering, 2015, 51(24): 90-96. doi: 10.3901/JME.2015.24.090
[9]	QI Y Y, DAI H Y. Influence of motor harmonic torque on wheel wear in high-speed trains[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(1): 32-42. doi: 10.1177/0954409719830808
[10]	侯茂锐,陈秉智,成棣,等. 两种典型动车组车轮磨耗演变规律及其动力学影响研究[J]. 机械工程学报,2022,58(4): 191-201. doi: 10.3901/JME.2022.04.191 HOU Maorui, CHEN Bingzhi, CHENG Di, et al. Two typical wheel wear evolution characteristics and its influence on dynamic performance of high-speed EMU[J]. Journal of Mechanical Engineering, 2022, 58(4): 191-201. doi: 10.3901/JME.2022.04.191
[11]	SANG H T, ZENG J, QI Y Y, et al. Study on wheel wear mechanism of high-speed train in accelerating conditions[J]. Wear, 2023, 516/517: 204597.1-204597.1-5.
[12]	LI Y Y, REN Z S, ENBLOM R, et al. Wheel wear prediction on a high-speed train in China[J]. Vehicle System Dynamics, 2020, 58(12): 1839-1858. doi: 10.1080/00423114.2019.1650941
[13]	孙丽霞,李晓峰,胡晓依,等. 高速动车组车轮磨耗对轮轨接触关系及车辆动力学性能的影响[J]. 中国铁道科学,2020,41(6): 117-126. SUN Lixia, LI Xiaofeng, HU Xiaoyi, et al. Influence of wheel wear on wheel-rail contact relationship and vehicle dynamic performance of high-speed EMU[J]. China Railway Science, 2020, 41(6): 117-126.
[14]	肖乾,周前哲,程玉琦,等. 高速列车车轮磨耗型面特征提取及参数化描述方法研究[J]. 机械工程学报,2023,59 (14) :245-253. XIAO Qian, ZHOU Qianzhe, CHENG Yuqi, et al. Study on extraction of wheel profile wear characteristics and curve parameterization description of high-speed train wheels[J]. Journal of Mechanical Engineering,2023,59 (14) :245-253.
[15]	YE Y G, HECHT M. Wear concentration index: an alternative to the target T-gamma in railway wheel profile optimization[C]//The IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks. Cham: Springer, 2022: 522-532.
[16]	宋志坤,任海星,胡晓依,等. 动车组车轮多边形磨耗发展历程模拟及车轮粗糙度的影响[J]. 铁道学报,2021,43(6): 23-28. SONG Zhikun, REN Haixing, HU Xiaoyi, et al. Research on development process simulation and influencing factors of polygonal wear of high-speed train wheels[J]. Journal of the China Railway Society, 2021, 43(6): 23-28.
[17]	YE Y G, ZHU B, HUANG P, et al. OORNet: a deep learning model for on-board condition monitoring and fault diagnosis of out-of-round wheels of high-speed trains[J]. Measurement, 2022, 199: 111268.1-111268.60.
[18]	CUI X L, BAO P Y, LI T, et al. Research on the failure mechanism of elastic strip fracture in corrugated sections of metros[J]. Engineering Failure Analysis, 2023, 143: 106837.1-106837.12.
[19]	QI Y Y, DAI H Y, GAN F, et al. Optimization of rail profile design for high-speed lines based on Gaussian function correction method[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2023: 095440972311525.1-095440972311525.11.
[20]	杨麒陆,王平. WJ-7型高速铁路扣件胶垫刚度温变性的测试与分析[J]. 中国铁路,2017(8): 58-63. YANG Qilu, WANG Ping. Tests and analysis of rubber pad stiffness of WJ-7 HSR fastening against temperature changes[J]. China Railway, 2017(8): 58-63.
[21]	中华人民共和国国家市场监督管理总局,中国国家标准化管理委员会. 机车车辆动力学性能评定及试验鉴定规范:GB/T 5599—2019[S]. 北京:中国标准出版社,2019.
[22]	石怀龙,罗仁,曾京. 国内外高速列车动力学评价标准综述[J]. 交通运输工程学报,2021,21(1): 36-58. SHI Huailong, LUO Ren, ZENG Jing. Review on domestic and foreign dynamics evaluation criteria of high-speed train[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 36-58.
[23]	黄彩虹,罗仁,曾京,等. 系统参数对高速列车车轮踏面凹陷磨耗的影响[J]. 交通运输工程学报,2016,16(3): 55-62. HUANG Caihong, LUO Ren, ZENG Jing, et al. Effect of system parameters on tread-hollow wear of high-speed train wheels[J]. Journal of Traffic and Transportation Engineering, 2016, 16(3): 55-62.
[24]	祁亚运,戴焕云,干锋,等. 高速动车组车轮偏磨影响因素与限值研究[J]. 表面技术,2023,52(5): 51-60. QI Yayun, DAI Huanyun, GAN Feng, et al. Influencing factors and limits of asymmetrical wheel wear of high-speed EMUs[J]. Surface Technology, 2023, 52(5): 51-60.
[25]	JENDEL T. Prediction of wheel profile wear— comparisons with field measurements[J]. Wear, 2002, 253(1/2): 89-99.
[26]	TUNNA J, SINCLAIR J, PEREZ J. The development of a wheel wear and rolling contact fatigue model[J]. Engineering Materials Science, 2007, 9: 106951664.1-106951664.12.