地铁弓网系统摩擦自激振动研究

冯晓航; 陈光雄; 梅桂明; 董丙杰; 赵鹏鹏; 李先航

doi:10.3969/j.issn.0258-2724.20220873

地铁弓网系统摩擦自激振动研究

doi: 10.3969/j.issn.0258-2724.20220873

1.
西南交通大学机械工程学院，四川成都 610031
2.
西南交通大学轨道交通运载系统全国重点实验室，四川成都 610031

基金项目: 国家自然科学基金项目（52175189）

详细信息

作者简介:
冯晓航（1998—），男，博士研究生，研究方向为轮轨摩擦学，E-mail：fxh1010@my.swjtu.edu.cn

通讯作者:
陈光雄（1962—），男，教授，博士，研究方向为摩擦振动与噪声，E-mail：chen_guangx@163.com

中图分类号: O323
计量
- 文章访问数: 253
- HTML全文浏览量: 117
- PDF下载量: 20
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-19
- 修回日期: 2023-02-21
- 网络出版日期: 2024-06-04

Frictional Self-Excited Vibration of a Metro Pantograph-Catenary System

1.
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
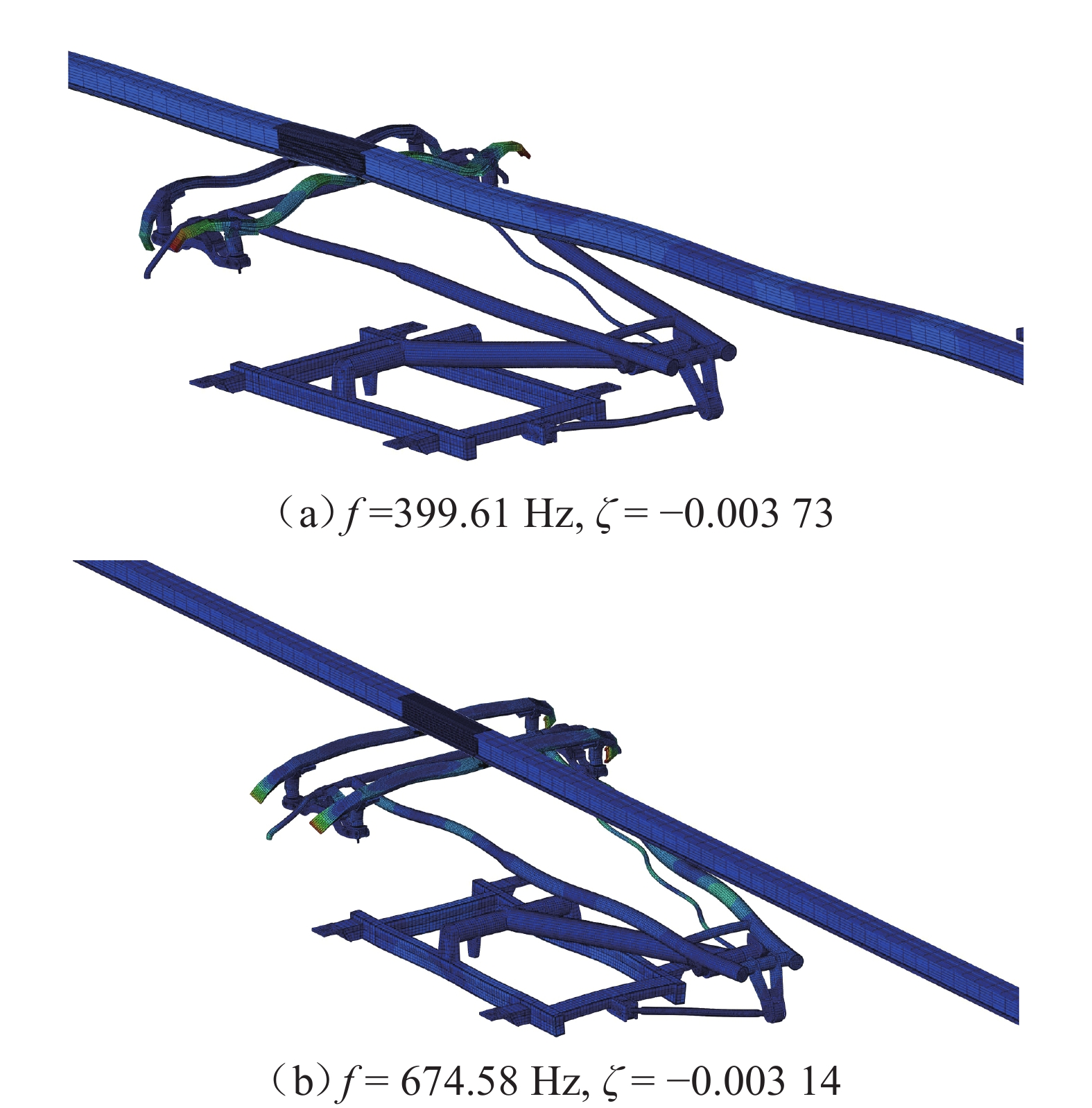
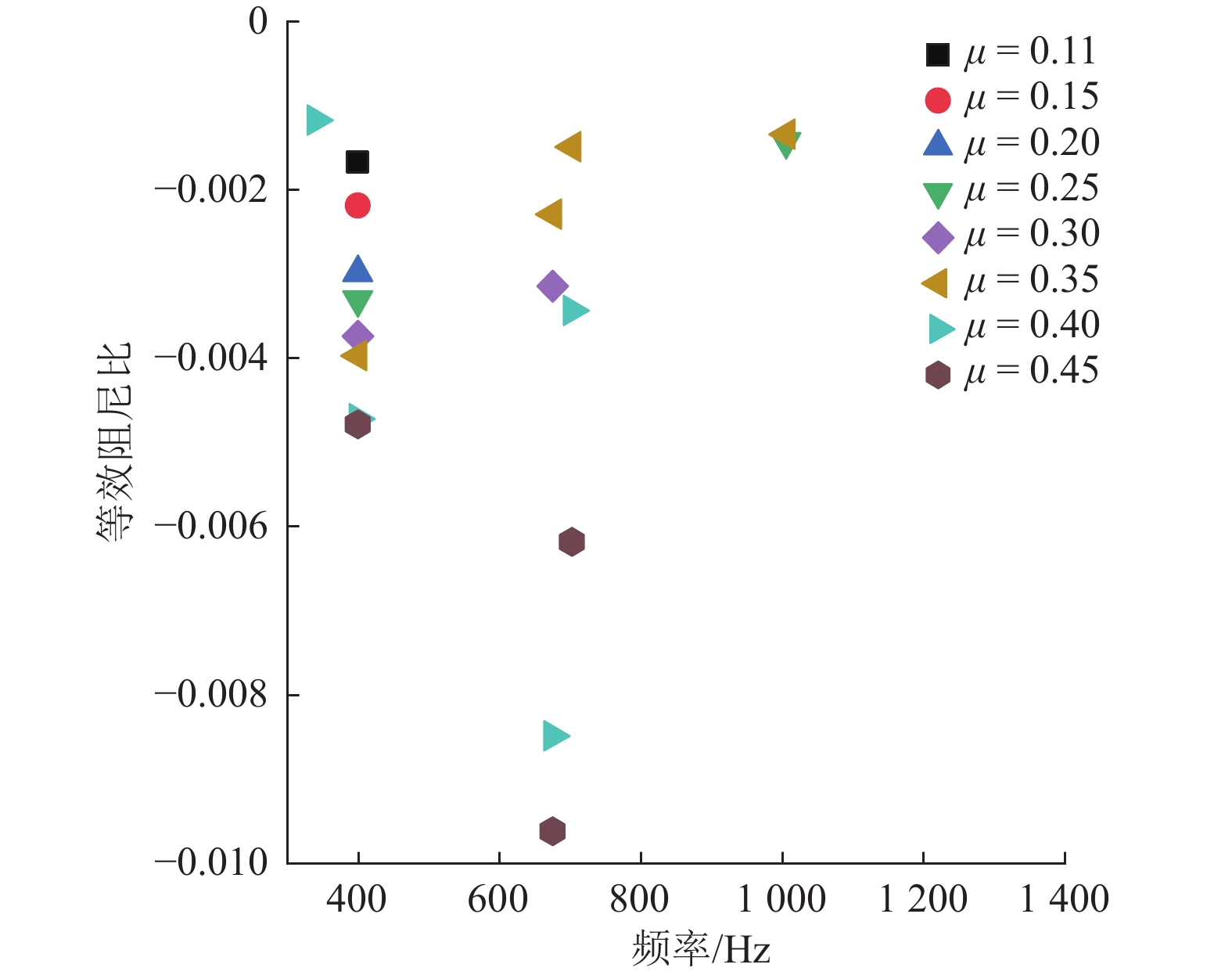
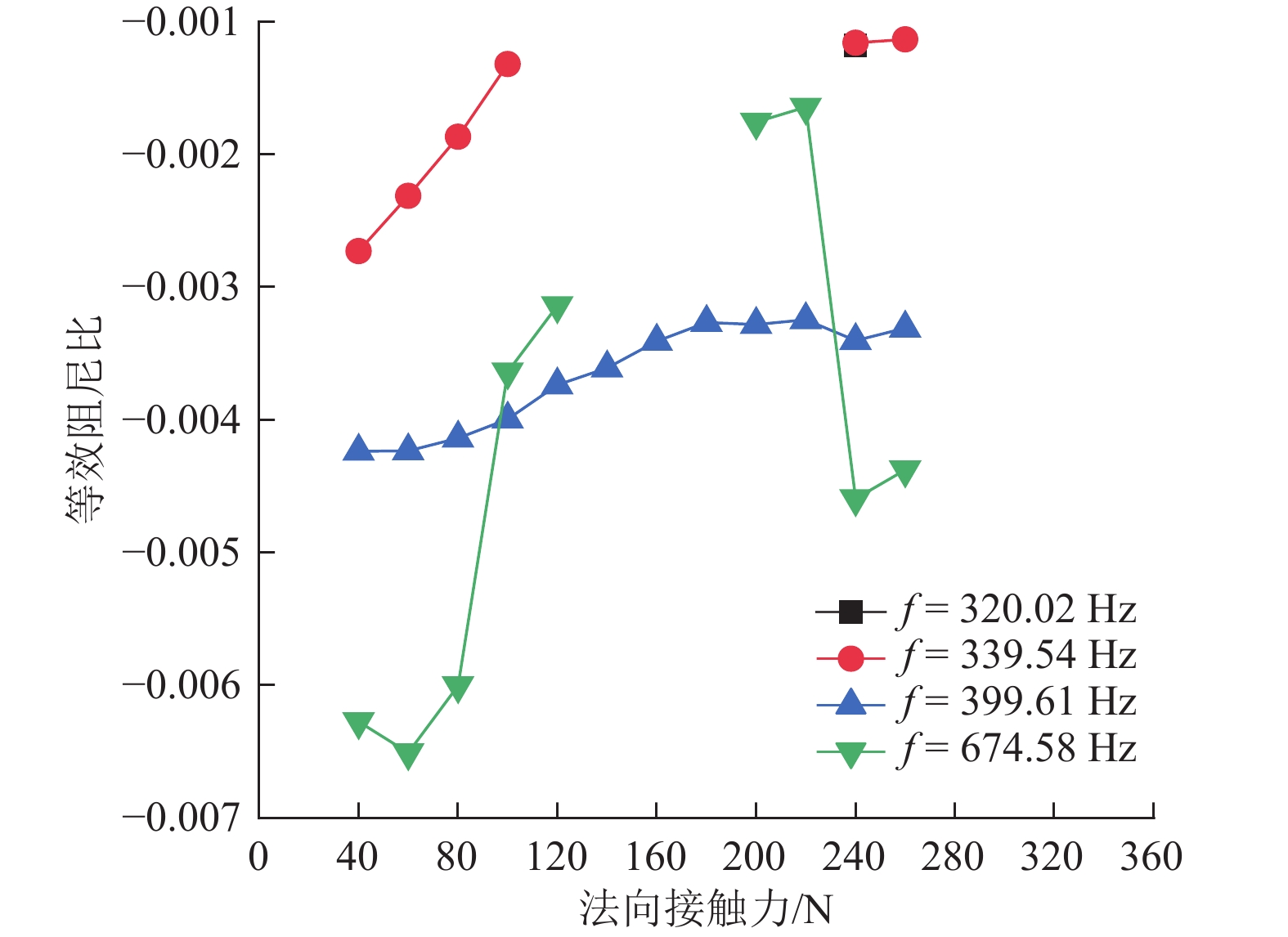
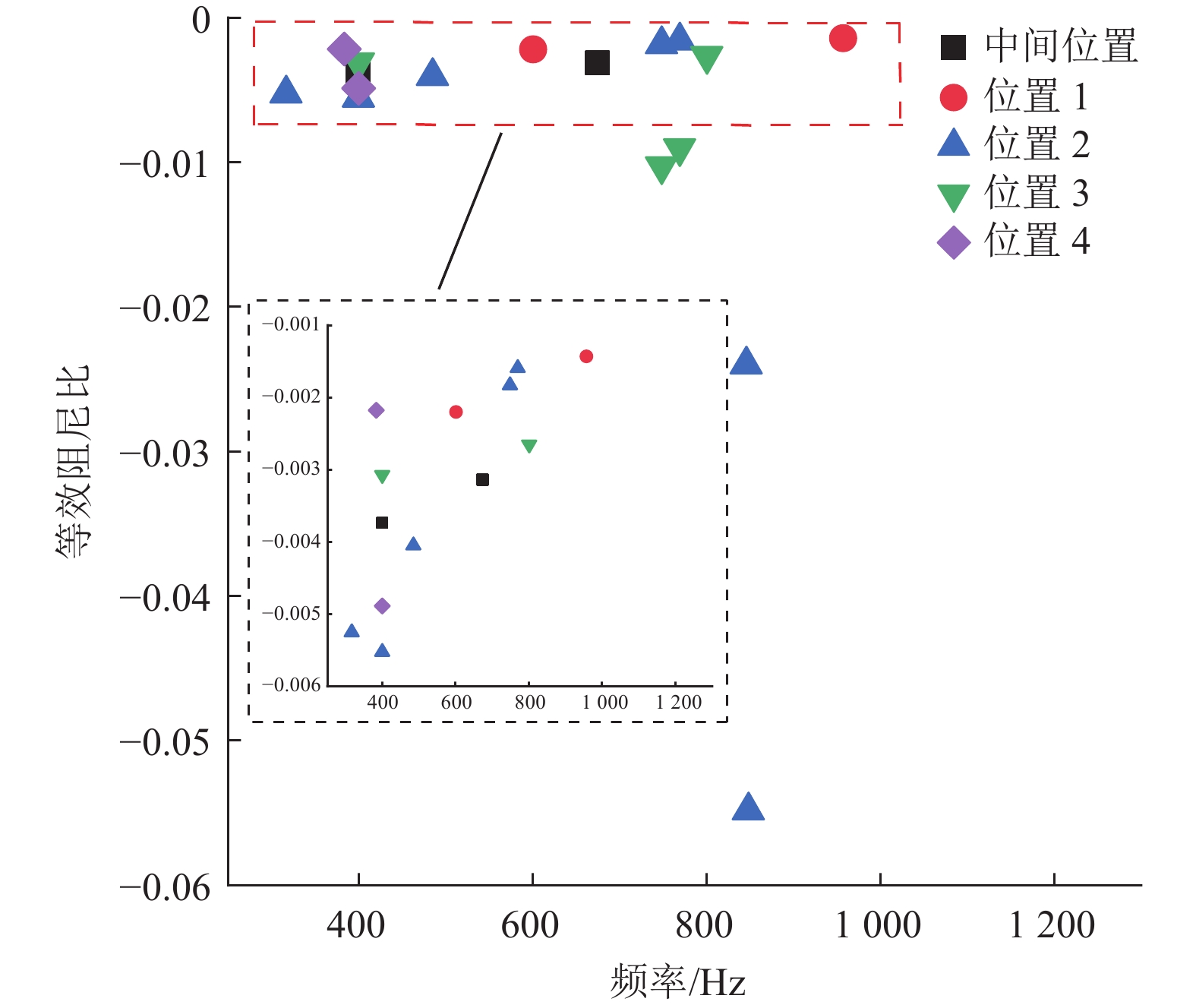
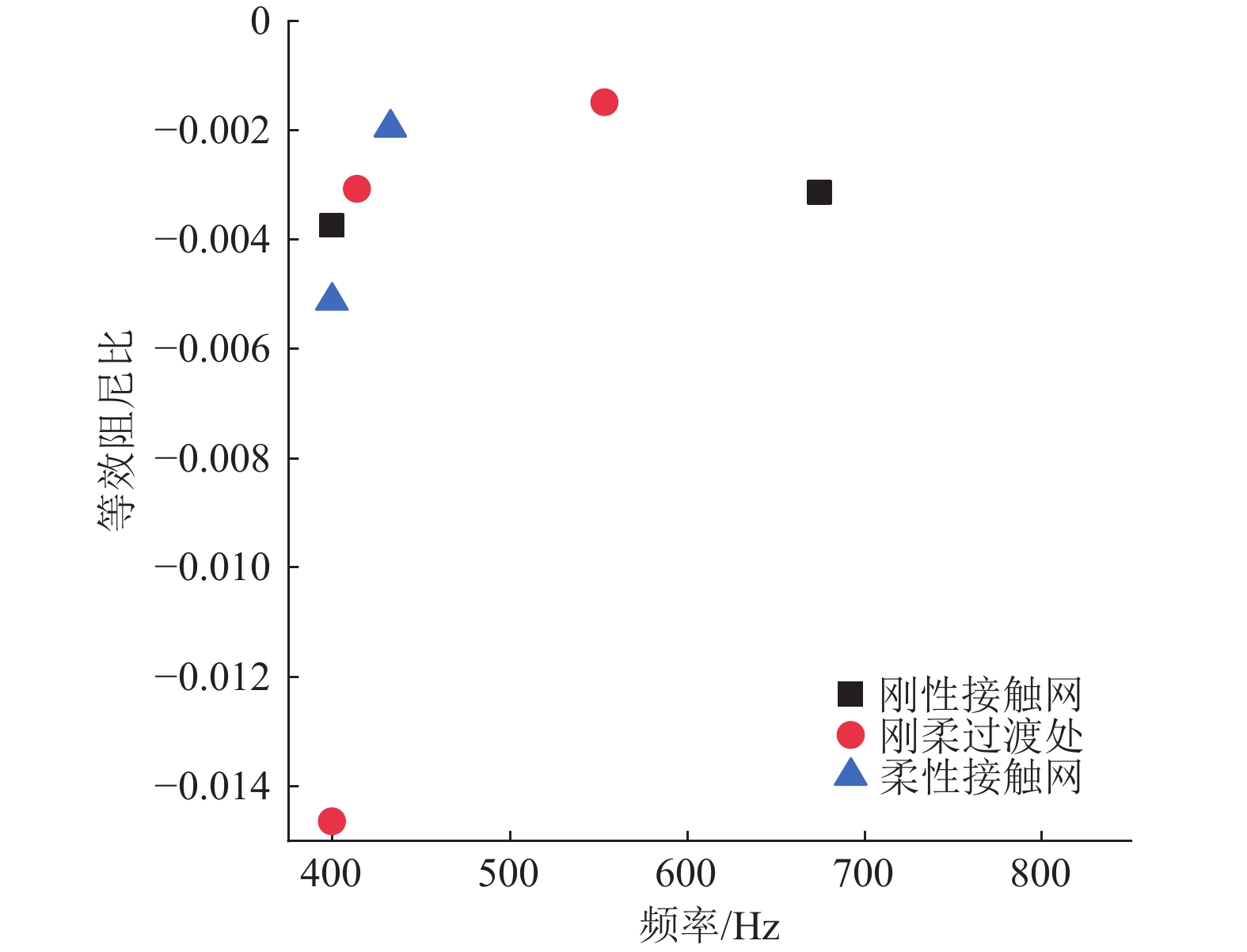
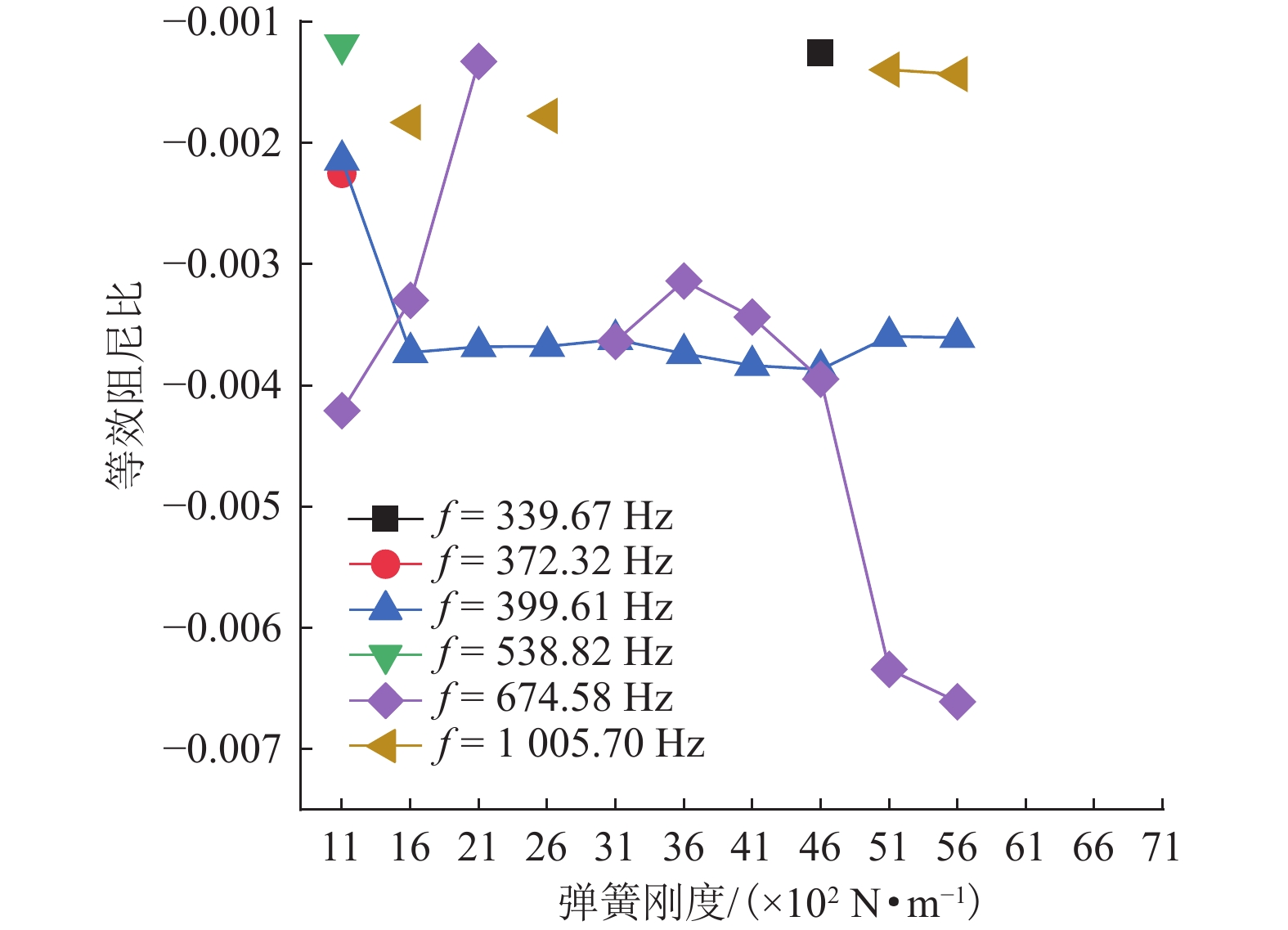
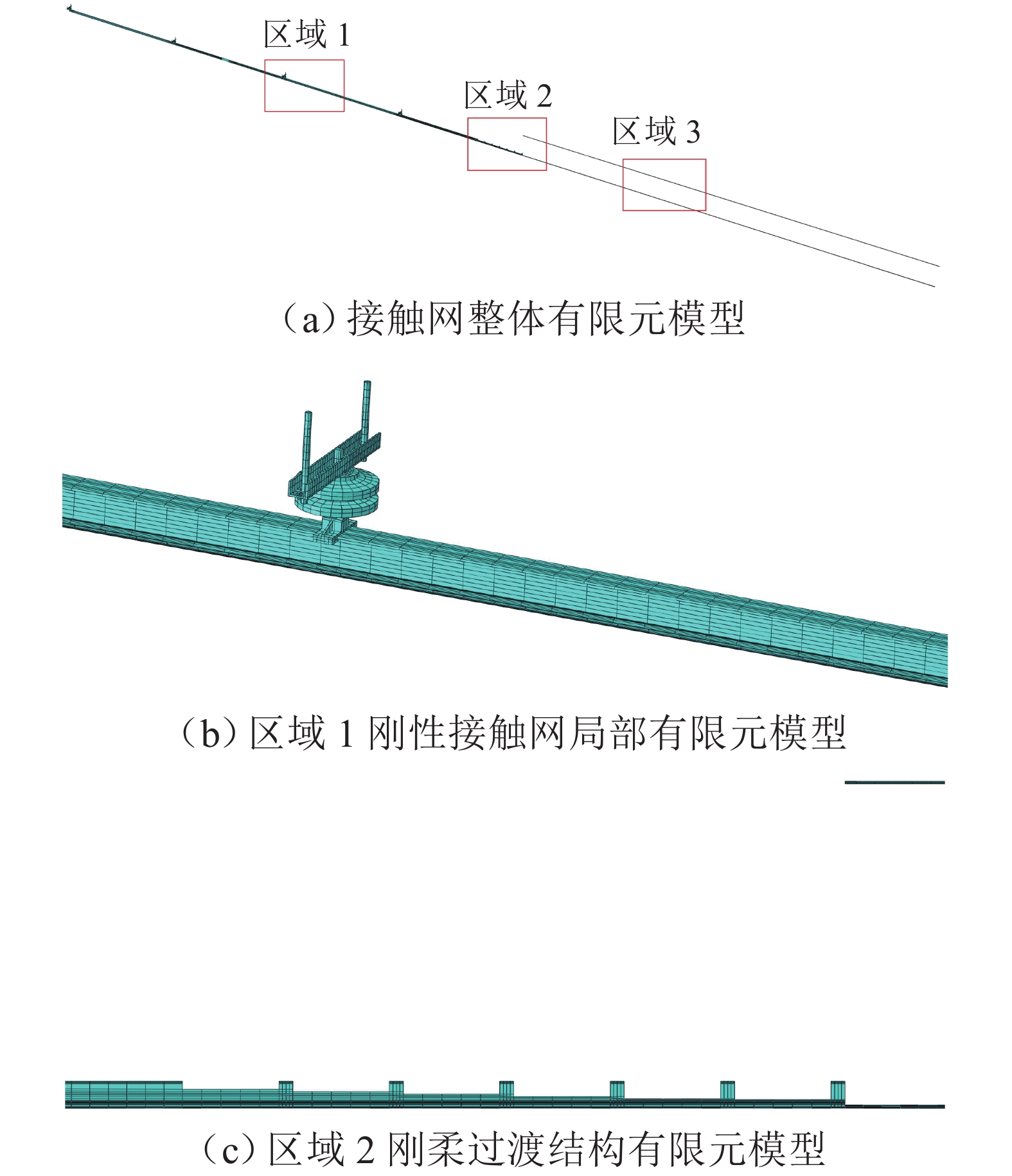
为研究弓网系统摩擦自激振动对碳滑板与接触线之间接触损耗的影响，基于摩擦自激振动理论，建立地铁刚柔过渡段处受电弓-接触网系统有限元模型，并利用复特征值分析方法研究不同弓网参数对该系统摩擦自激振动的影响. 分析结果显示：弓网系统由摩擦自激振动引起接触线波磨产生的主频为399.61 Hz；当摩擦系数大于或等于0.11时，受电弓-接触网系统出现不稳定振动，且摩擦系数越大，该系统出现不稳定振动的趋势越强；法向接触力、碳滑板与接触线的接触位置以及弓头弹簧刚度对弓网系统摩擦自激振动的产生有很大影响；摩擦系数低于0.11并且选择合适的法向接触力或调整弓头弹簧刚度可以抑制甚至消除弓网系统的摩擦自激振动，进而减少弓/网间摩擦引起的接触损耗.
- 弓网系统 /
- 刚柔过渡 /
- 摩擦自激振动 /
- 复特征值分析 /
- 数值仿真
Abstract:
In order to study the influence of frictional self-excited vibration of a pantograph-catenary system on the contact loss between the carbon strip and contact wire, a finite element model of the pantograph-catenary system at the rigid and flexible transition section of a metro was established based on the theory of frictional self-excited vibration. The complex eigenvalue analysis method was used to study the influence of different pantograph-catenary parameters on the frictional self-excited vibration of the system. The analysis results show that the main frequency of contact line corrugation caused by frictional self-excited vibration of the pantograph-catenary system is 399.61 Hz. When the friction coefficient is greater than or equal to 0.11, the pantograph-catenary system has unstable vibration, and with the increase in the friction coefficient, the unstable vibration tends to be stronger. The normal contact force, the contact position between the carbon strip and the contact wire, and the stiffness of the pantograph bow spring have great influences on the occurrence of the frictional self-excited vibration of the pantograph-catenary system. When the friction coefficient is less than 0.11, selecting the appropriate normal contact force or adjusting the stiffness of the pantograph bow spring can restrain or even eliminate the frictional self-excited vibration of the pantograph-catenary system and then reduce the contact loss caused by the friction between the pantograph and catenary.
- pantograph-catenary system /
- rigid and flexible transition /
- frictional self-excited vibration /
- complex eigenvalue analysis /
- numerical simulation

HTML全文

图 1 接触网有限元模型

Figure 1. Finite element model of catenary

下载: 全尺寸图片幻灯片

图 2 柔性接触网模型

Figure 2. Flexible catenary model

下载: 全尺寸图片幻灯片

图 3 受电弓有限元模型

Figure 3. Finite element model of pantograph

下载: 全尺寸图片幻灯片

图 4 弓网系统有限元模型

Figure 4. Finite element model of pantograph-catenary system

下载: 全尺寸图片幻灯片

图 5 刚性弓网系统不稳定振动模态

Figure 5. Unstable vibration mode shapes of rigid pantograph-catenary system

下载: 全尺寸图片幻灯片

图 6 接触线波磨波长

Figure 6. Wavelength of contact wire corrugation

下载: 全尺寸图片幻灯片

图 7 等效阻尼比和频率的变化关系

Figure 7. Variation of equivalent damping ratio with frequency under different friction coefficients

下载: 全尺寸图片幻灯片

图 8 系统不稳定振动频率对应的等效阻尼比随法向接触力的变化

Figure 8. Variation of equivalent damping ratio of unstable vibration frequency of system with normal contact force

下载: 全尺寸图片幻灯片

图 9 实际线路中碳滑板磨损位置

Figure 9. Wear position of a carbon strip in actual lines

下载: 全尺寸图片幻灯片

图 10 有限元模型中碳滑板接触位置

Figure 10. Contact position of carbon strip in finite element model

下载: 全尺寸图片幻灯片

图 11 碳滑板接触位置变化，等效阻尼比与频率的变化关系

Figure 11. Variation of contact position of carbon strip and variation of equivalent damping ratio with frequency

下载: 全尺寸图片幻灯片

图 12 不同接触网位置下，等效阻尼比与频率的变化关系

Figure 12. Variation of equivalent damping ratio with frequency under different catenary positions

下载: 全尺寸图片幻灯片

图 13 不同频率下，等效阻尼比ζ与弓头弹簧刚度的变化关系

Figure 13. Variation of equivalent damping ratio with stiffness of pantograph bow spring under different frequencies

下载: 全尺寸图片幻灯片

表 1 刚性接触网模型参数

Table 1. Rigid catenary model parameters

部件	材料	密度/ （× 10³ kg•m⁻³）	弹性模量/ GPa	泊松比
汇流排	6101B	2.71	69	0.33
接触线	CTHA120	8.92	130	0.30
定位线夹	铝合金	2.70	70	0.34
绝缘子	陶瓷	3.80	340	0.22

下载: 导出CSV

表 2 柔性接触网模型参数

Table 2. Flexible catenary model parameters

部件	材料	密度/ （× 10³ kg•m⁻³）	弹性模量/ GPa	泊松比
承力索	JT150	9.20	105	0.30
接触线	CTHA120	8.92	130	0.30

下载: 导出CSV

表 3 受电弓各部件材料

Table 3. Material properties of pantograph components

部件	材料	密度/ （ × 10³ kg•m^–3）	弹性模量/ GPa	泊松比
平衡杆	碳纤维	1.9	231	0.23
碳滑板	铜、碳	2.4	12.6	0.43
下臂杆	铝合金	2.8	72	0.33
弓头支架	钛合金	4.5	117	0.34
其他部件	Q235	7.8	210	0.30

下载: 导出CSV

表 4 弓网系统计算参数变化范围

Table 4. Variation range of calculation parameters of pantograph-catenary system

参数	数值
摩擦系数	0.11～0.45
法向接触力/N	40～260
碳滑板接触位置	中间位置，位置 1～4
接触网类型	刚性接触网、刚柔过渡处、柔性接触网
弓头弹簧刚度/ （N•m⁻¹）	1100～5600

下载: 导出CSV

参考文献(24)

[1]	关金发,田志军,吴积钦. 基于弓网动力仿真的160 km/h刚柔过渡系统方案研究[J]. 铁道学报,2018,40(9): 48-56. GUAN Jinfa, TIAN Zhijun, WU Jiqin. Research of 160 km/h transition structure proposal between overhead conductor railand contact line based on dynamic simulation[J]. Journal of the China Railway Society, 2018, 40(9): 48-56.
[2]	王建红. 重庆轨道六号线支线二期工程接触网刚柔过渡[J]. 现代制造技术与装备,2022,58(9): 127-129. WANG Jianhong. Rigid flexible transition of OCS of Chongqing rail line 6 branch line phase Ⅱ project[J]. Modern Manufacturing Technology and Equipment, 2022, 58(9): 127-129.
[3]	杨清太. 既有线铁路接触网刚柔过渡问题探析[J]. 工程建设与设计,2021(13): 74-76. YANG Qingtai. A study on rigid and flexible catenary transition for existing rail-line[J]. Construction & Design for Engineering, 2021(13): 74-76.
[4]	梅桂明. 刚性接触网-受电弓载流磨损性能的试验研究[J]. 西南交通大学学报,2021,56(6): 1305-1310. MEI Guiming. Experimental study on wear performance of rigid catenary-pantograph system with direct current[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1305-1310.
[5]	周宁,支兴帅,张静,等. 电气化铁路弓网系统摩擦磨损性能研究进展[J]. 西南交通大学学报,2024,59(5):990-1005. ZHOU Ning, ZHI Xingshuai, ZHANG Jing, et al. Friction and wear performance of pantograph-catenary system in electrified railways: State of the art[J]. Journal of Southwest Jiaotong University, 2024, 59(5):990-1005.
[6]	范杰,刘达毅,董丙杰,等. 地铁刚性弓网系统接触线磨损特性试验研究[J]. 润滑与密封,2022,47(6): 45-51. FAN Jie, LIU Dayi, DONG Bingjie, et al. Experimental study on the wear characteristics of contact wire of metro rigid pantograph-catenary systems[J]. Lubrication Engineering, 2022, 47(6): 45-51.
[7]	YANG H J, LI C, LIU Y H, et al. Study on the delamination wear and its influence on the conductivity of the carbon contact strip in pantograph-catenary system under high-speed current-carrying condition[J]. Wear, 2021, 477:203823.1-203823.14.
[8]	MANDAI T, HARADA S, SHIMIZU M, et al. Improvement of rigid conductor lines[J]. Quarterly Report of RTRI, 2003, 44(2): 78-81. doi: 10.2219/rtriqr.44.78
[9]	WU T X, BRENNAN M J. Dynamic stiffness of a railway overhead wire system and its effect on pantograph-catenary system dynamics[J]. Journal of Sound and Vibration, 1999, 219(3): 483-502. doi: 10.1006/jsvi.1998.1869
[10]	CHEN L, LIU Z G, ZHANG J, et al. Influence of key parameters on high speed overhead conductor rail and pantograph system[C]//The IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks. Cham: Springer, 2020: 201-211.
[11]	SHIMIZU M, HARADA S, OYA A, et al. Improving performance of type T overhead rigid conductor lines[J]. Quarterly Report of RTRI, 2006, 47(1): 52-58. doi: 10.2219/rtriqr.47.52
[12]	钱世勇,陈珍宝,陈明国,等. 地铁弓网动态试验研究及分析[J]. 科协论坛(下半月),2012(5): 26-27. QIAN Shiyong, CHEN Zhenbao, CHEN Mingguo, et al. Research and analysis on dynamic test of metro pantograph and catenary[J]. Science & Technology Association Forum, 2012(5): 26-27.
[13]	谭冬华. 架空刚性接触悬挂弓网磨耗异常的解决办法[J]. 都市快轨交通,2007,20(2): 88-91. TAN Donghua. Causes and solutions for the abnormal pantograph-catenary attrition of rigid catenary[J]. Urban Rapid Rail Transit, 2007, 20(2): 88-91.
[14]	裴志禹. AC25 kV刚性接触网过渡段结构优化研究[D]. 成都:西南交通大学,2018.
[15]	QIAN W J, CHEN G X, ZHANG W H, et al. Friction-induced, self-excited vibration of a pantograph-catenary system[J]. Journal of Vibration and Acoustics, 2013, 135(5): 051021.1- 051021. 8
[16]	WU B W, SHANG Z Y, PAN J B, et al. Analysis on the formation cause for the high-order wheel polygonization of the high-speed trains based on the finite element method[J]. Vehicle System Dynamics, 2023, 61(1): 1-18. doi: 10.1080/00423114.2022.2035777
[17]	CUI X L, CHENG Z, YANG Z C, et al. Study on the phenomenon of rail corrugation on high-speed rail based on the friction-induced vibration and feedback vibration[J]. Vehicle System Dynamics, 2022, 60(2): 413-432. doi: 10.1080/00423114.2020.1817507
[18]	康熙,陈光雄,吕金洲,等. 缩尺轮轨模型中钢轨波磨的相似性[J]. 西南交通大学学报,2020,55(6): 1320-1327. KANG Xi, CHEN Guangxiong, LÜ Jinzhou, et al. Similarity of small-scale wheelset-track model for investigation of rail corrugation[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1320-1327.
[19]	陈光雄. 钢轨波磨预测模型验证工况的研究[J]. 西南交通大学学报,2022,57(5): 1017-1023,1054. CHEN Guangxiong. Study on validation conditions of rail corrugation prediction models[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 1017-1023,1054.
[20]	田珂. 地铁受电弓—刚性接触网建模及仿真研究[D]. 成都:西南交通大学,2018.
[21]	朱志增. 基于有限元分析的刚性悬挂弓网接触压力仿真研究[D]. 成都:西南交通大学,2014.
[22]	杨艺,周宁,李瑞平,等. 基于有限元法的弓网过渡段处动态性能仿真分析[J]. 振动与冲击,2016,35(18): 71-75,116. YANG Yi, ZHOU Ning, LI Ruiping, et al. Dynamic performance analysis of different sections of overhead catenary based on finite element model[J]. Journal of Vibration and Shock, 2016, 35(18): 71-75,116.
[23]	YUAN Y. An eigenvalue analysis approach to break squeal problem[C]// Proceedings of the 29th ISATA conference on automotive braking systems. Florence: ISATA, 1996: 3-6.
[24]	黄之元. 两种地铁刚性接触网摩擦副异常磨耗的试验研究[D]. 成都:西南交通大学,2020.