基于聚类和随机森林耦合模型的崩滑灾害易发性评估

杜映锦; 席传杰; 胡卸文; 吴建利; 刘波; 何坤

doi:10.3969/j.issn.0258-2724.20220864

基于聚类和随机森林耦合模型的崩滑灾害易发性评估

doi: 10.3969/j.issn.0258-2724.20220864

杜映锦^1,,
席传杰¹,
胡卸文^{1, 2, ,},
吴建利¹,
刘波¹,
何坤^{1, 2}

1.
西南交通大学地球科学与工程学院，四川成都 610031
2.
四川省环青藏高原交通廊道地质灾害生态化防治工程技术研究中心，四川成都 610031

基金项目: 国家重点研发计划（2018YFC1505401）

详细信息

作者简介:
杜映锦（1979—），男，博士研究生，研究方向为地质灾害及防治工程，E-mail：dyj@swjtu.cn

通讯作者:
胡卸文（1963—），男，教授，博士，研究方向为工程地质、环境地质，E-mail：huxiewen@163.com

中图分类号: X43
计量
- 文章访问数: 287
- HTML全文浏览量: 116
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-13
- 修回日期: 2023-09-01
- 网络出版日期: 2024-07-09
- 刊出日期: 2023-09-25

Susceptibility Assessment of Collapses and Landslides Based on Cluster and Random Forest Coupled Model

DU Yingjin^1
,,
XI Chuanjie¹,
HU Xiewen^{1, 2
, ,},
WU Jianli¹,
LIU Bo¹,
HE Kun^{1, 2}

1.
Faculty of Geosciences and Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
Sichuan Province Engineering Technology Research Center of Ecological Mitigation of Geohazards in Tibet Plateau Transportation Corridors, Chengdu 610031, China

摘要

摘要:
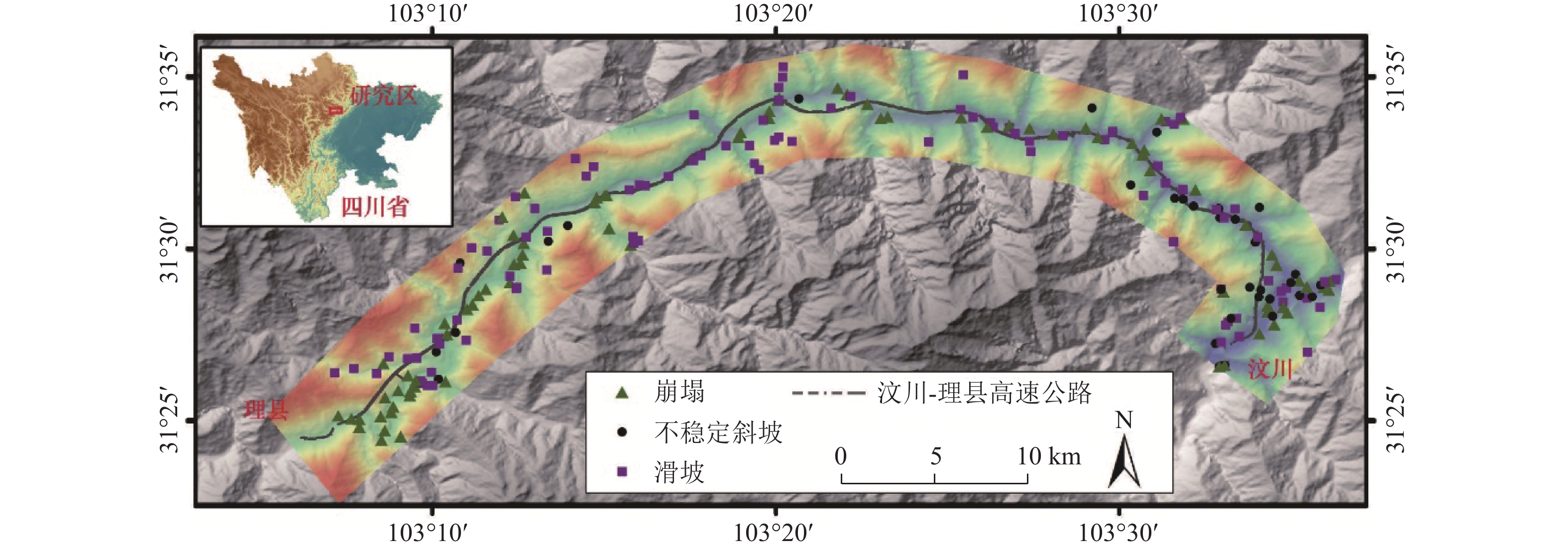
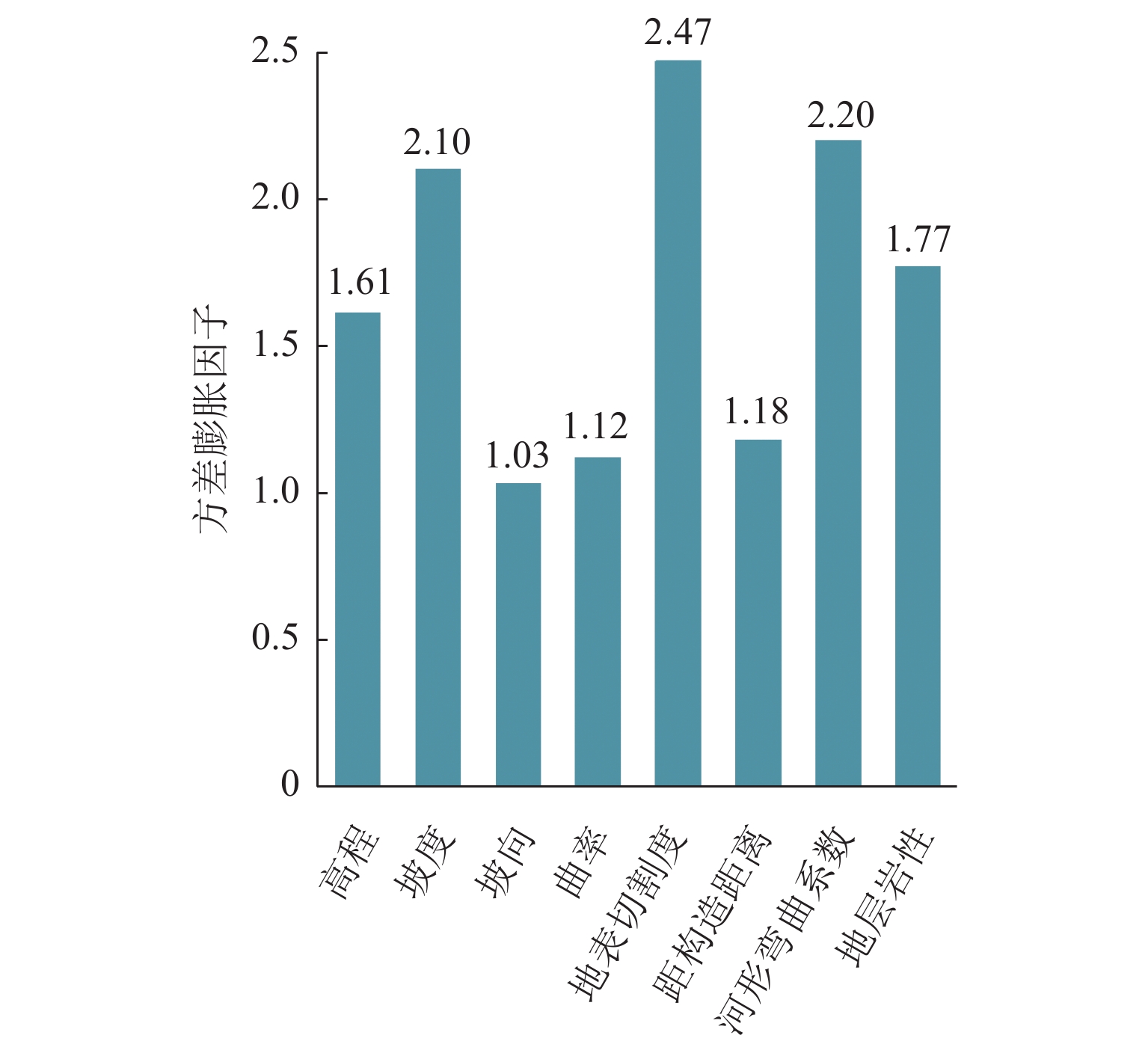
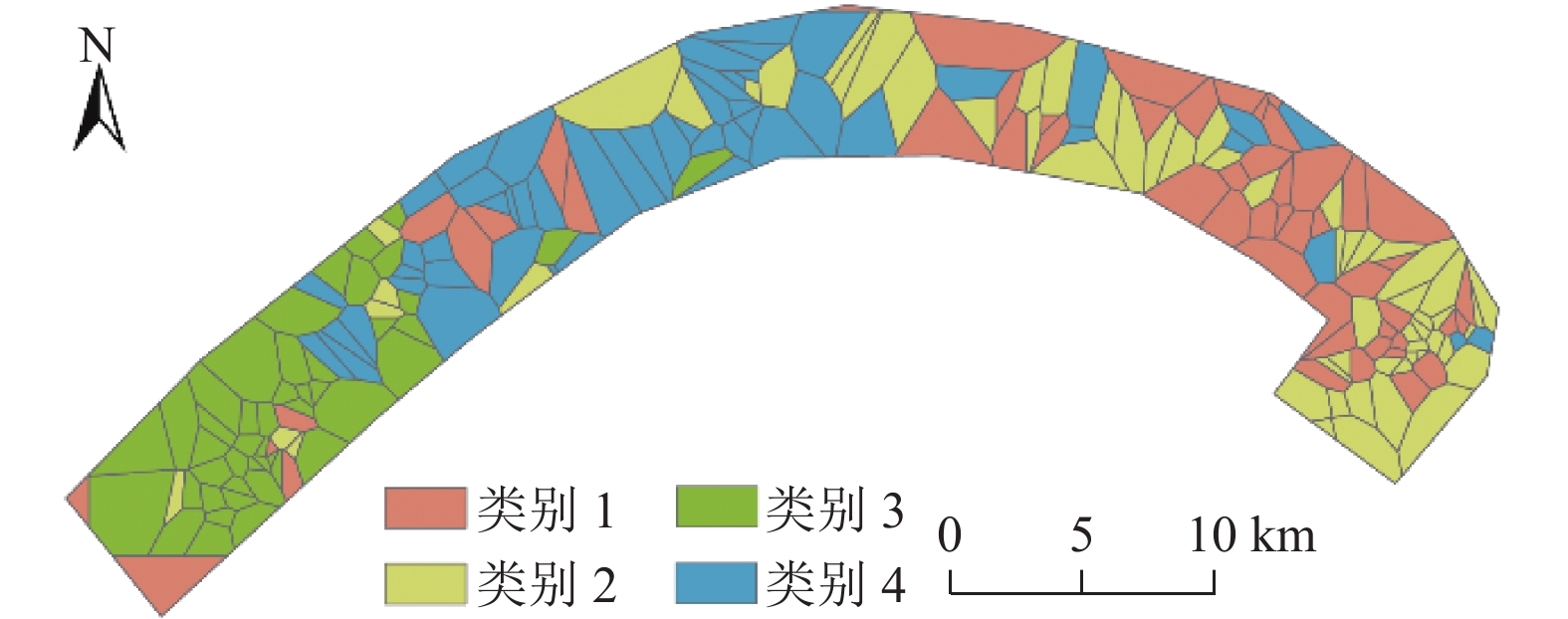
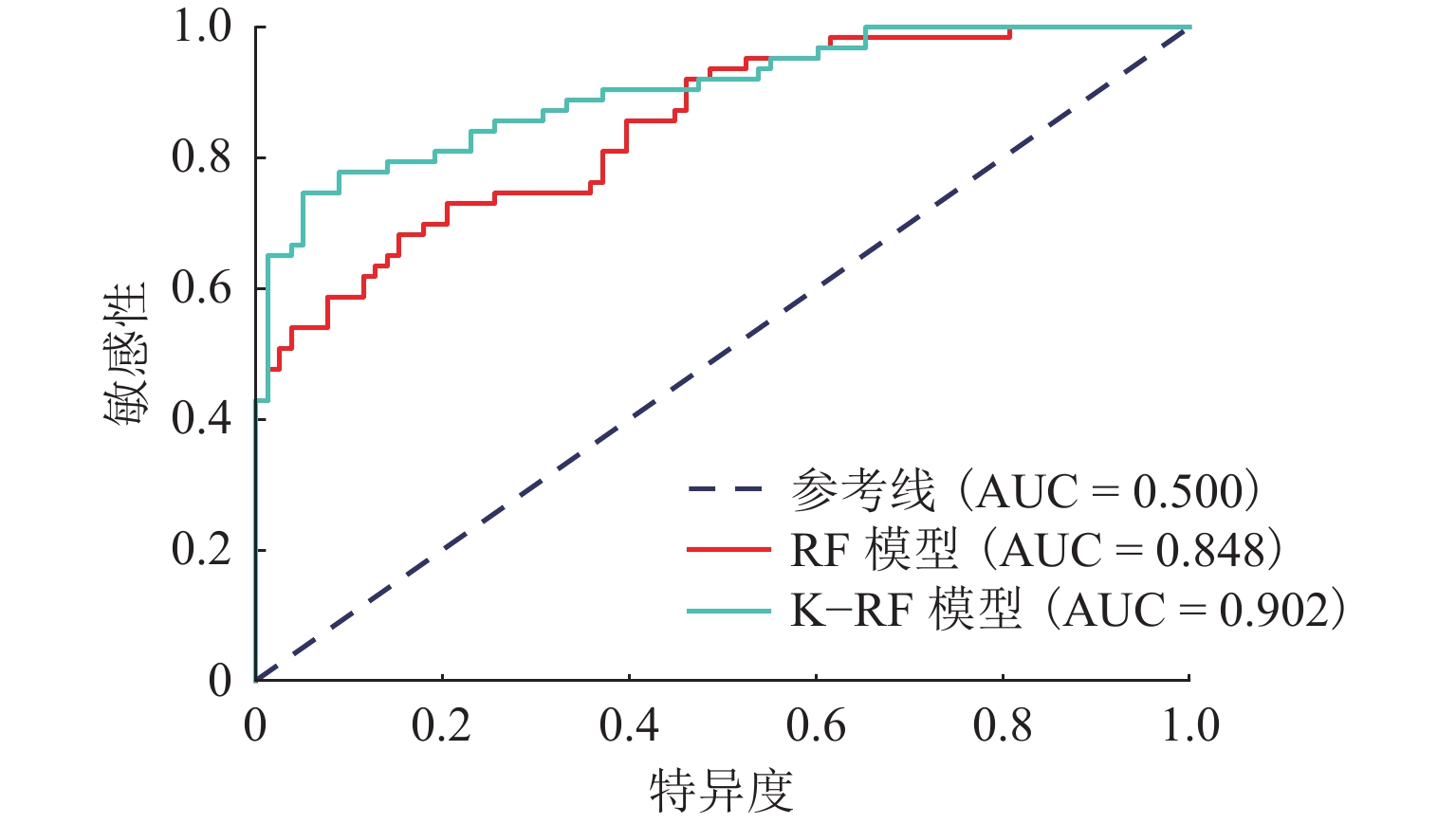
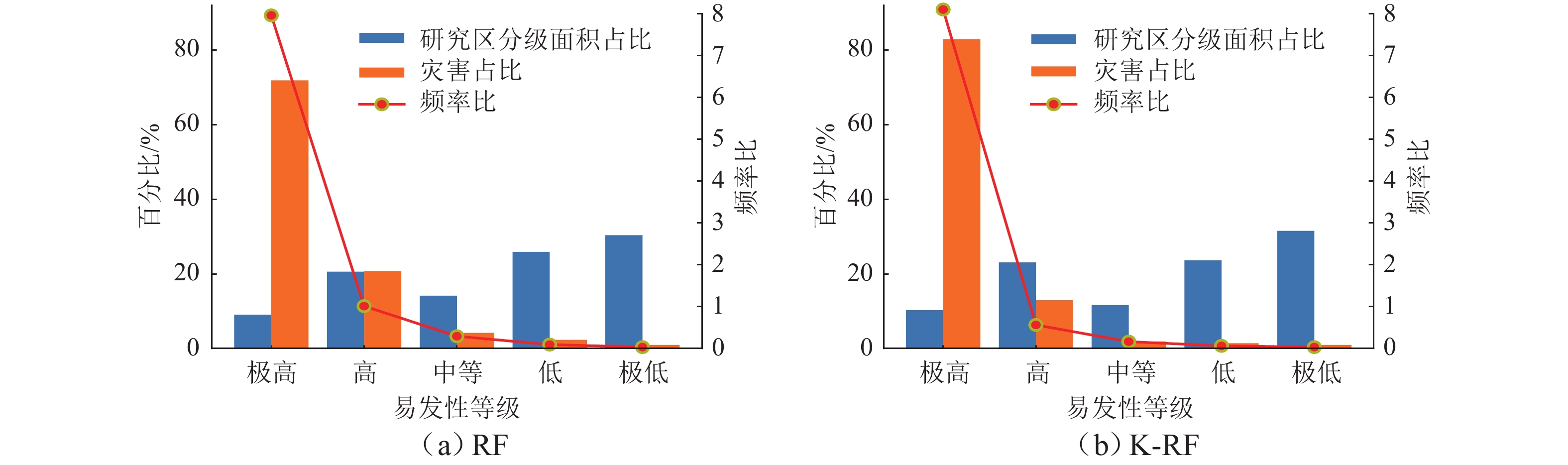
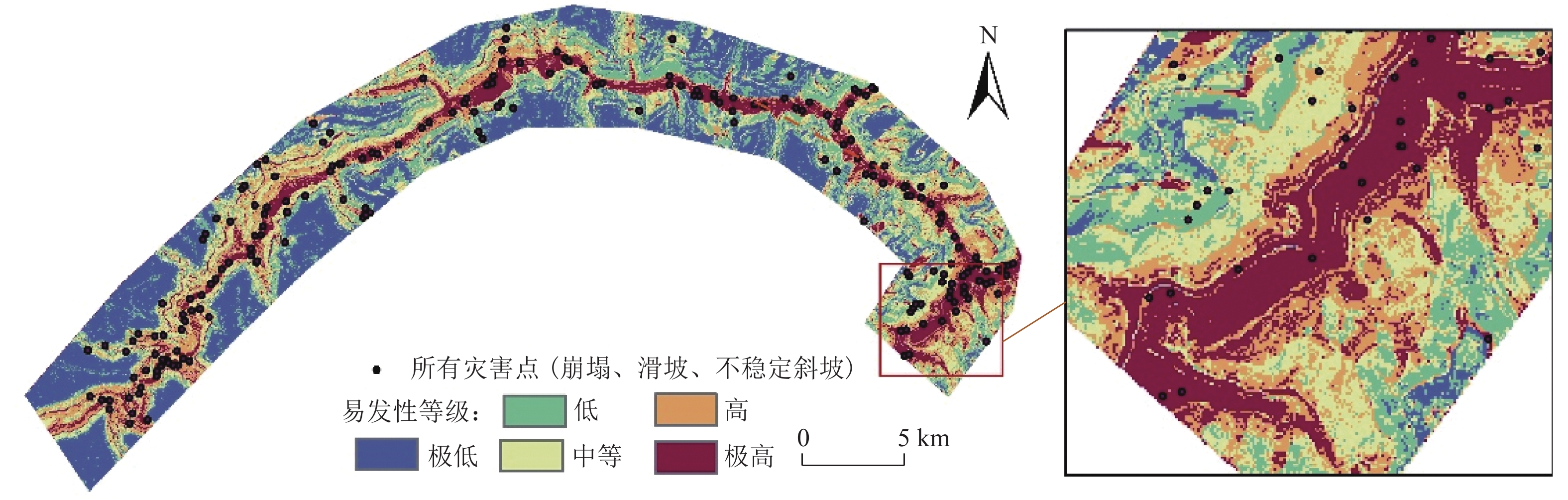
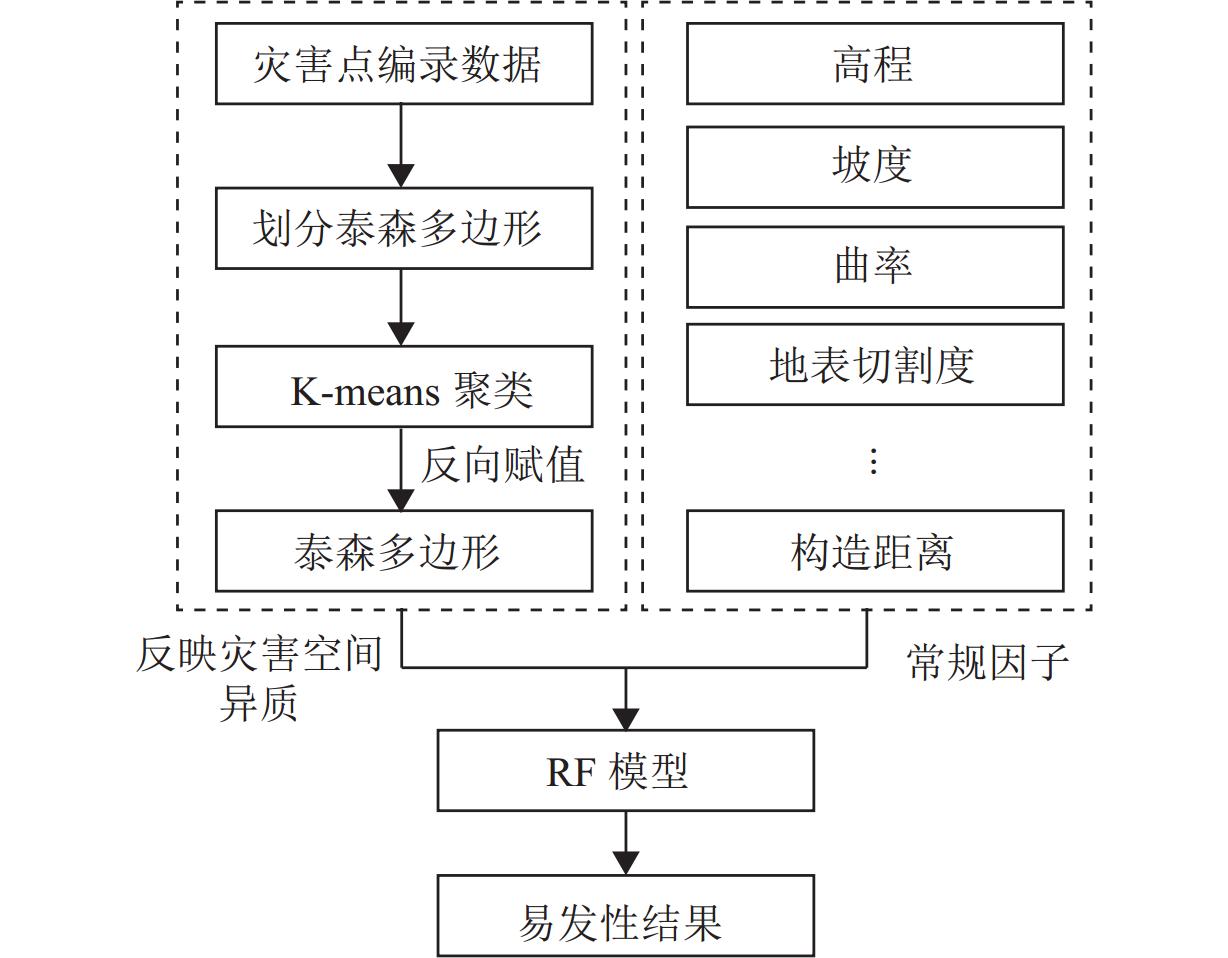
灾害易发性评估通常是基于灾害空间分布特征进行概率建模，然而灾害本身存在空间异质性. 本文以汶马高速汶川至理县段沿线崩滑灾害为例，为解决灾害的空间异质性问题，利用K-means算法将研究区灾害威胁对象（人员、财产）及危险程度（损毁房屋面积、损毁道路长度）进行空间聚类并赋予研究区不同聚类属性；从水文、地质、地貌条件等方面综合选取坡度、高程、坡向、曲率、地表切割度、河型弯曲系数、距构造带距离、岸坡坡体结构和地层岩性9个因子，将样本划分为70%的训练数据、30%的测试数据，对比K-RF模型与传统RF模型在易发性评估中的性能，以期为高速公路的运营安全及灾害防治提供理论支撑. 结果表明：K-RF模型极高易发区共包含82.95%灾害点，相较于单一RF模型取得了更好的评价结果（AUC值提高5.4%）；采用聚类的方法解决灾害空间异质性是可行的，但本文局限性在于未能从灾害本身反映灾害空间异质性，耦合模型结果本质上是易发性和易损性的综合反映.
- 崩滑灾害 /
- 机器学习 /
- 易发性 /
- 空间异质性
Abstract:
Hazard susceptibility assessment is generally a probabilistic modeling based on the spatial distribution characteristics of hazards, but the hazards have spatial heterogeneity. In order to solve the spatial heterogeneity of hazards, the collapses and landslides along the Wenchuan−Lixian section in the Wenchuan−Maerkang Expressway were studied. By using the K-means algorithm, the hazard-threaten objects (people and property) and risk degree (damaged house area and damaged road length) in the study area were spatially clustered, and different clustering attributes were assigned to the study area. Then, nine factors including slope angle, elevation, slope aspect, curvature, surface cutting degree, river curvature coefficient, distance from the tectonic zone, bank slope structure, and formation lithology were selected in terms of hydrology, geology, and geomorphic conditions. The samples were divided into 70% training data and 30% test data. The performance of the K-RF model and the traditional random forest (RF) model in susceptibility assessment was compared to provide theoretical support for operation safety and hazard prevention of expressways. The results show that the K-RF model contains a total of 82.95% of the hazard points in the areas with extremely high susceptibility, which has better assessment results than the single RF model (with AUC value increased by 5.4%). Therefore, it is feasible to use clustering to solve the spatial heterogeneity of hazards. However, the research limitation is that it fails to reflect the spatial heterogeneity of hazards from the hazard itself. The coupled model is a comprehensive reflection of susceptibility and vulnerability in essence.
- hazard /
- machine learning /
- susceptibility /
- spatial heterogeneity

HTML全文

信息技术的高速发展推动着便携式电子设备向低成本、小型化、高转换效率、长续航方向发展. 采用单电感双输出（single-inductor dual-output，SIDO）开关变换器作为供电电源，可以减少电感数量、降低其重量和体积、提高能量转换效率^[1-2]. 但SIDO开关变换器两输出支路共用一个电感传输能量，这导致其中某一支路工况的改变会影响另一支路，即存在交叉影响. 这种交叉影响是评估SIDO开关变换器稳态和瞬态性能的重要指标. 因此，抑制交叉影响已成为研究SIDO开关变换器的热点问题^[3-5].

SIDO开关变换器工作在连续导电模式（continuous conduction mode，CCM）时，变换器效率高、工作范围大，输出电压及电感电流纹波小，但是输出支路间存在严重的交叉影响^[6-7]. 根据变换器在一个工作周期中电感电流能量转换的次数，SIDO变换器分为共享充放和独立充放2种工作时序. 在共享充放时序时，在一个开关周期内电感充电一次后逐一向各输出支路供能；而在独立充放时序时，在一个开关周期内每条输出支路导通期间，电感都要进行充电和放电. 相较于共享充放时序，SIDO开关变换器工作在独立充放时序时降低了电感电流纹波以及输出电压纹波，且减小了两输出支路间的耦合，进而抑制交叉影响，提高瞬态响应性能^[8-10].

文献[11]研究了CCM SIDO buck变换器电容电流纹波控制技术，有效降低输出支路间的交叉影响，大幅度提高变换器的瞬态响应性能，但这种控制方法的负载范围有限. 文献[12]采用模型预测电压型控制方法，通过计算在交叉影响最小时各开关管的所有可能占空比，让变换器工作在上述情况下，以此抑制输出支路间的交叉影响，但该方法计算量较大. 文献[13]提出一种共享充放时序恒定谷值电流型变频控制SIDO变换器，虽然有效抑制了输出支路间的交叉影响，但电感电流纹波较大，且控制电路不能适用于输入输出电压宽范围变化. 文献[14]建立了共模-差模电压型控制SIDO开关变换器的控制环路小信号模型，根据交叉影响阻抗传递函数的Bode图，分析变换器在不同输出电压等级下两输出支路的交叉影响特性. 文献[15]研究了电容电流-电容电压纹波控制SIDO开关变换器，在提高变换器的瞬态响应性能、减小输出支路间交叉影响的同时，增大负载稳定工作范围，并利用Bode图分析变换器在不同负载电流下两输出支路的交叉影响特性. 文献[14-15]只单独讨论了不同输出电压等级或负载电流时输出支路间的交叉影响特性，并没有综合论述上述2个因素与变换器交叉影响特性间的关系. 实际中，分析不同输出电压、负载下输出支路间的交叉影响，得到的结论对输出支路采用重载、轻载、高压或低压输出的选择具有指导意义.

为改善CCM SIDO开关变换器工作性能，本文提出独立充放时序CCM SIDO buck变换器电流型变频控制（current mode variable frequency control，C-VF）技术，详细分析其控制原理、工作时序及系统频率，构建频域小信号模型，解得控制环路交叉影响阻抗、输出阻抗传递函数，分析不同输出电压、负载条件时输出支路间的交叉影响，最后通过仿真和实验证明了上述结论的准确性.

1. 工作原理

图1为独立充放时序C-VF CCM SIDO buck变换器主功率电路和控制环路原理. 主功率电路由输入电压V_in、主开关管S₁、二极管VD、电感L和输出支路a、b组成；输出支路a由支路开关管S_a、负载R_a、输出滤波电容C_oa及其等效串联电阻R_ca组成；输出支路b由支路开关管S_b、负载R_b、输出滤波电容C_ob及其等效串联电阻R_cb组成. 控制环路由误差放大器EA₁、EA₂，比较器CMP₁～CMP₃，与门AND₁、AND₂，或门OR，触发器RS、D及非门NOT组成. 图中：控制脉冲信号P_WM1、P_WMa、P_WMb分别为控制S₁、S_a、S_b导通与关断的开关，V_oa、V_ob分别为支路a、b的输出电压，V_ca、V_cb分别为滤波电容C_oa、C_ob的两端电压，V_refa、V_refb分别为支路a、b输出电压参考信号，i_V为谷值电流参考信号，i_L为电感电流信号，I_ref1、I_ref2为电感电流参考信号，V_c1、V_c2、V_c3（V_a1、V_a2、V_R）为比较器电路（逻辑门电路）输出的控制信号.

图 1 独立式充放时序C-VF CCM SIDO buck变换器

Figure 1. C-VF CCM SIDO buck converter with independent charge and discharge sequence

下载: 全尺寸图片幻灯片

独立充放时序C-VF CCM SIDO buck变换器的工作时序见图2. 图中：d₁、d₂分别为主开关在支路a、b工作时的导通占空比，d_a、d_b分别为支路a、b开关管导通占空比，T为开关周期，f_s为开关频率，t为时间.

图 2 工作时序

Figure 2. Working sequence

下载: 全尺寸图片幻灯片

电感电流信号i_L和谷值电流参考信号i_V经比较器CMP₁后，输出信号V_c1，进而使能D触发器，产生输出支路开关管S_a、S_b的控制脉冲P_WMa、P_WMb，使两输出支路在一个周期内互补导通. 以支路a工作期间为例，对主开关管S₁的工作原理进行描述：支路a刚开始导通时，i_L=i_V，比较器CMP₁输出信号V_c1为高电平，使得触发器RS的Q端输出信号P_WM1为高电平，主开关管S₁导通，i_L以斜率(V_in–V_oa)/L上升；当i_L上升到控制信号I_ref1时，使得触发器RS的Q端输出信号P_WM1为低电平，此时，主开关管S₁关断，支路开关管S_a仍然导通，电感电流以斜率 –V_oa/L下降至谷值电流i_V时，比较器CMP₁输出信号V_c1为高电平，触发器D的输出端Q输出高电平，支路开关管S_a关断、S_b导通. 支路b导通期间，主开关管S₁的控制信号P_WM1的产生过程与支路a导通期间相似.

2. 独立充放时序CCM SIDO buck变换器小信号建模与频域特性分析

2.1 主功率电路小信号建模

根据时间平均等效原理，将二极管VD和支路b开关管S_b分别由受控电压 $\hat{v}_{{\rm{D}}}(s)$ 和 $\hat{v}_{\mathrm{Sb}}(s)$ 替换，s为拉氏变换复变量；主开关管S₁和支路a开关管S_a由受控电流源 $\hat{i}_{{\rm{S}}1}(s)$ 和 $\hat{i}_{\mathrm{Sa}}(s)$ 分别替换，可得到独立充放时序CCM SIDO buck变换器的小信号等效电路，如所示. 图中： $\hat{{i}}_{\mathrm{L}}(s)$ 为电感电流i_L的小信号扰动， $\hat{v}_{\text {in }}(s)$ 为输入电压V_in的小信号扰动， ${\hat v_{{\text{oa}}}}(s)$ 、 ${\hat v_{{\text{ob}}}}(s)$ 分别为输出支路两端电压V_oa、V_ob的小信号扰动， $\hat{v}_{\mathrm{ca}}(s)$ 、 $\hat{v}_{{\rm{cb}}}(s)$ 分别为滤波电容两端电压V_ca、V_cb的小信号扰动. 图3中受控源的小信号表达式分别为

图 3 独立充放时序CCM SIDO buck变换器小信号等效电路

Figure 3. Small signal equivalent circuit of CCM SIDO buck converter with independent charge and discharge sequence

下载: 全尺寸图片幻灯片

$\left\{ \begin{array}{*{35}{l}} {{{\hat{i}}}_{\text{S1}}}(s)=\left( {{D}_{\text{1}}} + {{D}_{\text{2}}} \right){{{\hat{i}}}_{\text{L}}}(s) + {{I}_{\text{L}}}\left( {{{\hat{d}}}_{\text{1}}}(s) + {{{\hat{d}}}_{\text{2}}}(s) \right), \\ {{{\hat{i}}}_{\text{Sa}}}(s)={{D}_{\text{a}}}{{{\hat{i}}}_{\text{L}}}(s) + {{I}_{\text{L}}}{{{\hat{d}}}_{\text{a}}}(s), \\ {{{\hat{v}}}_{\text{D}}}(s)=\left( {{D}_{1}} + {{D}_{2}} \right){{{\hat{v}}}_{\text{in}}}(s) + {{V}_{\text{in}}}\left( {{{\hat{d}}}_{1}}(s) + {{{\hat{d}}}_{2}}(s) \right) ,\\ {{{\hat{v}}}_{\text{Sb}}}(s)={{D}_{\text{a}}}\left( {{{\hat{v}}}_{\text{cb}}}(s)-{{{\hat{v}}}_{\text{ca}}}(s) \right) + \left( {{V}_{\text{cb}}}-{{V}_{\text{ca}}} \right){{{\hat{d}}}_{\text{a}}(s)}, \end{array} \right.$

(1)

式中：D₁和D₂分别为主开关管在输出支路a、b导通期间的占空比，D_a为输出支路a导通占空比，I_L为电感电流平均值， $\hat d_1(s)$ 、 $\hat d_2(s)$ 、 $\hat d_{\rm{a}}(s)$ 分别为d₁、d₂、d_a的小信号扰动.

根据基尔霍夫电压定律（KCL）和基尔霍夫电流定律（KVL），由图3可以得到

$\left\{ {\begin{array}{*{20}{l}} {{{\hat i}_{\text{L}}}(s) = {{\hat v}_{{\text{oa}}}}(s)/{R_{{\text{eqa}}}}(s) + {{\hat v}_{{\text{ob}}}}(s)/{R_{{\text{eqb}}}}(s)}， \\ {{{\hat v}_{\text{D}}}(s) = sL{{\hat {i}}_{\text{L}}}(s) + {{\hat v}_{{\text{oa}}}}(s) - {{\hat v}_{{\text{Sb}}}}(s)} ， \end{array}} \right.$

(2)

式中：R_eqa(s) = R_a∥(R_ca + 1/(sC_oa))，R_eqb(s) = R_b∥(R_cb + 1/(sC_ob)).

求解式（2），可得CCM SIDO buck变换器输出支路a的控制-输出传递函数 $G_{\mathrm{ad1}}(s)$ 、 $G_{\mathrm{ad2}}(s)$ 、 $G_{\mathrm{ada}}(s)$ ，输出支路b的控制-输出传递函数 $G_{\mathrm{bd1}}(s)$ 、 $G_{\mathrm{bd2}}(s)$ 、 $G_{\mathrm{bda}}(s)$ 及控制-电感电流传递函数 $G_{\mathrm{Ld1}}(s)$ 、 $G_{\mathrm{Ld2}}(s)$ 、 $G_{\mathrm{Lda}}(s)$ ，支路a、b的输入电压-输出电压传递函数 $G_{\mathrm{avin}}(s)$ 、 $G_{\mathrm{bvin}}(s)$ 及输入电压-电感电流传递函数 $G_{\mathrm{Lvin}}(s)$ ，支路a、b的输出阻抗 $Z_{\mathrm{aa}}(s)$ 、 $Z_{\mathrm{bb}}(s)$ 及交叉影响阻抗 $Z_{\mathrm{ab}}(s)$ 、 $Z_{\mathrm{ba}}(s)$ 和输出-电感电流传递函数 $G_{\mathrm{La}}(s)$ 、 $G_{\mathrm{Lb}}(s)$ . 上述各传递函数表达式见附加材料A.

输入交流小信号包括控制信号扰动量 $\hat{d}_{1}(s)$ 、 $\hat{d}_{2}(s)$ 、 $\hat{d}_{\mathrm{a}}(s)$ 、输入电压扰动量 $\hat{v}_{\text {in }}(s)$ 和负载电流扰动量 $\hat{i}_{\mathrm{oa}}(s)$ 、 $\hat{{i}}_{\mathrm{ob}}(s)$ ，可以得到支路a、b输出电压小信号扰动量 $\hat{v}_{\mathrm{oa}}(s)$ 、 $\hat{v}_{{\rm{ob}}}(s)$ 以及电感电流小信号扰动量 $\hat{{i}}_{\mathrm{L}}(s)$ ，分别如式（3）～（5）所示.

$\begin{split} & {{{\hat{v}}}_{\text{oa}}}(s)={{G}_{\text{avin}}}(s){{{\hat{v}}}_{\text{in}}}(s) + {{G}_{\text{ad1}}}(s){{{\hat{d}}}_{1}}(s) + {{G}_{\text{ad2}}}(s){{{\hat{d}}}_{2}}(s)+ \\ &\quad {{G}_{\text{ada}}}(s){{{\hat{d}}}_{\text{a}}}(s) + {{Z}_{\text{aa}}}(s){{{\hat{i}}}_{\text{oa}}}(s) + {{Z}_{\text{ab}}}(s){{{\hat{i}}}_{\text{ob}}}(s), \end{split}$

(3)

$\begin{split} & {{{\hat{v}}}_{\text{ob}}}(s)={{G}_{\text{bvin}}}(s){{{\hat{v}}}_{\text{in}}}(s) + {{G}_{\text{bd1}}}(s){{{\hat{d}}}_{1}}(s) + {{G}_{\text{bd2}}}(s){{{\hat{d}}}_{2}}(s)+ \\ &\quad {{G}_{\text{bda}}}(s){{{\hat{d}}}_{\text{a}}}(s) + {{Z}_{\text{ba}}}(s){{{\hat{i}}}_{\text{oa}}}(s) + {{Z}_{\text{bb}}}(s){{{\hat{i}}}_{\text{ob}}}(s), \end{split}$

(4)

$\begin{split} & {{{\hat{i}}}_{\text{L}}}(s)={{G}_{\text{Lvin}}}(s){{{\hat{v}}}_{\text{in}}}(s) + {{G}_{\text{Ld1}}}(s){{{\hat{d}}}_{1}}(s) + {{G}_{\text{Ld2}}}(s){{{\hat{d}}}_{2}}(s)+ \\ &\quad {{G}_{\text{Lda}}}(s){{{\hat{d}}}_{\text{a}}}(s) + {{G}_{\text{La}}}(s){{{\hat{i}}}_{\text{oa}}}(s) + {{G}_{\text{Lb}}}(s){{{\hat{i}}}_{\text{ob}}}(s). \end{split}$

(5)

2.2 C-VF小信号模型

本文提出的独立充放时序C-VF CCM SIDO buck变换器的电感电流在一个开关周期内的波形如图4所示. 图中：m_a1（m_a2）、m_b1（m_b2）分别为输出支路a、b工作时电感电流的上升（下降）斜率.

图 4 独立充放时序C-VF变换器电感电流波形

Figure 4. Inductor current waveforms of C-VF converter with independent charge and discharge sequence

下载: 全尺寸图片幻灯片

由图4电感电流波形的几何关系，可得控制电流i_ref1、i_ref2以及电感电流平均值 $\bar i_{\rm{L}}$ 分别为

${{i}_{\text{ref}1}}={{i}_{\text{V}}} + {{m}_{\text{a}1}}{{D}_{1}}T,$

(6)

${{i}_{\text{ref2}}}={{i}_{\text{ref1}}} + {{m}_{\text{a2}}}\left( {{D}_{\text{a}}}-{{D}_{1}} \right)T + {{m}_{\text{b}1}}{{D}_{2}}T,$

(7)

$\begin{split} & {{{\bar{i}}}_{\text{L}}}=\frac{1}{2}\left( {{i}_{\text{V}}} + {{i}_{\text{ref}1}} \right){{D}_{\text{a}}} + \frac{1}{2}\left( {{i}_{\text{V}}} + {{i}_{\text{ref2}}} \right){{D}_{2}} +\\ &\quad \left( 1-{{D}_{\text{a}}}-{{D}_{2}} \right){{i}_{\text{ref}2}} + \frac{1}{2}{{\left( 1-{{D}_{\text{a}}}-{{D}_{2}} \right)}^{2}}{{m}_{\text{b}2}}T, \end{split}$

(8)

式中：m_a1 = (V_in–V_oa)/L，m_b1 = (V_in–V_ob)/L，m_a2 = –V_oa/L，m_b2 = –V_ob/L.

对式（6）～（8）变量分离扰动，忽略直流量和高阶扰动量，整理可得电感电流参考值 ${{{\hat{i}}}_{\text{ref1}}}(s)、{{{\hat{i}}}_{\text{ref2}}}(s)$ 及电感电流小信号扰动量 ${{{\hat{i}}}_{\text{L}}}(s)$ 分别为

$\begin{split} & {{{\hat{i}}}_{\text{ref}1}}(s)={{G}_{11}}{{{\hat{i}}}_{\text{v}}}(s) + {{G}_{12}}{{{\hat{v}}}_{\text{in}}}(s) \;+ \\ &\quad {{G}_{13}}{{{\hat{v}}}_{\text{oa}}}(s) + {{G}_{14}}{{{\hat{d}}}_{1}}(s), \end{split}$

(9)

$\begin{split} & {{{\hat{i}}}_{\text{ref2}}}(s)={{G}_{21}}{{{\hat{i}}}_{\text{ref}1}}(s) + {{G}_{22}}{{{\hat{v}}}_{\text{in}}}(s) \;+ \\ &\quad {{G}_{23}}{{{\hat{v}}}_{\text{oa}}}(s) + {{G}_{24}}{{{\hat{v}}}_{\text{ob}}}(s) + {{G}_{25}}{{{\hat{d}}}_{1}}(s)\;+ \\ &\quad {{G}_{26}}{{{\hat{d}}}_{2}}(s) + {{G}_{27}}{{{\hat{d}}}_{\text{a}}}(s) , \end{split}$

(10)

$\begin{split} & {{{\hat{i}}}_{\text{L}}}(s)={{G}_{31}}{{{\hat{i}}}_{\text{v}}}(s) + {{G}_{32}}{{{\hat{i}}}_{\text{ref}1}}(s) + {{G}_{33}}{{{\hat{i}}}_{\text{ref2}}}(s)\;+ \\ &\quad {{G}_{34}}{{{\hat{v}}}_{\text{ob}}}(s) + {{G}_{35}}{{{\hat{d}}}_{2}}(s) + {{G}_{36}}{{{\hat{d}}}_{\text{a}}}(s), \end{split}$

(11)

式中：G₁₁～G₁₄、G₂₁～G₂₇、G₃₁～G₃₆见附加材料B.

根据式（9）～（11）建立C-VF CCM SIDO buck变换器工作时主开关管及支路开关管小信号模型，如所示. 图中： $H_{\mathrm{va}}(s)$ 、 $H_{\text {vb }}(s)$ 分别为输出支路a、b的采样比例系数； $\hat v_{\rm{refa}}{(s)}$ 、 $\hat v_{\rm{refb}}{(s)}$ 分别为输出支路a、b的参考电压； $G_{\mathrm{PIa}}(s)$ 、 $G_{\mathrm{PIb}}(s)$ 分别为输出支路a、b的比例积分控制器传递函数；F₁₁～F₁₄、F₂₁～F₂₇分别为输出支路a、b的闭环输出阻抗；F_a1～F_a6为交叉影响阻抗传递函数，见附加材料C. 由于支路b导通期间电感电流平均值与支路a导通期间不同，故支路b导通期间主开关管占空比小信号扰动 $\hat{d}_{2}(s)$ 的表达式更为复杂；两支路开关管互补导通，所以两支路开关管占空比扰动与各输入信号扰动量的关系通过一个表达式即可完整描述.

图 5 独立充放时序C-VF小信号模型

Figure 5. Small signal model of C-VF with independent charge and discharge sequence

下载: 全尺寸图片幻灯片

2.3 开关频率与主电路参数的关系

独立充放时序C-VF CCM SIDO buck变换器的开关频率随着主电路参数的变化而变化. 为合理选取谷值电流参考值以及变换器元器件参数，确定开关频率和电路各元件参数的关系具有重要意义.

记V_S为电感两端电压瞬时值，I_S为流过电感的电流瞬时值，I_oa、I_ob分别为输出支路a、b的输出电流平均值，忽略电路中的功率损耗，由功率守恒得

$\frac{1}{T}\left( \int_{0}^{{{D}_{1}}T}{{{V}_{\text{s}}}{{I}_{\text{s}}}{\rm{d}}t + \int_{{{D}_{\text{a}}}T}^{\left( {{D}_{\text{a}}} + {{D}_{2}} \right)T}{{{V}_{\text{s}}}{{I}_{\text{s}}}{\rm{d}}t}} \right)={{V}_{\text{oa}}}{{I}_{\text{oa}}} + {{V}_{\text{ob}}}{{I}_{\text{ob}}},$

(12)

式中：I_oa = V_oa/R_oa，I_ob = V_ob/R_ob，R_oa、R_ob分别为输出支路a、b负载.

由式（12）可求得

${{f}_{\text{s}}}=\frac{{{V}_{\text{in}}}\left[ {{D}_{1}^{2}}\left( {{V}_{\text{in}}}-{{V}_{\text{oa}}} \right) + {{D}_{2}^{2}}\left( {{V}_{\text{in}}}-{{V}_{\text{ob}}} \right) \right]}{2L\left[ {{V}_{\text{oa}}}{{I}_{\text{oa}}} + {{V}_{\text{ob}}}{{I}_{\text{ob}}}-\left( {{D}_{1}} + {{D}_{2}} \right){{i}_{\text{V}}}{{V}_{\text{in}}} \right]}.$

(13)

因此，可以通过式（13）选定开关频率，进行主电路元器件的选型及谷值电流参考值的选取.

为更直观地展示开关频率和谷值电流参考值间的关系，根据表1所示主电路参数，绘制f_s与i_V的曲线，如图6所示. 由图可知，f_s随着i_V的增大而增大. 因此，可以通过选定开关频率，来选取合适的谷值电流参考值，最后进行主电路元器件的选型.

表 1 独立充放时序C-VF CCM SIDO buck变换器电路参数表

Table 1. Circuit parameters of C-VF CCM SIDO buck converter with independent charge and discharge sequence

参数	取值	参数	取值
V_in/V	20	I_oa/A	1
L/μH	22	I_ob/A	1
V_oa/V	12	C_oa/μF	470
V_ob/V	5	C_ob/μF	470

下载: 导出CSV

| 显示表格

图 6 开关频率与谷值电流参考值的关系

Figure 6. Relationship between switching frequency and valley current reference value

下载: 全尺寸图片幻灯片

2.4 交叉影响特性频域分析

由图5建立的独立充放时序C-VF CCM SIDO buck变换器控制环路小信号模型，通过两支路不同负载电压、输出电流情况下交叉影响传递函数的Bode图，对比分析该控制方法下两输出支路的交叉影响特性.

图7（a）是在两支路输出电压不同、负载不等时控制环路交叉影响传递函数的Bode图. 当V_oa = 12 V，V_ob = 5 V时，支路a在轻载工况下对支路b的交叉影响阻抗低频增益低于其在重载工况下；支路b在轻载工况下对支路a的交叉影响阻抗低频增益低于其在重载工况下. 图7（b）是在两输出支路负载电压相等、负载不同时控制环路交叉影响传递函数的Bode图. 当V_oa = V_ob = 5 V时，支路b在重载工况下对支路a的交叉影响阻抗低频增益低于支路a对支路b；支路a在重载工况下对支路b的交叉影响阻抗低频增益低于支路b对支路a.

图 7 负载不同时的闭环交叉影响阻抗Bode图

Figure 7. Bode diagrams of closed-loop cross-regulation impedance with different loads

下载: 全尺寸图片幻灯片

传递函数幅频曲线低频增益值大小反映交叉影响大小，低频增益越小，交叉影响越小^[16]. 根据上述分析可以得到以下结论：1）当两支路负载电压不等时，减轻某一支路负载电流可以降低该支路对另一支路的交叉影响； 2）当两支路负载电压相同但负载不同时，重载支路对轻载支路的交叉影响更小.

3. 实验验证

3.1 实验验证

采用表1的电路参数搭建独立充放时序C-VF CCM SIDO buck变换器实验装置（图8）进行验证. 图8（a）中，电流采样电路采用LM7171运放芯片，主电路中采用LM5101A栅极驱动芯片、IRF3205 MOSFET开关管、RB081L肖特基二极管；图8（b）中控制电路使用OPA2330双路运算放大器搭建误差放大器，采用LM319双路电压比较器芯片搭建比较电路，由SN74系列与门、或门、或非门和D触发器搭建控制逻辑电路.

图 8 独立充放时序C-VF CCM SIDO buck变换器实验装置

Figure 8. Experimental device of C-VF CCM SIDO buck converter with independent charge and discharge sequence

下载: 全尺寸图片幻灯片

图9（a）、（b）分别为谷值参考电流i_V= 0.5 A和i_V= 1.1 A时独立充放时序C-VF CCM SIDO buck变换器的电感电流i_L、输入电压V_in、输出电压V_oa和V_ob的稳态实验波形. 由图9可知：当谷值电流参考值i_V = 0.5 A时，变换器开关周期T = 32.3 μs，开关频率f_s = 31.0 kHz；当谷值电流参考值i_V = 1.1 A时，变换器开关周期T = 18.1 μs，开关频率f_s = 55.1 kHz. 这分别与理论计算出的32.1 kHz和52.5 kHz基本一致，验证了理论分析的正确性.

图 9 i_V= 0.5, 1.1 A时稳态实验波形

Figure 9. Steady-state experimental waveforms with i_V = 0.5, 1.1 A

下载: 全尺寸图片幻灯片

i_V= 0.8 A，V_oa= 12 V，V_ob= 5 V，i_ob= 1.0 A，输出支路a负载跳变时，i_oa、V_in、V_oa、V_ob的直流波形和纹波波形如图10所示. 由图可知：支路a负载从1.0 A→1.5 A跳变时，V_oa、V_ob分别经过约0.186、0.098 ms的调节时间后重新进入稳态，V_ob在调节过程中的交叉影响为106 mV；在支路a负载从1.5 A→2.0 A跳变时，V_oa、V_ob分别经过约0.257、0.109 ms的调节时间后重新进入稳态，V_ob在调节过程中的交叉影响为120 mV.

图 10 负载不同、负载电压不等时i_oa跳变的瞬态实验波形

Figure 10. Transient experimental waveforms with sudden variation of i_oa under different loads and unequal load voltages

下载: 全尺寸图片幻灯片

图11为i_V = 0.8 A，V_oa = 12 V，V_ob = 5 V，i_oa = 1.0 A，输出支路b负载跳变时，i_ob、V_in、V_oa、V_ob的直流波形和纹波波形. 由图11可知：在支路b负载从1.0 A→1.5 A跳变时，V_oa和V_ob分别经过约0.165 ms和0.102 ms的调节时间后重新进入稳态，V_oa在调节过程中的交叉影响为104 mV；在支路b负载从1.5 A→2.0 A跳变时，V_oa和V_ob分别经过约0.121 ms和0.214 ms的调节时间后重新进入稳态，V_oa在调节过程中的交叉影响为120 mV.

图 11 负载不同、负载电压不等时i_ob跳变的瞬态实验波形

Figure 11. Transient experimental waveforms with sudden sudden variation of i_ob with different loads and unequal load voltages

下载: 全尺寸图片幻灯片

图12为i_V= 0.8 A，V_oa= V_ob= 5 V，支路a、b负载跳变时，i_oa、i_ob、V_in、V_oa、V_ob的直流波形和纹波波形. 由图12（a）、（b）可知：在支路a负载电流从1.0 A→1.5 A跳变时，V_oa和V_ob分别经过约0.199 ms和0.126 ms的调节时间后重新进入稳态，V_ob在调节过程中的交叉影响为190 mV；在支路b负载电流从1.5 A→2.0 A跳变时，V_oa和V_ob分别经过约0.147 ms和0.161 ms的调节时间后重新进入稳态，V_oa在调节过程中的交叉影响为112 mV. 由图12（c）、（d）可知：在支路a负载电流从1.5 A→2.0 A跳变时，V_oa和V_ob分别经过约0.169 ms和0.096 ms的调节时间后重新进入稳态，V_ob在调节过程中的交叉影响为101 mV；在支路b负载电流从1.0 A→1.5 A跳变时，V_oa和V_ob分别经过约0.178 ms和0.166 ms的调节时间后重新进入稳态，V_oa在调节过程中的交叉影响为203 mV.

图 12 负载不同、负载电压相等时负载跳变的瞬态实验波形

Figure 12. Transient experimental waveforms with sudden variation of loads under different loads and equal load voltages

下载: 全尺寸图片幻灯片

表2描述了C-VF CCM SIDO buck变换器在时域仿真中不同工况下两支路间的交叉影响. 交叉影响系数是量化SIDO变换器交叉影响特性的性能指标^[16]，支路b负载跳变对支路a的交叉影响系数为

表 2 不同工况下闭环交叉影响

Table 2. Closed-loop cross-regulation under different working conditions

输出电压/V	负载电流/A	负载跳变/A	F_a
V_oa=12，V_ob=5	i_oa=1.0，i_ob=1.0	i_oa：1.0→1.5	0.0424
	i_oa=1.5，i_ob=1.0	i_oa：1.5→2.0	0.0720
	i_oa=1.0，i_ob=1.0	i_ob：1.0→1.5	0.0173
	i_oa=1.0，i_ob=1.5	i_ob：1.5→2.0	0.0300
V_oa=5，V_ob=5	i_oa=1.0，i_ob=1.5	i_oa：1.0→1.5	0.0760
	i_oa=1.0，i_ob=1.5	i_ob：1.5→2.0	0.0672
	i_oa=1.5，i_ob=1.0	i_oa：1.5→2.0	0.0606
	i_oa=1.5，i_ob=1.0	i_ob： 1.0→1.5	0.0812

下载: 导出CSV

| 显示表格

${F_{\text{a}}}=\frac{\left| \vartriangle {{v}_{\text{oa}}} \right|/{{v}_{\text{oa}}}}{\left| \vartriangle {{i}_{\text{ob}}} \right|/{{i}_{\text{ob}}}},$

(14)

式中：Δv_oa、Δi_ob分别为支路a负载电压和支路b负载电流的变化量.

由图9～12可知：当负载跳变时，本文提出的独立充放时序C-VF CCM SIDO buck变换器具有更小的电感电流纹波，更小的交叉影响，更快的瞬态性能；在两输出支路电压不等时，减小某一输出支路负载能够减小该支路对另一输出支路的交叉影响；在两输出支路电压相同但负载不同时，重载输出支路对轻载输出支路的交叉影响小于轻载输出支路对重载输出支路的交叉影响. 图9～12验证了理论分析的正确性.

3.2 性能对比

为更好地说明独立充放时序C-VF CCM SIDO buck变换器电感电流纹波、交叉影响及瞬态响应性能的优势，将其与现有文献中的SIDO变换器进行性能对比，比较结果见表3. 由表3可知，本文所提出的独立充放电时序C-VF CCM SIDO buck变换器的电感电流纹波率最低，交叉影响系数最小，变换器瞬态响应最多仅需7.0T即可回到稳态，证明了独立充放电时序C-VF CCM SIDO buck变换器具有优异的工作性能.

表 3 不同SIDO变换器性能的对比

Table 3. Performance comparison of different SIDO converters

来源	工作模式	输入电压/V	输出电容/μF	输出电压/V	输出功率/W	电感/μH	开关频率/kHz	电感电流纹波率	交叉影响系数	负载瞬态响应
本文	CCM	20	470	12.0, 5.0	17.0	22	55.1	1.05	0.0128	7.0T
文献[12]	CCM	12	100	24.0, 15.0	19.5	20	68.0	1.48	0.0146	142.8T
文献[13]	CCM	12	470	24.0, 15.0	19.5	50	50.0	1.23	0.1240	215.0T
文献[14]	CCM	10	470	3.3, 5.0	16.1	100	50.0		0.0800	28.0T

下载: 导出CSV

| 显示表格

4. 结　论

本文提出一种适用于独立充放时序C-VF技术，详细描述了独立充放时序C-VF CCM SIDO buck变换器的工作原理，构建闭环小信号模型，得到交叉阻抗传递函数，并分析在不同工况下变换器的交叉影响特性. 研究结果表明：

1）相较于共享充放时序，独立充放时序C-VF CCM SIDO buck变换器解决了电路参数宽范围变化下控制电路不能正常工作的问题，具有更小的电感电流纹波，能更好地抑制输出支路间的交叉影响，提高了变换器的瞬态性能；

2）当两支路输出电压、负载电流不同时，减轻其中一条支路的负载电流可以降低该支路对另一支路的交叉影响；

3）当两支路输出电压相同但负载电流不同时，重载支路对轻载支路的交叉影响比轻载支路对重载支路的交叉影响更小.

备注：附加材料在西南交通大学学报官网或中国知网本文的详情页中获取.

图 1 K-RF建模流程

Figure 1. Flow chart of K-RF model

下载: 全尺寸图片幻灯片

图 2 研究区位置及灾害编录

Figure 2. Location of study area and hazard inventories

下载: 全尺寸图片幻灯片

图 3 影响因子

Figure 3. Influencing factors

下载: 全尺寸图片幻灯片

图 4 VIF检验结果

Figure 4. Results of VIF test

下载: 全尺寸图片幻灯片

图 5 模型聚类结果

Figure 5. Model clustering results

下载: 全尺寸图片幻灯片

图 6 ROC曲线对比

Figure 6. Comparison of ROC curves

下载: 全尺寸图片幻灯片

图 7 易发性统计结果

Figure 7. Statistics results of susceptibility

下载: 全尺寸图片幻灯片

图 8 K-RF模型易发性制图结果

Figure 8. Mapping results of susceptibility of K-RF model

下载: 全尺寸图片幻灯片

图 9 RF模型易发性制图结果

Figure 9. Mapping results of susceptibility of RF model

下载: 全尺寸图片幻灯片

表 1 聚类结果

Table 1. Clustering results

类别	灾害数量/处	平均威胁人员数量/人	平均威胁财产/万元	平均损毁房屋面积/m²	平均损毁道路长度/m
1	53	95	337.2	8.90	0
2	65	50	164.6	1.80	0
3	46	36	113.5	0.43	0
4	53	59	80.4	1.38	10.2

下载: 导出CSV

表 2 验证指标计算结果

Table 2. Calculation results of validation indicators

模型	P_re	A_cc	R	AUC
RF	0.681	0.730	0.746	0.848
K-RF	0.726	0.787	0.841	0.902

下载: 导出CSV

表 3 易发性分级统计结果

Table 3. Statistical results of susceptibility levels

模型	易发性等级	分区面积/km²	灾害点个数/个	研究区分级面积占比/%	灾害占比/%	频率比
K-RF	极高	35.70	180	10.24	82.95	8.10
	高	80.37	28	23.05	12.90	0.56
	中等	40.27	4	11.55	1.84	0.16
	低	82.50	3	23.66	1.38	0.06
	极低	109.90	2	31.52	0.92	0.03
RF	极高	31.50	156	9.03	71.89	7.96
	高	71.74	45	20.57	20.74	1.01
	中等	49.27	9	14.13	4.15	0.29
	低	90.30	5	25.90	2.30	0.09
	极低	105.90	2	30.37	0.92	0.03

下载: 导出CSV

参考文献(23)

[1]	FELL R, COROMINAS J, BONNARD C, et al. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning[J]. Engineering Geology, 2008, 102(3/4): 85-98.
[2]	NHU V H, HOANG N D, NGUYEN H, et al. Effectiveness assessment of Keras based deep learning with different robust optimization algorithms for shallow landslide susceptibility mapping at tropical area[J]. Catena, 2020, 188: 104458.1-104458.13.
[3]	李利峰,杨华,张娟,等. 基于人工神经网络的区域滑坡预测研究[J]. 气象与环境科学,2020,43(3): 65-70. LI Lifeng, YANG Hua, ZHANG Juan, et al. Research on regional landslide prediction based on artificial neural network[J]. Meteorological and Environmental Sciences, 2020, 43(3): 65-70.
[4]	常晁瑜,薄景山,李孝波,等. 地震黄土滑坡滑距预测的BP神经网络模型[J]. 地震工程学报,2020,42(6): 1609-1614. doi: 10.3969/j.issn.1000-0844.2020.06.1609 CHANG Chaoyu, BO Jingshan, LI Xiaobo, et al. A BP neural network model for forecasting sliding distance of seismic loess landslides[J]. China Earthquake Engineering Journal, 2020, 42(6): 1609-1614. doi: 10.3969/j.issn.1000-0844.2020.06.1609
[5]	许冲,徐锡伟. 逻辑回归模型在玉树地震滑坡危险性评价中的应用与检验[J]. 工程地质学报,2012,20(3): 326-333. doi: 10.3969/j.issn.1004-9665.2012.03.004 XU Chong, XU Xiwei. Logistic regression model and its validation for hazard mapping of landslides triggered by Yushu earthquake[J]. Journal of Engineering Geology, 2012, 20(3): 326-333. doi: 10.3969/j.issn.1004-9665.2012.03.004
[6]	吴博,赵法锁,贺子光,等. 基于BA-LSSVM模型的黄土滑坡致灾范围预测[J]. 中国地质灾害与防治学报,2020,31(5): 1-6. WU Bo, ZHAO Fasuo, HE Ziguang, et al. Prediction of the disaster area of loess landslide based on least square support vector machine optimized by bat algorithm[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(5): 1-6.
[7]	XI C J, HAN M, HU X W, et al. Effectiveness of Newmark-based sampling strategy for coseismic landslide susceptibility mapping using deep learning, support vector machine, and logistic regression[J]. Bulletin of Engineering Geology and the Environment, 2022, 81(5): 174-196. doi: 10.1007/s10064-022-02664-5
[8]	文海家,胡东萍,王桂林. 汶川县地震滑坡易发性LR与NN评价比较研究[J]. 土木工程学报,2014,47(增1): 17-23. WEN Haijia, HU Dongping, WANG Guilin. Comparative study on LR and NN evaluation of earthquake landslide susceptibility in Wenchuan County[J]. China Civil Engineering Journal, 2014, 47(S1): 17-23.
[9]	YAO X, THAM L G, DAI F C. Landslide susceptibility mapping based on Support Vector Machine: a case study on natural slopes of Hong Kong, China[J]. Geomorphology, 2008, 101(4): 572-582. doi: 10.1016/j.geomorph.2008.02.011
[10]	许冲,徐锡伟. 基于不同核函数的2010年玉树地震滑坡空间预测模型研究[J]. 地球物理学报,2012,55(9): 2994-3005. doi: 10.6038/j.issn.0001-5733.2012.09.018 XU Chong, XU Xiwei. The 2010 Yushu earthquake triggered landslides spatial prediction models based on several kernel function types[J]. Chinese Journal of Geophysics, 2012, 55(9): 2994-3005. doi: 10.6038/j.issn.0001-5733.2012.09.018
[11]	TRUONG X, MITAMURA M, KONO Y, et al. Enhancing prediction performance of landslide susceptibility model using hybrid machine learning approach of bagging ensemble and logistic model tree[J]. Applied Sciences, 2018, 8(7): 1046.1-1046.22.
[12]	BREIMAN L. Random forests[J]. Machine Learning, 2001, 45: 5-32. doi: 10.1023/A:1010933404324
[13]	FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. doi: 10.1006/jcss.1997.1504
[14]	FRIEDMAN J H. Greedy function approximation: a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. doi: 10.1214/aos/1013203450
[15]	WANG Y M, FENG L W, LI S J, et al. A hybrid model considering spatial heterogeneity for landslide susceptibility mapping in Zhejiang Province, China[J]. Catena, 2020, 188: 104425.1-104425.13.
[16]	DENG M, YANG W T, LIU Q L, et al. Heterogeneous space–time artificial neural networks for space–time series prediction[J]. Transactions in GIS, 2018, 22(1): 183-201. doi: 10.1111/tgis.12302
[17]	黄发明,殷坤龙,蒋水华,等. 基于聚类分析和支持向量机的滑坡易发性评价[J]. 岩石力学与工程学报,2018,37(1): 156-167. HUANG Faming, YIN Kunlong, JIANG Shuihua, et al. Landslide susceptibility assessment based on clustering analysis and support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 156-167.
[18]	兰恒星,伍法权,王思敬. 基于GIS的滑坡CF多元回归模型及其应用[J]. 山地学报,2002,20(6): 732-737. doi: 10.3969/j.issn.1008-2786.2002.06.015 LAN Hengxing, WU Faquan, WANG Sijing. GIS based landslide CF multi-variable regression model and its application[J]. Journal of Mountain Research, 2002, 20(6): 732-737. doi: 10.3969/j.issn.1008-2786.2002.06.015
[19]	陈晓利,冉洪流,祁生文. 1976年龙陵地震诱发滑坡的影响因子敏感性分析[J]. 北京大学学报(自然科学版),2009,45(1): 104-110. doi: 10.3321/j.issn:0479-8023.2009.01.016 CHEN Xiaoli, RAN Hongliu, QI Shengwen. Triggering factors susceptibility of earthquake-induced landslides in 1976 Longling earthquake[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2009, 45(1): 104-110. doi: 10.3321/j.issn:0479-8023.2009.01.016
[20]	许冲,戴福初,姚鑫,等. 基于GIS的汶川地震滑坡灾害影响因子确定性系数分析[J]. 岩石力学与工程学报,2010,29(增1): 2972-2981. XU Chong, DAI Fuchu, YAO Xin, et al. Analysis of deterministic coefficient of influencing factors of Wenchuan earthquake landslide disaster based on GIS[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2972-2981.
[21]	陈绪坚,陈清扬. 黄河下游河型转换及弯曲变化机理[J]. 泥沙研究,2013(1): 1-6. doi: 10.3969/j.issn.0468-155X.2013.01.001 CHEN Xujian, CHEN Qingyang. Theory of river pattern transformation and change of channel sinuosity ratio in Lower Yellow River[J]. Journal of Sediment Research, 2013(1): 1-6. doi: 10.3969/j.issn.0468-155X.2013.01.001
[22]	CHEN Z, LIANG S Y, KE Y T, et al. Landslide susceptibility assessment using different slope units based on the evidential belief function model[J]. Geocarto International, 2020, 35(15): 1641-1664. doi: 10.1080/10106049.2019.1582716
[23]	WEN H, WU X Y, LIAO X, et al. Application of machine learning methods for snow avalanche susceptibility mapping in the Parlung Tsangpo Catchment, southeastern Qinghai−Tibet Plateau[J]. Cold Regions Science and Technology, 2022, 198: 103535.1-103535.12.

施引文献

附加材料(0)

访问统计

点击查看大图

图(9) / 表(3)

计量

文章访问数: 287
HTML全文浏览量: 116
PDF下载量: 57
被引次数: 0

1. 工作原理
2. 独立充放时序CCM SIDO buck变换器小信号建模与频域特性分析
2.1 主功率电路小信号建模
2.2 C-VF小信号模型
2.3 开关频率与主电路参数的关系
2.4 交叉影响特性频域分析
3. 实验验证
3.1 实验验证
3.2 性能对比
4. 结　论

基于聚类和随机森林耦合模型的崩滑灾害易发性评估

doi: 10.3969/j.issn.0258-2724.20220864

作者简介: 杜映锦（1979—），男，博士研究生，研究方向为地质灾害及防治工程，E-mail：dyj@swjtu.cn

通讯作者: 胡卸文（1963—），男，教授，博士，研究方向为工程地质、环境地质，E-mail：huxiewen@163.com

计量

出版历程

Susceptibility Assessment of Collapses and Landslides Based on Cluster and Random Forest Coupled Model

1. 工作原理

2. 独立充放时序CCM SIDO buck变换器小信号建模与频域特性分析

2.1 主功率电路小信号建模

2.2 C-VF小信号模型

2.3 开关频率与主电路参数的关系

2.4 交叉影响特性频域分析

3. 实验验证

3.1 实验验证

3.2 性能对比

4. 结 论

计量

出版历程

目录

1. 工作原理

2. 独立充放时序CCM SIDO buck变换器小信号建模与频域特性分析

2.1 主功率电路小信号建模

2.2 C-VF小信号模型

2.3 开关频率与主电路参数的关系

2.4 交叉影响特性频域分析

3. 实验验证

3.1 实验验证

3.2 性能对比

4. 结 论

作者简介:
杜映锦（1979—），男，博士研究生，研究方向为地质灾害及防治工程，E-mail：dyj@swjtu.cn

通讯作者:
胡卸文（1963—），男，教授，博士，研究方向为工程地质、环境地质，E-mail：huxiewen@163.com

4. 结　论

4. 结　论