超高速永磁电动悬浮系统性能优化

胡永攀; 曾杰伟; 王志强; 龙志强

doi:10.3969/j.issn.0258-2724.20220856

超高速永磁电动悬浮系统性能优化

doi: 10.3969/j.issn.0258-2724.20220856

胡永攀^{1, 2,},
曾杰伟¹,
王志强¹,
龙志强^1, ,

1.
国防科技大学智能科学学院，湖南长沙 410073
2.
同济大学国家磁浮交通工程技术研究中心，上海 201804

基金项目: 国家自然科学基金（52232013）

详细信息

作者简介:
胡永攀（1988—），男，博士研究生，研究方向为电磁悬浮与推进技术，E-mail：18745953753@139.com

通讯作者:
龙志强（1967—），男，教授，博士，研究方向为电磁悬浮与推进控制、智能诊断与容错控制、智能系统安全控制，E-mail：zhqlong@nudt.edu.cn

中图分类号: TP273
计量
- 文章访问数: 280
- HTML全文浏览量: 137
- PDF下载量: 36
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-11
- 修回日期: 2023-05-25
- 网络出版日期: 2023-06-15
- 刊出日期: 2023-07-06

Performance Optimization of Ultra-High Speed Permanent Magnet Electrodynamic Suspension System

1.
College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China
2.
National Maglev Transportation Engineering R & D Center, Tongji University, Shanghai 201804, China

摘要

摘要:
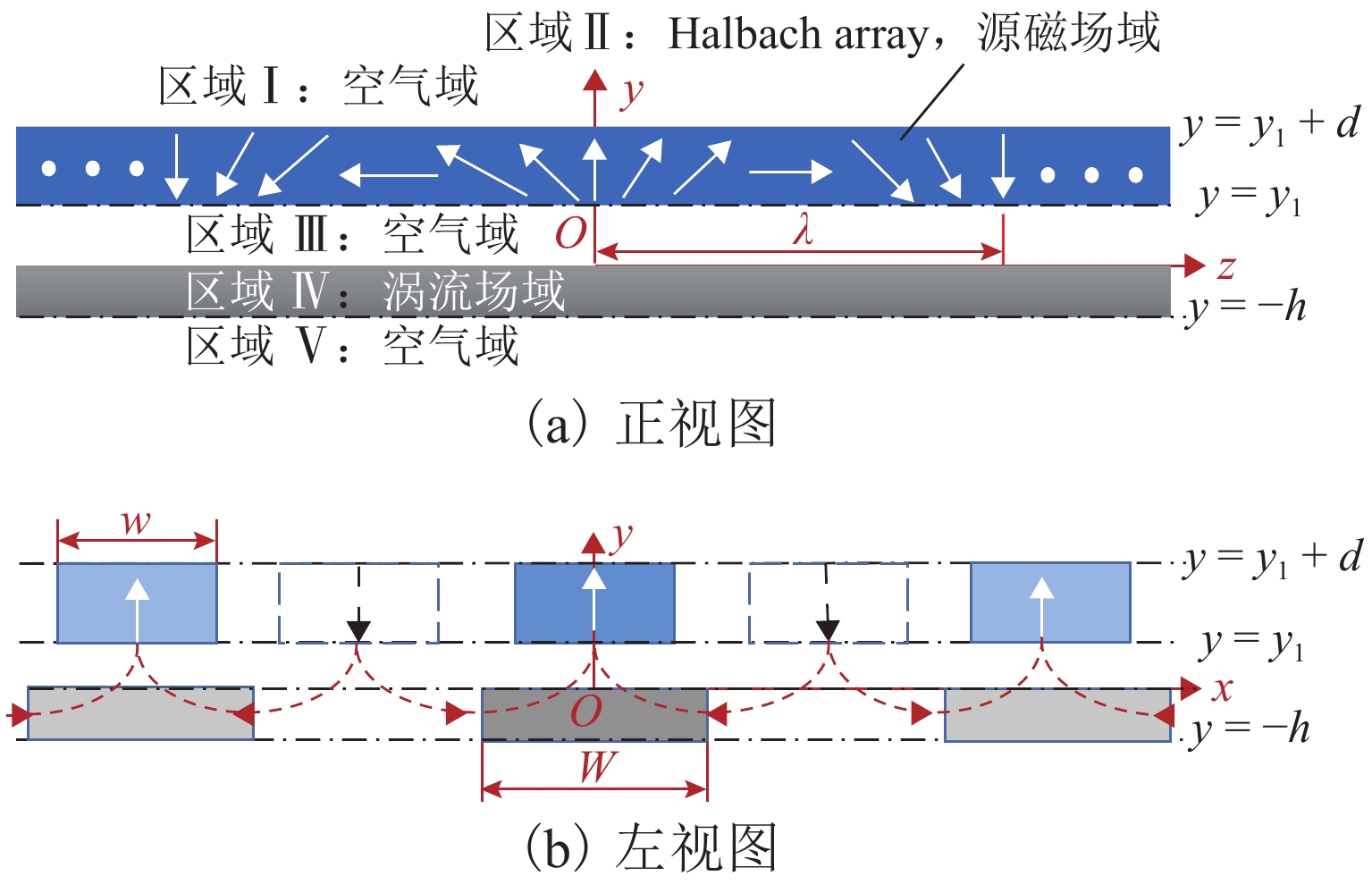
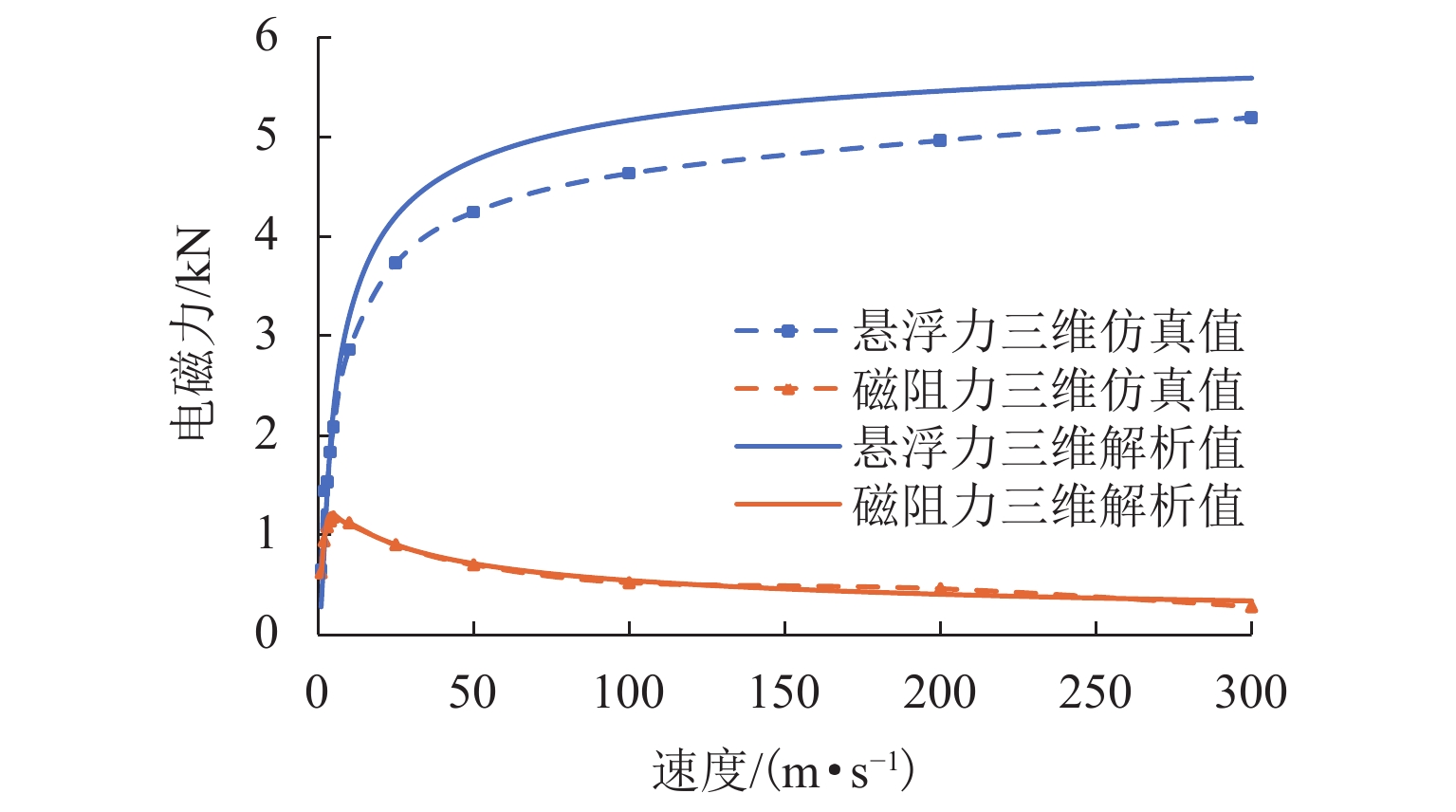
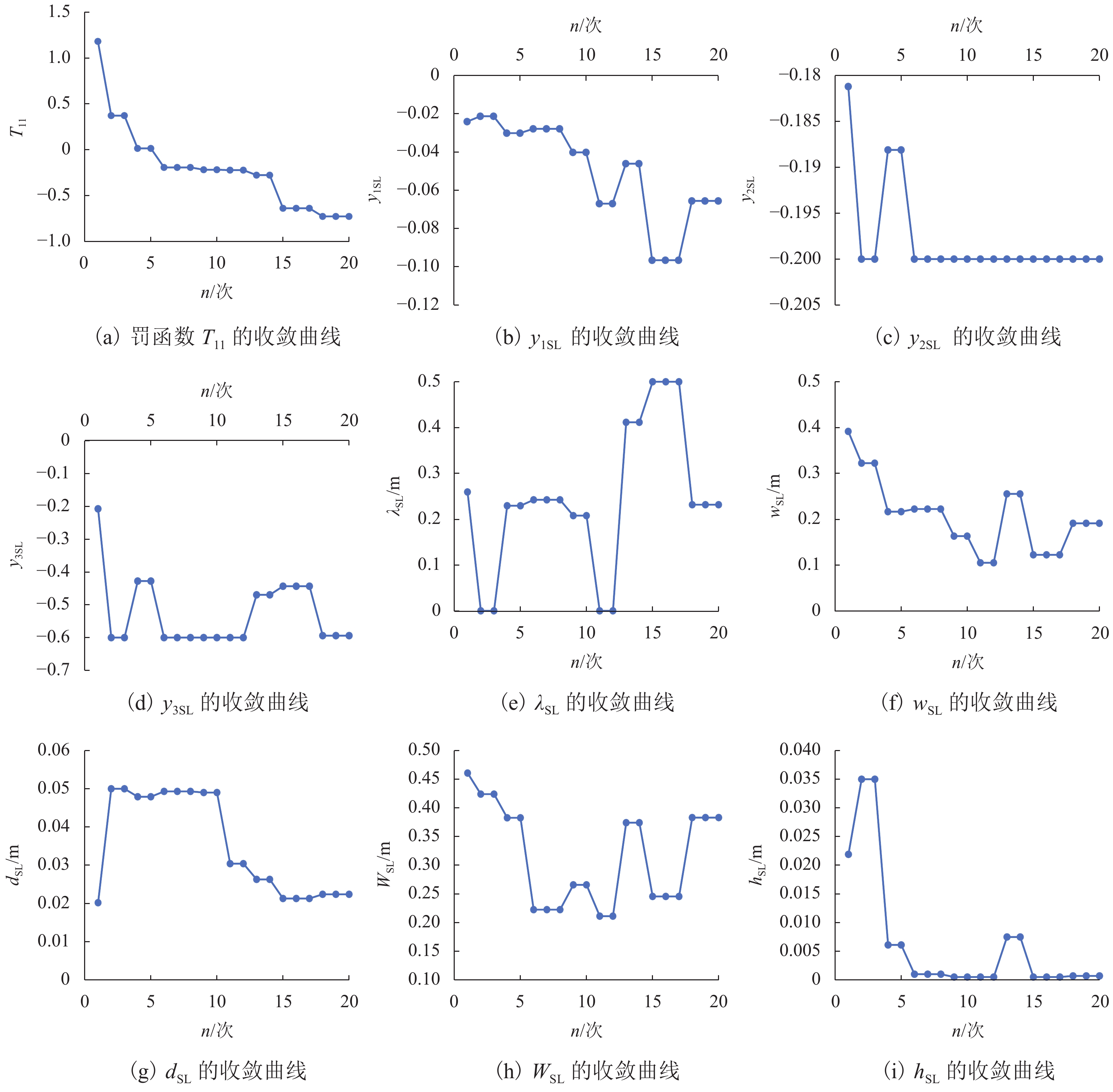
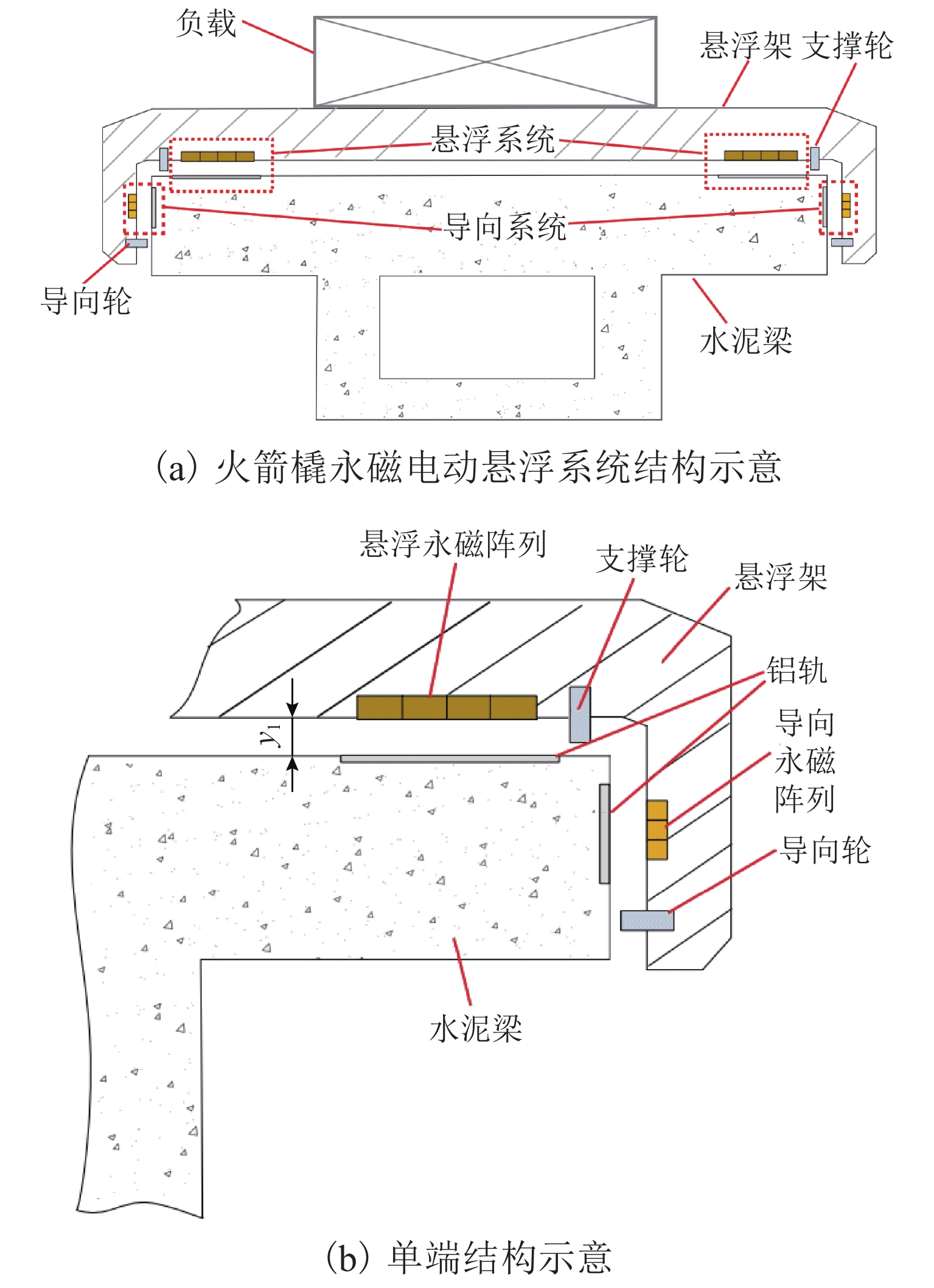
为提高超高速永磁电动悬浮系统的综合性能，围绕浮重比、浮阻比和悬浮刚度3个重要指标开展了多目标性能优化研究. 首先，对永磁电动悬浮系统进行横向延拓，推导三维电磁力模型，并进行有限元仿真分析；然后，针对浮重比、浮阻比和悬浮刚度的多目标优化问题，提出基于“系统级+子系统级”架构的并行优化策略，实现了线性加权意义下的系统性能最优. 最后，搭建了“Halbach永磁阵列+凸缘式铝制转盘”实验平台，验证上述优化策略在提高系统性能上的有效性. 研究结果表明：在超高速工况下，理论解析计算得到悬浮力与仿真结果误差在8%以内，而磁阻力几乎没有误差；通过优化设计，浮重比从11.0提升至18.3，增幅为75.50%；浮阻比从3.5提升至3.8，增幅为7.50%；单位质量永磁阵列的悬浮刚度从6.1 kN/m提升至20.6 kN/m，增幅为235.94%.
- 永磁 /
- 电磁悬浮 /
- 多目标优化
Abstract:
In order to improve the overall performance of the ultra-high speed permanent magnet electrodynamic suspension system, multi-objective performance optimization was carried out based on three important indexes: lift-to-weight ratio, lift-to-drag ratio, and suspension stiffness. Firstly, the transverse continuation of the permanent magnet electrodynamic suspension system was carried out, and a three-dimensional electromagnetic force model was derived. In addition, the finite element simulation was performed. Then, in view of the multi-objective optimization problem involving lift-to-weight ratio, lift-to-drag ratio, and suspension stiffness, a parallel optimization strategy based on “system + subsystem” architecture was proposed to obtain the optimal system performance in the sense of linear weighting. Finally, the experimental platform of “Halbach permanent magnet array + flanged aluminum turntable” was built, which demonstrated the effectiveness of the above optimization strategy in improving system performance. Research results show that the suspension force error between theoretical analysis and simulation results is less than 8%, and the error of magnetic resistance is little. By optimization design, the lift-to-weight ratio is increased by 75.50% from 11.0 to 18.3; the lift-drag ratio is increased by 7.50% from 3.5 to 3.8; the suspension stiffness of the unit mass permanent magnet array is increased by 235.94% from 6.1 kN/m to 20.6 kN/m.
- permanent magnet /
- electromagnetic suspension /
- multi-objective optimization

HTML全文

图 1 超高速火箭橇永磁电动悬浮方案

Figure 1. Permanene electrodynamic suspension scheme for ultra-high spend rocket sled

下载: 全尺寸图片幻灯片

图 2 永磁电动悬浮系统延拓示意

Figure 2. Continuation of permanent magnet electrodynamic suspension system

下载: 全尺寸图片幻灯片

图 3 永磁电动悬浮电磁力仿真与理论对比

Figure 3. Electromagnetic force comparison of permanent magnet electrodynamic suspension system between simulation and theoretical results

下载: 全尺寸图片幻灯片

图 4 多目标优化优化策略流程

Figure 4. Flow chart of multi-objective optimization strategy

下载: 全尺寸图片幻灯片

图 5 各个变量的迭代过程

Figure 5. Iterative process of each variable

下载: 全尺寸图片幻灯片

图 6 永磁电动悬浮系统悬浮、导向一体化实验台

Figure 6. Suspension and guidance integrated experimental platform for permanent magnet electrodynamic suspension system

下载: 全尺寸图片幻灯片

图 7 电磁力理论值与实验值的对比

Figure 7. Electromagnetic force comparison between experimental and theoretical results

下载: 全尺寸图片幻灯片

表 1 M=4，8时，ε_n、γ_n的取值

Table 1. Values of ε_nand γ_n when M = 4，8

M	n/次	ε_n	γ_n
4	1	sin π/4	sin π/4
	3	1/3sin π/4	−1/3sin π/4
	5	−1/5sin π/4	−1/5sin π/4
	7	−1/7sin π/4	1/7sin π/4
	9	1/9sin π/4	1/9sin π/4
8	1	2sin π/8	2sin π/8
	7	2/7sin π/8	−2/7sin π/8
	9	−2/9sin π/8	−2/9sin π/8
	15	−2/15sin π/8	2/15sin π/8
	17	2/17sin π/8	2/17sin π/8

下载: 导出CSV

表 2 电动悬浮系统特征参数

Table 2. Parameters of electrodynamic suspension system

参数	B_r/T	M	λ/mm	l/mm	w/mm	d/mm	W/mm	h/mm	y₁/mm
取值	1.44	8	0.24	0.27	60	30	100	30	15

下载: 导出CSV

表 3 基于PSO和PCS的多目标优化结果对比

Table 3. Comparison of multi-objective optimization results

参数	PSO	PCS
λ/mm	162.5	232.1
w/mm	86.8	191.6
d/mm	22.8	22.4
W/mm	130.1	383.1
h/mm	3.2	1.0
ζ₁	72.6	74.9
ζ₂	15.0	16.3
ζ₃/（MN·m⁻¹）	0.5	0.7

下载: 导出CSV

表 4 优化前、后永磁电动悬浮系统的性能对比

Table 4. Performance comparison of permanent magnet electrodynamic suspension system before and after optimization

参数及指标	优化前	优化后
永磁阵列尺寸/mm	200（波长）， 40（宽），40（厚）	153.6（波长）， 66.8（宽），23.4（厚）
v/（m·s⁻¹）	60	60
y₁/mm	20	20
浮重比	11.0	18.3
浮阻比	3.5	3.8
悬浮刚度/ （（kN·m⁻¹）·mg⁻¹）	6.1	20.6

下载: 导出CSV

参考文献(26)

[1]	夏有财,孙其会,肖军,等. 火箭橇运动计算算法优化与试验验证[J]. 航空动力学报,2021,36(7): 1564-1568. XIA Youcai, SUN Qihui, XIAO Jun, et al. Optimization and test verification of rocket sled motion calculation algorithm[J]. Journal of Aerospace Power, 2021, 36(7): 1564-1568.
[2]	GIERAS J F. Ultra high-speed ground transportation systems: Current Status and a vision for the future[J]. Przeglad Elektrotechniczny, 2020, 9: 3-9.
[3]	李冠醇,李杰,陈强. 应用于高速滑撬的电动悬浮和电磁推进系统设计[J]. 推进技术,2017,38(7): 1468-1474. LI Guanchun, LI Jie, CHEN Qiang. Design of an electrodynamic suspension and electromagnetic propulsion system for high speed test track[J]. Journal of Propulsion Technology, 2017, 38(7): 1468-1474.
[4]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530.
[5]	张瑞华,刘育红,徐善纲. 美国Magplane磁悬浮列车方案介绍[J]. 变流技术与电力牵引,2005(5): 40-43. ZHANG Ruihua, LIU Yuhong, XU Shangang. American magplane schemes[J]. Converter Technology & Electric Traction, 2005(5): 40-43.
[6]	李云钢,常文森,闫宇壮. 美国新型结构磁悬浮交通技术分析与比较[J]. 机车电传动,2006(3): 6-9,39. doi: 10.3969/j.issn.1000-128X.2006.03.002 LI Yungang, CHANG Wensen, YAN Yuzhuang. Analysis and comparison of new maglev transport technology in USA[J]. Electric Drive for Locomotives, 2006(3): 6-9,39. doi: 10.3969/j.issn.1000-128X.2006.03.002
[7]	ROSS P E. Hyperloop: No pressure[J]. IEEE Spectrum, 2016, 53(1): 51-54. doi: 10.1109/MSPEC.2016.7367468
[8]	HAN Q H. Analysis and modeling of the EDS maglev system based on the Halbach permanent magnet array [D]. Orlando: University of Central Florida, 2004.
[9]	DAVEY K. Optimization shows Halbach arrays to be non-ideal for induction devices[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1035-1038. doi: 10.1109/20.877618
[10]	李春生,杜玉梅,严陆光. 应用于磁浮列车的直线型Halbach磁体结构的优化设计[J]. 高技术通讯,2007,17(7): 724-729. doi: 10.3321/j.issn:1002-0470.2007.07.013 LI Chunsheng, DU Yumei, YAN Luguang. Optimal design of linear PM Halbach array for EDS maglev[J]. Chinese High Technology Letters, 2007, 17(7): 724-729. doi: 10.3321/j.issn:1002-0470.2007.07.013
[11]	王江波,李耀华,严陆光. 直线Halbach磁体用于磁浮列车涡流制动的研究[J]. 电气传动,2010,40(5): 8-11. WANG Jiangbo, LI Yaohua, YAN Luguang. Study on applying the linear halbach array to eddy current brake system for maglev[J]. Electric Drive, 2010, 40(5): 8-11.
[12]	ZHANG Z H, SHI L M, WANG K, et al. Characteristics investigation of single-sided ironless PMLSM based on Halbach Array for medium-speed maglev train[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2017(4): 375-382.
[13]	ZHAO M T, GE Q X, GAO Z, et al. Analysis of electromagnetic and damping characteristics of permanent magnet electrodynamic suspension system[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA). Wuhan: IEEE, 2021: 1-6.
[14]	DUAN J H, XIAO S, ZHANG K L, et al. Analysis and optimization of asymmetrical double-sided electrodynamic suspension devices[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-5.
[15]	LUO C, ZHANG K L, ZHANG W L, et al. 3D analytical model of permanent magnet and electromagnetic hybrid halbach array electrodynamic suspension system[J]. Journal of Electrical Engineering & Technology, 2020, 15(4): 1713-1721.
[16]	罗成. 永磁电磁混合Halbach阵列电动悬浮特性及稳定控制研究[D]. 成都: 西南交通大学, 2021.
[17]	罗成,张昆仑,王滢. 永磁电磁混合Halbach阵列电动悬浮的稳定性控制[J]. 西南交通大学学报,2022,57(3): 574-581. doi: 10.3969/j.issn.0258-2724.20210868 LUO Cheng, ZHANG Kunlun, WANG Ying. Stability control of electrodynamic suspension with permanent magnet and electromagnet hybrid halbach array[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 574-581. doi: 10.3969/j.issn.0258-2724.20210868
[18]	巫川,李冠醇,王东. 永磁电动悬浮系统三维解析建模与电磁力优化分析[J]. 电工技术学报,2021,36(5): 924-934. doi: 10.19595/j.cnki.1000-6753.tces.201099 WU Chuan, LI Guanchun, WANG Dong. 3-D analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 924-934. doi: 10.19595/j.cnki.1000-6753.tces.201099
[19]	LONG Z Q, HE G, XUE S. Study of EDS & EMS hybrid suspension system with permanent-magnet halbach array[J]. IEEE Transactions on Magnetics, 2011, 47(12): 4717-4724. doi: 10.1109/TMAG.2011.2159237
[20]	HU Y P, LONG Z Q, XU Y S, et al. Control-oriented modeling for the electrodynamic levitation with permanent magnet Halbach array[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 67(3): 375-392. doi: 10.3233/JAE-210007
[21]	贺光. 基于Halbach结构的永磁电动与电磁混合悬浮技术研究[D]. 长沙: 国防科学技术大学, 2010.
[22]	王厚生. 永磁电动式导体板磁悬浮列车轨道结构及相关研究[D]. 北京: 中国科学院, 2004.
[23]	李春生. 永磁电动式磁悬浮的研究[D]. 北京: 中国科学院, 2007.
[24]	HU Y P, LONG Z Q, ZENG J W, et al. Analytical optimization of electrodynamic suspension for ultrahigh-speed ground transportation[J]. IEEE Transactions on Magnetics, 2021, 57(8): 1-11.
[25]	WANG F Y, ZHANG J L, ZHAO J D, et al. Two dimensional analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[C]//2021 13th International Symposium on Linear Drives for Industry Applications (LDIA). Wuhan: IEEE, 2021: 1-5.
[26]	段家珩. 永磁板式电动悬浮边端效应及三维电磁力特性的研究[D]. 成都: 西南交通大学, 2021.