Extremum Conditions of Response of Maglev Guideway Under Train Loads
-
摘要:
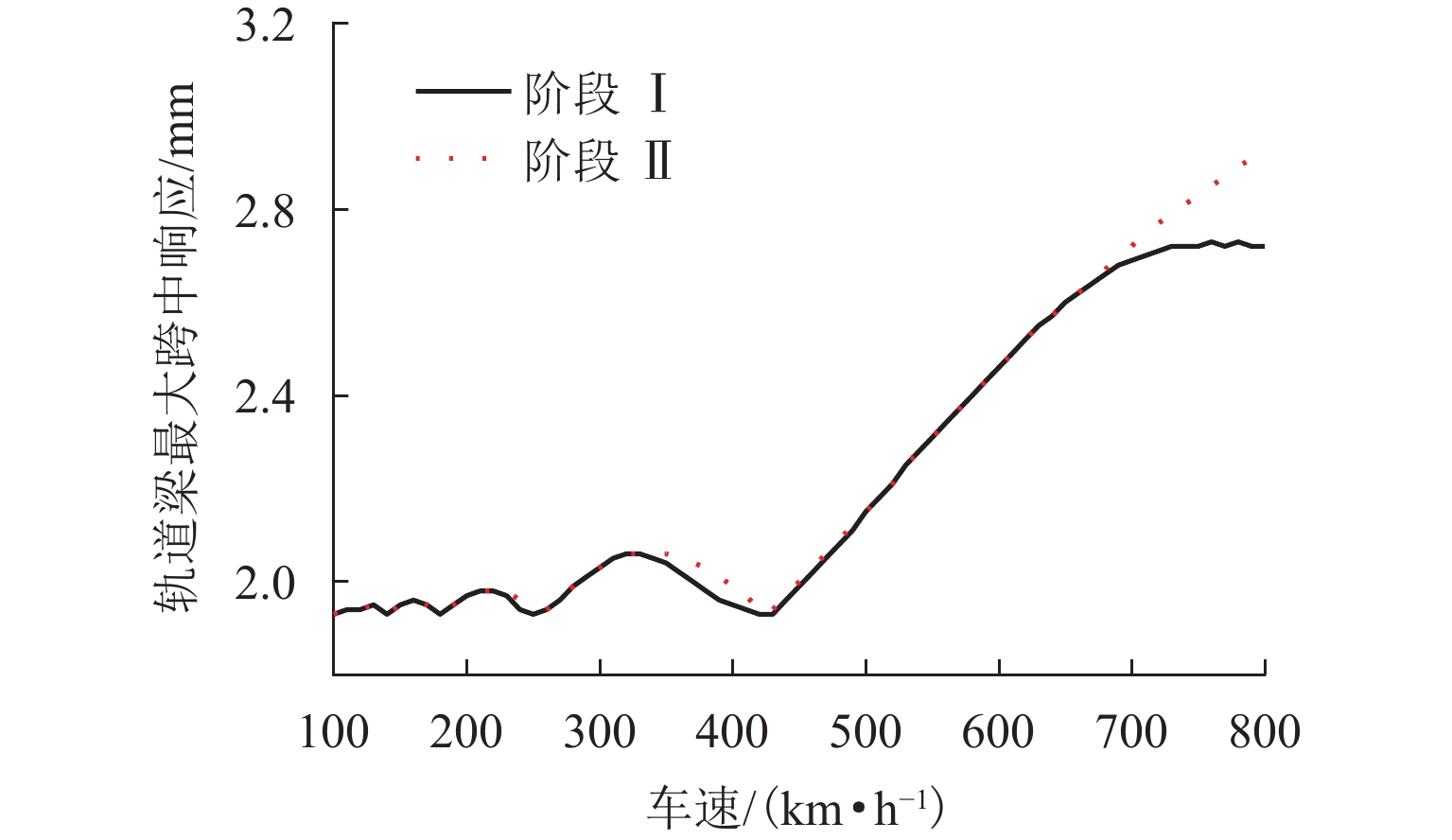
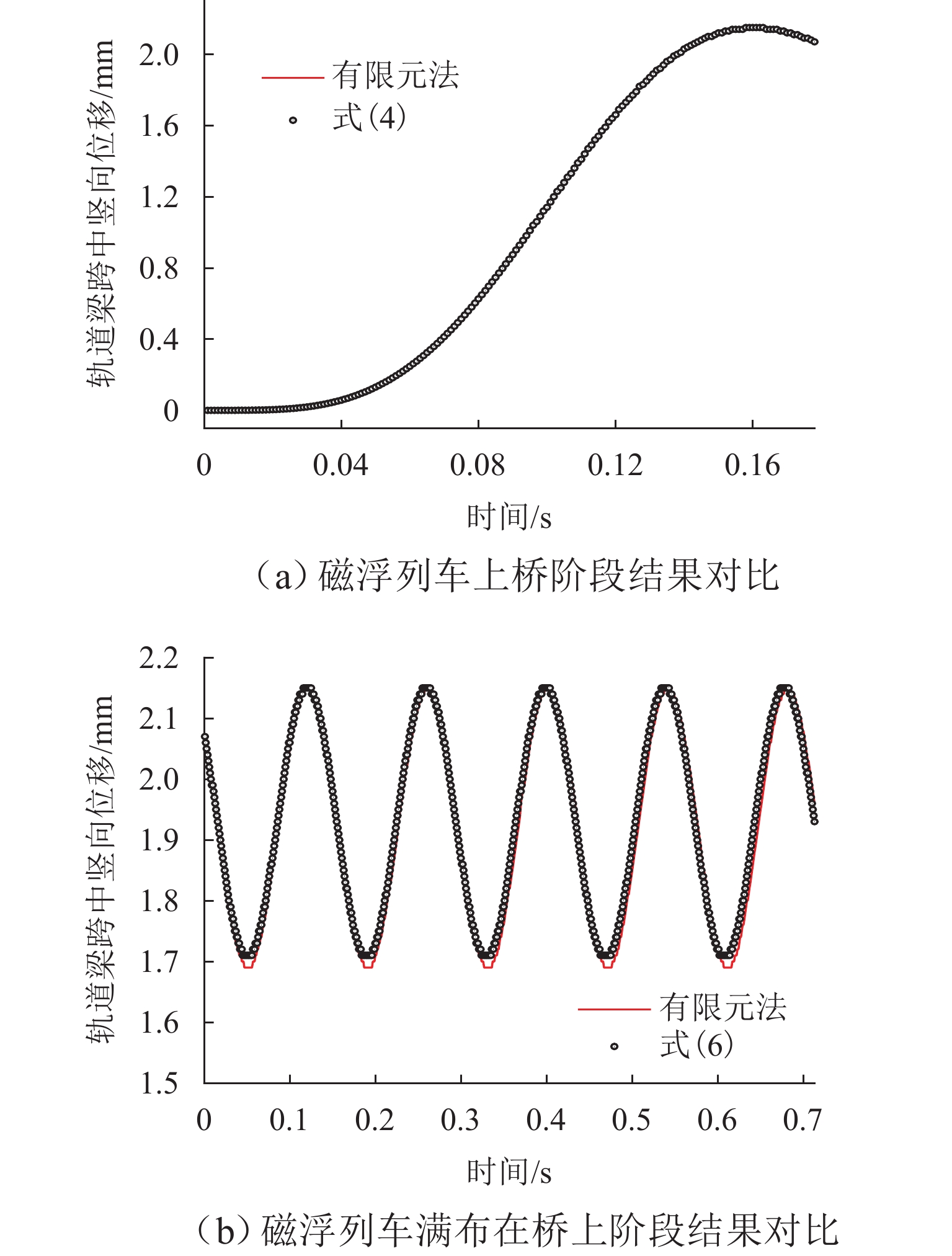
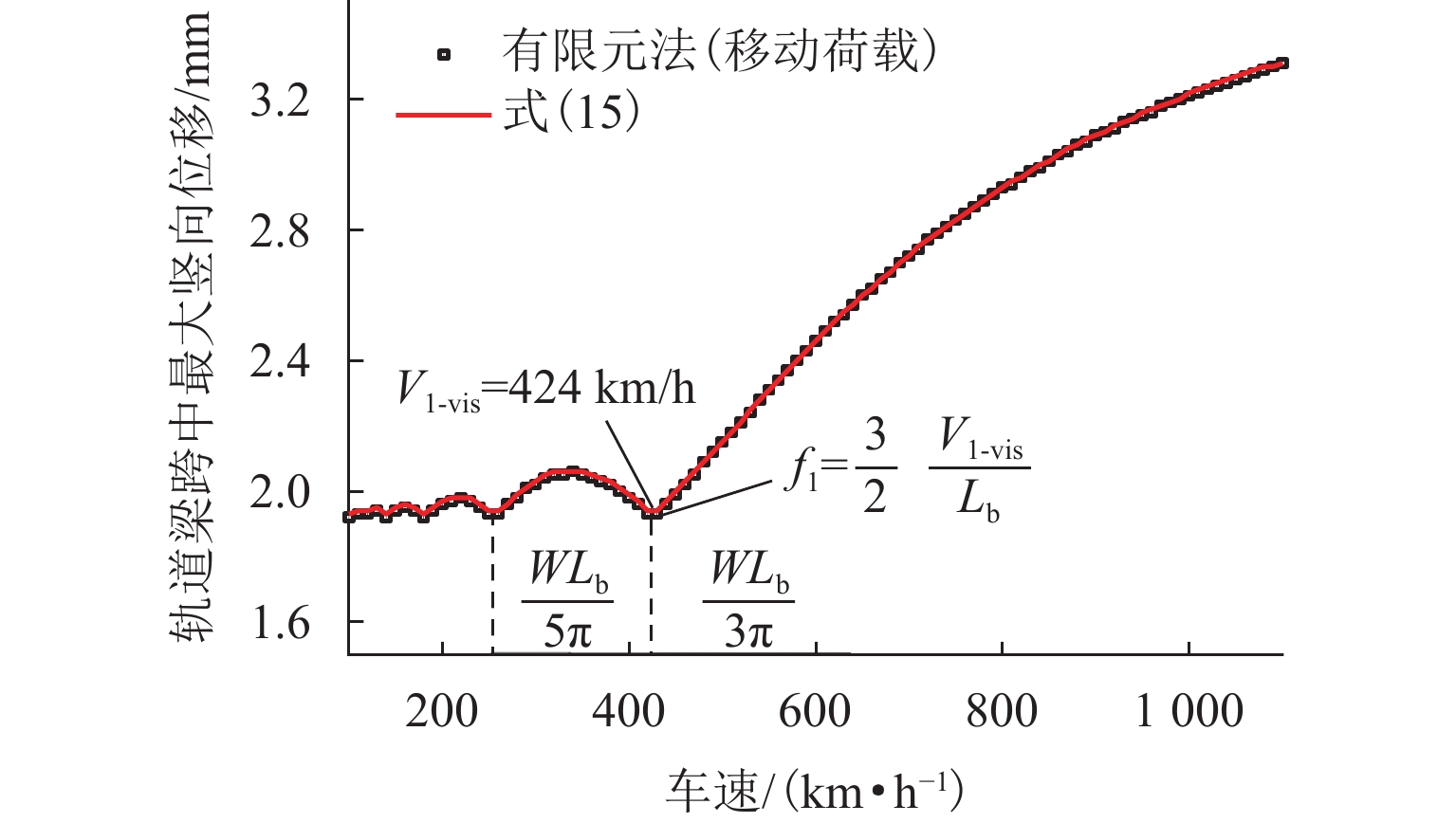
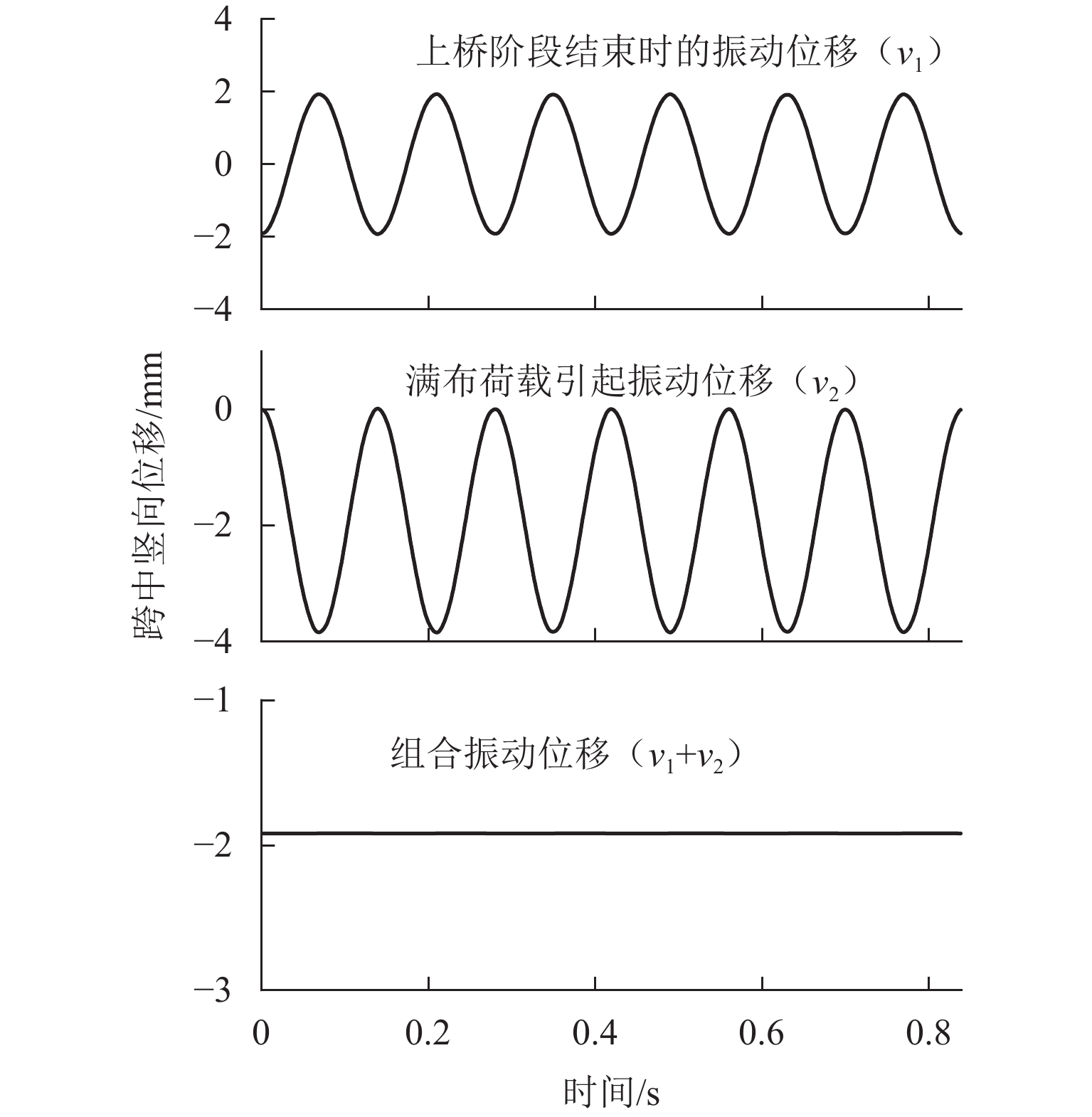
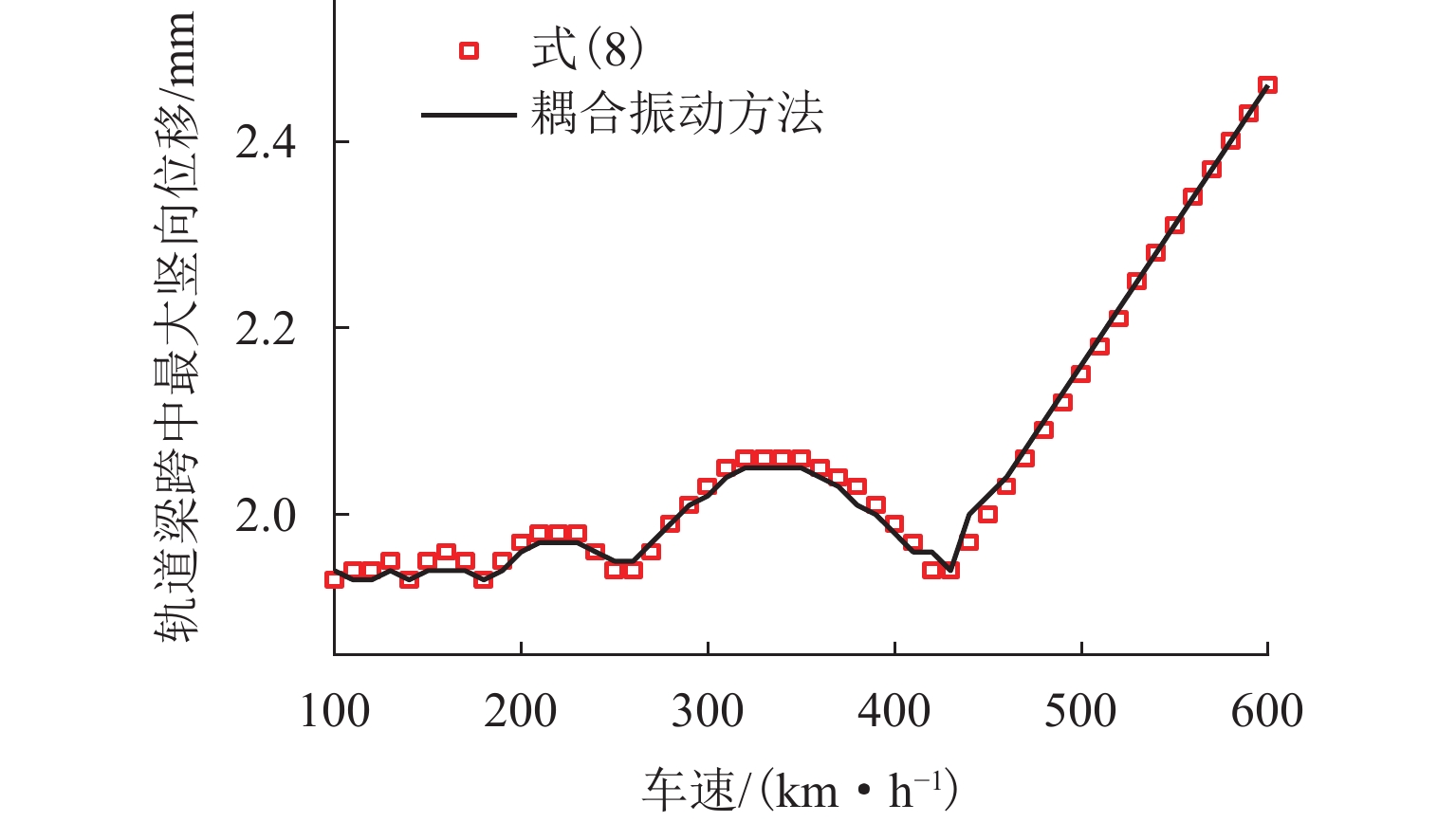
为研究磁浮轨道梁动力响应的变化规律，将磁浮列车简化为移动的均布荷载，采用解析法得到简支轨道梁动力响应的解析解，并讨论轨道梁最大值随车速、跨度等参数的变化规律，推导磁浮轨道梁动力响应的极值条件，利用有限元方法和车-桥耦合振动方法进行验证. 结果表明：列车与轨道梁跨度比值较大时，随列车速度的增加轨道梁跨中最大响应以波动形式增加，最大响应存在极值，轨道梁响应随轨道梁跨度、质量等参数也有类似规律；当车速和跨度的乘积为特定常数，或轨道梁一阶竖弯频率与跨度的乘积为车速特定倍数时，轨道梁产生消振现象.
Abstract:To reveal the variation law of dynamic response of maglev guideways, maglev trains were simplified as moving uniform loads, and analytical methods were employed to obtain the analytical solutions for dynamic response of simply supported guideways. The variation laws of the maximum response of guideways with train speed and guideway span were discussed, and the extremum conditions of response of maglev guideways were derived, which were verified by finite element and train-bridge coupling vibration methods. The results show that under the condition of a large train-guideway span ratio, the maximum response of midspan increases with fluctuations as the train speed increases and has extremums. Guideway response also has similar change laws with the variations of guideway span, mass, and other parameters. When the product of span and speed is a specific constant, or the product of the first-order vertical frequency and span of guideway is a specific time the train speed, the guideway produces vibration isolation.
-
Key words:
- maglev guideway /
- dynamic response /
- uniform loads /
- analytical method /
- vibration isolation
-
图 2 阶段Ⅰ、Ⅱ轨道梁最大跨中响应比较
Figure 2. Comparison of the maximum midspan response of the guideway at stage Ⅰ and stage Ⅱ
图 8 消振车速下阶段Ⅱ振动分解
Figure 8. Vibration decomposition diagram at stage Ⅱ at a train speed producing vibration isolation
图 9 解析法与耦合振动法结果比较
Figure 9. Comparison of analytical method and coupling vibration method
表 1 φ取值表
Table 1. Value of the auxiliary angle φ
车速范围/
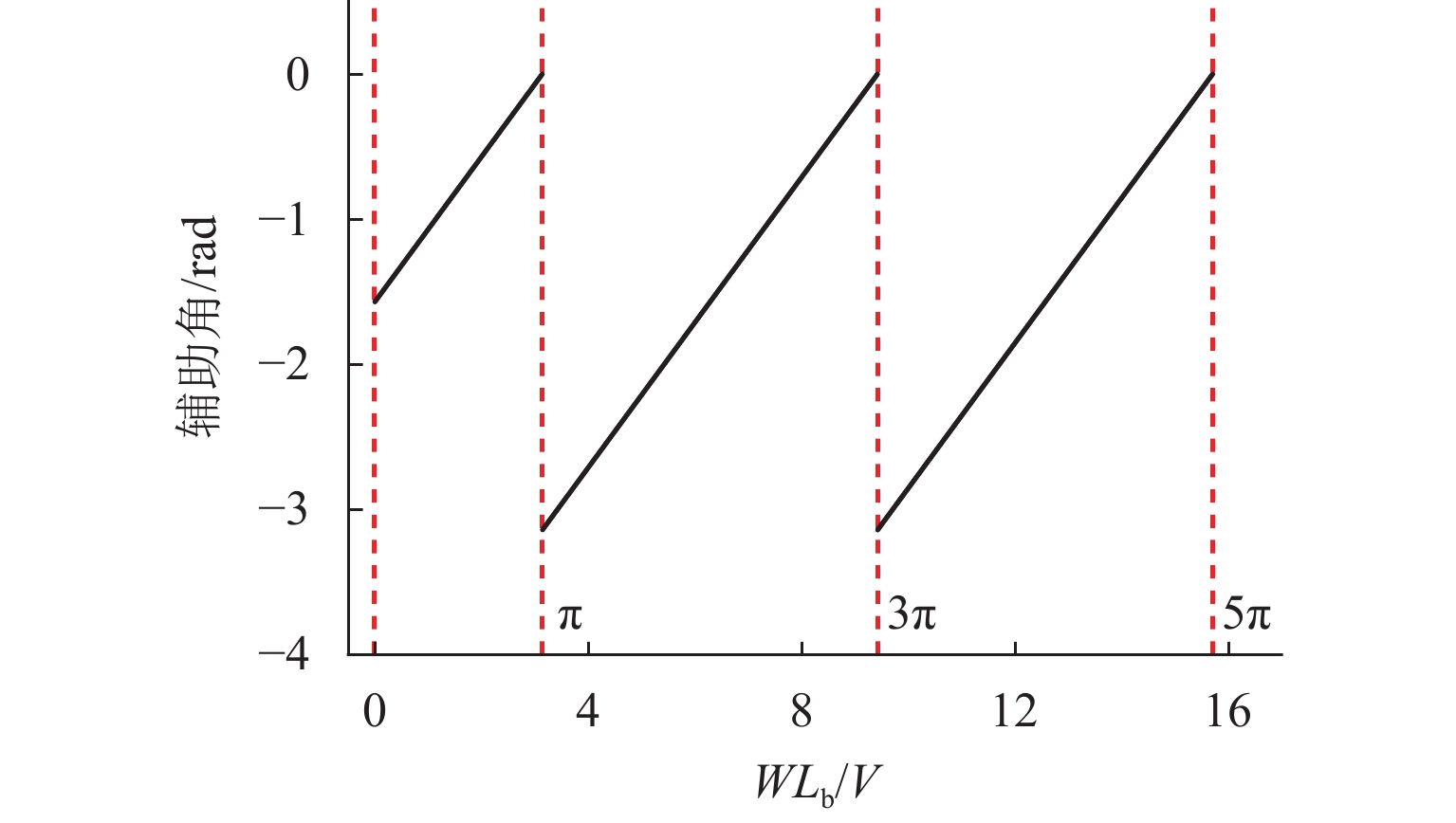
（km·h−1）φ 取值/rad 备注 $ \left[\dfrac{{W{L_{\text{b}}}}}{{{\text{π}} + 2k{\text{π}} }},\dfrac{{W{L_{\text{b}}}}}{{2k{\text{π}} }}\right] $ $ \dfrac{{W{L_{\text{b}}}}}{{2V}} - \dfrac{{\text{π}} }{2} - k{\text{π}} $ $k = 1,2,\cdots $ $ \left[\dfrac{{W{L_{\text{b}}}}}{{2{\text{π}} + 2k{\text{π}} }},{\dfrac{{W{L_{\text{b}}}}}{{{\text{π}}+ 2k{\text{π}} }} }\right) $ $ \dfrac{{W{L_{\text{b}}}}}{{2V}} - \dfrac{{\text{π}} }{2} - (k + 1){\text{π}} $ $k = 0,1,\cdots $ $ \left({\dfrac{{W{L_{\text{b}}}}}{{\text{π}} }}, + \infty \right) $ $ \dfrac{{W{L_{\text{b}}}}}{{2V}} - \dfrac{{\text{π}} }{2} $ 
下载: 导出CSV
-
[1] LIN G B, SHENG X W. Application and further development of maglev transportation in China[J]. Transportation Systems and Technology, 2018, 4(3): 36-43 doi: 10.17816/transsyst20184336-43 [2] ZHANG L, HUANG J Y. Dynamic interaction analysis of the high-speed maglev vehicle/guideway system based on a field measurement and model updating method[J]. Engineering Structures, 2019, 180: 1-17. doi: 10.1016/j.engstruct.2018.11.031 [3] PALMER C. Engineered to go fast, maglev trains inch forward[J]. Engineering, 2021, 7(7): 891-893. doi: 10.1016/j.eng.2021.06.001 [4] LI M, LUO S H, MA W H, et al. Experimental study on dynamic performance of medium and low speed maglev train-track-bridge system[J]. International Journal of Rail Transportation, 2021, 9(3): 232-255. doi: 10.1080/23248378.2020.1798294 [5] LIANG X, JIANG T, HONG Y, et al. Vibration response analysis of simply supported box girder bridge-maglev train in accelerated test of Changsha maglev express[J]. Advances in Materials Science and Engineering, 2020, 2020(1): 9563747.1-9563747.18. [6] 李小珍,金鑫,王党雄,等. 长沙中低速磁浮运营线列车-桥梁系统耦合振动试验研究[J]. 振动与冲击,2019,38(13): 57-63.LI Xiaozhen, JIN Xin, WANG Dangxiong, et al. Tests for coupled vibration of a train-bridge system on Changsha low-medium speed maglev line[J]. Journal of Vibration and Shock, 2019, 38(13): 57-63. [7] KIM K J, HAN J B, HAN H S, et al. Coupled vibration analysis of Maglev vehicle-guideway while standing still or moving at low speeds[J]. Vehicle System Dynamics, 2015, 53(4): 587-601. doi: 10.1080/00423114.2015.1013039 [8] TIAN X F, XIANG H Y, ZHU J, et al. Effect of long-wave deviation of stator plane on high-speed maglev train and guideway system[J]. Journal of Vibration and Control, 2023, 29(9/10): 2348-2362. [9] WANG D X, LI X Z, LIANG L, et al. Dynamic interaction analysis of bridges induced by a low-to-medium-speed maglev train[J]. Journal of Vibration and Control, 2020, 26(21/22): 2013-2025. [10] XIANG H Y, TIAN X F, LI Y L, et al. Dynamic interaction analysis of high-speed maglev train and guideway with a control loop failure[J]. International Journal of Structural Stability and Dynamics, 2022, 22(10): 2241012.1-2241012.28. [11] YAU J D. Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration, 2009, 321(1/2): 184-200. [12] ZHAO C F, ZHAI W M. Maglev vehicle/guideway vertical random response and ride quality[J]. Vehicle System Dynamics, 2002, 38(3): 185-210. doi: 10.1076/vesd.38.3.185.8289 [13] ZHENG X J, WU J J, ZHOU Y H. Numerical analyses on dynamic control of five-degree-of-freedom maglev vehicle moving on flexible guideways[J]. Journal of Sound and Vibration, 2000, 235(1): 43-61. doi: 10.1006/jsvi.1999.2911 [14] 王贞,侯金佑,吴斌,等. 高速磁浮列车-桥梁耦合振动实时混合试验的数值仿真研究[J]. 振动与冲击,2022,41(8): 270-276.WANG Zhen, HOU Jinyou, WU Bin, et al. A numerical simulation study of a real-time hybrid test for high-speed maglev train-bridge coupling vibration[J]. Journal of Vibration and Shock, 2022, 41(8): 270-276. [15] 陈绪黎,向活跃,田祥富,等. 常导高速磁浮桥梁预拱度形式研究[J]. 振动工程学报,2023,36(3): 652-661.CHEN Xuli, XIANG Huoyue, TIAN Xiangfu, et al. Analysis on pre-camber forms of high-speed EMS maglev bridge[J]. Journal of Vibration Engineering, 2023, 36(3): 652-661. [16] ZHANG L, HUANG J Y. Stiffness of coupling connection and bearing support for high-speed maglev guideways[J]. Journal of Bridge Engineering, 2018, 23(9): 04018064.1-04018064.14 [17] 邓建良,吴定俊,李奇. 移动均布荷载作用下简支梁桥动力系数分析[J]. 工程力学,2013,30(5): 56-62.DENG Jianliang, WU Dingjun, LI Qi. Impact factor analysis of simply-supported girder bridges traversed by uniformly-distributed moving loads[J]. Engineering Mechanics, 2013, 30(5): 56-62. [18] WANG H P, LI J, ZHANG K. Vibration analysis of the maglev guideway with the moving load[J]. Journal of Sound and Vibration, 2007, 305(4/5): 621-640. [19] SONG X D, WU D J, LI Q. Dynamic impact analysis of double-tower cable-stayed maglev bridges using a simple model[J]. Journal of Bridge Engineering, 2014, 19(1): 34-43. doi: 10.1061/(ASCE)BE.1943-5592.0000498 [20] 中华人民共和国住房和城乡建设部. 高速磁浮交通设计标准:CJJ/T 310—2021[S]. 北京:中国建筑工业出版社,2019. [21] REN S B, ROMEIJN A, KLAP K. Dynamic simulation of the maglev vehicle/guideway system[J]. Journal of Bridge Engineering, 2010, 15(3): 269-278. doi: 10.1061/(ASCE)BE.1943-5592.0000071 [22] WANG Z L, XU Y L, LI G Q, et al. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility[J]. Vehicle System Dynamics, 2019, 57(2): 161-191. doi: 10.1080/00423114.2018.1450517 [23] 吴祥明. 磁浮列车[M]. 上海:上海科学技术出版社,2003. [24] SHI J, FANG W S, WANG Y J, et al. Measurements and analysis of track irregularities on high speed maglev lines[J]. Journal of Zhejiang University SCIENCE A, 2014, 15(6): 385-394. doi: 10.1631/jzus.A1300163 -
下载:
点击查看大图
计量
- 文章访问数: 57
- HTML全文浏览量: 21
- PDF下载量: 11
- 被引次数: 0