Application of Good Lattice Point with Power Generator Method in Stochastic Dynamic Analysis of Vehicle-Bridge System
-
摘要:
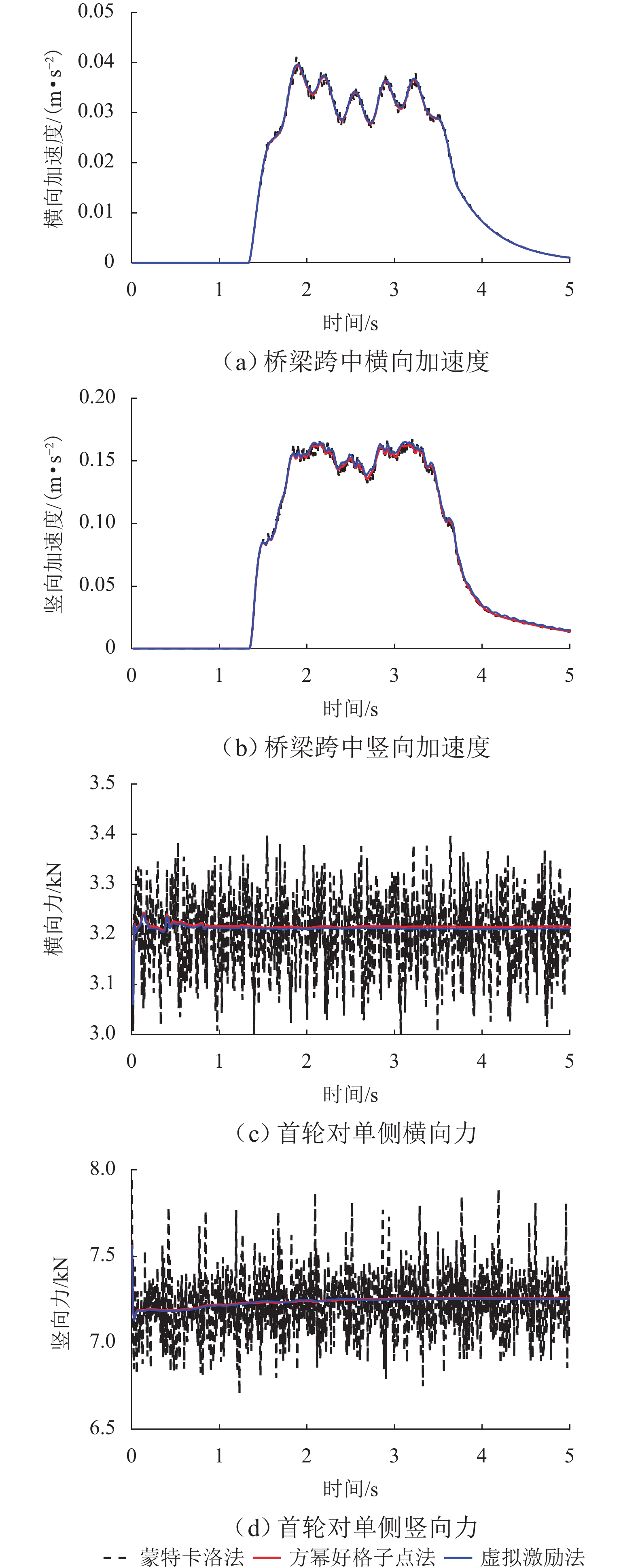
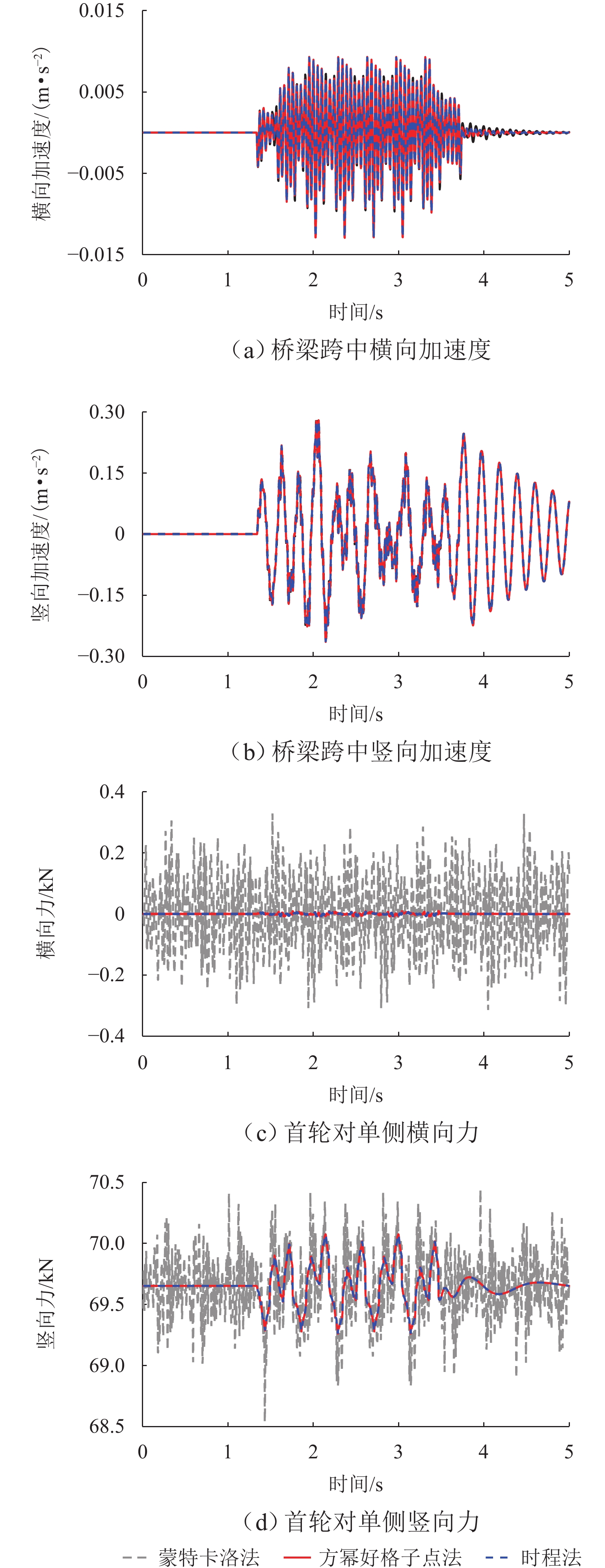
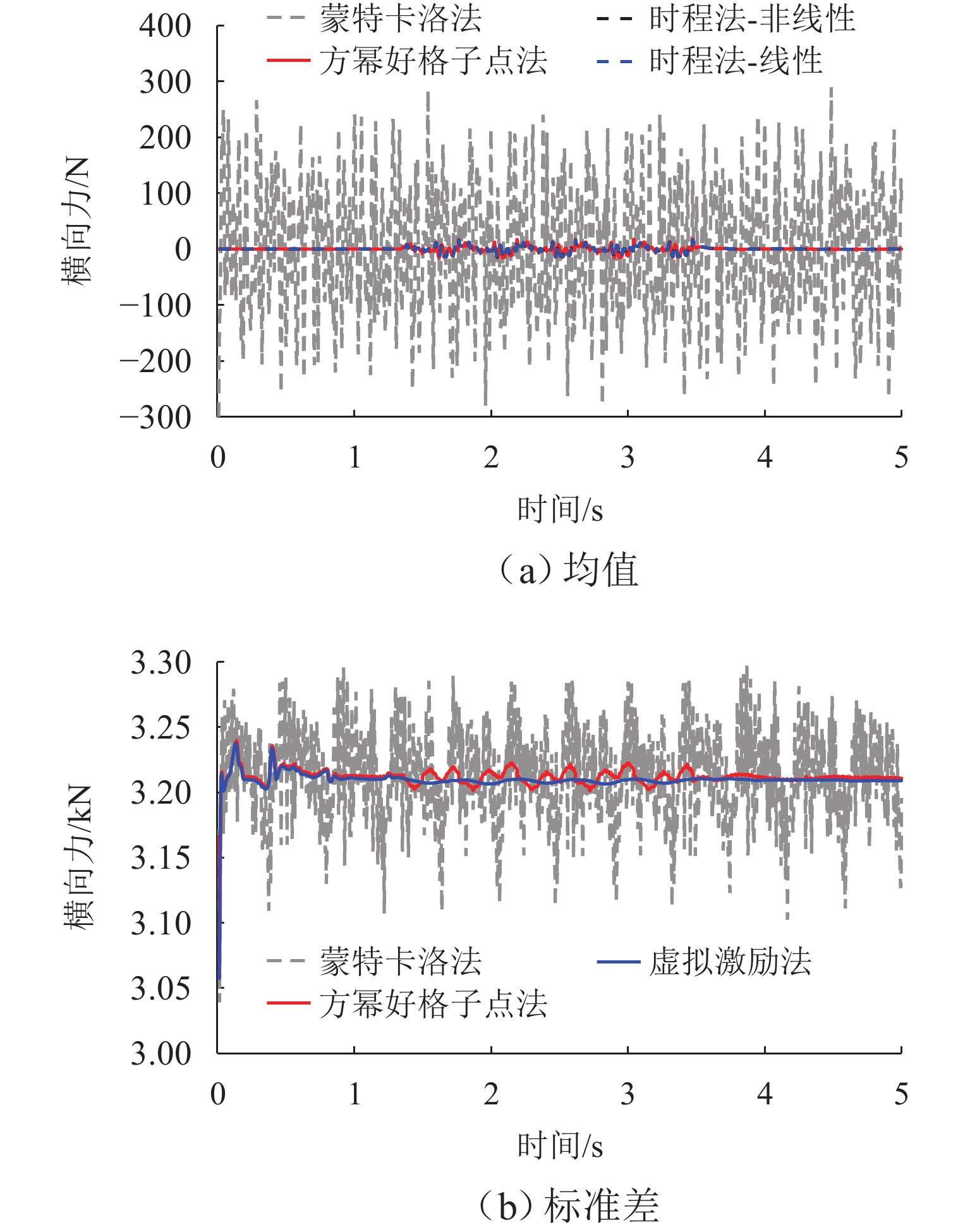
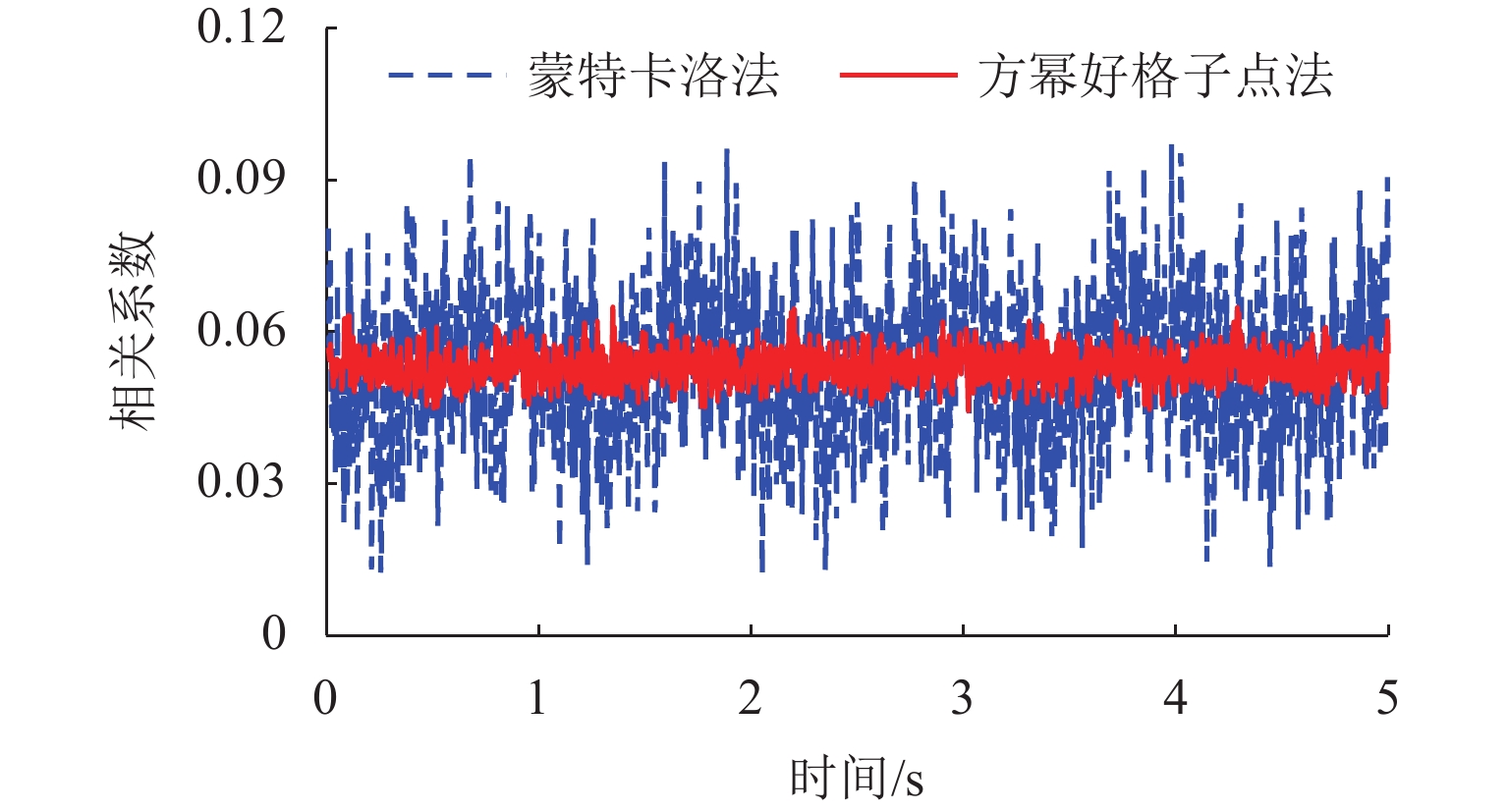
针对难以精确选取具有代表性的超高维随机相位角问题，采用方幂好格子点法生成代表性轨道不平顺样本，并将该样本作用于车-桥系统，得到轮轨力的均值与标准差；然后，通过对比虚拟激励法、确定性时程法和蒙特卡洛法的计算结果来探究该方法的计算精度与计算效率；最后，采用线性与非线性轮轨接触关系研究考虑列车日运营量的脱轨系数阈值. 以和谐号通过桥梁为例，计算结果表明：与蒙特卡洛法相比，采用方幂好格子点法生成不同方向的轨道不平顺样本之间的均匀性较好；方幂好格子点法求得的随机动力响应的概率特征参数与其他方法相比，具有较高的计算精度，其计算效率较蒙特卡洛法提高了近5倍；分别采用线性与非线性轮轨接触关系时所得的脱轨系数阈值相差达4.68%，方幂好格子点法具有较广泛适用性.
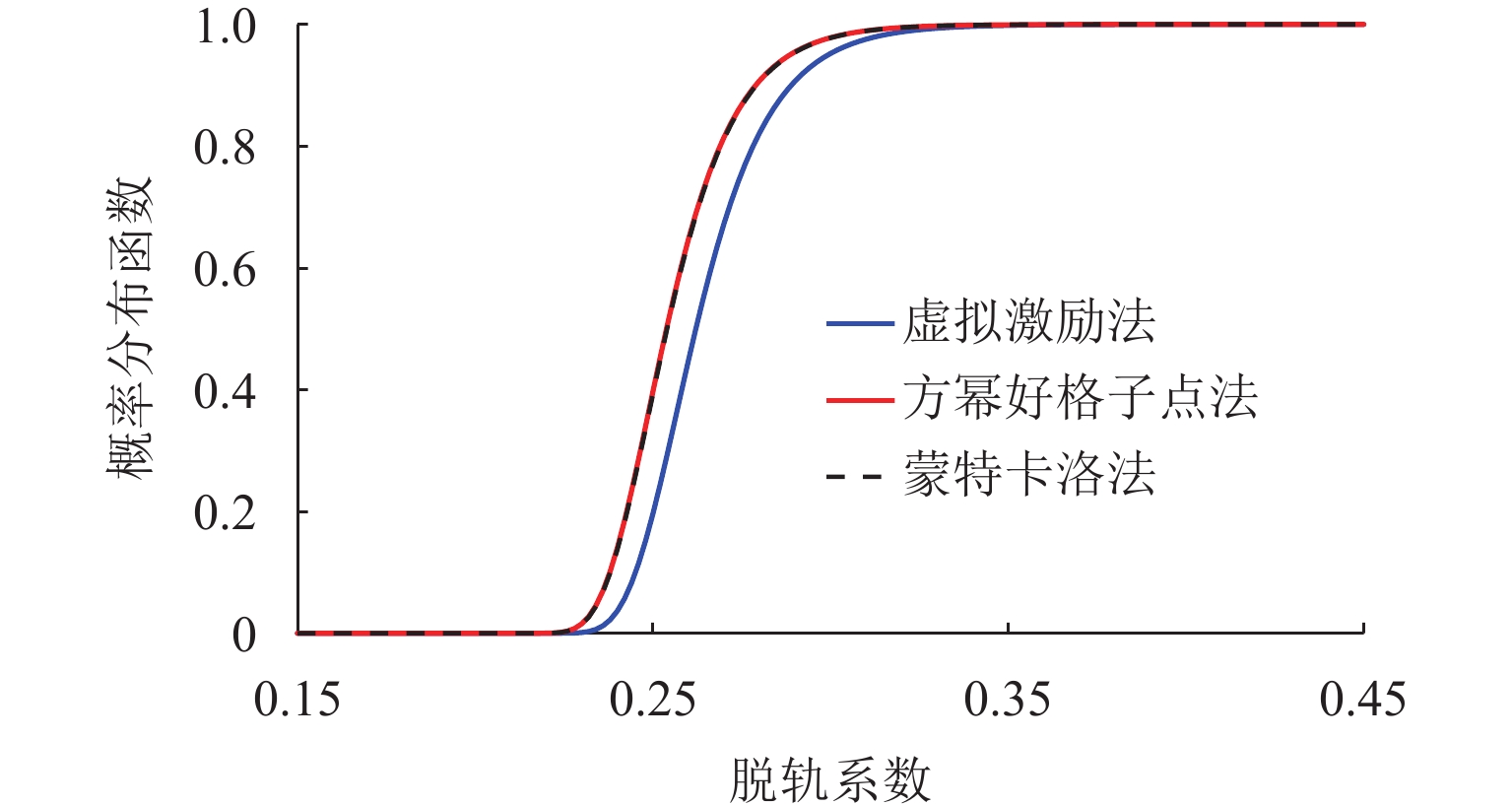
Abstract:Since it is difficult to accurately select representative super-high-dimensional random phase angles, the good lattice point with power generator method (GLPPGM) was utilized to generate samples of representative track irregularities, which were applied to the vehicle-bridge system to obtain the mean and standard deviation of random dynamic responses. Then, the calculation accuracy and efficiency of this method were explored by comparing the results of the pseudo-excitation method, deterministic time history method, and Monte Carlo method (MCM). Finally, the threshold value of the derailment factor considering the daily operation volume of trains was studied by using linear and nonlinear wheel-rail contact relationships. The Harmony train passing over a bridge was studied, and the results show that compared with that by the MCM, the uniformity between the samples of track irregularities generated by the GLPPGM in different directions is better. The probability characteristic parameters of the random dynamic response obtained by the GLPPGM have higher calculation accuracy than different methods, and its calculation efficiency is nearly five times higher than that of the MCM. When linear and nonlinear wheel-rail contact relationships are considered, the threshold value of the derailment factor differs by 4.68%, and the GLPPGM has a wider applicability.
-
图 4 车-桥系统动力响应的标准差
Figure 4. Standard deviation of dynamic response of vehicle-bridge system
图 7 横、竖向轮轨力的相关系数
Figure 7. Correlation coefficient of lateral and vertical wheel-rail forces
表 1 车辆参数
Table 1. Train parameters
名称 拖车 动车 名称 拖车 动车 转向架轴距/m 2.5 2.5 x 向转向架转动惯量/（t•m2） 3.2 1.6 车辆定距/m 18 18 y 向转向架转动惯量/（t•m2） 7.2 1.7 一系悬挂横向跨距/m 0.33 0.34 z 向转向架转动惯量/（t•m2） 6.8 1.7 转向架导一系悬挂/m 2.05 2.05 一系纵向阻尼（单侧）/（kN•s•m−1） 960 960 二系悬挂横向跨距/m 2.05 2.05 一系横向阻尼（单侧）/（kN•s•m−1） 960 960 车体中心到二系悬挂/m 0.36 0.83 一系竖向阻尼（单侧）/（kN•s•m−1） 1040 700 二系悬挂到转向架/m 0.24 0.15 二系纵向阻尼（单侧）/（kN•s•m−1） 240 210 轮对滚动园半径/m 0.4575 0.4575 二系横向阻尼（单侧）/（kN•s•m−1） 240 210 轮对质量/t 1.9 2.2 二系竖向阻尼（单侧）/（kN•s•m−1） 400 350 轮对转动惯量/（t•m2） 1.067 1.63 一系纵向阻尼（单侧）/（kN•s•m−1） 0 0 转向架质量/t 3.4 1.7 一系横向阻尼（单侧）/（kN•s•m−1） 0 0 x 向车体转动惯量/（t•m2） 101.5 74 一系竖向阻尼（单侧）/（kN•s•m−1） 30 38 y 向车体转动惯量/（t•m2） 1064.4 1370 二系纵向阻尼（单侧）/（kN•s•m−1） 120 150 z 向车体转动惯量/（t•m2） 867.2 1370 二系横向阻尼（单侧）/（kN•s•m−1） 30 15 车体质量/t 42.4 44 二系竖向阻尼（单侧）/（kN•s•m−1） 33 40 
下载: 导出CSV
-
[1] 雷虎军,黄江泽. 考虑桩土相互作用的车-轨-桥系统地震响应分析[J]. 西南交通大学学报,2021,56(2): 229-237.LEI Hujun, HUANG Jiangze. Seismic responses analysis of train-track-bridge system considering pile-soil interaction[J]. Journal of Southwest Jiaotong University, 2021, 56(2): 229-237. [2] 何佳骏,向活跃,龙俊廷,等. 桥隧过渡段高速列车行车抗风安全分析[J]. 西南交通大学学报,2021,56(5): 1056-1064.HE Jiajun, XIANG Huoyue, LONG Junting, et al. Wind-resistant safety analysis of high-speed trains passing through bridge-tunnel transition[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 1056-1064. [3] 王伟,张亚辉,欧阳华江. 考虑轨道不平顺随机性的车轨耦合系统动力可靠度分析[J]. 大连理工大学学报,2019,59(2): 111-117.WANG Wei, ZHANG Yahui, OUYANG Huajiang. Dynamic reliability analysis of vehicle-track coupled systems considering randomness of track irregularities[J]. Journal of Dalian University of Technology, 2019, 59(2): 111-117. [4] 林家浩,张亚辉,赵岩. 虚拟激励法在国内外工程界的应用回顾与展望[J]. 应用数学和力学,2017,38(1): 1-31. doi: 10.1007/s10483-016-2152-6LIN Jiahao, ZHANG Yahui, ZHAO Yan. The pseudo-excitation method and its industrial applications in China and abroad[J]. Applied Mathematics and Mechanics, 2017, 38(1): 1-31. doi: 10.1007/s10483-016-2152-6 [5] XU L, ZHAI W M. Probabilistic assessment of railway vehicle-curved track systems considering track random irregularities[J]. Vehicle System Dynamics, 2018, 56(10): 1552-1576. doi: 10.1080/00423114.2018.1424916 [6] XIA C Y, XIA H, DE ROECK G. Dynamic response of a train-bridge system under collision loads and running safety evaluation of high-speed trains[J]. Computers & Structures, 2014, 140: 23-38. [7] 朱艳,李小珍,强士中. 高速铁路简支梁桥车桥系统随机响应[J]. 西南交通大学学报,2011,46(4): 535-540. doi: 10.3969/j.issn.0258-2724.2011.04.002ZHU Yan, LI Xiaozhen, QIANG Shizhong. Stochastic responses of train-bridge coupling system for simply-supported high-speed railway bridge[J]. Journal of Southwest Jiaotong University, 2011, 46(4): 535-540. doi: 10.3969/j.issn.0258-2724.2011.04.002 [8] HE X H, SHI K, WU T. An efficient analysis framework for high-speed train-bridge coupled vibration under non-stationary winds[J]. Structure and Infrastructure Engineering, 2020, 16(9): 1326-1346. doi: 10.1080/15732479.2019.1704800 [9] 赵岩,张亚辉,林家浩. 列车-结构耦合作用的随机振动分析方法[M]. 北京:科学出版社,2018:156-190. [10] ZHANG N, ZHOU Z J, WU Z Z. Safety evaluation of a vehicle-bridge interaction system using the pseudo-excitation method[J]. Railway Engineering Science, 2022, 30(1): 41-56. doi: 10.1007/s40534-021-00259-6 [11] 李杰,陈建兵. 随机动力系统中的概率密度演化方程及其研究进展[J]. 力学进展,2010,40(2): 170-188. doi: 10.6052/1000-0992-2010-2-J2009-105LI Jie, CHEN Jianbing. Advances in the research on probability density evolution equations of stochastic dynamical systems[J]. Advances in Mechanics, 2010, 40(2): 170-188. doi: 10.6052/1000-0992-2010-2-J2009-105 [12] YU Z W, MAO J F. A stochastic dynamic model of train-track-bridge coupled system based on probability density evolution method[J]. Applied Mathematical Modelling, 2018, 59: 205-232. doi: 10.1016/j.apm.2018.01.038 [13] XU L, ZHAI W M, GAO J M. A probabilistic model for track random irregularities in vehicle/track coupled dynamics[J]. Applied Mathematical Modelling, 2017, 51: 145-158. doi: 10.1016/j.apm.2017.06.027 [14] 刘章军,张传勇,齐东春. 高速列车乘坐舒适度评价的概率密度演化方法[J]. 振动与冲击,2018,37(14): 149-155.LIU Zhangjun, ZHANG Chuanyong, QI Dongchun. Probability density evolution method for the ride comfort evaluation of high speed trains[J]. Journal of Vibration and Shock, 2018, 37(14): 149-155. [15] LIU Z J, LIU Z H, PENG Y B. Simulation of multivariate stationary stochastic processes using dimension-reduction representation methods[J]. Journal of Sound and Vibration, 2018, 418: 144-162. doi: 10.1016/j.jsv.2017.12.029 [16] ZHANG N, XIA H. Dynamic analysis of coupled vehicle–bridge system based on inter-system iteration method[J]. Computers & Structures, 2013, 114/115: 26-34. [17] 张楠,郭薇薇,夏禾. 高速铁路车桥耦合动力学[M]. 北京:北京交通大学出版社,2018:171-177. [18] 方开泰,刘民千,覃红,等. 均匀试验设计的理论和应用[M]. 北京:北京科学出版社,2018. [19] MARSAGLIA G. Ratios of normal variables[J]. Journal of Statistical Software, 2006, 16(4): 1-10. [20] ZHU Y, LI X Z, JIN Z B. Three-dimensional random vibrations of a high-speed-train–bridge time-varying system with track irregularities[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail and Rapid Transit, 2015, 230(8): 1851-1876. [21] 翟婉明. 车辆-轨道耦合动力学(上册)[M]. 4版. 北京:科学出版社,2015:120-128. -
下载:
点击查看大图
计量
- 文章访问数: 73
- HTML全文浏览量: 35
- PDF下载量: 8
- 被引次数: 0