一种高静-低动刚度磁弹簧的建模与特性分析

张明; 谢延松; 李洪涛; 孙凤; 徐方超; 张磊

doi:10.3969/j.issn.0258-2724.20220821

一种高静-低动刚度磁弹簧的建模与特性分析

doi: 10.3969/j.issn.0258-2724.20220821

张明^1, ,,
谢延松¹,
李洪涛¹,
孙凤¹,
徐方超¹,
张磊²

1.
沈阳工业大学机械工程学院，辽宁沈阳 110870
2.
辽宁科技学院机械工程学院，辽宁本溪 117004

基金项目: 国家自然科学基金（52005344，52005345）；国家重点研发计划（2020YFC2006701）；辽宁省自然科学基金（2022-MS-271）；辽宁省教育厅青年项目（LJKQZ2021044）；辽宁省教育厅科学研究经费（202007141）

详细信息

通讯作者:
张明（1988—），男，副教授，研究方向为磁力减震与柔性机器人技术，E-mail：mingzhang@sut.edu.cn

中图分类号: TH135；TB535.1
计量
- 文章访问数: 337
- HTML全文浏览量: 589
- PDF下载量: 57
- 被引次数: 1
出版历程
- 收稿日期: 2022-11-24
- 修回日期: 2023-03-17
- 网络出版日期: 2023-06-16
- 刊出日期: 2023-03-30

Modeling and Characteristic Analysis of a Magnetic Spring with High Static Stiffness and Low Dynamic Stiffness

1.
School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China
2.
School of Mechanical Engineering, Liaoning Institute of Science and Technology, Benxi 117004, China

摘要

摘要:
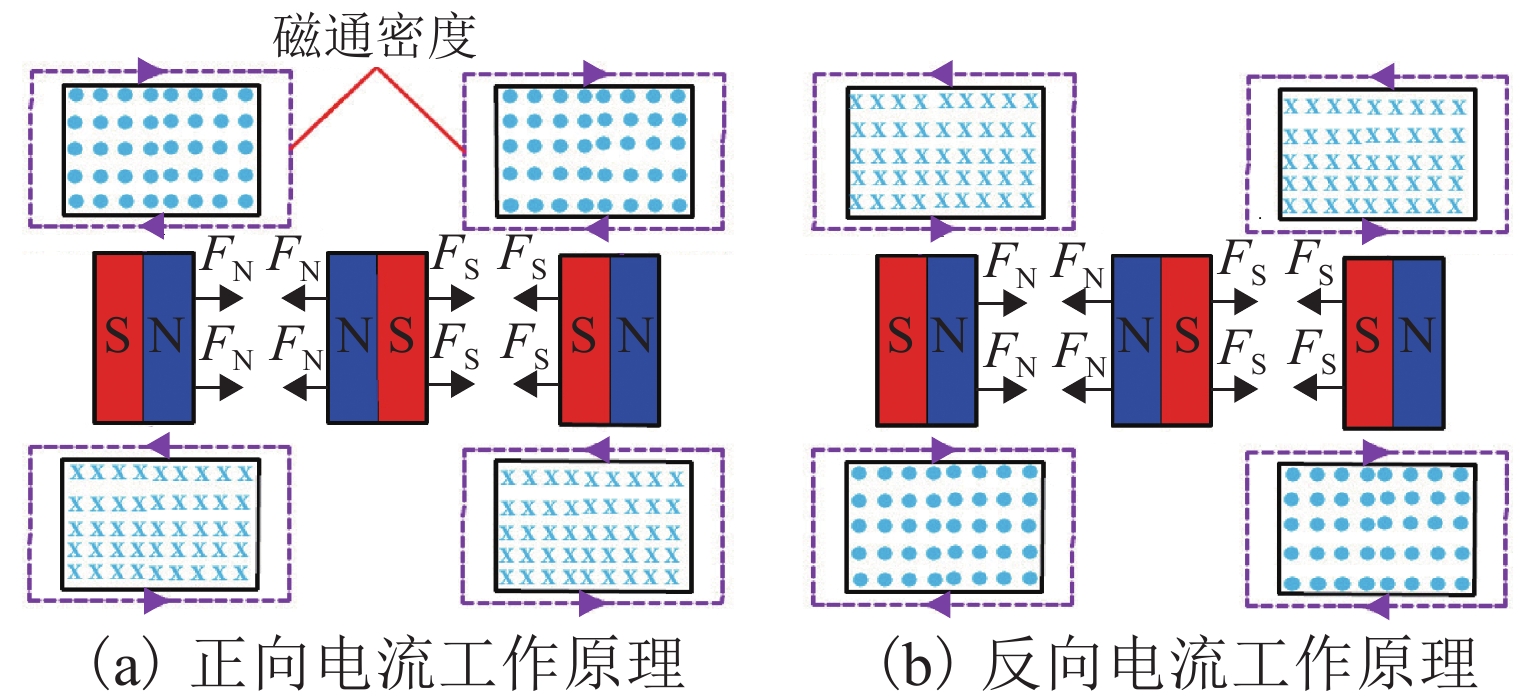
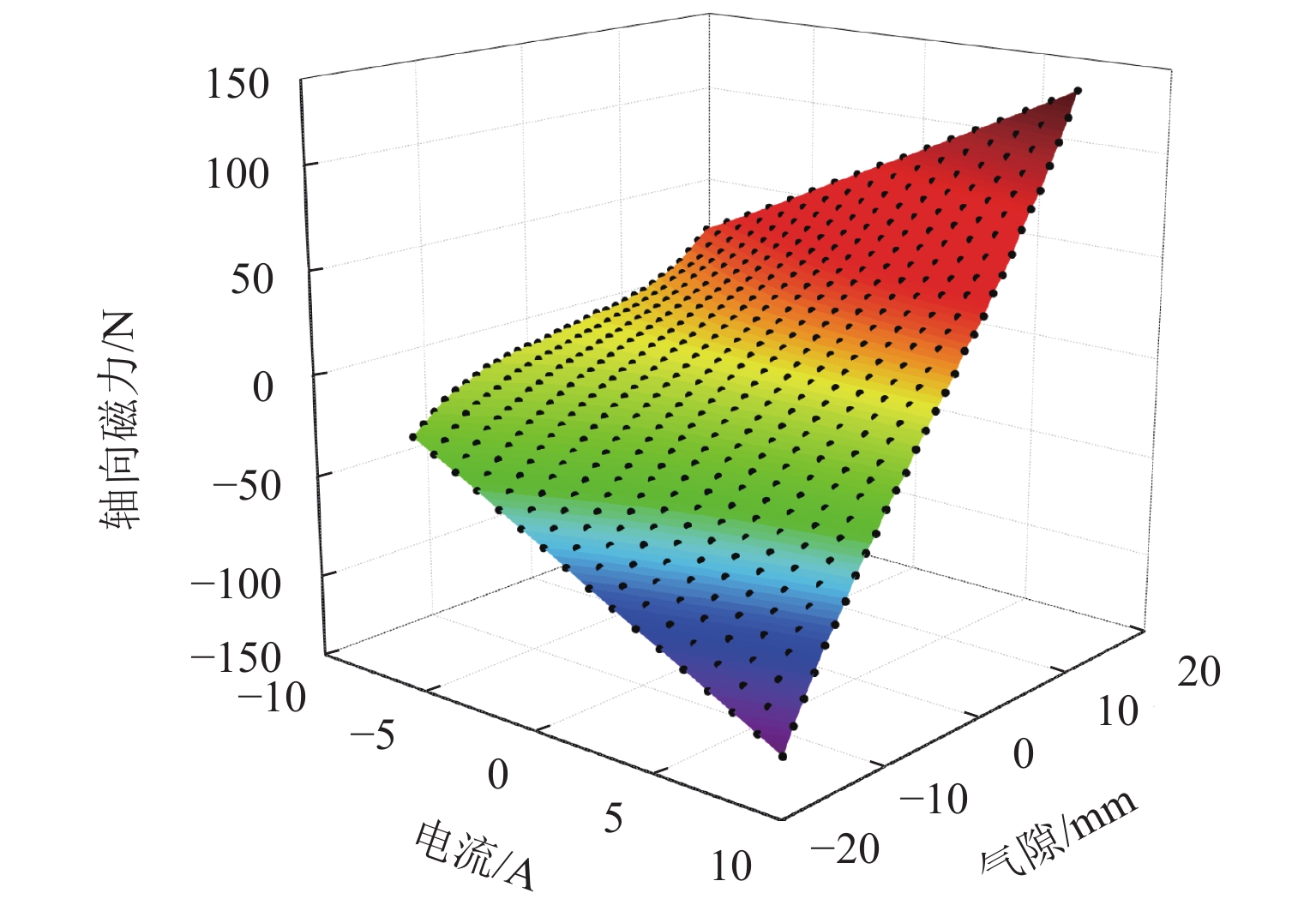
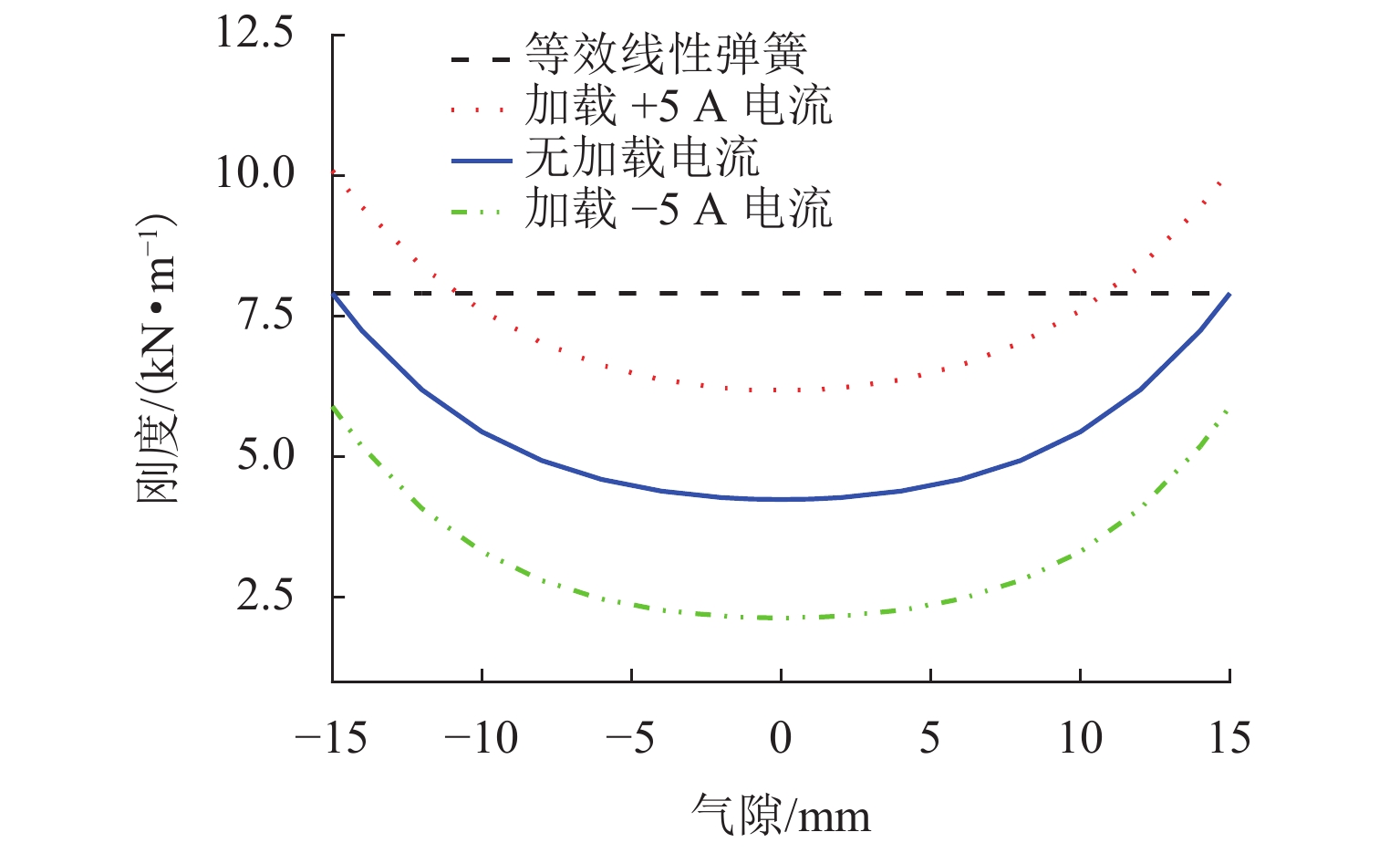
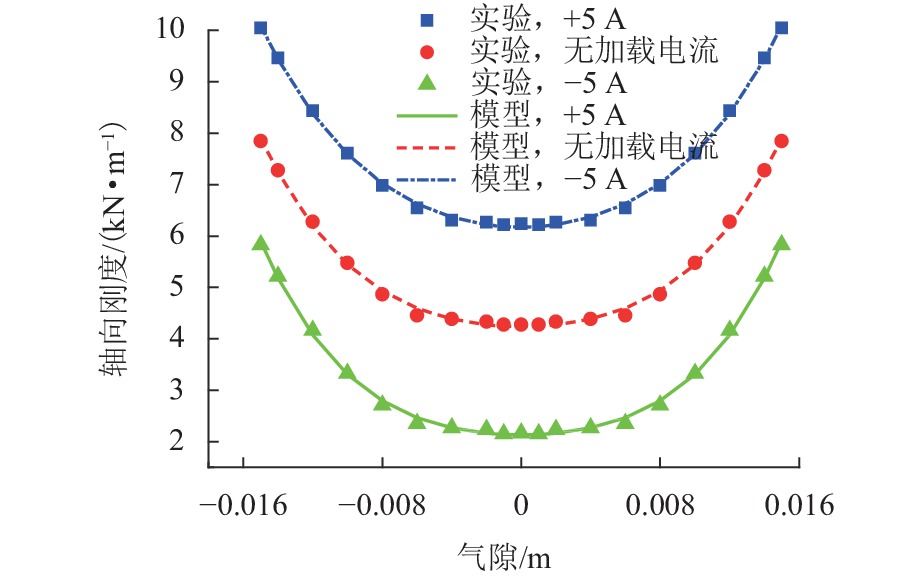
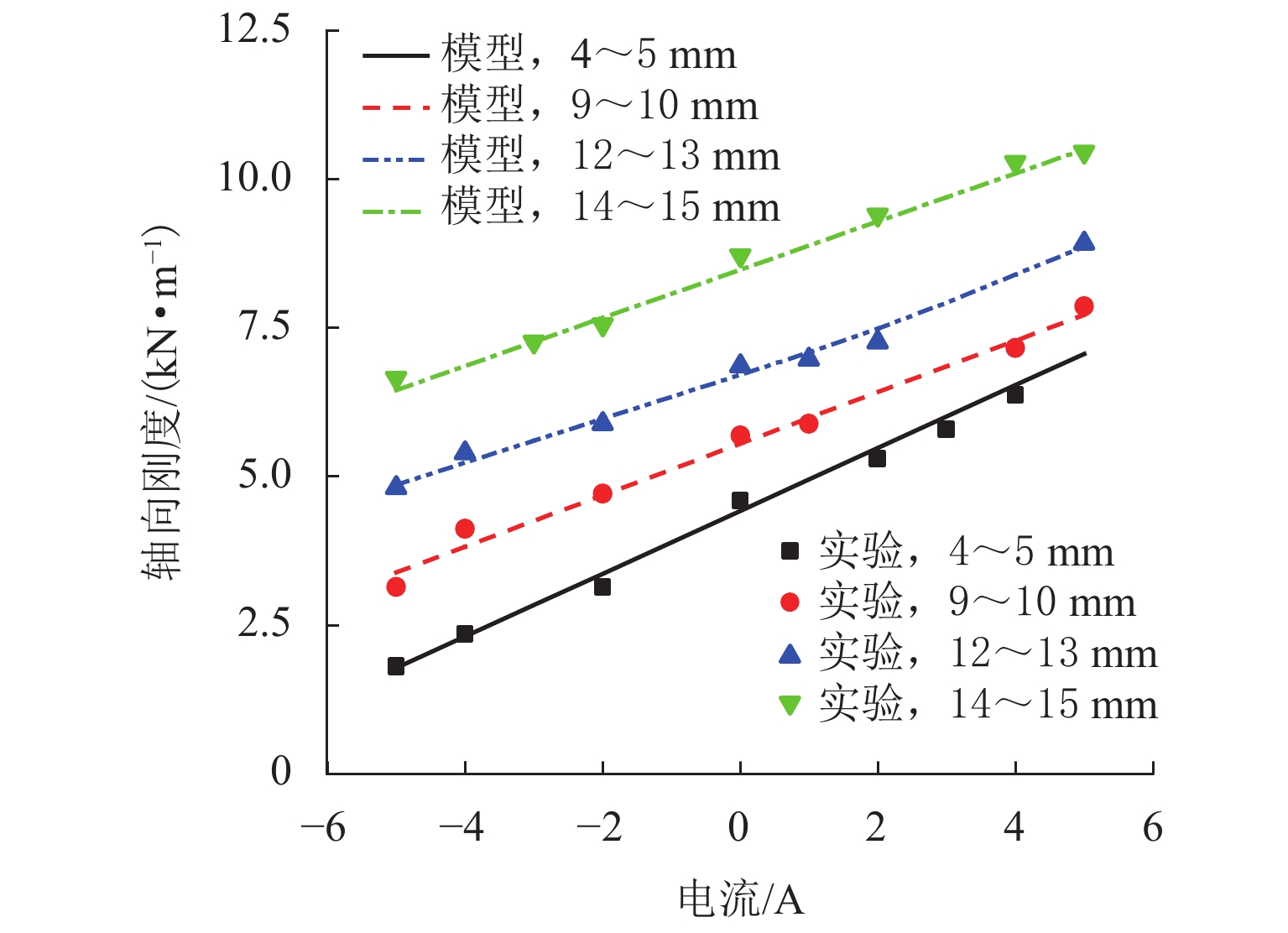
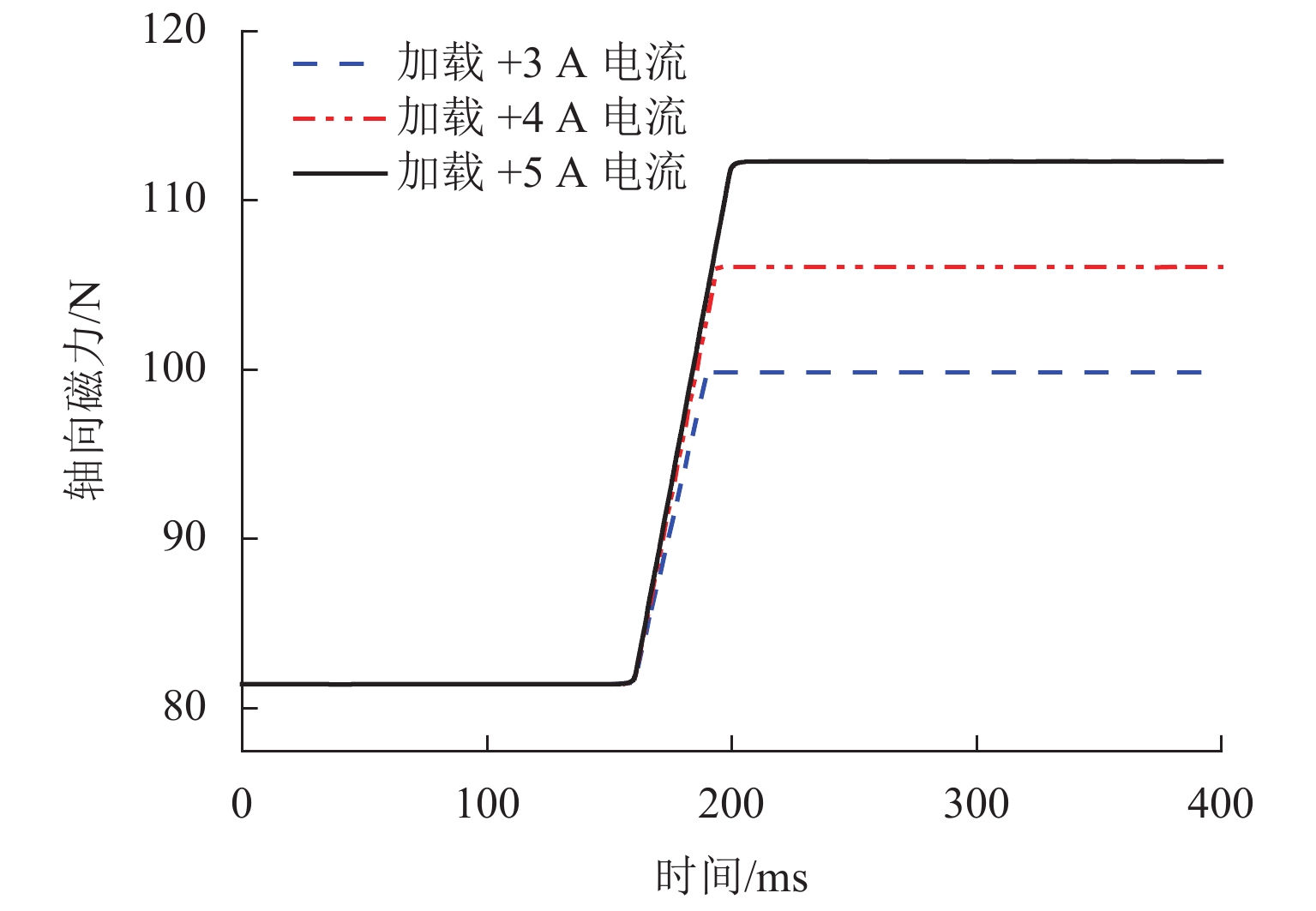
为解决低频隔振领域存在的低固有频率和高承载力之间的矛盾，设计了一种新型高静-低动刚度磁弹簧元件. 首先，基于电磁场理论和分子电流法建立磁弹簧的弹簧力和刚度模型；其次，建立系统的动力学模型，同时分析线圈通入不同电流时对位移传递率的影响，并与等效线性弹簧进行比较；最后，研制实验样机并进行实验研究. 仿真与实验结果表明：磁弹簧气隙-刚度曲线呈先平缓后急剧的非线性关系，具有明显的高静-低动刚度特性；其刚度与电流近似线性关系，磁弹簧可通过改变电流实现较大范围的刚度调整，且刚度响应迅速；在未通入电流时，相对于等效线性弹簧，起始隔振频率和传递率峰值降低26%，在通入负向额定电流时，起始隔振频率和传递率峰值降低了41%.
- 低频隔振 /
- 高静-低动 /
- 磁弹簧 /
- 电流 /
- 非线性
Abstract:
A novel magnetic spring element with high static stiffness and low dynamic stiffness was designed to address the conflict between low natural frequency and high bearing capacity in the field of low-frequency vibration isolation. First, the spring force and stiffness models of the magnetic spring were built based on electromagnetic field theory and molecular current method; secondly, the dynamics model of the system was established, and the influence of coils with different currents on displacement transmissibility was analyzed and compared with the equivalent linear spring; finally, an experimental prototype was developed, and an experimental study was carried out. The simulation and experimental results show that the air-gap stiffness curve of the magnetic spring presents a nonlinear relationship of being initially flat and then sharp, which indicates obvious characteristics of high static stiffness and low dynamic stiffness. The stiffness is approximately linear with the current. The magnetic spring can achieve a wide range of stiffness adjustment by changing the current, and the stiffness response is rapid; when no current is applied, the starting vibration isolation frequency and peak transmissibility are decreased by 26% compared with the equivalent linear spring. When a negative rated current is applied, the starting vibration isolation frequency and peak transmissibility are reduced by 41%.
- low-frequency vibration isolation /
- high static stiffness and low dynamic stiffness /
- magnetic spring /
- current /
- nonlinear

HTML全文

高速磁悬浮列车因具有速度快、爬坡强、噪声小、平稳性好等优点，成为一种新型轨道交通工具. 在磁浮列车高速运行时，由于车体与轨道不接触，所以列车的受流需采用无接触受流方式. 因此，高速磁悬浮列车的辅助供电是关键技术之一，无接触式直线谐波发电机成为重要研究方向^[1-3].

高速磁悬浮列车用直线谐波发电机主要应用于常导电磁悬浮系统（electromagnetic suspension, EMS）和超导电动悬浮系统（electrodynamic suspension, EDS）^[4-7]. 电磁悬浮系统直线发电机的研究主要包括：磁悬浮列车低速运行时，向长定子中注入高频电流和在列车的磁极上加绕一组直线发电机线圈，实现磁悬浮列车在低速运行时车载蓄电池的充足供电^[8]. 文献[9]利用有限元法构建发电机数学模型，在发电机输出特性基础上，定义了目标函数，并针对目标函数优化发电机的配置，得到输出特性的最优解. 文献[10]利用有限元仿真求解出直线发电机感应电动势. 文献[11]通过解析计算求得发电机的磁通密度以及感应电动势. 文献[12]通过解析计算，推导出直线发电机电阻、电感等主要参数.

在超导电动悬浮系统领域，文献[13]针对超导电动悬浮系统直线发电机，利用ANSYS有限元软件建立其三维模型，分析其在多运行工况下感应电动势、输出功率等特性. 文献[14]在前者基础之上，补充了超导线圈杜瓦外壳的涡流对直线发电机输出特性的影响，并对杜瓦外壳结构进行优化，优化后的杜瓦外壳能增大集电功率. 文献[15-16]提出直线发电机的电流控制方法，利用瞬时电流补偿无功功率，实现直线发电机等效电路功率因数为1. 文献[17-18]提出用于EDS系统的直线发电机，不但具备发电功能，而且具备调节电动悬浮列车转向架阻尼的特性，磁悬浮列车的悬浮力随集电线圈感应电流的相位变化而变化，通过改变相位获得电磁力，从而提高磁浮列车转向架阻尼. 文献[19]针对改进的集电线圈的尺寸和布置，提出一种采用零序电流控制的直线发电机系统，向集电线圈注入零序电流，在垂直方向产生电磁力，通过试验验证，发现该系统能有效抑制转向架振动. 文献[20]提出一种无传感器的垂向阻尼器，通过向直线发电机集电线圈中注入零序电流以产生垂直方向电磁力，提升转向架阻尼. 目前，对电动悬浮系统直线发电机的研究局限于有限元仿真以及直线发电机的阻尼特性分析，对超导电动悬浮系统直线谐波发电机发电特性的研究不足.

综上，本文针对超导电动悬浮系统用直线谐波发电机的发电特性（超导线圈磁感应强度、悬浮线圈电流以及谐波磁场、集电线圈感应电动势）展开研究. 以日本山梨线MLX01型磁浮列车作为工程研究对象，提出超导线圈的磁动势分布模型，利用解析计算的方法推导出集电线圈感应电动势，通过与有限元、实测数据的比较，验证解析模型的有效性，该解析模型求解速度快，在电动悬浮系统直线谐波发电机的发电特性分析上具备较大优势，为电动悬浮系统直线发电机的设计和控制提供理论基础.

1. 直线发电机结构和工作原理

超导电动悬浮系统直线发电机的拓扑结构如图1所示. 直线发电机主要由超导线圈、悬浮线圈、集电线圈组成，v为磁浮列车运行速度. 超导线圈安装在磁悬浮列车转向架两侧，集电线圈固定于超导线圈外侧，悬浮线圈位于轨道侧壁，沿线路铺设，用于悬浮和导向功能. 转向架单侧有4个超导线圈，相邻超导线圈的极性相反，一个超导线圈极距下对应一组悬浮线圈和一组集电线圈. 其中，悬浮线圈3个为一组，集电线圈4个为一组.

图 1 直线谐波发电机结构与安装位置

Figure 1. Linear harmonic generator structure and installation location

下载: 全尺寸图片幻灯片

电动悬浮系统直线谐波发电机的线圈排布如图2所示. 超导线圈在x轴方向极距为τ，悬浮线圈极距为τ₁. 超导线圈长度为a₀，悬浮线圈长度为a₁. 一组集电线圈由2个R相、1个S相和1个T相组成. R相、S相和T相集电线圈长度分别为a_2R、a_2S和a_2T. S、T两相极距为4τ/15，R相之间极距为x_2R.

图 2 直线谐波发电机的线圈排布

Figure 2. Coil arrangement of linear harmonic generator

下载: 全尺寸图片幻灯片

直线谐波发电机的运行原理为：高速磁浮列车运行时，通电的超导线圈掠过悬浮线圈，在悬浮线圈内产生感应电动势，从而产生感应电流和磁场^[6]. 同时，集电线圈与悬浮线圈存在相对位移，集电线圈切割悬浮线圈感应磁场，产生感应电动势.

2. 解析方法

2.1 超导线圈磁感应强度

利用空间谐波法，在x、z方向分别构建超导线圈磁动势周期性模型. 其中：x方向为实际存在的超导线圈，z方向为假设存在无限多的超导线圈，如图3所示. 图中：F_x(x)、F_z(z)分别为超导线圈在x、z轴方向的磁动势；F_z0(x) 为超导线圈在中心z = z₀的磁动势；b₀为超导线圈高度；τ_z为z方向极距；N_s为超导线圈匝数；I_s为单匝线圈电流.

图 3 超导线圈磁动势分布模型

Figure 3. Magnetomotive force distribution model of superconducting coil

下载: 全尺寸图片幻灯片

由于相邻超导线圈极性相反，其磁动势沿x方向分布如图3（a）所示. 超导线圈中心z = z₀，将超导线圈磁动势展开为傅里叶级数，如式（1）所示.

${F_{{{\textit{z}}_0}}}(x) = \sum\limits_{m = 1}^\infty {{a_{xm}}\cos \left(\frac{{m{\text{π }}}}{\tau}x\right)},$

(1)

${a_{xm}} = \frac{1}{\tau}\int_{ - \tau}^\tau {{F_x}(x)\cos \left(\frac{{m{\text{π }}}}{\tau}x\right)} {\text{d}}x,$

(2)

式中：a_xm 为x轴方向傅里叶级数系数.

超导线圈磁动势沿z方向分布如图3（b）所示，其傅里叶级数系数a_zn （n = 1，2，3，…）为

${a_{{\textit{z}}n}} = \frac{1}{{{\tau_{\textit{z}}}}}\int_{ - {\tau_{\textit{z}}}}^{{\tau_{\textit{z}}}} {{F_{\textit{z}}}({\textit{z}})\cos \left(\frac{{n{\text{π }}}}{{{\tau_{\textit{z}}}}}{\textit{z}}\right){\text{d}}{\textit{z}}}.$

(3)

由此，可推出超导线圈磁动势在xOz平面的分布为

$\begin{split} & F(x,{\textit{z}}) = \sum\limits_{n = 1}^\infty {{a_{{\textit{z}}n}}\cos \left[\frac{{n{\text{π}}}}{{{\tau_{\textit{z}}}}}({\textit{z}} - {{\textit{z}}_0})\right]} {\text{ = }}\frac{{16{{{N}}_s}{{{I}}_s}}}{{{{\text{π}}^{\mathbf{2}}}}}\times\\ &\quad \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {mn{c_{xm}}{c_{{\textit{z}}n}}\cos ({{{k}}_{{{xm}}}}{{x}})\cos } } \left[ {{{{k}}_{{{{\textit{z}}n}}}}({{{\textit{z}} - }}{{{{\textit{z}}}}_{{0}}})} \right] , \end{split}$

(4)

式中：${k_{xm}} = {{m{\text{π }}}}/\tau；{k_{{\textit{z}}n}} = {{n{\text{π }}}}/{{{\tau_{\textit{z}}}}}；{\text{ }}{c_{xm}} = \sin ({{{k_{xm}}{a_0}}}/{2})； {c_{{\textit{z}}n}} = \sin ({{{k_{{\textit{z}}n}}{b_0}}}/{{\text{2}}}) $.

由边界条件和拉普拉斯方程求出超导线圈的标量磁位ψ（x,y,z），如式（5）所示.

$\left\{ \begin{gathered} \psi (x,0,{\textit{z}}) = F(x,{\textit{z}})/2, \\ \psi (x,\infty ,{\textit{z}}) = 0 , \\ {\nabla ^2}\psi (x,y,{\textit{z}}) = 0. \\ \end{gathered} \right.$

(5)

利用磁位与磁感应强度的关系式，得到超导线圈在y方向的磁感应强度为

${B_y} = - {\mu _0}\frac{{\partial \psi (x,y,{\textit{z}})}}{{\partial y}},$

(6)

式中：μ₀为真空磁导率.

求解式（6）得

$\begin{split} &{B_y} = \frac{{8{\mu _0}{{{N}}_s}{{{I}}_s}}}{{{{\text{π}}^2}}}\sum\limits_{m = 1}^\infty \sum\limits_{n = 1}^\infty mn{\lambda _{mn}}{c_{xm}}{c_{{\textit{z}}n}}{{\rm{e}}^{ - {\lambda _{mn}}(y - {y_0})}}\times \\ &\quad \cos ({k_{xm}}x)\cos \left[ {{k_{{\textit{z}}n}}({\textit{z}} - {{\textit{z}}_0})} \right], \end{split}$

(7)

式中：$ {\lambda _{mn}} = \sqrt {k_{xm}^2 + k_{{\textit{z}}n}^2} $； y₀为超导线圈中心纵坐标.

2.2 悬浮线圈电流及其磁感应强度

超导线圈、集电线圈和悬浮线圈在yOz平面的位置关系如图4所示. 原点为列车转向架中心. 超导线圈中心位置为（x₀，y₀，z₀），集电线圈中心坐标为（x₂，y₂，0），悬浮线圈中心坐标为（x₁，y₁，0）. z_1U、z_1B分别为悬浮线圈上线圈中心、下线圈中心的z轴坐标；z_2U、z_2B分别为集电线圈上线圈中心、下线圈中心的z轴坐标.

图 4 yOz平面内线圈间位置关系

Figure 4. Positional relationship between coils in the yOz plane

下载: 全尺寸图片幻灯片

悬浮线圈固定于轨道侧壁，与地面保持静止，而超导线圈固定于车体，并随列车一同移动. 设时间t = 0时超导线圈中心正对的悬浮线圈编号为0号，沿x正方向依次为0，1，2，…，第V个悬浮线圈中心的x轴坐标为

${x_V} = V{\tau_1} - vt，$

(8)

式中：τ₁为磁浮线圈的极距.

根据超导线圈的磁场与悬浮线圈存在交链关系，对超导线圈磁场与集电线圈所在区域进行积分，求解得到超导线圈磁感应强度与悬浮线圈上线圈的交链磁通ϕ_1U以及超导线圈磁感应强度与悬浮线圈下线圈的交链磁通ϕ_1B，分别如式（9）、（10）所示.

${\phi _{{\text{1U}}}}{\text{ = }}\int_{{x_1} - {a_1}/2}^{{x_1} + {a_1}/2} {\int_{{{\textit{z}}_{{\text{1U}}}} - {b_1}/2}^{{{\textit{z}}_{{\text{1U}}}} + {b_1}/2} {{B_y}{\text{d}}x{\text{d}}{\textit{z}}} },$

(9)

${\phi _{{\text{1B}}}}{\text{ = }}\int_{{x_1} - {a_1}/2}^{{x_1} + {a_1}/2} {\int_{{{\textit{z}}_{{\text{1B}}}} - {b_1}/2}^{{{\textit{z}}_{{\text{1B}}}} + {b_1}/2} {{B_y}{\text{d}}x{\text{d}}{\textit{z}}} },$

(10)

式中：b₁为悬浮线圈上线圈与下线圈的高度.

超导线圈磁感应强度与悬浮线圈交链的总磁通量为

${\phi _1} = {\phi _{1{\text{B}}}} - {\phi _{{\text{1U}}}}.$

(11)

悬浮线圈电流的回路方程为

${R_1}{i_V} + {L_1}\frac{{{\text{d}}{i_1}}}{{{\text{d}}t}} = - {{{N}}_{\text{1}}}\frac{{{\text{d}}{\phi _1}}}{{{\text{d}}t}}，$

(12)

式中：R₁为悬浮线圈电阻； L₁为悬浮线圈电感； N₁为悬浮线圈的匝数；i_V为第V个悬浮线圈感应电流，如式（13）所示.

${i_V} = {{{N}}_1}{g_1}(\omega )\sum\limits_{m = 1}^\infty {m({P_{\text{B}}} - {P_{\text{U}}})\cos (m\omega t - m{\text{π}}V/3)} \text{，}$

(13)

$\omega = \frac{{\text{π }}}{\tau}v,$

(14)

${g_1}(\omega ) = - \frac{{{\text{j}}\omega }}{{{R_1} + {\text{j}}\omega {L_1}}},$

(15)

式中：ω为悬浮线圈电流的基波频率；g₁(ω)为能够反映悬浮线圈的导纳.

P_i为悬浮线圈与超导线圈间的位置函数，反映了超导和悬浮线圈间的电磁耦合紧密程度，i∈{B,U}，U代表上线圈，B代表下线圈.

$\begin{split} &{P_i} = \dfrac{{32{\mu _0}{{{N}}_{\text{s}}}{{{I}}_s}}}{{\tau{\tau_{\textit{z}}}}}\times\\ &\quad \sum\limits_{n = 1}^\infty {{\lambda _{mn}}{{{S}} _{{\text{sc}}}}{{{S}} _{{\text{lev}}}}{{\rm{e}}^{ - {\lambda _{mn}}({y_1} - {y_2})}}} \cos \left[ {{k_{{\textit{z}}n}}({{\textit{z}}_{1i}} - {{\textit{z}}_0})} \right] , \end{split}$

(16)

式中：S_sc、S_lev为系数，见式（17）.

$\left\{ \begin{gathered} {{{S}} _{{\text{sc}}}} = \frac{{\sin ({k_{xm}}{a_0}/2)\sin ({k_{{\textit{z}}n}}{b_0}/2)}}{{{k_{xm}}{k_{{\textit{z}}n}}}}, \\ {{{S}} _{{\text{lev}}}} = \frac{{\sin ({k_{xm}}{a_1}/2)\sin ({k_{{\textit{z}}n}}{b_1}/2)}}{{{k_{xm}}{k_{{\textit{z}}n}}}}. \\ \end{gathered} \right.$

(17)

悬浮线圈电流的谐波分量随时间的变化曲线如图5所示. 由图可知：悬浮线圈电流主要由基波分量和三次谐波分量构成. 本文只考虑悬浮线圈电流的基波分量以及三次谐波分量产生的磁感应强度. 悬浮线圈电流的基波分量幅值I_V1、三次谐波分量幅值I_V3分别如式（18）、（19）所示.

图 5 悬浮线圈电流谐波分析

Figure 5. Current harmonic analysis of suspension coil

下载: 全尺寸图片幻灯片

${I_{V{\text{1}}}} = {{{N}}_{\text{1}}}{g_1}(\omega )({P_{\text{B}}} - {P_{\text{U}}}),$

(18)

${I_{V3}} = 3{{{N}}_{\text{1}}}{g_1}(3\omega )({P_{\text{B}}} - {P_{\text{U}}}).$

(19)

悬浮线圈电流的磁感应强度求解步骤和推导超导线圈磁感应强度的方法类似，此处不再赘述. 求解得到基波电流的磁感应强度B_11i和三次谐波电流的磁感应强度B_13i分别如式（20）、（21）所示.

${B_{11{{i}}}} = \left\{ \begin{gathered} \frac{{ - 12{{{N}}_{\text{1}}}{\mu _0}}}{{\tau {\tau _{\textit{z}}}}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty \begin{gathered} {I_{V{\text{1}}}}{\lambda _{mn}}{{{S}} _{{\text{lev}}}}\cos [{k_{{\textit{z}}n}}({\textit{z}} - {{\textit{z}}_{{{1i}}}})] {{\rm{e}}^{ - {\lambda _{mn}}|y - {y_1}|}}\cos \left[ {{k_{xm}}x - (m - 1)\omega t} \right],\quad m{\text{ = 1，7，13}}，\cdots, \end{gathered} } \\ \frac{{ - 12{{{N}}_{\text{1}}}{\mu _0}}}{{\tau {\tau _{\textit{z}}}}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty \begin{gathered} {I_{V{\text{1}}}}{\lambda _{mn}}{{{S}} _{{\text{lev}}}}\cos [{k_{{\textit{z}}n}}({\textit{z}} - {{\textit{z}}_{{{1i}}}})] {{\rm{e}}^{ - {\lambda _{mn}}|y - {y_1}|}}\cos \left[ {{k_{xm}}x{\text{ + }}(m{\text{ + }}1)\omega t} \right] ,\quad m{\text{ = 5，11，17}}，\cdots, \end{gathered} } \end{gathered} \right.$

(20)

$\begin{gathered} {B_{{{13i}}}} = \frac{{24{{{N}}_{\text{1}}}{\mu _0}}}{{\tau {\tau _{\textit{z}}}}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty \begin{gathered} {I_{V{\text{3}}}}{\lambda _{3m,n}}{{{S}} _{{\text{lev}}}}\cos (3m\omega t + 3{k_{xm}}x) \cos \left( {3\omega t} \right)\cos [{k_{{\textit{z}}n}}({\textit{z}} - {{\textit{z}}_{{{1i}}}})]{{\rm{e}}^{ - {\lambda _{mn}}|y - {y_1}|}}, \quad m = 3，9，15，\cdots. \end{gathered} } \end{gathered}$

(21)

悬浮线圈电流产生的谐波磁场如图6所示，分析得知：悬浮线圈电流的感应磁场主要由基波磁场、五次谐波磁场构成. 由于基波磁场与随列车一同运动的集电线圈间不存在相对位移，无法在集电线圈中产生感应电动势. 而五次谐波磁场与集电线圈存在相对位移，五次谐波磁场切割集电线圈，继而产生感应电动势. 由于五次以上的高次谐波磁场含量很小，为简化计算，可忽略五次以上谐波磁场，故本文将五次谐波磁场作为发电磁场.

图 6 悬浮线圈电流产生的谐波磁场

Figure 6. Harmonic magnetic field generated by suspension coil current

下载: 全尺寸图片幻灯片

令式（20）中m = 5，则五次谐波磁场的磁感应强度如式（22）所示.

$\begin{split} &{B_{15i}} = \frac{{ - 12{{{N}}_{\text{1}}}{\mu _0}}}{{\tau{\tau_{\textit{z}}}}} \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{I_{V{\text{1}}}}{\lambda _{mn}}{{{S}} _{{\text{lev}}}}} {{\rm{e}}^{ - {\lambda _{mn}}|y - {y_1}|}}} \times \\ &\quad \cos [{k_{{\textit{z}}n}}({\textit{z}} - {{\textit{z}}_{{{1i}}}})]\cos \left[ {{k_{xm}}x{\text{ + }}(m{\text{ + }}1)\omega t} \right] . \end{split}$

(22)

2.3 集电线圈感应电动势

悬浮线圈电流产生的五次谐波磁场在集电线圈所在区域进行积分，求解得到悬浮线圈上、下线圈与集电线圈上、下线圈的交链磁通，如式（23）、（24）所示.

${\phi _{i{\text{U}}}} = \int_{{x_2} - \tfrac{{{x_{2{\text{R}}}}}}{2} - \tfrac{{{a_{2{\text{R}}}}}}{2}}^{{x_2} - \tfrac{{{x_{2{\text{R}}}}}}{2} + \tfrac{{{a_{2{\text{R}}}}}}{2}} {\int_{{{\textit{z}}_{{\text{2U}}}} - \tfrac{{{b_{{\text{2U}}}}}}{2}}^{{{\textit{z}}_{{\text{2U}}}} + \tfrac{{{b_{{\text{2U}}}}}}{2}} {{B_{{{15i}}}}{\text{d}}x{\text{d}}{\textit{z}}} },$

(23)

${\phi _{i{\text{B}}}} = \int_{{x_2}-\tfrac{{{x_{2{\text{R}}}}}}{2} - \tfrac{{{a_{2{\text{R}}}}}}{2}}^{{x_2}-\tfrac{{{x_{2{\text{R}}}}}}{2} + \tfrac{{{a_{2{\text{R}}}}}}{2}} {\int_{{{\textit{z}}_{{\text{2B}}}} - \tfrac{{{b_{{\text{2B}}}}}}{2}}^{{{\textit{z}}_{{\text{2B}}}} + \tfrac{{{b_{{\text{2B}}}}}}{2}} {{B_{{{15i}}}}{\text{d}}x{\text{d}}{\textit{z}}} },$

(24)

式中：ϕ_UU为集电线圈上线圈与悬浮线圈上线圈磁感应强度的交链磁通；ϕ_BU为集电线圈上线圈与悬浮线圈下线圈磁感应强度的交链磁通；ϕ_UB为集电线圈下线圈与悬浮线圈上线圈磁感应强度的交链磁通；ϕ_BB为集电线圈下线圈与悬浮线圈下线圈磁感应强度的交链磁通；b_2B为集电线圈下线圈的高度；b_2U为集电线圈上线圈的高度.

R相集电线圈与悬浮线圈五次谐波磁场交链磁通ϕ₂如式（25）所示.

$\qquad\begin{gathered} {\phi _2} = {\phi _{{\text{UU}}}} - {\phi _{{\text{UB}}}} + {\phi _{{\text{BB}}}} - {\phi _{{\text{BU}}}} = - \frac{{48{{{N}}_{\text{1}}}{\mu _0}}}{{\tau {\tau _{\textit{z}}}}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty \begin{gathered} {I_{V1}}{\lambda _{mn}}{{{S}} _{{\text{lev}}}}{{K}}{{\rm{e}}^{ - {\lambda _{mn}}|{y_2} - {y_1}|}} \cos \left[ {{k_{xm}}({x_2} - {x_{2{\text{R}}}}/2) + 6\omega t} \right] , \end{gathered} } \end{gathered}$

(25)

$\qquad\begin{gathered} {{K}} = {{{S}} _{\text{U}}}\cos \left[ {{k_{{\textit{z}}n}}({{\textit{z}}_{{\text{1U}}}} - {{\textit{z}}_{{\text{2U}}}})} \right] - {{{S}} _{\text{U}}}\cos \left[ {{k_{{\textit{z}}n}}({{\textit{z}}_{{\text{1B}}}} - {{\textit{z}}_{{\text{2U}}}})} \right] {\text{ }} + {{{S}} _{\text{B}}}\cos \left[ {{k_{{\textit{z}}n}}({{\textit{z}}_{{\text{1B}}}} - {{\textit{z}}_{{\text{2B}}}})} \right] - {{{S}} _{\text{B}}}\cos \left[ {{k_{{\textit{z}}n}}({{\textit{z}}_{{\text{1U}}}} - {{\textit{z}}_{{\text{2B}}}})} \right] , \end{gathered}$

(26)

式中：S_B、S_U为系数，见式（27）.

$\left\{ \begin{gathered} {{{S}} _{\text{B}}} = \frac{{\sin ({k_{xm}}{a_{{\text{2R}}}}/2)\sin ({k_{{\textit{z}}n}}{b_{2{\text{B}}}}/2)}}{{{k_{xm}}{k_{{\textit{z}}n}}}} , \\ {{{S}} _{\text{U}}} = \frac{{\sin ({k_{xm}}{a_{2{\text{R}}}}/2)\sin ({k_{{\textit{z}}n}}{b_{2{\text{U}}}}/2)}}{{{k_{xm}}{k_{{\textit{z}}n}}}}. \\ \end{gathered} \right.$

(27)

R相集电线圈感应电动势e_R与交链磁通ϕ₂的关系如式（28）所示.

${e_{\text{R}}} = - \frac{{{\text{d}}{\phi _2}}}{{{\text{d}}t}}.$

(28)

推导得出

$\begin{split} & {e_{\text{R}}} = \frac{{288\omega {{{N}}_{\text{1}}}{\mu _0}}}{{\tau{\tau_{\textit{z}}}}}\sum\limits_{m = 1}^\infty \sum\limits_{n = 1}^\infty {I_{V1}}{\lambda _{mn}}{{{S}} _{{\text{lev}}}}{{K}}{{\rm{e}}^{ - {\lambda _{mn}}|{y_2} - {y_1}|}} \times\\ &\quad \sin \left[ {6\omega t + {k_{xm}}({x_2} - {x_{2u}}/2)} \right] . \end{split}$

(29)

由感应电动势表达式可知：感应电动势幅值与列车运行速度相关，其频率是悬浮线圈电流基波频率的6倍. 其余相集电线圈感应电动势求解与上述求解过程类似，此处不再赘述.

3. 结果分析

根据日本山梨线电动悬浮系统直线谐波发电机的基本参数^[18,21]（如表1所示），通过ANSYS有限元软件建立直线谐波发电机的三维有限元仿真模型（如图7所示），且利用日本山梨线实测数据^[19,22]进行对比，进一步验证磁动势分布模型、解析公式的正确性. 图8为试验装置图^[23].

表 1 直线谐波发电机基本参数

Table 1. Parameters of linear harmonic generator

线圈	参数	数值
集电线圈	a_2R/mm	200
	a_2S/mm	245
	a_2T/mm	245
	b_2U/mm	435
	b_2B/mm	245
	与超导线圈间距/mm	75
悬浮线圈	a₁/mm	350
	b₁/mm	340
	N₁/匝	24
	τ₁/mm	450
	与超导线圈间距/mm	185
超导线圈	a₀/mm	1070
	b₀/mm	500
	N_s/匝	1400
	τ/mm	1350
	I_s/A	500

下载: 导出CSV

| 显示表格

图 7 利用ANSYS 2019 R2建立的三维模型

Figure 7. 3D model created with ANSYS 2019 R2

下载: 全尺寸图片幻灯片

图 8 试验装置

Figure 8. Test device

下载: 全尺寸图片幻灯片

超导线圈磁感应强度B_y沿着x轴方向分布如图9所示. 可知：两条曲线均呈马鞍形，解析计算峰值为885.7 mT，峰值的有限元结果为875.8 mT，相对误差为1.1%，验证了磁动势分布模型的有效性.

图 9 超导线圈磁感应强度

Figure 9. Magnetic induction intensity of superconducting coil

下载: 全尺寸图片幻灯片

列车速度500 km/h，悬浮线圈电流的解析值与有限元仿真的对比如图10所示. 解析计算的峰值为918 A，有限元结果为888 A，相对误差为3.2%，验证了解析模型的正确性.

图 10 悬浮线圈电流

Figure 10. Suspension coil current

下载: 全尺寸图片幻灯片

列车速度400 km/h，集电线圈感应电动势的解析值与有限元仿真的对比如图11所示. 感应电动势的解析值为133.0 V，而感应电动势的有限元仿真值为129.5 V，误差为2.6%，且两者相位几乎相等.

图 11 感应电动势解析计算与有限元仿真对比

Figure 11. Comparison between analytical calculation and finite element simulation of induced electromotive force

下载: 全尺寸图片幻灯片

集电线圈感应电动势随速度的变化曲线如图12所示. 可知：感应电动势与列车速度呈线性关系，是由于速度大于100 km/h，悬浮线圈谐波磁场趋于饱和，此时感应电动势几乎只与速度相关. 感应电动势的解析值与测试数据相对误差约为10%，验证了本文推导的集电线圈感应电动势公式的有效性.

图 12 感应电动势解析计算与试验数据对比

Figure 12. Comparison between analytical calculation and experimental data of induced electromotive force

下载: 全尺寸图片幻灯片

集电功率的解析值、有限元仿真和测试数据的对比如图13所示. 列车速度500 km/h，解析计算得到输出功率为43.3 kW，有限元结果为41.8 kW，试验数据为39.5 kW. 解析结果与试验数据之间平均误差为8.0%，有限元与试验数据平均误差为5.5%. 列车速度380 km/h，直线谐波发电机达到25.0 kW的目标集电功率，此时能够满足车载供电需求，证明了直线谐波发电机作为高速磁悬浮系统辅助供电的可靠性.

图 13 集电功率解析计算与有限元、试验对比

Figure 13. Comparison of collector powers between analytical calculation, finite element simulation and experimental data

下载: 全尺寸图片幻灯片

图14（a）描述了列车速度500 km/h，悬浮线圈电流及其磁感应强度随速度的变化曲线. 由图可知：悬浮线圈电流先随速度增加，在速度约大于100 km/h后进入饱和区段，其数值基本保持恒定的910 A. 而悬浮线圈电流产生的磁感应强度类似，磁感应强度先随速度增大，在速度大于100 km/h后趋于饱和，其数值基本恒定在52.7 mT.

图 14 悬浮线圈电流及其磁感应强度

Figure 14. Suspension coil current and its magnetic induction

下载: 全尺寸图片幻灯片

图14（b）描述了列车速度500 km/h，悬浮线圈电流谐波磁场的磁感应强度随速度的变化曲线. 基波、五次、七次谐波磁场的磁感应强度变化趋势类似，均在速度大于100 km/h后进入饱和区段.

这是由于随着列车速度提升，悬浮线圈中的磁通变化率增大，使得悬浮线圈电流以及磁感应强度随之增大. 然而，列车速度不断提升，悬浮线圈的趋肤效应的影响随之变大，增加了悬浮线圈的有效电阻，使悬浮线圈电流的缓慢变化，同时也使其磁感应强度在高速区段近乎饱和^[7].

图15（a）描述了不同运行速度下，集电线圈感应电动势随时间的变化曲线. 随着列车速度增大，感应电动势和频率随之增大. 这是由于感应电动势频率为6ω，由ω=k_x1v得知，感应电动势频率与列车速度成正比关系. 图15（b）描述了列车速度500 km/h，集电线圈各相感应电动势随时间的变化. 图15（c）描述了三相集电线圈感应电动随速度变化关系. 集电线圈的三相电压相位互差120°，R相感应电动势幅值略小于S/T相，是由集电线圈尺寸大小所决定. 三相感应电动势不平衡，连接时会存在零序电流，将零序电流注入集电线圈能够产生电磁力，提升转向架阻尼，进而衰减磁悬浮列车运行时转向架的振动.

图 15 集电线圈感应电动势

Figure 15. Induced electromotive force of collector coil

下载: 全尺寸图片幻灯片

4. 结　论

以日本山梨线MLX01为研究对象，通过与日本山梨线实测数据和有限元结果的比较验证了模型的有效性. 结论如下：

1）基于空间谐波法构建的超导线圈磁动势分布模型，解析求解的超导线圈磁感应强度和有限元结果的曲线高度吻合，验证了磁动势模型的有效性.

2）超导电动悬浮系统用直线谐波发电机感应发电主要利用悬浮线圈电流的五次谐波磁场，且感应电动势的频率是悬浮线圈电流基波频率的6倍. 磁浮列车速度大于100 km/h，由于趋肤效应的影响，悬浮线圈电流以及其磁感应强度趋于饱和.

3）集电线圈感应电动势与速度呈线性关系，感应电动势大小主要与列车运行速度、超导线圈极距相关和磁动势相关. 随着列车速度增加，速度约为380 km/h时，集电功率达到25.0 kW，此时便达到车载供电需求. 通过将感应电动势、功率的解析值与有限元、试验数据进行对比，验证了本文解析模型的正确性.

图 1 高静-低动刚度磁弹簧示意

Figure 1. Magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

图 2 高静-低动刚度磁弹簧工作原理

Figure 2. Working principle of magnetic spring with high static stiffness and low dynamic stiffness

下载: 全尺寸图片幻灯片

图 3 磁弹簧磁场分布

Figure 3. Magnetic field distribution of magnetic spring

下载: 全尺寸图片幻灯片

图 4 永磁体磁场分布

Figure 4. Magnetic field distribution of permanent magnet

下载: 全尺寸图片幻灯片

图 5 磁力理论计算与实验测量对比

Figure 5. Comparison of theoretically calculated magnetic force and experimentally measured magnetic force

下载: 全尺寸图片幻灯片

图 6 磁弹簧动力学模型

Figure 6. Dynamics model of magnetic spring

下载: 全尺寸图片幻灯片

图 7 磁弹簧理论刚度

Figure 7. Theoretical stiffness of magnetic spring

下载: 全尺寸图片幻灯片

图 8 振动传递率仿真对比

Figure 8. Simulation comparison of vibration transmissibility

下载: 全尺寸图片幻灯片

图 9 轴向磁力测量实验平台

Figure 9. Experimental platform formeasuring axial magnetic force

下载: 全尺寸图片幻灯片

图 10 轴向磁力与轴向气隙的关系

Figure 10. Relationship between axial magnetic force and axial air gap

下载: 全尺寸图片幻灯片

图 11 轴向磁力与电流的关系

Figure 11. Relationship between axial magnetic force and current

下载: 全尺寸图片幻灯片

图 12 轴向刚度与气隙的关系

Figure 12. Relationship between axial stiffness and air gap

下载: 全尺寸图片幻灯片

图 13 轴向刚度与电流的关系

Figure 13. Relationship between axial stiffness and current

下载: 全尺寸图片幻灯片

图 14 刚度阶跃响应

Figure 14. Stiffness step response

下载: 全尺寸图片幻灯片

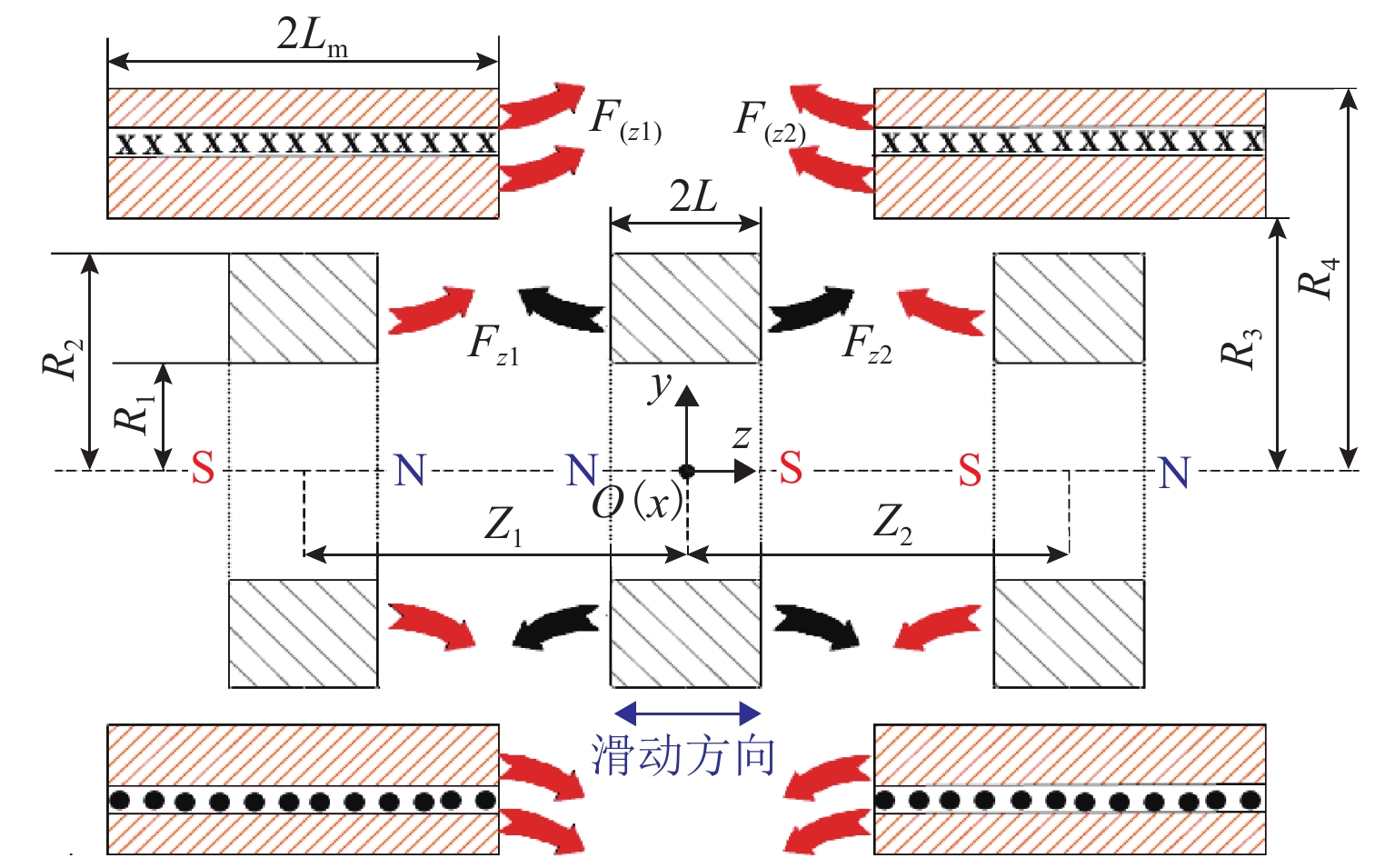
表 1 高静-低动刚度磁弹簧结构参数

Table 1. Structural parameters of magnetic spring with high static stiffness and low dynamic stiffness mm

参数 R₁ R₂ Z_d1 Z_d2 2L R₃ R₄ 2L_m
数值 15 30 15 15 20 35 52 52

下载: 导出CSV

参考文献(13)

[1]	刘尚举,晏巨,陈虬. 电磁永磁混合悬浮隔振系统控制研究[J]. 西南交通大学学报,1999,34(3): 279-283. doi: 10.3969/j.issn.0258-2724.1999.03.006 LIU Shangju, YAN Ju, CHEN Qiu. Study of controlling of an electromagnet and permanent magnet suspension isolation system[J]. Journal of Southwest Jiaotong University, 1999, 34(3): 279-283. doi: 10.3969/j.issn.0258-2724.1999.03.006
[2]	韩俊淑,孙景工,孟令帅. 一种曲面-弹簧-滚子机构的非线性隔振器特性分析[J]. 振动与冲击,2019,38(3): 170-178. doi: 10.13465/j.cnki.jvs.2019.03.024 HAN Junshu, SUN Jinggong, MENG Lingshuai. Design and characteristics analysis of a nonlinear vibration isolator using a curved surface-spring-roller mechanism as negative stiffness element[J]. Journal of Vibration and Shock, 2019, 38(3): 170-178. doi: 10.13465/j.cnki.jvs.2019.03.024
[3]	赵川,孙凤,裴文哲,等. 永磁悬浮平台的分散串级控制方法[J]. 西南交通大学学报,2022,57(3): 618-626. ZHAO Chuan, SUN Feng, PEI Wenzhe, et al. Independent cascade control method for permanent magnetic levitation platform[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 618-626.
[4]	李爽,楼京俊,杨庆超,等. 双环永磁体型高静低动刚度隔振器设计、建模与试验研究[J]. 振动工程学报,2019,32(4): 675-684. doi: 10.16385/j.cnki.issn.1004-4523.2019.04.015 LI Shuang, LOU Jingjun, YANG Qingchao, et al. Design and experiment of a vibration isolator using double-ring permanent magnets springs with negative stiffness[J]. Journal of Vibration Engineering, 2019, 32(4): 675-684. doi: 10.16385/j.cnki.issn.1004-4523.2019.04.015
[5]	高双,朱翔,谌宗琦,等. 基于欧拉梁的准零刚度隔振系统动力特性分析[J]. 中国机械工程,2016,27(21): 2869-2876. doi: 10.3969/j.issn.1004-132X.2016.21.006 GAO Shuang, ZHU Xiang, SHEN Zongqi, et al. Analyses on dynamics characteristics of a quasi-zero-stiffness vibration isolation system based on Euler beam[J]. China Mechanical Engineering, 2016, 27(21): 2869-2876. doi: 10.3969/j.issn.1004-132X.2016.21.006
[6]	CARRELLA A, BRENNAN M J, WATERS T P, et al. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J]. Journal of Sound and Vibration, 2008, 315(3): 712-720. doi: 10.1016/j.jsv.2008.01.046
[7]	ZHANG F, XU M L, SHAO S B, et al. A new high-static-low-dynamic stiffness vibration isolator based on magnetic negative stiffness mechanism employing variable reluctance stress[J]. Journal of Sound and Vibration, 2020, 476: 115322.1-115322.17
[8]	ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. doi: 10.1016/j.jsv.2009.11.001
[9]	王迎春,柴凯,刘树勇,等. 永磁体型高静低动刚度隔振器试验研究[J]. 噪声与振动控制,2019,39(5): 223-230. doi: 10.3969/j.issn.1006-1355.2019.05.042 WANG Yingchun, CHAI Kai, LIU Shuyong, et al. Experimental study on the permanent magnets vibration isolators with high-static and low-dynamic stiffness[J]. Noise and Vibration Control, 2019, 39(5): 223-230. doi: 10.3969/j.issn.1006-1355.2019.05.042
[10]	ZHAO Y, YU J, WANG H, et al. Design of an electromagnetic prismatic joint with variable stiffness[J]. Industrial Robot, 2017, 44(2): 222-230. doi: 10.1108/IR-09-2016-0249
[11]	EBRAHIMI B, KHAMESEE M B, GOLNARAGHI M F. Design and modeling of a magnetic shock absorber based on eddy current damping effect[J]. Journal of Sound and Vibration, 2008, 315(4/5): 875-889.
[12]	曹琪,王皓,余觉. 基于电磁变刚度的力控制装置研究[J]. 机械设计与研究,2020,36(3): 170-175,181. doi: 10.13952/j.cnki.jofmdr.2020.0124 CAO Qi, WANG Hao, YU Jue. Research on the force control device based on electromagnetic variable stiffness principle[J]. Machine Design & Research, 2020, 36(3): 170-175,181. doi: 10.13952/j.cnki.jofmdr.2020.0124
[13]	孟凯,顾勇,刘豫喜,等. 基于可控电磁负刚度的半主动隔振器传递率特性研究[J]. 振动与冲击,2022,41(7): 228-234. doi: 10.13465/j.cnki.jvs.2022.07.030 MENG Kai, GU Yong, LIU Yuxi, et al. Transmissibility characteristics of semi-active vibration isolator based on controllable electro-magnetic negative stiffness[J]. Journal of Vibration and Shock, 2022, 41(7): 228-234. doi: 10.13465/j.cnki.jvs.2022.07.030

施引文献

期刊类型引用(0)
其他类型引用(1)

附加材料(0)

访问统计

点击查看大图

图(14) / 表(1)

计量

文章访问数: 337
HTML全文浏览量: 589
PDF下载量: 57
被引次数: 1

1. 直线发电机结构和工作原理
2. 解析方法
2.1 超导线圈磁感应强度
2.2 悬浮线圈电流及其磁感应强度
2.3 集电线圈感应电动势
3. 结果分析
4. 结　论

参数	R₁	R₂	Z_d1	Z_d2	2L	R₃	R₄	2L_m
数值	15	30	15	15	20	35	52	52

一种高静-低动刚度磁弹簧的建模与特性分析

doi: 10.3969/j.issn.0258-2724.20220821

通讯作者: 张明（1988—），男，副教授，研究方向为磁力减震与柔性机器人技术，E-mail：mingzhang@sut.edu.cn

计量

出版历程

Modeling and Characteristic Analysis of a Magnetic Spring with High Static Stiffness and Low Dynamic Stiffness

1. 直线发电机结构和工作原理

2. 解析方法

2.1 超导线圈磁感应强度

2.2 悬浮线圈电流及其磁感应强度

2.3 集电线圈感应电动势

3. 结果分析

4. 结 论

期刊类型引用(0)

其他类型引用(1)

计量

出版历程

目录

1. 直线发电机结构和工作原理

2. 解析方法

2.1 超导线圈磁感应强度

2.2 悬浮线圈电流及其磁感应强度

2.3 集电线圈感应电动势

3. 结果分析

4. 结 论

通讯作者:
张明（1988—），男，副教授，研究方向为磁力减震与柔性机器人技术，E-mail：mingzhang@sut.edu.cn

4. 结　论

4. 结　论