基于二维离散混沌系统和DNA的图像加密方案

徐昌彪; 许浩南; 明志飞

doi:10.3969/j.issn.0258-2724.20220810

基于二维离散混沌系统和DNA的图像加密方案

doi: 10.3969/j.issn.0258-2724.20220810

重庆邮电大学光电工程学院，重庆 400065

基金项目: 国家自然科学基金（62071077）

详细信息

作者简介:
徐昌彪（1972—），男，教授，博士，研究方向为混沌理论，E-mail：xucb@cqupt.edu.cn

中图分类号: O415.5；TN918.4
计量
- 文章访问数: 362
- HTML全文浏览量: 230
- PDF下载量: 48
- 被引次数: 7
出版历程
- 收稿日期: 2022-11-21
- 修回日期: 2023-02-20
- 网络出版日期: 2023-12-19
- 刊出日期: 2023-03-02

Image Encryption Scheme Based on 2D Discrete Chaotic System and Deoxyribonucleic Acid

School of Optoelectronic Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

摘要

摘要:
为丰富低维离散混沌系统的动力学特性以及克服脱氧核糖核酸（deoxyribonucleic acid, DNA）编码的引入使混沌图像加密系统安全性易于降低的问题，基于Arnold映射构建具有恒定正Lyapunov指数的2维离散混沌系统，并将其与DNA编码结合，设计一个混沌图像加密方案. 所设计的混沌系统模型中不含非线性项，系统具有超混沌动力学行为；加密方案中用于加密的混沌序列为明文图像像素与密钥的加取模运算结果，图像按4 × 4大小予以分块，扩散算法中的DNA加减、异或、同或等运算分别基于DNA编码规则1、规则4和规则7. 仿真实验和性能分析结果表明：加密方案的密钥空间达到2²⁶⁶，信息熵为7.9993 bit，密钥灵敏度达到10⁻¹⁵，平均像素变化率（number of pixel change rate, NPCR）、统一平均变化强度（unified average change intensity, UACI）、块平均变化强度（block average change intensity, BACI）分别为99.6092%、33.4664%、26.7718%.
- 离散混沌系统 /
- 超混沌 /
- Lyapunov指数 /
- 图像加密
Abstract:
In order to enrich the dynamic characteristics of a low-dimensional discrete chaotic system and overcome the problem of low security of chaotic image encryption system caused by the introduction of deoxyribonucleic acid (DNA) coding, a 2D discrete chaotic system with constant positive Lyapunov exponent was constructed based on Arnold map. In addition, a chaotic image encryption scheme was designed by combining the system with DNA coding. The designed chaotic system model did not have nonlinear terms and had hyperchaotic dynamic behavior. The chaotic sequence used for encryption in the encryption scheme was the result of addition and module operation between the plaintext image pixels and the key. Images were divided into blocks by the size of 4 × 4. The operations of DNA addition and subtraction, XOR, and XNOR in the diffusion algorithm were based on DNA coding rule 1, rule 4, and rule 7, respectively. The simulation and performance analysis results show that the key space of the encryption scheme is 2²⁶⁶; the information entropy is 7.999 3 bit; the key sensitivity is 10⁻¹⁵, and the average number of pixel change rate (NPCR), unified average change intensity (UACI), and block average change intensity (BACI) are 99.609 2%, 33.466 4%, and 26.771 8%, respectively.
- discrete chaotic system /
- hyperchaotic /
- Lyapunov exponent /
- image encryption

HTML全文

高速列车的行驶引起了许多空气动力学问题，其中列车行驶过程产生的脉动风压所带来的问题受到广泛关注. 脉动风压产生于列车在高速行驶下对其周围的空气所产生的强烈扰动，当行驶的列车通过声屏障时，这一扰动将会加剧，使周围的空气产生的空气压力发生突变，形成一种瞬态的冲击压力，在很短的时间内(约几十毫秒)相继出现正、负压力峰值，这种瞬态压力冲击即为列车驶过声屏障时产生的压力波，即称为脉动风压. 刘海涛^[1]曾对比分析得到了不同桥宽、不同车型、不同速度下脉动风压的分布规律，这种压力波的存在实际会对声屏障结构产生巨大影响，如果不加以重视，会引起声屏障许多结构问题和疲劳问题，很多学者都曾针对脉动风压开展了相关研究. 声屏障风荷载体型系数上，刘磊等^[2]通过缩尺风洞实验，确定了声屏障迎风面净体型系数超过1.40，背风面体型系数接近0.30. 郑史雄等^[3]建议桥梁声屏障的风荷载体型系数取1.65，路基声屏障的风荷载体型系数取1.99. 声屏障脉动风压响应上，焦长洲等^[4]对脉动风压导致的声屏障结构振动进行了研究. 邓跞等^[5]研究了金属立柱插板式声屏障在脉动风压静态作用下的静力响应. 刘功玉^[6]研究了不同车速下声屏障结构在脉动风压作用下动力响应规律，发现随着车速的提高，列车经过声屏障区域时的气动压力和气动吸力也越来越大. 康健^[7]研究了不同中心距的声屏障结构在列车速度为350 km/h时产生的脉动风压作用下疲劳性能规律. 张田等^[8]发现防风板的应力远高于立柱的应力，疲劳问题也更为显著. 马驰^[9]研究了货运铁路大型全封闭声屏障结构，发现较大的疲劳荷载作用下声屏障柱脚螺栓会发生轻微松动，在设计过程中可以严格控制拧紧力矩防止螺栓松动发生，并定期对螺栓进行检查. 结构优化方面，申真真^[10]研究了不同的单元壁厚度和材料的高速铁路插板式冷弯声屏障的静动力响应及疲劳性能规律，提出了一种综合效益突出的结构组合. 赵允刚等^[11]针对采用声屏障时高速列车运行过程中表面气动阻力较大的问题，提出利用减载式声屏障降低列车运行过程中受到的气动阻力. 苏卫青^[12]研究了高速铁路声源特性、作用于高速铁路声屏障的气动压力和声屏障结构的动力响应. 针对前述的研究，发现目前针对不同顶部开口长度的双侧封闭式声屏障和不同顶部覆盖长度的单侧封闭式声屏障在脉动风压作用下的结构响应和疲劳性能规律的研究较少，事实上，顶部结构变化对列车行驶过程中气流的释放和结构优化有一定的意义. 本文研究不同顶部开口长度的双侧封闭式声屏障和不同顶部覆盖长度的单侧封闭式声屏障受力特征规律，并探究声屏障的关键连接部位耐久性、疲劳特性，为高铁桥上半封闭式声屏障的设计提供有力的技术支持.

1. 工程概况

某高铁声屏障结构采用单双侧封闭直立型金属插板式声屏障形式，列车运行车速为350 km/h，金属插板式声屏障主要由 H 型钢立柱、H 型钢底板、铝合金单元板、橡胶等结构组成，钢架部分采用Q345- B焊接工字钢；铝合金单元板采用标号不低于5A03、厚度不小于1.5 mm的铝合金材料，面板和背板需进行铬酸钝化或类似的预处理；通透吸声板采用厚度不小于20.0 mm的透明板，具有防撞击、防破损保护措施及防鸟撞击标志. 单元板及透明板四面加设铝合金框，铝合金框与型钢立柱间采用插入式柔性连接^[11].

声屏障结构截面沿顶部直线段分割情况及列车所在位置（图示右轨道）共分为3部分：近轨竖直声屏障部分、远轨竖直声屏障部分及顶部横向声屏障部分. 声屏障结构截面示意如图1所示.

图 1 声屏障结构截面示意

Figure 1. Cross sections of sound barrier structures

下载: 全尺寸图片幻灯片

2. 模型建立过程

本文探讨双侧封闭声屏障顶部开口间距为（即顶部不设置通透隔声板和吸声板）2、4、6、8 m以及单侧封闭式声屏障顶部覆盖长度为（即顶部设置通透隔声板）2、4、6、8 m 8种情况下声屏障结构的受力特征. 工况参数如表1所示.

表 1 工况参数

Table 1. Operating parameters

工况参数名称	取值
车型	CRH3
列车速度/(km•h⁻¹)	350
双侧封闭式声屏障顶部开口间距/m	2、	4、	6、	8
单侧封闭式声屏障顶部覆盖长度/m	2、	4、	6、	8

下载: 导出CSV

| 显示表格

2.1 脉动风压时程函数提取

本文脉动风压计算及结果参照李小珍等^[13-14]的脉动风压的CFD （computation fluid dynamics）模型，该模型为行进中的高速铁路半封闭声屏障的列车通过开口间距双侧封闭声屏障和顶部不同的覆盖长度单侧封闭声屏障产生的. 用动态铺层技术模拟移动列车表面流场，动网格部分模拟了高速列车表层及列车周围因列车高速前进，受列车移动影响最大的空气，模型如图2所示. 在此CFD模型中，近轨竖直声屏障部分分为17个区域，自下到上分别用N₁～N₁₇标记测点；远轨竖直声屏障部分设置17个区域，自下到上分别用F₁～F₁₇标记测点（单侧封闭式声屏障不布置）；顶部横向声屏障部分根据顶部开口间距的不同区域有所变化，靠近轨一侧由近轨至开口处用T₁～T₁₀标记测点，靠远轨用T₁₅～T₂₄标记测点，开口间距每增加2 m，顶部两侧测点从大序号依次各减少两个. 测点的整体布置（双侧封闭式声屏障顶部开口间距2 m和单侧封闭式声屏障顶部覆盖长度8 m）如图3.

图 2 CFD模型

Figure 2. CFD model

下载: 全尺寸图片幻灯片

一趟CRH3完整驶过后，记录各个测点随时间变化的受力情况，得到脉动风压作用的时程曲线，梳理罗云柯^[14]模型数据结果，以双侧封闭式顶部开口2 m模型为例，声屏障近轨、远轨、顶部风压时程函数如图4，结果用于整体模型动力计算.

考虑最不利的静力风压情况，提取其中风压极值计算结果如图5，结果用于整体模型静力计算.

图 3 声屏障结构测点布置

Figure 3. Layout of measuring points of sound barrier structures

下载: 全尺寸图片幻灯片

图 4 双侧封闭式声屏障顶部开口间距2 m模型脉动风压时程函数

Figure 4. Time histories of pulsating wind pressure on the double-side closed sound barrier model with 2 m top opening spacing

下载: 全尺寸图片幻灯片

图 5 脉动风压峰值

Figure 5. Peak values of pulsating wind pressure

下载: 全尺寸图片幻灯片

2.2 整体模型建立

得到脉动风压的时程曲线后，利用midas civil有限元软件分别建立了顶部不同的开口间距双侧封闭式声屏障及顶部不同覆盖长度的单侧封闭式声屏障整体模型，用于分析自然风、静力风压和脉动风压分别作用下，声屏障立柱顶部位移、立柱根部弯矩、轴力及应力计算结果，并计算动力放大系数.

模型共截取10个声屏障节段，声屏障结构共计长度20 m，宽度间距12 m，高度7.75 m. 梁体材料选用C30，采用梁单元模拟；声屏障立柱材料选用Q345钢，采用梁单元模拟；声屏障铝合金复合吸声板及通透吸声板根据实际设计参数进行材料拟定，材料性能指标见表2和表3，采用板单元模拟.

8种不同开口形式的声屏障整体结构如图6、7所示.

表 2 铝合金复合吸声板的性能指标

Table 2. Performance indexes of aluminum alloy composite sound absorption board

指标名称	性能指标
降噪系数	≥ 0.7
隔声量	≥ 25 dB
面密度	≤ 40 kg/m²，且≥ 20 kg/m²
抗风压性能	≥ 8.0 kPa
抗冲击	符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010）
抗火性能	防火等级应满足《建筑材料及制品燃烧性能分级》（GB 8624—2012）规定的 B1 级及以上
防腐蚀	声屏障声学构件的金属部件的防腐蚀年限应 ≥ 25 a
抗变形性能	符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010）最大弹性挠度 ≤ L/100
耐候性能	符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010）
使用年限	≥ 25 a

下载: 导出CSV

| 显示表格

表 3 通透隔声板的性能指标

Table 3. Performance indexes of transparent sound insulation board

指标名称	性能指标
隔声量	≥ 25 dB
密度	≤ 1 200 kg/m³
透光率	透光率不应小于 90%，10 年内透光率下降为 10%
拉伸强度	≥ 70 MPa
弯曲强度	≥ 98 MPa
弹性模量	≥ 3 100 MPa
断裂伸长率	≥ 4%
防火性能	复合《建筑材料的燃烧等级分级》（GB 8624—2012）规定的 B1 级及以上
0～50 ℃ 以内线性热膨胀系数	≤ 0.000 07
允许最高长期使用温度	≤ 70 ℃
软化温度	≥ 110 ℃
抗冲击	符合《铁路声屏障声学构件技术要求和测试方法》（TB/T 3122—2010）
板厚	≥ 20 mm
使用年限	≥ 25 a

下载: 导出CSV

| 显示表格

图 6 不同顶部开口间距的双侧封闭式声屏障整体模型

Figure 6. Global model of the double-side closed sound barrier with different top opening spacings

下载: 全尺寸图片幻灯片

图 7 不同顶部覆盖长度的单侧封闭式声屏障整体模型

Figure 7. Global model of the single-side closed sound barrier with different top covering lengths

下载: 全尺寸图片幻灯片

结构约束关系上，立柱底部与梁体固结，立柱与声屏障板之间采用弹性约束模拟纵桥向橡胶连接作用，声屏障板与板之间释放部分端部约束模拟真实接触效果.

2.3 瑞利阻尼

振型是结构的一个重要动力特性，振型的数量和各阶振型对结构总体反应的贡献直接影响到结构地震反应的计算结果.

本文通过振型分解将多自由度体系的振动转化为单自由度体系振动的组合问题进行计算，模型结构的质量和刚度分布不均匀，振型分解反应谱法所需的振型数取振型参与质量达到总质量的90%时所需的振型数，8个模型所需振型数为93～101个. 若假设阻尼与质量矩阵和刚度矩阵的组合成比例，则可表示为

${{{\boldsymbol{c}}}}=\alpha {{{\boldsymbol{m}}}} + \beta {{{\boldsymbol{k}}}} \text{，}$

(1)

式中： ${{{\boldsymbol{c}}}}$ 为阻尼矩阵； $\alpha$ 和 $\beta$ 均为与频率相关的参数； ${{{\boldsymbol{m}}}}$ 和 ${{{\boldsymbol{k}}}}$ 分别为质量矩阵和刚度矩阵.

这种阻尼称为瑞利阻尼. 利用瑞利阻尼法公式计算得到各阶瑞利阻尼比为

$\frac{\alpha }{2 \omega } + \frac{\omega \beta }{2}=\xi \text{，}$

(2)

式中： $\omega$ 为模态对应频率； $\xi$ 为阻尼比.

依据钢结构抗震要求^[15-16]， $\xi$ 取0.02，相关参数 $\alpha$ 和 $\beta$ 是随频率变化的，用频率范围的下限和上限代入式（2），联立求解得到各个声屏障结构的 $\alpha$ 和 $\beta$ ，结果如表4.

各个声屏障结构的 $\alpha$ 和 $\beta$ 代入瑞利阻尼公式，计算得到声屏障结构各阶振型的阻尼比，用于动力计算.

表 4 各个声屏障结构的

$\alpha$ 和

$\beta$

Table 4. Values of

$\alpha$ and

$\beta$ of each sound barrier structure

结构形式	参数	开口间距/m
结构形式	参数	2	4	6	8
双侧封闭式声屏障	$\alpha$	0.46773	0.47596	0.48947	0.50614
双侧封闭式声屏障	$\beta$	0.00063	0.00060	0.00054	0.00048
单侧封闭式声屏障	$\alpha$	0.67421	0.55969	0.51430	0.42194
单侧封闭式声屏障	$\beta$	0.00034	0.00041	0.00051	0.00060

下载: 导出CSV

| 显示表格

2.4 风压时程函数输入

加载原则上，静力作用时，考虑最不利的受力情况，提取各位置脉动风压的峰值，按静力方式作用于声屏障结构，得到最大静力响应结果a；动力计算采用振型叠加法，利用前述瑞利阻尼法计算所得的每一阶振型的阻尼进行动力计算，动力计算分析采用CFD，取一个荷载子步为0.005 s动力时长共30 s，按各个测点分块，按2 m一个节间，根据时程递进，将脉动风压时程曲线施加于整个声屏障结构上得到静力响应同一测点的动力响应结果b. b/a得到结构动力放大系数.

3. 计算结果

不同开口形式的声屏障结构在立柱的位移、应力、弯矩、轴向力、水平力的峰值位置基本一致，最大位移位置主要分布在近轨部分的立柱顶部；最大应力、最大弯矩位置主要分布在近轨部分的立柱底部；立柱结构最大轴力位置分布在远轨部分的立柱底部；立柱结构最大水平力位置分布在近轨部分的立柱底部，以双侧顶部开口间距2 m的双侧封闭声屏障为例，静力动力计算结果示意如图8、9.

所有声屏障结构计算结果汇总见表5.

从计算结果来看，对于双侧封闭式声屏障，随着顶部开口间距的增大，响应减小，对于开口4、6 m内力变化影响不大，开口2 m的立柱动应力是开口8 m的立柱动应力的1.15倍，放大系数相差0.12，对于单侧封闭式声屏障中，覆盖的长度增加，响应增大，覆盖长度4～6 m后有较大变化，覆盖8 m的立柱动应力是覆盖2 m的立柱动应力的1.28倍，放大系数相差0.37.

图 8 双侧封闭顶部开口间距2 m声屏障立柱静力响应结果

Figure 8. Static responses of the double-side closed sound barrier columns with 2 m top opening spacing

下载: 全尺寸图片幻灯片

表 5 受力特征结果

Table 5. Force characteristic results

型式	类别	立柱底部应力/MPa	立柱顶部位移/mm	立柱弯矩/（kN•m）	轴向力/kN	水平力/kN
双侧封闭式顶部开口间距 2 m	动力作用	20.60	5.82	37.24	19.42	52.09
	放大系数	2.10	3.75	2.10	3.26	1.94
	静力作用	9.62	1.49	17.48	5.50	26.51
双侧封闭式顶部开口间距 4 m	动力作用	19.55	5.47	34.90	17.14	51.45
	放大系数	2.03	4.08	2.00	3.14	1.83
	静力作用	9.60	1.54	17.38	5.50	25.95
双侧封闭式顶部开口间距 6 m	动力作用	19.48	5.09	34.81	16.90	50.35
	放大系数	2.02	3.43	2.00	3.15	1.97
	静力作用	8.99	1.51	16.27	3.09	24.20
双侧封闭式顶部开口间距 8 m	动力作用	17.88	4.62	32.18	11.31	45.84
	放大系数	1.98	3.75	1.97	3.73	2.01
	静力作用	8.83	1.34	15.99	2.35	23.31
单侧封闭式顶部覆盖长度 2 m	动力作用	19.02	5.09	34.37	8.24	51.10
	放大系数	2.15	3.80	2.15	3.50	2.19
	静力作用	9.24	1.49	16.74	2.62	27.41
单侧封闭式顶部覆盖长度 4 m	动力作用	20.10	5.33	36.34	5.33	51.15
	放大系数	2.18	3.61	2.17	2.03	2.00
	静力作用	9.62	1.54	17.42	1.74	26.28
单侧封闭式顶部覆盖长度 6 m	动力作用	23.19	5.89	41.56	6.16	59.75
	放大系数	2.41	3.41	2.39	3.54	2.01
	静力作用	9.69	1.52	17.51	2.65	26.42
单侧封闭式顶部覆盖长度 8 m	动力作用	24.44	6.27	44.08	6.57	62.25
	放大系数	2.52	4.13	2.52	2.48	2.36
	静力作用	9.78	1.55	17.74	5.95	26.83

下载: 导出CSV

| 显示表格

图 9 双侧封闭式声屏障顶部开口间距2 m模型动力时程响应曲线结果

Figure 9. Dynamic response time-histories of the double-side closed sound barrier model with 2 m top opening spacing

下载: 全尺寸图片幻灯片

4. 结　论

1）立柱结构最大位移位置分布在近轨部分的立柱顶部；立柱结构最大弯矩位置分布在近轨部分的立柱底部；立柱结构最大轴力位置分布在远轨部分的立柱底部；立柱结构最大水平力位置分布在近轨部分的立柱底部；立柱结构最大应力位置分布在近轨部分的立柱底部.

2）双侧封闭式声屏障结构中，立柱最大弯矩、最大应力和放大系数随着顶部开口间距的增加有减小的趋势；同理，单侧封闭式声屏障中，立柱最大弯矩、最大应力和动力放大系数随着顶部覆盖程长度的增加有增大的趋势.

3）双侧封闭式声屏障中，最不利结构为顶部开口间距2 m的双侧封闭式声屏障结构，单侧封闭式声屏障中，最不利结构为顶部覆盖8 m的单侧封闭式声屏障结构. 两种结构形式不同，单侧封闭式声屏障内力变化对顶部覆盖长度更为敏感，且单侧封闭式引起的动力响应更大，可能是由于双侧封闭后，远轨侧同样受到了脉动风作用，近远轨侧脉动风的作用叠加减小了内力响应.

图 1 系统相图

Figure 1. Phase diagram of the system

下载: 全尺寸图片幻灯片

图 2 系统的0-1测试

Figure 2. Results of 0-1 test of the system

下载: 全尺寸图片幻灯片

图 3 系统Lyapunov指数谱

Figure 3. Lyapunov exponential spectrum of the system

下载: 全尺寸图片幻灯片

图 4 系统分岔图

Figure 4. Bifurcation diagrams of the system

下载: 全尺寸图片幻灯片

图 5 系统SE复杂度谱图

Figure 5. SE complexity spectrum of the system

下载: 全尺寸图片幻灯片

图 6 系统C₀复杂度谱图

Figure 6. C₀ complexity spectrum of the system

下载: 全尺寸图片幻灯片

图 7 系统运行时间

Figure 7. Running time of the system

下载: 全尺寸图片幻灯片

图 8 加密方案流程

Figure 8. Flow chart of encryption scheme

下载: 全尺寸图片幻灯片

图 9 解密方案流程

Figure 9. Flowchart of decryption scheme

下载: 全尺寸图片幻灯片

图 10 明文图像与密文图像直方图

Figure 10. Histogram of plaintext image and ciphertext image

下载: 全尺寸图片幻灯片

图 11 鲁棒性

Figure 11. Robustness

下载: 全尺寸图片幻灯片

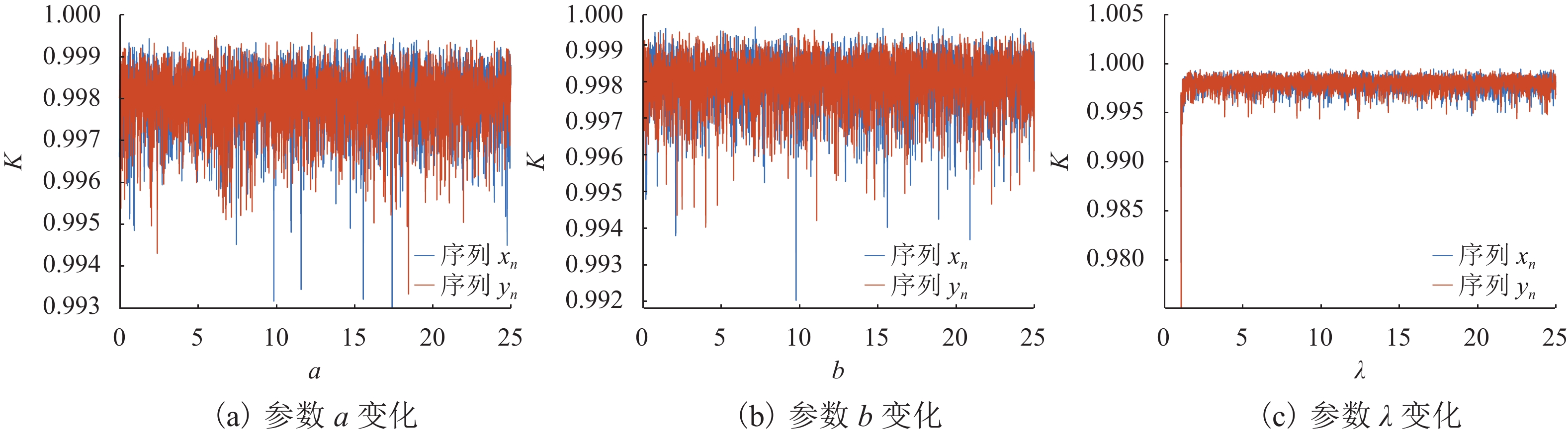
表 1 x_n、y_n的SE、C₀测度平均值

Table 1. Average of SE and C₀ for x_n and y_n

参数	x_n 的测度平均值		y_n 的测度平均值
参数	SE	C₀	SE	C₀
a	0.9460	0.2501	0.9459	0.2962
b	0.9459	0.2500	0.9459	0.2515
λ	0.9452	0.2515	0.9452	0.2702

下载: 导出CSV

表 2 相关系统的模型复杂度与结构复杂度

Table 2. Model complexity and structural complexity of related systems

系统	指标维度/维	参数/个	非线性项数/个	非线性项形式	SE 杂度均值	C₀杂度均值	硬件实现难度	硬件实现成本
本文	2	3	0		0.9457	0.2505	低	低
文献[11]	2	2	1	$x_n^2$	0.9460	0.2501	中	中
文献[12]	2	3	1	cos²(carccos x_n)	0.9457	0.2499	高	高
文献[13]	4	16	0		0.9460	0.2501	低	中
文献[14]	6	44	0		0.9198	0.1645	中	中
文献[15]	6	36	0		0.9461	0.2501	低	中

下载: 导出CSV

表 3 DNA编码规则

Table 3. DNA encoding rules

编码	规则 1	规则 2	规则 3	规则 4	规则 5	规则 6	规则 7	规则 8
00	A	A	T	T	G	G	C	C
01	G	C	G	C	A	T	A	T
10	C	G	C	G	T	A	T	A
11	T	T	A	A	C	C	G	G

下载: 导出CSV

表 4 本文采用的DNA加法运算规则

Table 4. Operation rules of DNA addition

项目	A	G	C	T
A	A	G	C	T
G	G	C	T	A
C	C	T	A	G
T	T	A	G	C

下载: 导出CSV

表 5 本文采用的DNA减法运算规则

Table 5. Operation rules of DNA substraction

项目	A	G	C	T
A	A	T	C	G
G	G	A	T	C
C	C	G	A	T
T	T	C	G	A

下载: 导出CSV

表 6 本文采用的DNA异或运算规则

Table 6. Operation rules of DNA XOR

项目	A	G	C	T
A	C	T	A	G
G	T	C	G	A
C	A	G	C	T
T	G	A	T	C

下载: 导出CSV

表 7 本文采用的DNA同或运算规则

Table 7. Operation rules of DNA XNOR

项目	A	G	C	T
A	A	G	C	T
G	G	A	T	C
C	C	T	A	G
T	T	C	G	A

下载: 导出CSV

表 8 加解密方案测试结果

Table 8. Test results of encryption and decryption schemes

下载: 导出CSV

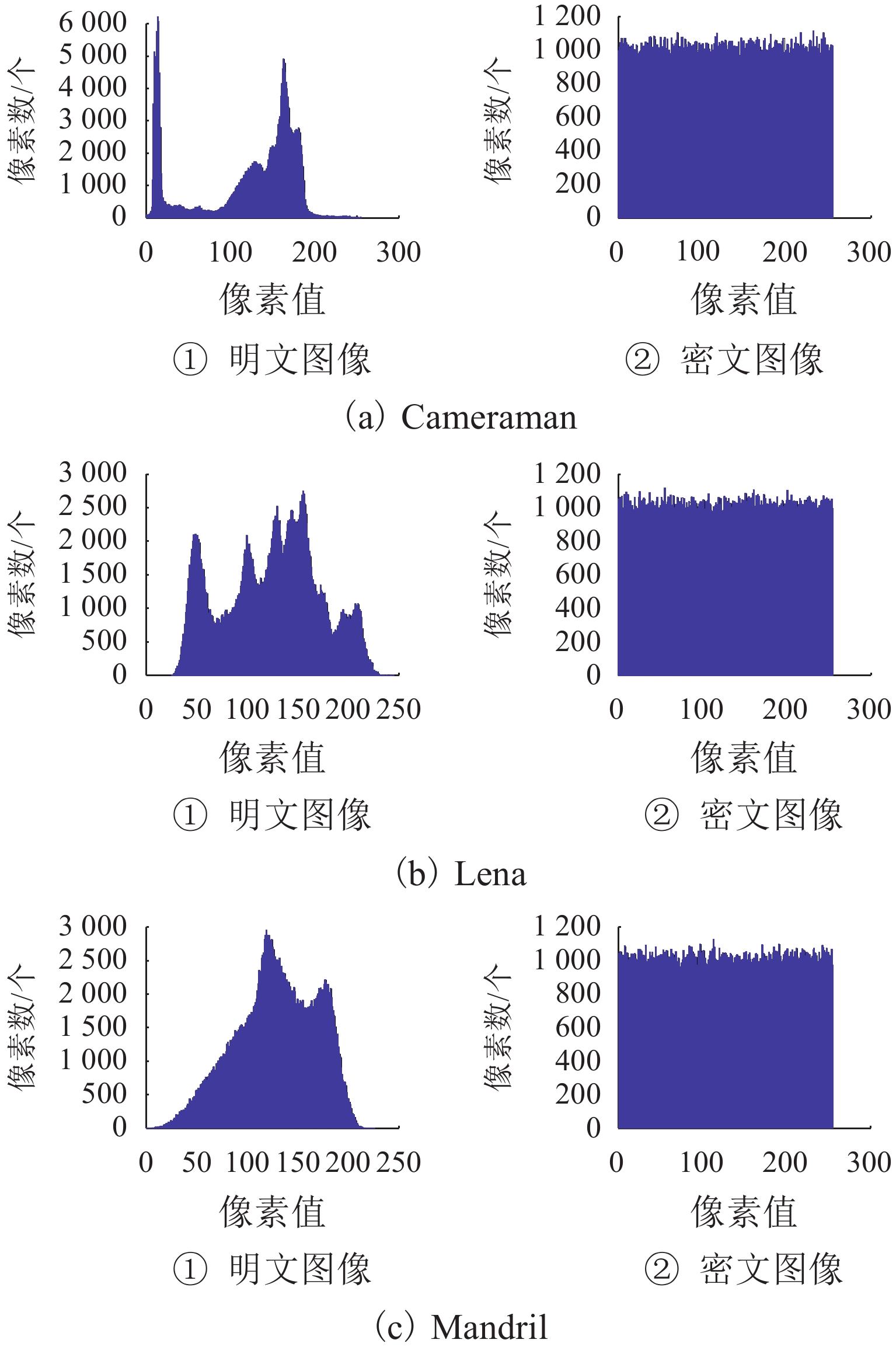
表 9 信息熵

Table 9. Information entropy bit

方案	图像	密文	明文
本文	Cameraman	7.9993	7.0480
	Lena	7.9993	7.4451
	Mandril	7.9993	7.2925
文献[16]	Lena	7.9969
	Cameraman	7.9973
	Horse	7.9974
文献[17]	Lena	7.9977
	Mandril	7.9973
	Peppers	7.9974

下载: 导出CSV

表 10 χ²检验结果

Table 10. Test results of χ² bit

图像	明文/ × 10⁵	密文
Cameraman	4.1853	248.6660
Lena	1.5834	256.6152
Mandril	2.1137	262.8926

下载: 导出CSV

表 11 相关性系数计算结果

Table 11. Calculation results of correlation coefficient

方案	图像	明/密文	水平	垂直	正对角	反对角
本文	Cameraman	明文	0.9881	0.9840	0.9795	0.9779
	Cameraman	密文	−0.0027	0.0101	0.0124	0.0069
	Lena	明文	0.9849	0.9726	0.9585	0.9689
	Lena	密文	0.0115	0.0326	0.0352	−0.0252
	Mandril	明文	0.9122	0.9220	0.8692	0.8592
	Mandril	密文	−0.0295	0.0135	0.0175	0.0294
文献[16]	Lena	明文	0.9237	0.9420	0.8906
	Lena	密文	0.0040	−0.0012	−0.0021
	Cameraman	明文	0.9333	0.9569	0.9052
	Cameraman	密文	−0.0031	−0.0006	0.0011
	Horse	明文	0.6425	0.6682	0.5179
	Horse	密文	0.0034	0.0012	−0.0035
文献[17]	Couple	明文	0.9023	0.9478	0.8688
	Couple	密文	−0.0325	−0.0025	0.0223
	Aerial	明文	0.8818	0.8960	0.7885
	Aerial	密文	0.0069	0.0221	0.0172
	Stream and bridge	明文	0.9258	0.9387	0.8958
	Stream and bridge	密文	0.2180	0.0468	−0.0318

下载: 导出CSV

表 12 本文所用灰度图像与随机图像间的UACI与BACI值

Table 12. UACI and BACI between gray image and random image used in this paper %

图像	UACI 值	BACI 值
Cameraman	31.1146	22.8078
Lena	28.6241	21.3218
Mandril	27.5411	20.2075

下载: 导出CSV

表 13 加解密过程密钥灵敏度分析

Table 13. Key sensitivity analysis during encryption and decryption processes %

参数	指标	加密过程			解密过程
参数	指标	Cameraman	Lena	Mandril	Cameraman	Lena	Mandril
k₁	NPCR	99.6090	99.6840	99.6113	99.6090	99.6840	99.6113
	UACI	33.4643	33.4662	33.4725	31.1195	28.6277	27.5460
	BACI	26.7728	26.7719	26.7732	22.8148	21.3235	20.2097
k₂	NPCR	99.6091	99.6099	99.6099	99.6091	99.6099	99.6099
	UACI	33.4637	33.4617	33.4592	31.1154	28.6221	27.5354
	BACI	26.7674	26.7661	26.7693	22.8043	21.3200	20.2060
k₃	NPCR	99.6101	99.6112	99.6103	99.6101	99.6112	99.6103
	UACI	33.4639	33.4655	33.4671	31.1202	28.6278	27.5393
	BACI	26.7738	26.7742	26.7646	22.8075	21.3248	20.2062
k₄	NPCR	99.6086	99.6083	99.6091	99.6086	99.6083	99.6091
k₄	UACI	33.4610	33.4643	33.4641	31.1114	28.6197	27.5388
	BACI	26.7706	26.7708	26.7692	22.8061	21.3174	20.2045
k₅	NPCR	99.6084	99.6112	99.6101	99.6084	99.6112	99.6101
	UACI	33.4664	33.4640	33.4669	31.1209	28.6228	27.5393
	BACI	26.7689	26.7722	26.7703	22.8104	21.3222	20.2043
r₁	NPCR	99.6088	99.6101	99.6111	99.6088	99.6101	99.6111
	UACI	33.4608	33.4679	33.4650	31.1200	28.6299	27.5404
	BACI	26.7701	26.7751	26.7702	22.8104	21.3216	20.2061
r₂	NPCR	99.6101	99.6089	99.6112	99.6101	99.6089	99.6112
	UACI	33.4619	33.4692	33.4615	31.1186	28.6137	27.5363
	BACI	26.7667	26.7729	26.7712	22.8089	21.3215	20.2069
r₃	NPCR				99.6101	99.6089	99.6112
	UACI				31.1189	28.6300	27.5466
	BACI				22.8143	21.3210	20.2117
r₄	NPCR				99.6101	99.6089	99.6112
	UACI				31.1175	28.6251	27.5375
	BACI				22.8048	21.3235	20.2015

下载: 导出CSV

表 14 明文敏感性

Table 14. Plaintext sensitivity %

图像	NPCR	UACI	BACI
Cameraman	99.6083	33.4632	26.7711
Lena	99.6106	33.4685	26.7711
Mandril	99.6087	33.4676	26.7733

下载: 导出CSV

参考文献(22)

[1]	LI W S, YAN W H, ZHANG R X, et al. A new 3D discrete hyperchaotic system and its application in secure transmission[J]. International Journal of Bifurcation and Chaos, 2019, 29(14): 1950206.1-1950206.14.
[2]	RAY A, GHOSH D. Another new chaotic system: bifurcation and chaos control[J]. International Journal of Bifurcation and Chaos, 2020, 30(11): 2050161.1-2050161.13.
[3]	YU F, QIAN S, CHEN X, et al. Chaos-based engineering applications with a 6D memristive multistable hyperchaotic system and a 2D SF-SIMM hyperchaotic map[J]. Complexity, 2021, 2021. 6683284.1- 6683284.21.
[4]	BELAZI A, HERMASSI H, RHOUMA R, et al. Algebraic analysis of a RGB image encryption algorithm based on DNA encoding and chaotic map[J]. Nonlinear Dynamics, 2014, 76(4): 1989-2004. doi: 10.1007/s11071-014-1263-y
[5]	WANG X Y, LI P, ZHANG Y Q, et al. A novel color image encryption scheme using DNA permutation based on the Lorenz system[J]. Multimedia Tools and Applications, 2018, 77(5): 6243-6265. doi: 10.1007/s11042-017-4534-z
[6]	WANG X Y, ZHANG H L, BAO X M. Color image encryption scheme using CML and DNA sequence operations[J]. Biosystems, 2016, 144: 18-26. doi: 10.1016/j.biosystems.2016.03.011
[7]	ZHANG X Q, WANG X S. Multiple-image encryption algorithm based on DNA encoding and chaotic system[J]. Multimedia Tools and Applications, 2019, 78(6): 7841-7869. doi: 10.1007/s11042-018-6496-1
[8]	JITHIN K C, SANKAR S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set[J]. Journal of Information Security and Applications, 2020, 50: 102428.1-102428.22.
[9]	LIU T M, BANERJEE S, YAN H Z, et al. Dynamical analysis of the improper fractional-order 2D-SCLMM and its DSP implementation[J]. The European Physical Journal Plus, 2021, 136(5): 506.1-506.17.
[10]	AKIF O Z, ALI S, ALI R S, et al. A new pseudorandom bits generator based on a 2D-chaotic system and diffusion property[J]. Bulletin of Electrical Engineering and Informatics, 2021, 10(3): 1580-1588. doi: 10.11591/eei.v10i3.2610
[11]	MERANZA-CASTILLÓN M O, MURILLO-ESCOBAR M A, LÓPEZ-GUTIÉRREZ R M, et al. Pseudorandom number generator based on enhanced Hénon map and its implementation[J]. International Journal of Electronics and Communications, 2019, 107: 239-251. doi: 10.1016/j.aeue.2019.05.028
[12]	LIU Y, QIN Z, LIAO X F, et al. A chaotic image encryption scheme based on Hénon-Chebyshev modulation map and genetic operations[J]. International Journal of Bifurcation and Chaos, 2020, 30(6): 2050090.1-2050090.22. doi: 10.1142/S021812742050090X
[13]	KANSO A, GHEBLEH M, ALAZEMI A. Efficient image encryption scheme based on 4-dimensional chaotic maps[J]. Informatica, 2020, 31(4): 793-820.
[14]	WANG Y J, WU C C, KANG S Q, et al. Multi-channel chaotic encryption algorithm for color image based on DNA coding[J]. Multimedia Tools and Applications, 2020, 79(25): 18317-18342.
[15]	SUN C Y, WANG E F, ZHAO B. Image encryption scheme with compressed sensing based on a new six-dimensional non-degenerate discrete hyperchaotic system and plaintext-related scrambling[J]. Entropy, 2021, 23(3): 291.1-291.25.
[16]	ZHANG S J, LIU L F. A novel image encryption algorithm based on SPWLCM and DNA coding[J]. Mathematics and Computers in Simulation, 2021, 190: 723-744. doi: 10.1016/j.matcom.2021.06.012
[17]	TIAN J F, LU Y, ZUO X Y, et al. A novel image encryption algorithm using PWLCM map-based CML chaotic system and dynamic DNA encryption[J]. Multimedia Tools and Applications, 2021, 80(21): 32841-32861.
[18]	KANG X J, GUO Z H. A new color image encryption scheme based on DNA encoding and spatiotemporal chaotic system[J]. Signal Processing: Image Communication, 2020, 80: 115670-115681. doi: 10.1016/j.image.2019.115670
[19]	WANG C F, FAN C L, FENG K, et al. Analysis of the time series generated by a new high-dimensional discrete chaotic system[J]. Complexity, 2018, 2018: 1-11.
[20]	SUN K H, LIU X, ZHU C X. The 0-1 test algorithm for chaos and its applications[J]. Chinese Physics B, 2010, 19(11): 204-210.
[21]	叶晓林,牟俊,王智森,等. 基于SE和C₀算法的连续混沌系统复杂度分析[J]. 大连工业大学学报,2018,37(1): 67-72. YE Xiaolin, MOU Jun, WANG Zhisen, et al. Analysis of continuous chaotic complexity based on SE and C₀ algorithm[J]. Journal of Dalian Polytechnic University, 2018, 37(1): 67-72.
[22]	孙克辉. 混沌保密通信原理与技术[M]. 北京: 清华大学出版社, 2015: 30-33.

施引文献

期刊类型引用(2)

1.	李涛，李梓响，郑晨昱，张子凯，张利平. 求解U型拆卸线平衡问题的多目标教与学优化. 组合机床与自动化加工技术. 2025(02): 229-235 . 百度学术
2.	张雷，耿笑荣，陶凯博. 考虑碳排放与收益的随机并行拆卸线平衡优化. 机械工程学报. 2023(07): 330-338 . 百度学术

其他类型引用(5)

附加材料(0)

访问统计

点击查看大图

图(11) / 表(14)

计量

文章访问数: 362
HTML全文浏览量: 230
PDF下载量: 48
被引次数: 7

1. 工程概况
2. 模型建立过程
2.1 脉动风压时程函数提取
2.2 整体模型建立
2.3 瑞利阻尼
2.4 风压时程函数输入
3. 计算结果
4. 结　论

基于二维离散混沌系统和DNA的图像加密方案

doi: 10.3969/j.issn.0258-2724.20220810

作者简介: 徐昌彪（1972—），男，教授，博士，研究方向为混沌理论，E-mail：xucb@cqupt.edu.cn

计量

出版历程

Image Encryption Scheme Based on 2D Discrete Chaotic System and Deoxyribonucleic Acid

1. 工程概况

2. 模型建立过程

2.1 脉动风压时程函数提取

2.2 整体模型建立

2.3 瑞利阻尼

2.4 风压时程函数输入

3. 计算结果

4. 结 论

期刊类型引用(2)

其他类型引用(5)

计量

出版历程

目录

1. 工程概况

2. 模型建立过程

2.1 脉动风压时程函数提取

2.2 整体模型建立

2.3 瑞利阻尼

2.4 风压时程函数输入

3. 计算结果

4. 结 论

作者简介:
徐昌彪（1972—），男，教授，博士，研究方向为混沌理论，E-mail：xucb@cqupt.edu.cn

4. 结　论

4. 结　论