基于改进Super-Twisting滑模观测器的永磁同步电机无传感器控制

王涛; 黄景春; 周行之; 金靖

doi:10.3969/j.issn.0258-2724.20220793

基于改进Super-Twisting滑模观测器的永磁同步电机无传感器控制

doi: 10.3969/j.issn.0258-2724.20220793

西南交通大学电气工程学院，四川成都 610031

基金项目: 国家自然科学基金项目（U21A20169）；四川省自然科学基金项目（2022NSFSC0451）

详细信息

作者简介:
王涛（1972—），男，教授，博士生导师，研究方向为电机鲁棒控制，E-mail：taowang@home.swjtu.edu.cn

中图分类号: TM341
计量
- 文章访问数: 192
- HTML全文浏览量: 65
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-17
- 修回日期: 2023-06-08
- 网络出版日期: 2025-01-13
- 刊出日期: 2023-11-27

Sensorless Control of Permanent Magnet Synchronous Motor Based on Improved Super-Twisting Sliding Mode Observer

School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
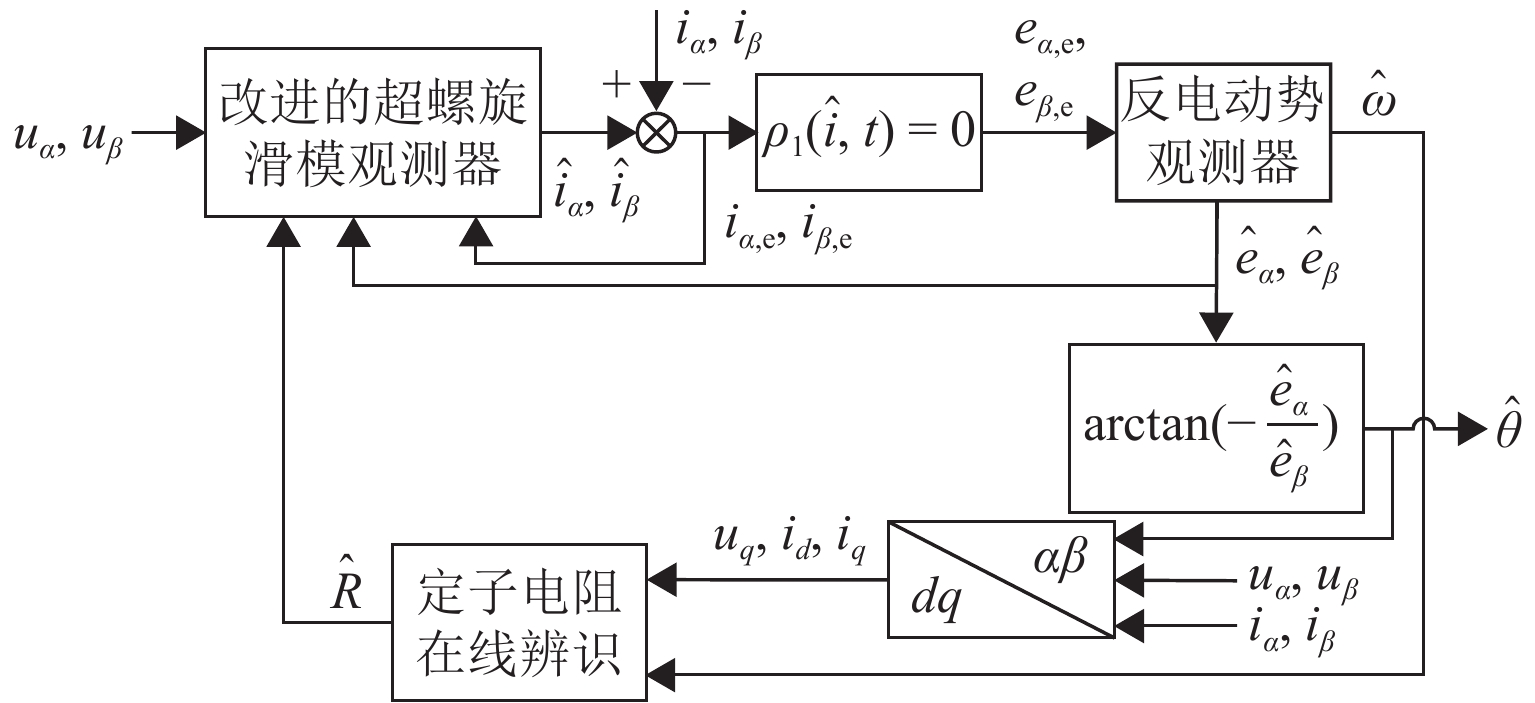
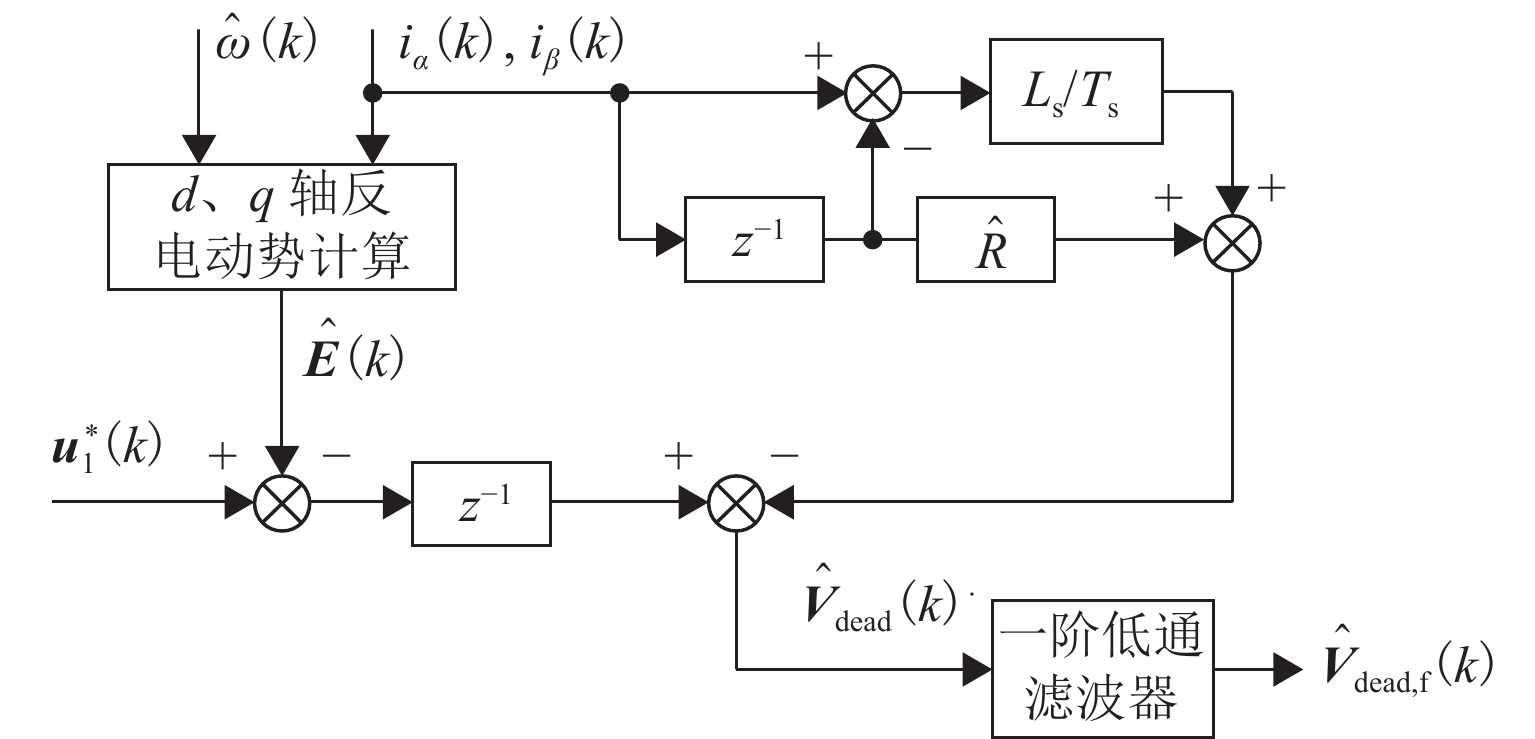
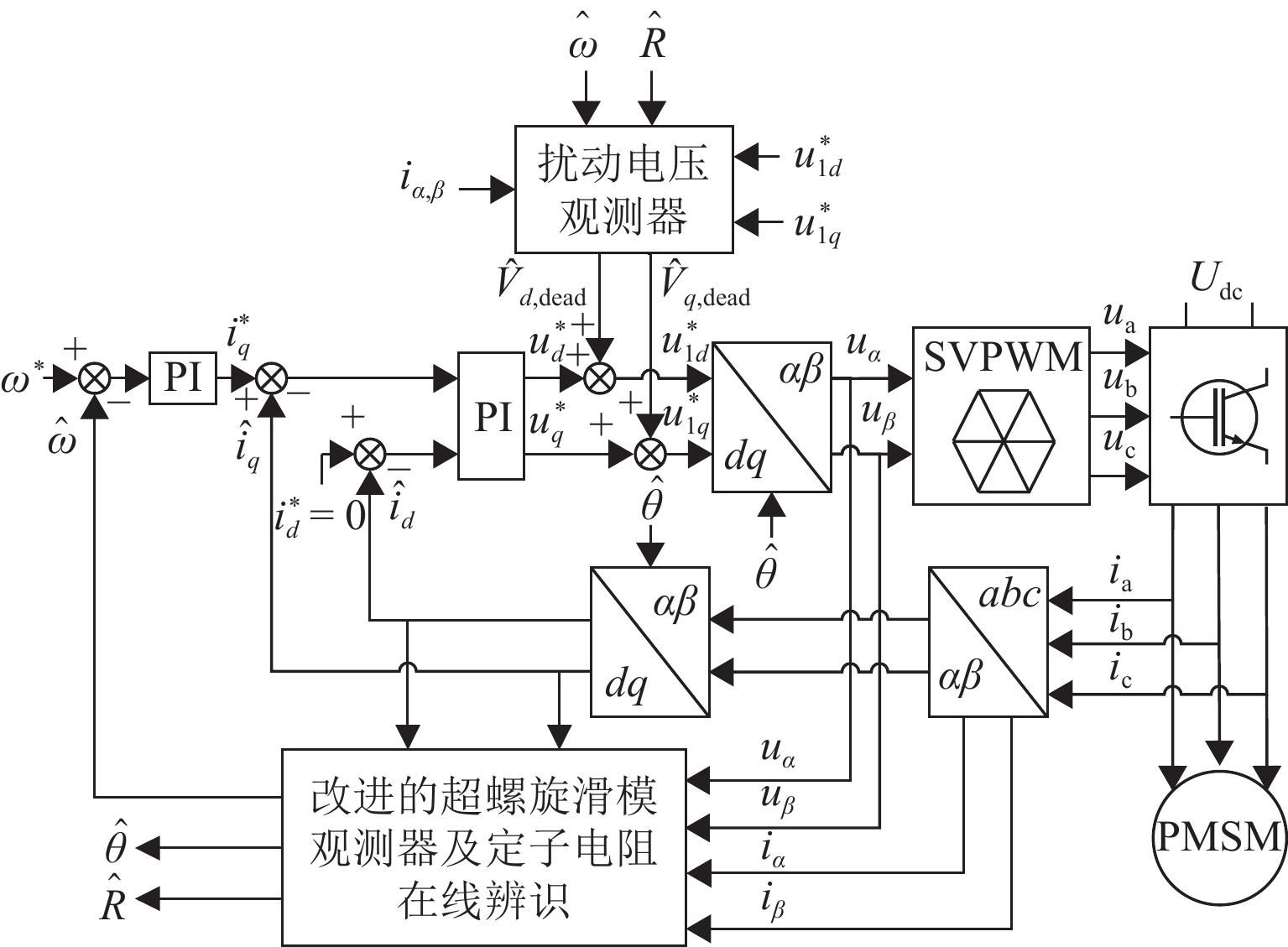
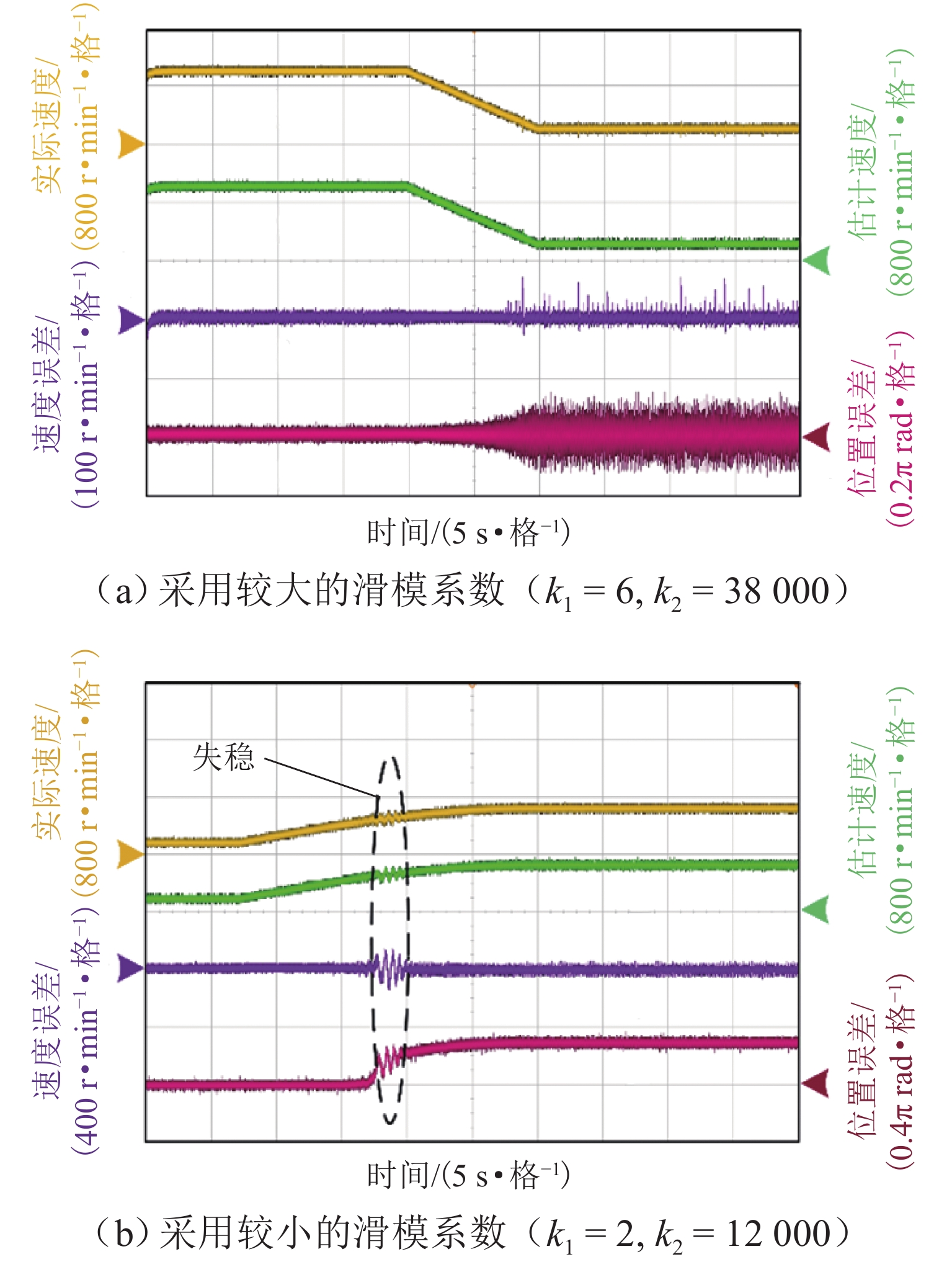
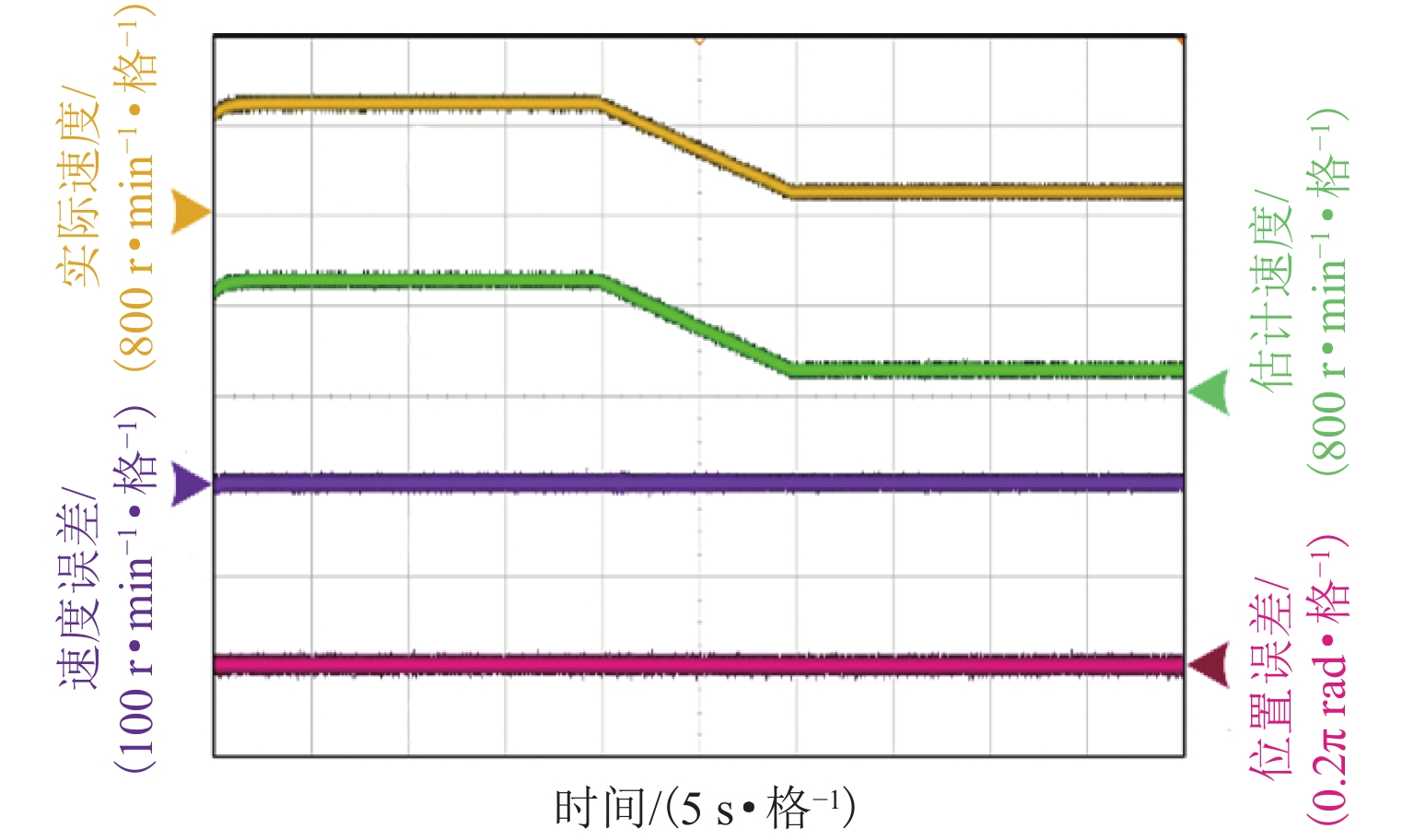
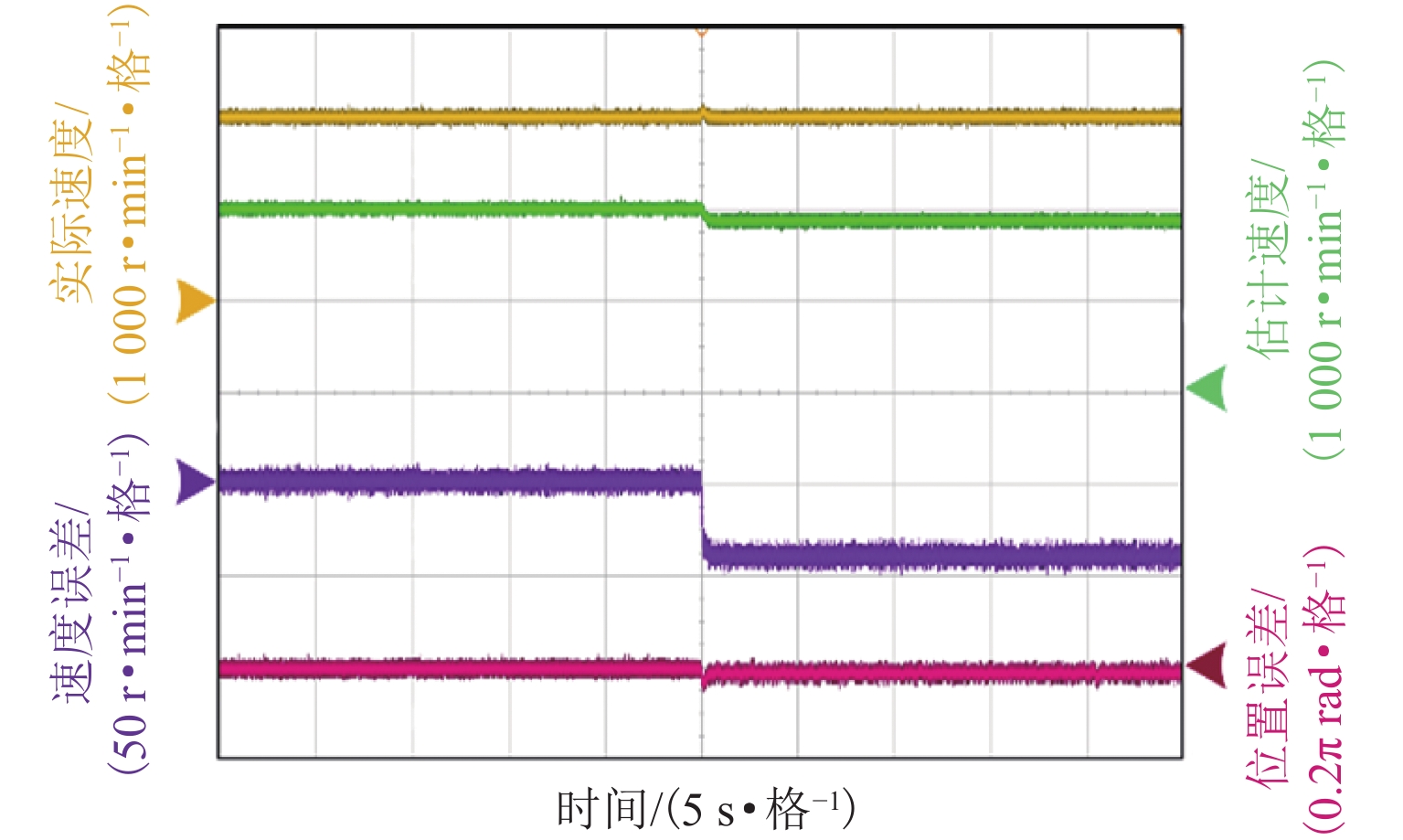
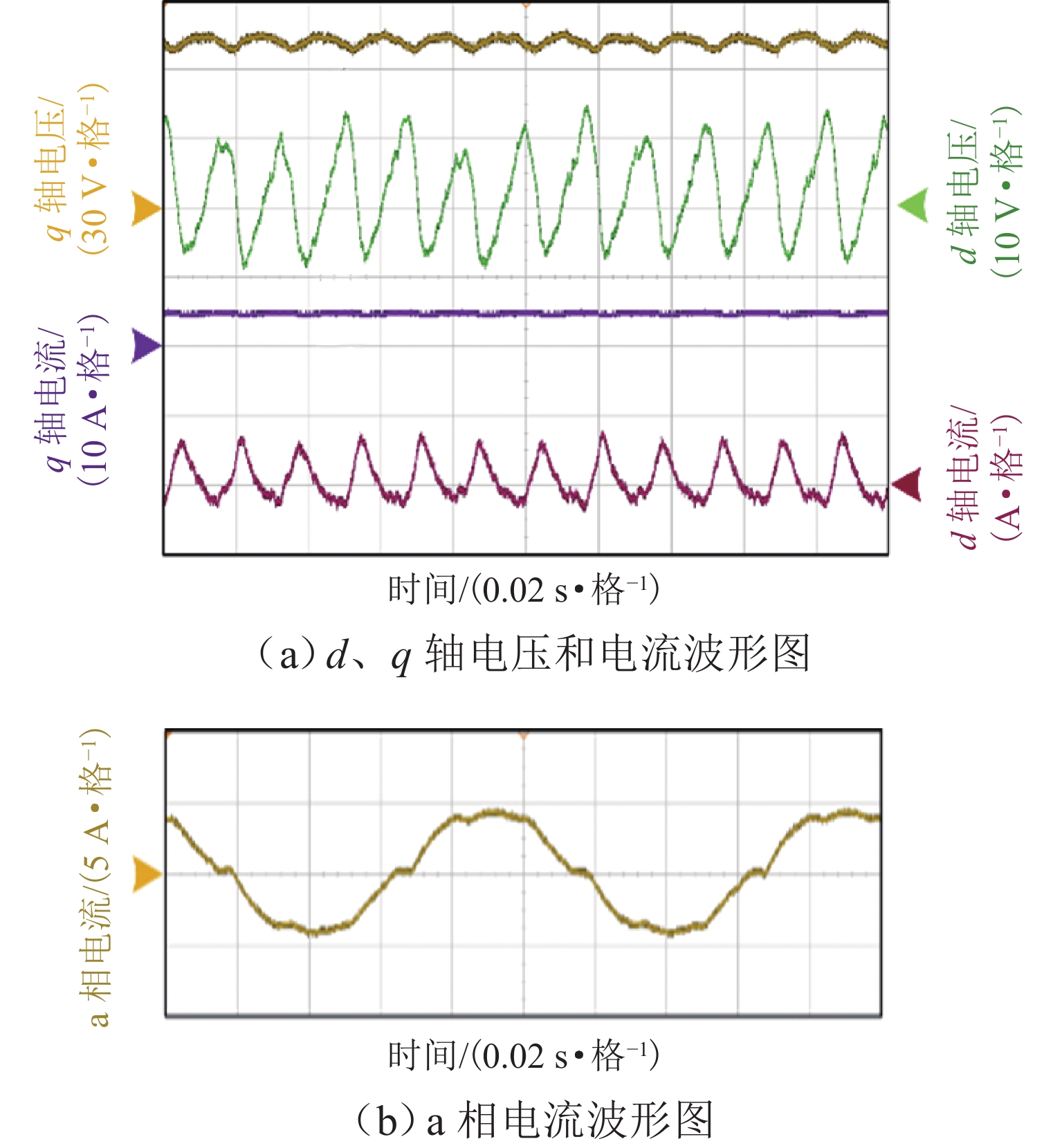
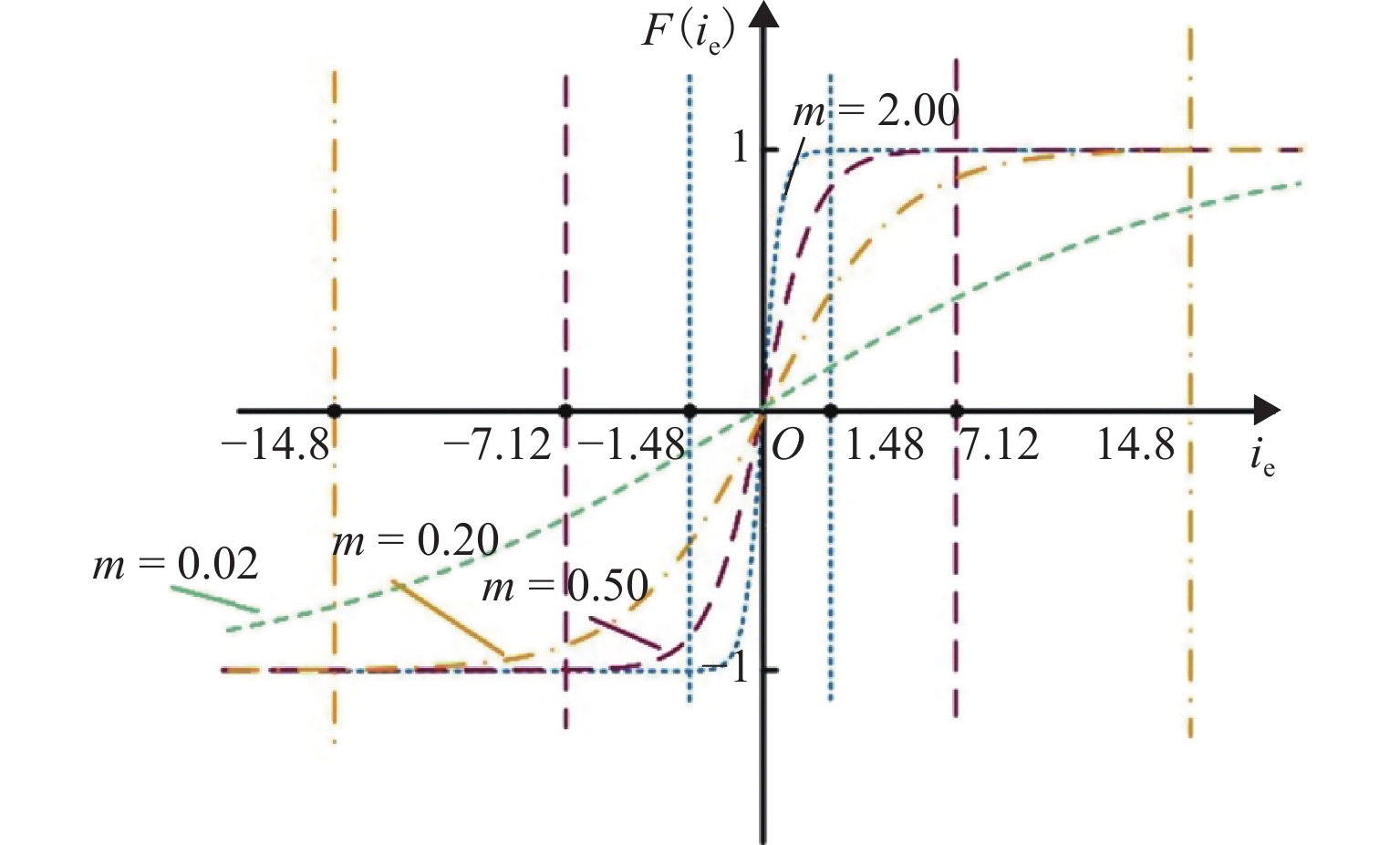
在无传感器控制宽调速范围内，传统super-twisting二阶滑模观测器算法在永磁同步电机中存在转子位置估计误差随速度变化而发生抖动的问题. 为减小转子位置估计误差并提升电机调速控制性能，本文基于双曲函数提出一种改进的滑模观测器，并设计定子电阻的在线辨识方案，同时开发扰动电压观测器以在线估计逆变器非线性引起的失真电压；最后，通过电机硬件在环实验测试进行验证. 测试结果表明：位置估计误差减小7.6%，速度估计精度提高5.8%.
- 永磁同步电机 /
- 无传感器控制 /
- 改进super-twisting算法 /
- 定子电阻在线辨识 /
- 逆变器非线性补偿
Abstract:
In the wide speed range of sensorless control, the traditional super-twisting second-order sliding mode observer algorithm had a problem that the error of rotor position estimation would change with the speed in the permanent magnet synchronous motor (PMSM). In order to improve the control performance of the motor speed and reduce the error of rotor position estimation, an improved sliding mode observer based on hyperbolic function was proposed, and an online identification scheme of stator resistance was designed. A disturbance voltage observer was designed to estimate the distortion voltage caused by the nonlinearity of the inverter on line. Finally, the hardware-in-the-loop test was carried out to verify the feasibility of the scheme. The test results show that the error of position estimation can be reduced by 7.6%, and the accuracy of velocity estimation can be increased by 5.8%.
- permanent magnet synchronous motor /
- sensorless control /
- improved super-twisting algorithm /
- online identification of stator resistance /
- nonlinearity compensation of inverter

HTML全文

感知施工现场人员的位置信息、进行施工现场实体的追踪定位，能够为生产力分析、安全管理提供基础数据^[1]. 相比基于无线电的方法定位，如无线电射频识别（RFID）、超宽带（UWB）和基于传感器的全球定位系统（GPS），基于计算机视觉的位置信息采集技术有成本低、无接触、效率高等优点^[1-3].

基于计算机视觉的施工实体追踪与定位研究多采用手工设计的图像特征（如梯度直方图和色彩直方图）进行目标检测和数据关联^[1-2,4]. 数据关联即为目标检测结果分配ID，完成对目标的持续追踪. 相比基于深度学习的特征，手工设计特征是较为浅层的特征，鲁棒性差. 因此，Son等^[5]使用深度残差网络作为主干网络进行特征提取，实现高精度的施工现场人员检测. Son等^[3]使用YOLOv4^[6]进行目标检测，并利用基准卷积神经网络对检测结果进行特征提取以实现目标匹配. Angah等^[7]利用Mask RCNN （region-based convolutional neural networks）^[8]作为检测器，并使用不同基准卷积网络进行特征提取，完成施工人员的匹配. Zhang等^[9]利用行人重识别深度特征实现跨摄像头的施工现场人员匹配.

行人重识别原是多目标多摄像头追踪的子任务，后来分离成为独立的研究方向，旨在利用目标图像实现行人跨时空的准确检索^[10-11]. 上述人员追踪研究都仅仅将行人重识别方法用作特征提取器，并没有充分挖掘特征序列彼此之间的关联，以实现更准确的目标匹配；另一方面，行人重识别研究针对的场景大多为普通行人场景，相较之下，施工场景背景复杂、人员姿势丰富、着装更为相似、遮挡重叠更为严重，依靠外观特征进行匹配容易产生错误匹配，需要针对施工场景提出优化机制.

本文采用YOLOv5算法进行目标检测，并提出一种基于行人重识别的数据关联方法，以实现对施工人员的视觉追踪. 该方法包括基于重排序的距离度量技术，能够考虑深度特征之间的关联性，从而增强对难样本的识别能力. 此外，还引入一种后处理机制，结合缓冲机制和特征动态更新，旨在优化匹配结果，充分考虑施工环境的动态性、复杂性及人员着装的相似性，以提高追踪的准确性. 在视觉追踪的基础上，运用图像透视变换实现对施工人员在现场的真实2D坐标及运动信息的持续感知，为生产力分析提供基础数据.

1. 算法整体流程

算法由3个模块组成：目标检测、数据关联、坐标获取. 目标检测能够完成大类目标（如人员、机具、材料等）的识别与初步定位，但并不能实现大类下个体之间的区分，以及视频帧与帧之间目标的辨别. 因此，在目标检测的基础上进行数据关联，为被检测出的对象分配ID，实现目标的视觉追踪. 本文以行人重识别的视角建立了一种数据关联方法，每一帧通过目标检测网络输出的目标称为待检目标（query），这些目标需要和人员图像库（gallery，以下简称库）中的若干对象进行匹配，以为其分配ID. 完成数据关联后，基于图像透视变换完成施工人员现场真实位置信息获取，并结合帧率信息获取如运动距离、速度、时间等的基础生产力分析数据. 算法流程如图1所示，图中，q_i为第i个待检目标，g_j为库中第j个对象（库中储存图像是由深度网络提取到的深度特征而非直接存储图像，故称其为对象）.

图 1 算法流程示意

Figure 1. Algorithm process

下载: 全尺寸图片幻灯片

2. 目标检测

采用基于深度学习的单阶段目标检测方法YOLOv5^[12]，该方法是单阶段算法YOLO系列的第5版，为目前主流的单阶段算法之一. 实际采用YOLOv5l网络架构，并利用An等^[13]提出的施工现场数据集，提取其中包含工人的部分图片和对应的标注信息，结合现场采集的图片，构建训练集以及验证集，其中，训练集6085张图片，验证集1522张图片.

训练初始学习率为3.2 × 10^-3，最终OneCycle学习率为0.12，动量为0.853，权重衰减为3.6 × 10^-4，训练轮数为400轮，每轮样本数为16个. 训练目标框损失变化情况见图2. 在验证集中，训练后的网络检测平均精度均值（mean average precision，mAP）达到87.5%.

图 2 目标检测网络目标框损失变化曲线

Figure 2. Target frame loss curves of target detection network

下载: 全尺寸图片幻灯片

3. 基于行人重识别的数据关联

3.1 基于重排序的距离度量

通过基于深度学习的行人重识别网络提取代表目标外观特征的特征向量，利用特征向量之间的欧氏距离进行度量和对比，从而实现对施工现场不同工人的识别，并在遮挡和重叠情况下有效“重识别”同一目标.

采用Luo等^[14]提出的基准网络，如图3所示. 图中，GAP、BN、FC分别为全局平均池化层、批正则化层、全连接层. 网络的输出ID用于训练，而特征向量则用于推理和模型训练. 在测试阶段，使用在行人重识别标准数据集Market1501^[15]上预训练的模型.

图 3 行人重识别算法网络结构

Figure 3. Network structure of person re-identification algorithm

下载: 全尺寸图片幻灯片

将待检测目标与数据库中所有对象进行欧氏距离度量，并按距离从小到大对对象进行排序，生成初始序列，如式（1）所示. 在这个序列中，靠前的对象与待检测目标越相似，则为该待检测目标分配序列中第1个对象对应的ID.

$\begin{split} & L_0\left(q_i\right)=\left\{g_1, g_2, \cdots, g_J\right\},\quad d_1\left(q_i, g_j\right)\lt d_1\left(q_i, g_{j + 1}\right), \\ &\quad j=1,2, \cdots, J-1, \end{split}$

(1)

$d_1\left(q_i, g_j\right)=\left\|\boldsymbol{f}_{q i}, \boldsymbol{f}_{g j}\right\|_2,$

(2)

式中： $d_{1}\left(q_{i}, g_{j}\right)$ 为q_i和g_j间的欧氏距离，J为库中对象数， ${\boldsymbol{f}}_{qi}$ 和 ${\boldsymbol{f}}_{gj}$ 分别为q_i和g_j对应的特征向量.

施工场景下人员穿着相似，排序靠前对象可能并非该待检目标的正确配对. 此外，ID分配仅考虑了外观特征的相似度，所构建序列的排序信息未得到充分利用，而目标和对象若属于同一ID，则二者的近邻之间有较高的相似度^[16]. 为此，引入行人重识别研究中的重排序（re-ranking）概念，针对数据关联任务，提出一种基于k最邻近的重排序方法，并对重排序后的序列进行特征局部扩展，以获得更为鲁棒的特征表示，从而生成最终的优化序列，以提高算法在施工人员外观相似情况下的匹配准确性，如所示. 图中，g_j右侧括号内的 $h_{p}^{(l)}$ 表示序列中对象g_j的真实ID为l，并且在排序中是序列中第p个ID为l的对象， $L_{1}\left(q_{i}\right)$ 、 $L_{*}\left(q_{i}\right)$ 分别为经过k最邻近重排序后的序列（优化序列1）和最终匹配序列， $N\left(g_{j}, k\right)$ 为库中对象g_j的k最邻近集（定义见3.1.1节）， $q_{i}^{*}$ 为特征局部扩展后的待检目标.

图 4 重排序示意

Figure 4. Re-ranking

下载: 全尺寸图片幻灯片

3.1.1 基于k最邻近的重排序

取待检目标的k最邻近集 $N\left(q_{i}, k\right)$ ，也即初始匹配序列 $L_{0}\left(q_{i}\right)$ 中的前k项中满足距离阈值要求的对象集，如式（3）所示. 其中，k取值见式（4）. 使用同样的方法，对 $N\left(q_{i}, k\right)$ 中每个对象计算其k最邻近对象集 $N\left(g_{j}, k\right)$ （排除该对象本身）. 基于建立好的近邻集，利用Jaccard距离^[17]，计算待检目标与其k最邻近集中对象的邻近距离 $d_{2}\left(q_{i}, g_{j}\right)$ ，表征集合间的相似度，如式（5）所示，对于待检目标的非k最邻近对象，该值取1. 采用欧氏距离与最邻近距离加权获得重排序后的序列，如式（6）所示，其中距离的计算见式（7）.

$N\left(q_i, k\right)=\left\{g_1, g_2, \cdots, g_k\right\},\quad g_j \in L_0\left(q_i\right),$

(3)

$\begin{split} & k=\min \left\{k_0, j_{\max }\right\}, \quad d_1\left(q_i, g_j\right)\lt d_0, \\&\quad j=1,2, \cdots, J, \end{split}$

(4)

$d_2\left(q_i, g_j\right)=\left\{\begin{array}{l} 1-\dfrac{N\left(q_i, k\right) \cap N\left(g_j, k\right)}{N\left(q_i, k\right) \cup N\left(g_j, k\right)},\quad j \leqslant k, \\ 1,\quad j \gt k \end{array}\right.$

(5)

$\begin{split} & L_1\left(q_i\right)=\left\{g_1, g_2, \cdots, g_J\right\}, \quad d\left(q_i, g_j\right) \lt d\left(q_i, g_{j + 1}\right), \\&\quad j=1,2, \cdots, J-1, \end{split}$

(6)

$d\left(q_i, g_j\right)=\left(1-\lambda_1\right) d_1\left(q_i, g_j\right) + \lambda_1 d_2\left(q_i, g_j\right),$

(7)

式中： $k_{0}$ 为设定的邻近数， $d_{0}$ 为一距离阈值， $\lambda_{1}$ 为近邻距离权重.

3.1.2 特征局部扩展

将待检目标本身的图像特征向量与重排序后序列的前 $k_{{\mathrm{e}}}$ 个对象对应的图像特征向量进行加权，如式（8）所示，其中 $k_{{\mathrm{e}}}$ 的取值见式（9）. 该加权方法考虑了排序信息，根据对象特征在排序中的位置进行该对象特征权重的调整，能够确保越相近的对象被赋予更高的权重. 利用扩展的特征向量再次进行距离度量，获取该待检目标的最终匹配序列，如式（10）所示.

$\boldsymbol{f}_{q_i}^*=\left(1-\lambda_2\right) \boldsymbol{f}_{q_i} + \lambda_2 \frac{\displaystyle\sum_{j=1}^{k_{\mathrm{e}}}\left(k_{\mathrm{e}}-j + 1\right) \boldsymbol{f}_{g_j}}{\displaystyle\sum_{j=1}^{k_{\mathrm{e}}}\left(k_{\mathrm{e}}-j + 1\right)}，$

(8)

$\begin{split} & k_{\mathrm{e}}=\min \left\{k_{{\mathrm{e}} 0}, \max (j)\right\},\quad d\left(q_i, g_j\right) \lt d_{{\mathrm{e}} 0}, \\&\quad j=1,2, \cdots, J, \end{split}$

(9)

$\begin{split} & L_*\left(q_i\right)=\left\{g_1, g_2, \cdots, g_J\right\}, \quad d_1\left(q_i^*, g_j\right)\lt d_1\left(q_i^*, g_{j + 1}\right), \\&\quad j=1,2, \cdots, J-1, \end{split}$

(10)

式中： $\lambda_{2}$ 为扩展权重， $k_{{\mathrm{e}} 0}$ 为设定的扩展邻近数， $d_{{\mathrm{e}}0}$ 为扩展距离阈值.

3.2 匹　配

匹配也即为待检目标分配ID. 跟行人重识别研究不同，数据关联任务中，每个待检目标获取的ID是唯一的，也即不存在多个待检目标被分配同一ID的情况，另外追踪过程中可能会出现此前库中没有的新目标，更类似于开放世界行人重识别任务^[11]. 因此，为正确分配ID，不同于3.1节中仅度量待检目标与库中对象之间的距离，这里利用最终匹配序列 $L_{*}\left(q_{i}\right)$ 获取待检目标 $q_{i}$ 与库中ID间的距离. 计算所有待检目标与所有ID的距离以建立距离矩阵D，如式（11）所示.

$\boldsymbol{D}=\left(\begin{array}{cccccc} d_{11} & d_{12} & \cdots & d_{1 l} & \cdots & d_{1 n} \\ d_{21} & d_{22} & \cdots & d_{2 l} & \cdots & d_{2 n}\\ \vdots & \vdots & & \vdots & & \vdots \\ d_{i 1} & d_{i 2} & \cdots & d_{i l} & \cdots & d_{i n}\\ \vdots & \vdots & & \vdots & & \vdots \\ d_{m 1} & d_{m 2} & \cdots & d_{m l } & \cdots & d_{m n} \end{array}\right)_{m \times n},$

(11)

式中： $d_{il}$ 为待检目标q_i与 $L_{*}\left(q_{i}\right)$ 中ID为l的第1个对象间的欧式距离，也即 $d_{1}\left(q_{i}^{*}, h_{1}^{(l)}\right)$ ，m和n分别为这一帧的待检目标数和库中所有ID数.

基于建立好的距离矩阵，采用改进的Jonker-Volgenant方法^[18]为每个待检目标分配ID. 对于被分配ID为l的待检目标q_i，若d_il小于匹配阈值，则认为匹配成功，为其分配对应的ID；否则认为出现了库中没有的新目标，为其分配新的ID；此外若m>n，则表示出现了库中没有的目标，为这些没有被匹配到的待检目标分配新ID.

3.3 匹配结果后处理

3.3.1 缓冲机制

施工场景复杂，常常出现遮挡和姿态变化等情况，使得即使待检目标确实属于某一数据库ID，也可能面临匹配失败. 此外，目标检测过程中可能存在误检，如果此时错误地赋予新ID，将导致匹配错误和误判. 为解决这一问题，引入缓冲机制，如图5所示. 该机制通过建立一个缓冲库来类比原始库. 每一帧的待检目标首先与库进行匹配，如果匹配失败，则会与缓冲库进行匹配. 如果成功，则该特征将被添加到缓冲库中. 当缓冲库中对应ID的特征向量数量达到设定阈值时，会将该待检目标加入主库并赋予新ID. 如果仍然匹配失败，则在缓冲库中为该待检目标创建新ID并存储其特征向量. 同时，缓冲库中连续若干帧匹配失败的ID将被删除. 最终的追踪结果由两个部分贡献组成：一是与库中目标成功匹配的目标，二是缓冲库中满足特征向量数量要求的目标. 该缓冲机制提高了算法的容错性，从而减少了错误匹配的发生.

图 5 匹配结果后处理方法示意

Figure 5. Post-processing method for matching results

下载: 全尺寸图片幻灯片

3.3.2 特征动态更新机制

对于匹配成功的若干待检目标，计算其两两间目标框的交并比（2个矩形相交面积与相并面积之比），若任意一个待检目标与其余待检目标的目标框交并比均小于阈值，则认为不存在较大重叠，将该待检目标的图像特征存入库中对应ID下，若该ID特征数满足限值，则随机替换非初始图像特征，见图5. 由于库并不能无限储存特征，特征的动态更新确保库中始终保留与当前目标相近的图像特征，从而提高姿态变化情况下的追踪准确率，并有效避免库中出现重叠的图像特征，减少错误匹配的发生.

4. 坐标获取

上述目标追踪方法只能获取人员与ID对应的像素坐标，为获取现场真实位置信息，需要进行坐标变换. 假定所有施工人员均位于同一施工平面，则可忽略深度信息，通过透视变换获取目标在平面上的真实2D坐标^[19]. 在变换前需对相机进行基本的畸变矫正，如图1，这里不再赘述其过程.

图像透视变换本质是利用图像的单应性实现2D图像之间的映射，在变换前后直线仍为直线，效果见. 图像坐标系 $uov$ 通过透视变换转换为设定的 $u^{\prime} o^{\prime} v^{\prime}$ 坐标系，与结构图对应. 透视变换式见式（12）. 为求解透视变换矩阵，需选择4对参考点，例如图6中的4个点柱节点，实际计算时可选择超过4个点，利用随机抽样一致法（random sample consensus，RANSAC）获得更鲁棒的结果.

图 6 透视变换示意

Figure 6. Perspective transformation

下载: 全尺寸图片幻灯片

$w(\begin{array}{l} x \quad y \quad 1 \end{array})^{\mathrm{T}}=\boldsymbol{A}_{3 \times 3}(\begin{array}{c} x_0 \quad y_0 \quad 1 \end{array})^{\mathrm{T}},$

(12)

式中： $\left(x_{0}\;\;\; y_{0}\;\;\; 1\right)^{{\mathrm{T}}}$ 和 $(x\;\;\; y\;\;\; 1)^{{\mathrm{T}}}$ 分别为变换前、后对应点的齐次坐标（变换前坐标采用目标框底边中点像素坐标）， $w$ 为比例系数， ${\boldsymbol{A}}_{3 \times 3}$ 为透视变换矩阵.

获取坐标后，结合视频帧率可以分析人员的运动信息. 通过设置采样频率，计算指定区间内的平均移速，如果该速度满足阈值要求，则判定目标处于运动状态. 同时，更新目标的运动距离和时间.

5. 实验验证与模型评价

5.1 实验案例概况

在上海市某房屋建筑施工现场收集视频资料，并从不同视角和施工阶段中选取了具有各种施工现场特点的视频，以制作标准测试视频用于算法测试. 其详细信息见表1. 所有视频均以25帧/s的速度拍摄，且大部分场景中目标的外观相似度较高. 算法测试的软硬件配置如表2所示.

表 1 标准测试视频详细信息

Table 1. Details of standard test videos

编号	主要施工活动	视角	帧数/帧	目标数/个	难点
1	混凝土浇筑	平视	1479	10136	尺寸差异、遮挡
2	结构测设	平视	769	4606	尺寸差异、遮挡
3	混凝土浇筑	俯视	754	9803	夜间、遮挡
4	结构测设	俯视	616	8101	小目标、遮挡
5	钢筋绑扎	俯视	1230	26922	小目标、遮挡
6	混凝土浇筑	俯视	704	8427	夜间、小目标
7	混凝土模板搭设	俯视	1131	5656	姿态改变、背景复杂
8	预制柱吊装	俯视	1374	11220	动态性强、遮挡
9	预制板吊装	俯视	866	4221	动态性强、遮挡
10	脚手架搭建	俯视	497	6853	背景复杂
11	钢筋加工	俯视	632	3265	人员离开又重进入

下载: 导出CSV

| 显示表格

表 2 软硬件配置详情

Table 2. Software and hardware configuration

项目	详情
监控设备	6寸球机型号：DS-2DC6423IW-AE
CPU	Intel（R） Core（TM） i9-10900X @3.70 GHz
GPU	NVIDIA GeForce GTX 2080 Ti
操作系统	Ubuntu 20.04.3
编程环境	Python 3.8.8
深度学习框架	Pytorch 1.9.1 + cu102

下载: 导出CSV

| 显示表格

5.2 模型评价方法

采用多目标追踪准确度（multiple object tracking accuracy，MOTA）和IDF1（ID的F1得分）对目标追踪效果进行评价，其计算分别如式（13）、（14）所示.

$A_{\mathrm{{MOT}}}=1-\frac{\displaystyle \sum_{t=1}^T\left(M_t + W_t + M_t\right)}{\displaystyle \sum_{t=1}^T G_t} \times 100{\text{%}},$

(13)

$\begin{aligned} F_{{\mathrm{ID}}}=\frac{2}{1 / P + 1 / R} \times 100 {\text{%}}, \end{aligned}$

(14)

式中： $M_{t}$ 、 $W_{t}$ 、 $M_{t}$ 、 $G_{t}$ 分别为第 $t$ 帧中的漏检数、误检数、ID切换数、真实目标数；T为视频总帧数，反映追踪的稳定性；P和R分别为ID的准确率和召回率，能够综合反映ID的准确性.

5.3 视觉追踪

按照实验结果选取参数配置：匹配阈值0.6，缓冲库图像特征限值15个，库中每个目标的特征数限值20个，交并比阈值0.8. 其余参数设置为： $k_{0}=20$ 个， $d_{0}=1.0$ ， $\lambda_{1}=0.8$ ， $k_{{\mathrm{e}} 0}=10$ 个， $d_{{\mathrm{e}}0}=0.6$ ， $\lambda_{2}=0.5$ . 部分场景追踪效果如图7所示，算法运行平均帧率达到15.2帧/s.

图 7 不同场景视觉追踪效果

Figure 7. Visual tracking results in different scenes

下载: 全尺寸图片幻灯片

为验证算法的有效性，在不同场景中和其他追踪算法进行对比，结果见表3. 在大部分场景下，本文算法获得了最好的结果，平均IDF1和MOTA分别为85.4%和75.4%.

表 3 不同算法在标准测试视频中的结果（IDF1/MOTA，%）

Table 3. Performance of different algorithms on standard test videos （IDF1/MOTA, %）

算法	场景 1	场景 2	场景 3	场景 4	场景 5	场景 6	场景 7	场景 8	场景 9	场景 10	场景 11
DAN*^[20]	61.5/65.8	44.2/55.4	66.8/67.8	79.2/77.9	73.1/61.5	78.9/81.3	95.3/86.4	76.7/84.2	78.6/81.3	65.5/59.0	93.5/96.2
TraDeS^[21]	43.4/27.0	32.2/21.2	8.2/5.3	10.4/-10.8	8.8/-6.8	40.3/28.8	4.2/2.6	30.2/36.2	5.4/-0.7	10.5/2.8	40.4/16.6
FairMOT^[22]	48.7/47.0	51.4/54.0	18.4/13.5	47.9/40.5	12.0/0	61.9/45	10.1/9.6	29.1/33.6	28.2/18.2	11.6/5.7	49.8/43.5
Trackformer*^[23]	61.7/55.3	49.8/44.4	29.5/23.0	58.0/54.5	37.2/22.7	68.7/58.9	40.6/24.1	36.7/52.3	32.8/30.6	37.5/38.1	83.8/95.7
Unicorn^[24]	61.4/57.5	70.5/64.0	13.2/4.6	62.6/46.9	20.1/16.4	72.5/66.3	3.2/3.4	54.6/58.7	34.3/29.2	40.4/34.2	81.7/79.9
ByteTrack^[25]	73.4/63.7	67.3/62.4	64.6/58.2	82.1/73.5	38.5/29.6	77.6/71.2	33.4/31.1	61.8/67.1	52.6/54.1	47.0/34.4	83.0/75.8
本文算法*	78.0/66.0	73.3/57.1	82.4/67.8	87.2/77.7	78.0/63.1	89.1/81.6	97.8/95.6	91.8/84.8	90.5/81.5	73.8/58.3	97.5/96.4
注：带*的方法使用了相同的目标检测结果，最优结果加粗表示.

下载: 导出CSV

| 显示表格

为评估本文提出的基于重排序的距离度量方法及匹配后处理优化机制对算法性能的影响，对比了不同架构下的实验结果，详见表4. 结果显示，包含重排序方法和匹配后处理优化机制（包括缓冲机制和动态更新机制）的算法，相比于去除这二者后的算法，平均提高了52.8%的IDF1和3.8%的MOTA.

表 4 不同架构下追踪结果详情（IDF1/MOTA，%）

Table 4. Tracking results with different architectures （IDF1/MOTA, %）

架构	场景 1	场景 2	场景 3	场景 4	场景 5	场景 6	场景 7	场景 8	场景 9	场景 10	场景 11
完整	78.0/66.0	73.3/57.1	82.4/67.8	87.2/77.7	78.0/63.1	89.1/81.6	97.8/95.6	91.8/84.8	90.5/81.5	73.8/58.3	97.5/96.4
无重排序	77.3/66.0	60.1/56.6	81.6/67.6	77.8/77.5	74.8/61.9	88.1/81.4	97.8/95.6	80.6/84.2	90.4/81.3	66.8/58.3	95.9/92.6
无缓冲	76.9/66.0	56.8/55.6	79.3/68.0	81.5/77.9	76.0/61.5	87.1/81.6	97.8/95.6	91.3/84.2	89.5/81.0	72.8/59.1	96.0/96.4
无动态更新	67.0/62.9	47.1/53.5	46.7/60.5	56.1/66.4	45.0/54.7	69.2/77.8	68.4/91.9	60.4/79.4	69.1/78.5	51.3/51.2	92.3/93.7
仅动态更新	70.0/65.9	55.5/55.5	76.4/67.9	74.0/77.7	64.7/61.5	84.5/81.5	93.9/95.6	78.0/84.1	81.4/81.1	63.3/58.9	88.0/96.2
仅缓冲	60.6/63.6	31.0/53.0	30.1/59.3	36.2/68.9	28.3/53.9	60.3/77.2	40.2/87.3	37.5/78.8	45.1/77.0	27.0/52.3	44.7/90.2
仅重排序	63.0/63.9	45.0/54.6	38.8/64.4	41.5/72.6	36.8/56.6	64.0/79.9	58.3/92.4	52.8/80.3	69.5/77.8	38.3/55.8	63.2/94.0
无优化方法	47.8/63.4	27.8/53.4	22.9/62.5	29.6/73.3	21.7/56.2	49.2/79.0	31.6/91.3	29.1/80.4	37.7/77.9	24.5/56.4	36.7/94.1

下载: 导出CSV

| 显示表格

施工场景动态性强，人员除了大量的反复移动之外，姿态相较于普通行人场景更为丰富. 在动态更新机制作用下，视频帧率足够高，即使目标处于运动状态，目标帧间的变化也较小，帧间特征较为相似，确保了持续准确的匹配；此外，动态更新还能对重叠的特征进行过滤，减小目标框重叠导致的错误匹配. 重排序通过考虑特征序列之间相似度，进一步增强待检目标与其对应ID的相似性，从而提高匹配的准确性. 缓冲机制则在目标特征变化匹配失败时发挥作用，避免立刻分配新的ID，虽然可能会带来部分漏检，但提升了长时间追踪下的准确性.

5.4 坐标获取

在俯视视角下选择如图6所示的现场坐标系，利用柱中心点、梁梁节点中心点共9对参考点求解透视变换矩阵，得到施工人员的坐标和轨迹信息如图8，移动距离采样为每25帧一次，运动状态判定阈值为0.5 m，获得位置信息数据如表5，坐标精确到cm.

图 8 完整位置信息感知效果

Figure 8. Result of comprehensive location information perception

下载: 全尺寸图片幻灯片

5.5 结果讨论

本文提出的方法在施工场景下获得较高的追踪准确度，提升追踪精度. 然后，在部分场景下仍存在漏检、误检、错误匹配等现象. 在小目标场景下（如图7（b）），目标检测易出现漏检，此时依靠后续数据关联并不能恢复目标框，而目标本身的行人外观特征也不明显，特别是目标处于蹲姿的情况下，易发生错误匹配. 此外，施工现场重叠较多，由其是在平视且目标穿着相似的情况下. 如图9，在场景2平视视角下，3个相似目标出现了严重重叠，甚至是完全遮挡. 在遮挡后视野中出现穿着相似的新目标会引起ID切换. 一般情况下，遮挡后可利用行人重识别特征进行“重识别”，但在严重重叠的情况下，目标检测可能失效，且因外观高度相似，重识别特征也难保证准确匹配.

表 5 运动数据获取结果

Table 5. Attained movement data

ID	移动距离/m	在场总时间/s	移动时间/s	平均速度/ （m•s⁻¹）
0	52.2	78.0	37.8	1.4
1	12.3	78.0	9.0	1.4
2	0.5	78.0	0.6	0.8
3	7.0	77.8	7.0	1.0
4	28.0	76.1	25.6	1.1
5	17.4	33.5	16.6	1.0

下载: 导出CSV

| 显示表格

图 9 测试场景2中的错误匹配情况

Figure 9. Mismatch in scene 2

下载: 全尺寸图片幻灯片

为进一步改善追踪的效果，首先，针对小目标，可以优化目标检测网络以提升检测性能^[26]；其次，引入先验信息，例如根据现场布局或结构图纸预先标记可能的遮挡物，并预测重新出现的位置，同时结合多摄像头数据优化匹配结果；此外，还可考虑建立施工场景的行人重识别数据集，并融合多源数据进行开放世界人员重识别. 在算法效率方面，由于本文算法在有限硬件设备下未能实现实时图像处理，因此可以考虑采用轻量化行人重识别网络来提高算法的效率. 最后，本文基于图像透视变换获取了现场真实坐标，但由于施工现场动态性较强、人员密集，并没有对获取的精度进行检验，未来可考虑结合传感器等设备对坐标精度进行验证.

6. 结　论

1）本文提出的基于行人重识别的方法能够在不同施工场景下进行准确的人员追踪，并获得现场真实坐标与运动信息，在测试视频中平均IDF1和MOTA分别达到85.4%和75.4%.

2）提出的基于重排序的距离度量方法对目标序列排序结果进行了优化，提高了目标间相似性度量的准确性，有效提升了追踪的准确度.

3）提出的包含缓冲机制和动态更新机制的匹配后处理方法充分考虑了施工场景的动态性、复杂性，能够有效减少由于重叠、遮挡等带来的错误匹配.

图 1 不同m值下的双曲函数

Figure 1. Hyperbolic functions under different values of m

下载: 全尺寸图片幻灯片

图 2 提出的具有定子电阻在线辨识的改进的super-twisting滑模观测器结构框

Figure 2. Structure of proposed improved super-twisting sliding mode observer with online identification of stator resistance

下载: 全尺寸图片幻灯片

图 3 提出的逆变器非线性补偿方法结构框图

Figure 3. Structure of proposed inverter nonlinearity compensation method

下载: 全尺寸图片幻灯片

图 4 PMSM无传感器控制系统框图

Figure 4. Sensorless control system of PMSM

下载: 全尺寸图片幻灯片

图 5 硬件在环测试系统框图

Figure 5. Hardware-in-the-loop test system

下载: 全尺寸图片幻灯片

图 6 采用常值滑模系数的传统super-twisting滑模观测器测试结果

Figure 6. Test results of traditional super-twisting sliding mode observer using constant sliding mode coefficients

下载: 全尺寸图片幻灯片

图 7 基于改进super-twisting滑模观测器的实验测试结果

Figure 7. Test results of improved super-twisting sliding mode observer

下载: 全尺寸图片幻灯片

图 8 不具有定子电阻在线辨识的基于改进super-twisting滑模观测器的实验测试结果

Figure 8. Test results of improved super-twisting sliding mode observer without online identification of stator resistance

下载: 全尺寸图片幻灯片

图 9 具有定子电阻在线辨识的基于改进super-twisting滑模观测器的实验测试结果

Figure 9. Test results of improved super-twisting sliding mode observer with online identification of stator resistance

下载: 全尺寸图片幻灯片

图 10 传统super-twisting滑模观测器测试结果

Figure 10. Test results of traditional super-twisting sliding mode observer

下载: 全尺寸图片幻灯片

图 11 逆变器非线性补偿策略的改进super-twisting滑模观测器测试结果

Figure 11. Test results of improved super-twisting sliding mode observer based on inverter nonlinearity compensation strategy

下载: 全尺寸图片幻灯片

表 1 PMSM相关参数

Table 1. Related parameters of PMSM

参数	值	参数	值
定子电阻/Ω	2.875	额定转矩/（N•m）	5
定子电感/H	0.008	额定电流/A	4.6
极对数/对	4	开通延迟/μs	0.6～1.8
永磁磁链/Wb	0.175	关断延迟/μs	1.8～3.0
m	0.01	死区时间/μs	3.0
额定速度/（r·min⁻¹）	1500	二极管正向压降/V	2.0～3.2
直流母线电压/V	310	饱和压降/V	1.9～2.8

下载: 导出CSV

参考文献(15)

[1]	邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001 DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. doi: 10.3969/j.issn.0258-2724.20220001
[2]	孙友刚,徐俊起,贺祯宇,等. 基于误差交叉耦合的多电磁铁悬浮系统滑模协同控制[J]. 西南交通大学学报,2022,57(3): 558-565. doi: 10.3969/j.issn.0258-2724.20210924 SUN Yougang, XU Junqi, HE Zhenyu, et al. Sliding mode cooperative control of multi-electromagnet suspension system based on error cross coupling[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 558-565. doi: 10.3969/j.issn.0258-2724.20210924
[3]	尚喆,赵荣祥,窦汝振. 基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J]. 中国电机工程学报,2007,3: 23-27. doi: 10.3321/j.issn:0258-8013.2007.26.005 SHANG Zhe, ZHAO Rongxiang, DOU Ruzhen. Research on sensorless control of PMSM based on adaptive sliding mode observer[J]. Proceedings of the CSEE, 2007, 3: 23-27. doi: 10.3321/j.issn:0258-8013.2007.26.005
[4]	王高林,张国强,贵献国,等. 永磁同步电机无位置传感器混合控制策略[J]. 中国电机工程报,2012,32(24): 103-109. WANG Gaolin, ZHANG Guoqiang, GUI Xianguo, et al. Hybrid sensorless control strategy for permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2012, 32(24): 103-109.
[5]	XIE G, LU K Y, DWIVEDI S K, et al. Minimum-voltage vector injection method for sensorless control of PMSM for low-speed operations[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1785-1794. doi: 10.1109/TPEL.2015.2426200
[6]	张磊,高春侠. 一种变增益宽速度范围的永磁同步电机无位置传感器控制[J]. 电机与控制学报,2015,19(8): 36-40,46. ZHANG Lei, GAO Chunxia. Research on variable gain wide speed region sensor-less controltheme for permanent magnet synchronous motors[J]. Electrical Machines and Control, 2015, 19(8): 36-40,46.
[7]	BOUKATTAYA M, GASSARA H. Time-varying nonsingular terminal sliding mode control foruncertain second-order nonlinear systems with prespecified time[J]. International Journal of Adaptive Control and Signal Processing, 2022, 36(8): 2017-2040. doi: 10.1002/acs.3445
[8]	CHI S, XU L Y, ZHANG Z. Sliding mode sensorless control of PM synchronous motor for direct-driven washing machines[C]//Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting. Tampa: IEEE, 2006: 873-879.
[9]	WANG H M, GE X L, LIU Y C. Second-order sliding-mode MRAS observer-based sensorless vector control of linear induction motor drives for medium-low speed maglev applications[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9938-9952. doi: 10.1109/TIE.2018.2818664
[10]	LIANG D L, LI J, QU R H. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3672-3682. doi: 10.1109/TIA.2017.2690218
[11]	YI S C, ZHAI J Y. Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators[J]. ISA Transactions, 2019, 90: 41-51. doi: 10.1016/j.isatra.2018.12.046
[12]	张勇军,汪伟,张小庆,等. 带电阻在线辨识的改进型永磁同步电机滑模观测方法[J]. 电机与控制学报,2017,21(6): 10-17. ZHANG Yongjun, WANG Wei, ZHANG Xiaoqing, et al. Study on improved sliding-mode control with resistance estimation of PMSM[J]. Electrical Machines and Control, 2017, 21(6): 10-17.
[13]	LI Z Y, ZHAI J Y, KARIMI H R. Adaptive finite-time super-twisting sliding mode control for robotic manipulators with control backlash[J]. International Journal of Robust and Nonlinear Control, 2021, 31(17): 8537-8550. doi: 10.1002/rnc.5744
[14]	KIM H, SON J, LEE J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069-4077. doi: 10.1109/TIE.2010.2098357
[15]	HWANG S H, KIM J M. Dead time compensation method for voltage-fed PWM inverter[J]. IEEE Transactions on Energy Conversion, 2010, 25(1): 1-10. doi: 10.1109/TEC.2009.2031811

施引文献

附加材料(0)

访问统计

点击查看大图

图(11) / 表(1)

计量

文章访问数: 192
HTML全文浏览量: 65
PDF下载量: 26
被引次数: 0

1. 算法整体流程
2. 目标检测
3. 基于行人重识别的数据关联
3.1 基于重排序的距离度量
3.2 匹　配
3.3 匹配结果后处理
4. 坐标获取
5. 实验验证与模型评价
5.1 实验案例概况
5.2 模型评价方法
5.3 视觉追踪
5.4 坐标获取
5.5 结果讨论
6. 结　论

基于改进Super-Twisting滑模观测器的永磁同步电机无传感器控制

doi: 10.3969/j.issn.0258-2724.20220793

作者简介: 王涛（1972—），男，教授，博士生导师，研究方向为电机鲁棒控制，E-mail：taowang@home.swjtu.edu.cn

计量

出版历程

Sensorless Control of Permanent Magnet Synchronous Motor Based on Improved Super-Twisting Sliding Mode Observer

1. 算法整体流程

2. 目标检测

3. 基于行人重识别的数据关联

3.1 基于重排序的距离度量

3.1.1 基于k最邻近的重排序

3.1.2 特征局部扩展

3.2 匹 配

3.3 匹配结果后处理

3.3.1 缓冲机制

3.3.2 特征动态更新机制

4. 坐标获取

5. 实验验证与模型评价

5.1 实验案例概况

5.2 模型评价方法

5.3 视觉追踪

5.4 坐标获取

5.5 结果讨论

6. 结 论

计量

出版历程

目录

1. 算法整体流程

2. 目标检测

3. 基于行人重识别的数据关联

3.1 基于重排序的距离度量

3.2 匹 配

3.3 匹配结果后处理

4. 坐标获取

5. 实验验证与模型评价

5.1 实验案例概况

5.2 模型评价方法

5.3 视觉追踪

5.4 坐标获取

5.5 结果讨论

6. 结 论

作者简介:
王涛（1972—），男，教授，博士生导师，研究方向为电机鲁棒控制，E-mail：taowang@home.swjtu.edu.cn

3.2 匹　配

6. 结　论

3.2 匹　配

6. 结　论