Density-Reducing Monte Carlo Method for 7 Degrees of Freedom Humanoid Robot Arm Workspace Solution
-
摘要:
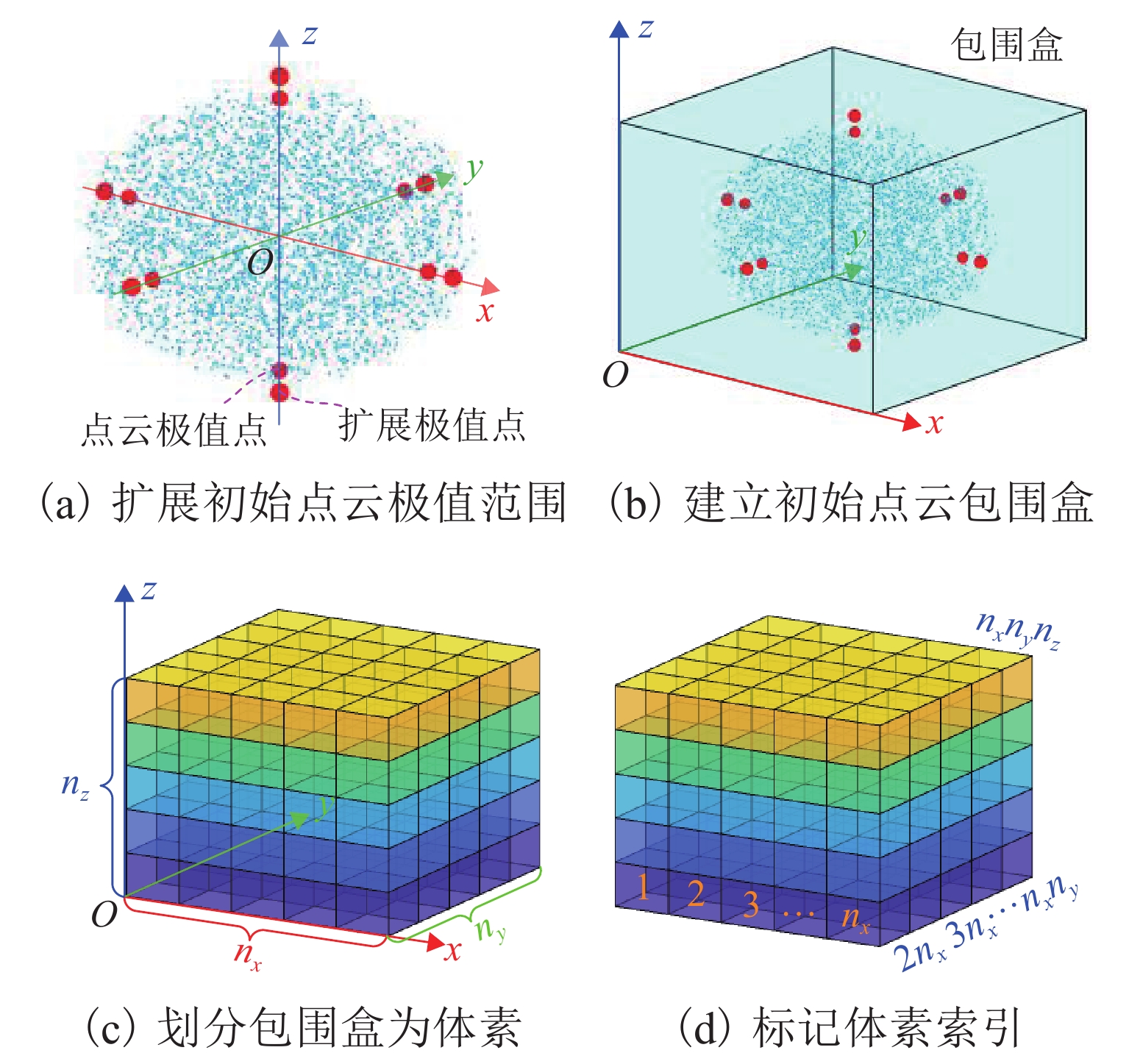
针对蒙特卡洛法和改进蒙特卡洛法在求解机械臂工作空间时存在精度不够准确和加密点云浪费的问题，提出一种降密蒙特卡洛法. 首先，基于蒙特卡洛法中随机点分布不均的特性，对机械臂初始工作空间进行均匀加密，使空间的内部与边界区域分明；然后，采用扩展关节角度和循环加密随机点的方式，只对边界区域进行加密，达到降低工作空间随机点云密度的目的；同时，还研究了该方法中初始点云数量、各轴向分割体素数量、精度阈值、扩展关节角度和循环次数等参数对工作空间精度的影响；最后，通过仿真分析对降密蒙特卡洛法的有效性进行验证. 结果表明：相比于蒙特卡洛法，降密蒙特卡洛法在工作空间平均误差率为0.02242%时，总随机点云数量降幅为93.89%；相比于改进蒙特卡洛法，在循环次数为2次和4次时，降密蒙特卡洛法工作空间的平均误差率分别降低0.13853%和0.11329%，总随机点云数量降幅分别为44.83%和64.52%.
Abstract:A density-reducing Monte Carlo method was proposed to address the problems of inaccurate precision and waste of encrypted point cloud in the Monte Carlo method and the improved Monte Carlo method for solving robot arm workspace. Firstly, based on the characteristic of uneven distribution of random points in the Monte Carlo method, the initial workspace of the robot arm was uniformly densified to make the inner and boundary regions of the space clear. Then, only the boundary region was encrypted by adopting the extended joint angle and the cyclic encryption of random points, so as to reduce the density of the random point cloud in the workspace. Meanwhile, the influence of initial point cloud quantity, axial segmentation voxel quantity, precision threshold, extended joint angle, and cycle number on the precision of the workspace was studied. Finally, the effectiveness of the density-reducing Monte Carlo method was verified by simulation analysis. The results show that compared with the Monte Carlo method, the total number of random point clouds of the density-reducing Monte Carlo method decreases by 93.89% when the average error rate of the workspace is 0.022 42%. In addition, compared with the improved Monte Carlo method, the density-reducing Monte Carlo method reduces the average error rate of the workspace by 0.138 53% and 0.113 29% when the number of cycles is 2 and 4, and the total number of random point clouds decreases by 44.83% and 64.52%.
-
图 5 扩展关节角度对工作空间精度的影响
Figure 5. Influence of extended joint angle on workspace precision
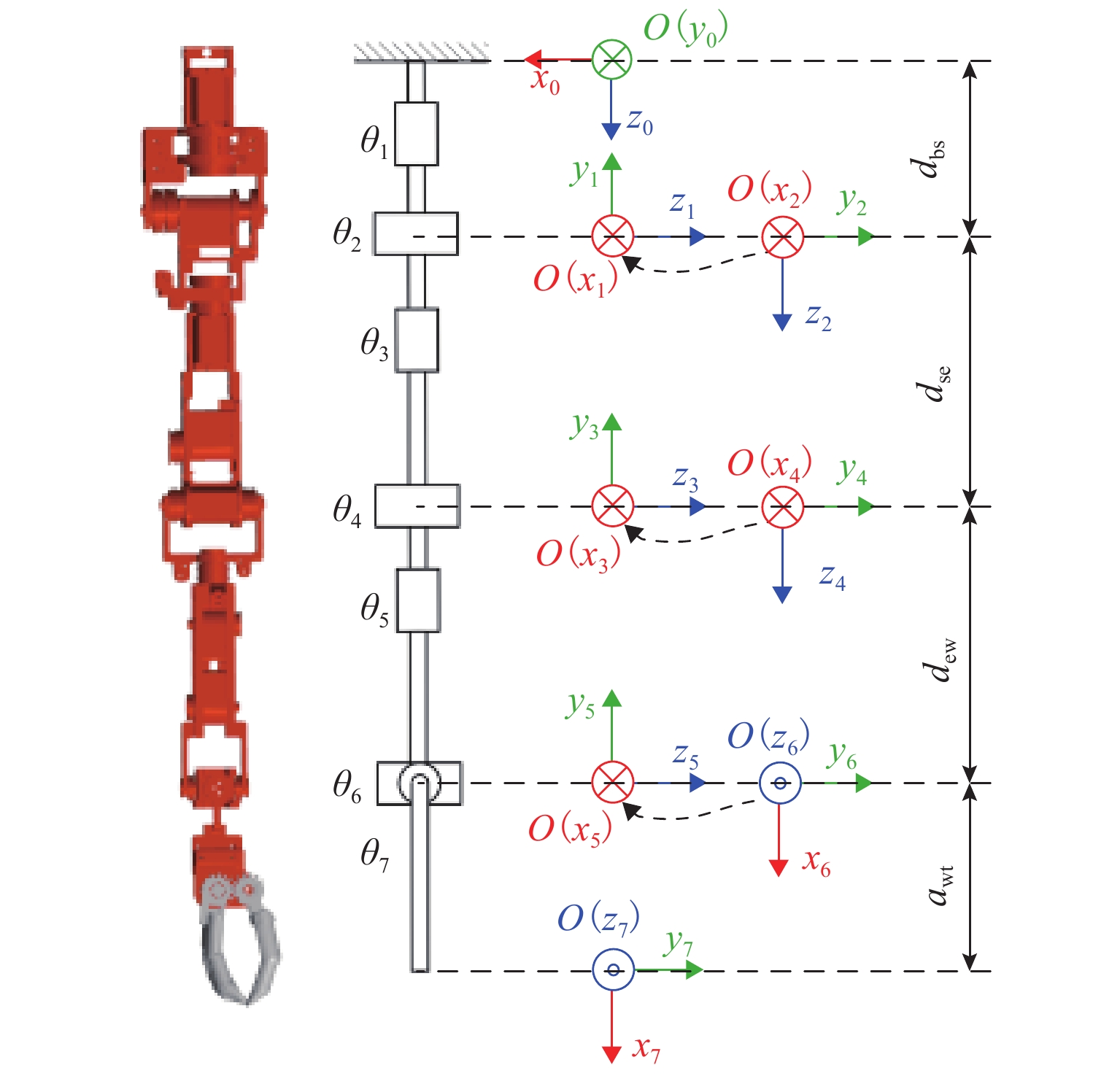
表 1 仿人机械臂关节限位
Table 1. Joint limit of humanoid robot arm
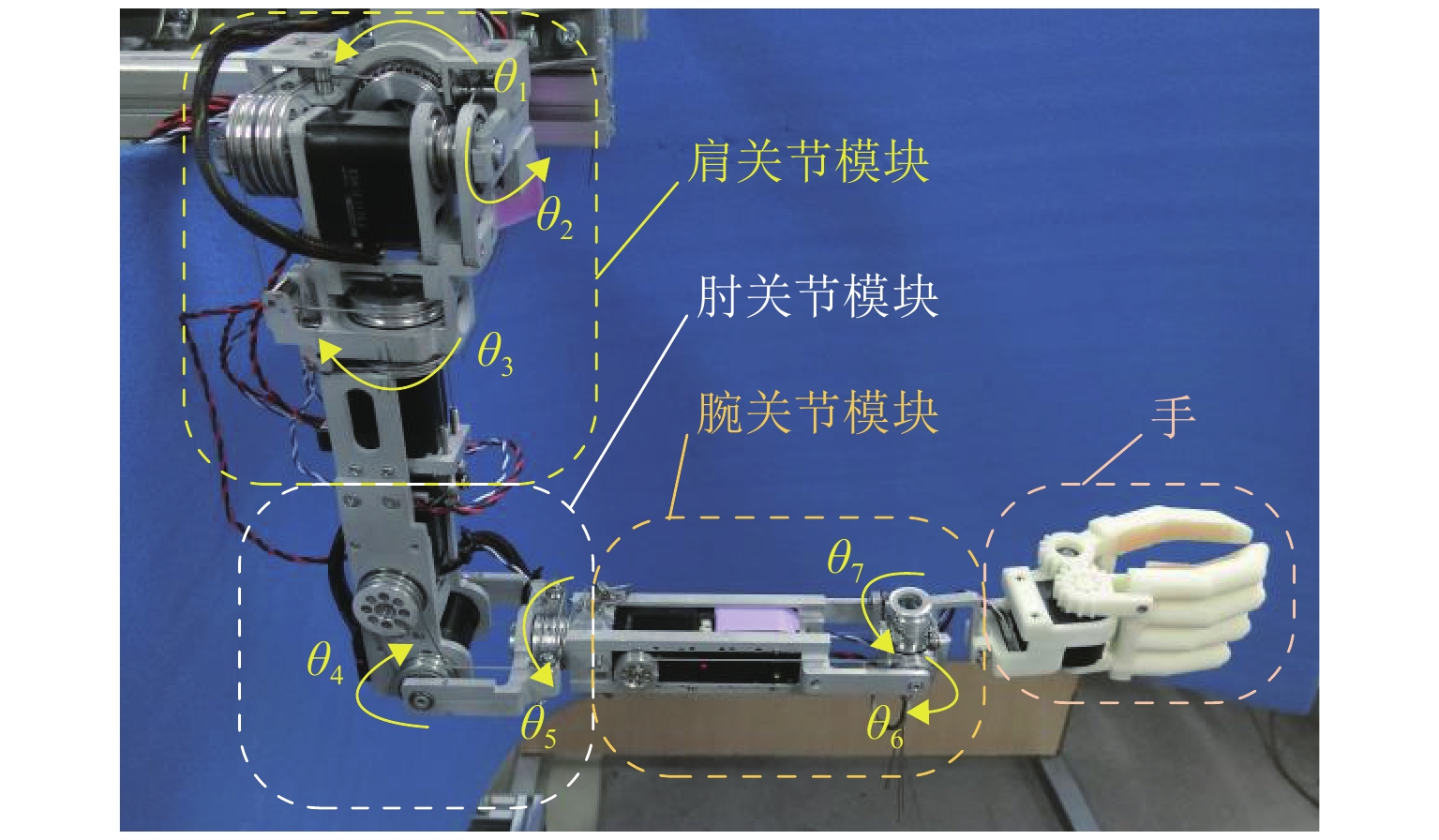
关节角度 最大值/（°） 最小值/（°） θ1 180 −90 θ2 10 −180 θ3 120 −90 θ4 130 −60 θ5 180 −180 θ6 80 −80 θ7 90 −90 
下载: 导出CSV
表 2 仿人机械臂D-H参数
Table 2. D-H parameters for humanoid robot arm
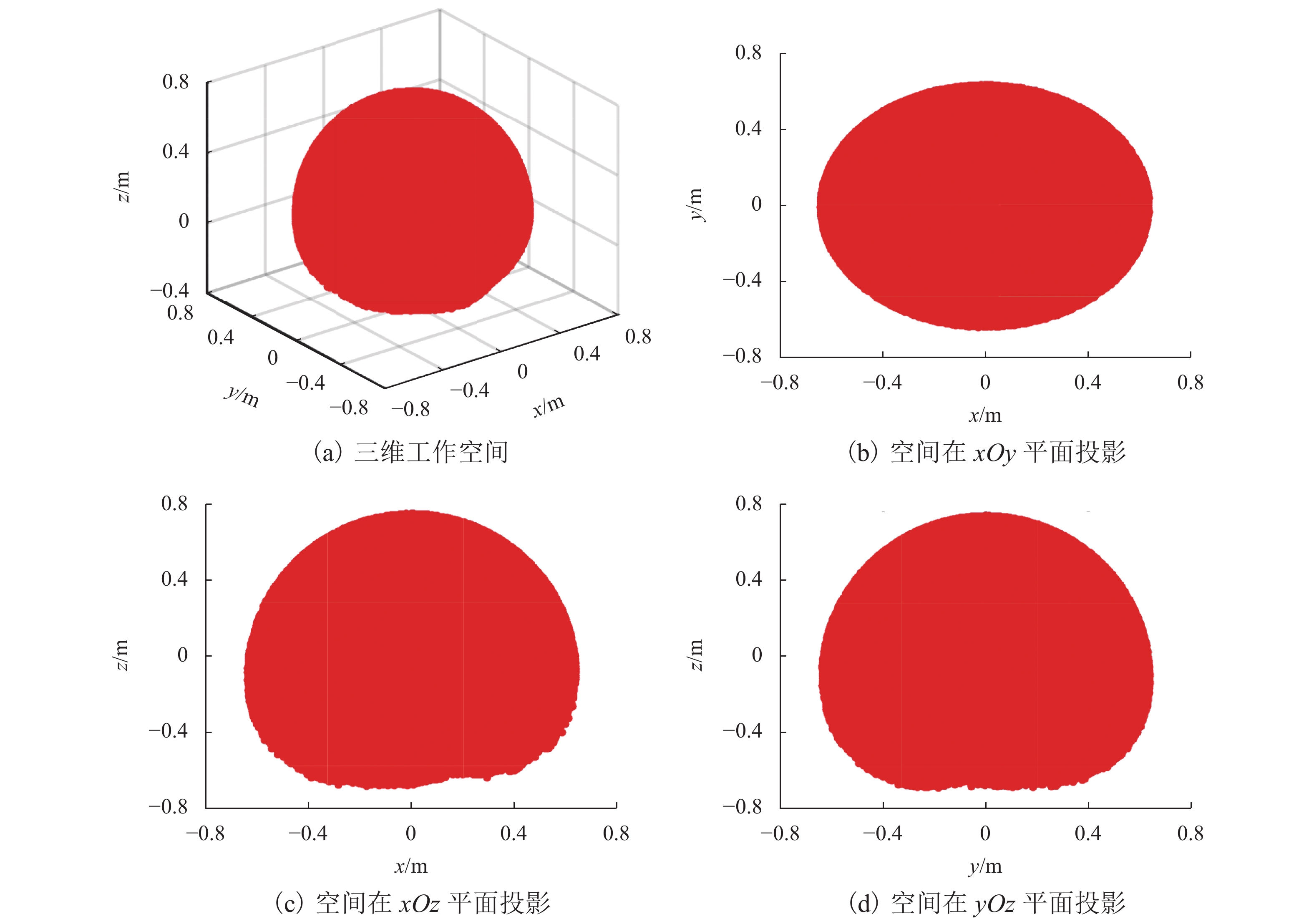
i θi /（º） di /m ai /m αi / （º） 1 90 dbs 0 −90 2 0 0 0 90 3 0 dse 0 −90 4 0 0 0 90 5 0 dew 0 −90 6 −90 0 0 90 7 0 0 awt 0
下载: 导出CSV
表 3 机械臂实际工作空间范围
Table 3. Actual workspace range of robot arm
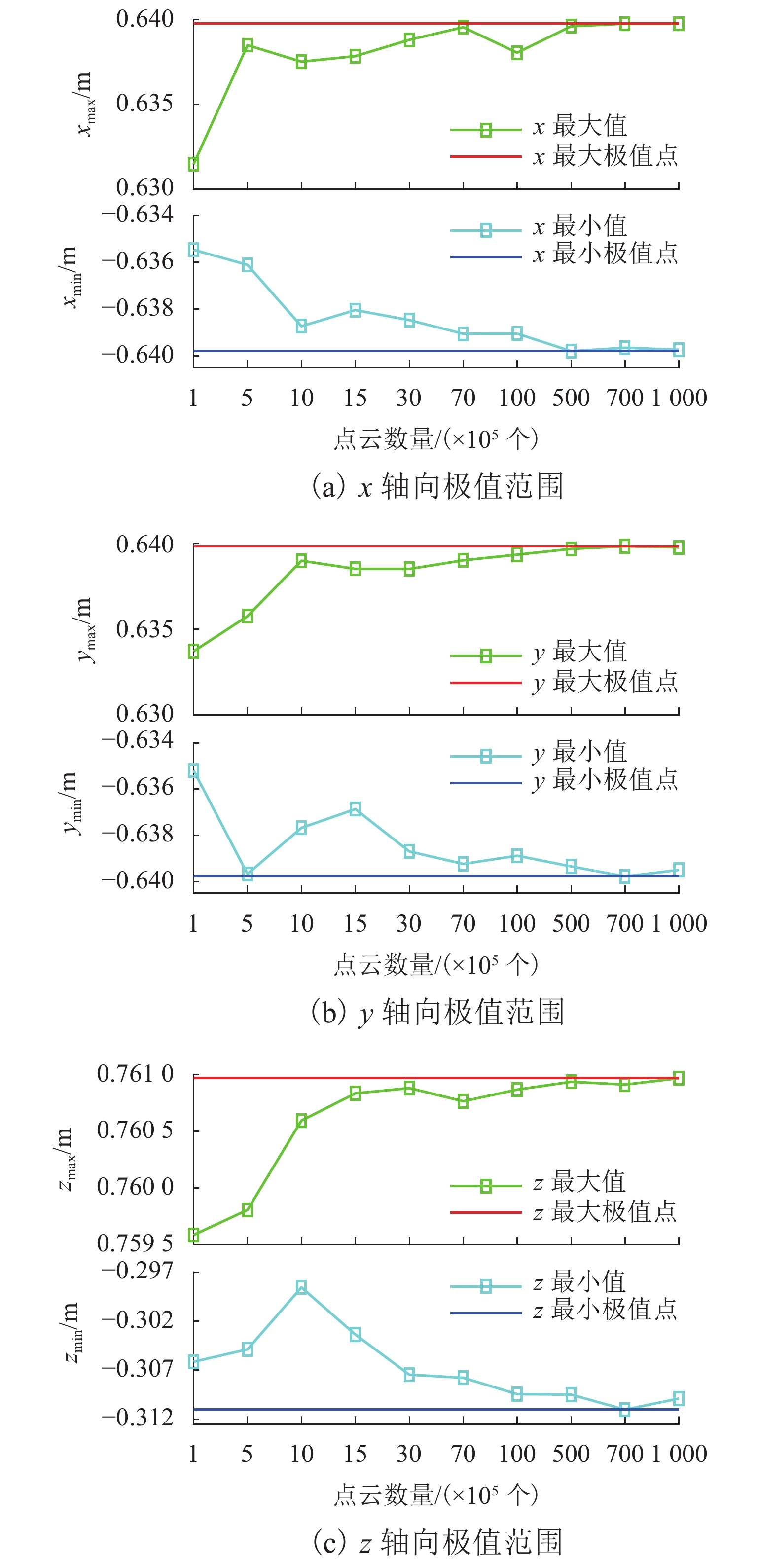
m 轴向 最大值 最小值 x 0.63975 −0.63979 y 0.63982 −0.63978 z 0.76096 −0.31102
下载: 导出CSV
表 4 初始点云数量对工作空间精度的影响
Table 4. Influence of initial point cloud quantity on workspace precision
Pinit/个 xmin/m xmax/m ymin/m ymax/m zmin/m zmax/m εa/% 5000 −0.63738 0.63639 −0.63458 0.63739 −0.29514 0.76061 1.20751 10000 −0.63909 0.63447 −0.63770 0.63850 −0.30532 0.76083 0.55259 50000 −0.63939 0.63772 −0.63644 0.63939 −0.30078 0.76069 0.71627 100000 −0.63960 0.63689 −0.63531 0.63619 −0.29769 0.76089 1.00622
下载: 导出CSV
表 5 体素数量对工作空间精度的影响
Table 5. Influence of voxel quantity on workspace precision
各轴向体素数量/个 xmin/m xmax/m ymin/m ymax/m zmin/m zmax/m εa/% 6 −0.63730 0.63468 −0.63729 0.63618 −0.29272 0.76062 1.34452 10 −0.63939 0.63772 −0.63644 0.63939 −0.30078 0.76069 0.71627 14 −0.63781 0.63859 −0.63663 0.63872 −0.30624 0.76076 0.45310 18 −0.63839 0.63899 −0.63931 0.63895 −0.30600 0.76087 0.36249
下载: 导出CSV
表 6 精度阈值对工作空间精度的影响
Table 6. Influence of precision threshold on workspace precision
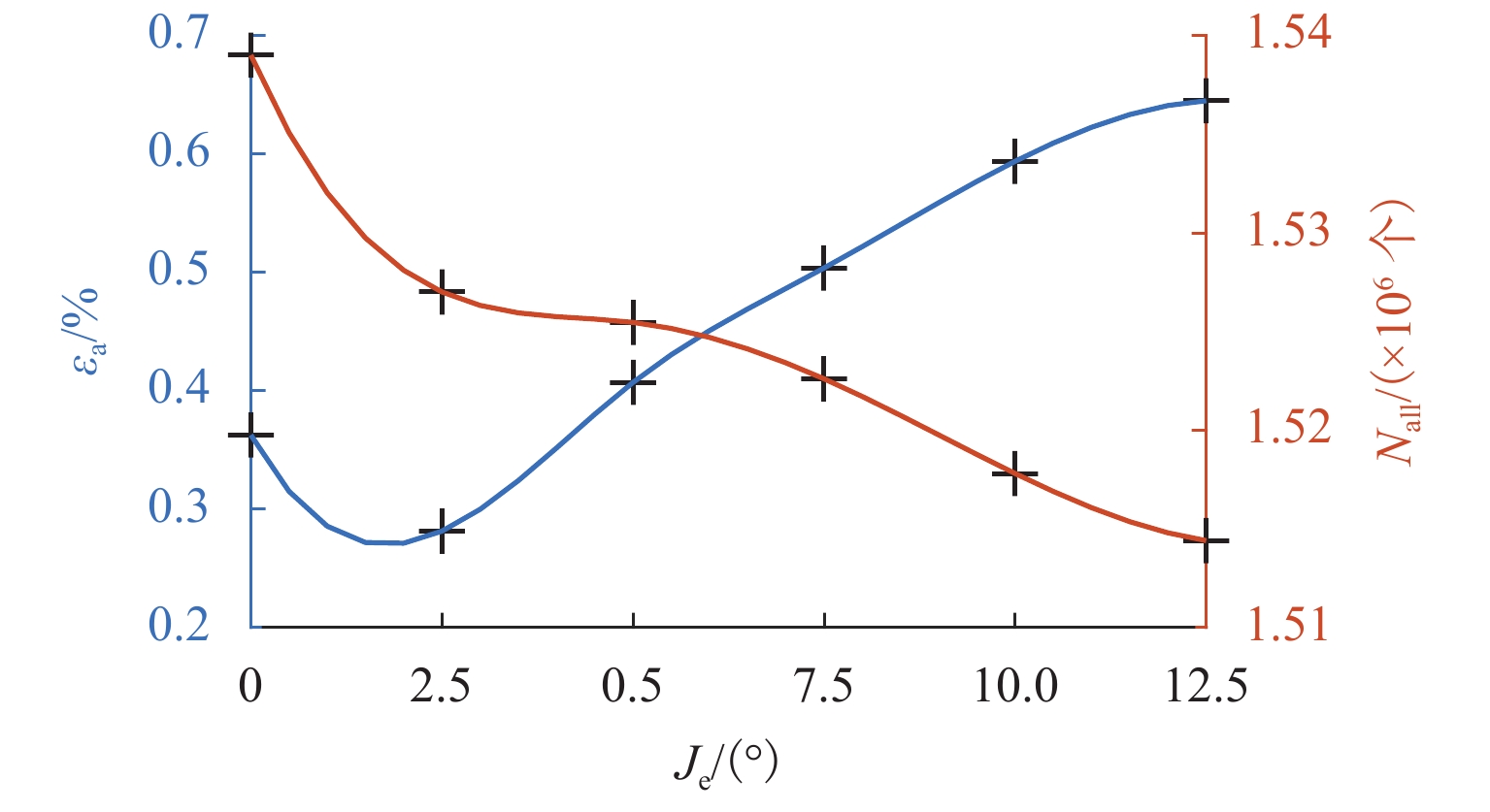
Nε xmin/m xmax/m ymin/m ymax/m zmin/m zmax/m εa/% 300 −0.63789 0.63678 −0.63716 0.63912 −0.30574 0.76089 0.49774 600 −0.63839 0.63899 −0.63931 0.63895 −0.30600 0.76087 0.36249 900 −0.63864 0.63646 −0.63758 0.63900 −0.30816 0.76086 0.35013
下载: 导出CSV
表 7 最大循环次数对工作空间精度的影响
Table 7. Influence of maximum cycle number on workspace precision
Cm/次 xmin/m xmax/m ymin/m ymax/m zmin/m zmax/m εa/% 5 −0.63839 0.63899 −0.63931 0.63895 −0.30600 0.76087 0.36249 8 −0.63940 0.63868 −0.63974 0.63907 −0.30554 0.76078 0.35615 16 −0.63945 0.63785 −0.63838 0.63973 −0.30664 0.76093 0.33245
下载: 导出CSV
表 8 降密蒙特卡洛法中工作空间范围及其误差率
Table 8. Workspace range and error rate by density-reducing Monte Carlo method
项目 xmin/m xmax/m ymin/m ymax/m zmin/m zmax/m 极值 −0.63961 0.63937 −0.63900 0.63956 −0.31113 0.76091 误差率 0.00018 0.00038 −0.00078 0.00026 −0.00011 0.00005
下载: 导出CSV
表 9 降密蒙特卡洛法与改进蒙特卡洛法对比
Table 9. Comparison between density-reducing Monte Carlo method and improved Monte Carlo method
方法 循环
次数/次总点云数/
（×105 个）εa/% 耗时/h 改进蒙特卡洛法 2 5.8 0.68532 4.591 4 9.3 0.55971 13.841 降密蒙特卡洛法 2 3.2 0.54679 0.997 4 3.3 0.44642 1.051
下载: 导出CSV
-
[1] 赵雅婷,赵韩,梁昌勇,等. 养老服务机器人现状及其发展建议[J]. 机械工程学报,2019,55(23): 13-24. doi: 10.3901/JME.2019.23.013ZHAO Yating, ZHAO Han, LIANG Changyong, et al. Current situation and development suggestions of old-age service robot[J]. Journal of Mechanical Engineering, 2019, 55(23): 13-24. doi: 10.3901/JME.2019.23.013 [2] 杨林川,朱庆. 建成环境对老年人出行行为影响的空间异质性[J]. 西南交通大学学报,2023,58(3): 696-703.YANG Linchuan, ZHU Qing. Spatially heterogeneous effects of the built environment on the travel behavior of older adults[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 696-703. [3] 刘欣,仇原鹰,盛英,等. 平面冗余并联机器人的综合性能优化设计[J]. 西南交通大学学报,2008,43(5): 626-632. doi: 10.3969/j.issn.0258-2724.2008.05.014LIU Xin, QIU Yuanying, SHENG Ying, et al. Optimization of comprehensive performance of planar redundant parallel manipulator[J]. Journal of Southwest Jiaotong University, 2008, 43(5): 626-632. doi: 10.3969/j.issn.0258-2724.2008.05.014 [4] YIN G Q, HE F Y, LI Z F, et al. Workspace description and simulation of a backhoe device for hydraulic excavators[J]. Automation in Construction, 2020, 119: 103325.1-103325.8. [5] 东辉,杜志江. 基于工作空间密度函数的平面冗余机器人的逆运动学求解算法[J]. 机械工程学报,2015,51(17): 8-14. doi: 10.3901/JME.2015.17.008DONG Hui, DU Zhijiang. Inverse kinematics of planar redundant manipulators based on workspace density function[J]. Journal of Mechanical Engineering, 2015, 51(17): 8-14. doi: 10.3901/JME.2015.17.008 [6] XU Z T, ZHAO Y H, XIAN L W, et al. Workspace solution and space trajectory planning of 5-DOF manipulator[J]. Journal of Physics: Conference Series, 2022, 2239(1): 012015.1-012015.5. [7] 赵智远,徐振邦,何俊培,等. 基于工作空间分析的9自由度超冗余串联机械臂构型优化[J]. 机械工程学报,2019,55(21): 51-63.ZHAO Zhiyuan, XU Zhenbang, HE Junpei, et al. Configuration optimization of nine degree of freedom super-redundant serial manipulator based on workspace analysis[J]. Journal of Mechanical Engineering, 2019, 55(21): 51-63. [8] CAO Y, LU K, LI X J, et al. Accurate numerical methods for computing 2D and 3D robot workspace[J]. International Journal of Advanced Robotic Systems, 2011, 8(6): 76.1-76.13. [9] 吴虎,李鑫宁,杨先海. 基于网格划分理论连杆机器人工作空间的研究[J]. 济南大学学报(自然科学版),2022,36(4): 476-483.WU Hu, LI Xinning, YANG Xianhai. Research on workspace for multi-linkages robots based on grid partition theory[J]. Journal of University of Jinan (Science and Technology), 2022, 36(4): 476-483. [10] 李钊,樊桂菊,梁昭,等. 基于D-H法的果园作业平台工作空间分析与试验[J]. 农业工程学报,2020,36(16): 25-34. doi: 10.11975/j.issn.1002-6819.2020.16.004LI Zhao, FAN Guiju, LIANG Zhao, et al. Workspace analysis and experiments of orchard platform based on D-H method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(16): 25-34. doi: 10.11975/j.issn.1002-6819.2020.16.004 [11] 王春,韩秋实. 六自由度串联机械臂运动学及其工作空间研究[J]. 组合机床与自动化加工技术,2020(6): 32-36. doi: 10.13462/j.cnki.mmtamt.2020.06.008WANG Chun, HAN Qiushi. Kinematics of six-degree-of-freedom series manipulator and its working space[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(6): 32-36. doi: 10.13462/j.cnki.mmtamt.2020.06.008 [12] 田海波,马宏伟,魏娟. 串联机器人机械臂工作空间与结构参数研究[J]. 农业机械学报,2013,44(4): 196-201. doi: 10.6041/j.issn.1000-1298.2013.04.034TIAN Haibo, MA Hongwei, WEI Juan. Workspace and structural parameters analysis for manipulator of serial robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 196-201. doi: 10.6041/j.issn.1000-1298.2013.04.034 [13] PEIDRÓ A, REINOSO Ó, GIL A, et al. An improved Monte Carlo method based on Gaussian growth to calculate the workspace of robots[J]. Engineering Applications of Artificial Intelligence, 2017, 64: 197-207. doi: 10.1016/j.engappai.2017.06.009 [14] HE B, ZHU X R, ZHANG D. Boundary encryption-based Monte Carlo learning method for workspace modeling[J]. Journal of Computing and Information Science in Engineering, 2020, 20(3): 034502.1-034502.6. [15] 刘志忠,柳洪义,罗忠,等. 机器人工作空间求解的蒙特卡洛法改进[J]. 农业机械学报,2013,44(1): 230-235. doi: 10.6041/j.issn.1000-1298.2013.01.043LIU Zhizhong, LIU Hongyi, LUO Zhong, et al. Improvement on Monte Carlo method for robot workspace determination[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 230-235. doi: 10.6041/j.issn.1000-1298.2013.01.043 [16] 徐振邦,赵智远,贺帅,等. 机器人工作空间求解的蒙特卡洛法改进和体积求取[J]. 光学 精密工程,2018,26(11): 2703-2713. doi: 10.3788/OPE.20182611.2703XU Zhenbang, ZHAO Zhiyuan, HE Shuai, et al. Improvement of Monte Carlo method for robot workspace solution and volume calculation[J]. Optics and Precision Engineering, 2018, 26(11): 2703-2713. doi: 10.3788/OPE.20182611.2703 [17] ZHAO Z Y, HE S, ZHAO Y P, et al. Workspace analysis for a 9-DOF hyper-redundant manipulator based on an improved Monte Carlo method and voxel algorithm[C]//2018 IEEE International Conference on Mechatronics and Automation (ICMA). Changchun: IEEE, 2018: 637-642. [18] DOU R T, YU S B, LI W Y, et al. Inverse kinematics for a 7-DOF humanoid robotic arm with joint limit and end pose coupling[J]. Mechanism and Machine Theory, 2022, 169: 104637.1-104637.23. [19] LI W Y, CHEN P, BAI D C, et al. Modularization of 2- and 3-DOF coupled tendon-driven joints[J]. IEEE Transactions on Robotics, 2021, 37(3): 905-917. doi: 10.1109/TRO.2020.3038687 [20] 肖正涛,高健,吴东庆,等. 面向三维点云识别的体素网格降采样[J]. 组合机床与自动化加工技术,2021(11): 43-47. doi: 10.13462/j.cnki.mmtamt.2021.11.011XIAO Zhengtao, GAO Jian, WU Dongqing, et al. Voxel grid downsampling for 3D point cloud recognition[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(11): 43-47. doi: 10.13462/j.cnki.mmtamt.2021.11.011 -
下载:
点击查看大图
计量
- 文章访问数: 232
- HTML全文浏览量: 78
- PDF下载量: 36
- 被引次数: 0