Simulation on Decoupling Control of Maglev Flexible Rotor System
-
摘要:
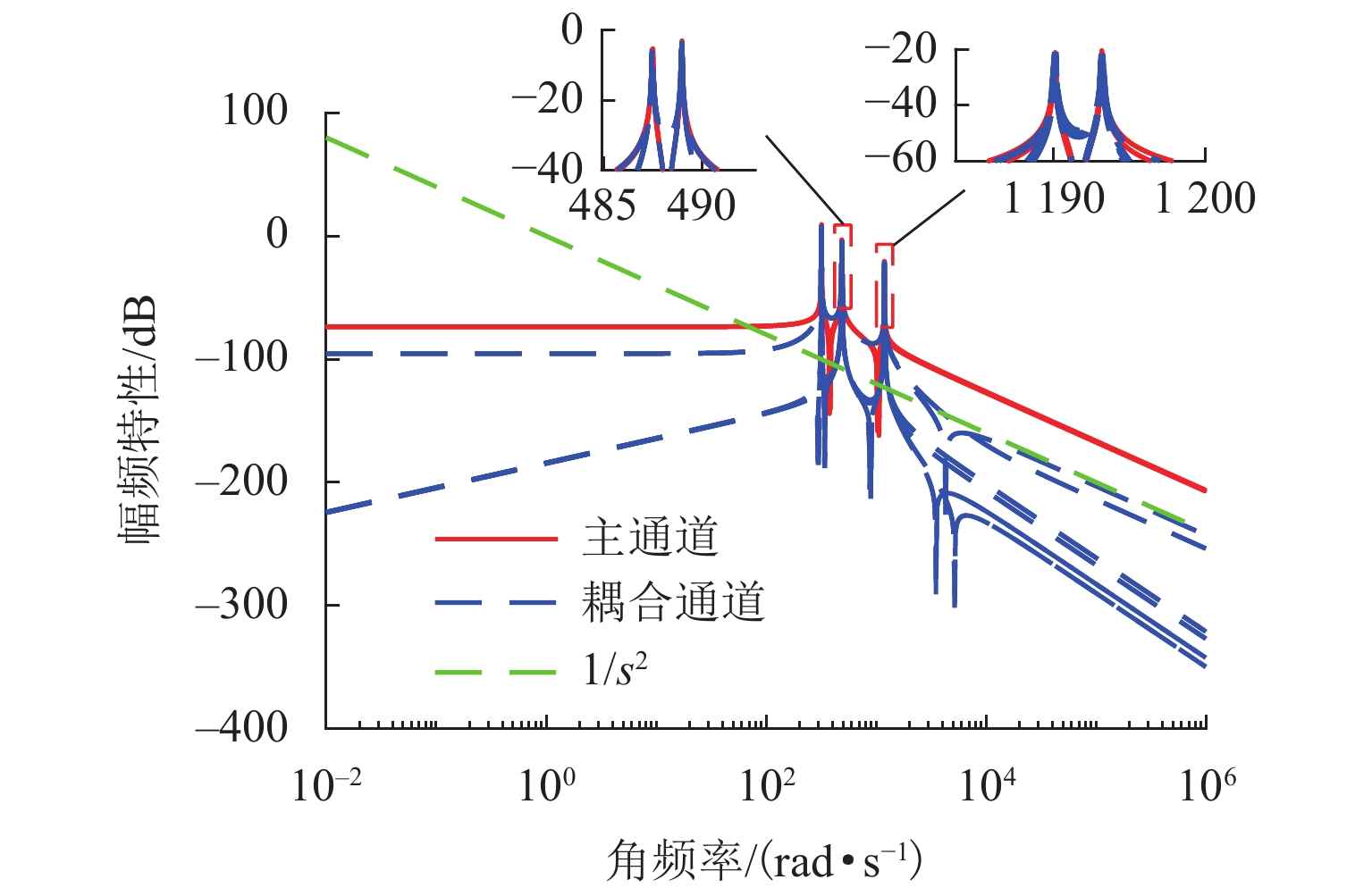
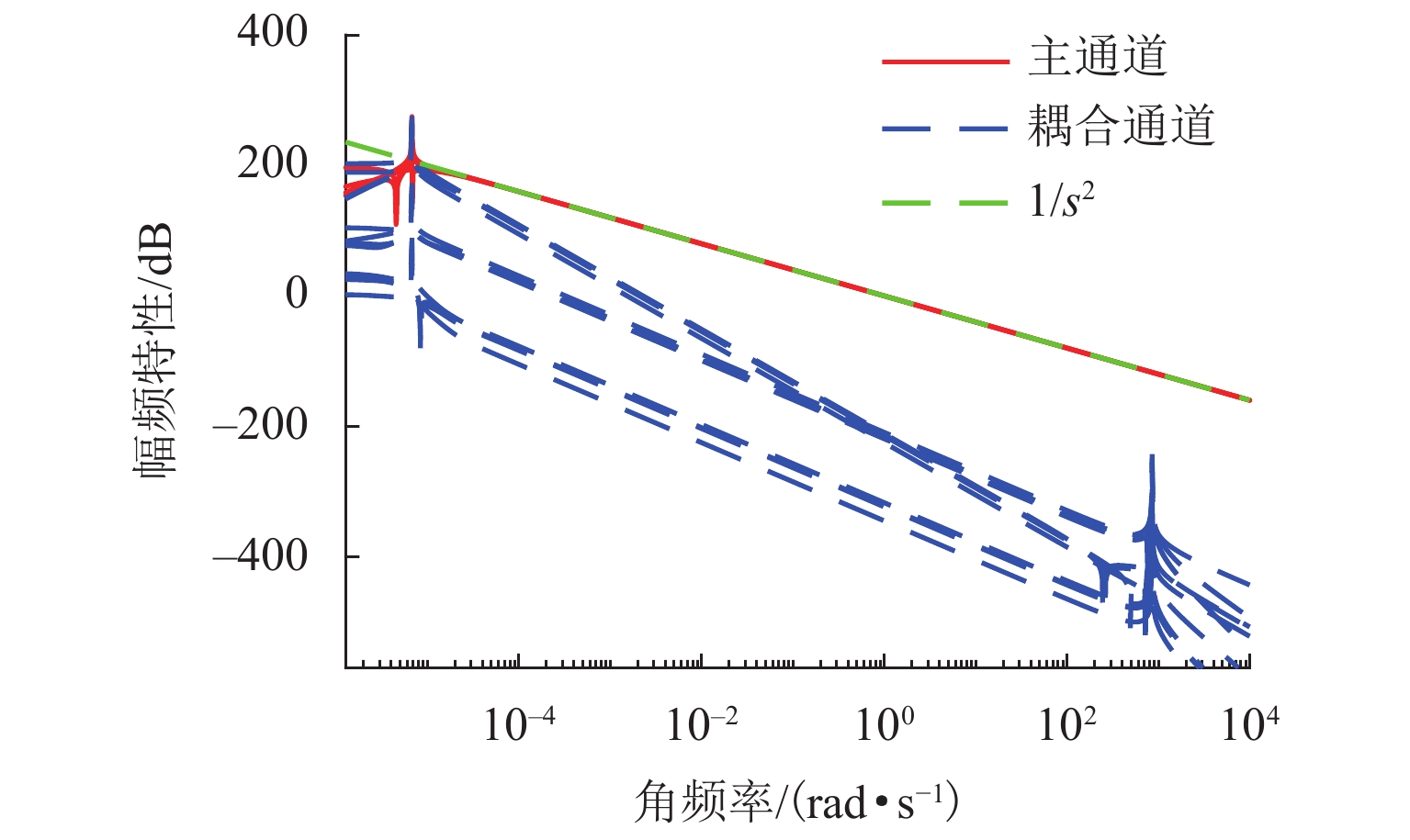
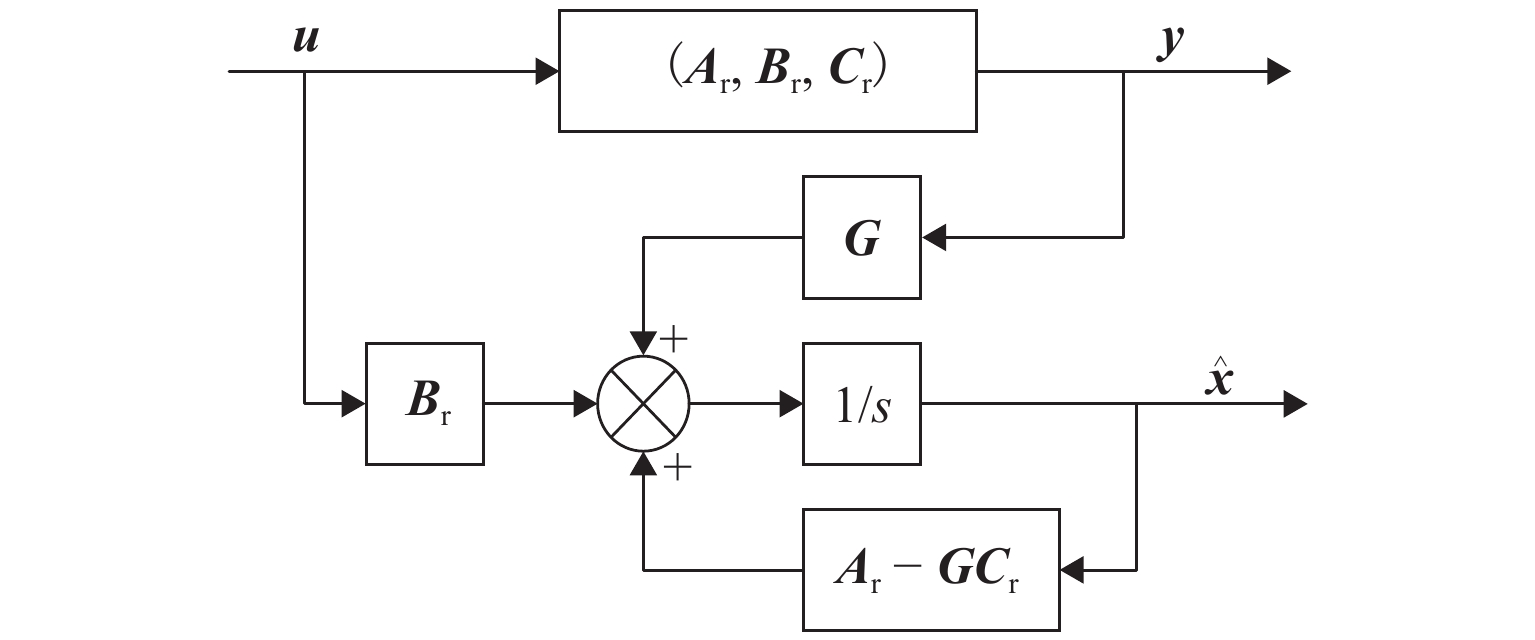
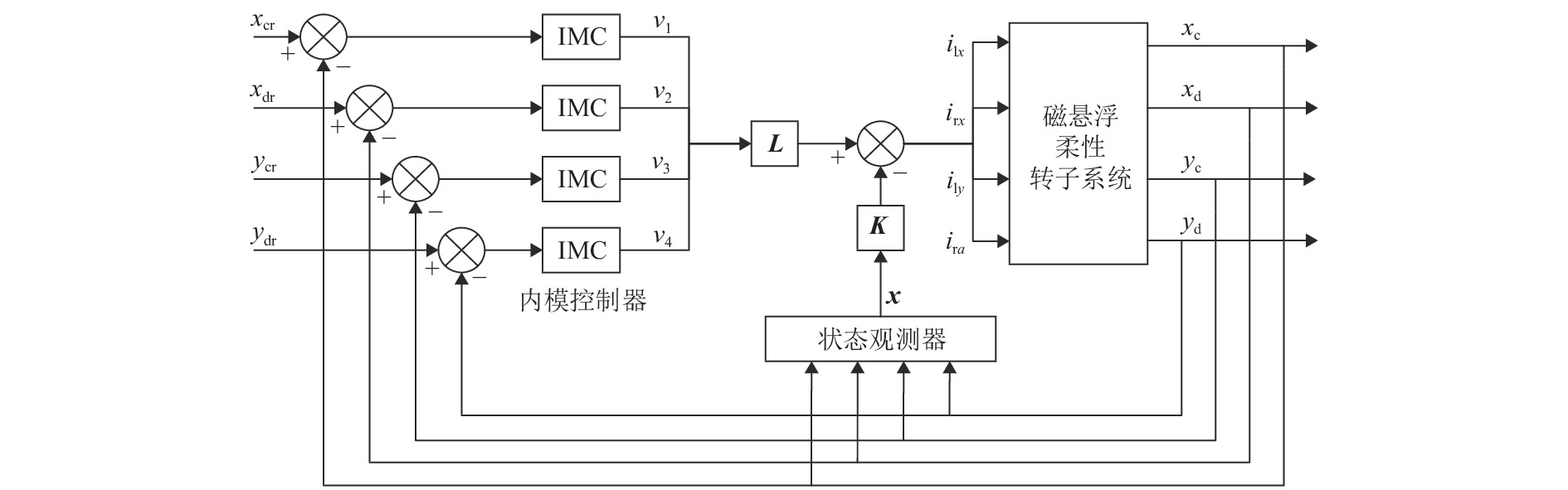
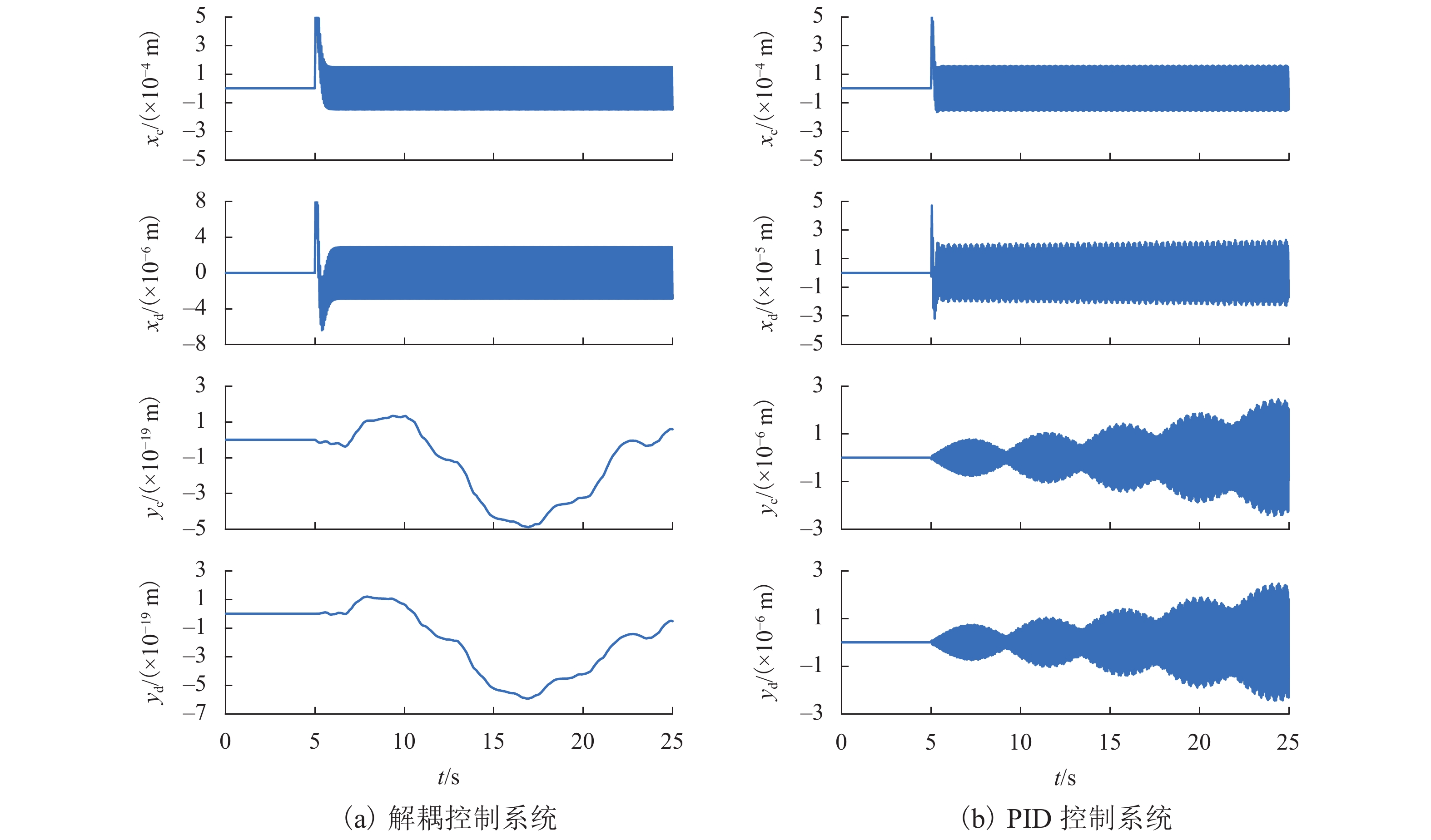
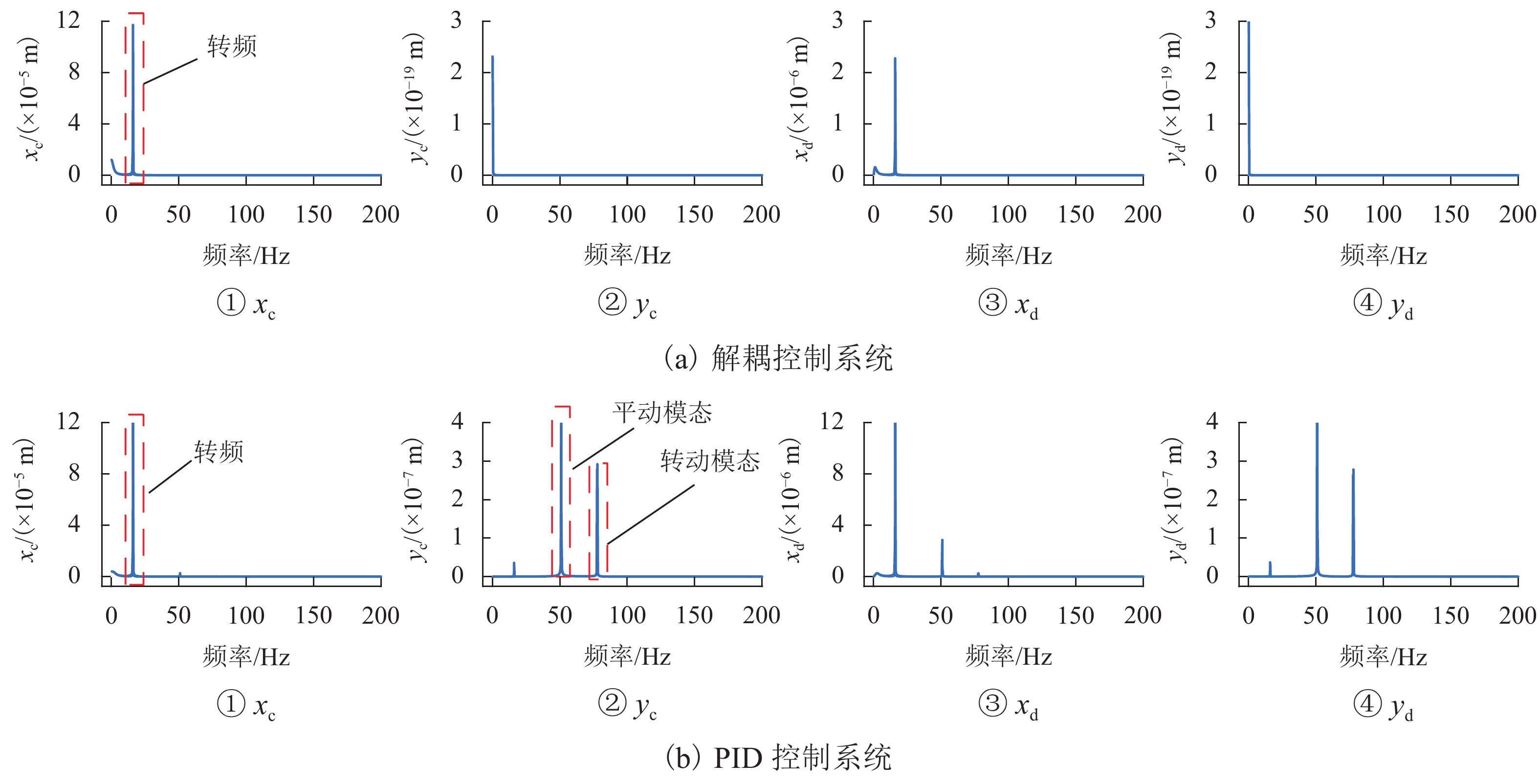
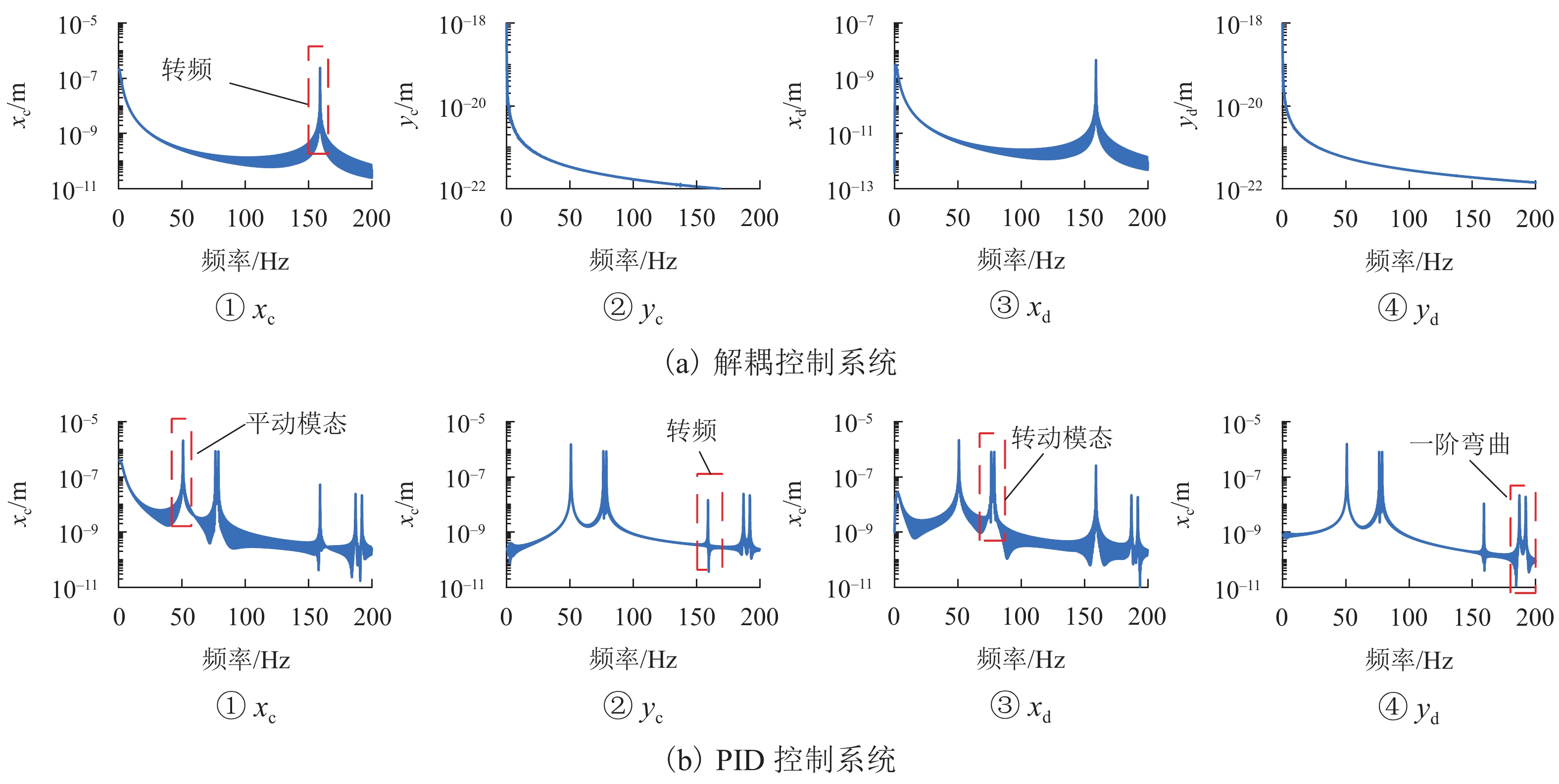
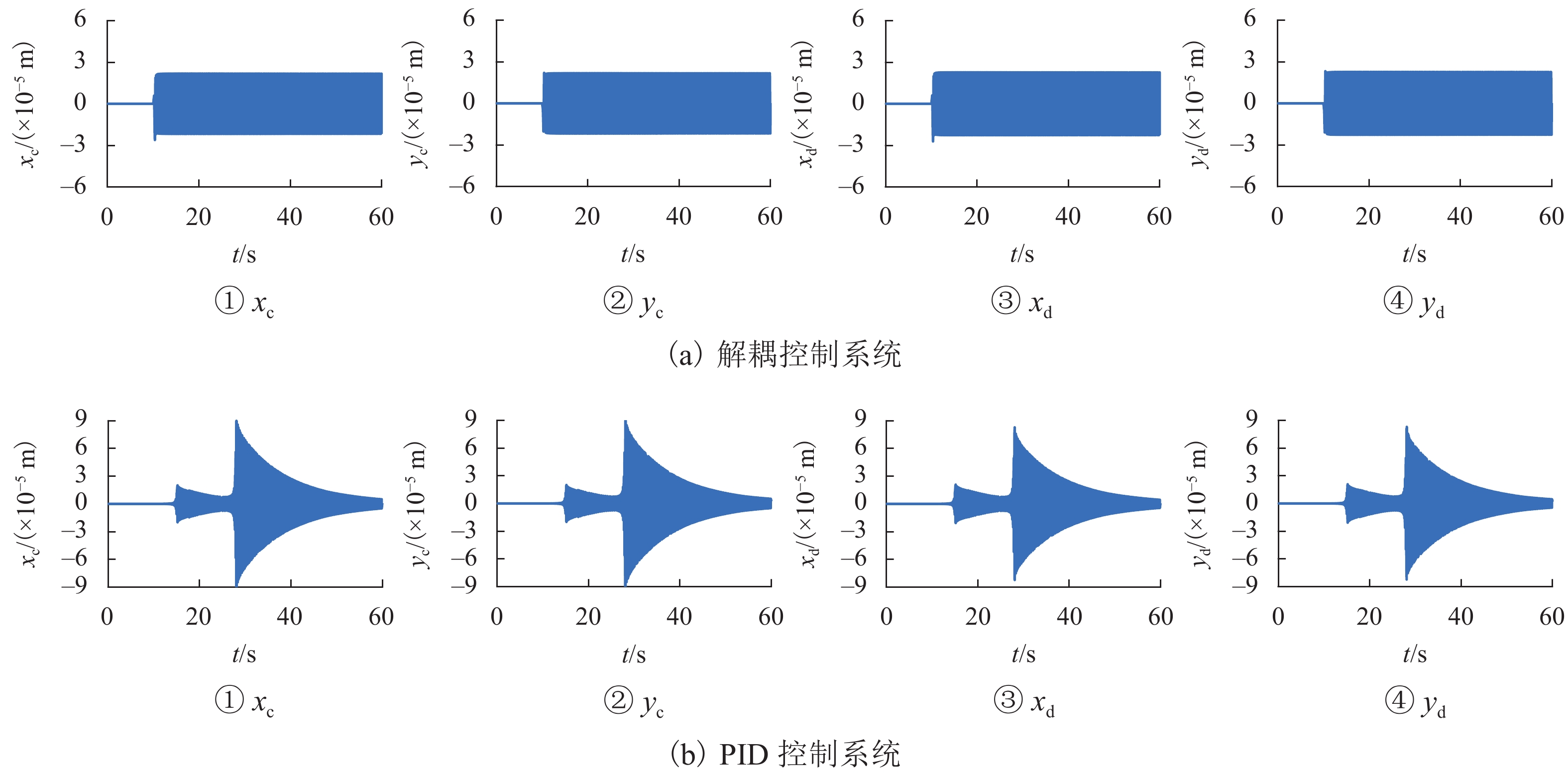
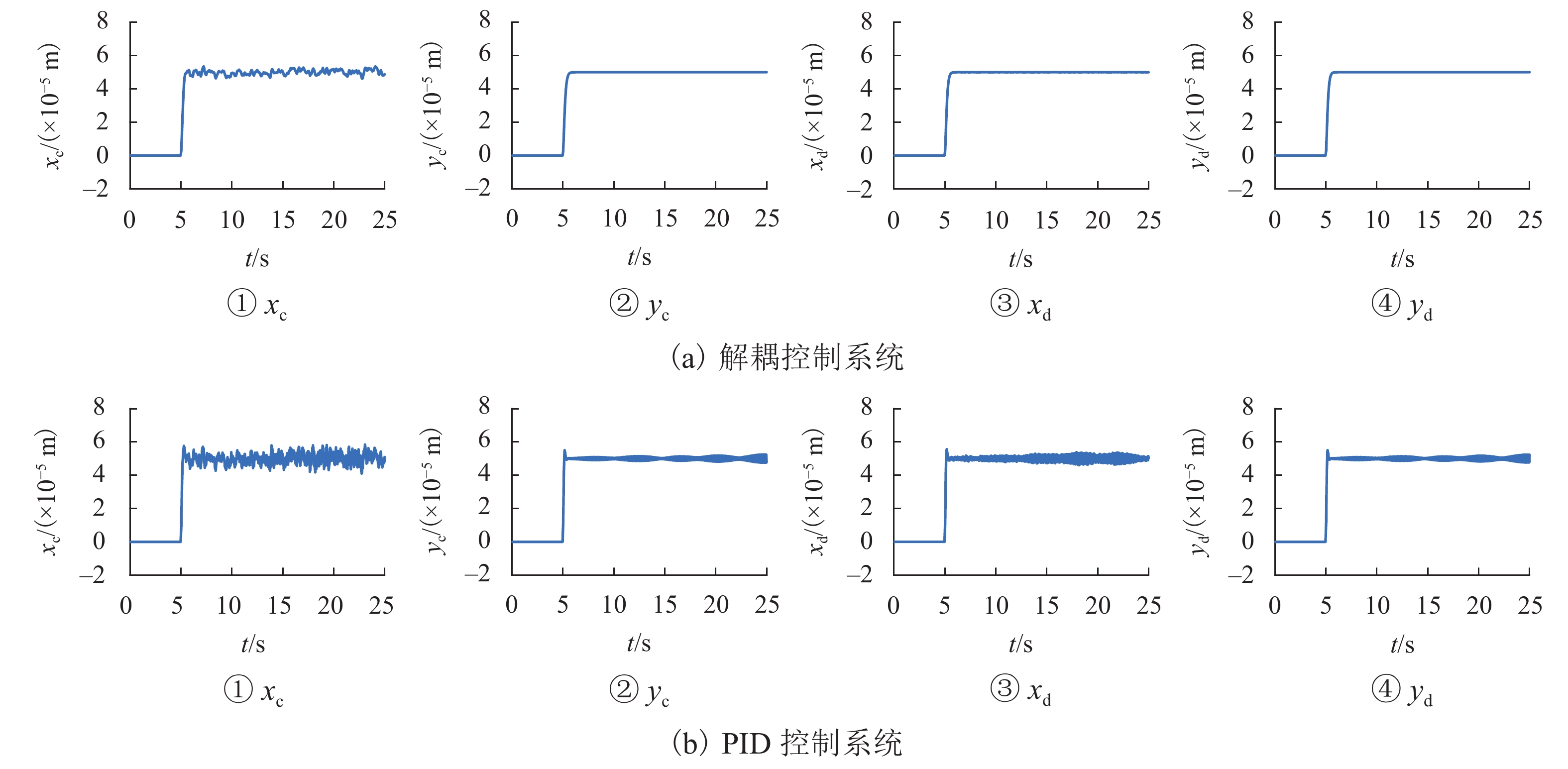
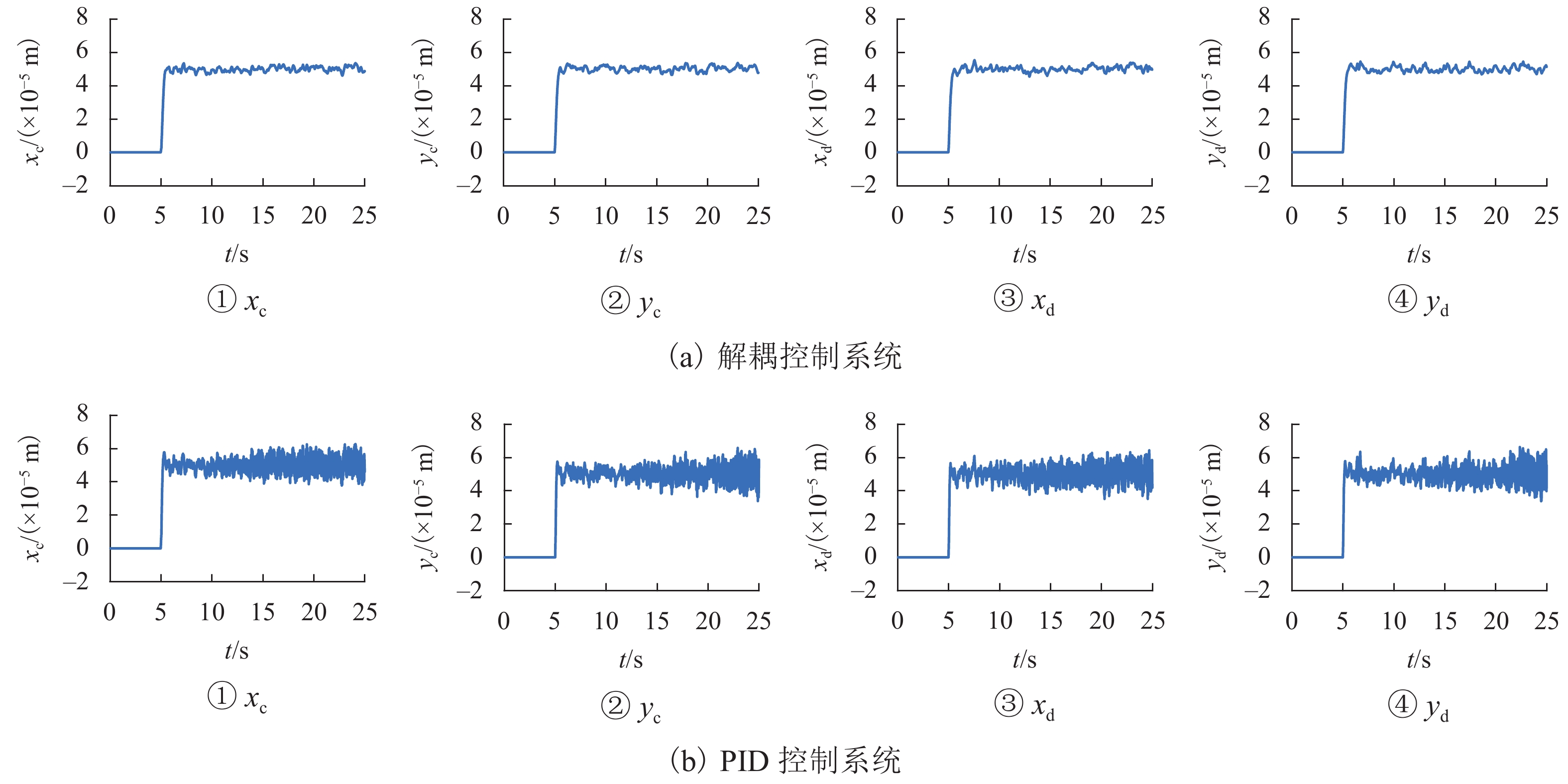
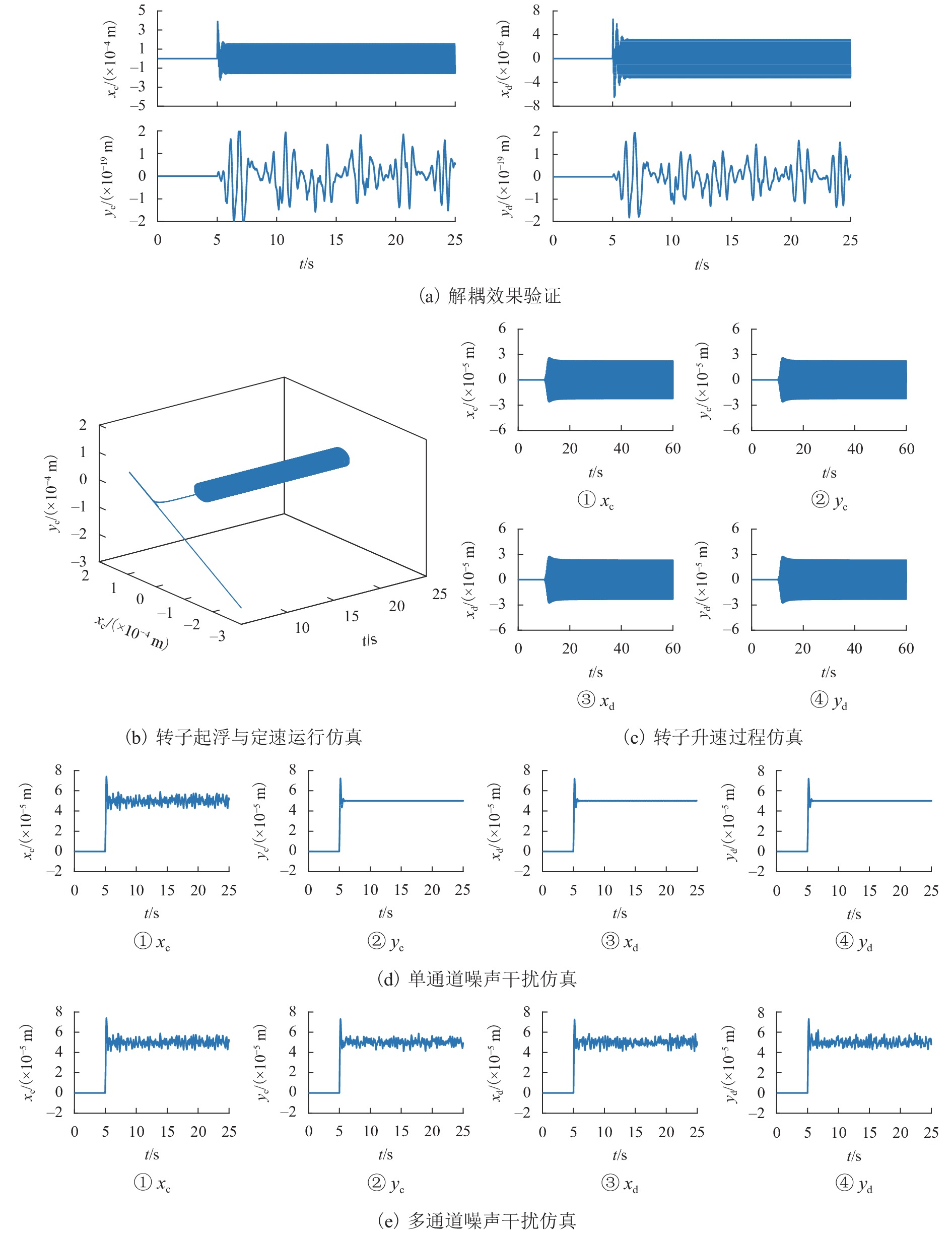
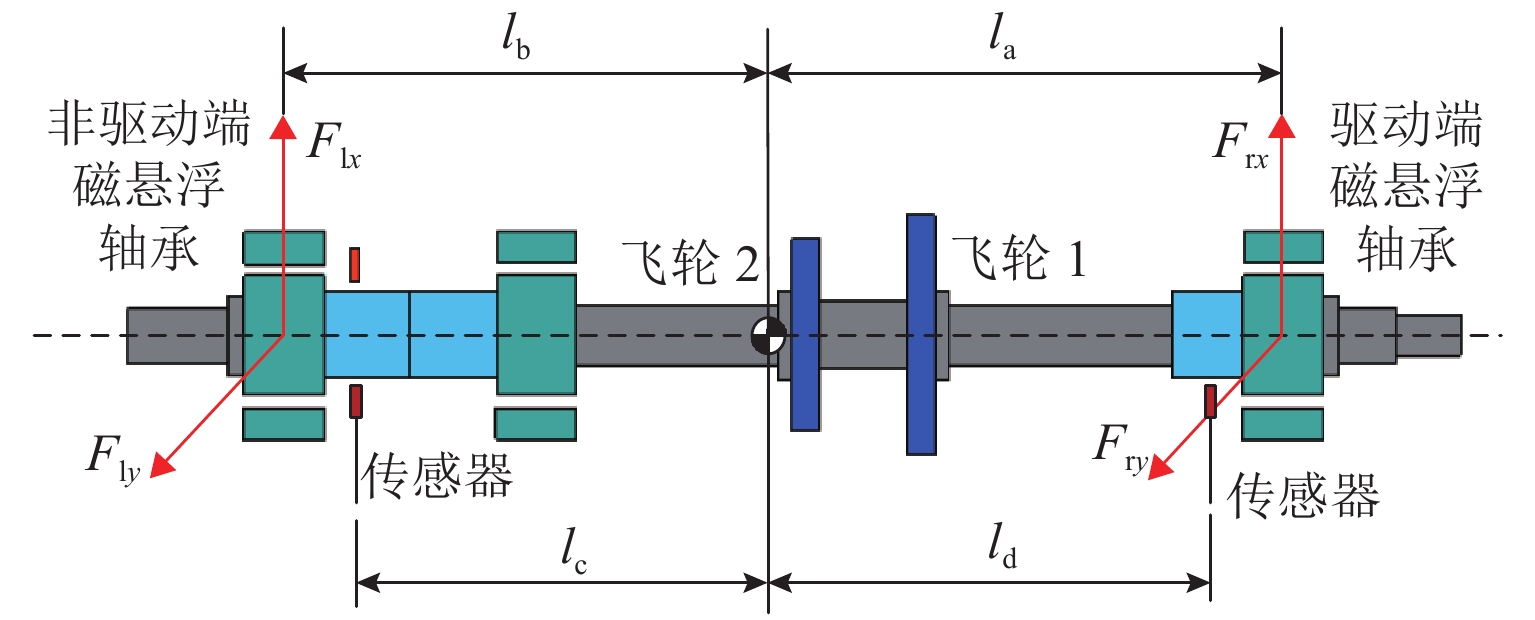
目前磁悬浮转子系统的解耦控制研究主要基于刚性转子系统，但在高转速、高支撑刚度下，转子的弹性模态不能忽视. 针对磁悬浮柔性转子的解耦控制问题，首先，建立柔性转子模型，采用模态截断法进行简化，通过状态反馈解耦得到解耦系统；然后，基于解耦系统设计了内模控制器，针对状态变量不易通过传感器获取的特点设计状态观测器；最后，仿真分析系统的解耦效果. 仿真结果表明：未解耦系统的位移响应中含有与系统固有频率相关的多个频率成分，而解耦后系统的位移响应仅含激励同频成分；同一坐标平面内的机械耦合由10−5 m数量级减小到${10^{ - 6}}$ m数量级，由陀螺效应引起的两径向方向间的耦合由${10^{ - 6}}$ m数量级减小到${10^{ - 19}}$ m数量级，机械耦合和陀螺效应耦合均得到了有效控制；稳定悬浮时轴心到参考点距离的标准差由$6.52 \times {10^{ - 9}}$ m减小到$6.38 \times $$ {10^{ - 12}}$ m，解耦后系统的运行波动更小；转子升速时和受到噪声干扰时系统响应不再受到固有频率影响，始终保持平稳；采用状态反馈解耦对不同的控制方法同样有效.
Abstract:At present, the decoupling control research on maglev rotor systems is mainly based on rigid rotor systems, but the elastic mode of the rotor cannot be ignored under high speed and high support stiffness. Aiming at the decoupling control problem of maglev flexible rotors, this paper first built a flexible rotor model, simplified the model by modal truncation method, and obtained the decoupled system through state feedback decoupling; then an internal model controller was designed based on the decoupled system, and the state observer was designed according to the characteristic that the state variables were not easily obtained by the sensors; finally, the decoupling effect of the system was simulated. The simulation results show that the displacement response of the uncoupled system contains multiple frequency components related to the natural frequency of the system, while that of the decoupled system only contains the same frequency component of the excitation; the mechanical coupling within the same coordinate plane has decreased from the order of 10−5 m to ${10^{ - 6}}$ m, and the coupling between the two radial directions caused by the gyroscopic effect has decreased from the order of ${10^{ - 6}}$ m to${10^{ - 19}}$ m, with both mechanical coupling and gyroscopic effect coupling effectively controlled; the standard deviation of the distance from the axis to the reference point during stable levitation has decreased from $6.52 \times {10^{ - 9}}$ m to $6.38 \times {10^{ - 12}}$ m, and the operation fluctuation of the system is smaller after decoupling; when the rotor accelerates and is disturbed by noises, the system response is no longer affected by the natural frequency and always remains stable; the state feedback decoupling is also effective for different control methods.
-
Key words:
- maglev bearings /
- state feedback /
- decoupled system /
- internal model control
-
图 2 模态参与因子随激励频率的变化
Figure 2. Variation of modal participation factor with excitation frequency
图 4 原系统各通道幅频特性曲线
Figure 4. Amplitude-frequency characteristic curves of each channel of the original system
图 5 解耦系统各通道幅频特性曲线
Figure 5. Amplitude-frequency characteristic curves of each channel of the decoupled system
图 9 单通道简谐激励下各通道响应
Figure 9. Response of each channel under single-channel harmonic excitation
图 11 高频激励下各通道位移响应FFT分析
Figure 11. FFT analysis of displacement response of each channel under high-frequency excitation
图 14 单通道噪声扰动下各通道响应
Figure 14. Response of each channel under single-channel noise disturbance
图 15 多通道噪声扰动下各通道响应
Figure 15. Response of each channel under multi-channel noise disturbance
-
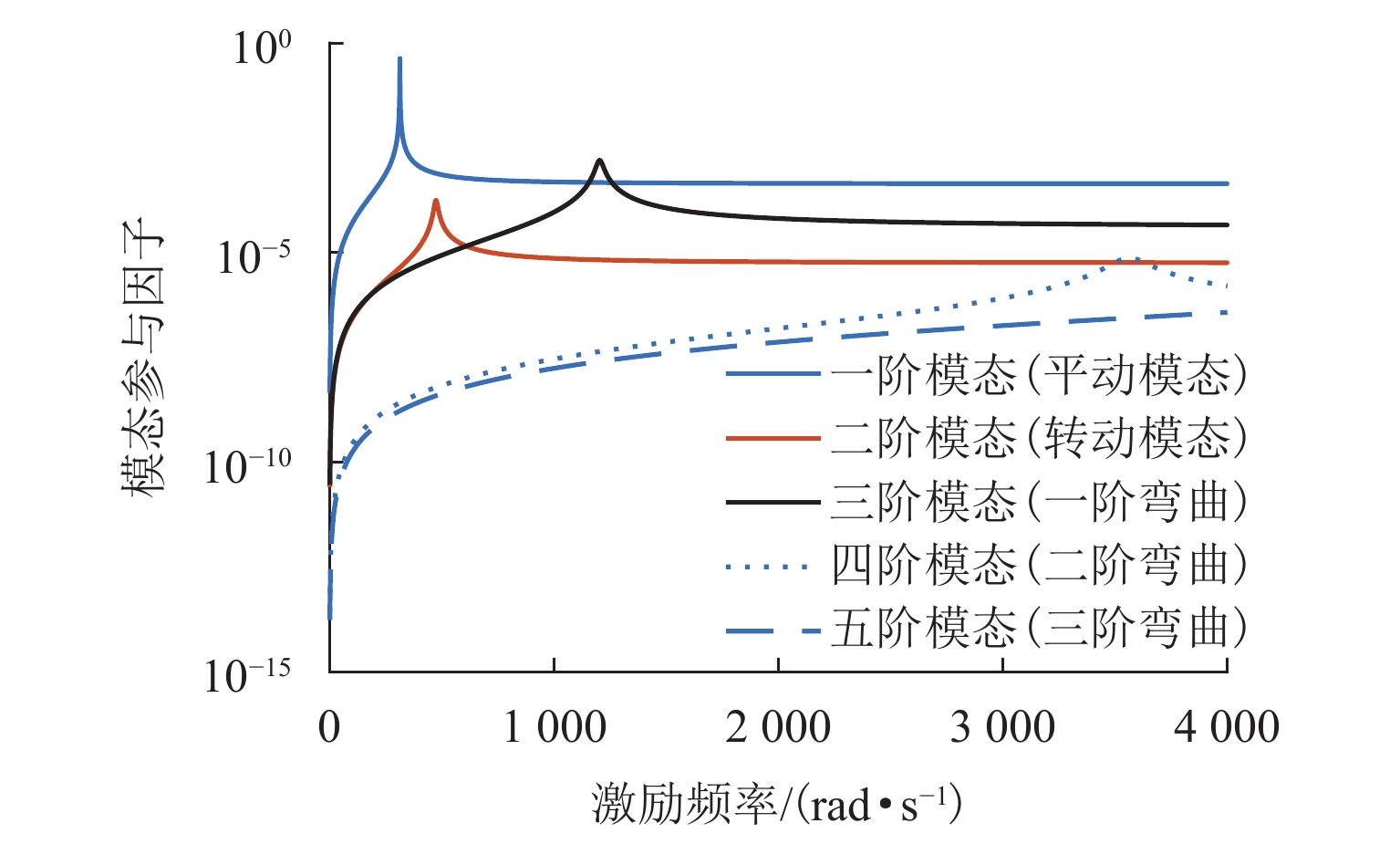
[1] 谢振宇. 电磁轴承系统及其工业应用[D]. 西安: 西安交通大学, 2000. [2] 王晓光,胡业发,江征风,等. 磁悬浮系统机械耦合的研究[J]. 武汉理工大学学报,2002(12): 65-68.WANG Xiaoguang, HU Yefa, JANG Zhengfeng, et al. Research on mechanical coupling of magnetic suspension system[J]. Journal of Wuhan University of Technology, 2002(12): 65-68. [3] 沈钺,孙岩桦,王世琥,等. 磁悬浮飞轮系统陀螺效应的抑制[J]. 西安交通大学学报,2003,37(11): 1105-1109.SHEN Yue, SUN Yanhua, WANG Shihu, et al. The suppression of gyroscopic effect of magnetically suspended flywheel system[J]. Journal of Xi’an Jiaotong University, 2003, 37(11): 1105-1109. [4] 刘峰,王德明,欧阳慧珉,等. 基于交叉解耦的滑模控制在磁轴承中的应用[J]. 轴承,2014(11): 12-15,47.LIU Feng, WANG Deming, OUYANG Huimin et al. Application of sliding mode control based on cross decoupling in magnetic bearings[J]. Bearing, 2014(11): 12-15,47. [5] QIAO X L, TANG X P. The stability of magnetic levitation milling system based on modal decoupling control[J]. Shock and Vibration, 2020, 2020: 1-9. [6] 毛川. 主动电磁轴承—刚性飞轮转子系统的分析与控制[D]. 浙江: 浙江大学, 2017. [7] 尹增愿,蔡远文,任元,等. 磁悬浮转子状态反馈解耦自抗扰控制方法[J]. 北京航空航天大学学报,2022,48(7): 1210-1221. doi: 10.13700/j.bh.1001-5965.2021.0021YIN Zengyuan, CAI Yuanwen, REN Yuan, et al. Decoupled active disturbance rejection control method for magnetically suspended rotor based on state feedback[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(7): 1210-1221. doi: 10.13700/j.bh.1001-5965.2021.0021 [8] CHENG X, CHENG B X, DENG S, et al. State-feedback decoupling control of 5-DOF magnetic bearings based on α-order inverse system[J]. Mechatronics, 2020, 68: 102358.1-102358.10. [9] LI Y Y, ZHU H Q. Decoupling control of three degrees of freedom hybrid magnetic bearing based on LS-SVM[J]. Applied Mechanics and Materials, 2014, 529: 534-538. doi: 10.4028/www.scientific.net/AMM.529.534 [10] 魏子航,宋春生,李俊,等. 变刚度支承下电磁轴承−转子系统振动特性研究[J]. 轴承,2022(3): 15-22. doi: 10.19533/j.issn1000-3762.2022.03.003WEI Zihang, SONG Chunsheng, LI Jun, et al. Research on vibration characteristics of magnetic suspension bearing-rotor system under variable supporting stiffness[J]. Bearing, 2022(3): 15-22. doi: 10.19533/j.issn1000-3762.2022.03.003 [11] 冉少林. 基于鲁棒控制的磁悬浮柔性转子建模及稳定性控制研究[D]. 武汉: 武汉理工大学, 2019. [12] 徐园平. 柔性转子磁悬浮轴承支承特性辨识[D]. 南京: 南京航空航天大学, 2018. [13] 朱伟明,杨艳,刘泽远,等. 基于模态参与因子的无轴承开关磁阻电机振动分析与抑制[J]. 微电机,2022,55(10): 8-15. doi: 10.3969/j.issn.1001-6848.2022.10.002ZHU Weiming, YANG Yan, LIU Zeyuan, et al. Vibration analysis of bearingless switched reluctance motor based on modal participation factor[J]. Micromotors, 2022, 55(10): 8-15. doi: 10.3969/j.issn.1001-6848.2022.10.002 [14] 孙兆萍. 非线性系统内模控制策略[D]. 北京: 北京化工大学, 2014. [15] 刘芸. 内模控制及逆系统算法在船舶运动控制中的仿真研究[J]. 舰船科学技术,2016,38(11): 111-115,119.LIU Yun. Research on internal model control and inverse system theory in the simulation of ship motion control[J]. Ship Science and Technology, 2016, 38(11): 111-115,119. [16] 王孝武. 现代控制理论基础[M]. 3版. 北京: 机械工业出版社, 2013. [17] GAO H, MENG X H, QIAN K J. The impact analysis of beating vibration for active magnetic bearing[J]. IEEE Access, 2019, 7: 134104-134112. doi: 10.1109/ACCESS.2019.2932723 [18] 韩军,高德平,胡绚,等. 航空发动机双转子系统的拍振分析[J]. 航空学报,2007,28(6): 1369-1373. doi: 10.3321/j.issn:1000-6893.2007.06.017 -
下载:
点击查看大图
计量
- 文章访问数: 288
- HTML全文浏览量: 57
- PDF下载量: 36
- 被引次数: 0