Anomaly Detection of Suspension System in Maglev Train Based on Missed Detection Rate
-
摘要:
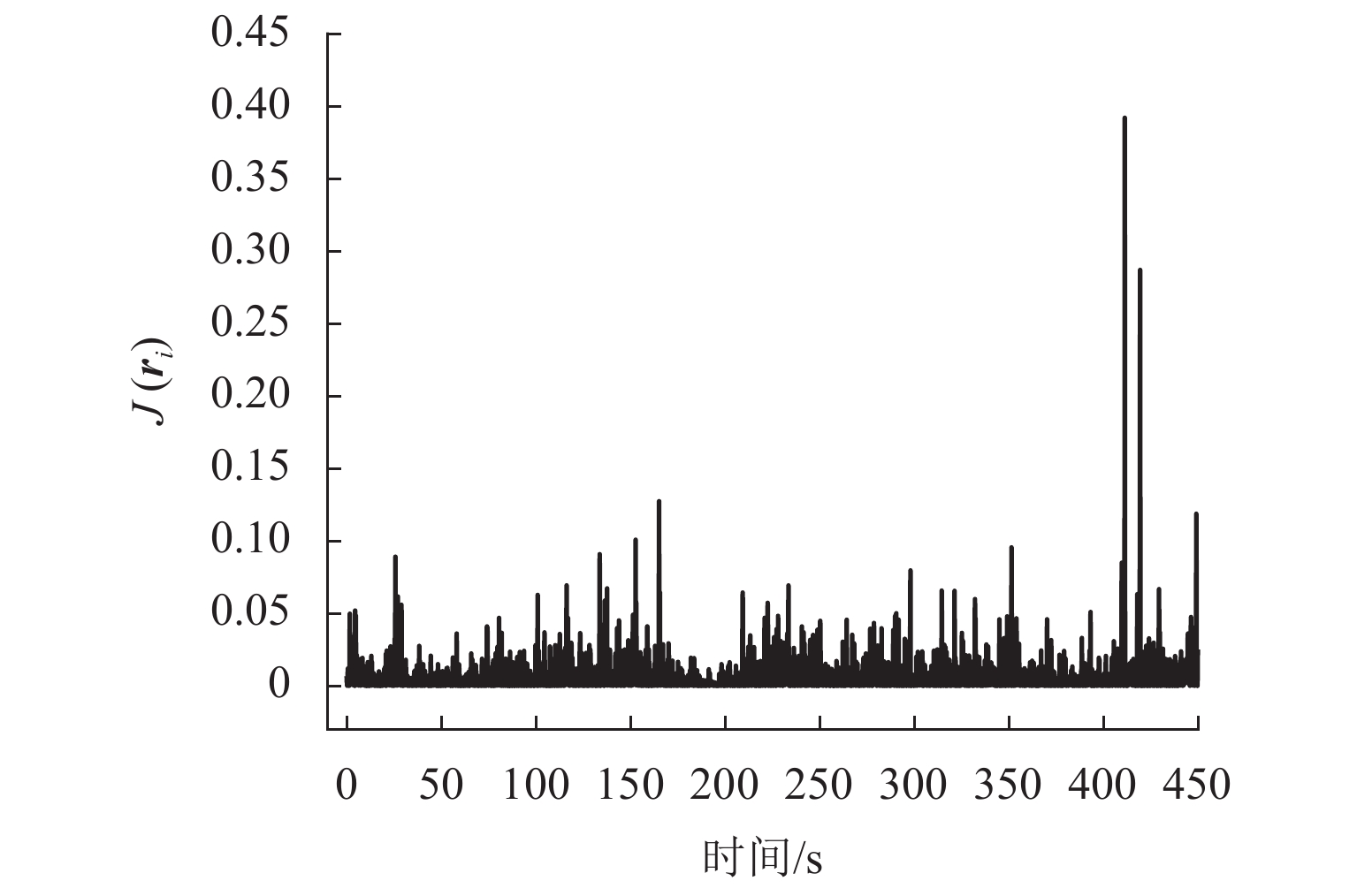
为实现中速磁浮列车悬浮系统的数据驱动异常检测，首先，引入基于参数化残差的异常检测方法；然后，针对当前悬浮系统的异常先验信息非常缺乏的问题，建立悬浮系统健康数据置信集和异常数据置信集，确定悬浮系统的异常检测评估函数与阈值；接着，异常误报率固定时以最小化异常漏检率为设计目标，从数理角度设计满足该目标的最优参数向量，并以此构建基于最低漏检率的悬浮系统异常检测算法；最后，以长沙磁浮快线的悬浮系统运行数据为例，对悬浮系统的间隙突变异常、砸轨异常和加速度传感器异常进行分析和检测. 结果表明，在异常误报率为5%时，所提出的方法能够实现3种典型异常的全部检测，不存在对3种异常的漏检和对正常数据段的误检，最大异常检测滞后0.2 s.
Abstract:In order to detect data-driven anomalies of the suspension system in medium-speed maglev trains, firstly, the paper introduced an anomaly detection method based on parameterized residuals. Secondly, in response to the lack of prior information on anomalies in the current suspension system, the paper established a confidence set for the health data and anomaly data of the suspension system and determined the anomaly detection and evaluation function and threshold for the suspension system. Thirdly, to minimize the missed detection rate of anomalies at a fixed anomaly false alarm rate, the paper designed an optimal parameter vector from a mathematical perspective and constructed an anomaly detection algorithm for the suspension system based on the minimum missed detection rate. Finally, taking the operational data of the suspension system in the Changsha Maglev Express as an example, the paper detected the gap mutation anomaly, rail smashing anomaly, and acceleration sensor anomaly of the suspension system. The experimental results show that the proposed method can detect all three typical anomalies at a false alarm rate of 5%, without any missed detections of the three anomalies or false detections of normal data segments. The maximum anomaly detection delay is 0.2 s.
-
图 2 间隙突变异常时间隙、电流、加速度和电压
Figure 2. Gap, current, acceleration, and voltage at gap mutation anomaly
图 3 砸轨异常时的间隙、电流、加速度和电压
Figure 3. Gap, current, acceleration, and voltage at rail smashing anomaly
图 4 加速度计异常时的间隙、电流、加速度和电压
Figure 4. Gap, current, acceleration, and voltage at accelerometer anomaly
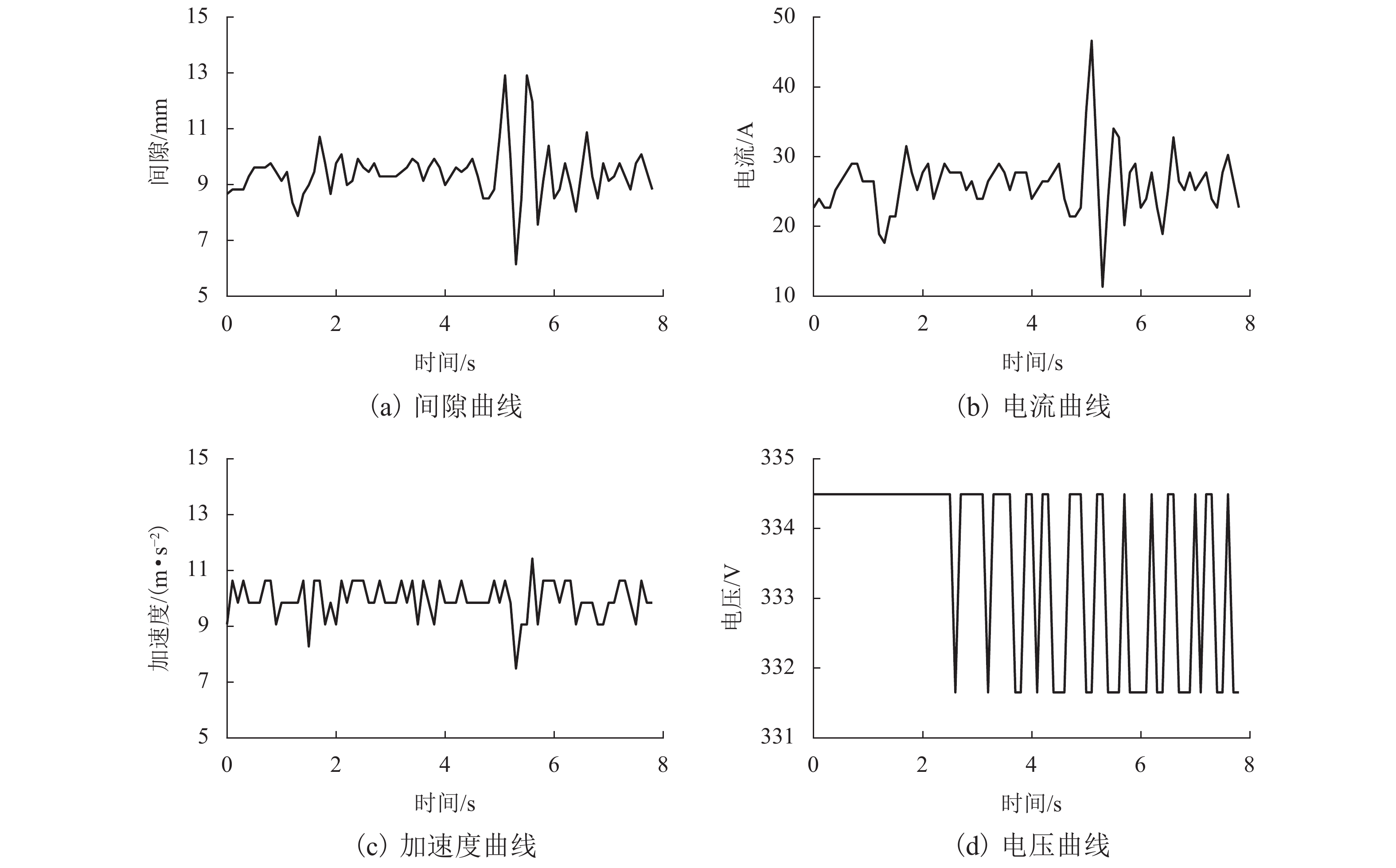
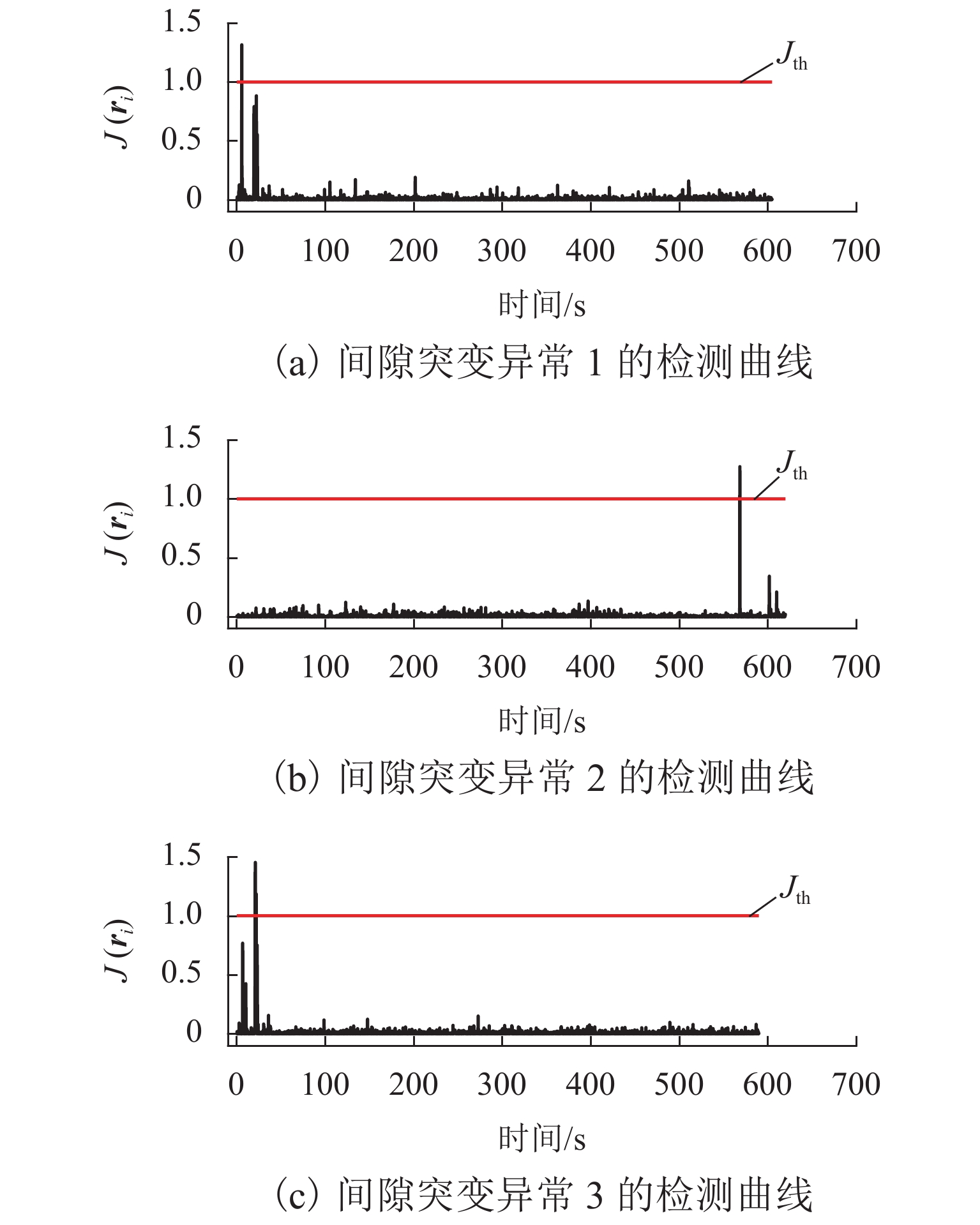
表 1 间隙突变异常的检测位置与异常实际发生位置
Table 1. Detection position and actual occurrence position of gap mutation anomalies
异常 检测位置/s 实际位置/s 间隙异常 1 5.9 5.7 间隙异常 2 568.7 568.5 间隙异常 3 21.1 21.1 
下载: 导出CSV
表 2 砸轨异常的检测位置与异常实际发生位置
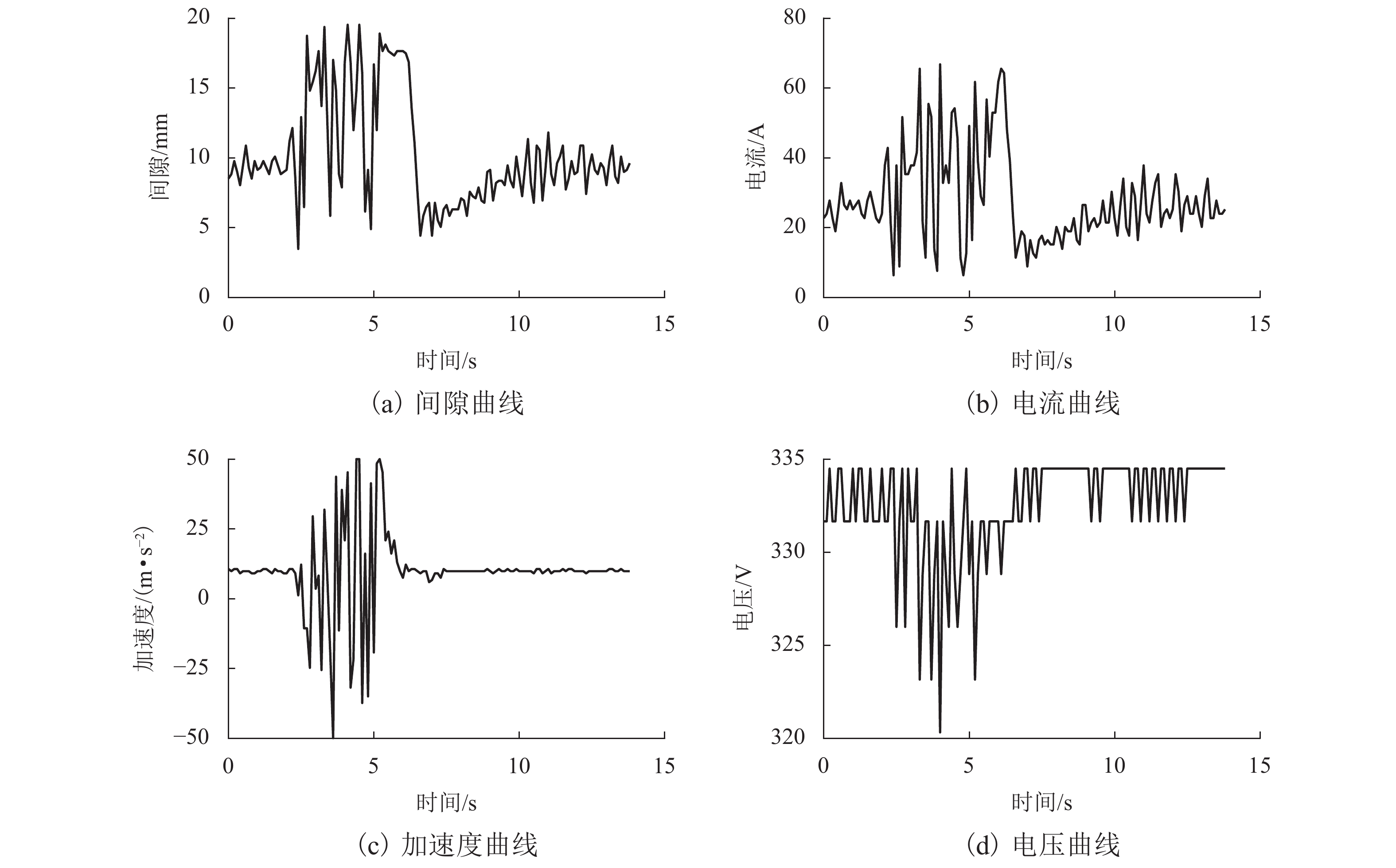
Table 2. Detection position and actual occurrence position of rail smashing anomalies
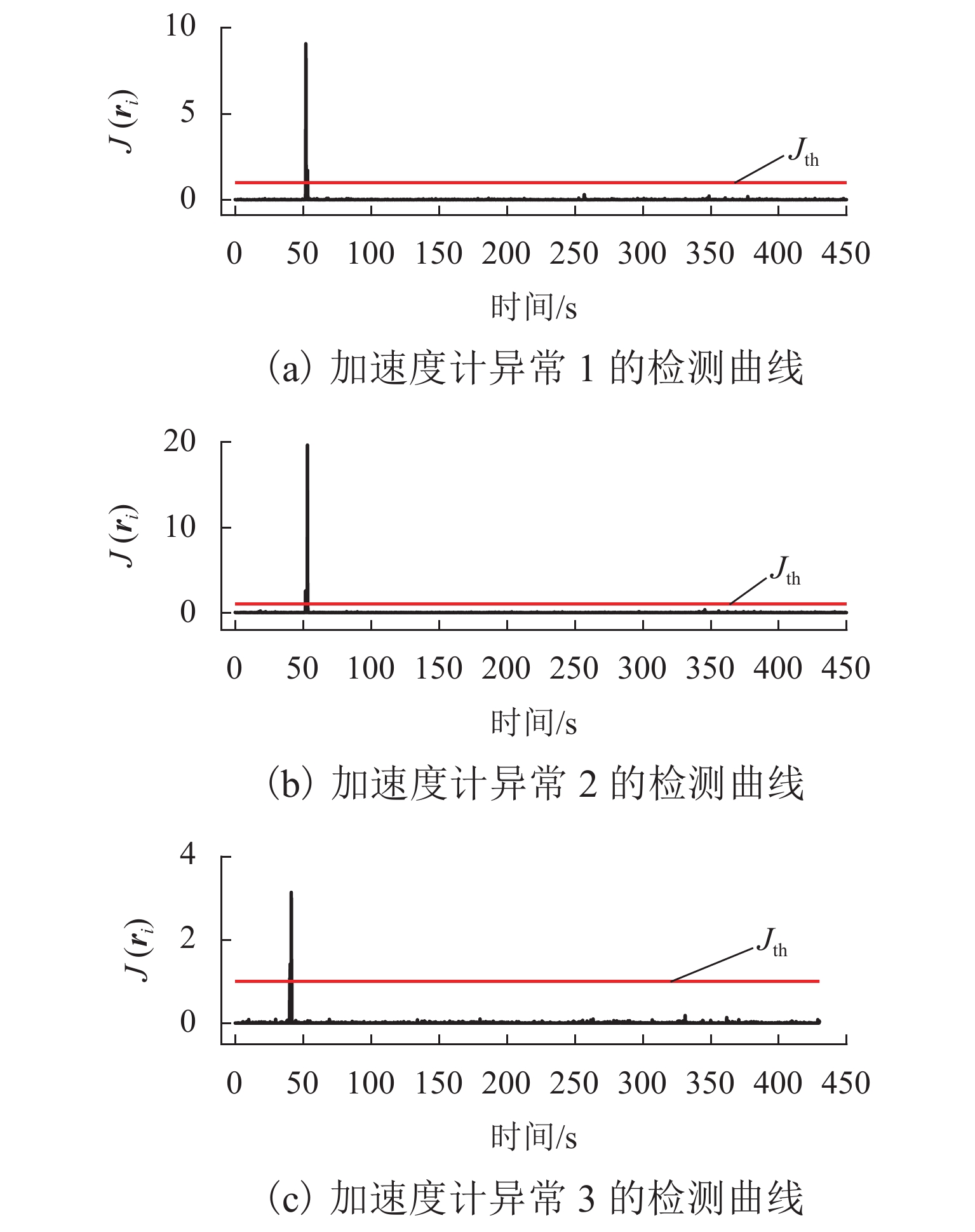
异常 检测位置/s 实际位置/s 砸轨异常 1 7.1 7.0 砸轨异常 2 20.2 20.0
下载: 导出CSV
表 3 加速度计异常的检测位置与异常实际发生位置
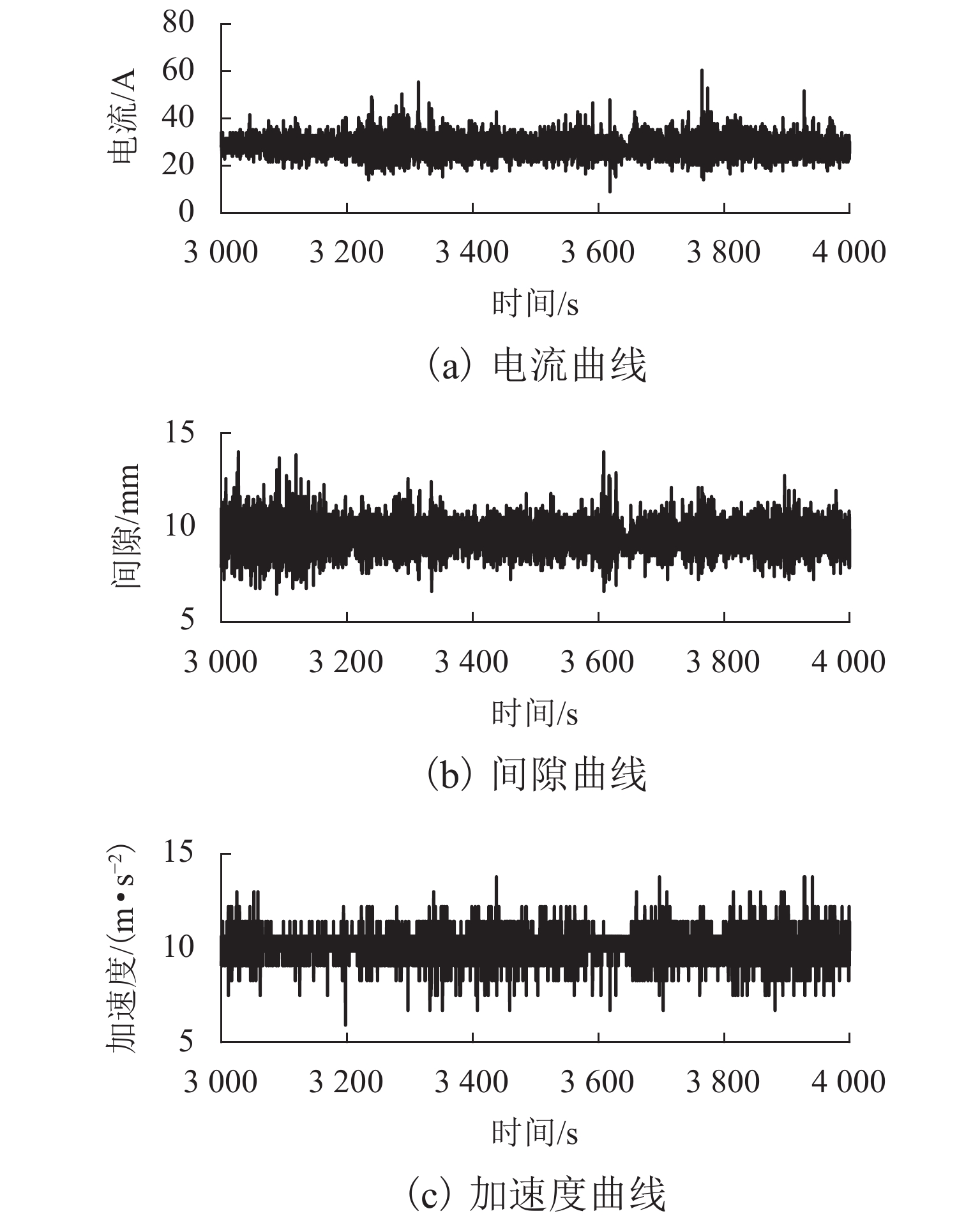
Table 3. Detection position and actual occurrence position of accelerometer anomalies
异常 检测位置/s 实际位置/s 加速度计异常 1 52.2 52.2 加速度计异常 2 52.1 52.1 加速度计异常 3 40.5 40.5
下载: 导出CSV
-
[1] 邓自刚,刘宗鑫,李海涛,等. 磁悬浮列车发展现状与展望[J]. 西南交通大学学报,2022,57(3): 455-474,530.DENG Zigang, LIU Zongxin, LI Haitao, et al. Development status and prospect of maglev train[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 455-474,530. [2] 翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226.ZHAI Wanming, ZHAO Chunfa. Frontiers and Challenges of Sciences and Technologies in Modern Railway Engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. [3] 柳阳阳. 中低速磁浮列车悬浮控制系统在线监测与故障诊断系统研究[D]. 成都: 西南交通大学, 2018 [4] 王志强. 高速磁浮列车悬浮系统故障诊断与容错控制研究[D]. 长沙: 国防科技大学, 2019. [5] ZHENG Z, LIU W, LIU R, et al. Anomaly detection of metro station tracks based on sequential updatable anomaly detection framework[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2022, 32(11): 7677-7691. doi: 10.1109/TCSVT.2022.3181452 [6] ZHANG Y Z, CHAO C, WU J, et al. Magnetic anomaly of long track detection method based on wavelet combining with fractal for high speed maglev transit[J]. Measurement and Control, 2022, 55(7/8): 717-728. [7] DENG Z G, ZHOU X C, HUANG H, et al. Measurement and characterization method of permanent magnetic guideway irregularity in HTS maglev system[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(2): 1-7. [8] 罗茹丹. 高速磁浮长定子异常情况下牵引行波主漏磁场的分析及其检测系统设计[D]. 长沙: 国防科技大学. [9] 林国斌, 陈健, 徐俊起, 等. 一种基于车轨状态监测的悬浮冗余控制系统及方法: CN202110987666.0[P]. 2021-10-29. [10] 杨杰, 高涛, 周发助. 一种基于悬挂式磁悬浮轨道交通系统的轨道维护设备: CN201911216341.1[P]. 2020-04-14. [11] KE Z H, DENG Z G, CHEN Y N, et al. Vibration states detection of HTS pinning maglev system based on deep learning algorithm[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(6): 1-6. [12] 朱跃欧, 罗华军, 佟来生, 等. 磁浮列车、悬浮控制器及悬浮间隙异常预警方法、系统: CN202110546646.X[P]. 2021-08-10. [13] 王平,梅子,龙志强. 基于超球体高斯分布的悬浮系统异常检测[J]. 机车电传动,2021(6): 9-17.WANG Ping, MEI Zi, LONG Zhiqiang. Anomaly detection for suspension systems based on the Gaussian distribution of hyperspheres[J]. Electric Drive for Locomotives, 2021(6): 9-17. [14] 王平,梅子,龙志强. 基于改进典型相关分析的中低速悬浮系统异常检测方法[J]. 同济大学学报(自然科学版),2022,50(2): 241-252. doi: 10.11908/j.issn.0253-374x.21186WANG Ping, MEI Zi, LONG Zhiqiang. Anomaly detection method of middle-low speed suspension system based on improved canonical correlation analysis[J]. Journal of Tongji University (Natural Science), 2022, 50(2): 241-252. doi: 10.11908/j.issn.0253-374x.21186 [15] 马政. 永磁磁浮列车远程监控系统研究[D]. 赣州: 江西理工大学, 2021 . [16] WANG L C, YU P C, LI J H, et al. Suspension system status detection of maglev train based on machine learning using levitation sensors[C]//2017 29th Chinese Control and Decision Conference (CCDC). Chongqing: IEEE, 2017: 7579-7584. [17] MA D R, PEICHANG Y, LI J. Research on operational state monitoring of maglev train based on machine learning[C]//2019 Chinese Automation Congress (CAC). Hangzhou: IEEE, 2020: 4679-4683. [18] 王志强, 龙志强, 高明, 等. 一种基于数据驱动的磁浮列车悬浮系统故障检测方法: CN202010319948.9[P]. 2020-08-14. [19] STEVEN X D, LI L L, KRÜGER M. Application of randomized algorithms to assessment and design of observer-based fault detection systems[J]. Automatica, 2019, 107: 175-182. doi: 10.1016/j.automatica.2019.05.037 [20] STEVEN X D, YANG Y, Y. ZHANG, LI L. Data-driven realizations of kernel and image representations and their application to fault detection and control system design[J]. Automatica, 2014, 50(10): 2615-2623. doi: 10.1016/j.automatica.2014.08.022 [21] SONG Y, ZHONG MY, XUE T, et al. Parity space-based fault isolation using minimum error minimax probability machine[J]. Control Engineering Practice, 2020, 95: 104242.1-104242.13. [22] YIN S, DING S X, XIE X C, et al. A review on basic data-driven approaches for industrial process monitoring[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6418-6428. doi: 10.1109/TIE.2014.2301773 [23] NADERI E, KHORASANI K. A data-driven approach to actuator and sensor fault detection, isolation and estimation in discrete-time linear systems[J]. Automatica, 2017, 85: 165-178. [24] JIANG B B, GUO Z F, ZHU Q X, et al. Dynamic minimax probability machine-based approach for fault diagnosis using pairwise discriminate analysis[J]. IEEE Transactions on Control Systems Technology, 2017: 1-8. [25] XUE T, DING S X, ZHONG M Y, et al. A distribution independent data-driven design scheme of optimal dynamic fault detection systems[J]. Journal of Process Control, 2020, 95: 1-9. doi: 10.1016/j.jprocont.2020.09.004 [26] ZYMLER S, KUHN D, RUSTEM B. Distributionally robust joint chance constraints with second-order moment information[J]. Mathematical Programming, 2013, 137(1/2): 167-198. [27] ZHONG M Y, XUE T, SONG Y, et al. Parity space vector machine approach to robust fault detection for linear discrete-time systems[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(7): 4251-4261. doi: 10.1109/TSMC.2019.2930805 [28] 温韬,夏文韬,周旭,等. 基于数据驱动的磁浮列车悬浮系统参数整定[J]. 西南交通大学学报,2022,57(3): 506-513.WEN Tao, XIA Wentao, ZHOU Xu, et al. Data-driven parameter tuning for maglev train levitation system[J]. Journal of Southwest Jiaotong University, 2022, 57(3): 506-513. -
下载:
点击查看大图
计量
- 文章访问数: 292
- HTML全文浏览量: 98
- PDF下载量: 33
- 被引次数: 0