Vulnerability Analysis of En-route Network Based on Cascading Failure
-
摘要:
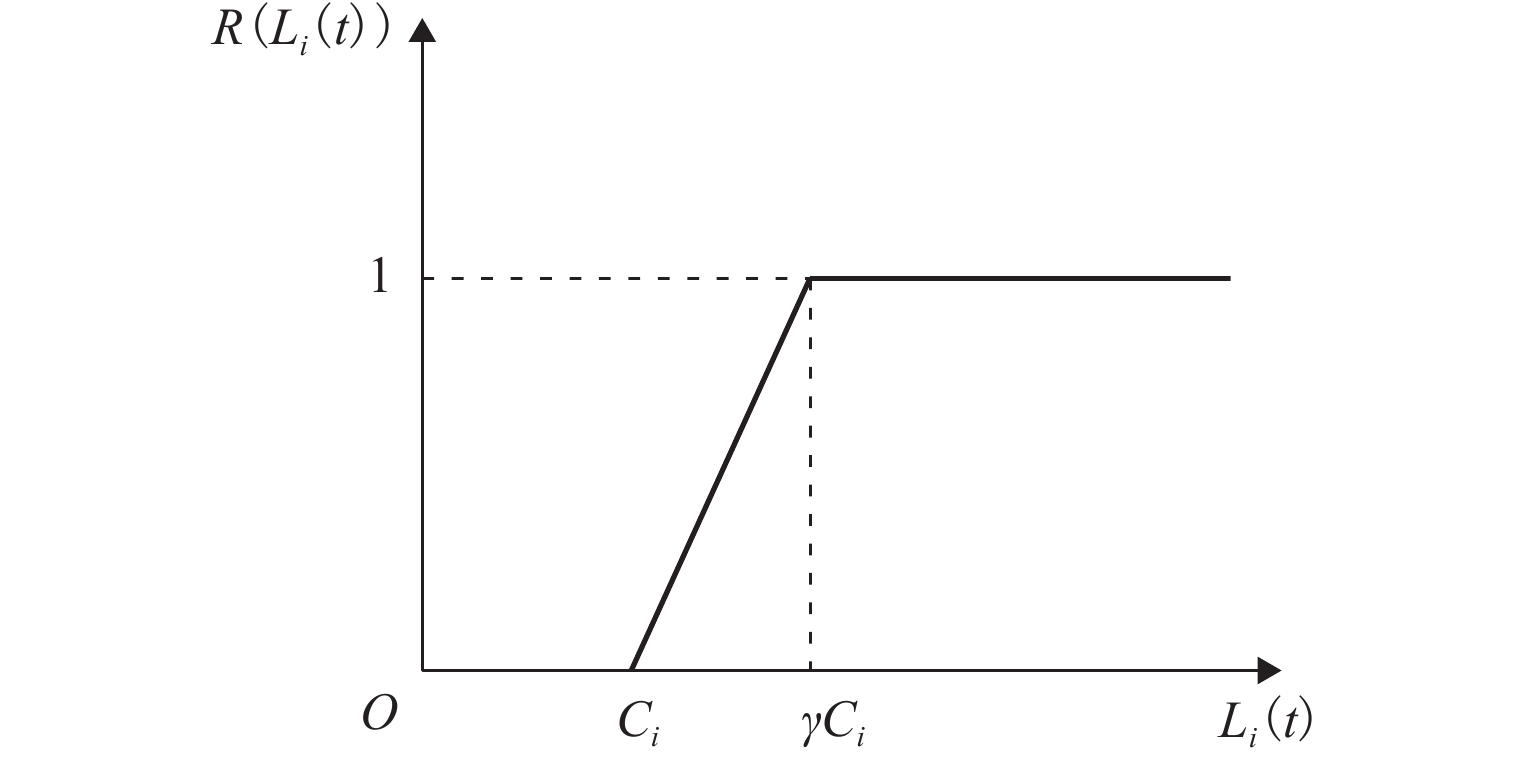
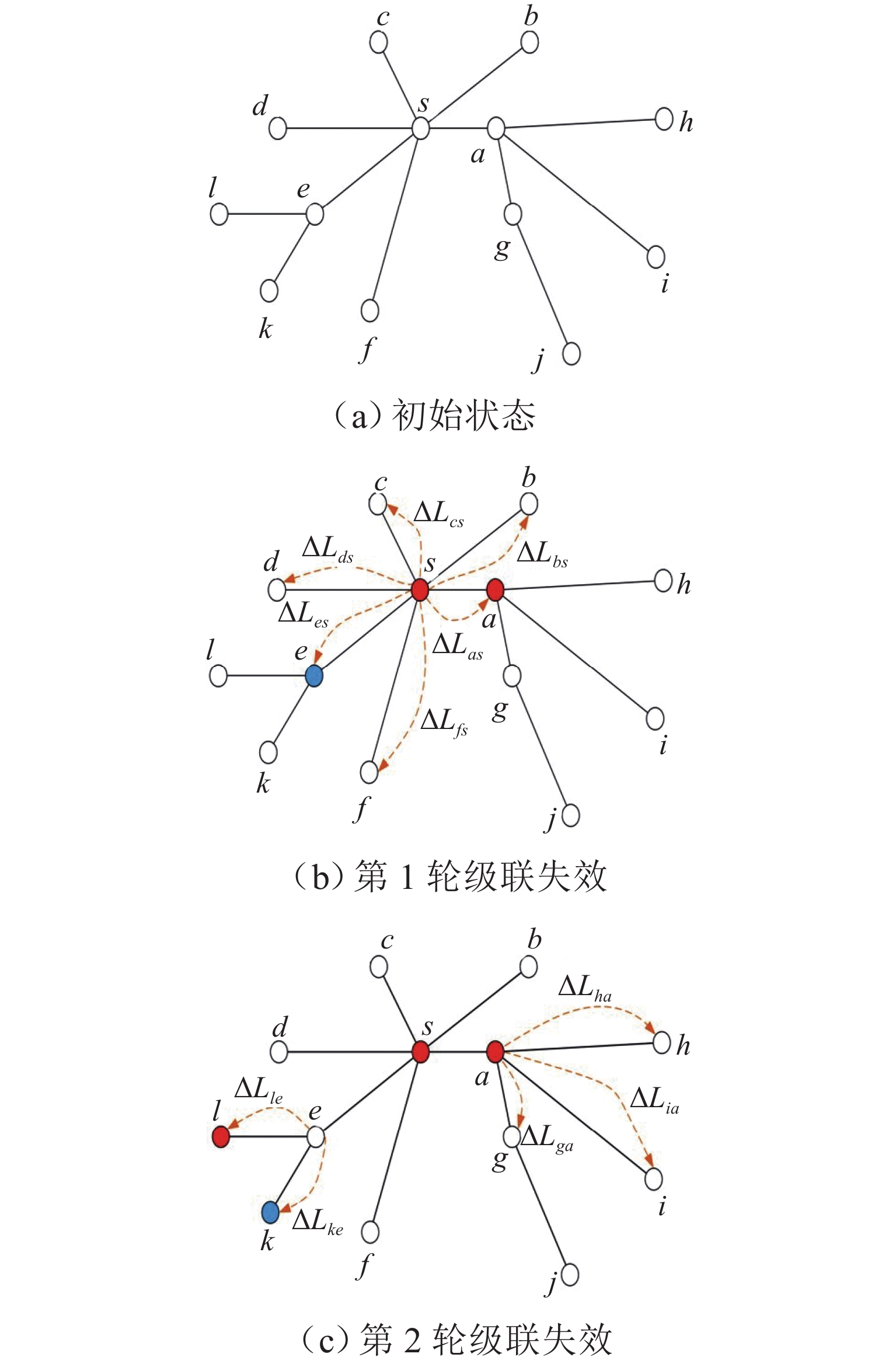
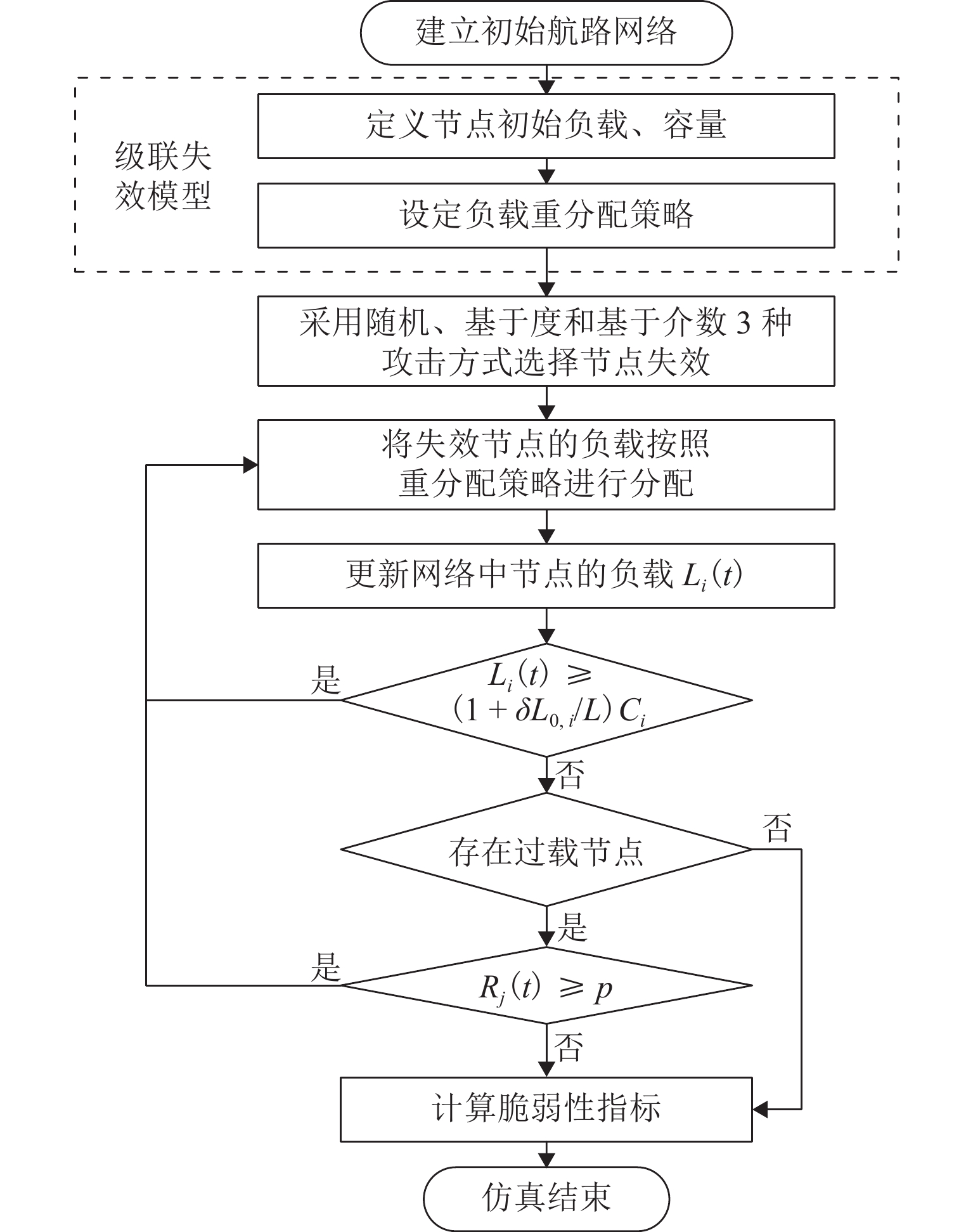
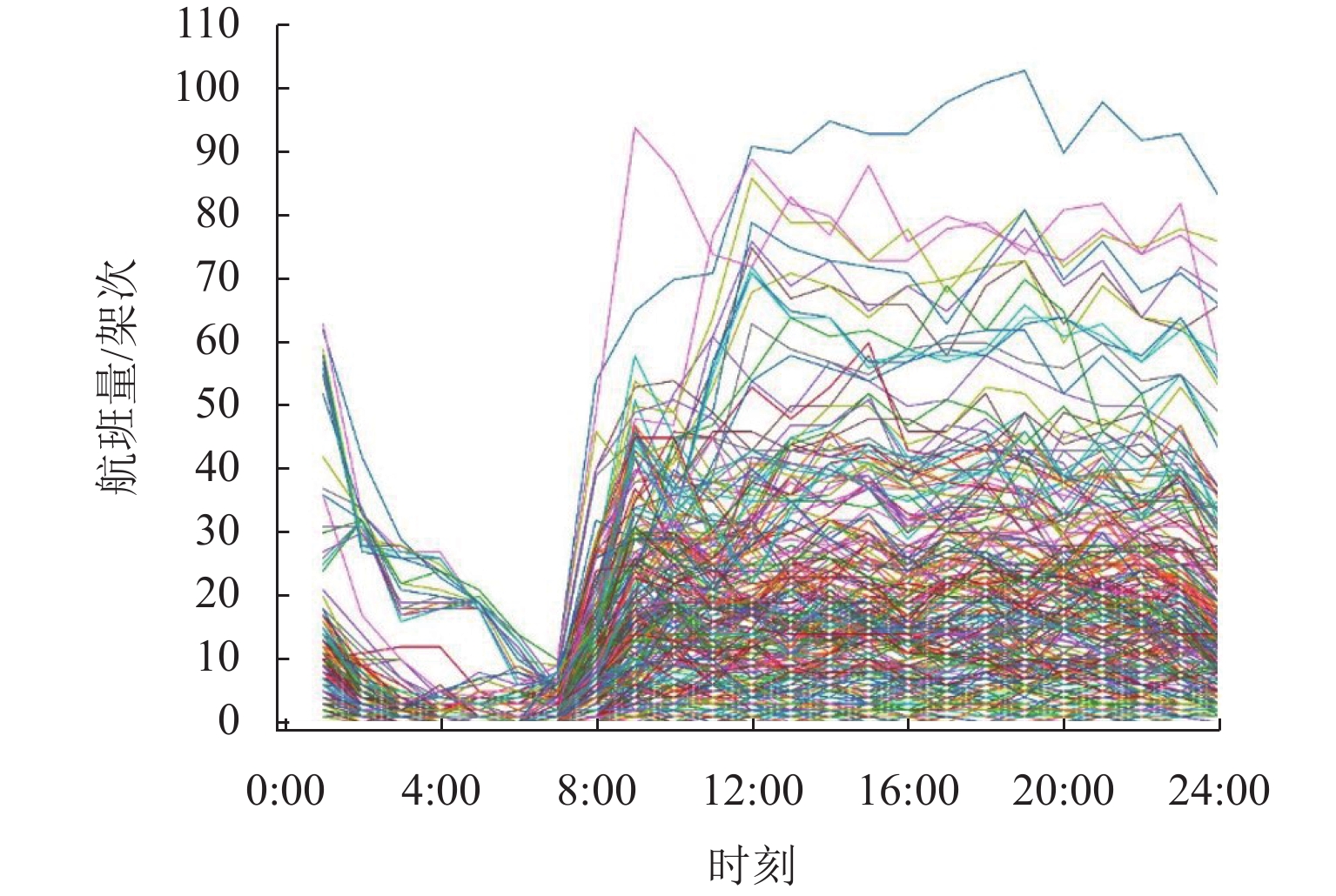
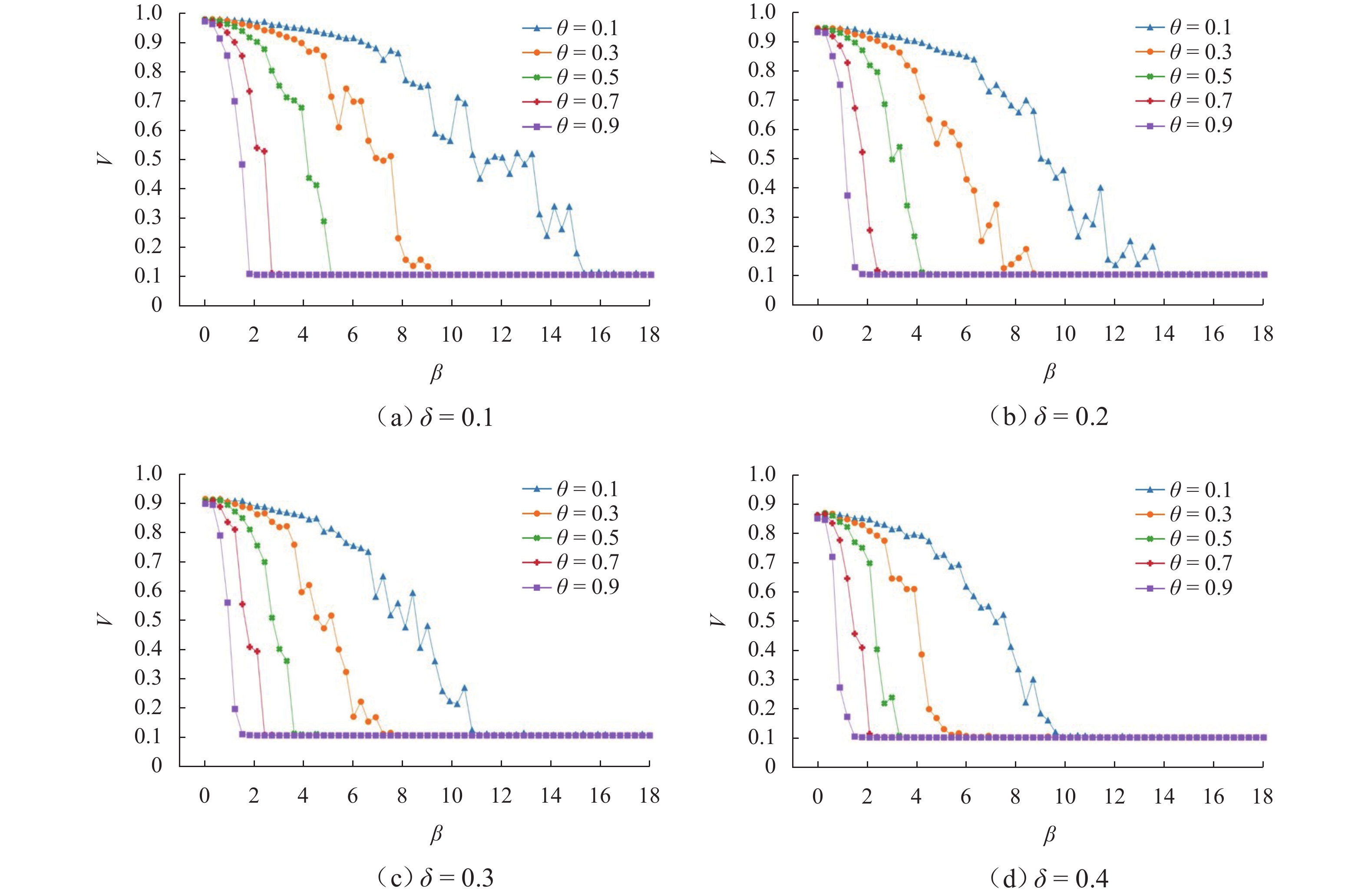
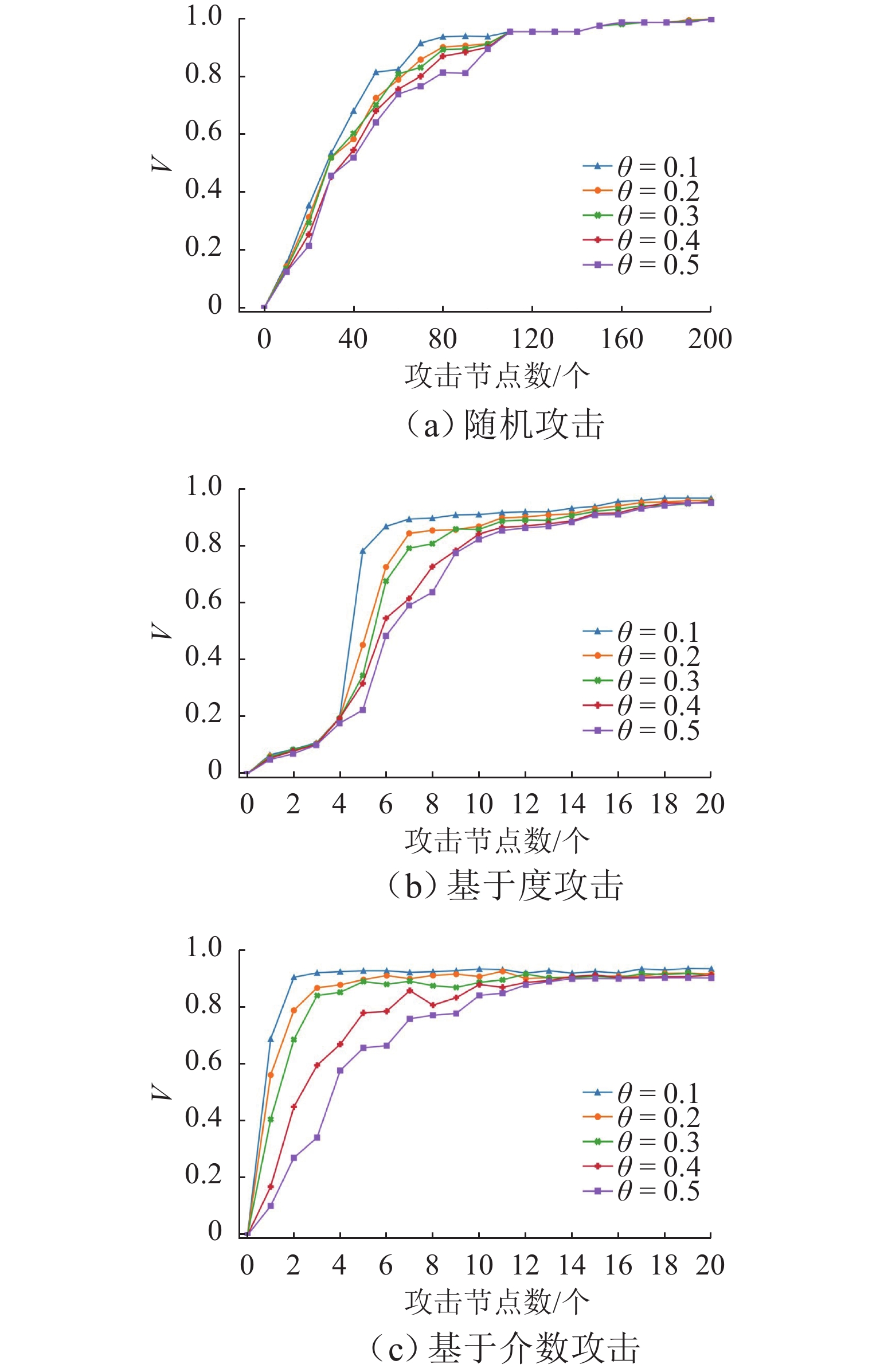
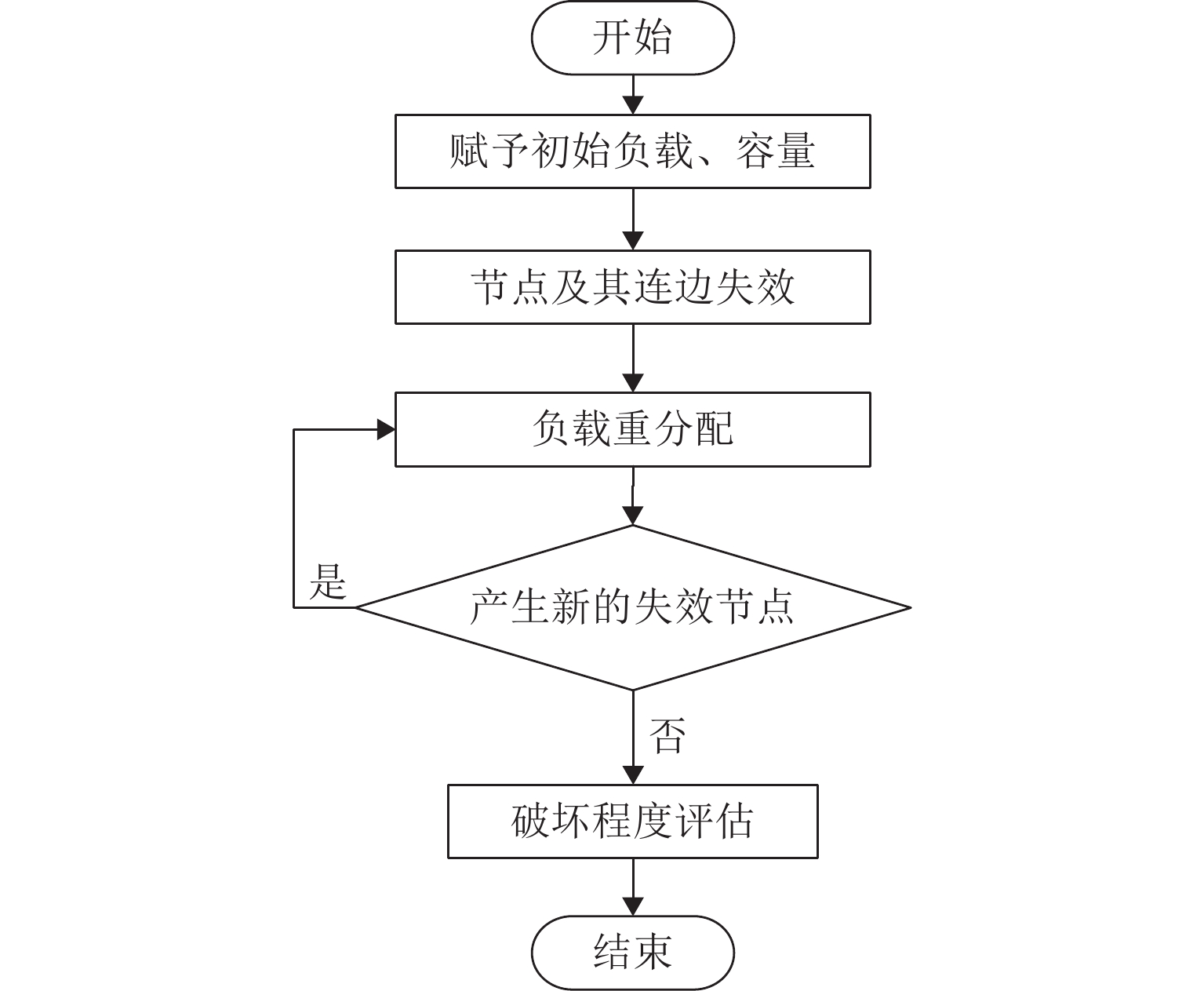
为探究级联失效所造成的航路网络脆弱性变化规律，基于不同攻击方式的级联失效过程对航路网络脆弱性进行分析. 首先，结合航路网络超容运行实际，提取非失效状态节点的过载运行、节点失效的概率性和节点所经负载的可分流性3个特点，构建航路网络级联失效模型和不同攻击方式的级联失效过程；然后，从航路点运行能力损失角度提出航路网络级脆弱性指标以及与级联失效模型相结合的脆弱性分析方法；最后，以民航华东区域为实例，分析航路网络脆弱性与所建模型参数的关联性，探究不同参数条件下航路网络脆弱性指标的变化规律，并设计了3种攻击实验. 研究表明：各航路点运行能力随着负载流量的超容范围增加而提升，航路网络脆弱性随之降低；航路网络对选择性攻击方式较为敏感，尤其是基于介数的攻击.
Abstract:In order to explore the variation of the vulnerability of the en-route network caused by cascading failure, the vulnerability of the en-route network was analyzed based on the cascading failure process of different attack methods. By combining with the actual overcapacity operation of the en-route network, the overload operation of the nodes in the non-failure state, the probability of node failure, and the divertability of the load passed by the nodes were extracted. The cascading failure model of the en-route network and the cascading failure process based on different attack methods were constructed, and the en-route network-level vulnerability index was proposed from the perspective of the loss of waypoint operation capacity, as well as the vulnerability analysis method combined with the cascading failure model. The correlation between the vulnerability of the en-route network and the proposed model parameters was analyzed by studying the operation data in Eastern China, and the change rule of the vulnerability index of the en-route network under different parameters was explored. Three kinds of attack experiments were designed, and the results show that the operation capacity of each waypoint increases with the overcapacity range of the load flow, and the vulnerability of the en-route network decreases; the en-route network is more sensitive to selective attack methods, especially those based on the betweenness.
-
Key words:
- air traffic /
- en-route network /
- complex networks /
- cascading failure /
- vulnerability
-
随着我国城市化进程不断加快，隧道数量和复杂性都在不断增加. 目前，我国已成为世界上隧道数量最多、条件最复杂、技术发展最快的国家[1-2]. 为解决交通便捷性需求，城市隧道结构逐渐丰富，各类分岔隧道数量也急剧增加.
火灾作为隧道中危害性最大的灾害，一旦发生，将造成严重的人员财产损失. 相较于普通地面建筑，隧道中火灾的烟气蔓延情况及控制手段都更为复杂，使得隧道发生火灾时人员的安全疏散及灭火救援难度高于普通地面建筑[3-4].
针对于单直隧道火灾，国内外进行了大量的研究. Alpert[5]首次提出了预测顶棚射流最高羽流温度的经验模型；Kurioka等[6]通过改变隧道的横截面以及火源的热释放速率进行实验，提出隧道顶棚下的最高温度模型；Li等[7]考虑连续火焰长度低于顶棚高度的情况下，通过理论分析及实验研究，探讨2种不同尺寸隧道中，不同热释放速率、纵向通风风速及隧道几何形状对顶棚下烟气最高温度的影响；王钟宽等[8]以美国Memorial隧道为原型，应用Froude准则建立1∶20缩尺隧道模型，探究不同坡度的隧道火灾自熄特性；姜学鹏等[9]提出侧部点式排烟模式隧道火灾临界风速的无量纲计算式.
随着地下空间的开发与应用，隧道结构逐渐丰富. 因此，针对于分岔隧道火灾的研究也快速展开. Yang等[10]采用理论分析和数值模拟相结合的方法，研究在具备机械排烟系统的倾斜分岔隧道中烟气流动的多重行为；Huang等[11]通过小尺寸分岔隧道火灾实验，研究隧道顶棚下气体最大超限温度，提出一个分为两部分的数学模型来预测分岔隧道的最大上限温度；Zhang等[12]研究T型分岔隧道结构火灾的顶棚最大温升，并提出在目前的模型结构规模和热释放率的研究范围内T型分岔隧道的最大顶烟温度随着无量纲支管宽度的增加而略有下降.
目前，空气幕也被广泛应用于隧道火灾排烟控制中，其工作原理是让高速喷出的空气流形成一道墙，以起到隔烟隔热的效果. 学者们研究了空气幕对火灾烟气蔓延的控制作用. Shu等[13]利用一系列典型的空气动力学性能曲线，建立一种在无风条件下计算空气幕效率系数的新模型，对分岔隧道火灾空气幕控烟有借鉴作用. Yu等[14]提出当动量比约为10∶1时，吹风角度垂直向下的空气幕封烟效果最佳，且其效果随缝宽和喷射角的增大而提升；当火源位于空气幕一侧时，空气幕的最佳喷射角为朝向火源倾斜30°. Li等[15]提出空气幕射流的均匀性受气幕单元的横截面影响，随着射流距离的增加，空气幕的射流速度先急剧下降，然后缓慢下降，直至为0.
隧道火灾中，单独使用纵向通风或空气幕对分岔隧道进行烟气的控制效果仍不尽如人意[16-17]. 而针对纵向通风与空气幕协同作用下的分岔隧道烟气控制及最高温度的研究还较少，故本文根据57组缩尺寸实验数据，对分岔隧道多向气流耦合下的烟气运动和最高温度变化进行研究.
1. 实验布置
如图1所示，在缩小比例（1∶10）分岔隧道模型中进行实验，隧道长10.0 m、宽1.0 m、高0.6 m，分岔隧道长5.0 m、宽1.0 m、高0.6 m，夹角45°. 以液化石油气为燃料，火源位于主隧道中间.
图 1 城市隧道分岔段火灾实验平台Figure 1. Experimental platform for fires in urban bifurcated tunnels分岔隧道的岔道口处安装有空气幕. 该空气幕采用铁制栅格通过软性连接与风机相连，并通过底部支架固定于隧道内，从而保证气流的稳定性，且各个位置的风速分布均匀. 同时，可通过侧面螺丝及手柄调节空气幕的角度A在 −45°～45° （面向主隧道为正，分岔隧道口为负），空气幕喷射宽度（厚度T）为0～0.15 m. 通过变频器也可随意调节空气幕风速大小，使空气幕射流速度$ {v_{{\mathrm{air}}}} $在0～4.0 m/s. 空气幕的整体结构如图1（b）、（c）所示. 在分岔隧道的左侧安装变频风机，用于控制纵向通风. 为监测隧道中最高温度的分布，将127个K型热电偶沿着主隧道和分岔隧道的中心轴放置，热电偶设置细节如图2所示. 纪杰等[18]研究狭长空间内的烟气流动特性发现，在小尺寸隧道中进行火灾实验，雷诺数Re （式（1））和弗洛德数Fr （式（2））对流体运动具有决定性影响.
Re=vlμ, (1) Fr=glv2， (2) 式中：$ v $为纵向通风速度，m/s；$ l $为长度尺寸，m；$ \mu $为流体的运动黏度.
基于几何相似原理，热量的相似关系可表示为
Qm=Qf(LmLf)5/2， (3) 式中：$ {Q_{\mathrm{m}}} $为模型尺寸热释放速率，kW；$ {Q_{\mathrm{f}}} $为全尺寸热释放速率，kW；$ {L_{\mathrm{m}}} $为模型隧道的长度，m；$ {L_{\mathrm{f}}} $为全尺寸隧道的长度，m.
基于该相似关系，当全尺寸隧道中热释放速率 （HRR）为5、15、25 MW时，缩尺寸隧道模型中分别对应为15.9、47.9、77.7 kW.
本文总共进行了57组实验，变量包括热释放速率、纵向通风速度、空气幕角度、厚度和风速，拟探究纵向通风与空气幕之间的耦合效应. 详细实验工况见表1.
表 1 实验工况Table 1. Experimental conditions工况 HRR/kW 纵向通风/（m•s−1） 空气幕风速/（m•s−1） 角度/（°） 厚度/m 1～15 15.9，47.9，77.7 0.4，0.8，1.2，1.6，2.0 1.0 0 0.15 16～33 47.9 0.4，0.8，1.2 1.5，2.0，2.5，3.0，3.5，4.0 0 0.15 34～51 47.9 0.4，0.8，1.2 3.5 −45，−30，−15，15，30，45 0.15 52～57 47.9 0.4，0.8，1.2 3.5 30 0.05，0.10 2. 不同纵向通风下的隧道温度分布
2.1 主线隧道
当空气幕射流速度较小且恒定（$ {v_{{\mathrm{air}}}} $=1.0 m/s）时，3种不同热释放速率下纵向通风大小对主隧道内温度分布影响如图3所示. 图中，横坐标x0为距离主隧道火源的距离. 由图可知，当纵向风速较小时（$ v $=0.4 m/s），其对烟气回流层的阻隔作用较小，从而导致隧道上游出现温度波动的情况，而火源热释放速率越大，该现象越明显. 当纵向风速为0.8 m/s及以上时，对主线隧道内烟气的降温效果由纵向通风主导，能在隧道上游形成空气屏障，有效缩短烟气回流层长度. 烟气的蔓延过程为非定常的三维湍流运动[19]，而空气幕的作用方向与烟气在顶棚形成的射流方向垂直，导致空气幕通风会对烟气的一维水平蔓延形成剪切作用，在此基础上再添加纵向通风，会对火灾烟气在主线隧道下游蔓延的湍流运动产生较大扰乱，且火源功率越小影响越大. 在3种热释放速率下，随着纵向风速的增加，不仅隧道内最高气温降低，而且烟气最高温度的位置也向隧道下游有一定偏移.
图 3 不同纵向通风下主隧道温度场分布Figure 3. Temperature field distribution in main tunnel with different longitudinal ventilation由图3（a）可知：当热释放速率为15.9 kW时，纵向风速从0.4 m/s增加到2.0 m/s，隧道顶棚最高温度从150.1 ℃降低到49.5 ℃；纵向风速达到2.0 m/s时，烟气温度已无明显峰值，火羽流在纵向通风的作用下向火源下游倾斜；当纵向通风增大时，火羽流的倾斜程度增加，对隧道顶棚的直接冲击作用减弱，因此，在隧道顶棚下方形成的高温区域逐渐减小，并且向火源下游偏移. 由图3（b）可知：当热释放速率为47.9 kW时，纵向通风从0.4 m/s增加到2.0 m/s，顶棚最高温度从381.4 ℃降低到83.6 ℃；当纵向风速为2.0 m/s时，隧道顶棚最高温度位置根据火源位置向下游偏移1.0 m. 由图3（c）可知：当热释放速率为77.7 kW时，纵向风速从0.4 m/s增加到2.0 m/s，最高温度从512.3 ℃降低到149.2 ℃，主线隧道下游沿程温度变化随纵向风速的增加而趋于稳定. 综上所述，当空气幕射流速度不变时，随着热释放速率的增大，主线隧道的纵向通风降温效果会达到阈值，因此，有必要探究纵向通风与空气幕协同作用时的最佳风速组合.
2.2 分岔隧道
当$ {v_{{\mathrm{air}}}} $=1.0 m/s时，不同热释放速率下纵向风速大小对分岔隧道温度分布影响如图4所示. 分岔隧道的最高温度随着热释放速率的增大而显著升高，因空气幕良好的隔热阻烟效果，温度在x0=0.8 m处呈断崖式下降. 当纵向风速不同时，分岔隧道中x0=−0.5 m处的温度差异较大. 纵向风速过小（如0.4、0.8 m/s）会导致高温烟气在火源附近滞留，并向分岔隧道蔓延. 然而，加大纵向风速虽能一定程度上避免烟气向分岔隧道蔓延，但会加剧主线隧道下游烟气的沉降效果.
图 4 不同纵向通风下分岔隧道温度分布Figure 4. Temperature distribution in bifurcated tunnel with different longitudinal ventilation综上，在城市隧道分岔段采用空气幕进行隔热阻烟具有一定的应用价值，其对火灾烟气的具体影响将在下文进行论述. 由于当纵向风速超过1.2 m/s时其降温效果不再显著变化，因此，后续实验选择在纵向风速为0.4、0.8、1.2 m/s条件下进行.
3. 空气幕对隧道最高温升的影响
3.1 空气幕射流速度
为探究不同纵向风速和空气幕射流速度条件下分岔隧道的最大温升，基于Chen等[20]的研究，建立式（4）～（7）所示关系.
ΔTmax=f(Q,Cp,g,v,ρ∞,T∞,H)， (4) ΔTmaxT∞=γ(Q2/30Fr1/3)ε， (5) Q0=Qρ∞CPT∞g1/2H5/2, (6) ΔTmaxT∞∼Q0Fr， (7) 式中：$ \gamma 、\varepsilon $为常数，当$ \dfrac{{\mathop Q\nolimits_{\text{0}}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}} }}{{F{r^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}} < 1.35 $时，$ \gamma =1.77，\varepsilon = \text{1}\text{.2} $，当$ \dfrac{{\mathop Q\nolimits_{\text{0}}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}} }}{{F{r^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}} \geqslant 1.35 $时，$ \gamma =\text{2}\text{.54}，\varepsilon =\text{0} $；$ \Delta {T_{\max }} $为隧道顶棚最高温升，K；$ Q $为热释放速率，kW；Cp为恒压比热容，kJ/（kg•K）；$ {\rho _\infty } $为环境空气密度，kg/m3；$ {T_\infty } $为环境温度，K；H为燃烧器表面到隧道顶棚的距离，m；$ \mathop Q\nolimits_{\text{0}} $为无量纲热释放速率.
根据陈贻来[21]的研究，单个汽车燃烧时的热释放速率为3～5 MW，当隧道中单个汽车发生火灾并引燃两侧汽车时，火灾热释放速率最高可达15 MW. 而夏永旭等[22]研究表明，大巴车在隧道中平均热释放速率为8 MW. 因此，为更好地与实际相结合，探究隧道火灾极端情况下不同纵向风速与空气幕对隧道顶棚温度的影响，后续实验选取热释放速率为15 MW，即在缩尺寸隧道中热释放速率为47.9 kW时进行. 因此，在该情况下，$ {Q_0} $可以作为一个常数而忽略，故而式（7）可以写为
ΔTmaxT∞∼Fr∼v2gH. (8) 图5显示在不同空气幕射流速度下$ {{{v^2}} / {gH}} $与$ {{\Delta {T_{\max }}} / {{T_\infty }}} $之间的关系. 图中，x、y分别为拟合曲线横、纵坐标参量，余图同. 由此可以得出，在不同空气幕射流速度的影响下，分岔隧道的最大温升与纵向通风之间的关系如式（9）所示.
图 5 不同空气幕射流速度下$ v^{2} / (g H) $与$ \Delta T_{\max } / T_{\infty} $之间的关系Figure 5. Relationship between $ v^{2} / (g H) $ and $ \Delta T_{\max } / T_{\infty} $at different jet velocities of air curtainΔTmaxT∞=m(v2gH)−n， (9) m=−0.2vair√gH+1.75， (10) n=−0.08vair√gH+0.18， (11) 式中：m、n为系数.
拟合的详细描述见图6.
图 6 $ {v_{{\mathrm{air}}}}/{(gH)^{1/2}} $与系数m和n之间的关系Figure 6. Relationship between$ {v_{{\mathrm{air}}}}/{(gH)^{1/2}} $and coefficients m and n将m和n代入式（9），便可以得到Q = 47.9 kW，空气幕角度为0° 时，纵向通风与空气幕协同作用下分岔隧道最大温升的理论模型，如式（12）所示.
ΔTmaxT∞=(−0.2vair√gH+1.75)(v2gH)0.08vair√gH−0.18. (12) 将不同空气幕射流速度下主隧道最大温升实验值与理论模型（式（12））中的预测值进行比较，如图7所示，其结果吻合度较高.
图 7 不同空气幕射流速度下无量纲预测与实验的最大温升对比Figure 7. Comparison of dimensionless predicted and experimental maximum temperature rise at different jet velocities of air curtain3.2 空气幕角度和厚度
根据图5可以看出，在3种纵向通风下，当空气幕射流速度达到3.5 m/s时，空气幕射流速度对主隧道最高温影响减弱，此时，空气幕和纵向通风产生的气流达到动态平衡. 因此，为探索空气幕的角度A和厚度T对隧道温度分布的影响，将空气幕的射流速度$ {v_{{\mathrm{air}}}} $设置为固定值3.5 m/s，以排除其影响.
不同空气幕角度下，$ {v^2}/(gH) $与$ {{\Delta {T_{\max }}} / {{T_\infty }}} $之间的关系如图8所示. 由此可以得出，在不同空气幕角度（−45° 除外）的影响下，分岔隧道最大温升与纵向通风的关系如图9所示，其拟合式如式（13）所示.
图 8 不同空气幕角度下$ {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {(gH)}}} \right. } {(gH)}} $与$ {{\Delta {T_{\max }}} \mathord{\left/ {\vphantom {{\Delta {T_{\max }}} {{T_\infty }}}} \right. } {{T_\infty }}} $的关系Figure 8. Relationship between $ v^{2} / ({gH}) $and $ \Delta T_{\max } / T_{\infty} $at different angles of air curtainΔTmaxT∞=αv2gH+β， (13) α = −0.9sin2A+0.8sinA−0.3， (14) β = −0.61sinA+1.57， (15) 式中：α、β为拟合系数.
将系数$ \alpha $和$ \beta $代入式（13）中，得到热释放速率为47.9 kW，$ {v_{{\mathrm{air}}}} $=3.5 m/s时，纵向通风与空气幕协同作用下空气幕角度对分岔隧道最大温升影响的理论模型，如式（16）所示.
ΔTmaxT∞=(−0.9sin2A+0.8sinA−0.3)v2gH−0.61sinA+1.57. (16) 如图10所示，当火源功率47.9 kW，$ {v_{{\mathrm{air}}}} $=3.5 m/s 时，不同空气幕角度下，隧道最大温升拟合得到的理论公式较好与实验结果基本一致.
图 10 不同空气幕角度下无量纲预测与实验的最大温升对比Figure 10. Comparison of dimensionless predicted and experimental maximum temperature rise at different angles of air curtain如图11所示，$ {v_{{\mathrm{air}}}} $=3.5 m/s，A=30° 条件下进行了3种不同空气幕厚度的实验，当T=0.10 m时分岔隧道降温效果最佳. 由图11可以得出，当vair=3.5 m/s，A=30° 时，在不同空气幕厚度的影响下，分叉隧道最大温升与纵向通风之间的关系如式（17）所示.
图 11 不同空气幕厚度下$ v/{(gH)^{1/2}} $与$ {{\Delta {T_{\max }}} \mathord{\left/ {\vphantom {{\Delta {T_{\max }}} {{T_\infty }}}} \right. } {{T_\infty }}} $之间的关系Figure 11. Relationship between $ v/{(gH)^{1/2}} $ and $ \Delta T_{\max } / T_{\infty} $at different angles of air curtainΔTmaxT∞=av2gH+bv√gH+c， (17) 式中：a、b、c为拟合系数，拟合的详细描述见图12.
图 12 T/H与系数a、b和c之间的关系Figure 12. Relationship between T/H and coefficients a, b, and c将系数a、b和c代入式（17）中，便可以得到热释放速率为47.9 kW时，纵向通风和空气幕协同作用下空气幕厚度对分岔隧道最大温升影响的理论模型，如式（18）所示.
ΔTmaxT∞=av2gH−bv√gH+24T2H2−13TH+2.7， (18) 式中：a = −26.88T2/H2−12T/H−0.44，b = −44.8T2/H2 +22T/H−1.3.
将不同空气幕喷射宽度下主隧道最大温升实验值与理论模型（式（18））中的预测值进行比较，如图13所示，具有较好的吻合性.
图 13 不同空气幕喷射宽度下无量纲预测与实验的最大温升对比Figure 13. Comparison of dimensionless predicted and experimental maximum temperature rise at different jet widths of air curtain4. 结 论
1） 空气幕能有效协助纵向通风降低主线隧道温度，防止烟气进入分岔隧道.
2） 当空气幕射流速度较小时（$ {v_{{\mathrm{air}}}} $=1.0 m/s），纵向风速的增加能有效防止烟气在分岔口积聚，提高空气幕对烟气的阻隔效率，降低隧道分岔点处的烟气温度.
3） 根据隧道火灾顶棚最大温升的无量纲经验相关公式，提出在固定热释放速率47.9 kW条件下，隧道最大温升与纵向通风和空气幕射流速度之间的关系，该模型的预测结果与实验结果吻合度较高.
4） 在固定热释放速率47.9 kW，空气幕射流速度3.5 m/s条件下，提出分岔隧道最大温升与纵向风速和空气幕角度之间的关系，其预测结果与实验结果吻合度较高.
5） 在固定热释放速率47.9 kW，空气幕射流速度3.5 m/s及空气幕角度30° 条件下，提出分岔隧道最大温升与纵向风速和空气幕厚度之间的关系，其预测结果与实验结果吻合度较高.
-
图 4 基于级联失效的航路网络脆弱性分析流程
Figure 4. Vulnerability analysis process of en-route network based on cascading failure
表 1 航路网络节点度分布情况
Table 1. Distribution of node degree of en-route network
度数 节点数/个 比例/% 1 24 7.0 2 151 44.0 3 67 19.5 4 65 19.0 5 16 4.7 6 13 3.8 7 3 0.9 8 1 0.3 9 2 0.6 10 1 0.3 
下载: 导出CSV
-
[1] 程光权,陆永中,张明星,等. 复杂网络节点重要度评估及网络脆弱性分析[J]. 国防科技大学学报,2017,39(1): 120-127.CHENG Guangquan, LU Yongzhong, ZHANG Mingxing, et al. Node importance evaluation and network vulnerability analysis on complex network[J]. Journal of National University of Defense Technology, 2017, 39(1): 120-127. [2] HU Y Q, ZHOU D, ZHANG R, et al. Percolation of interdependent networks with intersimilarity[J]. Physical Review E, 2013, 88(5): 052805.1-052805.7. [3] WANG J W, SUN E H, XU B, et al. Abnormal cascading failure spreading on complex networks[J]. Chaos, Solitons & Fractals, 2016, 91: 695-701. [4] KIM M, KIM J S. A model for cascading failures with the probability of failure described as a logistic function[J]. Scientific Reports, 2022, 12: 989-998. doi: 10.1038/s41598-021-04753-z [5] 徐伟举. 基于复杂网络的美国航空线路网络的抗毁性研究[D]. 成都:西南交通大学,2013. [6] 王兴隆,贺敏,刘明学. 空中交通CPS级联失效与缓解策略[J]. 北京航空航天大学学报,2021,47(12): 2426-2433.WANG Xinglong, HE Min, LIU Mingxue. Air traffic CPS cascading failure and mitigation strategy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(12): 2426-2433. [7] 汪凯强,王布宏,曾乐雅,等. 不同负载条件下的航空网络抗毁性研究[J]. 电光与控制,2022,29(7): 86-90.WANG Kaiqiang, WANG Buhong, ZENG Leya, et al. Survivability of airline network under different load models[J]. Electronics Optics & Control, 2022, 29(7): 86-90. [8] MIRZASOLEIMAN B, BABAEI M, JALILI M, et al. Cascaded failures in weighted networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84: 046114.1-046114.8. [9] CUMELLES J, LORDAN O, SALLAN J M. Cascading failures in airport networks[J]. Journal of Air Transport Management, 2021, 92: 102026.1-102026.10. [10] 齐雁楠,高经东. 空域扇区网络级联失效抗毁性及优化策略[J]. 航空学报,2018,39(12): 349-357.QI Yannan, GAO Jingdong. Cascading failure invulnerability and optimization strategy of airspace sector network[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 349-357. [11] 王兴隆,刘明学,高经东. 基于复杂网络的空域扇区网络建模与抗毁性研究[J]. 武汉理工大学学报,2018,40(11): 50-55.WANG Xinglong, LIU Mingxue, GAO Jingdong. Research on modeling analysis and invulnerability of sector network based on complex network[J]. Journal of Wuhan University of Technology, 2018, 40(11): 50-55. [12] 王兴隆,潘维煌,赵末. 华北航空相依网络统计特征与鲁棒性分析[J]. 科学技术与工程,2018,18(13): 180-185.WANG Xinglong, PAN Weihuang, ZHAO Mo. Analysis of network characteristics and robustness of aeronautical interdependent network in North China[J]. Science Technology and Engineering, 2018, 18(13): 180-185. [13] 王兴隆,潘维煌. 航空相依网络的弹性测度与分析[J]. 计算机仿真,2019,36(11): 40-43,58.WANG Xinglong, PAN Weihuang. The resilience measurement and analysis of aeronautical interdependent network[J]. Computer Simulation, 2019, 36(11): 40-43,58. [14] 王兴隆,潘维煌,赵末. 航空相依网络故障传播机理研究[J]. 武汉理工大学学报,2018,40(6): 41-46.WANG Xinglong, PAN Weihuang, ZHAO Mo. Research on fault propagation mechanism of aviation interdependent network[J]. Journal of Wuhan University of Technology, 2018, 40(6): 41-46. [15] ZHANG J, ZHANG Z H. A review of the research methods on vulnerability of transportation system[C]// CICTP 2019. Nanjing: American Society of Civil Engineers, 2019: 4294-4305. [16] GUZE S. Graph theory approach to the vulnerability of transportation networks[J]. Algorithms, 2019, 12(12): 270.1-270.12. [17] 王兴隆,潘维煌,赵末. 空中交通相依网络的脆弱性研究[J]. 航空学报,2018,39(12): 268-277.WANG Xinglong, PAN Weihuang, ZHAO Mo. Vulnerability of air traffic interdependent network[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 268-277. [18] 周子丰. 基于复杂网络理论的民航陆基空管保障系统脆弱性分析[D]. 广汉:中国民用航空飞行学院,2018. [19] WILKINSON S M, DUNN S, MA S. The vulnerability of the European air traffic network to spatial hazards[J]. Natural Hazards, 2012, 60(3): 1027-1036. doi: 10.1007/s11069-011-9885-6 [20] 李航,胡小兵. 一种改进的民用航空网络空间脆弱性模型[J]. 交通运输系统工程与信息,2018,18(4): 202-208.LI Hang, HU Xiaobing. An improved spatial vulnerability model for civil aviation network[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(4): 202-208. [21] JANIĆ M. Modelling the resilience, friability and costs of an air transport network affected by a large-scale disruptive event[J]. Transportation Research Part A: Policy and Practice, 2015, 71: 1-16. doi: 10.1016/j.tra.2014.10.023 [22] VOLTES-DORTA A, RODRÍGUEZ-DÉNIZ H, SUAU-SANCHEZ P. Vulnerability of the European air transport network to major airport closures from the perspective of passenger delays: ranking the most critical airports[J]. Transportation Research Part A: Policy and Practice, 2017, 96: 119-145. doi: 10.1016/j.tra.2016.12.009 [23] LORDAN O, KLOPHAUS R. Measuring the vulnerability of global airline alliances to member exits[J]. Transportation Research Procedia, 2017, 25: 7-16. doi: 10.1016/j.trpro.2017.05.189 [24] Roy S, Xue M, Sridhar B. Vulnerability metrics for the airspace system[C]//Twelfth USA/Europe Air Traffic Management Research and Development Seminar (ATM2017). Seattle: Curran Associates, 2017: 1-26. [25] TAMIMI A, HAHN A, ROY S. Cyber threat impact analysis to air traffic flows through dynamic queue networks[J]. ACM Transactions on Cyber-Physical Systems, 2020, 4(3): 1-22. [26] 田文,方琴,周雪芳,宋津津. 航路网络关键节点识别方法研究[J]. 西南交通大学学报,2025,60(1): 233-242.TIAN Wen, ZHOU Xuefang, FANG Qin, et al. Research on identification method of key nodes in en-route network[J]. Journal of Southwest Jiaotong University,2025,60(1): 233-242. [27] 种鹏云. 基于复杂网络的危险品运输网络拓扑特性、级联失效机制及抗毁性研究[D]. 成都:西南交通大学,2015. [28] 欧阳敏,费奇,余明辉,等. 复杂网络的功效性与脆弱性研究综述[J]. 计算机科学,2008,35(6): 1-4.OUYANG Min, FEI Qi, YU Minghui, et al. Survey on efficiency and vulnerability of complex network[J]. Computer Science, 2008, 35(6): 1-4. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 161
- HTML全文浏览量: 57
- PDF下载量: 20
- 被引次数: 0