Vortex-Induced Vibration Response of Bridges Considering Both Spanwise Variation of Vibration Amplitude and Correlation of Aerodynamic Forces
-
摘要:
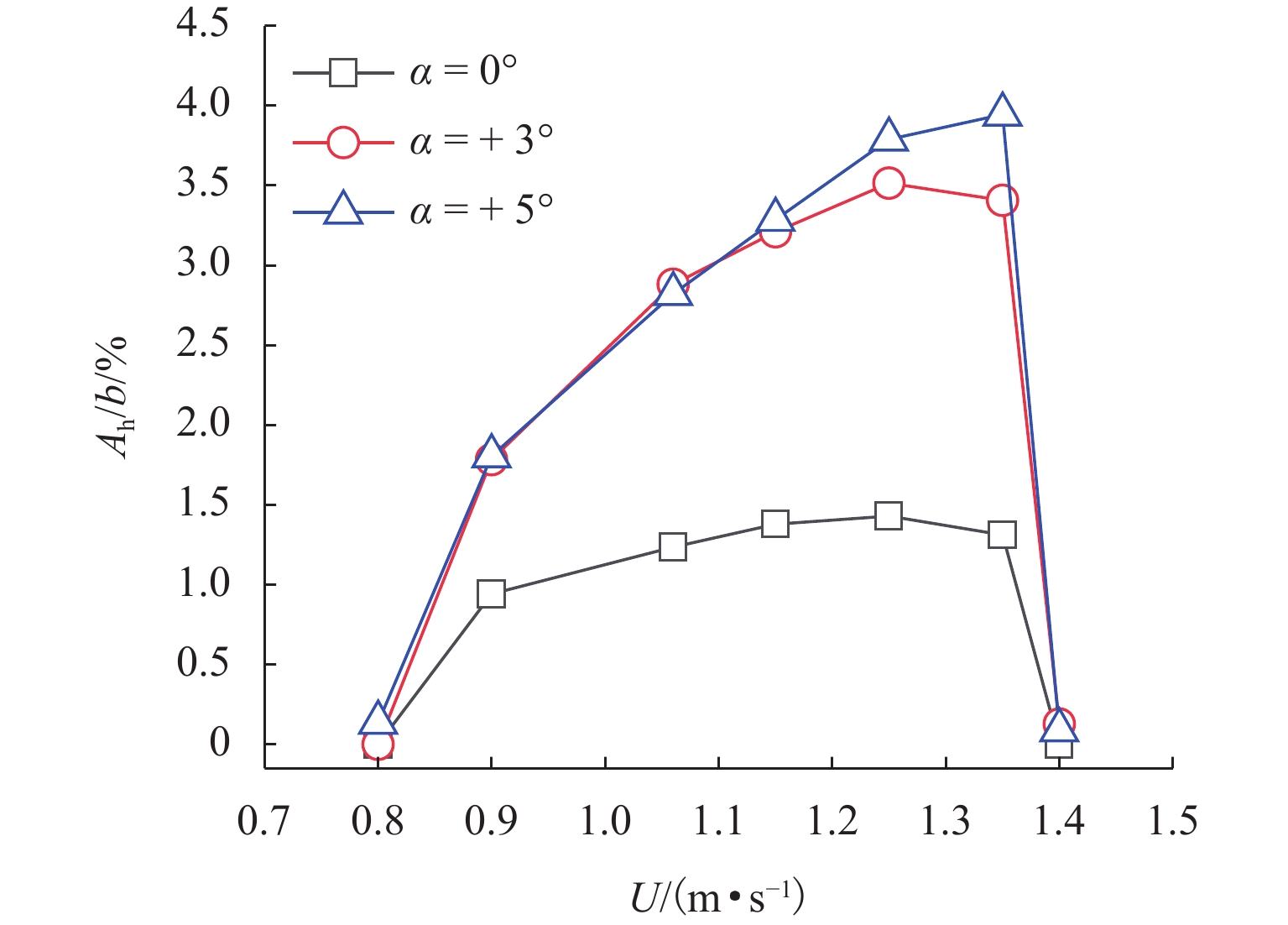
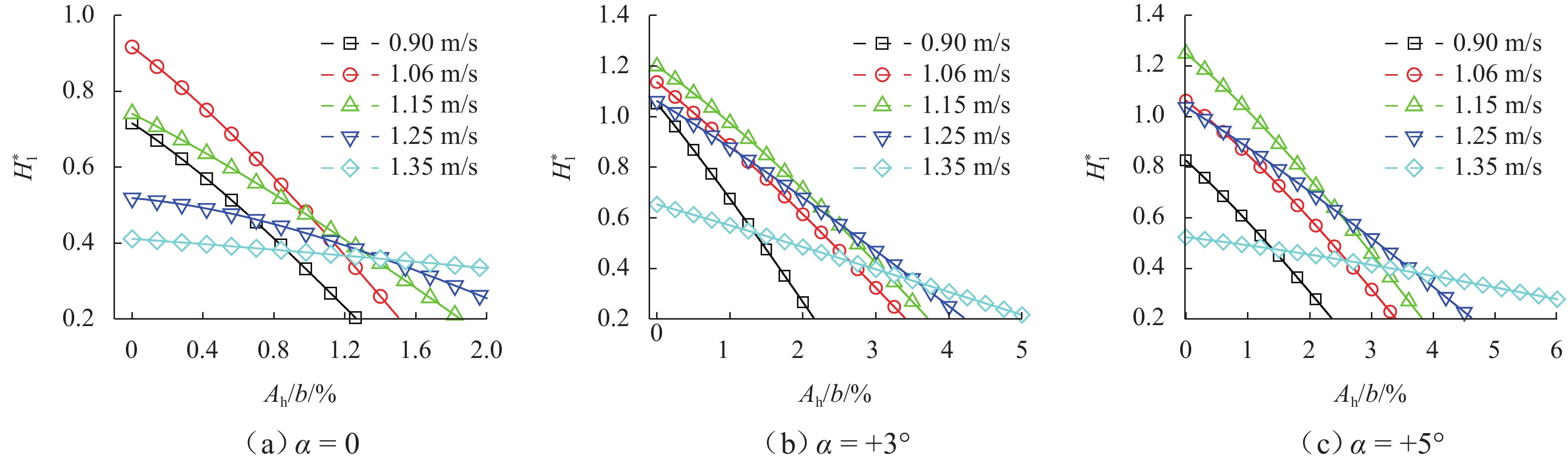
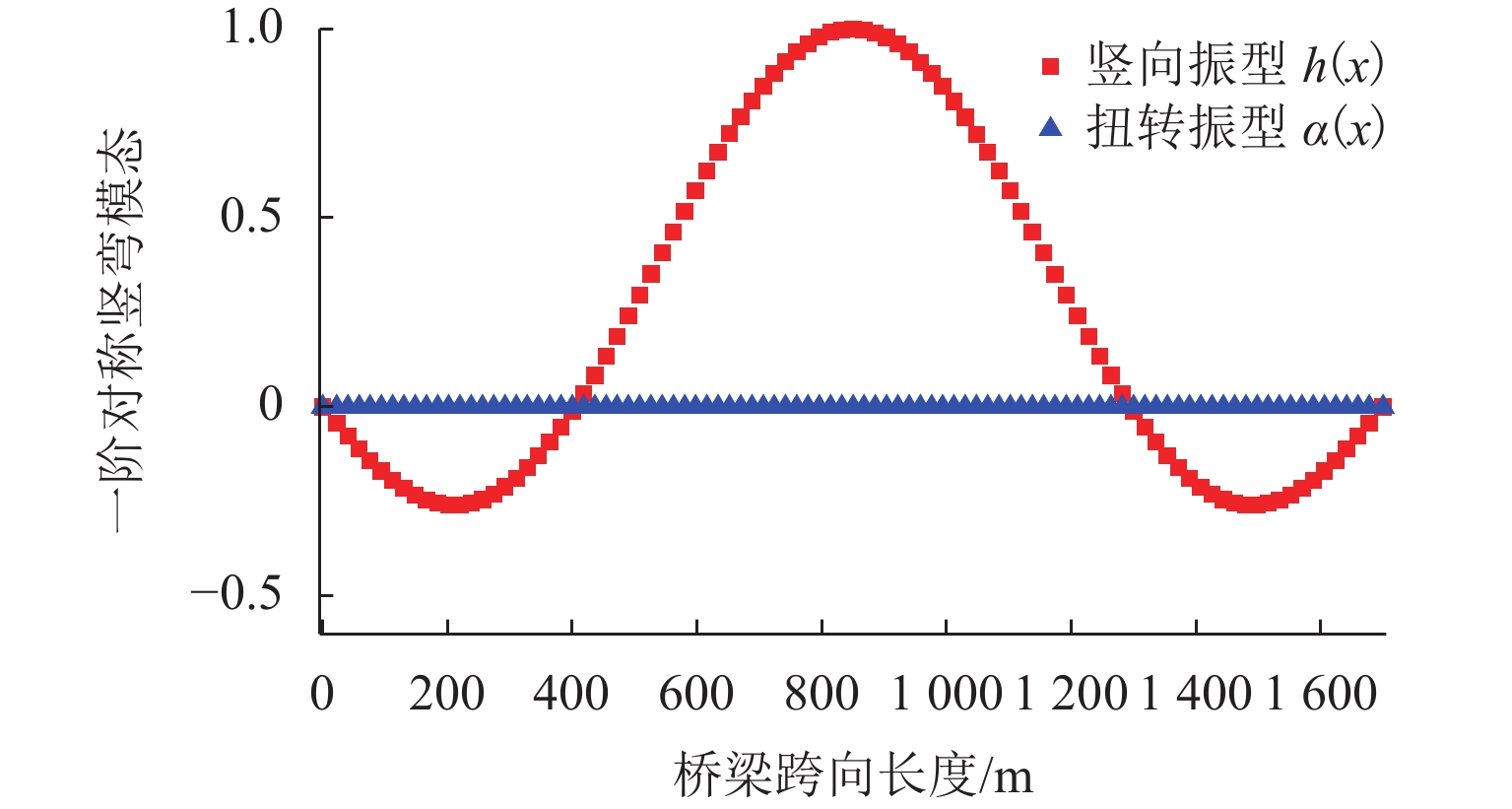
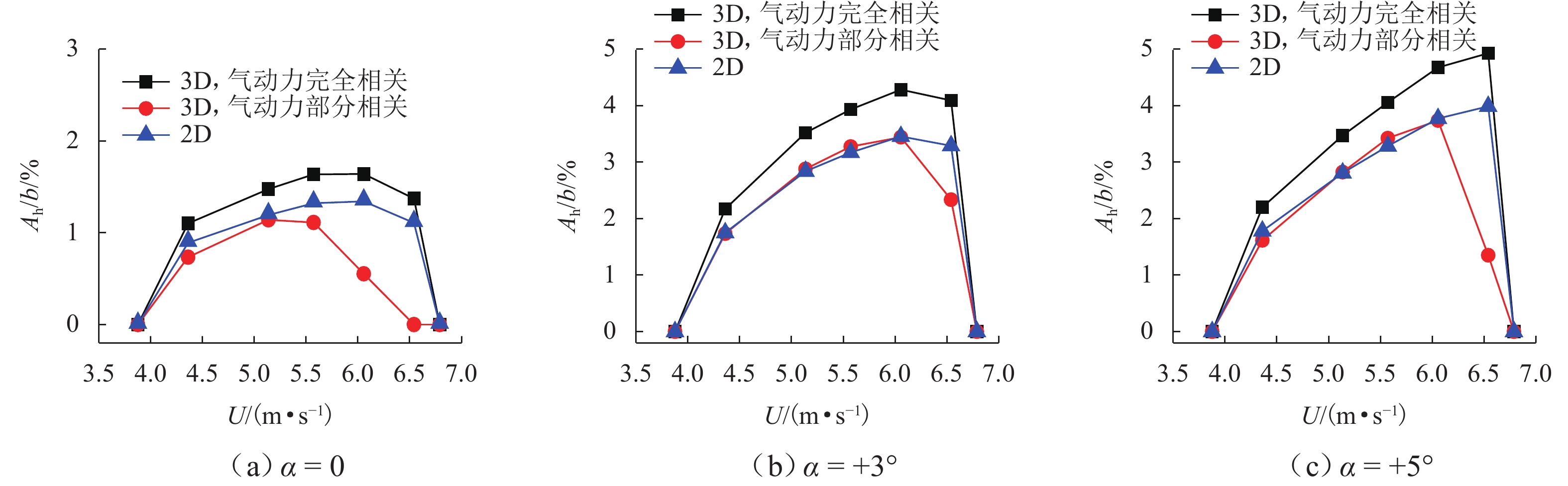
为研究非线性气动力跨向振幅依存性和跨向相关性对桥梁涡振响应的影响，首先，引入由振幅多项式表达的桥梁非线性气动力模型；其次，在二维涡振分析方法的基础上，通过理论分析提出同时考虑气动力的跨向振幅依存性和跨向相关性的三维涡振振幅响应分析方法；最后，以主跨1700 m的大跨度悬索桥为例，通过风洞实验识别其主梁在不同风攻角下的竖向涡振非线性气动力参数，进而分析不同风攻角下一阶正对称竖弯模态下的涡振振幅响应. 研究结果表明：当气动力沿跨向完全相关时，在气动力跨向振幅依存性的影响下，三维分析方法得到的各风速涡振响应明显大于二维分析，约大19%；当气动力沿跨向不完全相关时，三维分析的涡振振幅响应比不考虑相关性时降低明显，其中大部分风速下的降低范围在16%～30%，个别风速下约降低70%；证明了考虑气动力跨向不完全相关性和跨向振幅依存性对准确预测大跨度桥梁涡振响应的重要性;本文提出的分析方法对于扭转涡振及高阶模态下涡振分析同样适用.
Abstract:This paper aims to study the effect of spanwise variation of vibration amplitude and spanwise correlation of the nonlinear aerodynamic forces on the vortex-induced vibration (VIV) response of bridges. Firstly, a nonlinear aerodynamic force model of the bridge represented by polynomial functions of vibration amplitude was introduced. Secondly, on the basis of the two-dimensional VIV (2D VIV) analysis method, an approach for predicting the three-dimensional VIV (3D VIV) amplitude response with consideration of both spanwise variation of vibration amplitude and spanwise correlation of aerodynamic forces was proposed through theoretical analysis. Finally, by taking a 1 700 m long-span suspension bridge as an example, the nonlinear aerodynamic force parameters of vertical VIV of the bridge girder at different angles of wind attack were extracted through a wind tunnel test. Then, the VIV amplitude response of the suspension bridge under a first-order positive symmetrical vertical mode at different angles of wind attack was analyzed. The results prove that when the aerodynamic forces are assumed to be fully correlated along the span, the 3D analysis under different wind speeds leads to a significantly higher VIV amplitude response (about 19%) as compared with the 2D analysis method due to the effect of spanwise variation of vibration amplitude of the aerodynamic forces. However, when the aerodynamic forces are assumed to be partially correlated along the span, the VIV amplitude response by 3D analysis is reduced significantly, and the reduction range is about 16%–30% under most wind speeds and about 70% under certain wind speeds. It is proved that it is important to accurately predict the VIV amplitude response of long-span bridges by considering the spanwise variation of vibration amplitude and spanwise partial correlation of aerodynamic forces. The approach proposed in this paper is also applicable to the analysis of torsional VIV or VIV at higher-order modes.
-
图 4 竖弯涡振位移时程响应（$ \alpha = $ + 3°, U = 1.15 m/s）
Figure 4. Time history of displacement for vertical VIV （$ \alpha = $ + 3°, U = 1.15 m/s）
图 5 不同涡振风速下非线性气动导数$ {H}_{1}^{*} $随振幅的变化
Figure 5. Variation of nonlinear aerodynamic derivative $ {H}_{1}^{*} $ with amplitude at different VIV wind speeds
图 6 悬索桥一阶正对称竖弯模态
Figure 6. First-order positive symmetrical vertical mode of suspension bridge
图 7 考虑气动力跨向不完全相关性时的折减因子$ {\mathrm{\lambda }}_{{H}_{1}^{\mathrm{*}}} $
Figure 7. Reduction factor $ {\mathrm{\lambda }}_{{H}_{1}^{\mathrm{*}}} $ with consideration of spanwise partial correlation of aerodynamic forces
图 8 考虑气动力跨向不完全相关性时悬索桥非线性气动阻尼比$ {\xi }_{ha} $
Figure 8. Nonlinear aerodynamic damping ratio $ {\xi }_{ha} $ of suspension bridge with consideration of spanwise partial correlation of aerodynamic forces
-
[1] 李加武,方成,侯利明,等. 大跨径桥梁静风稳定参数的敏感性分析[J]. 振动与冲击,2014,33(4): 124-130.LI Jiawu, FANG Cheng, HOU Liming, et al. Sensitivity analysis for aerostatic stability parameter of a long-span bridge[J]. Journal of Vibration and Shock, 2014, 33(4): 124-130. [2] WU B, CHEN X Z, WANG Q, et al. Characterization of vibration amplitude of nonlinear bridge flutter from section model test to full bridge estimation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 197: 104048.1-104048.14. doi: 10.1016/j.jweia.2019.104048 [3] 朱金,黄旭,熊籽跞,等. 大跨度悬索桥竖弯涡振条件下驾驶员行车视线研究[J]. 西南交通大学学报,2023,58(1): 191-201.ZHU Jin, HUANG Xu, XIONG Ziluo, et al. Study on driver’s sight line under vertical vortex-induced vibration of long span suspension bridges[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 191-201. [4] CHEN X Z. Estimation of stochastic crosswind response of wind-excited tall buildings with nonlinear aerodynamic damping[J]. Engineering Structures, 2013, 56: 766-778. doi: 10.1016/j.engstruct.2013.05.044 [5] WANG Y F, CHEN X Z, LI Y L. Nonlinear self-excited forces and aerodynamic damping associated with vortex-induced vibration and flutter of long span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 204: 104207.1-104207.21. [6] 李永乐,侯光阳,向活跃,等. 大跨度悬索桥钢箱主梁涡振性能优化风洞试验研究[J]. 空气动力学学报,2011,29(6): 702-708. doi: 10.3969/j.issn.0258-1825.2011.06.004LI Yongle, HOU Guangyang, XIANG Huoyue, et al. Optimization of the vortex induced vibration for steel box girder of long span suspension bridges by wind tunnel test[J]. Acta Aerodynamica Sinica, 2011, 29(6): 702-708. doi: 10.3969/j.issn.0258-1825.2011.06.004 [7] 马存明,王俊鑫,罗楠,等. 宽幅分体箱梁涡振性能及其抑振措施[J]. 西南交通大学学报,2019,54(4): 724-730.MA Cunming, WANG Junxin, LUO Nan, et al. Vortex-induced vibration performance and control measures of wide twin-box girder[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 724-730. [8] 张天翼,孙延国,李明水,等. 宽幅双箱叠合梁涡振性能及抑振措施试验研究[J]. 中国公路学报,2019,32(10): 107-114,168.ZHANG Tianyi, SUN Yanguo, LI Mingshui, et al. Experimental study on vortex-induced vibration performance and aerodynamic countermeasures for a wide-width double-box composite beam[J]. China Journal of Highway and Transport, 2019, 32(10): 107-114,168. [9] 李明,孙延国,李明水,等. 宽幅流线型箱梁涡振性能及制振措施研究[J]. 西南交通大学学报,2018,53(4): 712-719.LI Ming, SUN Yanguo, LI Mingshui, et al. Vortex-induced vibration performance of wide streamlined box girder and aerodynamic countermeasure research[J]. Journal of Southwest Jiaotong University, 2018, 53(4): 712-719. [10] 葛耀君,赵林,许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报,2019,32(10): 1-18.GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 1-18. [11] EHSAN F, SCANLAN R H. Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics, 1990, 116(6): 1392-1411. doi: 10.1061/(ASCE)0733-9399(1990)116:6(1392) [12] LARSEN A. A generalized model for assessment of vortex-induced vibrations of flexible structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 281-294. [13] ZHU L D, MENG X L, GUO Z S. Nonlinear mathematical model of vortex-induced vertical force on a flat closed-box bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122: 69-82. doi: 10.1016/j.jweia.2013.07.008 [14] SUN Y G, LI M S, LIAO H L. Nonlinear approach of vortex-induced vibration for line-like structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 124: 1-6. doi: 10.1016/j.jweia.2013.10.011 [15] LI M S, LI S P, LIAO H L, et al. Spanwise correlation of aerodynamic forces on oscillating rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 154: 47-57. doi: 10.1016/j.jweia.2016.04.003 [16] ZHOU S, HUA X G, CHEN Z Q, et al. Experimental investigation of correction factor for VIV amplitude of flexible bridges from an aeroelastic model and its 1∶1 section model[J]. Engineering Structures, 2017, 141: 263-271. doi: 10.1016/j.engstruct.2017.03.023 [17] SCANLAN R H. The action of flexible bridges under wind, I: Flutter theory[J]. Journal of Sound and Vibration, 1978, 60(2): 187-199. doi: 10.1016/S0022-460X(78)80028-5 [18] MASHNAD M, JONES N P. A model for vortex-induced vibration analysis of long-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134: 96-108. doi: 10.1016/j.jweia.2014.09.002 [19] SIMIU E, SCANLAN R. Wind effects on structures: an introduction to wind engineering[M]. New York: John Wiley, 1986. -
下载:
点击查看大图
计量
- 文章访问数: 64
- HTML全文浏览量: 21
- PDF下载量: 14
- 被引次数: 0