Influence of Nose Rail Reconstruction Profile Parameters Based on B-Spline Curve
-
摘要:
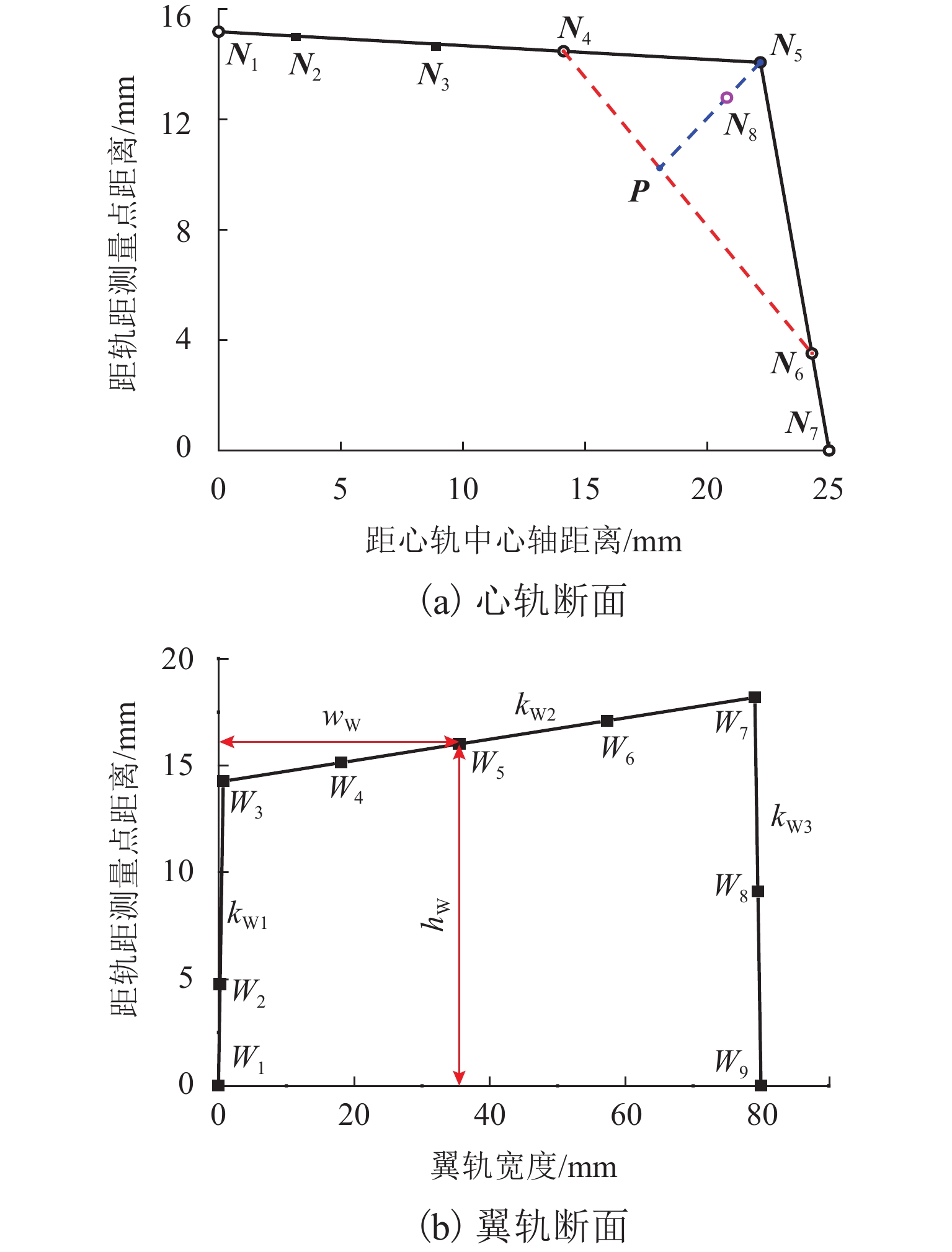
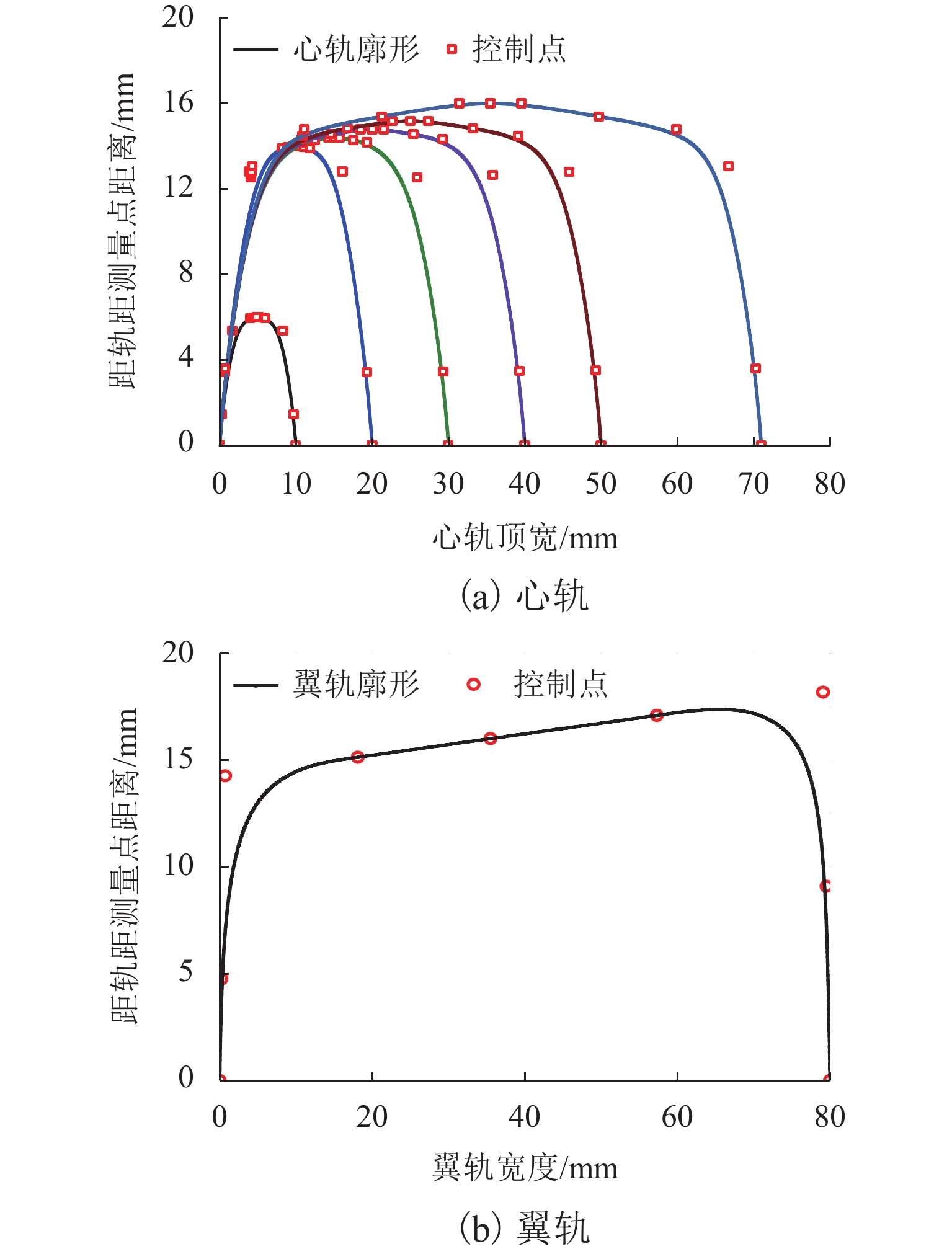
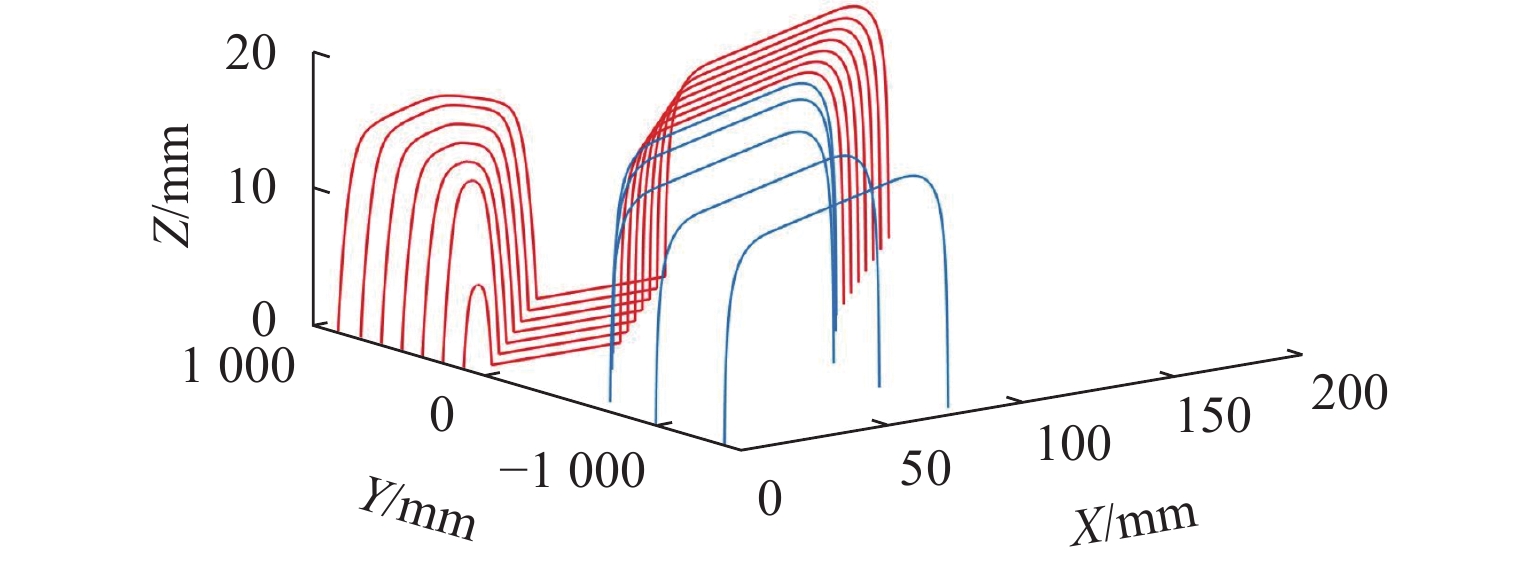
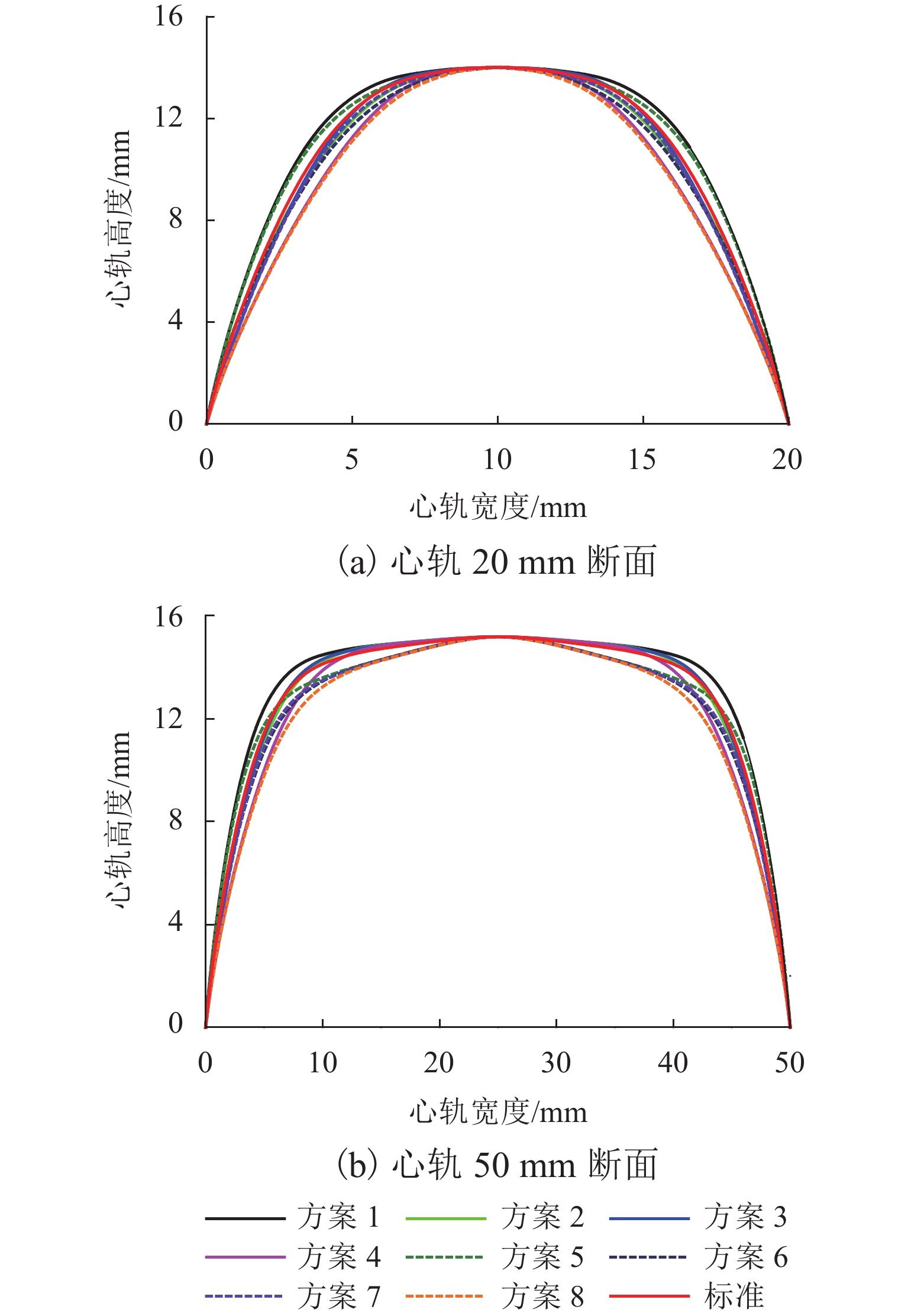
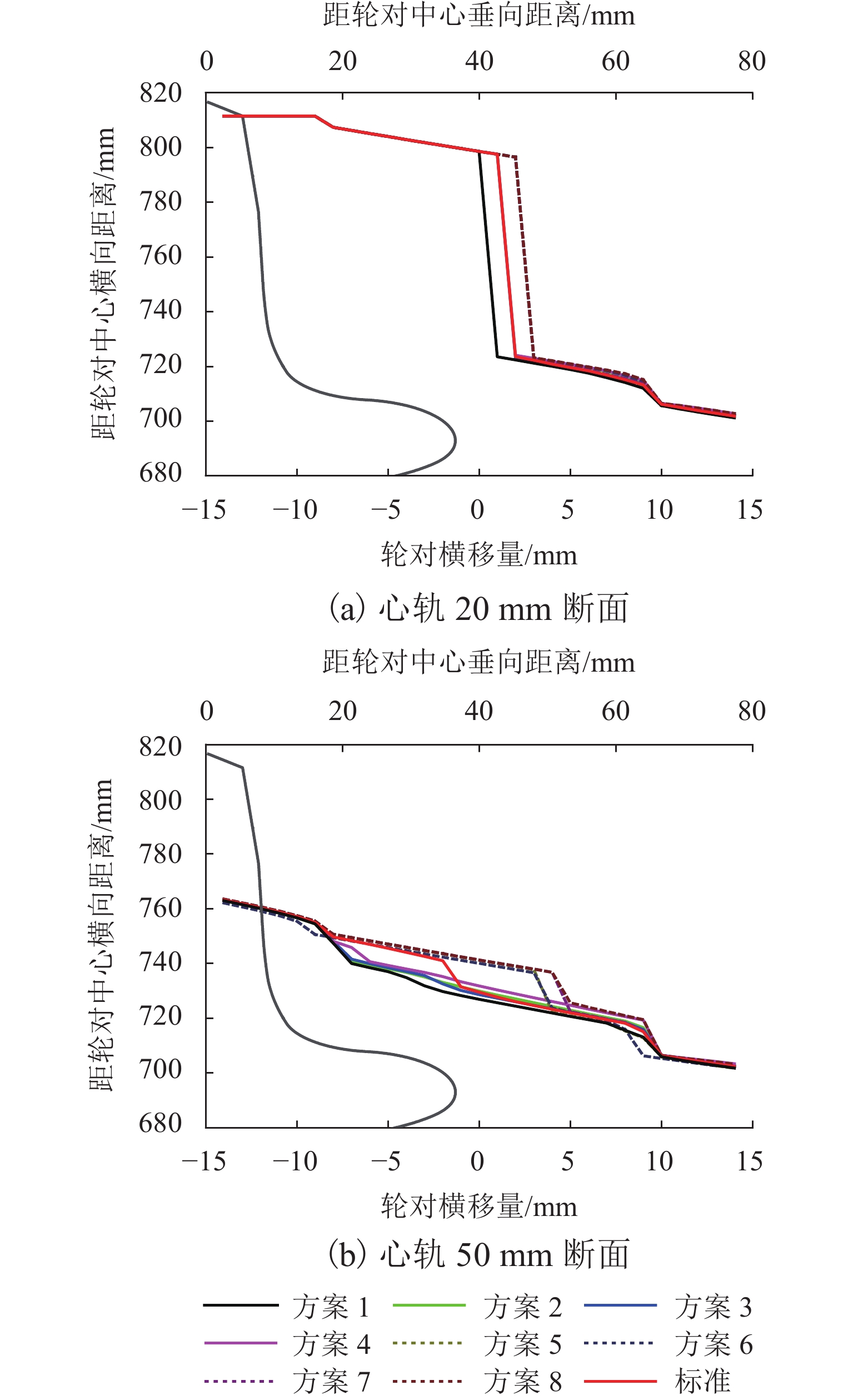
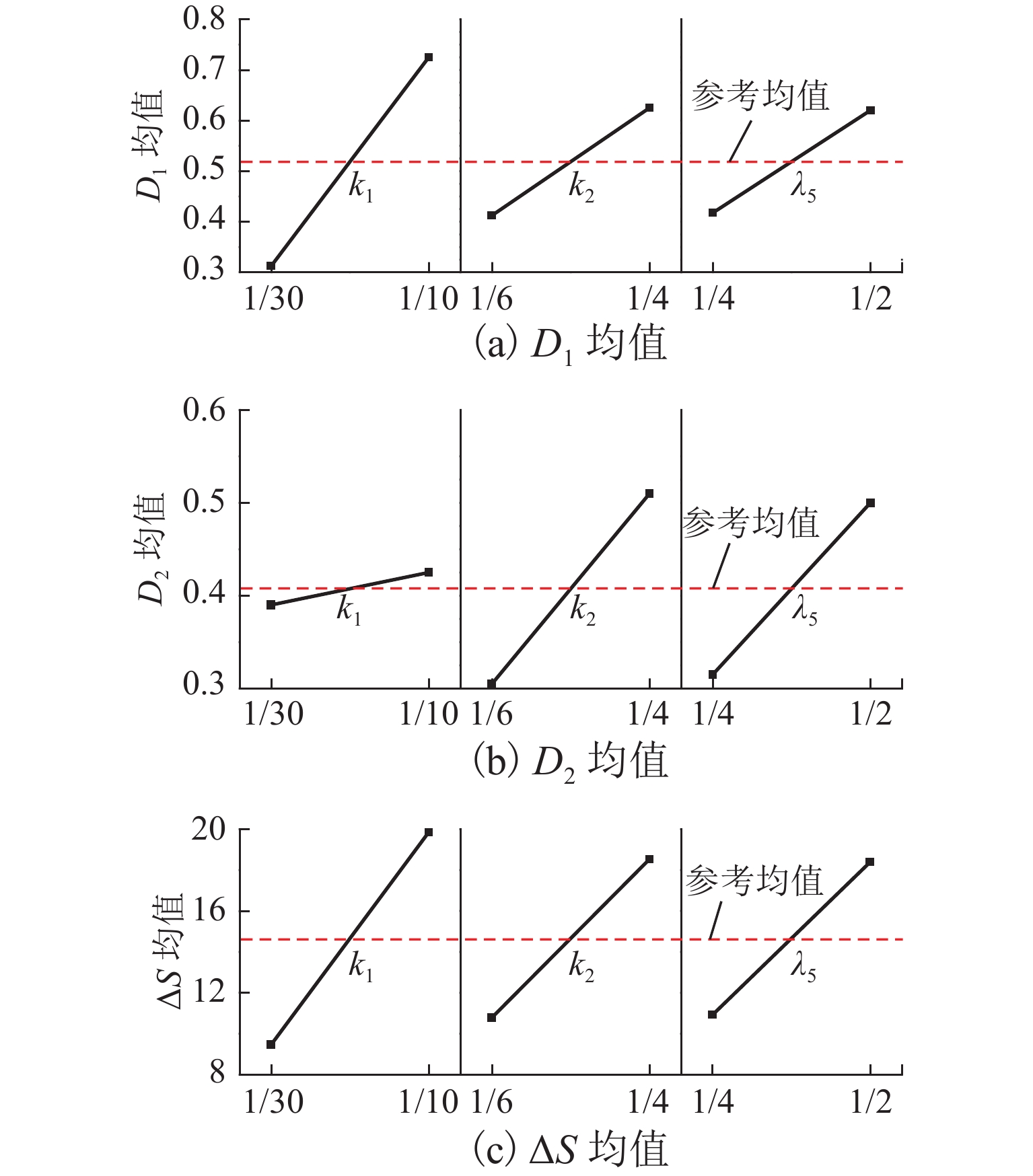
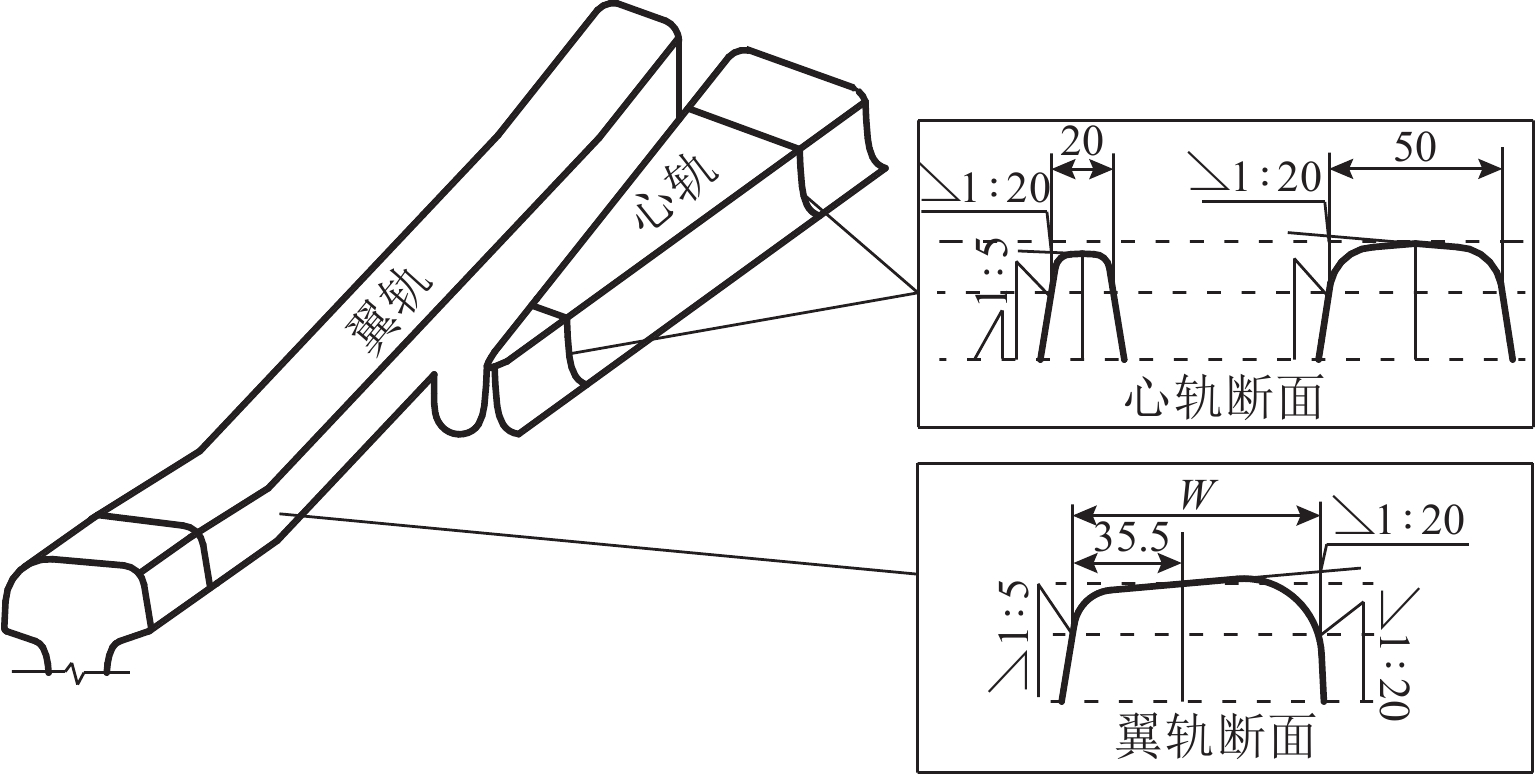
针对固定辙叉钢轨廓形不规则变化特点，基于B样条理论提出一种考虑固定辙叉钢轨断面廓形特征的参数化设计方法，并提出拟合钢轨廓形贴合度评价指标和关键控制参数对廓形贴合度影响权重指标；以60 kg/m钢轨12号固定辙叉为例，采用DOE （design of experiments）方法分析轨顶横坡、侧面纵坡和复合圆弧段比例系数对心轨轨头整体廓形、轨顶面廓形和侧面廓形的影响. 结果表明：1） 在心轨20 mm断面，轨顶横坡、侧面纵坡和复合圆弧段比例系数对心轨整体廓形变化的影响权重分别为21.08%、56.89%和22.02%，对心轨顶面廓形变化影响权重分别为8.42%、61.95%、29.63%；在心轨50 mm断面，各关键控制参数对心轨轨头整体廓形变化影响权重分别为55.9%、33.38%、10.72%；侧面纵坡对心轨20 mm和50 mm断面的侧面廓形变化影响权重分别为76.82%、66.04%. 2） 当心轨轨头宽度为20 mm时，侧面纵坡对各部分廓形变化影响均达到50%以上；随着心轨轨头宽度的增大，心轨轨顶横坡对整体廓形变化影响权重由21.8%增至55.9%，侧面纵坡和复合圆弧段比例系数影响权重则分别减小41.3%和51.3%.
Abstract:According to irregular changes in rail profiles in a fixed-nose crossing, a parametric design method was proposed based on the B-spline theory by considering the section characteristics of rail profiles in a fixed-nose crossing. In addition, the rail profile fitting evaluation indexes and the influence weights of key control parameters on the rail profile fitting were proposed. With No.12 turnout of fixed-nose crossing of 60 kg/m rail as an example, the design of experiment (DOE) was employed to analyze the influence of railhead slope, rail side slope, and proportion coefficient of composite circular arc on the changes in the full railhead profile, rail top profile, and rail side profile of the nose rail. The results show that 1) for nose rail with a section of 20 mm, the influence weights of railhead slope, rail side slope, and proportion coefficient of composite circular arc on the full railhead profile change are 21.08%, 56.89%, and 22.02%, respectively, and the influence weights on the rail top profile change of the nose rail are 8.42%, 61.95%, and 29.63%, respectively. For nose rail with a section of 50 mm, the influence weights of the key control parameters on the full railhead profile change are 55.9%, 33.38%, and 10.72%, respectively. For nose rails with a section of 20 mm and 50 mm, the influence weights of the rail side slope on the rail side profile change are 76.82% and 66.04%, respectively. 2) When the nose railhead width is 20 mm, the influence of the rail side slope on the nose profiles is more than 50%. As the nose railhead width increases, the influence weight of railhead slope on full railhead profile gradually increases from 21.8% to 55.9%, while that of rail side profile and proportion coefficient of composite circular arc is reduced by 41.3% and 51.3%, respectively.
-
Key words:
- turnout /
- fixed-nose crossing /
- B-spline curve /
- rail profile /
- parametric design /
- design of experiments
-
图 6 心轨关键断面车轮踏面接触点变化规律
Figure 6. Contact point variations on wheel tread for key nose rail sections
表 1 DOE全阶乘方案设计
Table 1. DOE full factorial scheme design
方案 k1 k2 λ5 方案 1 1/30 1/6 1/4 方案 2 1/30 1/6 1/2 方案 3 1/30 1/4 1/4 方案 4 1/30 1/4 1/2 方案 5 1/10 1/6 1/4 方案 6 1/10 1/6 1/2 方案 7 1/10 1/4 1/4 方案 8 1/10 1/4 1/2 标准 1/20 1/5 1/3 
下载: 导出CSV
-
[1] 高原,王平,陈嵘,等. 重载铁路固定辙叉区轮轨瞬态滚动接触行为分析[J]. 铁道学报,2020,42(6): 35-43.GAO Yuan, WANG Ping, CHEN Rong, et al. Analysis of 3D transient wheel-rail rolling contact behavior for fixed frog in heavy haul railways[J]. Journal of the China Railway Society, 2020, 42(6): 35-43. [2] 杨新文,张昭,孟玮,等. 道岔区固定辙叉心轨垂磨对轮轨动态接触的影响[J]. 同济大学学报(自然科学版),2020,48(11): 1595-1604.YANG Xinwen, ZHANG Zhao, MENG Wei, et al. Effect of vertical wear of unmovable frog nose rail on dynamical wheel-rail contact in turnout zone[J]. Journal of Tongji University (Natural Science), 2020, 48(11): 1595-1604. [3] MA Y W, MASHAL A A, MARKINE V L. Modelling and experimental validation of dynamic impact in 1: 9 railway crossing panel[J]. Tribology International, 2018, 118: 208-226. doi: 10.1016/j.triboint.2017.09.036 [4] WIEDORN J, DAVES W, OSSBERGER U, et al. Simplified explicit finite element model for the impact of a wheel on a crossing-Validation and parameter study[J]. Tribology International, 2017, 111: 254-264. doi: 10.1016/j.triboint.2017.03.023 [5] SKRYPNYK R, NIELSEN J C O, EKH M, et al. Metamodelling of wheel-rail normal contact in railway crossings with elasto-plastic material behaviour[J]. Engineering With Computers, 2019, 35(1): 139-155. doi: 10.1007/s00366-018-0589-3 [6] 于淼,张军,鹿广清,等. 重载货车作用下固定辙叉心轨磨耗分析[J]. 铁道学报,2014,36(7): 30-35.YU Miao, ZHANG Jun, LU Guangqing, et al. Analysis on wear of unmovable frog nose rail under the action of heavy-haul freight car[J]. Journal of the China Railway Society, 2014, 36(7): 30-35. [7] 王树国,葛晶,司道林,等. 固定辙叉查照间隔及心轨加宽研究[J]. 中国铁道科学,2014,35(1): 7-12.WANG Shuguo, GE Jing, SI Daolin, et al. Study on guard check gauge of fixed frog and design on widening nose rail[J]. China Railway Science, 2014, 35(1): 7-12. [8] 徐井芒,王平. 基于轮轨廓型的固定辙叉优化设计方法[J]. 中国铁道科学,2014,35(2): 1-6.XU Jingmang, WANG Ping. Optimization design method for rigid frog based on wheel/rail profile type[J]. China Railway Science, 2014, 35(2): 1-6. [9] 徐井芒,郑兆光,赖军,等. 轨道参数对高速道岔轮轨接触行为的影响[J]. 西南交通大学学报,2022,57(5): 990-999.XU Jingmang, ZHENG Zhaoguang, LAI Jun, et al. Influence of track parameters on wheel/rail contact behavior of high-speed turnout[J]. Journal of Southwest Jiaotong University, 2022, 57(5): 990-999. [10] 曹洋,王平. 固定辙叉心轨轨顶降低值优化[J]. 西南交通大学学报,2015,50(6): 1067-1073.CAO Yang, WANG Ping. Optimization of nose depth for rigid frog[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1067-1073. [11] 沈钢,汪徐江. 固定辙叉区心轨轨顶降低值优化设计方法[J]. 同济大学学报(自然科学版),2020,48(11): 1605-1611.SHEN Gang, WANG Xujiang. An optimization method for height of nose rail at turnout crossing[J]. Journal of Tongji University (Natural Science), 2020, 48(11): 1605-1611. [12] 张鹏飞,朱旭东,雷晓燕. 提速道岔辙叉翼轨的加高值方案优化[J]. 西南交通大学学报,2021,56(3): 602-610.ZHANG Pengfei, ZHU Xudong, LEI Xiaoyan. Optimization of wing rail lifting value for rigid frog of speed-up turnout[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 602-610. [13] WAN C, MARKINE V L, SHEVTSOV I Y. Improvement of vehicle−turnout interaction by optimising the shape of crossing nose[J]. Vehicle System Dynamics, 2014, 52(11): 1517-1540. doi: 10.1080/00423114.2014.944870 [14] WAN C, MARKINE V L, SHEVTSOV I. Optimisation of the elastic track properties of turnout crossings[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail and Rapid Transit, 2016, 230(2): 360-373. doi: 10.1177/0954409714542478 [15] 铁道部第三设计院. 道岔设计手册[M]. 北京: 人民铁道出版社, 1975: 413-503. [16] 韩江,江本赤,夏链,等. 基于轮廓关键点的B样条曲线拟合算法[J]. 应用数学和力学,2015,36(4): 423-431.HAN Jiang, JIANG Benchi, XIA Lian, et al. A B-spline curve fitting algorithm based on contour key points[J]. Applied Mathematics and Mechanics, 2015, 36(4): 423-431. [17] YANG Y, QIU W S, ZENG W, et al. A prediction method of rail grinding profile using non-uniform rational B-spline curves and Kriging model[J]. Journal of Central South University, 2018, 25(1): 230-240. doi: 10.1007/s11771-018-3732-9 [18] 温士明. 地铁线路小半径曲线钢轨打磨廓形研究[D]. 成都: 西南交通大学, 2018: 11-25. [19] 刘建桥. 地铁曲线轨道钢轨廓型优化研究[D]. 成都: 西南交通大学, 2019: 24-29. [20] 唐彦玲,吴磊,董勇,等. 重载铁路曲线钢轨廓形多目标优化设计[J]. 机械,2020,47(12): 1-9.TANG Yanling, WU Lei, DONG Yong, et al. Multi-objective optimization design of rail profiles on curve tracks of heavy haul railway[J]. Machinery, 2020, 47(12): 1-9. [21] 王亮,向伟彬,刘宏达,等. 小半径曲线钢轨非对称打磨目标型面优化[J]. 机械科学与技术,2021,40(6): 949-954.WANG Liang, XIANG Weibin, LIU Hongda, et al. Target profile optimization of asymmetrical grinding for rail with sharp-radius curve[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(6): 949-954. [22] 林凤涛,吴涛,杨洋,等. 高速铁路辙叉区钢轨打磨廓形设计方法[J]. 交通运输工程学报,2021,21(6): 124-135.LIN Fengtao, WU Tao, YANG Yang, et al. Design method of rail grinding profile in frog area of high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2021, 21(6): 124-135. [23] 史振帅. 基于NURBS曲面拟合的道岔打磨廓形研究[D]. 南昌: 华东交通大学, 2021: 22-27. [24] 陈雨,安博洋,潘自立,等. 考虑尖轨变截面廓形的轮轨接触与磨耗分析[J]. 西南交通大学学报,2022,57(6): 1250-1258.CHEN Yu, AN Boyang, PAN Zili, et al. Analysis of wheel-rail contact and wear considering variable cross-sections of switch rail[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1250-1258. [25] 王璞,王树国,赵振华,等. 基于改善轮轨共形度的60 kg/m钢轨廓形优化[J]. 西南交通大学学报,2022,57(6): 1233-1238.WANG Pu, WANG Shuguo, ZHAO Zhenhua, et al. Optimization of 60 kg/m rail profile based on improving wheel-rail conformal degree[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1233-1238. -
下载:
点击查看大图
计量
- 文章访问数: 236
- HTML全文浏览量: 82
- PDF下载量: 28
- 被引次数: 0