Flexural Performance of PP-ECC Beams Under Coupling of Freeze-Thaw Cycles and Bending Loads
-
摘要:
为探究冻融以及冻融-弯曲荷载耦合作用对聚丙烯纤维水泥基复合材料（PP-ECC）梁抗弯性能的影响，设置7种试验工况，采用三分点加载方式对PP-ECC梁抗弯性能进行研究，分析冻融及冻融-弯曲荷载耦合作用下PP-ECC梁的荷载-跨中挠度曲线、抗弯承载力及裂缝发展形态差异；基于计算假定和正常环境下PP-ECC梁抗弯承载力的计算模型，结合PP-ECC材料冻融劣化机理，推导出PP-ECC梁在冻融环境下抗弯承载力计算模型；在此基础上引入持荷损伤系数
γ ，建立冻融-弯曲荷载耦合作用下PP-ECC梁抗弯承载力计算模型. 研究结果表明：不同持荷比的PP-ECC梁极限抗弯承载力在冻融循环作用下出现不同程度降低，500次冻融循环后，持荷比为0、0.25、0.50的PP-ECC梁极限抗弯承载力分别降低了28.70%、27.09%、35.69%；受拉区PP-ECC材料开裂后不退出工作仍能协同受拉钢筋参与全截面受力；PP-ECC 梁在达到极限状态时，受拉区呈多条裂缝稳态发展模式，且随冻融损伤加剧，梁体最大裂缝宽度增大，裂缝数量减少；单一冻融以及冻融-弯曲荷载耦合作用下的PP-ECC梁仍满足平截面假定；基于平截面假定建立的冻融和冻融-弯曲荷载耦合作用下PP-ECC 梁的抗弯承载力计算模型吻合度分别在0.88～1.06和0.96～1.10.-
关键词:
- 冻融-弯曲荷载耦合作用 /
- 抗弯性能 /
- 聚丙烯纤维水泥基复合材料 /
- 抗弯承载力 /
- 多裂缝发展
Abstract:To investigate the effect of freeze-thaw cycles and coupling of freeze-thaw cycles and bending loads on the flexural performance of polypropylene fiber cement-based composite (PP-ECC) beams, seven experimental working conditions were set up. In addition, the three-point loading method was adopted to explore the flexural performance of PP-ECC beams. The differences in load-span deflection curves, flexural bearing capacity, and crack development patterns of PP-ECC beams under coupling of freeze-thaw cycles and bending loads were analyzed. Based on the calculation assumptions and the calculation model of the flexural bearing capacity of PP-ECC beams under normal environments, combined with the freeze-thaw deterioration mechanism of PP-ECC materials, the calculation model of flexural bearing capacity of PP-ECC beams under freeze-thaw environments was deduced. Furthermore, the load-bearing damage coefficient γ was introduced on this basis. The calculation model of the flexural bearing capacity of PP-ECC beams under the coupling of freeze-thaw cycles and bending loads was established. The research results show that the ultimate flexural bearing capacity of PP-ECC beams with different load-bearing ratios decreases to varying degrees under freeze-thaw cycles. After 500 freeze-thaw cycles, the ultimate flexural bearing capacity of PP-ECC beams with load-bearing ratios of 0, 0.25, and 0.5 decreases by 28.70%, 27.09%, and 35.69%, respectively. After cracking under tension, the PE-ECC material can still work with the rebar under tension and participate in the stress of the whole section. When the PP-ECC beam reaches the limit state, the zone under tension develops steadily with multiple cracks. With the aggravation of freeze-thaw damage, the width of the largest crack in the beam body increases, and the number of cracks decreases. The PP-ECC beam subjected to freeze-thaw cycles and coupling of freeze-thaw cycles and bending loads still satisfies the plane section assumption. The coincidence degree of the flexural bearing capacity calculation models of PP-ECC beams under freeze-thaw cycles and coupling of freeze-thaw cycles and bending loads established based on the plane section assumption is 0.88–1.06 and 0.96–1.10, respectively.
-
青藏铁路是当前世界上海拔最高、线路最长的高原铁路，其东起青海省西宁市，经格尔木市到达西藏自治区拉萨市. 其中，西宁至格尔木段（西格段）于2011年完成电气化改造，实现电气化运营；而格尔木至拉萨段（格拉段）目前仍然为非电气化铁路，采用内燃机车牵引，最大运行速度120 km/h. 因此，车辆需要在格尔木更换牵引机车，严重影响青藏线运输效率[1-2]. 内电双源动车组（后简称双源动车组）是我国研制的动力集中动车组，其最大运行速度160 km/h，能够同时满足电气化铁路和非电气化铁路[3]. 因此，双源动车组不仅能够提升青藏线的运行速度，还能够大大提升青藏线的运行效率. 然而，青藏线全程要经历山岭重丘、高原高寒、风沙荒漠、雷雨雪霜等多种极端地理环境和气候条件，恶劣的外部环境对轮轨间的黏着性能提出巨大挑战，对高原铁路的运营机车提出极大考验. 为了提高高原机车的黏着特性，专家学者开展了大量的研究：黄问盈等[4]从提高黏着富裕度的角度，阐明了高原机车轮轴功率和列车比功率与列车最高速度、保有加速度及列车质量之间的关系；王晨等[5]分析不同悬挂刚度比下高原机车转向架的低动力作用，以保证机车具有足够黏着；伍赛特[6]以NJ2型机车为研究对象，分析提高黏着利率的轴控技术应用情况；申瑞源[7]从高原铁路环境特点、高原列车的适应性技术以及新型高原内燃机车研制方面总结了我国高原机车的研究工作，研究表明，高原机车仍需要提高黏着利用率，使之适应各种恶劣条件.
因此，本文以机车的黏着特性为研究对象，建立不同状态下双源动车组和青藏线典型运营机车（HXN3型高原机车）动力学模型，通过对比2个机车在青藏线格拉段环境运行的黏着性能，分析双源动车组在不同线路工况下的高原黏着适应性，为双源动车组在青藏线运营提供一定的参考.
1. 高原机车
1.1 HXN3型高原机车
HXN3型高原机车是中车大连机车车辆有限公司研发的一款速度120 km/h的高原机车，是我国目前技术水平最高的交流传动内燃机车之一，主要运营在青藏铁路的格尔木—拉萨段[7]. 转向架采用2C0式（如图1所示），主要由构架、轮对、驱动装置、制动装置等组成，其中，轮对与构架通过一系悬挂（单拉杆双钢簧轴箱定位，并配有垂向减振器）连接；构架与车体之间的二系悬挂则由2组橡胶旁承、2个横向减振器、2个抗蛇行减振器以及横向止档组成；电机通过抱轴轴箱与轮对连接，通过电机吊杆与构架连接；牵引装置采用平行四边形平拉杆传递牵引力；制动装置则采用踏面制动提供制动力. HXN3机车轴重25 t，车轮轮径
1250 mm，车轮廓形采用JM3磨耗型踏面.1.2 FXN3型高原机车
FXN3型高原机车是中车大连机车车辆有限公司研发的一款速度160 km/h的高原机车[8]，目前应用在拉萨—林芝段，是双源动车组中的内燃机车（后续以FXN3型高原机车代替）. 转向架采用A-1-A式（如图2所示），主要由构架、轮对、驱动装置、制动装置等组成，其一系悬挂与HXN3机车相同；构架与车体通过二系悬挂（2组高挠钢簧、2个垂向减振器、2个横向减振器、2个抗蛇行减振器以及横向止档）连接；驱动装置仅布置在转向架的端轴位置，通过六连杆空心轴联器实现电机与轮对的连接；牵引装置则采用四连杆机构传递牵引力；制动力通过制动夹钳夹持轮盘获得. FXN3机车轴重23 t，车轮轮径
1250 mm，车轮廓形采用JM3磨耗型踏面.为了便于后续分析，表1列出了HXN3型机车与FXN3型机车的主要技术参数.
表 1 HXN3和FXN3机车主要技术参数Table 1. Main technical parameters of HXN3 and FXN3 locomotives序号 参数 HXN3 FXN3 1 轨距/mm 1435 1435 2 持续速度/（km·h−1） 23 28 3 定距/m 13.900 16.435 4 轴距/m 1.755/1.925 1.950/2.050 5 最大运用速度/（km·h−1） 120 160 6 柴油机装车功率/kW 3700 3500 7 起动牵引力/kN 620 245 8 持续牵引力/kN 598 200 9 牵引杆高度/m 0.725 0.685 10 牵引杆长度/m 1.238 1.350 2. 轮轨黏着
黏着是摩擦的表现方式之一，是机车发挥牵引或制动力的基本条件[9-10]. 在牵引状态下，机车车轮的接触点相对钢轨有微小宏观滑动，但由于轮轨材料弹性变形，接触点实际上是一个具有一定面积的接触斑. 进入接触斑前端的车轮和钢轨材料分别产生压应变和拉应变，两者有共同的应变速率但不产生真实滑动，称为接触斑黏着区；随着切向应变的增加，切向应力随之增加，达到摩擦极限后，轮轨材料应变速率产生差异，导致发生真实滑动，称为接触斑蠕滑区[11-15]. 通常黏着系数定义为实际达到的纵、横向摩擦力与法向力之比，因此，黏着系数可以分为纵向黏着系数（也称为牵引黏着系数）和横向黏着系数. 纵向黏着系数的绝对值与摩擦系数的比值称为黏着利用率，用于表示对轮轨摩擦利用程度，因此，纵向黏着系数的绝对值小于摩擦系数，黏着利用率总是不大于1.0.
纵向黏着系数的变化表征了轮轨间纵向力的变化，当电机或者制动装置所提供的扭矩超出了轮轨黏着力产生的反力矩时，将引发一系列的问题. 例如在牵引状态下易造成车轮的持续空转或颤振，在制动状态下易导致车轮打滑或抱死. 无论轮对空转、颤振、打滑或抱死都会对车轮和钢轨表面形成异常磨损或擦伤，并进一步加剧机车的振动和结构部件的动应力，影响部件的可靠性和机车运行的平稳性，同时也增加了钢轨和机车车辆的维护成本，降低轮轨使用寿命[16-17]. 空转或打滑造成车轮表面出现的擦伤和车轮擦伤剥离如图3.
黏着系数受到轮轨界面黏着特性的影响，然而轮轨界面的黏着特性复杂多变，受到轮轨界面状态、环境因素、轮轨接触状态、运行参数、牵引力发挥影响. 因此，黏着系数是一个具有不确定性的复杂时变参数，其变化范围大，影响因素多[18] . 以接触面为分界线，黏着系数的影响因素分为机车部分和线路部分：线路影响因素主要有线路曲率、坡道、几何不平顺以及轨面的温度、湿度、粗糙度和污染层等；机车影响因素主要包括车辆的速度、轴重以及轮对的材料、粗糙度、轮径等[19-20].
3. 机车动力学模型
机车是一种典型的多体系统，通常由车体、构架、轮对、电机以及牵引杆等部件组成. 本文采用成熟的多体动力学软件SIMPACK进行机车的建模仿真.
3.1 动力学模型
根据FXN3和HXN3型机车的结构特点、动力学参数和轮轨廓形，建立FXN3和HXN3机车的动力学模型，动力学参数见表1和表2. 为模拟机车的牵引状态，对每个轮对施加扭矩，用于模拟牵引电机提供的牵引力矩. 而为了避免瞬时冲击过大，采用线性递增的方式使得扭矩在一定时间范围内递增到最大，最大值为电机的扭矩曲线. 机车在牵引力作用下，车辆速度不断增加，但是电机的扭矩随着车速的增大而逐渐降低，施加在模型中的扭矩也跟着相应调整. 因此，该动力学模型适应于加速牵引工况（如图4所示）.
表 2 HXN3和FXN3机车动力学参数（部分）Table 2. Main dynamic parameters of HXN3 and FXN3 locomotives （part）序号 参数 HXN3 FXN3 1 一系纵向刚度/（MN·m−1） 30.00 28.59 2 一系横向刚度/（MN·m−1） 0.800 3.588 3 一系垂向刚度/（MN·m−1） 0.838 2.320 4 二系纵向刚度（橡胶堆或
钢簧）/（MN·m−1）0.300 0.192 5 二系横向刚度/（MN·m−1） 0.200 0.192 6 二系垂向刚度/（MN·m−1） 7.700 0 0.5185 7 抗蛇形减振器/（kN·s·m−1） 16.5@0.01 14.2@0.01 8 二系横向减振器/（kN·s·m−1） 4.5@0.10 2.8@0.05 9 轴重/t 25 23 
图 4 机车变速牵引工况动力学模型（以HXN3机车为例）Figure 4. Traction dynamic model of locomotive at variable speed （HXN3 locomotive）机车在运行过程中，受到车辆基本阻力、曲线阻力、空气阻力、坡道阻力等限制，当机车的牵引力与阻力相当时，机车处于匀速牵引工况. 为了模拟机车的匀速牵引工况，通过车钩连接一虚车体，虚车体沿着轨道恒速运行（9号铰），模拟车钩位置施加的车钩阻力，实现机车的匀速牵引[21]（图5）. 需要说明的是，FXN3机车采用内燃机车牵引时是双机牵引，即采用2台FXN3机车同时牵引，为便于后续分析，这里由前向后分别记为FXN3A和FXN3B.
图 5 机车匀速牵引工况动力学模型（以HXN3机车为例）Figure 5. Traction dynamic model of locomotive at constant speed （HXN3 locomotive）FXN3和HXN3型机车牵引均采用架控模式，即每个转向架的电机扭矩相同. 由于轴重转移的存在，假设轮轨之间的黏着系数不会出现突变，每个动轴可发挥的牵引力存在一定的差异，因此，每个转向架电机扭矩的最大值由该转向架动轴轴重最低值的决定.
3.2 轴重转移分析
轴重转移又称轴重再分配，是指机车产生牵引力时各轴重发生的变化. 影响轴重转移的因素很多，如车辆的一系悬挂、二系悬挂、车轮直径、定距、轴距以及牵引杆的高度、角度和长度等. 轴重转移的分析方法主要有数学分析法和多体动力学分析法：前者从理论的角度分析了轴重转移的原理以及相关参数的影响，但忽略了轮轨黏着等微观因素的影响；后者能够全面分析轴重转移的相关参数的影响规律.
由第1节的介绍可知，FXN3和HXN3的踏面廓形、轮径相同，但车辆的悬挂、定距、轴距等均存在较大的差异. 除上述车辆因素，线路中的坡道及轨道的温度、湿度、粗糙度等均会引起一定程度的轴重转移. 牵引黏着系数直接影响牵引力的发挥，而牵引力是导致机车轴重再分配的根本原因，因此，牵引黏着系数对机车的轴重转移有重大影响. 美国GM公司通过试验得到黏着系数0.35 时某内燃机车的轴重转移约10.0%，黏着系数0.25 时轴重转移仅7.0%[22].
机车牵引黏着受到各种条件的制约，目前采用交流传动技术的大功率内燃机车，其牵引黏着系数[23]为
μx≈0.31+330+10v， (1) 式中： $ v $为速度，km/h.
图6为机车以1 km/h运行，黏着系数为0.41时，高原机车的轴重转移. 由图可以看出，启动牵引时，机车的轴重最大减载均为第一位轮对（沿着机车前进方向，由前向后，带动力的车轴依次为1～4，wst为轮对的简称），2台机车的轴重转移均约为−9.9%. 因此，每个转向架的电机扭矩均为初始值的90.1%.
4. 直线段黏着对比分析
低温作为高原铁路的显著特点之一，文献[24]发现，低温环境有利于提高牵引黏着系数，然而提升幅度并未具体给出. 接触面的摩擦力是机械阻力的组成部分之一，在其余条件不变的情况下，低温环境同样会提高机械阻力. 文献[25]研究发现，高原低温环境（−30 ℃） 较常温环境，机械阻力存在一个修正系数$ {K}_{{\mathrm{t}}} $（$ K_{{\mathrm{t}}}=1 + 5 \times 10^{-4} v $，$ v $取值范围20～160 km/h）. 因此，本文采用该修正系数与式（1）的乘积作为低温环境的牵引黏着系数（方便与纵向蠕滑率对应，后续统一成为纵向黏着系数）.
4.1 恒速牵引工况
机车的纵向黏着系数如图7所示，由图可知：随着车速的增大，机车发挥最大牵引力时的纵向黏着系数逐渐降低；40 km/h时，HXN3机车完全发挥牵引力时的纵向黏着系数为 0.252，占最大纵向黏着系数的77.8%；FXN3机车完全发挥牵引力时的纵向黏着系数为 0.190，约占最大纵向黏着系数的59.0%；当最大纵向黏着系数下降时，HXN3机车轮对先出现打滑现象. FXN3机车在线路湿滑、结冰等条件下导致最大黏着系数降低的富裕度更高，对高原环境的适应性更强.
4.2 加速牵引工况
采用5 s内，牵引力等比例增大至对应速度的最大牵引力作为加速牵引工况. 图8为机车由20 km/h加速至120 km/h工况下导向轮对的纵向黏着系数，由图可以看出：HXN3机车加速至120 km/h所用的时间几乎为FXN3机车的一半，这是因为HXN3机车的单轴功率约等于FXN3机车的2倍；20～33 km/h时，FXN3机车的纵向黏着系数增大，这是因为牵引力等比例增速大于速度造成的纵向黏着系数降低速率， HXN3机车在20～44 km/h也展现了同样的现象；44～120 km/h，纵向黏着系数与恒速牵引工况相类似. 因此，FXN3机车在线路湿滑、结冰等因素导致最大黏着系数降低的富裕度更高，加速牵引工况下，对高原环境的适应性更强.
5. 曲线段黏着对比分析
机车的牵引力发挥与轮对的纵向蠕滑率息息相关，但是纵向蠕滑率与横向蠕滑率相互影响[24]，特别是曲线通过时，由于导向力的需求导致横向蠕滑率增大，纵向蠕滑率降低，进一步引起曲线上的纵向黏着降低，即曲线黏降. 文献[9]提出了曲线最大纵向黏着系数的公式，如式（2）所示.
μx,R=μ√1−(2l0ξR)2， (2) 式中：$ \mu $为轮轨最大纵向黏着系数；$ l_0 $为单个转向架端轴距离之半，m；$ \xi $为总蠕滑率，取值范围2.00%～2.50%；$ R $为曲线半径，m.
文献[26-27]发现，HXN3机车在青藏线（格尔木—拉萨段）运营过程中出现轮缘裂纹故障. 根据前期研究，线路中R800 m曲线频繁交替，可能是导致轮缘裂纹的原因之一，因此，选取R800 m为本文对比分析的曲线半径之一. 为了对比两者小半径曲线的情况，本文选取R300 m曲线为计算线路.
5.1 曲线起动工况
曲线超高取120 mm，以1 m/s的车速起动，电机的扭矩在缓和曲线段由零增加至对应速度的最大扭矩. 考虑低温和曲线黏降的影响，机车对应的最大纵向黏着系数为0.356.
图9为HXN3、FXN3机车通过R300 m曲线时导向轮对（1 st）牵引力的发挥情况，其中L、R分别为左、右车轮. 文献[21]表明，纵向蠕滑率绝对值大于1.25%（正负表示蠕滑率的方向）时，轮轨有发生黏滑振动的风险. 因此，以纵向蠕滑率−1.25% （图9纵向蠕滑率在−2.00%，出现明显打滑）作为机车仍能稳定发挥牵引力的临界值. 由图9可以看出：HXN3机车通过R300 m时，纵向黏着为直线时的72.2% （0.285/0.356−0.079=0.722×100%=72.2%，0.079是纵向黏着系数为0.285时轴重转移较0.356多计入0.079），该值与式（2）$ \xi $取2.00%的曲线黏降结果（79.0%）较为接近，验证了HXN3机车动力学模型和仿真结果的正确性；FXN3机车R300 m时纵向黏着为直线的68.2% （0.278/0.356−0.099=0.682×100%=68.2%，0.099是纵向黏着系数为0.278时轴重转移为90.9%），该值与式（2）$ \xi $取2.00%的曲线黏降结果74.5%较为接近，验证了FXN3机车动力学模型和仿真结果的正确性.
机车通过R300 m曲线时的纵向黏着系数相差0.007，但是由于轴重相差2 t，因此，HXN3机车在纵向蠕滑率为−1.25%时的牵引力明显大于FXN3型机车.
图10为HXN3、FXN3机车通过R800 m曲线时牵引力的发挥情况. 仍以−1.25%作为稳定发挥牵引力的临界值，由图可以看出：HXN3机车通过R800 m时纵向黏着为直线时的97.0% （0.338/0.356 + 0.021=0.970×100%=97%，0.021是因为牵引黏着系数为0.338时轴重转移较0.356多计入了2.1%），该值与式（2）$ \xi $取2.00%的结果97.3%较为接近；FXN3机车通过R800 m时，纵向蠕滑率均位于−1.25%～0%，机车一直保持有稳定的牵引力，且牵引力均低于HXN3型机车.
综上所述，R300 m曲线起动过程中，FXN3机车的曲线黏降大于HXN3机车，若忽略结构引起的差异，两者的曲线黏降幅度几乎相同.
6. 坡道黏着对比分析
青藏铁路中存在大量的坡道，最大坡道高达20‰，大坡道不仅带来大的坡道阻力，同时引起更大的轴重转移，降低机车牵引能力的发挥. 为方便对比分析，本文以20‰为研究对象，分析坡道起动和加速牵引的工况.
6.1 坡道起动工况
采用与4.1节类似的车速和最大纵向黏着，图11为机车爬升20‰ 坡道的纵向黏着和轮对转速情况，由图可以看出：1） HXN3机车纵向黏着为直线的92.5% （0.361/0.356−0.025−0.07=0.925×100%=92.5%，0.025是因为纵向黏着系数为0.361时轴重转移较0.356少计入了2.5%，0.07是因为爬升20‰ 坡道时，在纵向蠕滑率为−1.25%时，轮轨间的法向力降低了7%，同时也是导致纵向黏着系数大于轮轨之间摩擦系数的原因）. 2） 在该时刻，HXN3机车的轮对转速增大了1.3%，且在持续上升；FXN3机车爬升20‰ 坡道时，纵向蠕滑率均位于−1.25%～0%，且黏着系数均小于0.356，机车一直保持有稳定的牵引力；转速增大0.3%，远低于HXN3型机车.
图 11 纵向黏着系数、轮对转速（20‰ 坡道）Figure 11. Longitudinal adhesion coefficient and wheelset rotation speed（20‰ ramp）图12为不同输入扭矩的情况下HXN3机车的纵向黏着系数、轮轨转速示意，由图可以看出，降低初始电机扭矩（降低起动牵引力）可以使得机车在坡道起动时保证有足够的牵引力，避免车轮出现打滑.
图 12 HXN3机车纵向黏着系数、轮对转速（20‰ 坡道）Figure 12. HXN3 longitudinal adhesion coefficient and wheelset rotation speed（20‰ ramp）6.2 坡道通过工况
图13为机车以10～120 km/h的速度爬升20‰ 坡道时的纵向黏着系数和蠕滑率的示意，由图可以看出：纵向黏着和蠕滑率均先增大后减小，且其转折速度分别为23 km/h （HXN3）和28 km/h （FXN3），与机车的持续速度相对应；同时低速阶段（小于持续速度），纵向黏着系数大幅上升，中高速阶段纵向黏着系数则逐渐下降，且降速逐渐降低. 主要是由于低速阶段机车牵引力等比例增加（5 s增大阶段），中高速阶段随着机车进入恒功区，机车的牵引力随着车速的增大而减小，即机车的纵向黏着系数与牵引力成正比关系.
图 13 纵向蠕滑率、黏着系数（20‰ 坡道）Figure 13. Longitudinal creepages and adhesion coefficient （20‰ ramp）7. 结 论
为研究FXN3型高原机车的高原黏着适应性，本文采用仿真的方式，通过与青藏铁路成熟运营的HXN3机车对比，分别计算了直线段、曲线段和坡道时2个机车的纵向黏着系数、蠕滑率、牵引力和速度的关系曲线，从而分析了其高原黏着特性. 通过上述计算，可以得到如下结论：
1） 机车完全发挥牵引力运行在直线段时，FXN3型高原机车的黏着富裕度大于HXN3机车，其高原黏着适应性更强；
2） R300 m曲线时，忽略不同轴距引起的机车曲线黏降的差异，2个机车的曲线黏降幅度几乎相等；R800 m曲线时，则FXN3型高原机车起动时的曲线黏降幅度小于HXN3机车；
3） 20‰ 的坡道启动时，HXN3机车在纵向黏着为直线的92.5%，FXN3型高原机车仍然保持充足的纵向黏着.
4） 相同工况下，FXN3型高原机车的蠕滑率均低于HXN3机车，有利于减低车轮磨耗，减轻车轮的滚动接触疲劳，降低列车的运营维护成本.
本文建立的多体动力学模型，其曲线段黏着动力学仿真结果与曲线黏降的经验公式匹配良好，验证了动力学模型的正确性，为后续机车制动能力和制动特性的分析提供了一定的基础，也为文献[24] HXN3机车轮缘裂纹问题分析提供了一定的参考.
-
图 5 应变片布置
1—荷载传感器；2—分配工装；3—PP—ECC梁侧面；4—铰支座；5—应变片；6—百分表；7—PP-ECC梁顶面.
Figure 5. Strain gauge layout
图 9 冻融过程中PP-ECC的极限压缩性能变化
Figure 9. Variations in ultimate compression performance of PP-ECC during freeze-thaw process
图 10 冻融过程中PP-ECC的拉伸性能变化
Figure 10. Variations in tensile properties of PP-ECC during freeze-thaw process
表 1 PP-ECC梁具体试验参数
Table 1. Specific test parameters of PP-ECC beam
试验梁
分组试件编号 冻融循环
次数/次弯曲
荷载/%抗弯性能
试验第Ⅰ组 E0-0 0 是 第Ⅱ组 E0-300 300 E0-500 500 第Ⅲ组 E0.25-300 300 25 E0.25-500 500 第Ⅳ组 E0.50-300 300 50 E0.50-500 500 
下载: 导出CSV
表 2 钢筋性能指标
Table 2. Rebar performance indexes
型号 直径/
mm截面面
积/mm2屈服强
度/MPa极限强
度/MPa弹性模
量/GPaQ235 6 28.26 236 390 196 HRB400 6 28.26 406 576 197 HRB400 10 78.50 411 535 203
下载: 导出CSV
表 3 PP-ECC梁的配合比
Table 3. Mix proportion of PP-ECC beam
kg/m3 水泥 粉煤灰 PP纤维 水 820.0 442.0 18.2 504.8
下载: 导出CSV
表 4 PP-ECC梁四点弯曲试验结果
Table 4. Four-point bending test results of PP-ECC beam
试件编号 屈服荷载/kN 极限荷载/kN 极限抗弯承载力/（kN·m） 裂缝最大宽度/mm 最终裂缝数量/条 E0-0 33.95 33.97 5.10 0.90 36 E0-300 29.34 28.84 4.33 1.10 30 E0-500 24.82 24.22 3.63 1.34 25 E0.25-300 30.88 30.72 4.61 1.25 32 E0.25-500 24.64 25.02 3.75 1.42 29 E0.50-300 26.67 26.01 3.90 1.55 23 E0.50-500 21.21 21.87 3.28 1.80 18
下载: 导出CSV
表 5 PP-ECC材料本构参数
Table 5. Constitutive parameters of PP-ECC materials
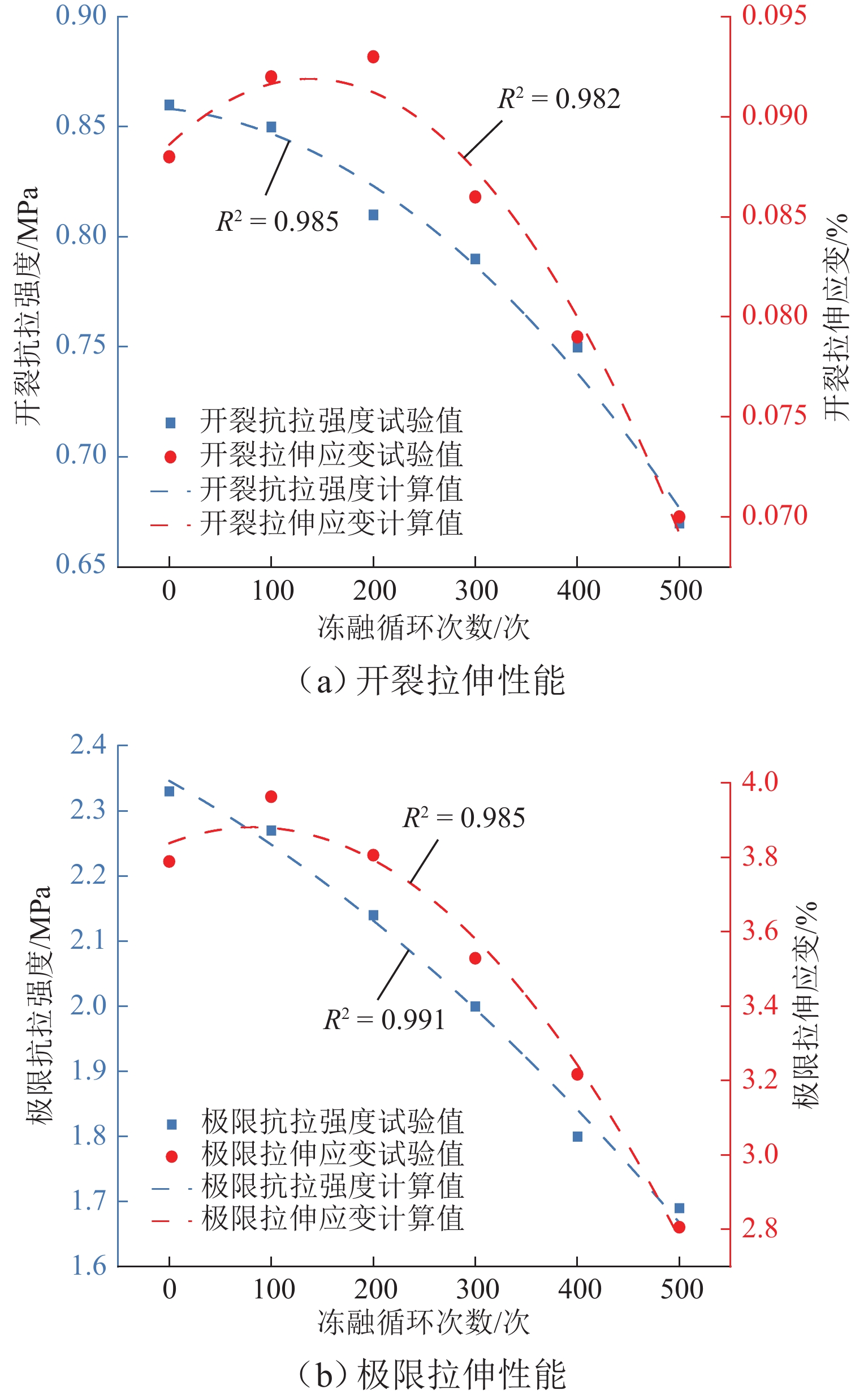
PP-ECC 单轴拉伸本构参数 单轴受压本构参数 σtc/MPa εtc/% σtu/MPa εtu/% σcu/MPa εcu/% 0.86 0.088 2.33 3.789 31.65 0.38
下载: 导出CSV
表 6 抗弯承载力对比
Table 6. Comparison of flexural bearing capacity
冻融循环
次数/次抗弯承载力 计算值/
试验值计算值/
（kN·m）试验值/
（kN·m）0 4.50 5.10 0.88 300 4.18 4.33 0.97 500 3.88 3.63 1.06
下载: 导出CSV
表 7 抗弯承载力对比
Table 7. Comparison of flexural bearing capacity
冻融循环
次数/次持荷比 抗弯承载力 计算值/
试验值计算值/
（kN·m）试验值/
（kN·m）300 0 4.18 4.33 0.97 0.25 4.46 4.61 0.97 0.50 3.75 3.90 0.96 500 0 3.88 3.63 1.07 0.25 4.14 3.75 1.10 0.50 3.48 3.28 1.06
下载: 导出CSV
-
[1] CAMPIONE G, CANNELLA F, CAVALERI L. Shear and flexural strength prediction of corroded R. C. beams[J]. Construction and Building Materials, 2017, 149: 395-405. doi: 10.1016/j.conbuildmat.2017.05.125 [2] LI V C, LEUNG C K Y. Steady-state and multiple cracking of short random fiber composites[J]. Journal of Engineering Mechanics, 1992, 118(11): 2246-2264. doi: 10.1061/(ASCE)0733-9399(1992)118:11(2246) [3] LI V C, WU H C. Conditions for pseudo strain-hardening in fiber reinforced brittle matrix composites[J]. Applied Mechanics Reviews, 1992, 45(8): 390-398. doi: 10.1115/1.3119767 [4] YUAN F, PAN J L, DONG L T, et al. Mechanical behaviors of steel reinforced ECC or ECC/concrete composite beams under reversed cyclic loading[J]. Journal of Materials in Civil Engineering, 2014, 26(8): 04014047.1-04014047.8. [5] POURFALAH S. Behaviour of engineered cementitious composites and hybrid engineered cementitious composites at high temperatures[J]. Construction and Building Materials, 2018, 158: 921-937. doi: 10.1016/j.conbuildmat.2017.10.077 [6] JIN H S, LI F H, HU D H. Research on the flexural performance of reinforced engineered cementitious composite beams[J]. Structural Concrete, 2022, 23(4): 2198-2220. doi: 10.1002/suco.202100012 [7] 黄士元. 近代混凝土技术[M]. 西安: 陕西科学技术出版社, 1998. [8] SUN W, ZHANG Y M, YAN H D, et al. Damage and damage resistance of high strength concrete under the action of load and freeze-thaw cycles[J]. Cement and Concrete Research, 1999, 29(9): 1519-1523. doi: 10.1016/S0008-8846(99)00097-6 [9] KOSIOR-KAZBERUK M, BERKOWSKI P. Surface scaling resistance of concrete subjected to freeze-thaw cycles and sustained load[J]. Procedia Engineering, 2017, 172: 513-520. doi: 10.1016/j.proeng.2017.02.060 [10] SHEN Y, LIU J, ZHOU S Y, et al. Experimental investigation on the freeze-thaw durability of concrete under compressive load and with joints[J]. Construction and Building Materials, 2019, 229: 116893.1-116893.12. doi: 10.1016/j.conbuildmat.2019.116893 [11] WANG Y, WANG G, GUAN Z W, et al. The effect of freeze-thaw cycles on flexural behaviour of FRP-reinforced ECC beams[J]. Archives of Civil and Mechanical Engineering, 2021, 21(3): 1-24. [12] ZHANG Y X, BAI S, ZHANG Q B, et al. Failure behavior of strain hardening cementitious composites for shear strengthening RC member[J]. Construction and Building Materials, 2015, 78: 470-473. doi: 10.1016/j.conbuildmat.2015.01.037 [13] DING Y, YU K Q, YU J T, et al. Structural behaviors of ultra-high performance engineered cementitious composites (UHP-ECC) beams subjected to bending-experimental study[J]. Construction and Building Materials, 2018, 177: 102-115. doi: 10.1016/j.conbuildmat.2018.05.122 [14] YUN H D, KIM S W, LEE Y O, et al. Tensile behavior of synthetic fiber-reinforced strain-hardening cement-based composite (SHCC) after freezing and thawing exposure[J]. Cold Regions Science and Technology, 2011, 67(1/2): 49-57. [15] 靳贺松,李福海,何肖云峰,等. 聚丙烯纤维水泥基复合材料的抗冻性能研究[J]. 材料导报,2020,34(8): 8071-8076,8082. doi: 10.11896/cldb.18080117JIN Hesong, LI Fuhai, HE Xiaoyunfeng, et al. Research on frost resistance of polypropylene fiber cement-based composite material[J]. Materials Reports, 2020, 34(8): 8071-8076,8082. doi: 10.11896/cldb.18080117 [16] DUAN A, LI Z Y, ZHANG W C, et al. Flexural behaviour of reinforced concrete beams under freeze-thaw cycles and sustained load[J]. Structure and Infrastructure Engineering, 2017, 13(10): 1350-1358. doi: 10.1080/15732479.2016.1268172 [17] 李福海,胡丁涵,余泳江,等. PP-ECC梁抗弯性能试验研究[J]. 西南交通大学学报,2021,56(2): 272-281.LI Fuhai, HU Dinghan, YU Yongjiang, et al. Experimental study on flexural capacity of PP-ECC beam[J]. Journal of Southwest Jiaotong University, 2021, 56(2): 272-281. [18] 崔晶波. 荷载冻融耦合作用下再生粗骨料自密实混凝土梁的受弯力学性能试验研究[D]. 乌鲁木齐: 新疆大学, 2020. [19] IAN T. Research on seismic behavior of steel tube reinforeed conerete bridge columns[D]. Dalian: Dalian University of Technology, 2019. [20] LI F H, WEN T, LI J Y, et al. Ultrasonic-detected damage and bending behavior of reinforced PP-ECC beams after coupled action of freeze-thaw cycles and constant flexural load[J]. Case Studies in Construction Materials, 2022, 17: e01284.1-e01284.15. [21] 徐港,李运攀,潘琪,等. 盐冻环境下钢筋混凝土梁抗弯性能试验研究[J]. 土木建筑与环境工程,2014,36(3): 86-91.XU Gang, LI Yunpan, PAN Qi, et al. Experimental analysis on flexural performance of reinforced concrete beam in salt-frost environment[J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(3): 86-91. [22] 刘泽军,李艳,温丛格. PVA-ECC劈裂抗拉强度与变形性能试验研究[J]. 建筑材料学报,2016,19(4): 746-751. doi: 10.3969/j.issn.1007-9629.2016.04.024LIU Zejun, LI Yan, WEN Congge. Experimental study on strength and deformation performance of PVA-ECC under splitting tension[J]. Journal of Building Materials, 2016, 19(4): 746-751. doi: 10.3969/j.issn.1007-9629.2016.04.024 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 291
- HTML全文浏览量: 119
- PDF下载量: 56
- 被引次数: 0