侧风下大跨拱桥变形对高速列车行车平稳性的影响机理

李小珍; 周彦希; 王铭

doi:10.3969/j.issn.0258-2724.20220598

侧风下大跨拱桥变形对高速列车行车平稳性的影响机理

doi: 10.3969/j.issn.0258-2724.20220598

李小珍^{1, 2,},
周彦希^{1, 2},
王铭^{1, 2, ,}

1.
西南交通大学土木工程学院，四川成都 610031
2.
西南交通大学桥梁智能与绿色建造全国重点实验室，四川成都 611756

基金项目: 国家自然科学基金项目（52208505，52278463）

详细信息

作者简介:
李小珍（1970—），男，教授，研究方向为风-车-桥耦合振动，E-mail：xzhli@swjtu.edu.cn

通讯作者:
王铭（1989—），男，副研究员，研究方向为风-车-桥耦合振动， E-mail：ming.wang@swjtu.edu.cn

中图分类号: U441.7；U211
计量
- 文章访问数: 426
- HTML全文浏览量: 190
- PDF下载量: 133
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-13
- 修回日期: 2022-11-30
- 网络出版日期: 2023-11-17
- 刊出日期: 2022-12-01

Influence Mechanism of Long-Span Arch Bridge Deformation on Running Stability of High-Speed Trains Under Crosswind

LI Xiaozhen^{1, 2
,},
ZHOU Yanxi^{1, 2},
WANG Ming^{1, 2
, ,}

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
State Key Laboratory of Bridge Intelligent and Green Construction, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
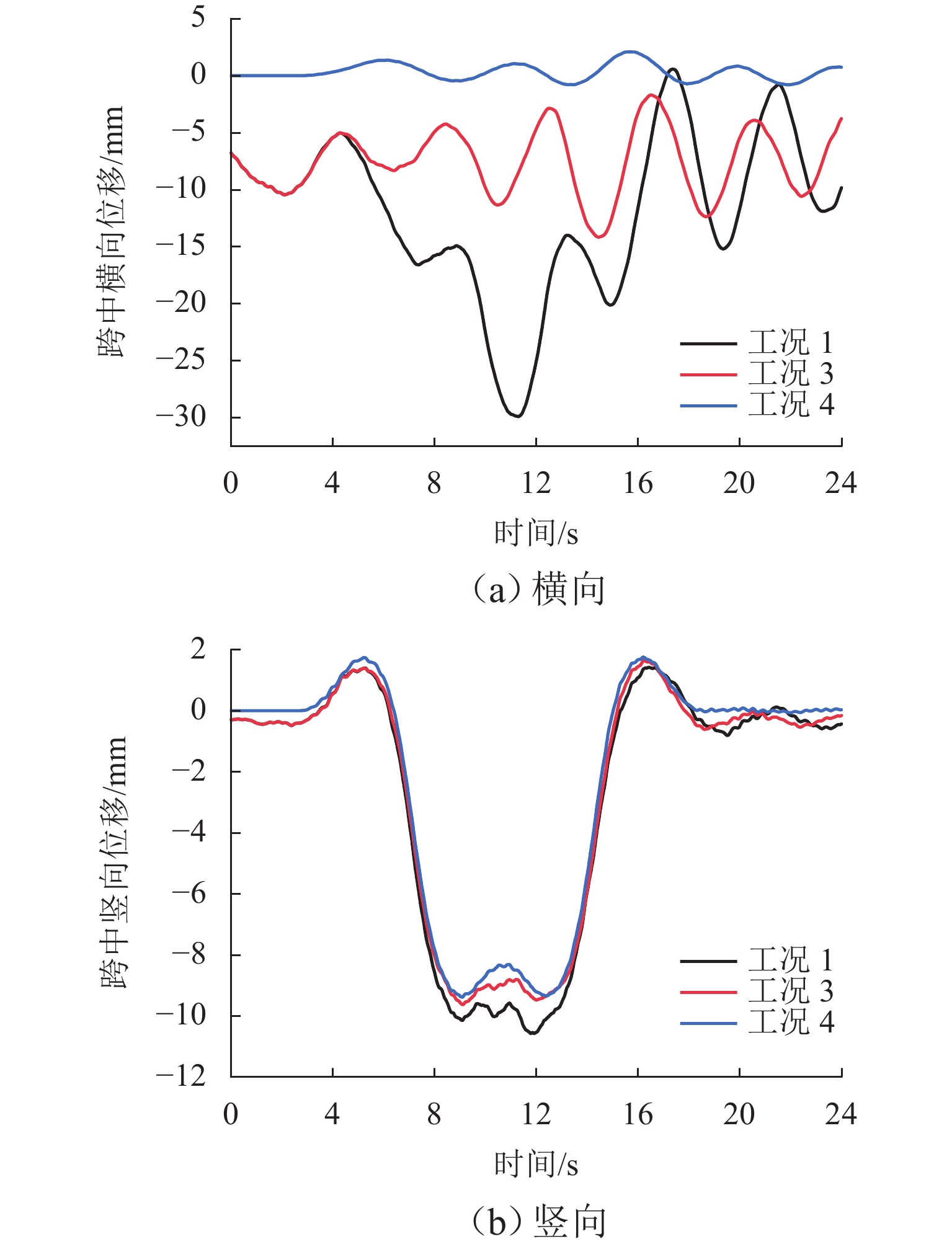
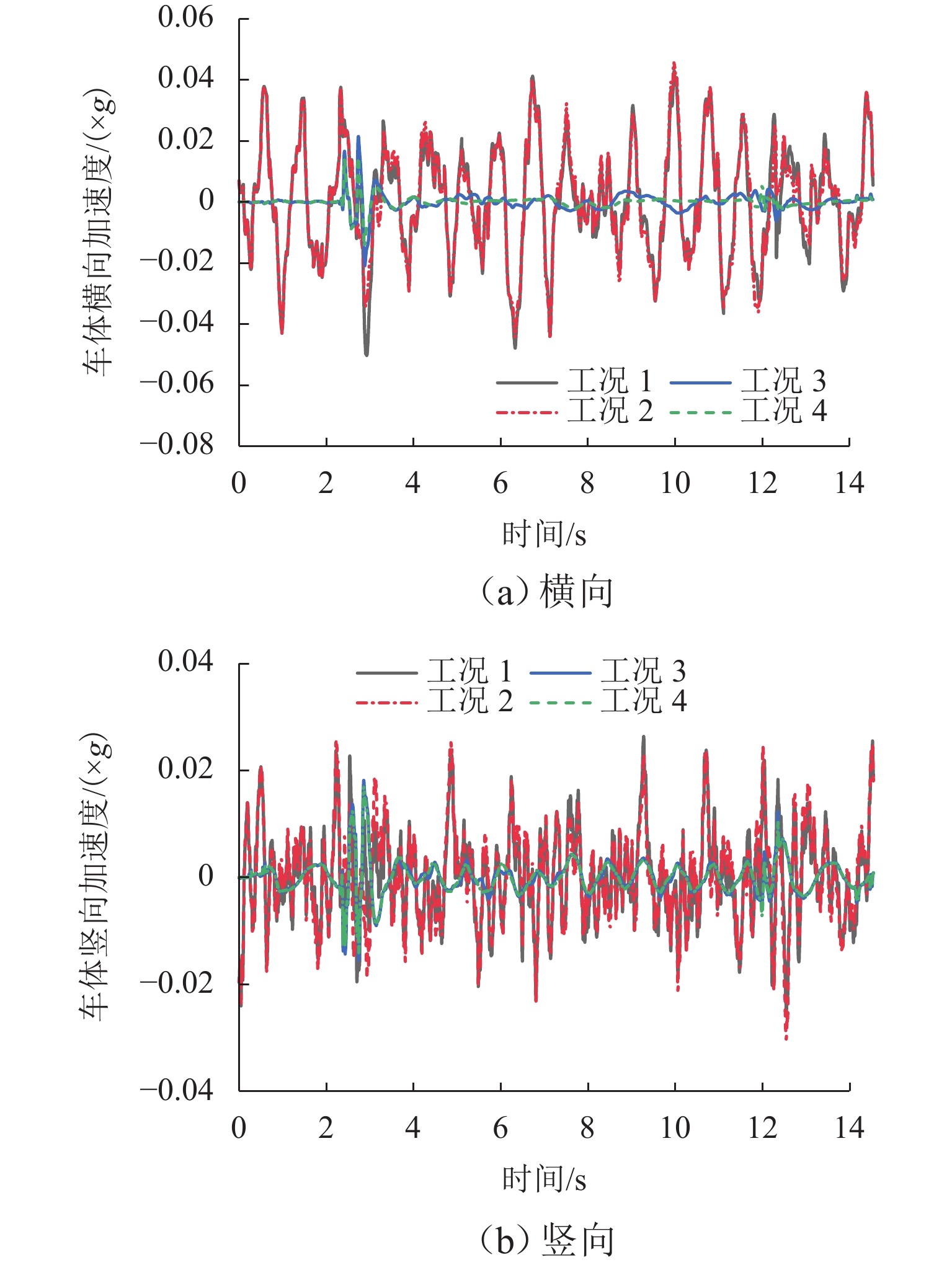
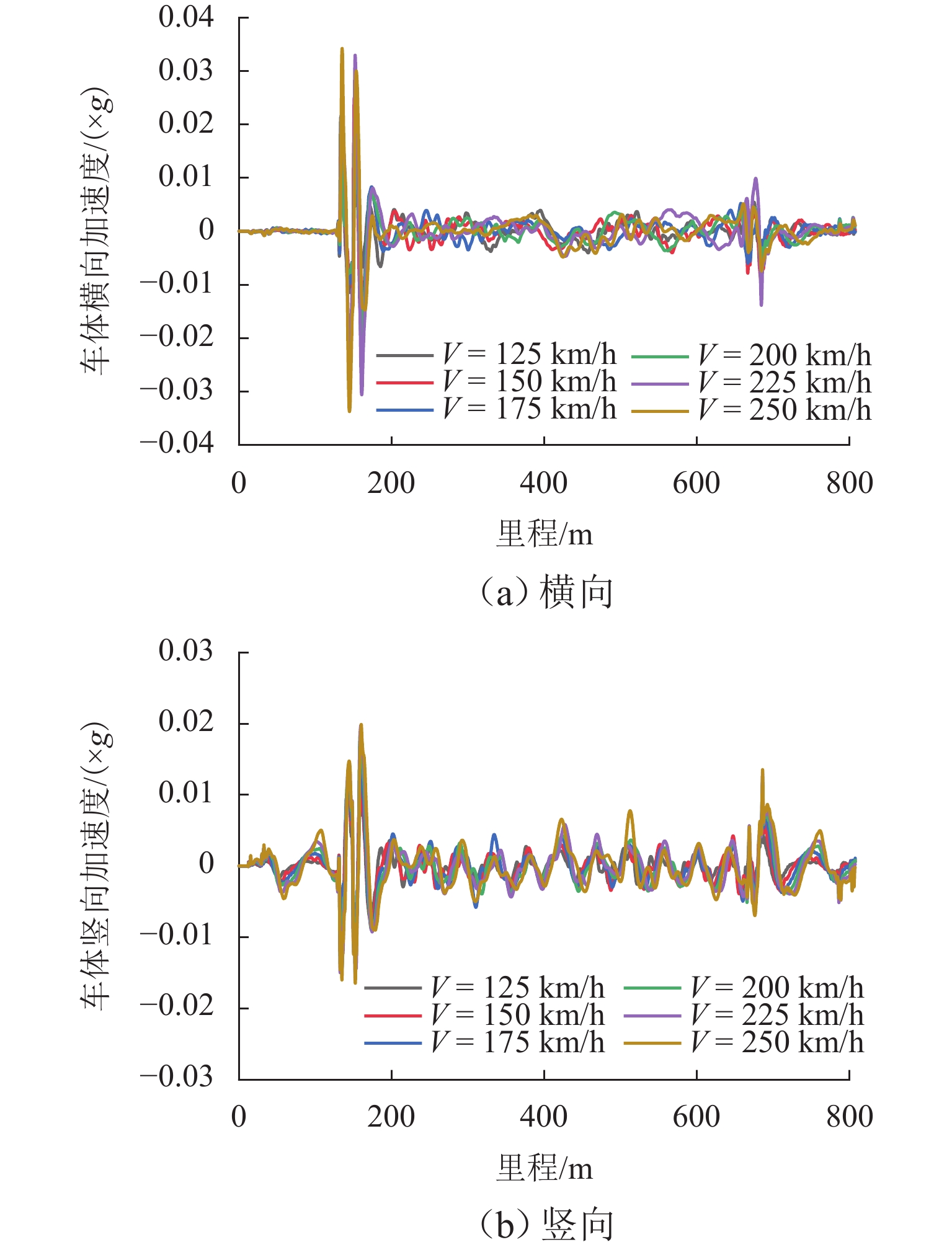
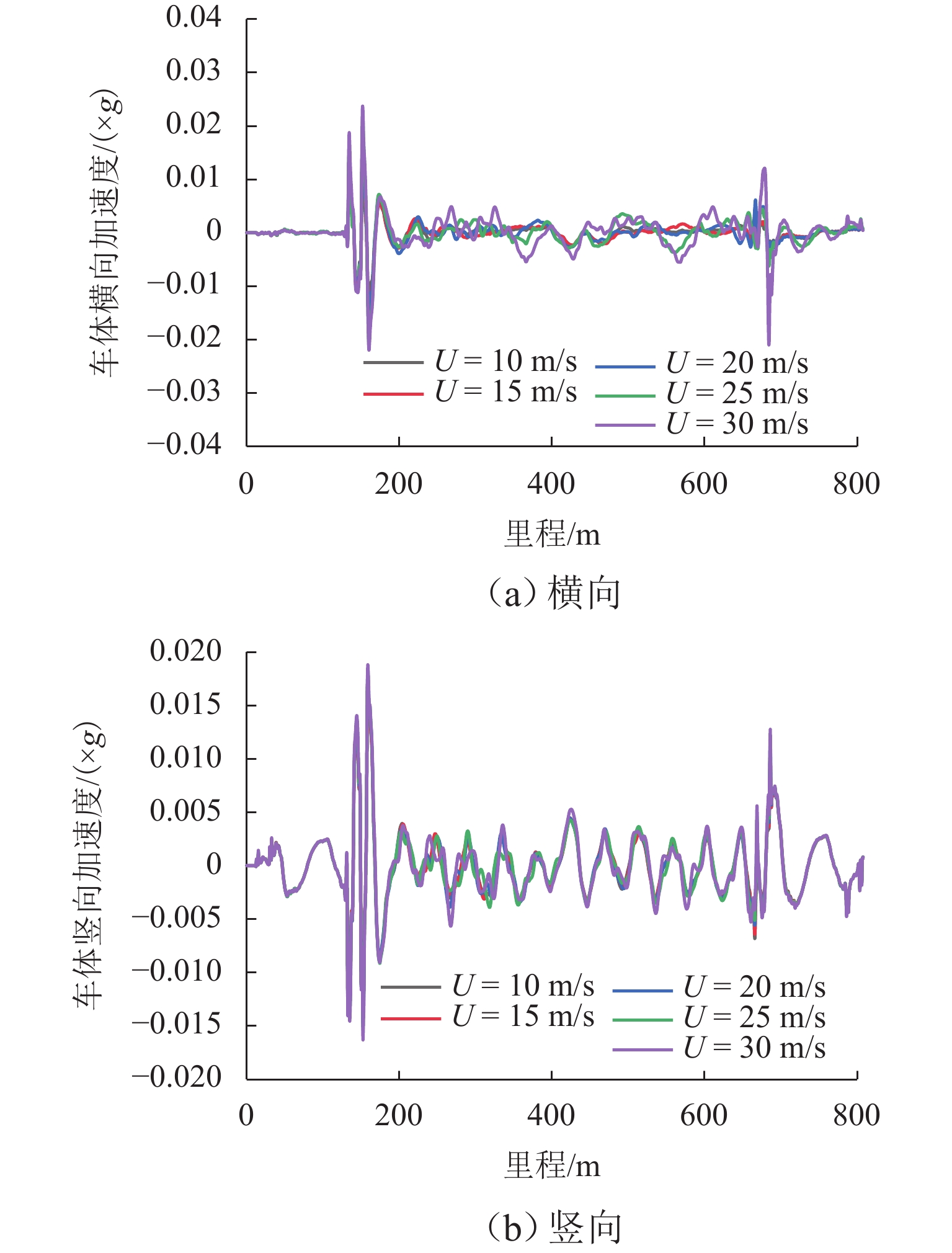
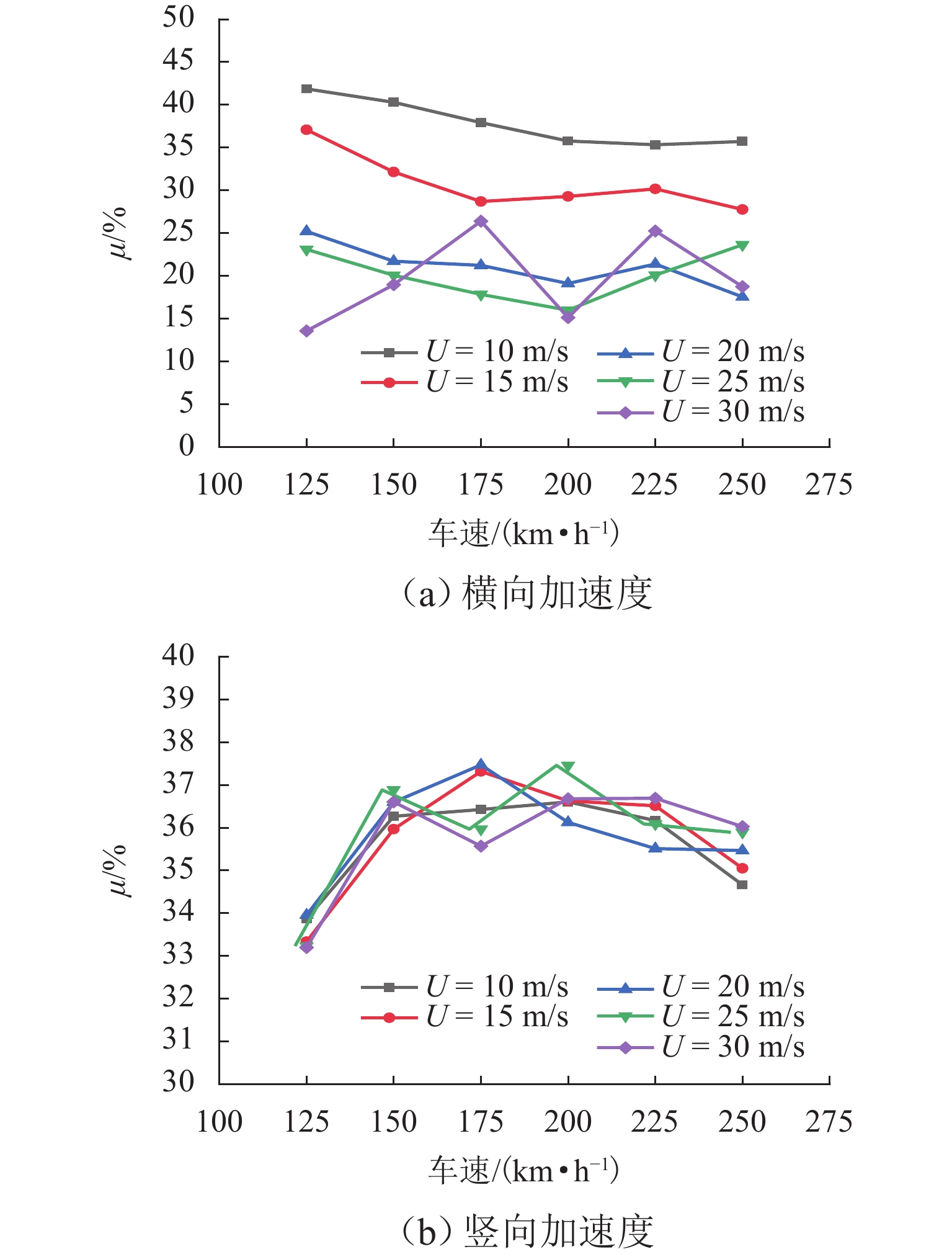
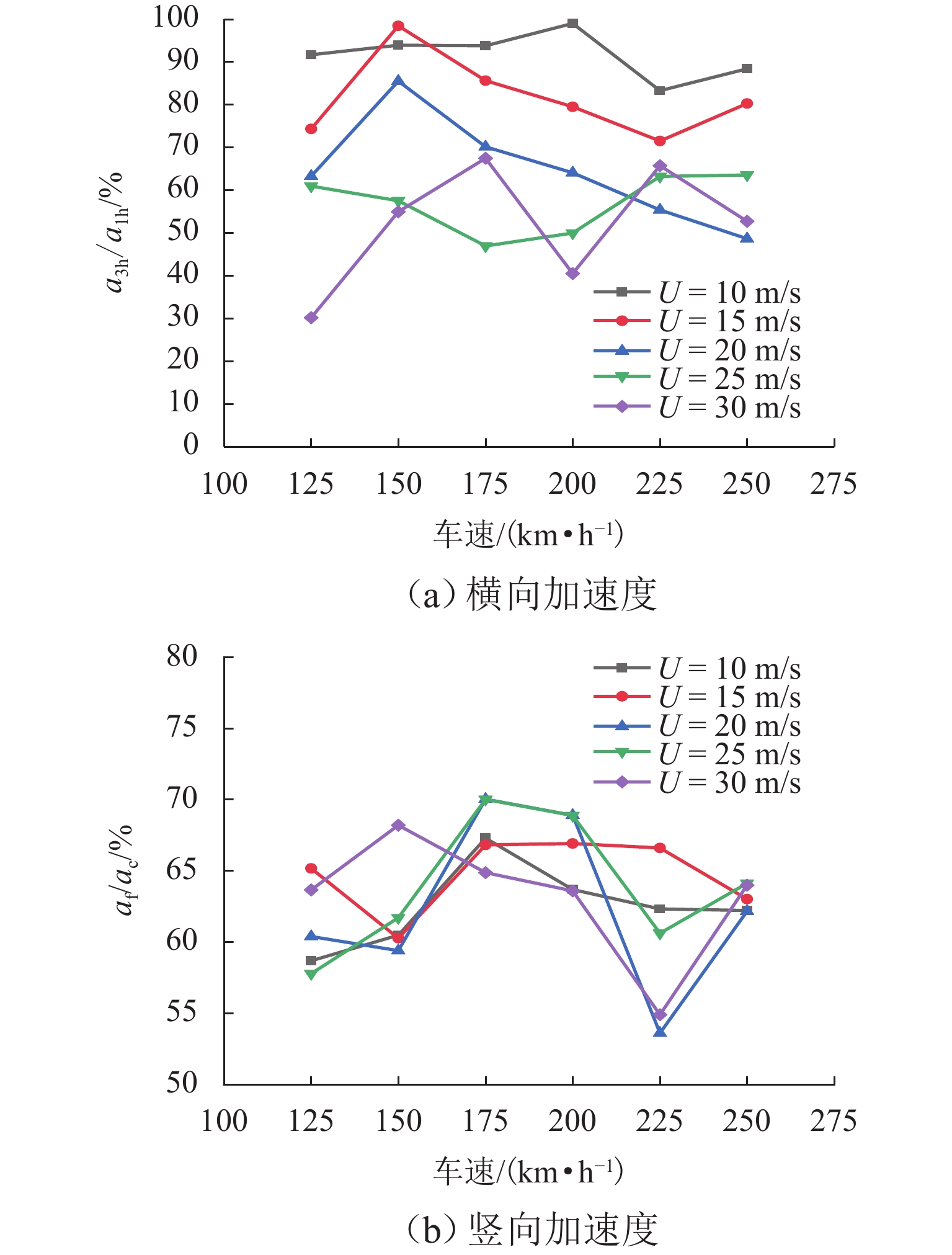
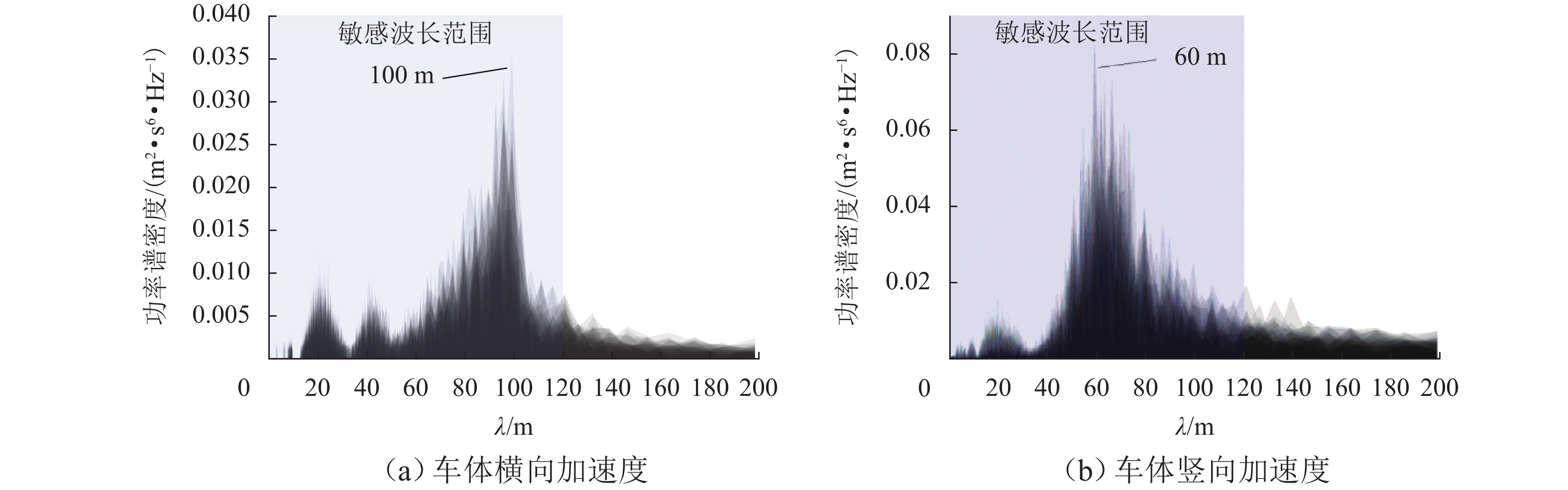
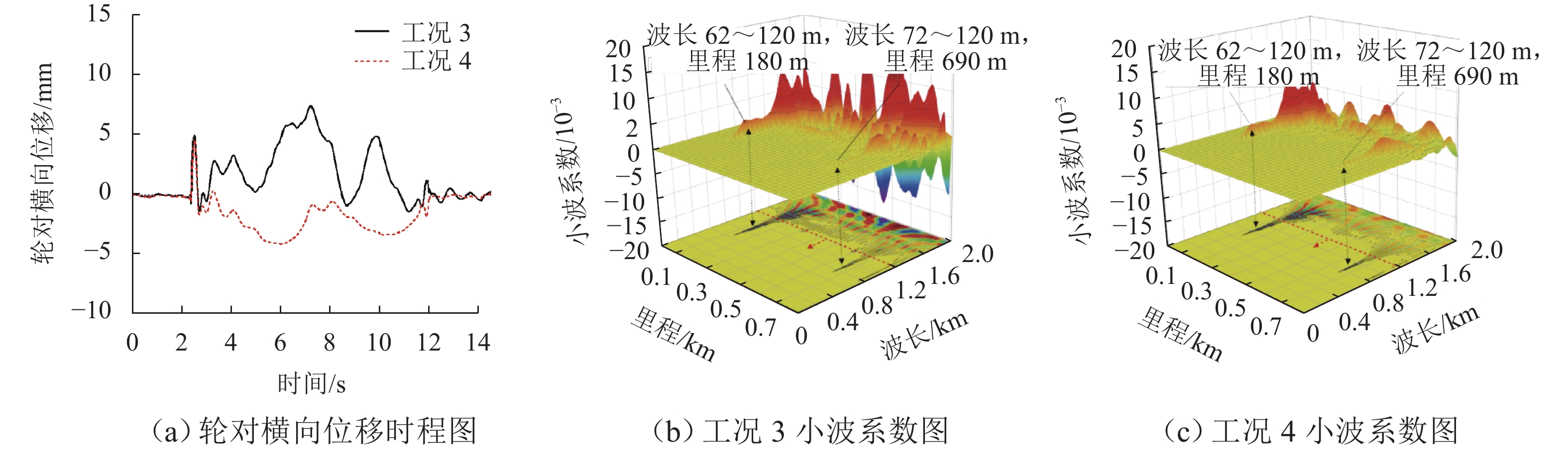
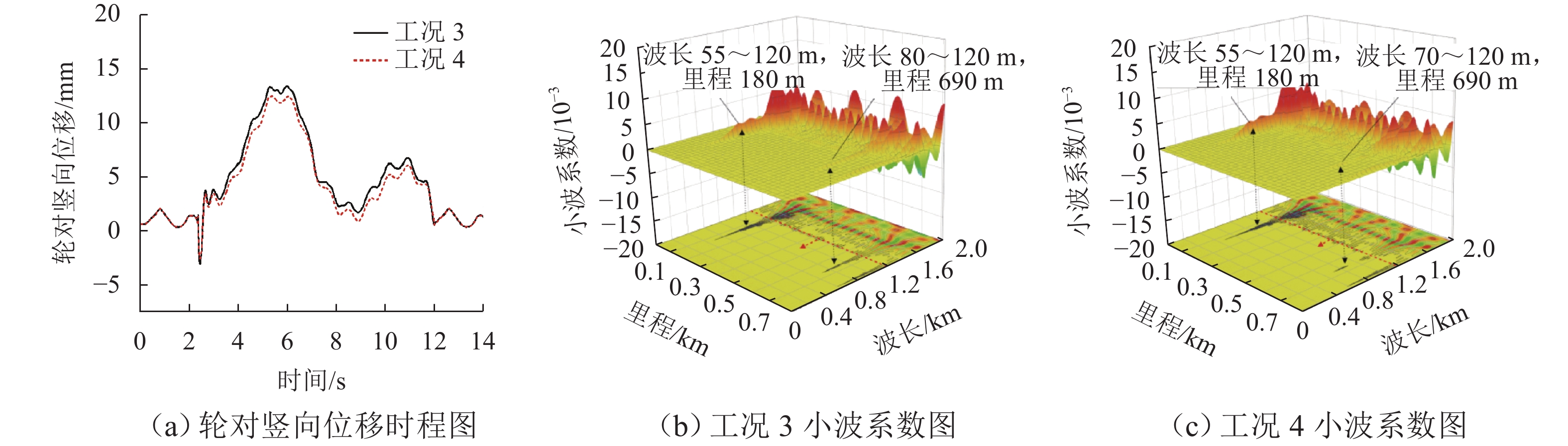
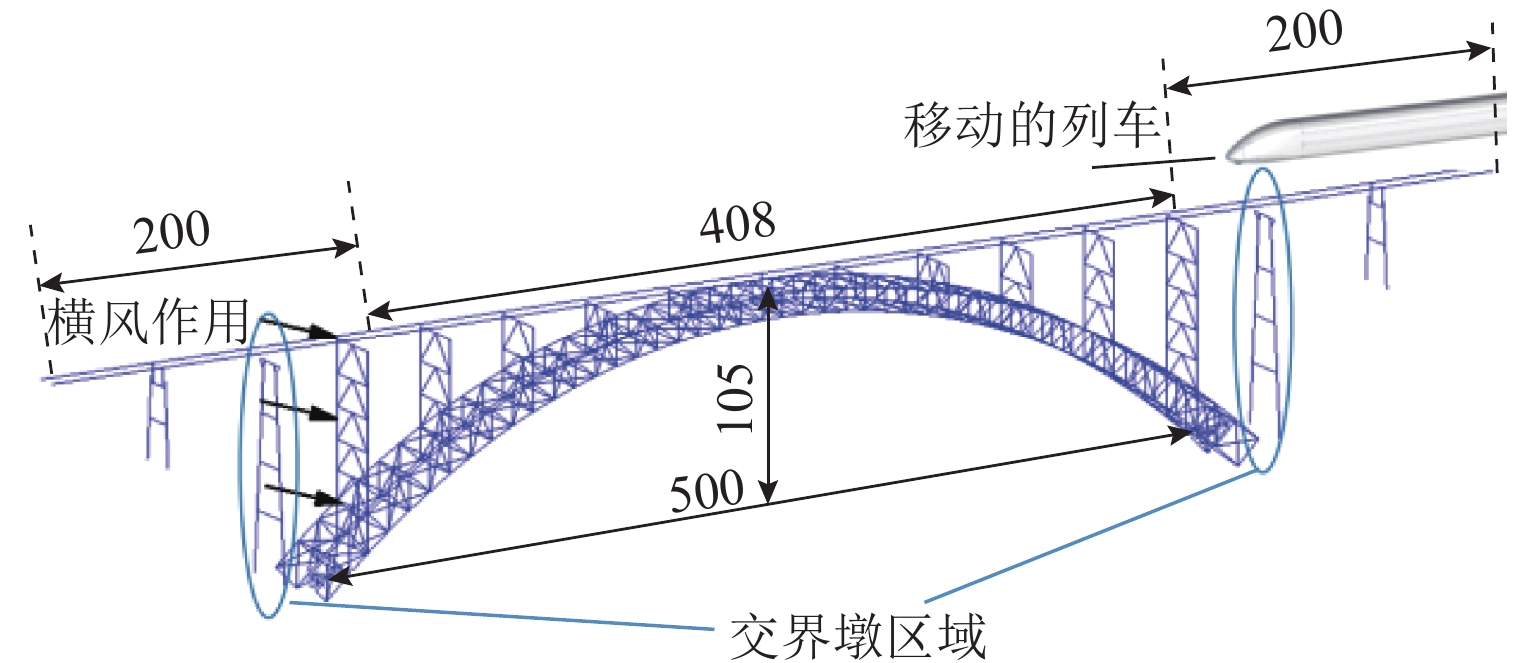
为探求侧风下的拱桥变形对列车平稳性的作用机理，通过风-车-桥耦合系统得到跨中横、竖向位移，分析不同风速、车速下的列车行车平稳性，量化桥梁变形对风-车-桥系统中列车横、竖向加速度的贡献；结合车体加速度响应的敏感波长及桥梁变形的时频特性，分析桥梁变形对行车平稳性影响机理. 结果表明：桥梁竖向位移差异较横向位移差异较小，且主要位移由车致桥梁变形产生，最大幅值达到了−9.2 mm；在列车及风荷载作用下，桥梁横向及竖向位移较为显著，但其对列车平稳性的影响主要体现在交界墩位置处，约为其余位置响应的4倍；除交界墩区域，桥上列车的行车平稳性主要由风致列车振动及轨道不平顺决定；车体横向及竖向加速度功率谱密度分布与轨道不平顺的波长密切相关，其对应的敏感波长区间均小于120 m；车体横向及竖向加速度主要受车辆荷载作用引起的桥梁变形影响，而风荷载引起的桥梁变形主要分布于主跨范围内，波长大于120 m，因而未对列车车体加速度产生显著影响.
- 高速列车 /
- 行车平稳性 /
- 桥梁变形 /
- 风荷载 /
- 风-车-桥系统
Abstract:
In order to explore the influence mechanism of arch bridge deformation on the running stability of the train under crosswind, the horizontal and vertical displacement of the mid-span was obtained through the wind, vehicle, and bridge coupling system, and the running stability of the train under different wind speeds and train speeds was analyzed. The contribution of bridge deformation to horizontal and vertical acceleration of the train in the wind, vehicle, and bridge system was quantified. Combined with the sensitive wavelength of the acceleration response of the train and the time-frequency characteristic of bridge deformation, the influence mechanism of bridge deformation on running stability was analyzed. The results show that the vertical displacement difference of the bridge is smaller than the horizontal displacement difference, and the main displacement is caused by the vehicle-induced bridge deformation. The maximum value reaches −9.2 mm. Under the action of train and wind load, the horizontal and vertical displacement of the bridge is more significant, but its influence on the stability of the train is mainly reflected in the position of the junction pier, which is about four times the response of other positions. Except for the junction pier area, the running stability of the train on the bridge is mainly determined by the wind-induced train vibration and track irregularity. The spectral density distribution of horizontal and vertical acceleration power of the train is closely related to the wavelength of track irregularity, and the corresponding sensitive wavelength range is less than 120 m. The horizontal and vertical acceleration of the train is mainly affected by the bridge deformation caused by the vehicle load, while the bridge deformation caused by wind load is mainly distributed in the main span, and the wavelength is larger than 120 m. Therefore, it does not exert a significant impact on the acceleration of the train.
- high-speed train /
- running stability /
- bridge deformation /
- wind load /
- wind, vehicle, and bridge system

HTML全文

拱桥由于其刚度大、跨越能力强的特点，常常被作为山区桥梁的结构形式^[1-2]. 受山区大风天气影响，大跨度铁路拱桥在强侧风及列车作用下会产生显著的桥梁变形，对桥上高速列车行车带来了巨大的挑战，使得侧风下桥上高速列车的行车平稳性评估成为当前高速列车安全运营领域的研究热点.

开展桥上列车行车平稳性研究涉及风场模拟、气动参数识别及车桥动力仿真等^[3-5]. 在风场模拟方面：Liu等^[6]结合可控的非高斯随机变量模拟目标非高斯速度分布；靖洪淼等^[7]基于计算流体动力学（CFD）软件改进了计算域形态，设置了地形过渡段，并获得了计算域入口风速条件；沈炼等^[8]基于WRF （weather research and forecasting）与CFD耦合模式对峡谷桥址风场进行精细化分析. 在气动参数识别方面：Li等^[9]研究了侧风作用下双车交会通过跨度为32 m的简支箱梁桥的气动特性；He等^[10]研究了风洞中大跨度桁架梁桥内部铁路车厢的静止模型的空气动力学，分析了桁架桥梁配置的主要参数对空气动力学的影响；Ma等^[11]研究了双箱梁的气动特性；于洪刚^[12]探讨了自激力和气动导纳等因素对抖振响应的影响. 在动力仿真方面：李永乐等^[13]分析了波高、风速、车速对耦合模型车辆和桥梁响应的影响；韩万水等^[14]对现有风-车-桥耦合振动系统进行精细化改进；韩艳等^[15]发展了一种可以考虑抖振力空间相关性的风-车-桥耦合振动分析方法；李沅璋^[16]计算了基于梁格法建模的车桥耦合振动响应，并根据规范对车辆的走行性进行了验证.

侧风作用下，桥上列车的行车平稳性取决于2个方面：一方面，风荷载会作用于列车车体本身，直接影响其动力性能；另一方面，风荷载会通过作用于桥梁结构，产生桥梁变形以改变列车的空间运行轨迹，从而间接地影响其动力性能. 风-车-桥耦合系统振动分析可以同时兼顾上述2个方面的影响，以有效评估其行车平稳性，但也不可避免地将风荷载导致的列车振动与桥梁振动对高速列车行车平稳性的影响融为一体，而无法明确其各自的影响. 本文基于风-车-桥耦合系统振动模型，针对大跨度拱桥桥梁变形对列车的行车平稳性影响，将列车气动力参数设置为0，得到风致桥梁变形对于列车行车平稳性影响；将桥梁气动力参数设置为0，得到风荷载对列车行车平稳性影响；对于上述工况中存在的轨道不平顺和列车自重的影响，再分别设置工况进行计算. 对比以上工况，可以揭示桥梁变形对侧风作用下桥上高速列车行车平稳性中的影响规律及作用机理，从而明确侧风作用下桥上高速列车行车平稳性的主要控制因素.

1. 分析模型

1.1 风-车-桥耦合系统

本文以某山区大跨度上承式钢管混凝土拱桥为工程背景，开展风-车-桥耦合振动分析. 如图1所示，桥梁全长808 m，全桥总布置为：（50＋2 × 75） m T构＋（1～500 m）上承式钢管混凝土拱＋（2 × 75＋50） m T构. 线路为国铁Ⅰ级的客货共线四线铁路，桥上线间距取5 m，桥面宽23.5 m，轨道类型为有砟轨道，设计速度200 km/h，列车采用CRH3型8节客车编组.

图 1 风-车-桥系统（单位：m）

Figure 1. Wind, vehicle, and bridge system (unit: m)

下载: 全尺寸图片幻灯片

风-车-桥耦合振动系统主要由3个动力学子模型组成，包括列车模型、轨道结构模型、大跨度拱桥模型和风荷载. CRH3列车由8辆相同的客车组成，每辆客车包含1个车体、2个相同的转向架和4个轮对，总共达到35个自由度^[17]，其车体的自振特性如表1所示；拱桥为MIDAS建立的三维有限元模型. 列车轮轨力通过轨道传递到桥面，考虑轨道系统的弹性效应；有砟轨道由钢轨、紧固件、钢筋混凝土轨枕和道床组成. 2条钢轨都被认为是基于离散弹性点支撑的无限长欧拉梁，而轨枕被认为是刚体，钢轨与轨枕、轨枕与道床、道床和路基之间由线性弹簧和黏性阻尼连接^[18]；作用在车桥系统上的风荷载考虑了横向、竖向和扭转方向，同时考虑了静风力和抖振力. 具体而言，可以根据沿桥梁跨度模拟点生成的风速时程^[19]获得作用在列车和桥梁上的抖振力时程. 在分析模型中，通过联合求解式（1）得到列车、轨道和桥梁子系统的动力响应结果.

表 1 列车自振特性

Table 1. Vibration characteristics of the train

阶数	频率/Hz	振型描述
1	0.451	车体绕下心
2	0.803	车体绕上心
3	0.840	车体沉浮
4	0.878	车体摇头
5	1.056	车体点头

下载: 导出CSV

| 显示表格

$\left\{\begin{aligned} &{M_{\text{b}}}{\ddot x_{\text{b}}} + {C_{\text{b}}}{\dot x_{\text{b}}} + {K_{\text{b}}}{x_{\text{b}}} = {F_{{\text{stb}}}} + {F_{{\text{bub}}}} + {F_{{\text{seb}}}} + {F_{{\text{tb}}}} ,\\ &{M_{\text{t}}}{\ddot x_{\text{t}}} + {C_{\text{t}}}{\dot x_{\text{t}}} + {K_{\text{t}}}{x_{\text{t}}} = {F_{{\text{bt}}}} + {F_{{\text{vt}}}},\\ &{M_{\text{v}}}{\ddot x_{\text{v}}} + {C_{\text{v}}}{\dot x_{\text{v}}} + {K_{\text{v}}}{x_{\text{v}}} = {F_{{\text{stv}}}} + {F_{{\text{buv}}}} + {F_{{\text{tv}}}} , \end{aligned}\right.$

(1)

式中： $M、C、K$ 分别为广义质量、广义阻尼和广义刚度，下标b、t、v分别代表桥梁、轨道、列车； $\ddot x、\dot x、x$ 分别为加速度、速度和位移； ${F_{{\text{stb}}}}、{F_{{\text{bub}}}}、{F_{{\text{seb}}}}$ 分别为桥梁受到的静风力、抖振力和自激力； ${F_{{\text{tb}}}}、{F_{{\text{bt}}}}$ 分别为轨道与桥梁间相互作用力； ${F_{{\text{tv}}}}、{F_{{\text{vt}}}}$ 分别为轨道与列车的相互作用力； ${F_{{\text{stv}}}}、{F_{{\text{buv}}}}$ 分别为列车受到的静风力和抖振力.

1.2 车-桥系统气动参数

列车及桥梁的三分力系数由风场试验获取，该试验在西南交通大学XNJD-1风洞中进行，试验段断面为2.4 m （宽） × 2.0 m （高）的矩形，最大来流风速为45 m/s，最小来流风速为0.5 m/s，如（a）. 试验段中设有专为桥梁节段模型静力三分力试验用的侧壁支撑及测力天平系统，选择了1∶50的缩尺比例模拟桥梁节段和列车. 该模型由环氧树脂板和优质木材制成. 静态三点受力试验中桥段模型有侧壁支撑和受力平衡系统. 由美国PSI公司生产的780B数据采集系统完成数据采集. 根据风轴坐标系，作用在列车截面上的静态三分力及参数如（b）所示，图中： ${M_{\text{z}}}$ 为车体受到的扭矩，H为列车模型高度， $B$ 为列车模型宽度.

图 2 参数定义及风洞试验

Figure 2. Parameter definition and wind tunnel test

下载: 全尺寸图片幻灯片

风轴坐标系中的阻力系数 ${C_{\text{D}}}$ 、升力系数 ${C_{\text{L}}}$ 和扭矩系数 ${C_{\text{M}}}$ 定义为^[20]

$\left\{\begin{aligned} &{C_{\text{D}}} = \frac{{2{F_{\text{y}}}}}{{\rho {U^2}HL}} ,\\ &{C_{\text{L}}} = \frac{{2{F_{\text{x}}}}}{{\rho {U^2}BL}},\\ & {C_{\text{M}}} = \frac{{2{M_{\text{z}}}}}{{\rho {U^2}{B^2}L}}, \end{aligned}\right.$

(2)

式中： ${F_{\text{y}}}$ 为车体所受到的阻力；L为列车模型长度； ${F_{\text{x}}}$ 为车体所受到的升力； $U$ 为平均风速； $\rho$ 为空气密度，取值 1.225 kg/m³.

本桥拱肋受风荷载影响显著，对于拱肋，其截面多为常规断面，其三分力系数可以参考《公路桥梁抗风设计规范（JTG/T 3360-01—2018）》^[21]第5.4.2条表5.4.2-1对常规断面三分力的建议值，本计算采用的是圆形截面的三分力系数，风-车-桥系统的气动参数如表2.

表 2 风-车-桥系统气动参数

Table 2. Aerodynamic parameters of wind-vehicle-bridge system

对象	C_D	C_L	C_M
主梁	1.098	0.010	−0.036
列车	1.257	0.070	0.068
拱肋	0.600

下载: 导出CSV

| 显示表格

1.3 风场模拟与轨道不平顺

本文使用分散点的风速而不是连续的空间风场来模拟桥梁周围的风场. 具体而言，采用IEC推荐的Kaimal谱和Davenport相干函数引入的谱分解生成随机风场^[22]. 以平均风速U=25 m/s，列车车速V = 200 km/h为例，模拟总长度为1000 m，间隔距离为4 m. 如图3所示，绘制了桥面跨中位置的横向和竖向风速. 通过模拟点与行驶列车的时空关系对模拟点处的风速进行插值得到作用于车体的风速.

图 3 桥面脉动风速与行进列车仿真时程

Figure 3. Simulated time history of fluctuating wind speed and running train at bridge deck

下载: 全尺寸图片幻灯片

通过使用德国轨道谱的反向傅里叶变换来模拟轨道不平顺^[22-24]. 本文最大运行速度为250 km/h，仿真取最小波长为0.5 m，最大波长为200.0 m.

1.4 计算工况

计算工况如表3所示,“√”表示考虑了该因素，否则不考虑. 列车车体平稳性由风荷载、轨道不平顺激励和桥梁位移三者共同决定，可以借助风-车-桥系统（工况1）综合考虑，其中，风荷载的作用主要体现在：一方面，风荷载通过直接作用于列车车体影响列车动力响应，由列车自身风荷载和随机不平顺激励产生的车体加速度可由工况2量化；另一方面，风荷载作用于桥梁结构上会引起桥梁变形，从而间接地影响列车动力响应，考虑到列车运行同样会引起桥梁变形，因此，风致及车致桥梁变形对车体加速度的影响可以由工况3获取，而列车单独作用下产生的车致桥梁变形对车体加速度的影响可以通过工况4计算获取.

表 3 风-车-桥耦合系统计算工况

Table 3. Working conditions of wind-vehicle-bridge coupling system

工况	车辆风荷载	轨道不平顺	桥梁风荷载	桥梁位移
工况 1	√	√	√	√
工况 2	√	√
工况 3			√	√
工况 4				√

下载: 导出CSV

| 显示表格

2. 风-车-桥系统耦合效应分析

图4绘制了V = 200 km/h，U = 25 m/s时，桥梁跨中点的横、竖向位移时程图，由于工况2未涉及桥梁变形，因此只绘制了工况1、3、4的结果. 从图4（a）可以看出：随着列车上桥，到抵达跨中位移，再到驶离跨中，3种工况下桥梁的横向位移呈现出不同的变化，其中，工况1横向位移最大值达到了−30 mm，工况3最大值为−13 mm，而工况4仅有−2 mm. 上述分析表明：跨中横向位移同时取决于列车响应和桥梁风荷载影响，由工况3和工况4对比可知，风致桥梁变形明显大于车致桥梁变形；由工况3和工况1对比可知，列车的自身风荷载和随机不平顺影响对跨中横向位移具有显著的影响. 从图4（b）可以看出：3个工况下桥梁的竖向位移差异较横向位移差异较小，且主要的位移由工况4中的车致桥梁变形产生，最大幅值达到了−9.2 mm；对比工况3和工况4可知，风致桥梁变形仅引起了−0.3 mm的竖向位移增幅；而考虑列车的自身风荷载和随机不平顺影响后，最大竖向位移由工况3中的−9.5 mm变为−10.5 mm.

图 4 桥梁跨中横、竖向变形

Figure 4. Horizontal and vertical deformations of bridge mid-span

下载: 全尺寸图片幻灯片

行车平稳性指标包含车体加速度和Sperling指标，其中Sperling指标由车体加速度决定，故在本文中选取车体横、竖向加速度开展行车平稳性影响分析.

图5给出了V = 200 km/h，U = 25 m/s时，4种工况下车体横向加速度的时程曲线. 从图5（a）发现：1）工况1的车体加速度主要由工况2贡献，仅在交界墩区有较为明显的差异，而工况3和工况4在该区域呈现出明显的加速度响应. 上述分析表明，在不考虑交界墩区域时，桥上其余位置处的列车动力响应主要由列车的自身风荷载和轨道随机不平顺贡献，而交界墩区的列车动力响应与风致/车致桥梁变形有关. 2）对比工况3和工况4的时程曲线发现，交界墩区车体横向加速度主要由车致桥梁变形贡献，风致桥梁变形的影响较小. 从图5（b）中可以看出：在绝大部分桥梁里程范围内，工况1的竖向加速度基本与工况2相当，在两处交界墩位置，二者存在明显差异；工况3和工况4呈现出相同的车体竖向加速度，且在交界墩位置处表现出明显的加速度响应；工况1与工况2的差异主要由工况3和工况4中的桥梁变形引起，且该桥梁变形主要是车致桥梁变形，风致桥梁变形的影响并不明显.

图 5 车体横、竖向加速度时程图

Figure 5. Time history of horizontal and vertical accelerations of train

下载: 全尺寸图片幻灯片

图6给出了U = 25 m/s时，车速对车体横、竖向加速度的影响. 从图6中可以看出：列车的横向加速度主要呈现在左、右桥墩位置处，其余区域加速度接近于0，且左侧桥墩位置处加速度响应要大于右侧桥墩区域；随着车速增大，左侧桥墩处的车体横向加速度有所增大，而其余区域变化不明显；图6（b）中列车的竖向加速度时程曲线沿桥跨的分布趋势与车体横向加速度一致，但车速的增加并未引起明显的车体竖向加速度变化.

图 6 车速对工况3车体横、竖向加速度影响

Figure 6. Influence of train speed on horizontal and vertical accelerations of train under working condition No.3

下载: 全尺寸图片幻灯片

图7给出了V = 200 km/h时，不同风速对车体横向、竖向加速度的影响. 从图7中可以看出：风速对车体加速度的影响仍然集中在两侧交界墩区域，其中左侧交界墩区域的横、竖向加速度大于右侧的；同时，随着风速的提高，交界墩区域的横向加速度略有增大，而竖向加速度几乎未受影响. 从上述分析可以看出，桥梁变形对列车车体加速度的影响主要体现在交界墩区域，且风速和车速的影响也仅仅是影响交界墩处的横向加速度响应，而竖向加速度受影响不明显.

图 7 风速对工况3车体横、竖向加速度影响

Figure 7. Influence of wind speed on horizontal and vertical accelerations of train under working condition No. 3

下载: 全尺寸图片幻灯片

为量化分析桥梁变形对风-车-桥系统中列车横、竖向加速度的贡献，结合上述风速及车速参数分析，基于工况1和工况3所获取的车体横、竖向加速度时程曲线开展样本统计分析，得到不同风速及车速下工况3与工况1的车体加速度标准差百分比μ，以量化风-车-桥系统中桥梁变形对车体加速度的贡献，如图8所示. 从图中可以看出：桥梁变形对车桥系统中列车横向加速度标准差的贡献最大为40%，发生在风速10 m/s时，随着风速的增大，该比值逐渐减小，说明高风速下风致列车振动的贡献越来越大；在各级风速下，车速的影响并未对标准差比值产生明显影响；对列车竖向加速度而言，工况3与工况1的标准差比值随车速和风速均发生明显变化，说明桥梁变形对风-车-桥系统中列车竖向加速度的贡献比较固定.

图 8 横、竖向加速度标准差占比统计

Figure 8. Standard deviation ratio of horizontal and vertical accelerations

下载: 全尺寸图片幻灯片

考虑到桥梁变形对列车加速度的影响主要体现在交界墩区域，图9统计了工况3与工况1的横、竖向加速度峰值比值. 图中：a_1h、a₃_h分别为工况1、3的横向加速度峰值，a_f、a_c分别为风桥、风车桥竖向加速度峰值. 从图中可以看出：当风速较低时，桥上列车的横向加速度主要由桥梁变形引起；当风速增大时，桥梁变形的贡献开始减弱，从峰值上看，其贡献最低为30%，发生在车速125 km/h、风速30 m/s时；随着车速的改变，工况3与工况1的横向加速度峰值比值略有波动；对竖向加速度而言，桥梁变形引起的峰值约为风-车-桥系统中车体竖向加速度峰值的65%；且风速和车速改变对该比值的影响较小. 上述分析表明，除两侧交界墩区域，桥上列车的行车平稳性主要由作用于列车上的风荷载和轨道不平顺决定，对于交界墩区域，其行车平稳性受桥梁变形影响较为显著，而桥梁变形对车体平稳性的贡献将随着风速的增大而逐渐减小.

图 9 横、竖向加速度峰值占比统计

Figure 9. Peak ratio of horizontal and vertical accelerations

下载: 全尺寸图片幻灯片

3. 桥梁变形对行车平稳性影响机理分析

由图4和图5可知，侧风及列车荷载作用下，桥梁虽产生了可观的风致及车致桥梁变形，但对桥上列车运行平稳性的影响并不显著，仅在交界墩处产生一定的影响. 为解释上述现象，本节将结合车体加速度响应的敏感波长分析及桥梁变形的时频特性分析，针对桥梁变形对行车平稳性影响机理展开研究.

无论是轨道不平顺还是桥梁变形，都是通过改变列车行驶过程中的轮对空间线形来影响列车行车平稳性的. 为探究列车车体加速度的轮对空间线形敏感波长信息，图10结合随机不平顺样本分析绘制了车体横、竖向加速度随波长分布的功率谱密度. 采用图3中的轨道不平顺反演方法生成了30个随机不平顺样本，上下截止波长分别为0.5～300.0 m. 由图10可知：车体的横向及竖向加速度功率谱密度分布与轨道不平顺的波长密切相关，以200 km/h时速为例，车体的横向及竖向加速度敏感波长λ分别为100 m和60 m，而对应的敏感波长区间均小于120 m波长. 当轨道不平顺的波长超过120 m时，其线形对车体横、竖向加速度的影响并不明显.

图 10 车体加速度敏感波长分析

Figure 10. Analysis of sensitive wavelength of train acceleration

下载: 全尺寸图片幻灯片

为探索桥上列车轮对空间线形的波长组成，获取列车第一轮对处的空间位移，并采用小波分析开展轮对空间位移的时频分析. 图11给出了V = 200 km/h，U = 25 m/s时，工况3、4下的轮对横向位移时程曲线及小波系数图. 由图11（a）可知：工况3中由于风荷载的存在，其轮对横向位移在主跨范围内明显大于工况4的轮对横向位移. 结合图11（b）中工况3轮对横向位移小波系数图可以发现：在车体横向加速度敏感波长120 m范围内，两侧交界墩区域存在明显的幅值，分别为左侧交界墩位置存在波长62～120 m的变形成分，右侧交界墩位置存在波长72～120 m的变形成分，其中，左侧交界墩处幅值要大于右侧交界墩处幅值，而其余位置处的线形幅值虽然十分明显，但其波长均大于120 m. 结合图10的车体加速度敏感波长分析得出，工况3的桥梁变形由于仅在两侧交界墩位置产生小于120 m的线形成分，所以导致了图5（a）车体横向加速度仅体现在两侧交界墩处. 同时，对比图11（b）和图11（c）中工况3和工况4的小波系数图看出：二者在波长120 m范围内具有相同的幅值，预示着交界墩位置处120 m波长范围内的桥梁变形主要是由工况4中的车致桥梁变形引起，而工况3中的风致桥梁变形主要引起的是桥梁主跨范围内的桥梁变形，且波长大于车体敏感波长.

图 11 轮对横向位移时程与小波系数图

Figure 11. Time history of wheel set horizontal displacement and wavelet coefficients

下载: 全尺寸图片幻灯片

图12为V = 200 km/h，U = 25 m/s时，工况3、工况4的轮对竖向位移时程曲线及小波系数图. 与横向轮对位移有所不同，工况3、4下的轮对竖向位移沿桥跨方向的变化趋势较为接近，列车接近桥梁跨中位置时，竖向位移达到最大值. 对比图12（b）、图12（c）发现，在120 m波长范围内，两侧交界墩区域存在明显的幅值，左侧交界墩位置存在波长55～120 m的变形成分，右侧交界墩位置存在波长80～120 m的变形成分，且左侧交界墩处幅值要大于右侧交界墩处幅值，与图5（b）车体竖向加速度沿桥跨分布趋势是吻合的. 上述分析说明：桥梁变形对车体横、竖向加速度的影响取决于桥梁线形中是否存在车体加速度敏感波长范围内的线形成分及其分布位置；针对大跨度拱桥，在风荷载及列车荷载作用产生的桥梁变形，对车体加速度有影响的是由列车荷载引起的桥梁变形成分，尽管风荷载会引起显著的桥梁横向变形，但该变形成分大于120 m波长，因而，未对列车车体加速度产生显著影响.

图 12 轮对竖向位移时程和小波系数图

Figure 12. Time history of wheel set vertical displacement and wavelet coefficients

下载: 全尺寸图片幻灯片

4. 结　论

1）侧风作用下，影响桥上列车行车平稳性的因素与桥梁跨径有关：在交界墩区域范围内，其行车平稳性同时受桥梁变形、风致列车振动及随机不平顺影响；在非交界墩区域范围，其行车平稳性由风致列车振动及随机不平顺激励决定，而桥梁变形的影响可以忽略.

2）在交界墩区域，由风荷载及列车荷载作用产生的风致及车致桥梁变形，对车体加速度起决定作用的是车致桥梁变形；随着风速增大，桥梁变形对风-车-桥耦合系统中列车行车平稳性的贡献逐渐减小，而车速对该贡献影响不明显.

3）轮对空间位移的时频分析表明：桥梁变形对行车平稳性沿桥跨方向的不同影响取决于桥梁线形中是否存在车体加速度敏感波长范围内的变形成分；侧风作用下，大跨度拱桥两侧交界墩区域存在上述变形成分，因而导致该区域出现明显的车体加速度响应；同时该变形成分主要由车致桥梁变形产生，风荷载主要引起大波长范围内的桥梁变形，因而对列车平稳性影响不显著.

图 1 风-车-桥系统（单位：m）

Figure 1. Wind, vehicle, and bridge system (unit: m)

下载: 全尺寸图片幻灯片

图 2 参数定义及风洞试验

Figure 2. Parameter definition and wind tunnel test

下载: 全尺寸图片幻灯片

图 3 桥面脉动风速与行进列车仿真时程

Figure 3. Simulated time history of fluctuating wind speed and running train at bridge deck

下载: 全尺寸图片幻灯片

图 4 桥梁跨中横、竖向变形

Figure 4. Horizontal and vertical deformations of bridge mid-span

下载: 全尺寸图片幻灯片

图 5 车体横、竖向加速度时程图

Figure 5. Time history of horizontal and vertical accelerations of train

下载: 全尺寸图片幻灯片

图 6 车速对工况3车体横、竖向加速度影响

Figure 6. Influence of train speed on horizontal and vertical accelerations of train under working condition No.3

下载: 全尺寸图片幻灯片

图 7 风速对工况3车体横、竖向加速度影响

Figure 7. Influence of wind speed on horizontal and vertical accelerations of train under working condition No. 3

下载: 全尺寸图片幻灯片

图 8 横、竖向加速度标准差占比统计

Figure 8. Standard deviation ratio of horizontal and vertical accelerations

下载: 全尺寸图片幻灯片

图 9 横、竖向加速度峰值占比统计

Figure 9. Peak ratio of horizontal and vertical accelerations

下载: 全尺寸图片幻灯片

图 10 车体加速度敏感波长分析

Figure 10. Analysis of sensitive wavelength of train acceleration

下载: 全尺寸图片幻灯片

图 11 轮对横向位移时程与小波系数图

Figure 11. Time history of wheel set horizontal displacement and wavelet coefficients

下载: 全尺寸图片幻灯片

图 12 轮对竖向位移时程和小波系数图

Figure 12. Time history of wheel set vertical displacement and wavelet coefficients

下载: 全尺寸图片幻灯片

表 1 列车自振特性

Table 1. Vibration characteristics of the train

阶数频率/Hz 振型描述

1 0.451 车体绕下心
2 0.803 车体绕上心
3 0.840 车体沉浮
4 0.878 车体摇头
5 1.056 车体点头

下载: 导出CSV

表 2 风-车-桥系统气动参数

Table 2. Aerodynamic parameters of wind-vehicle-bridge system

对象 C_D C_L C_M

主梁 1.098 0.010 −0.036
列车 1.257 0.070 0.068
拱肋 0.600

下载: 导出CSV

表 3 风-车-桥耦合系统计算工况

Table 3. Working conditions of wind-vehicle-bridge coupling system

工况车辆风荷载轨道不平顺桥梁风荷载桥梁位移

工况 1 √ √ √ √
工况 2 √ √
工况 3 √ √
工况 4 √

下载: 导出CSV

参考文献(24)

[1]	TAN Y B, HE X W, SHI L, et al. Reinforcement effect evaluation on dynamic characteristics of an arch bridge based on vehicle-bridge coupled vibration analysis[J]. Computer Modeling in Engineering & Sciences, 2022, 131(2): 1041-1061.
[2]	唐俊峰,何玮,郭向荣,等. 风攻角对强风下大跨度斜拉桥车-桥耦合振动的影响[J]. 中南大学学报(自然科学版),2018,49(7): 1760-1767. TANG Junfeng, HE Wei, GUO Xiangrong, et al. Influence of wind attack angle on vehicle-bridge coupling vibration for long-span cable-stayed bridge during strong wind[J]. Journal of Central South University (Science and Technology), 2018, 49(7): 1760-1767.
[3]	徐昕宇. 复杂山区铁路风—车—桥系统耦合振动研究[D]. 成都: 西南交通大学, 2017.
[4]	QIN S Q, FENG J C, ZHOU Y L, et al. Investigation on the dynamic impact factor of a concrete filled steel tube butterfly arch bridge[J]. Engineering Structures, 2022, 252: 113614.1-113614.14.
[5]	JING H M, LIAO H L, MA C M, et al. Field measurement study of wind characteristics at different measuring positions in a mountainous valley[J]. Experimental Thermal and Fluid Science, 2020, 112: 109991.1-109991.18.
[6]	LIU C, FU L, YANG D, et al. Non-gaussian Lagrangian stochastic model for wind field simulation in the surface layer[J]. Advances in Atmospheric Sciences, 2020, 37(1): 90-104. doi: 10.1007/s00376-019-9052-7
[7]	靖洪淼,廖海黎,周强,等. 一种山区峡谷桥址区风场特性数值模拟方法[J]. 振动与冲击,2019,38(16): 200-207. JING Hongmiao, LIAO Haili, ZHOU Qiang, et al. A numerical simulation method for wind field characteristics of mountainous valley at bridge site[J]. Journal of Vibration and Shock, 2019, 38(16): 200-207.
[8]	沈炼,华旭刚,韩艳,等. 高精度入口边界的峡谷桥址风场数值模拟[J]. 中国公路学报,2020,33(7): 114-123. SHEN Lian, HUA Xugang, HAN Yan, et al. Numerical simulation of wind field at canyon bridges with high precision inlet boundary[J]. China Journal of Highway and Transport, 2020, 33(7): 114-123.
[9]	LI X Z, TAN Y L, QIU X W, et al. Wind tunnel measurement of aerodynamic characteristics of trains passing each other on a simply supported box girder bridge[J]. Railway Engineering Science, 2021, 29(2): 152-162. doi: 10.1007/s40534-021-00231-4
[10]	HE X H, LI H, HU L, et al. Crosswind aerodynamic characteristics of a stationary interior railway carriage through a long-span truss-girder bridge[J]. Engineering Structures, 2020, 210: 110350.1-110350.19.
[11]	MA C M, PEI C, LIAO H L, et al. Field measurement and wind tunnel study of aerodynamic characteristics of twin-box girder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 202: 104209.1-104209.14.
[12]	于洪刚. 大跨度拱桥气动参数识别及风致响应研究[D]. 上海: 同济大学, 2008.
[13]	李永乐,房忱,向活跃. 风-浪联合作用下大跨度桥梁车-桥耦合振动分析[J]. 中国公路学报,2018,31(7): 119-125. LI Yongle, FANG Chen, XIANG Huoyue. Coupled vibration analysis of vehicle-bridge for long-span bridge under wind and wave[J]. China Journal of Highway and Transport, 2018, 31(7): 119-125.
[14]	韩万水,刘焕举,包大海,等. 大跨钢桁梁悬索桥风-车-桥分析系统建立与可视化实现[J]. 土木工程学报,2018,51(3): 99-108. HAN Wanshui, LIU Huanju, BAO Dahai, et al. Establishment and visualization of wind-vehicle-bridge analysis system for the large-span steel truss suspension bridge[J]. China Civil Engineering Journal, 2018, 51(3): 99-108.
[15]	韩艳,陈浩,刘跃飞,等. 桥梁抖振力空间相关性对风-车-桥耦合动力响应的影响[J]. 湖南大学学报(自然科学版),2015,42(9): 82-88. HAN Yan, CHEN Hao, LIU Yuefei, et al. Effect of the coherence of buffeting forces of bridges on the coupled dynamic responses of wind-vehicle-bridge system[J]. Journal of Hunan University (Natural Sciences), 2015, 42(9): 82-88.
[16]	李沅璋. 基于梁格法的刚构拱桥静动力力学性能分析[D]. 北京: 北京交通大学, 2017.
[17]	刘德军. 风-列车-线路-桥梁系统耦合振动研究[D]. 成都: 西南交通大学, 2010.
[18]	辛莉峰,李小珍,朱艳. 基于eFAST方法的车—线—桥耦合系统全局敏感性分析[J]. 中国铁道科学,2019,40(4): 46-51. XIN Lifeng, LI Xiaozhen, ZHU Yan. Global sensitivity analysis of vehicle-track-bridge coupling system based on eFAST method[J]. China Railway Science, 2019, 40(4): 46-51.
[19]	徐磊,翟婉明. 横风和轨道不平顺联合作用下的车辆-轨道系统随机分析模型[J]. 振动工程学报,2018,31(1): 39-48. XU Lei, ZHAI Wanming. The vehicle-track stochastic model considering joint effects of cross-winds and track random irregularities[J]. Journal of Vibration Engineering, 2018, 31(1): 39-48.
[20]	BULJAC A, KOZMAR H, POSPÍŠIL S, et al. Effects of wind-barrier layout and wind turbulence on aerodynamic stability of cable-supported bridges[J]. Journal of Bridge Engineering, 2020, 25(12): 04020102.1-04020102.18.
[21]	中华人民共和国交通运输部. 公路桥梁抗风设计规范: JTG/T 3360-01—2018[S]. 北京: 人民交通出版社, 2018.
[22]	宋玉鹏,陈建兵,彭勇波. 二维空间脉动风场波数-频率联合功率谱表达的FFT模拟[J]. 振动工程学报,2020,33(4): 660-666. SONG Yupeng, CHEN Jianbing, PENG Yongbo. Simulation of fluctuating wind field in two-spatial dimensions by FFT implementation of wavenumber-frequency joint power spectrum[J]. Journal of Vibration Engineering, 2020, 33(4): 660-666.
[23]	李小珍, 张效邦, 郑净, 等. 400 km/h高铁桥上直立式声屏障的列车风致振动[J]. 西南交通大学学报, 2024, 59（6）: 1415-1422 LI Xiaozhen, ZHANG Xiaobang, ZHENG Jing, et al. Wind-induced vibration of 400 km/h trains with vertical soundbarrier on highspeed railway bridge[J]. Journal of Southwest Jiaotong University, 2024, 59(6): 1415-1422
[24]	陈士军,凌贤长,朱占元,等. 轨道高低不平顺谱分析[J]. 地震工程与工程振动,2012,32(5): 33-38. CHEN Shijun, LING Xianchang, ZHU Zhanyuan, et al. Analyses of track vertical profile irregularity spectra[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(5): 33-38.

施引文献

附加材料(0)

访问统计

点击查看大图

图(12) / 表(3)

计量

文章访问数: 426
HTML全文浏览量: 190
PDF下载量: 133
被引次数: 0

1. 分析模型
1.1 风-车-桥耦合系统
1.2 车-桥系统气动参数
1.3 风场模拟与轨道不平顺
1.4 计算工况
2. 风-车-桥系统耦合效应分析
3. 桥梁变形对行车平稳性影响机理分析
4. 结　论

侧风下大跨拱桥变形对高速列车行车平稳性的影响机理

doi: 10.3969/j.issn.0258-2724.20220598

作者简介: 李小珍（1970—），男，教授，研究方向为风-车-桥耦合振动，E-mail：xzhli@swjtu.edu.cn

通讯作者: 王铭（1989—），男，副研究员，研究方向为风-车-桥耦合振动， E-mail：ming.wang@swjtu.edu.cn

计量

出版历程