基于机电液耦合的钢轨打磨模型

曾鲁庆; 崔大宾; 李立

doi:10.3969/j.issn.0258-2724.20220577

基于机电液耦合的钢轨打磨模型

doi: 10.3969/j.issn.0258-2724.20220577

曾鲁庆^{1, 2,},
崔大宾¹,
李立^1, ,

1.
西南交通大学机械工程学院，四川成都 610031
2.
成都工业学院智能制造学院，四川成都 610031

基金项目: 四川省科技计划（2021YJ0026）

详细信息

作者简介:
曾鲁庆（1981—），男，博士研究生，研究方向为钢轨打磨，E-mail：51642328@qq.com

通讯作者:
李立(1966—) ，女，教授，博士，研究方向为钢轨打磨、轮轨关系，E-mail：lili@swjtu.edu.cn

中图分类号: U216.65
计量
- 文章访问数: 135
- HTML全文浏览量: 56
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-20
- 修回日期: 2024-01-18
- 网络出版日期: 2024-07-25

Rail Grinding Model Based on Mechanical-Electric-Hydraulic Coupling

ZENG Luqing^{1, 2
,},
CUI Dabin¹,
LI Li^{1
, ,}

1.
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
School of Intelligent Manufacturing, Chengdu Technological University, Chengdu 610031, China

摘要

摘要:
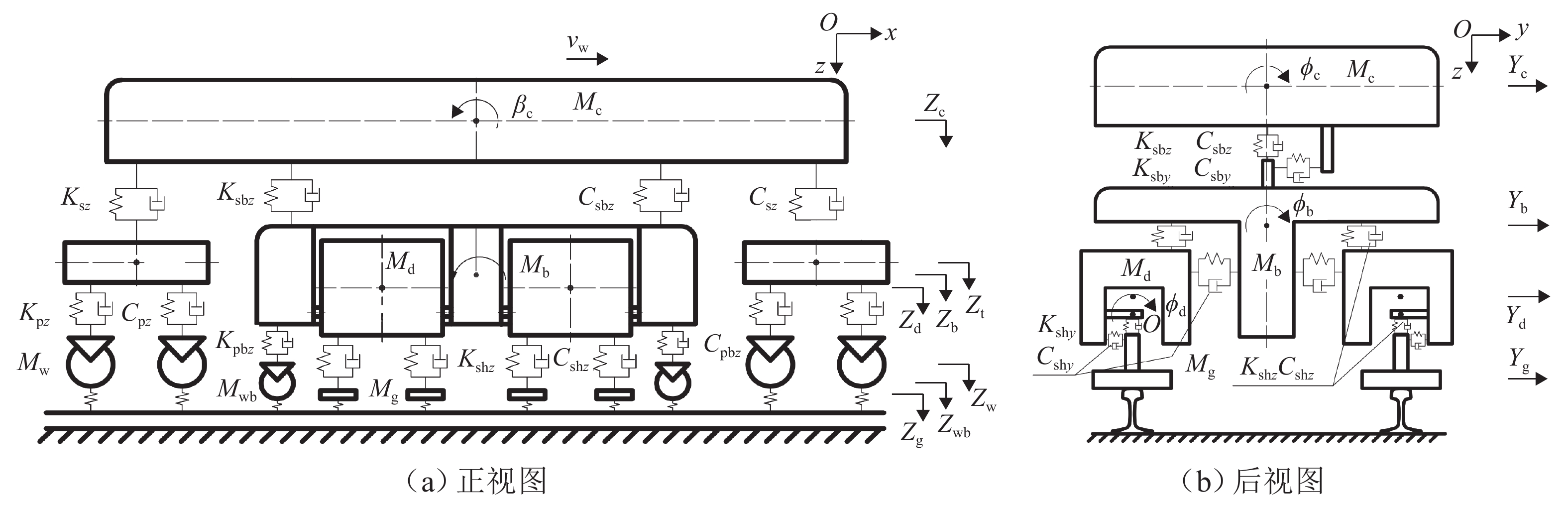
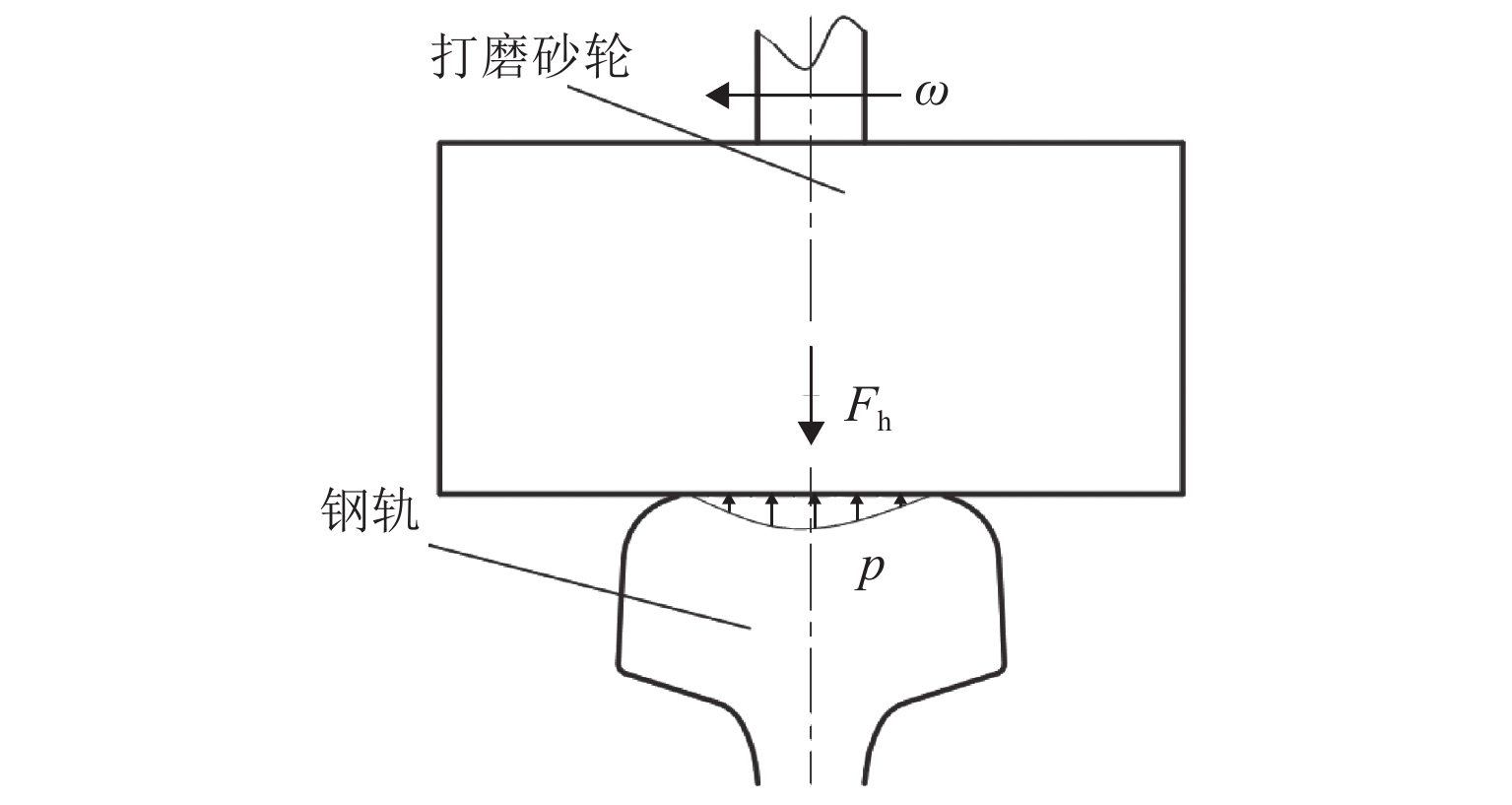
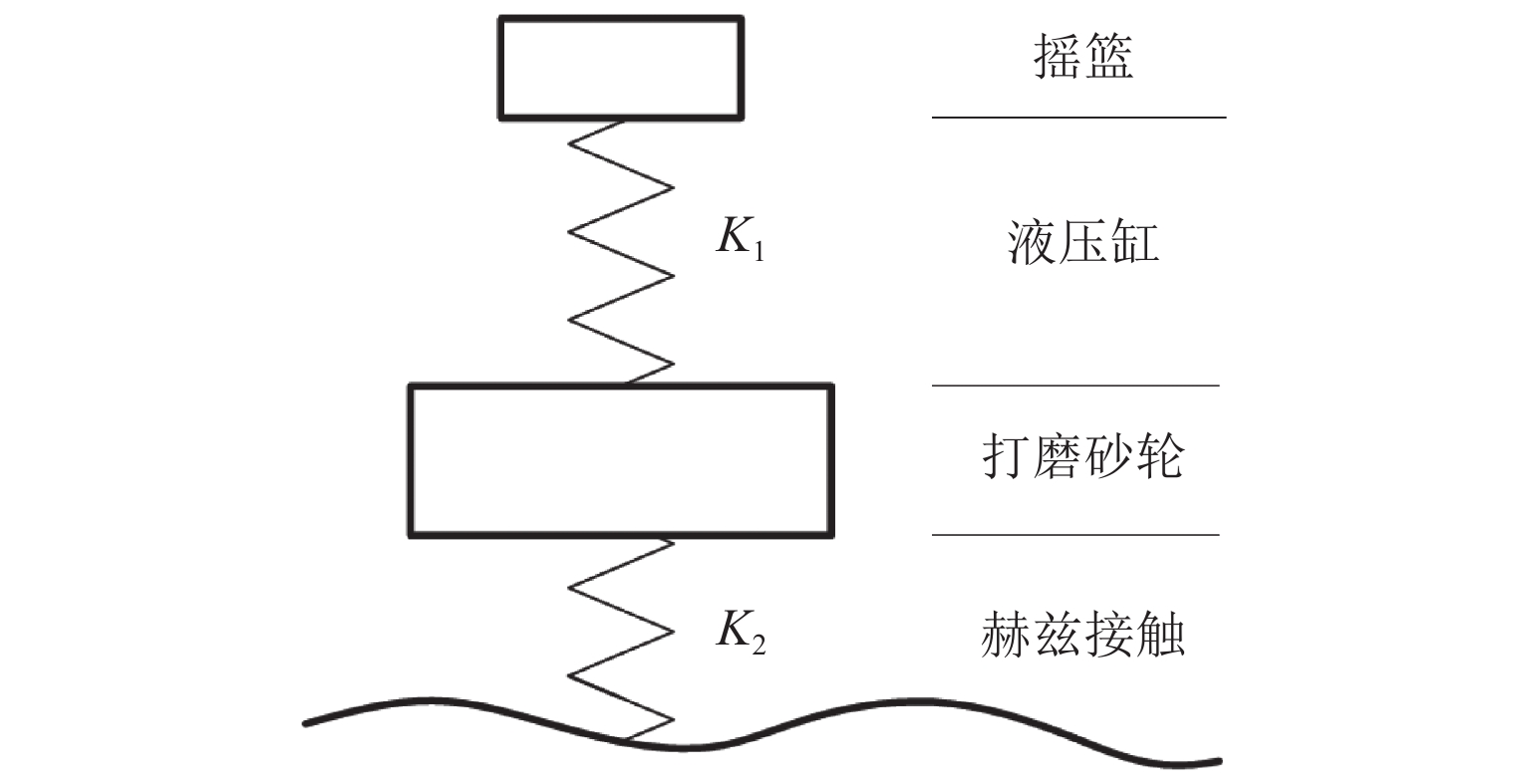
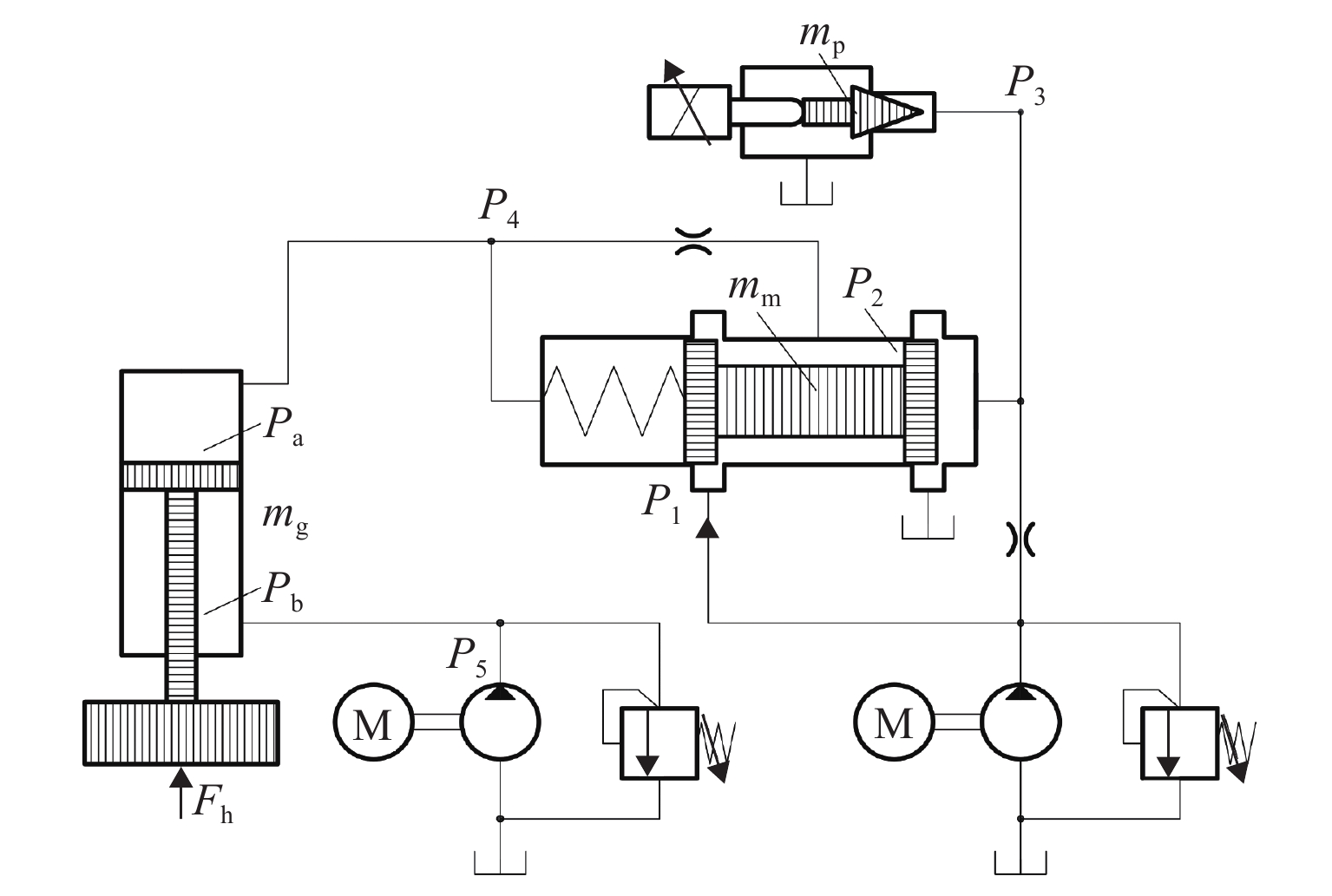
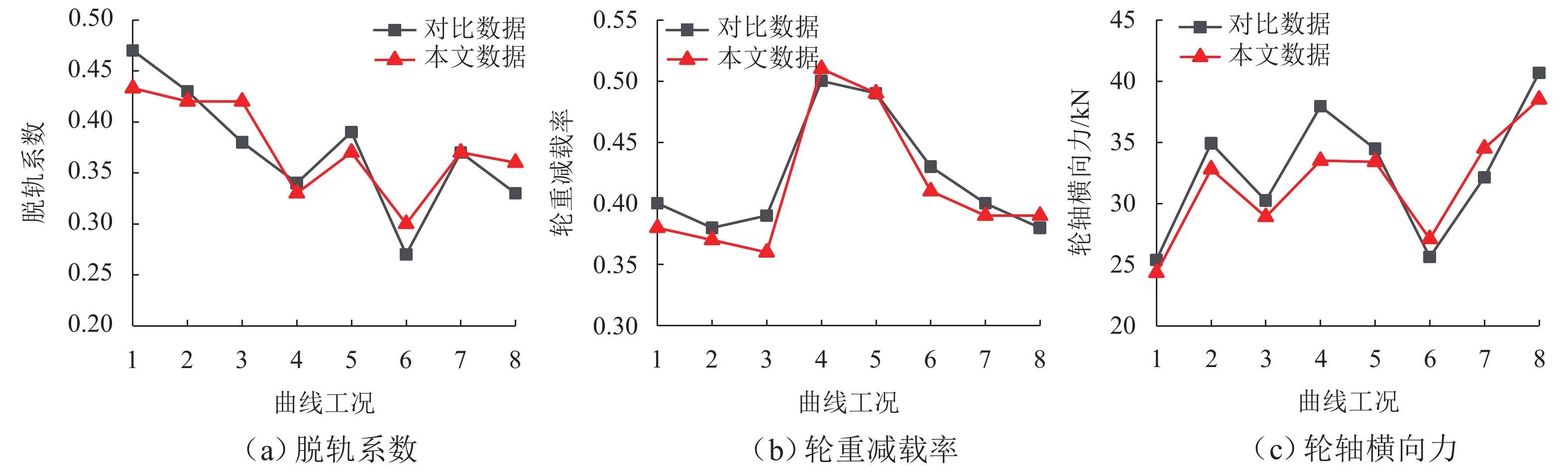
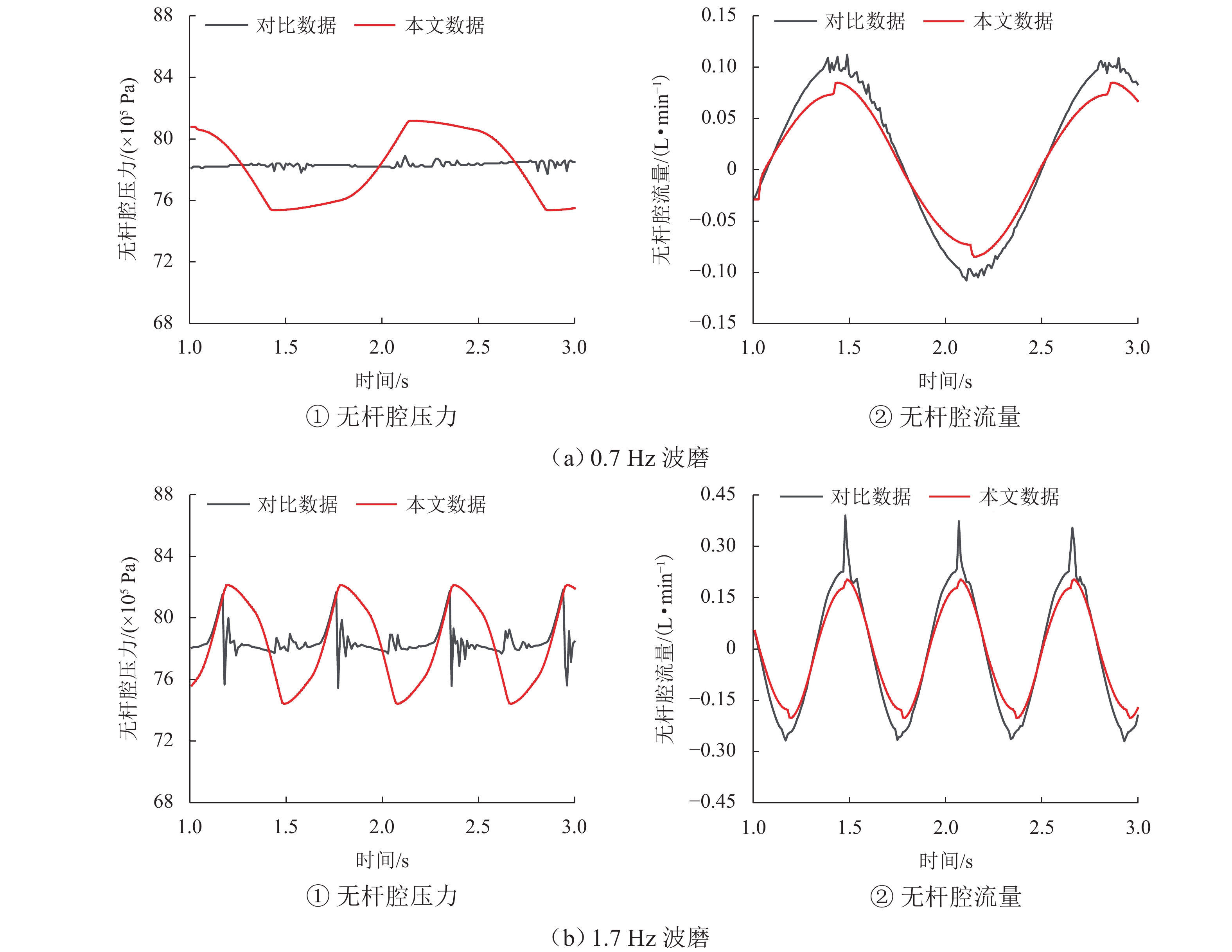
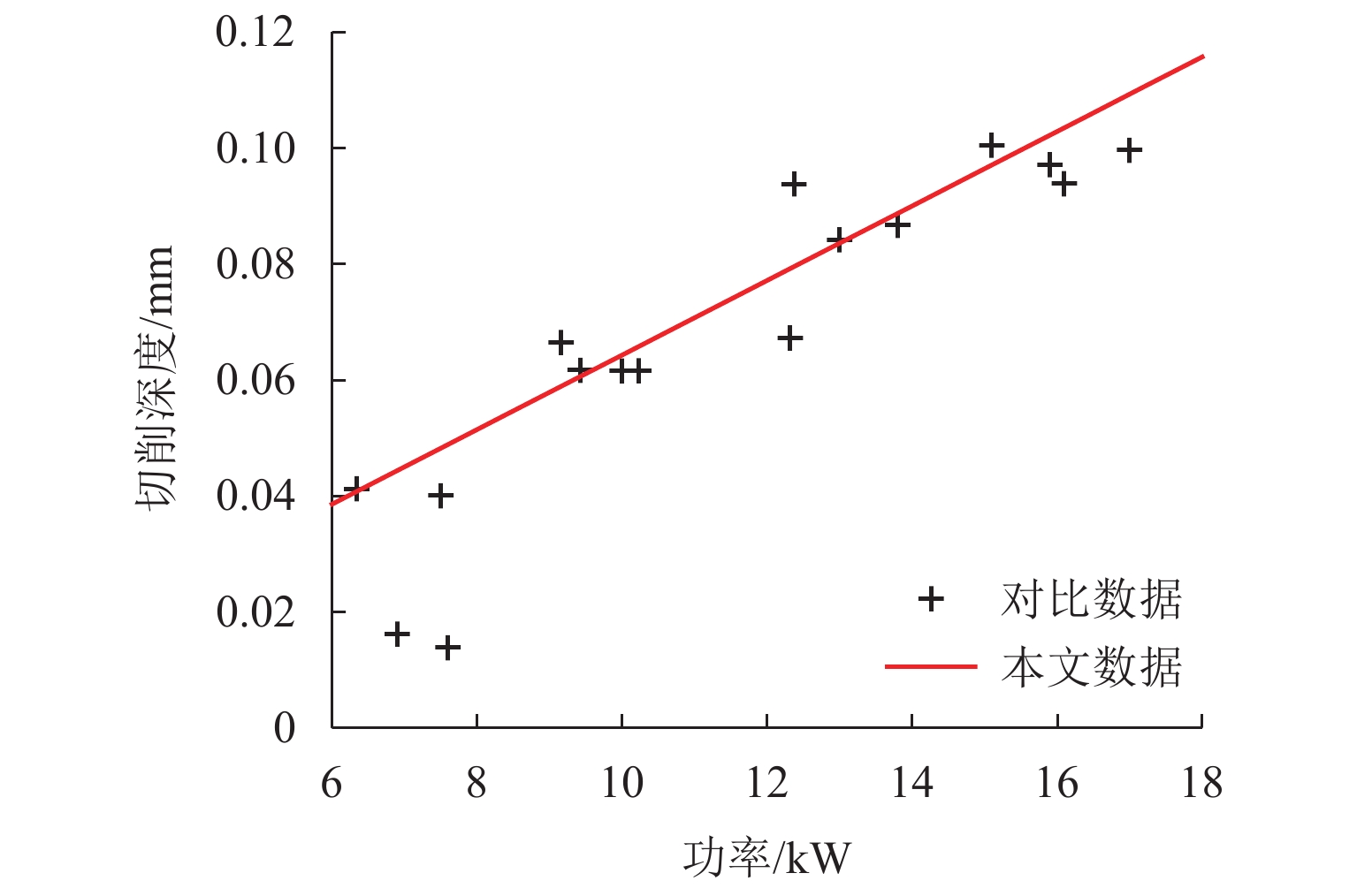
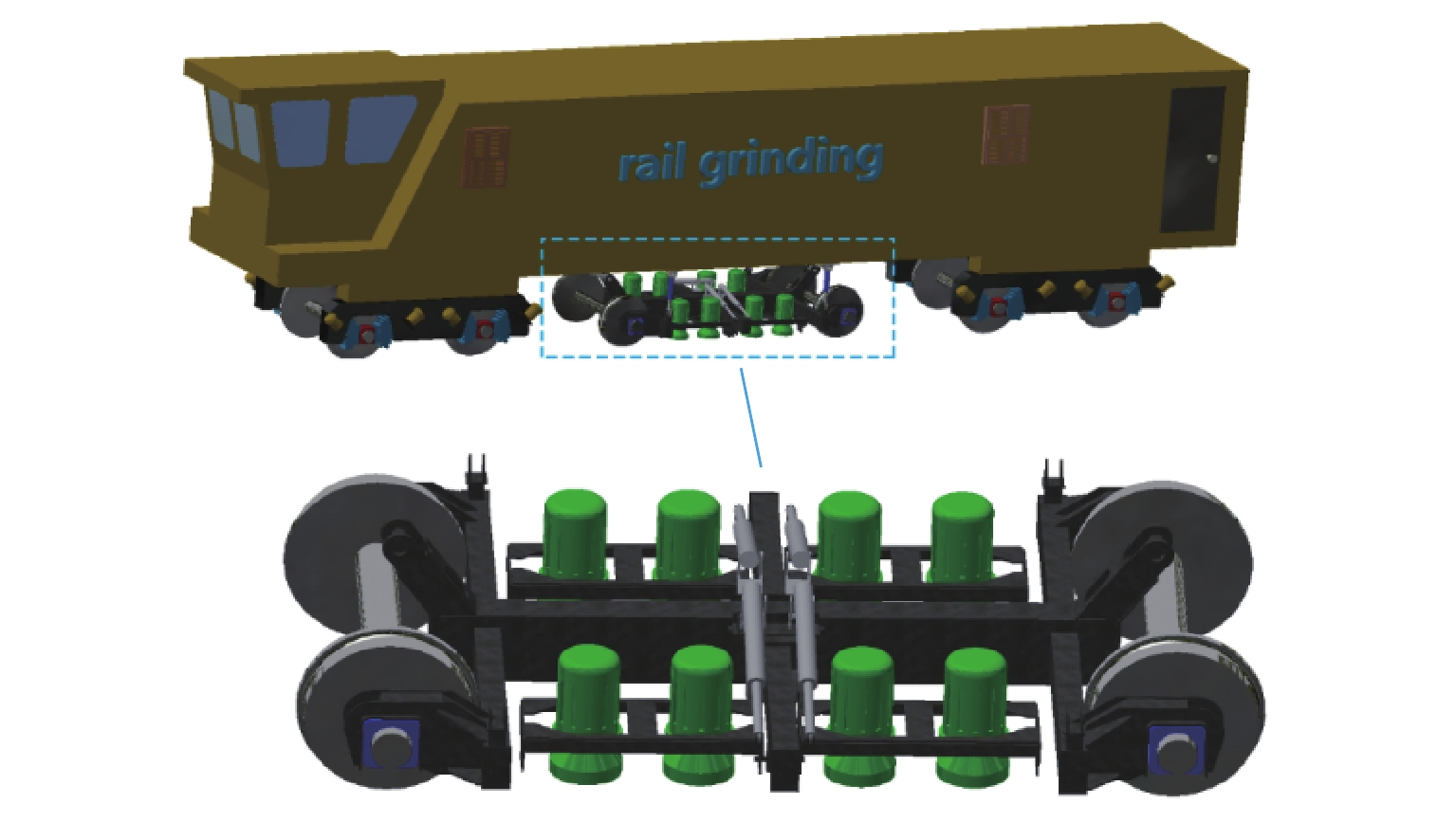
钢轨打磨发生在钢轨打磨车行驶过程中，会受到钢轨打磨车动力学性能的影响. 钢轨打磨一般设置为恒功率打磨，涉及到砂轮钢轨接触关系、砂轮钢轨磨削关系、液压系统、控制系统等，是一个机电液耦合过程. 在考虑机电液耦合的钢轨打磨过程中，基于车辆轨道耦合动力学，建立机电液耦合的钢轨打磨整体模型，包含车辆轨道耦合动力学子模型、砂轮钢轨接触子模型、磨削子模型、液压系统子模型；通过与已有的实验数据对比，对该钢轨打磨模型进行验证. 研究结果表明：车辆轨道动力学模型验证时，脱轨系数最大误差为11.11%，轮重减载率最大误差为7.69%，轮轴横向力最大误差为11.68%；液压控制模型验证时，在0.7 Hz与1.7 Hz波磨下，无杆腔压力偏差率分别为−2.96%～2.92%、−0.32%～1.38%，无杆腔流量偏差率为−24.11%～0、−48.72%～0；磨削模型验证时，整体趋势一致，最大偏差点处偏差量为0.036 mm；以上偏差均在可接受范围内，此模型能应用于实际的钢轨打磨研究中.
- 钢轨打磨 /
- 动力学性能 /
- 机电液耦合 /
- PID控制 /
- 赫兹接触
Abstract:
Rail grinding occurs when the rail grinder is in traveling status, which is affected by the dynamic performance of the vehicle. Rail grinding is generally set as constant power grinding, involving a wheel-track contact relationship, wheel-track grinding relationship, hydraulic system, and control system. It is a mechanical-electric-hydraulic coupling process. The whole model of rail grinding based on mechanical-electric-hydraulic coupling was formed by considering the mechanical-electric-hydraulic coupling of the rail grinding process on the basis of vehicle-track coupling dynamics. This model included a vehicle-track coupling dynamics submodel, wheel-track contact submodel, grinding submodel, and hydraulic system submodel. This rail grinding model was validated by comparing it with experimental data. The results show that in vehicle-track dynamics model verification, the maximum deviation of derailment coefficient is 11.11%, and the maximum deviation of wheel unloading rate is 7.69%. The maximum deviation of the lateral force of the wheel is 11.68%. In hydraulic and control model verification, under 0.7 Hz and 1.7 Hz rail corrugation, the deviation range of pressure in the rodless cavity are between (−2.96%–2.92%) and (−0.32%–1.38%), and the deviation range of flow in the rodless cavity are between (−24.11%–0) and (−48.72%–0). In grinding model verification, the trend is generally consistent, with a deviation of 0.036 mm at the point of maximum deviation. The above deviations are all within the acceptable range, proving that this model can be applied to practical rail grinding study.
- rail grinding /
- dynamic performance /
- mechanical-electric-hydraulic coupling /
- PID control /
- Hertz contact

HTML全文

图 1 钢轨打磨车

Figure 1. Rail grinder

下载: 全尺寸图片幻灯片

图 2 打磨车车辆-轨道空间耦合模型

Figure 2. Vehicle-track spatial coupling model of rail grinder

下载: 全尺寸图片幻灯片

图 3 砂轮钢轨接触图

Figure 3. Wheel-track contact

下载: 全尺寸图片幻灯片

图 4 等效弹簧

Figure 4. Equivalent spring

下载: 全尺寸图片幻灯片

图 5 液压模型

Figure 5. Hydraulic submodel

下载: 全尺寸图片幻灯片

图 6 基于机电液耦合钢轨打磨模型

Figure 6. Rail grinding model based on mechanical-electric-hydraulic coupling

下载: 全尺寸图片幻灯片

图 7 打磨作业车的动力学指标

Figure 7. Dynamic indicators of rail grinder

下载: 全尺寸图片幻灯片

图 8 波磨不平顺对打磨压力与流量的影响

Figure 8. Influence of rail irregularity on grinding pressure and flow

下载: 全尺寸图片幻灯片

图 9 磨削深度对比

Figure 9. Grinding depth comparison

下载: 全尺寸图片幻灯片

表 1 曲线设置

Table 1. Curve parameters

曲线工况	曲线半径/m	缓和曲线/m	外轨超高值/m	圆曲线长/m	通过速度/（km·h⁻¹）
1	400	120	0.12	100	70
2	500	110	0.11	100	80
3	600	100	0.10	100	80
4	700	100	0.10	100	100
5	800	100	0.10	100	100
6	1000	90	0.09	100	100
7	1000	90	0.09	100	110
8	1200	80	0.08	100	120

下载: 导出CSV

参考文献(36)

[1]	吴磊,康彦兵,董勇,等. 考虑打磨量的重载钢轨打磨廓形优化设计[J]. 西南交通大学学报,2022,57(4): 805-812. doi: 10.3969/j.issn.0258-2724.20210120 WU Lei, KANG Yanbing, DONG Yong, et al. Optimal design of heavy-haul rail grinding profile considering grinding amount[J]. Journal of Southwest Jiaotong University, 2022, 57(4): 805-812. doi: 10.3969/j.issn.0258-2724.20210120
[2]	王文健,陈明韬,郭俊,等. 高速铁路钢轨打磨技术及其应用[J]. 西南交通大学学报,2007,42(5): 574-577. doi: 10.3969/j.issn.0258-2724.2007.05.011 WANG Wenjian, CHEN Mingtao, GUO Jun, et al. Rail grinding technique and its application in high-speed railway[J]. Journal of Southwest Jiaotong University, 2007, 42(5): 574-577. doi: 10.3969/j.issn.0258-2724.2007.05.011
[3]	李伟,周志军,温泽峰. 地铁弹性短轨枕轨道的钢轨波磨萌生原因[J]. 西南交通大学学报,2021,56(3): 619-626. doi: 10.35741/issn.0258-2724.56.3.50 LI Wei, ZHOU Zhijun, WEN Zefeng. Initiation cause of subway rail corrugation on track with rubber-booted short sleepers[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 619-626. doi: 10.35741/issn.0258-2724.56.3.50
[4]	肖宏,陈鑫,赵越. 基于摩擦自激理论的单侧钢轨波磨机理分析[J]. 西南交通大学学报,2022,57(1): 83-89,119. doi: 10.3969/j.issn.0258-2724.20200033 XIAO Hong, CHEN Xin, ZHAO Yue. Analysis of unilateral rail corrugation mechanism based on friction self-excited theory[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 83-89,119. doi: 10.3969/j.issn.0258-2724.20200033
[5]	从建力,王源,徐舟,等. 振噪融合的地铁钢轨波磨快速测量方法[J]. 西南交通大学学报,2023,58(3): 677-684. doi: 10.3969/j.issn.0258-2724.20220260 CONG Jianli, WANG Yuan, XU Zhou, et al. Rail corrugation measurement method based on vibration-noise fusion in metro system[J]. Journal of Southwest Jiaotong University, 2023, 58(3): 677-684. doi: 10.3969/j.issn.0258-2724.20220260
[6]	ZENG L Q, CUI D B, FU Y D, et al. Analysis on curve negotiating ability of rail grinder in grinding state[J]. Scientific Reports, 2022, 12(1): 11668.1-11668.19.
[7]	ZENG L Q, CUI D B, LI L, et al. Improvement of the hydraulic system in a rail grinder based on the grinding effect[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2023, 237(9): 1140-1151. doi: 10.1177/09544097231156531
[8]	翟婉明. 车辆-轨道耦合动力学-上册[M]. 4版. 北京:科学出版社,2015.
[9]	ZHAI W M, WANG K Y, CAI C B. Fundamentals of vehicle–track coupled dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1349-1376. doi: 10.1080/00423110802621561
[10]	HAHN R S. On the mechanics of the grinding process under plunge cut conditions[J]. Journal of Engineering for Industry, 1966, 88(1): 72-79. doi: 10.1115/1.3670895
[11]	MARINESCU I D, ROWE W B, DIMITROV B, et al. Tribosystems of abrasive machining processes[M]//Tribology of Abrasive Machining Processes. Amsterdam: Elsevier, 2013: 13-31.
[12]	金学松,杜星,郭俊,等. 钢轨打磨技术研究进展[J]. 西南交通大学学报,2010,45(1): 1-11. doi: 10.3969/j.issn.0258-2724.2010.01.001 JIN Xuesong, DU Xing, GUO Jun, et al. State of arts of research on rail grinding[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 1-11. doi: 10.3969/j.issn.0258-2724.2010.01.001
[13]	ZHOU K, DING H H, WANG W J, et al. Influence of grinding pressure on removal behaviours of rail material[J]. Tribology International, 2019, 134: 417-426. doi: 10.1016/j.triboint.2019.02.004
[14]	ZHOU K, DING H H, ZHANG S Y, et al. Modelling and simulation of the grinding force in rail grinding that considers the swing angle of the grinding stone[J]. Tribology International, 2019, 137: 274-288. doi: 10.1016/j.triboint.2019.05.012
[15]	ZHI S D, LI J Y, ZAREMBSKI A M. Modelling of dynamic contact length in rail grinding process[J]. Frontiers of Mechanical Engineering, 2014, 9(3): 242-248. doi: 10.1007/s11465-014-0305-y
[16]	ZHI S D, ZAREMBSKI A M, LI J Y. Towards a better understanding of the rail grinding mechanism[C]// Proceedings of ASME 2013 Rail Transportation Division Fall Technical Conference. Altoona, Pennsylvania: [s.n.], 2013: 15-17.
[17]	LIN B, ZHOU K, GUO J, et al. Influence of grinding parameters on surface temperature and burn behaviors of grinding rail[J]. Tribology International, 2018, 122: 151-162. doi: 10.1016/j.triboint.2018.02.017
[18]	GU K K, LIN Q, WANG W J, et al. Analysis on the effects of rotational speed of grinding stone on removal behavior of rail material[J]. Wear, 2015, 342/343: 52-59. doi: 10.1016/j.wear.2015.08.008
[19]	WANG W J, GU K K, ZHOU K, et al. Influence of granularity of grinding stone on grinding force and material removal in the rail grinding process[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2019, 233(2): 355-365. doi: 10.1177/1350650118779495
[20]	张科元,王文健,郭俊,等. 钢轨打磨过程中打磨压力波动行为分析[J]. 机械强度,2016,38(3): 447-452. ZHANG Keyuan, WANG Wenjian, GUO Jun, et al. Analysis of pressure fluctuation behavior during the rail grinding process[J]. Journal of Mechanical Strength, 2016, 38(3): 447-452.
[21]	王璐颖,罗世辉,马卫华,等. 一系定位刚度对钢轨打磨车动力学性能的影响[J]. 重庆理工大学学报(自然科学),2012,26(8): 12-16. WANG Luying, LUO Shihui, MA Weihua, et al. Effect of primary positioning stiffness on dynamics performance of rail grinding train[J]. Journal of Chongqing University of Technology (Natural Science), 2012, 26(8): 12-16.
[22]	FAN W G, HOU G Y, WANG W X, et al. Dynamic analysis of a novel rail-grinding car using open-structured abrasive belt for high-speed railways[J]. Mathematical Problems in Engineering, 2019, 2019: 1748679.1-1748679.9.
[23]	DU X, JIN X S, ZHAO G T, et al. Rail corrugation of high-speed railway induced by rail grinding[J]. Shock and Vibration, 2021, 2021: 5546809.1-5546809.14.
[24]	付青云,吴磊,陈帅,等. 钢轨打磨对焊接接头区的不平顺及其动力学响应的影响[J]. 润滑与密封,2016,41(3): 66-70,80. doi: 10.3969/j.issn.0254-0150.2016.03.013 FU Qingyun, WU Lei, CHEN Shuai, et al. The effect of rail grinding on weld irregularity and dynamic response[J]. Lubrication Engineering, 2016, 41(3): 66-70,80. doi: 10.3969/j.issn.0254-0150.2016.03.013
[25]	汤万文,胡军科,周创辉. 钢轨打磨车恒压加载系统压力波动分析[J]. 铁道科学与工程学报,2013,10(3): 116-120. doi: 10.3969/j.issn.1672-7029.2013.03.024 TANG Wanwen, HU Junke, ZHOU Chuanghui. Pressure fluctuation analysis on the constant pressure loading system of rail grinding train[J]. Journal of Railway Science and Engineering, 2013, 10(3): 116-120. doi: 10.3969/j.issn.1672-7029.2013.03.024
[26]	聂蒙,李建勇,沈海阔. 基于容腔调节的钢轨打磨压力控制系统[J]. 西南交通大学学报,2015,50(5): 796-802. NIE Meng, LI Jianyong, SHEN Haikuo. Pressure control system for rail grinding based on chamber adjustment[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 796-802.
[27]	戴云飞. 液压缸液压刚度的计算[J]. 有色金属设计,1999,26(1): 62-64. DAI Yunfei. Calculation of hydraulic stiffness of hydraulic cylinder[J]. Nonferrous Metals Design, 1999, 26(1): 62-64.
[28]	张云波. 多体动力学接触与碰撞建模研究[D]. 武汉:华中科技大学,2007.
[29]	SONG P, KRAUS P, KUMAR V, et al. Analysis of rigid-body dynamic models for simulation of systems with frictional contacts[J]. Journal of Applied Mechanics, 2001, 68(1): 118-128. doi: 10.1115/1.1331060
[30]	JOHNSON K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985.
[31]	金学松,刘启跃. 轮轨摩擦学[M]. 北京:中国铁道出版社,2004.
[32]	波波夫. 接触力学与摩擦学的原理及其应用[M]. 2版. 北京:清华大学出版社,2019.
[33]	宋锦春,王长周,蔡衍. 液压系统建模与仿真分析[M]. 沈阳:东北大学出版社,2021.
[34]	杜成义. 某型钢轨打磨列车动力学特性研究[D]. 成都:西南交通大学,2018.
[35]	方立志. 钢轨打磨车打磨装置恒力加载系统的研究[D]. 长沙:中南大学,2012.
[36]	智少丹. 钢轨打磨车磨削过程建模研究[D]. 北京:北京交通大学,2015.