基于时空路径推算的城轨网络客流分配方法

茧敏; 王卓; 陈哲轩; 赵留杰; 陈钱飞; 陈绍宽

doi:10.3969/j.issn.0258-2724.20220545

基于时空路径推算的城轨网络客流分配方法

doi: 10.3969/j.issn.0258-2724.20220545

茧敏^{1, 2,},
王卓¹,
陈哲轩¹,
赵留杰³,
陈钱飞¹,
陈绍宽^{1, 2, ,}

1.
北京交通大学交通运输部综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044
2.
北京交通大学中国综合交通研究中心，北京 100044
3.
郑州地铁集团有限公司运营分公司，河南郑州 450000

基金项目: 国家自然科学基金（71890972，71890970）；北京市自然科学基金（L191023）

详细信息

作者简介:
茧敏（1995—），男，博士研究生，研究方向为交通运输规划与管理，E-mail：20114039@bjtu.edu.cn

通讯作者:
陈绍宽（1977—），男，教授，博士，研究方向为交通运输规划与管理，E-mail：shkchen@bjtu.edu.cn

中图分类号: U293.5
计量
- 文章访问数: 468
- HTML全文浏览量: 89
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-09
- 修回日期: 2022-10-21
- 网络出版日期: 2023-04-11
- 刊出日期: 2022-11-03

Passenger Flow Assignment Method for Urban Rail Transit Networks Based on Inference of Spatiotemporal Path

1.
MOT Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport, Beijing Jiaotong University, Beijing 100044, China
2.
Integrated Transport Research Center of China, Beijing Jiaotong University, Beijing 100044, China
3.
Operation Company of Zhengzhou Metro Co., Ltd., Zhengzhou 450000, China

摘要

摘要:
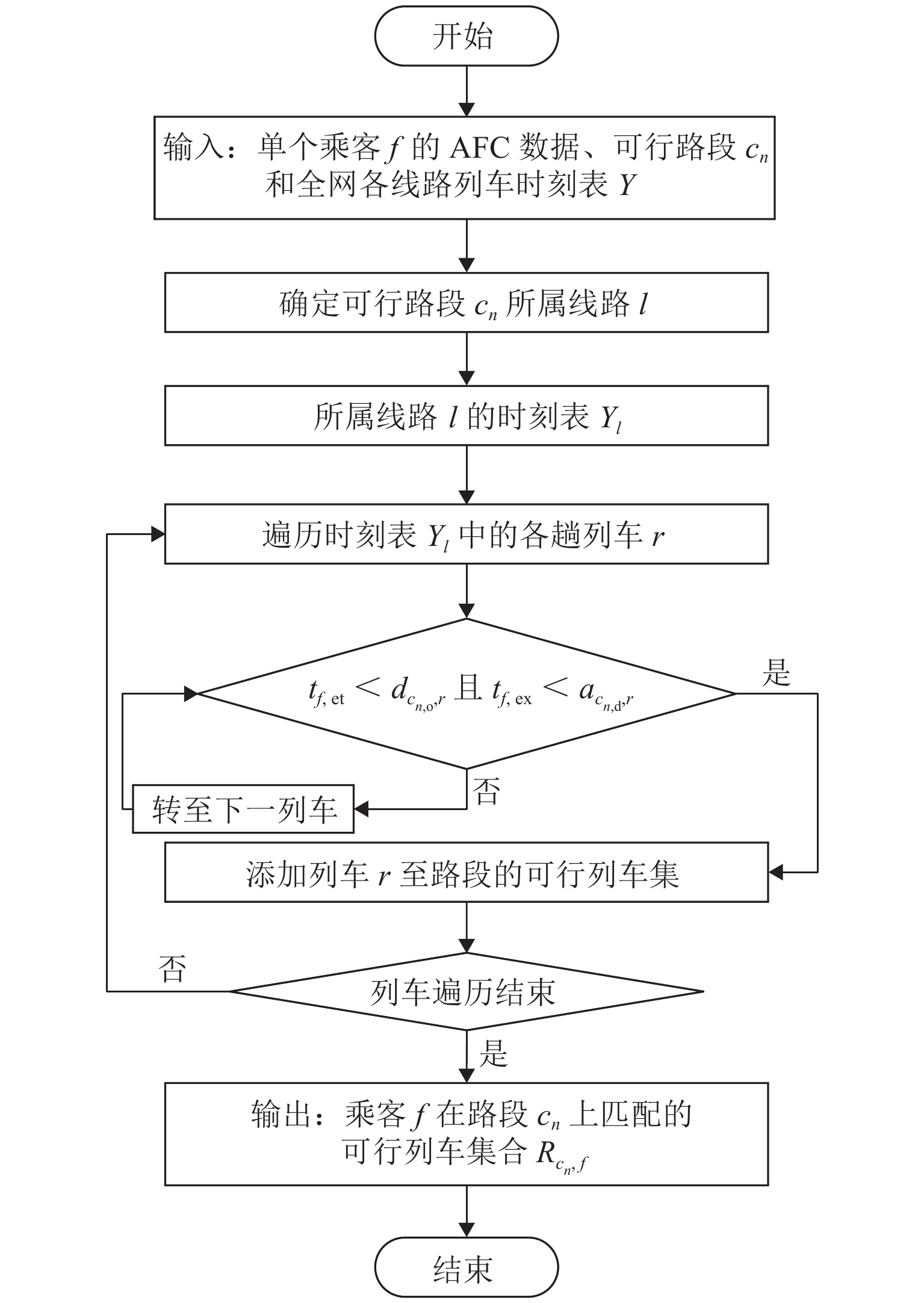
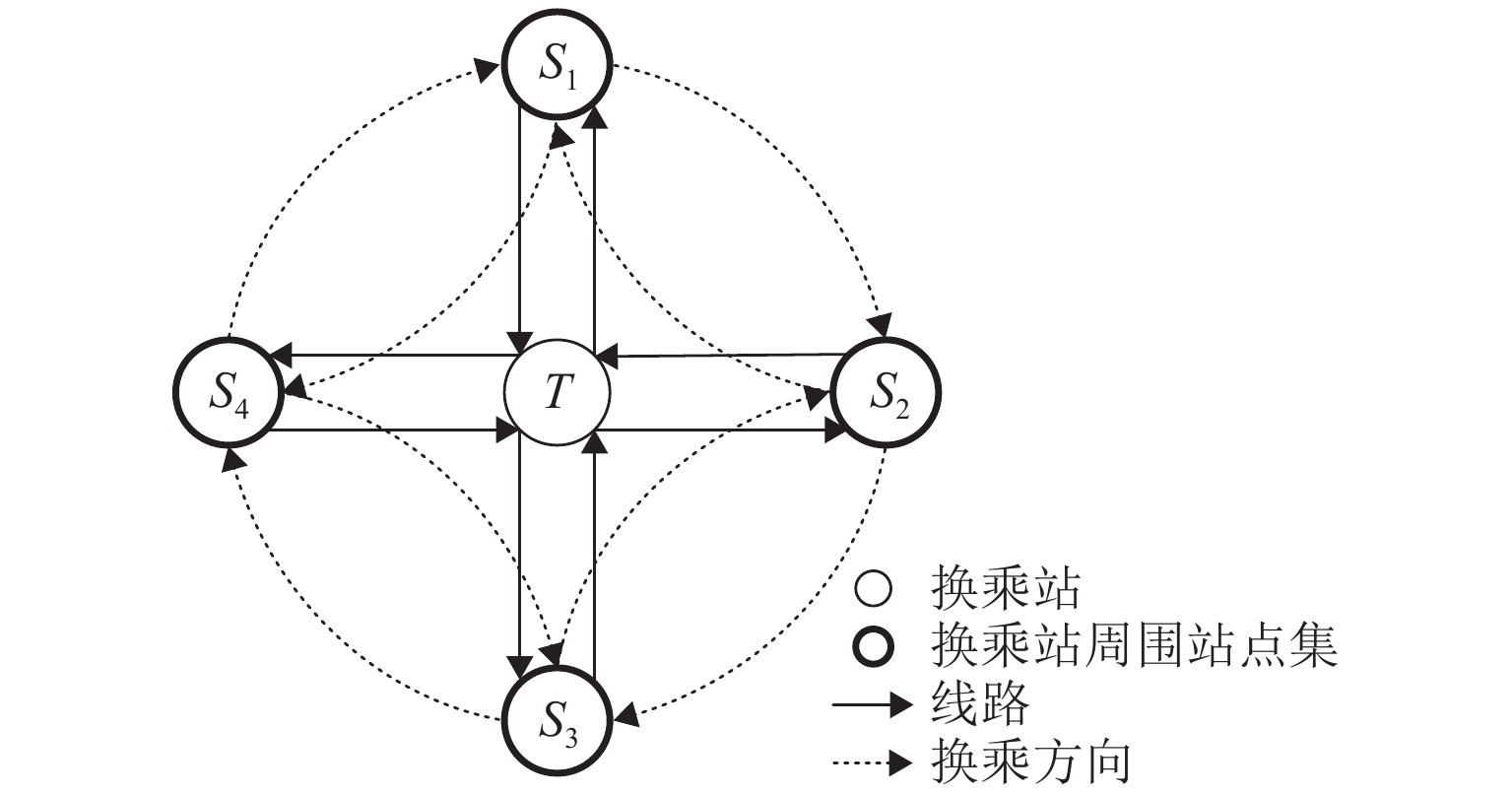
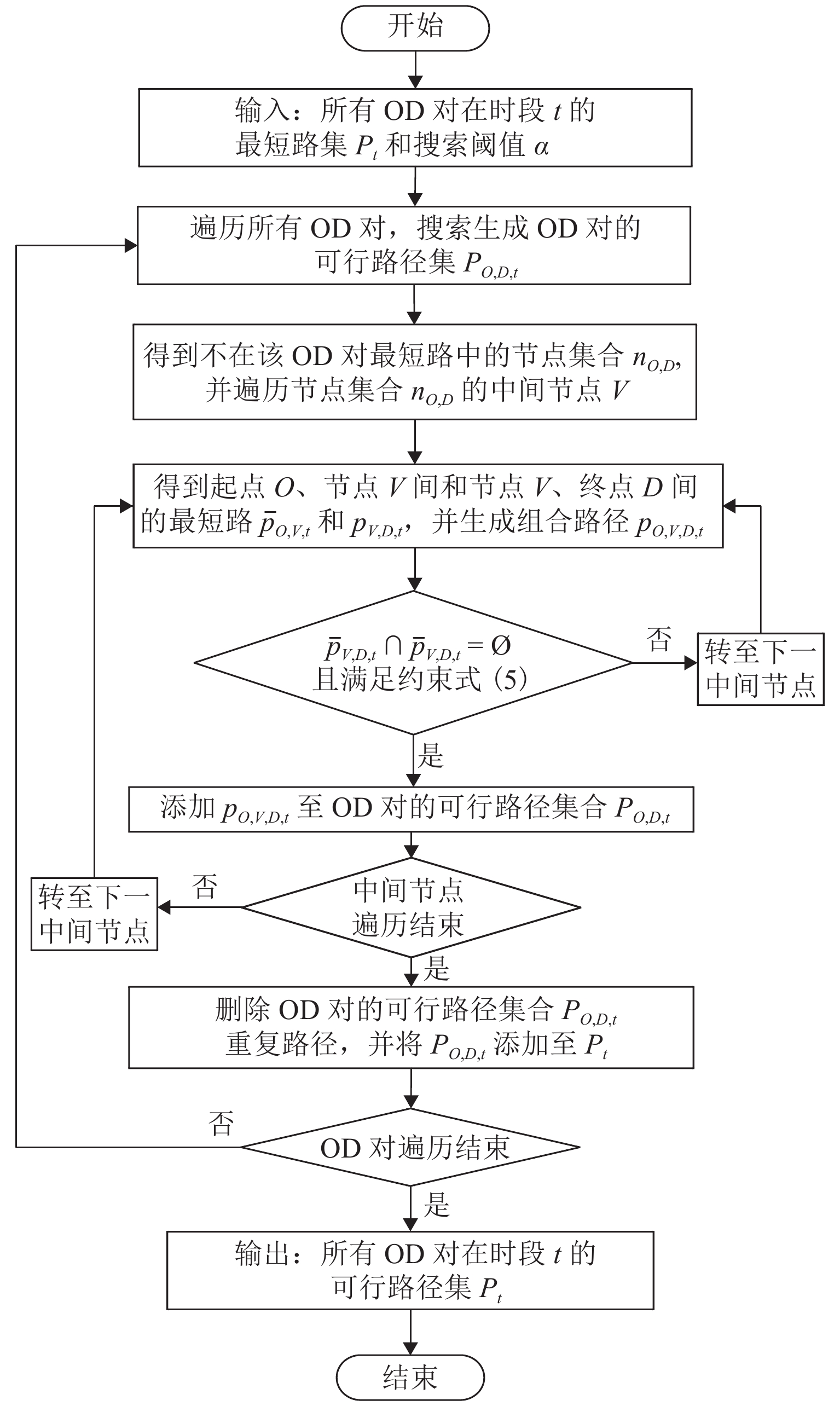
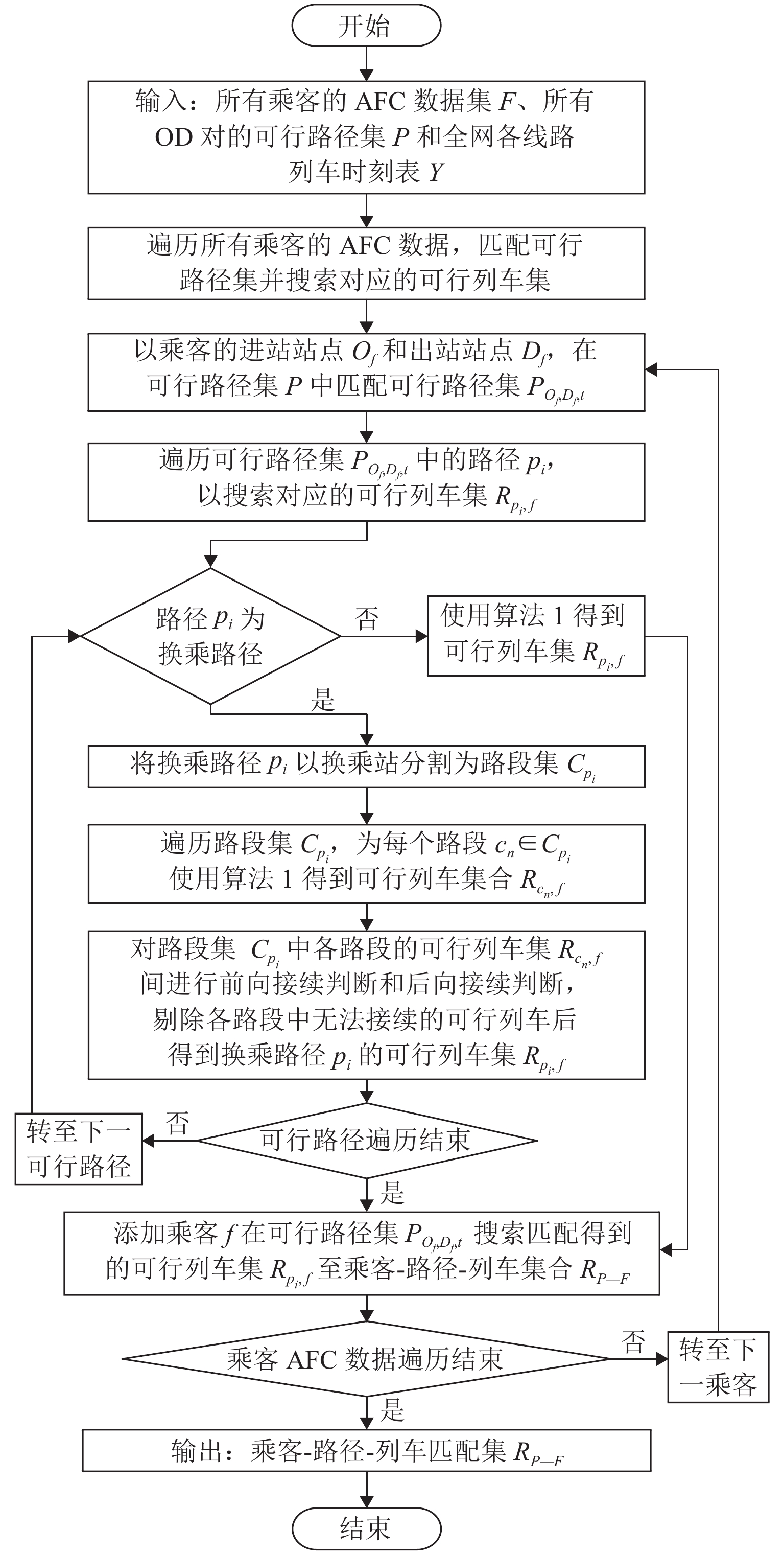
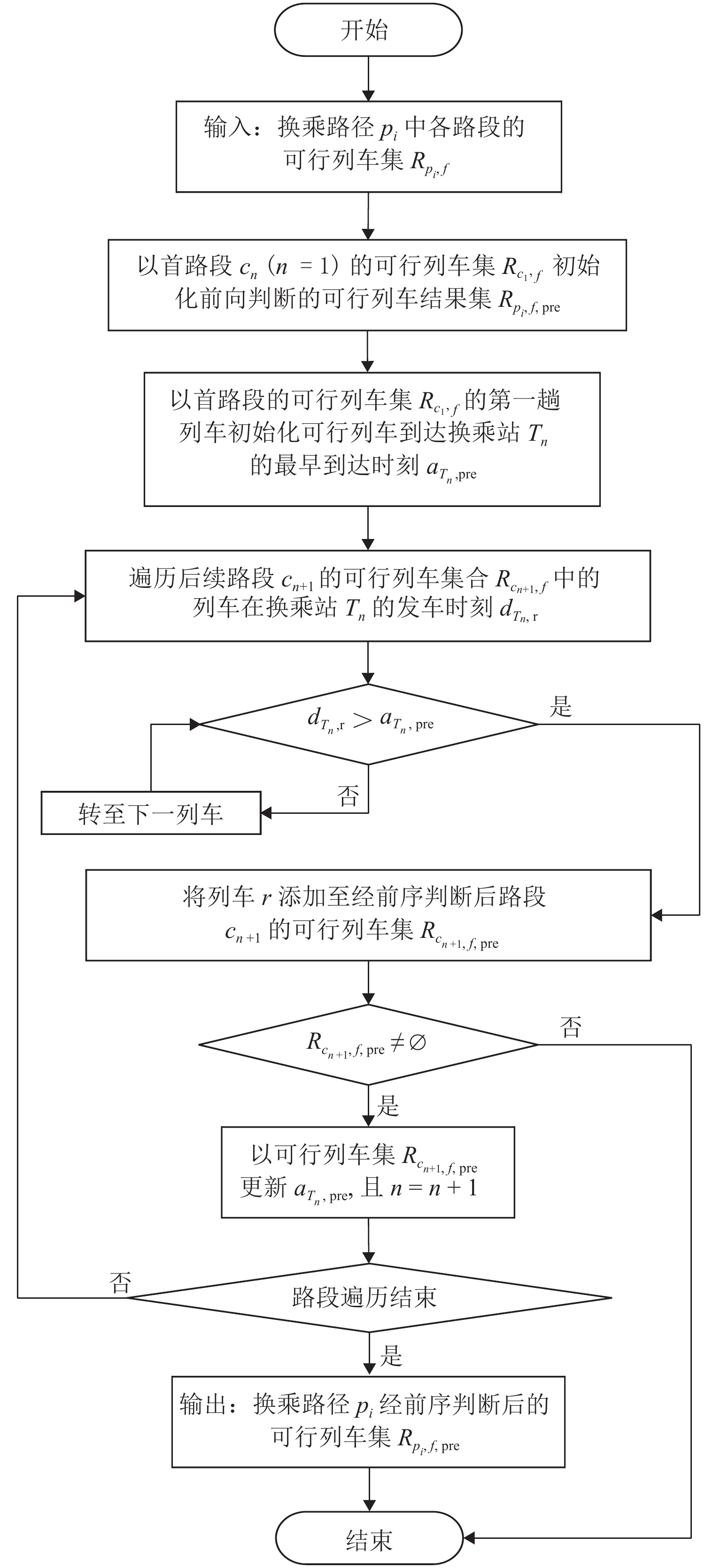
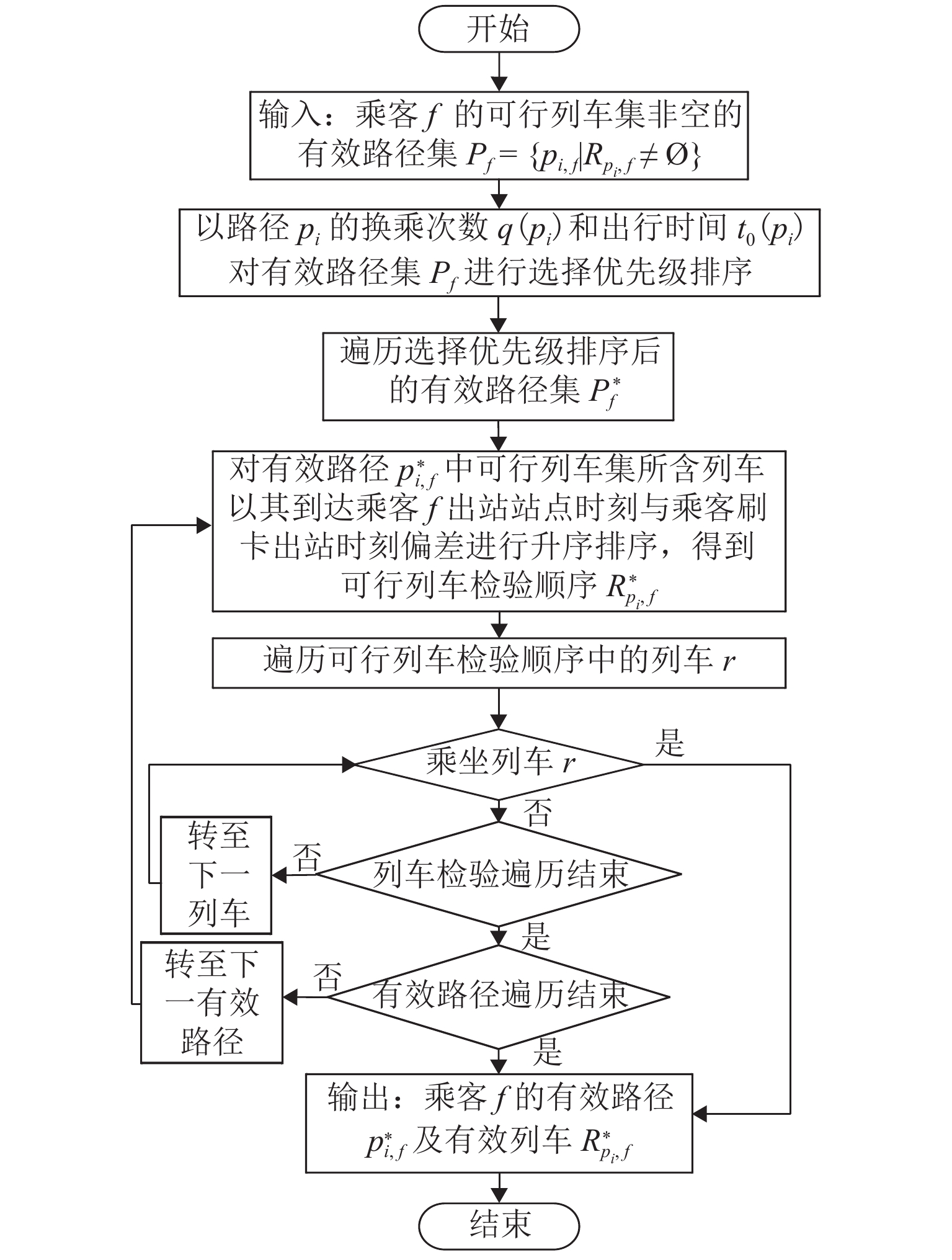
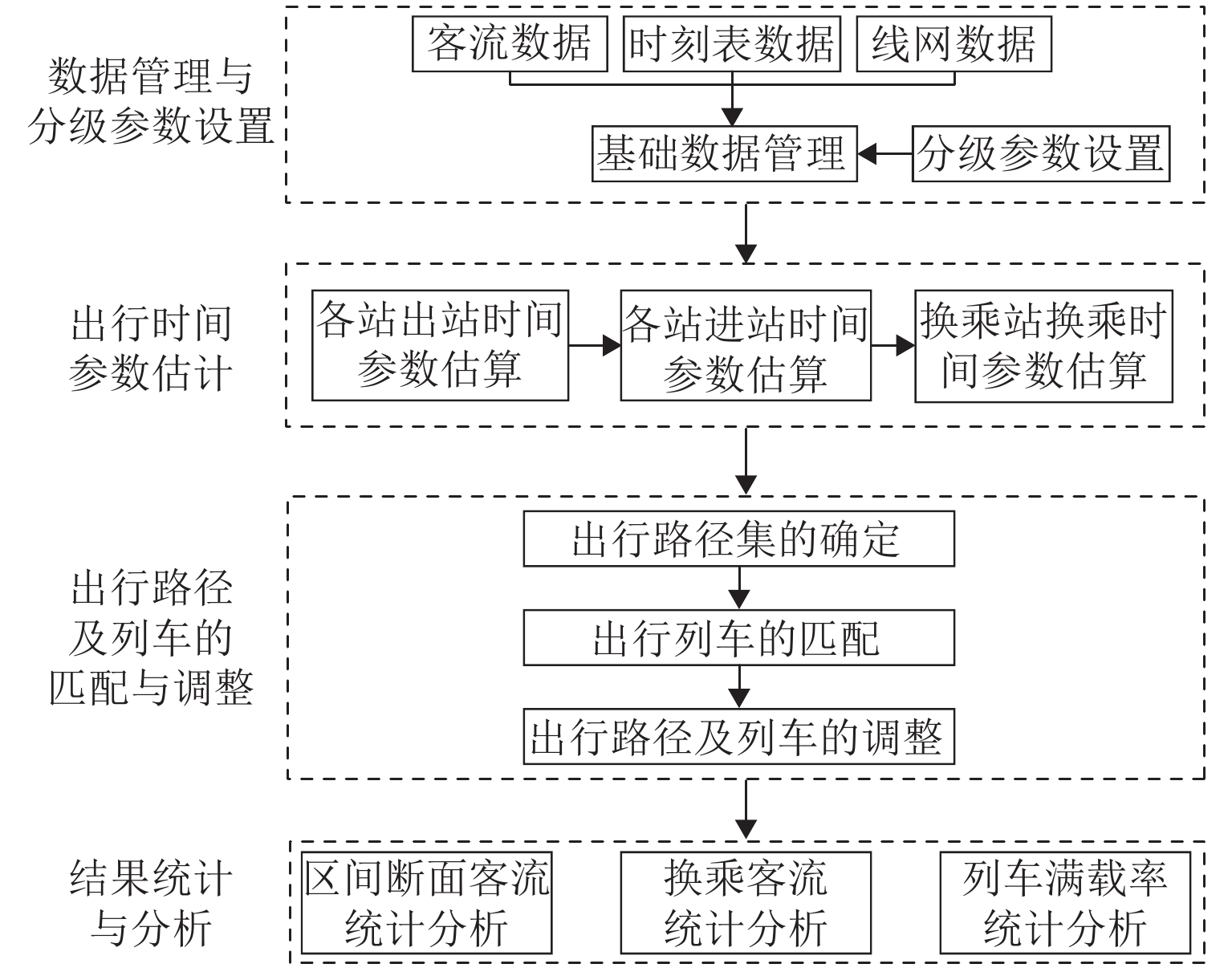
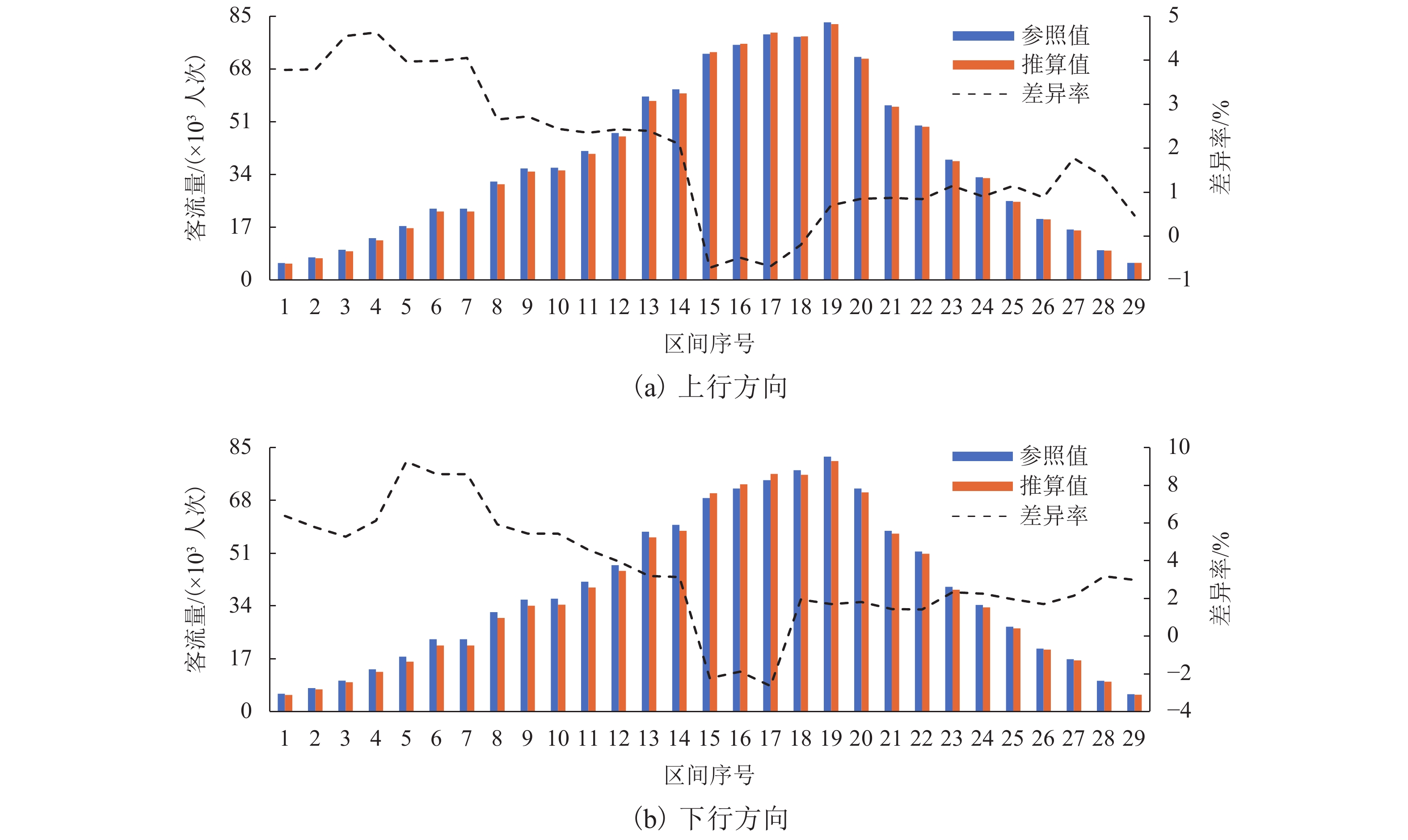
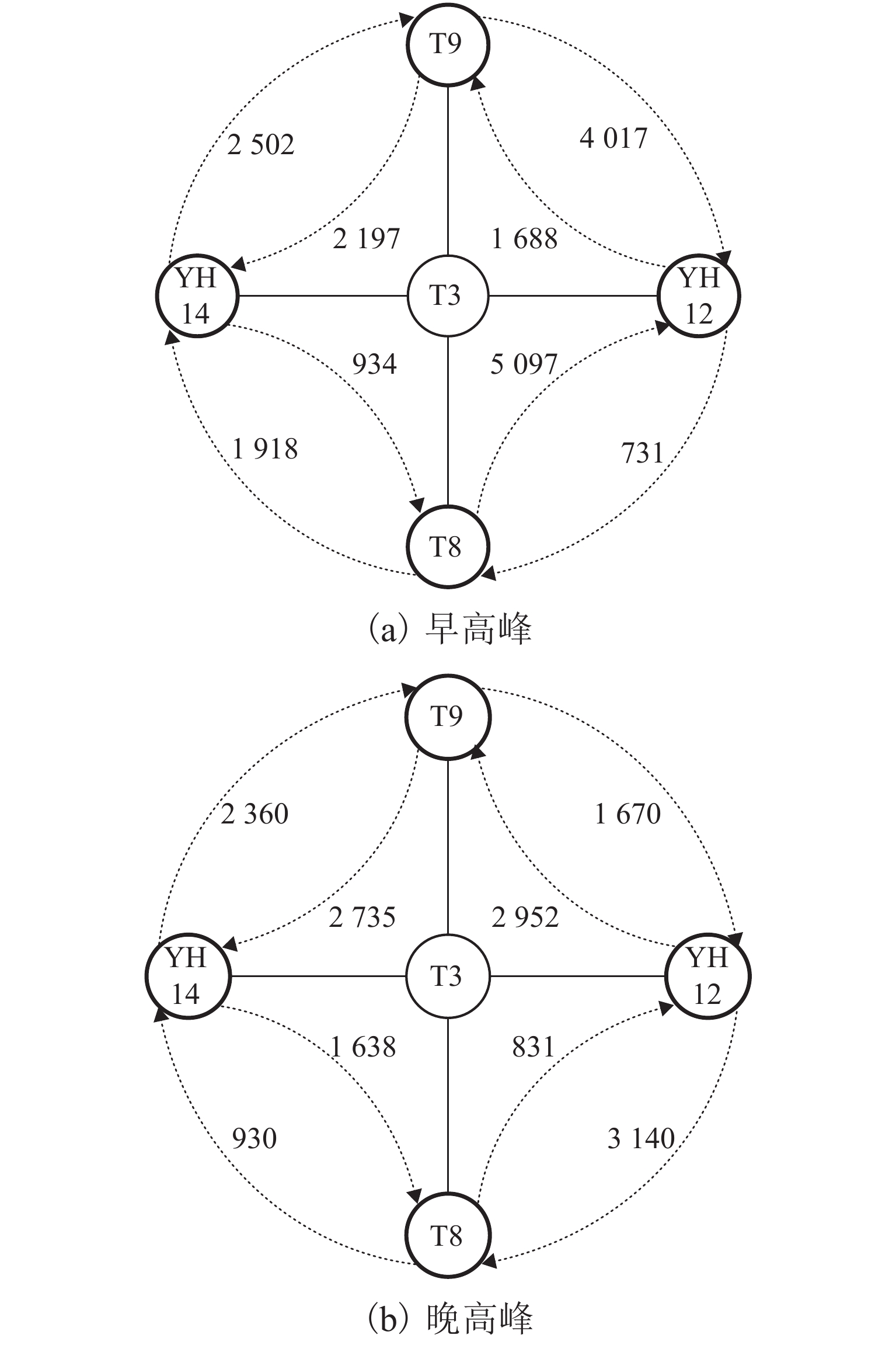
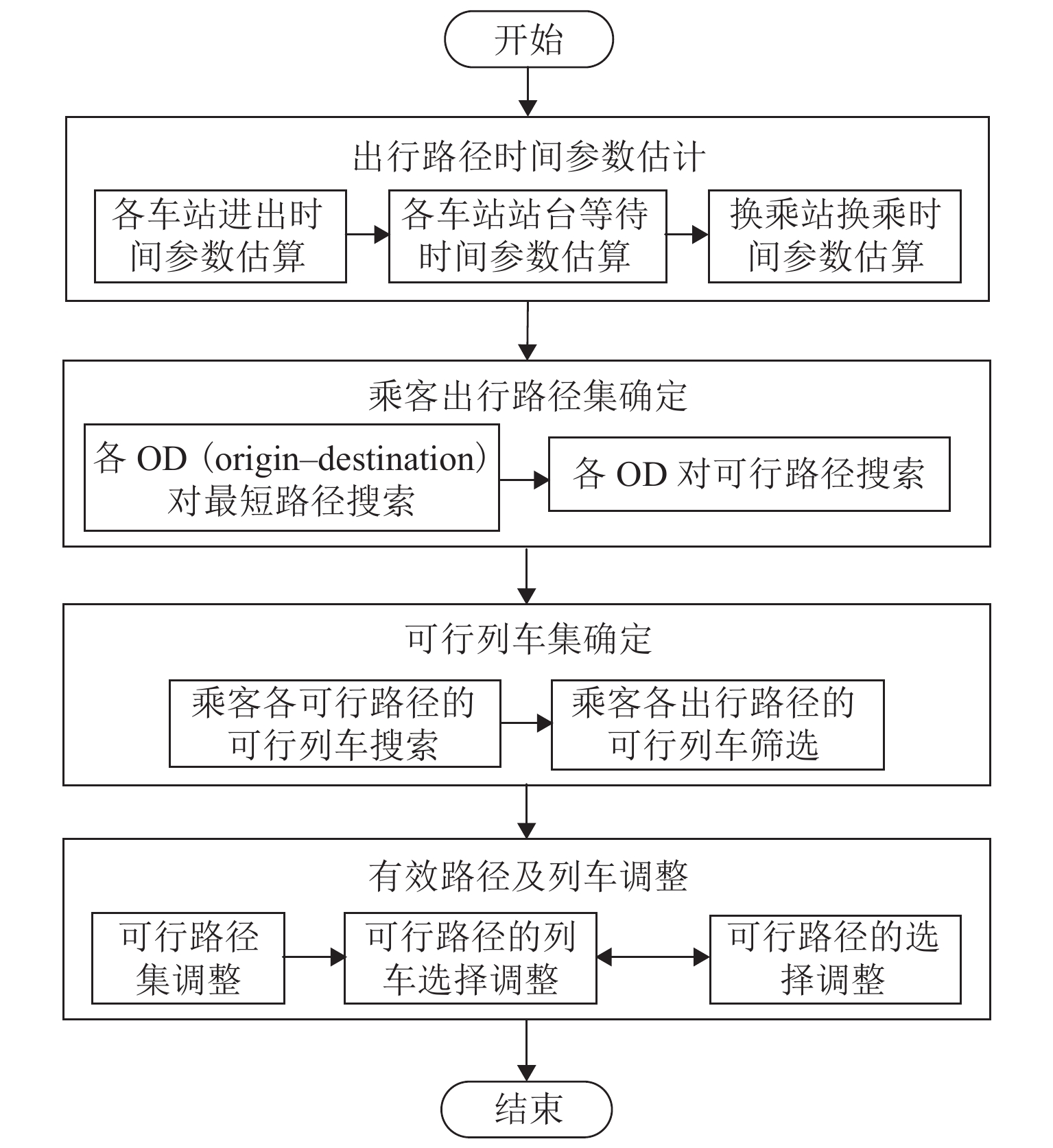
针对城市轨道交通客流分布推算问题，根据自动客票采集系统（AFC）数据和列车时刻表数据，提出基于乘客出行时空路径推算的网络客流分配方法. 首先，利用前述两类数据估算乘客出行时间参数；其次，使用基于插点法的可行路径搜索算法得到全网各OD （origin–destination）对的可行路径集合；再次，基于乘客进出站刷卡信息、列车时刻表数据及匹配的可行路径集合，构建乘客有效出行路径集和列车集的推算模型，获得有效出行结果集；进一步，结合所得有效结果集合与列车载客量限制，并根据列车时刻表完成列车运行推演，确定唯一的有效出行路径和所乘列车；最后，设计开发基于C# 语言的城市轨道交通网络客流推算系统，对某城市轨道交通工作日客流数据进行案例研究. 结果表明：客流推算系统所得的断面客流推算值与运营参照值的平均差异上、下行分别为2.03%、3.90%；列车满载率变化趋势符合线路路由特点；早晚高峰时段换乘站的换乘客流来源站点固定，但早高峰来源量比例较晚高峰稳定.
- 城市交通 /
- 城市轨道交通 /
- 客流分配 /
- 时空路径推算 /
- 自动客票采集系统（AFC）数据 /
- 列车时刻表
Abstract:
To calculate passenger flow distribution in urban rail transits, a passenger flow assignment method based on inference of passenger spatiotemporal path is proposed with the data collected from the automatic fare collection (AFC) and train timetables. Firstly, the passenger travel time parameters are estimated with the above two types of data. The feasible path set of each origin–destination (OD) in the whole network is then obtained by using the feasible path search algorithm based on the node-inserting method. Subsequently, according to the inbound and outbound information from passenger smart cards, train timetable and matched feasible path set, an inference model of passenger effective travel path and train set is built to obtain the effective travel result set. Finally, a train operation is developed with the obtained effective result set, train load capacity, and train timetable to determine the sole effective travel path and riding train. A calculation system for the passenger flow in urban rail transit networks is designed and developed, and a case study is conducted on weekday passenger flow data of urban rail transit. The results show that the average difference of section passenger flow between the calculated results and operation reference data of upstream and downstream is 2.03% and 3.90%, respectively, and the trend of train load rate confirms to the line routing. Moreover, the source of transfer passenger flow at transfer station is stable in the morning and evening peaks, but the proportion of sources in the morning peak is more stable that in the evening peak.
- urban transportation /
- urban rail transit /
- passenger flow assignment /
- inference of passenger spatiotemporal path /
- automatic fare collection (AFC) data /
- train timetable

HTML全文

图 1 网络客流推算流程

Figure 1. Calculation process for network-wide passenger flow

下载: 全尺寸图片幻灯片

图 2 单个乘客出行路段的可行列车集生成算法

Figure 2. Feasible train set algorithm for single passenger at path section

下载: 全尺寸图片幻灯片

图 3 一次换乘范围示意

Figure 3. Schematic of one-time transfer range

下载: 全尺寸图片幻灯片

图 4 基于插点法的可行路径搜索算法

Figure 4. Feasible path search algorithm based on the node-inserting method

下载: 全尺寸图片幻灯片

图 5 可行列车集匹配算法

Figure 5. Feasible train set matching algorithm

下载: 全尺寸图片幻灯片

图 6 换乘路径可行列车集的前向判断算法

Figure 6. Forward judge algorithm for feasible train set of transfer path

下载: 全尺寸图片幻灯片

图 7 确定有效路径及有效列车算法

Figure 7. Estimation algorithm for valid path and train

下载: 全尺寸图片幻灯片

图 8 城市轨道交通客流推算系统架构

Figure 8. Calculation system framework for urban rail transit passenger flow

下载: 全尺寸图片幻灯片

图 9 YH线各区间全日断面客流对比

Figure 9. Comparison of daily section passenger flows in each section of YH line

下载: 全尺寸图片幻灯片

图 10 T3站各换乘方向的换乘量对比（单位：人次）

Figure 10. Comparison of transfer volumes in each transfer direction at station T3 （unit: trips）

下载: 全尺寸图片幻灯片

表 1 乘客-路径-列车初始匹配结果类型

Table 1. Result types of matching initial passenger–route–train

类型	可行路径情况	可行列车情况	处理方式
类型 1	唯一	唯一	直接确定
类型 2	唯一	不唯一	算法 5
类型 3	不唯一	所有路径均唯一	算法 5
类型 4	不唯一	存在路径不唯一	算法 5

下载: 导出CSV

表 2 输入的数据名称及内容

Table 2. Name and content of input data

数据名称	数据内容
乘客行程信息	进站时间、进站车站名、出站时间、出站车站名
时刻表信息	所属线路名、车次号、车站名、到站时刻、发车时刻
线路属性	线路名称、线路类型、是否开通、线路颜色（RGB）
车站属性	车站编号、车站名、是否为换乘站、衔接线路、衔接线路车站
满载率分级参数	分级数量、各线各区间分级标准
车站客流分级参数	线路名称、分级数量、全线分级标准、全线各站分级标准

下载: 导出CSV

表 3 YH线早晚高峰换乘客流来源统计

Table 3. Statistics on source of transfer passenger flow for YH line in morning and evening peaks %

来源站名	早高峰来源量比例	来源站名	晚高峰来源量比例
RML	22.6	BSG	22.3
ZZHCZ	21.3	LCGC	21.6
LCGC	19.7	RML	20.1
BSG	19.6	ZZHCZ	19.7
YXY	16.9	QLL	16.3
标准差	1.91	标准差	2.08

下载: 导出CSV

表 4 EH线早晚高峰换乘客流来源统计

Table 4. Statistics on source of transfer passenger flow for EH line in morning and evening peaks %

来源站名	早高峰来源量比例	来源站名	晚高峰来源量比例
NSH	22.0	LHDL	21.8
JW	20.8	JW	21.1
SWL	20.1	LZ	20.6
LZ	18.9	LL	18.4
HNC	18.2	HHYBG	18.0
标准差	1.35	标准差	1.51

下载: 导出CSV

表 5 列车区间满载率分级

Table 5. Classification of train-section load rate %

等级	满载率范围	等级	满载率范围
等级 1	（0,50]	等级 4	（100,120]
等级 2	（50,80]	等级 5	（120,130]
等级 3	（80,100]	等级 6	（130,∞）

下载: 导出CSV

参考文献(10)

[1]	曾鸣凯,黄鉴,彭其渊. 客运专线旅客列车开行方案的客流分配方法[J]. 西南交通大学学报,2006,41(5): 571-574. doi: 10.3969/j.issn.0258-2724.2006.05.006 ZENG Mingkai, HUANG Jian, PENG Qiyuan. Research on assignment of passenger train plan for dedicated passenger train line[J]. Journal of Southwest Jiaotong University, 2006, 41(5): 571-574. doi: 10.3969/j.issn.0258-2724.2006.05.006
[2]	张思佳,贾顺平,毛保华,等. 乘客出行距离分布对轨道线网内公交竞争力的影响[J]. 浙江大学学报(工学版),2019,53(2): 292-298. doi: 10.3785/j.issn.1008-973X.2019.02.012 ZHANG Sijia, JIA Shunping, MAO Baohua, et al. Influence of passenger trip distance distribution on competitiveness of bus lines in urban rail transit network[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(2): 292-298. doi: 10.3785/j.issn.1008-973X.2019.02.012
[3]	许得杰,巩亮,朱宁,等. 城市轨道交通多交路共线运营客流分配方法[J]. 交通运输系统工程与信息,2021,21(5): 206-213. doi: 10.16097/j.cnki.1009-6744.2021.05.021 XU Dejie, GONG Liang, ZHU Ning, et al. Passenger flow assignment method for common-line operation with multi-routing of urban rail transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(5): 206-213. doi: 10.16097/j.cnki.1009-6744.2021.05.021
[4]	ASAKURA Y, IRYO T, NAKAJIMA Y, et al. Estimation of behavioural change of railway passengers using smart card data[J]. Public Transport, 2012, 4(1): 1-16. doi: 10.1007/s12469-011-0050-0
[5]	KUSAKABE T, IRYO T, ASAKURA Y. Estimation method for railway passengers’ train choice behavior with smart card transaction data[J]. Transportation, 2010, 37: 731-749.
[6]	YAO X M, HAN B M, YU D D, et al. Simulation-based dynamic passenger flow assignment modelling for a schedule-based transit network[J]. Discrete Dynamics in Nature and Society, 2017, 2017: 1-15.
[7]	刘峰博,周庭梁,王小敏. 城市轨道交通故障下客流分布计算及评估方法[J]. 西南交通大学学报,2021,56(5): 921-927,966. LIU Fengbo, ZHOU Tingliang, WANG Xiaomin. Calculation and evaluation method of passenger flow distribution under urban rail transit failure[J]. Journal of Southwest Jiaotong University, 2021, 56(5): 921-927,966.
[8]	ZHU Y W, KOUTSOPOULOS H N, WILSON N H M. A probabilistic passenger-to-train assignment model based on automated data[J]. Transportation Research Part B: Methodological, 2017, 104: 522-542.
[9]	陈钱飞. 城市轨道交通网络乘客时空路径估计与瓶颈识别方法研究[D]. 北京: 北京交通大学, 2021.
[10]	中华人民共和国建设部, 中华人民共和国国家发展和改革委员会. 城市轨道交通工程项目建设标准: 建标 104—2008[S]. 北京: 中国计划出版社, 2008.