Current-Mode Variable Frequency Control Technique for Single-Inductor Dual-Output Switching Converter with Independent Charge and Discharge Sequence
-
摘要:
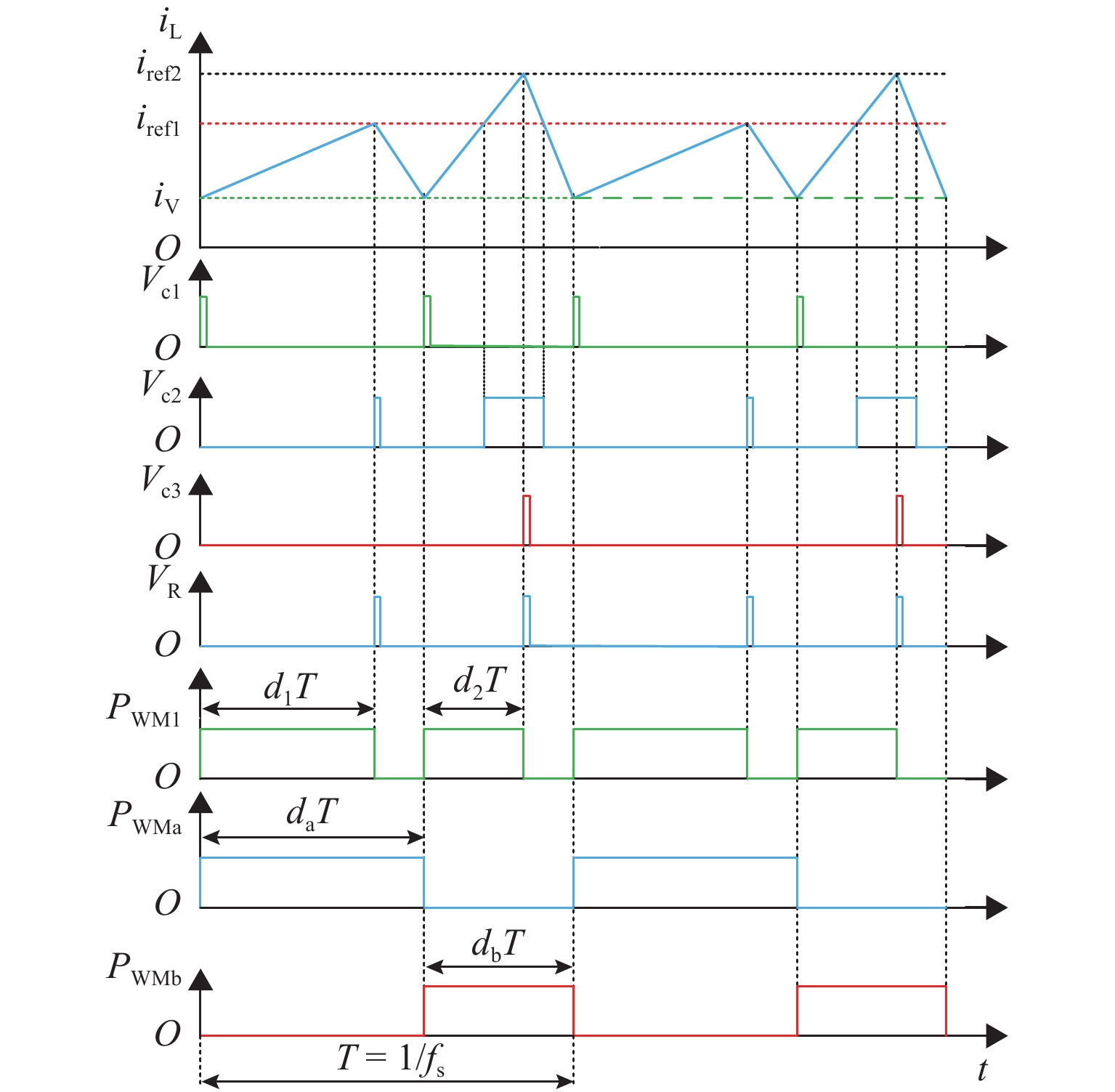
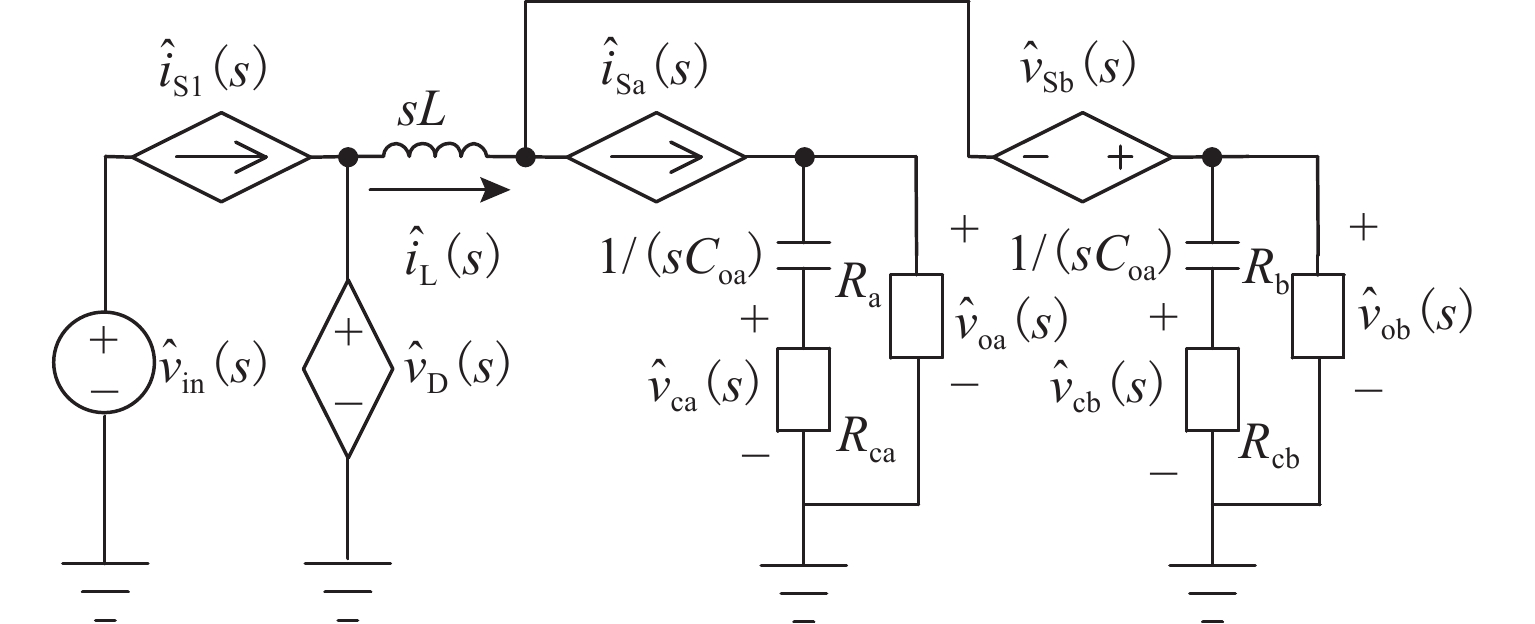
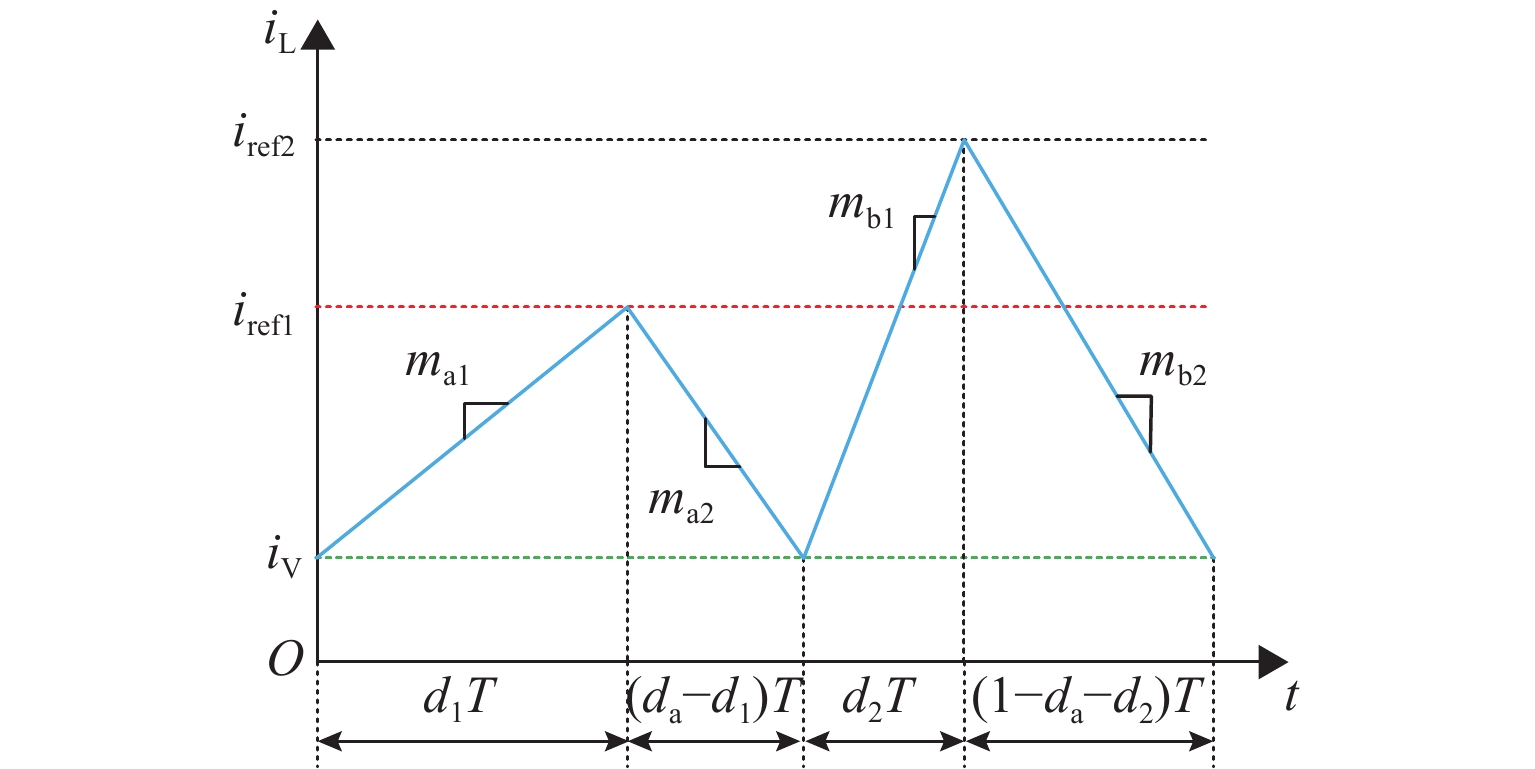
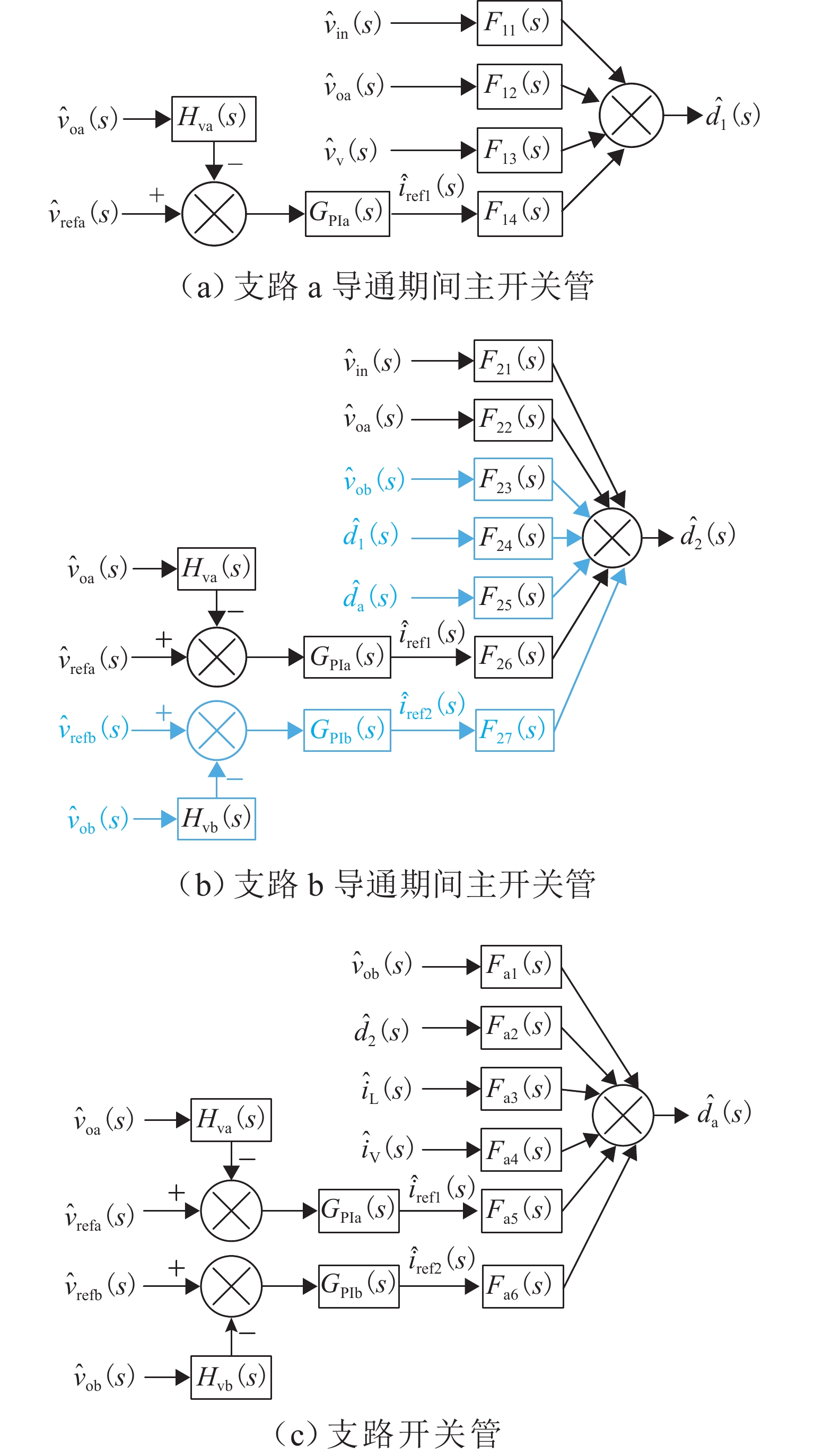
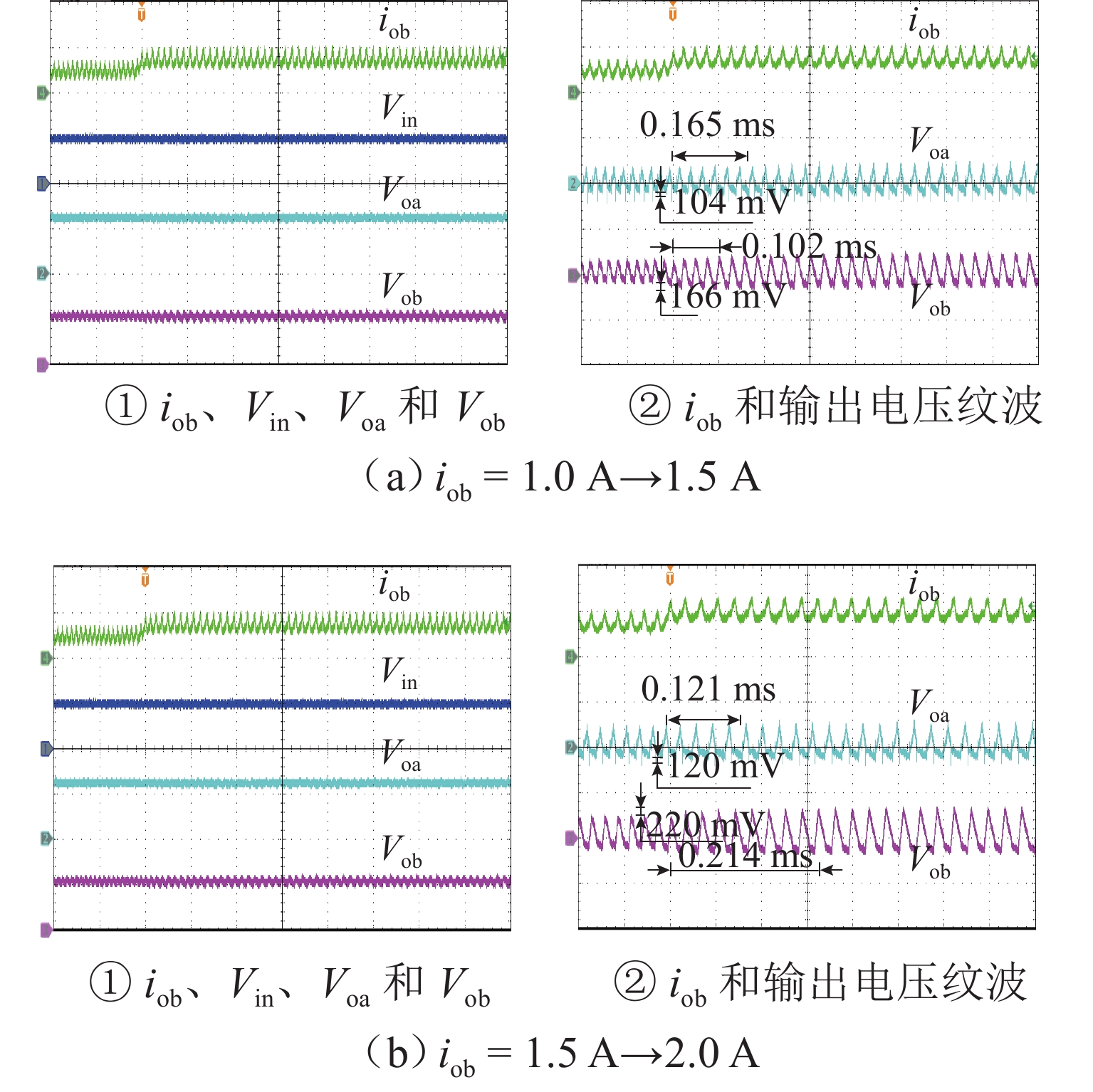
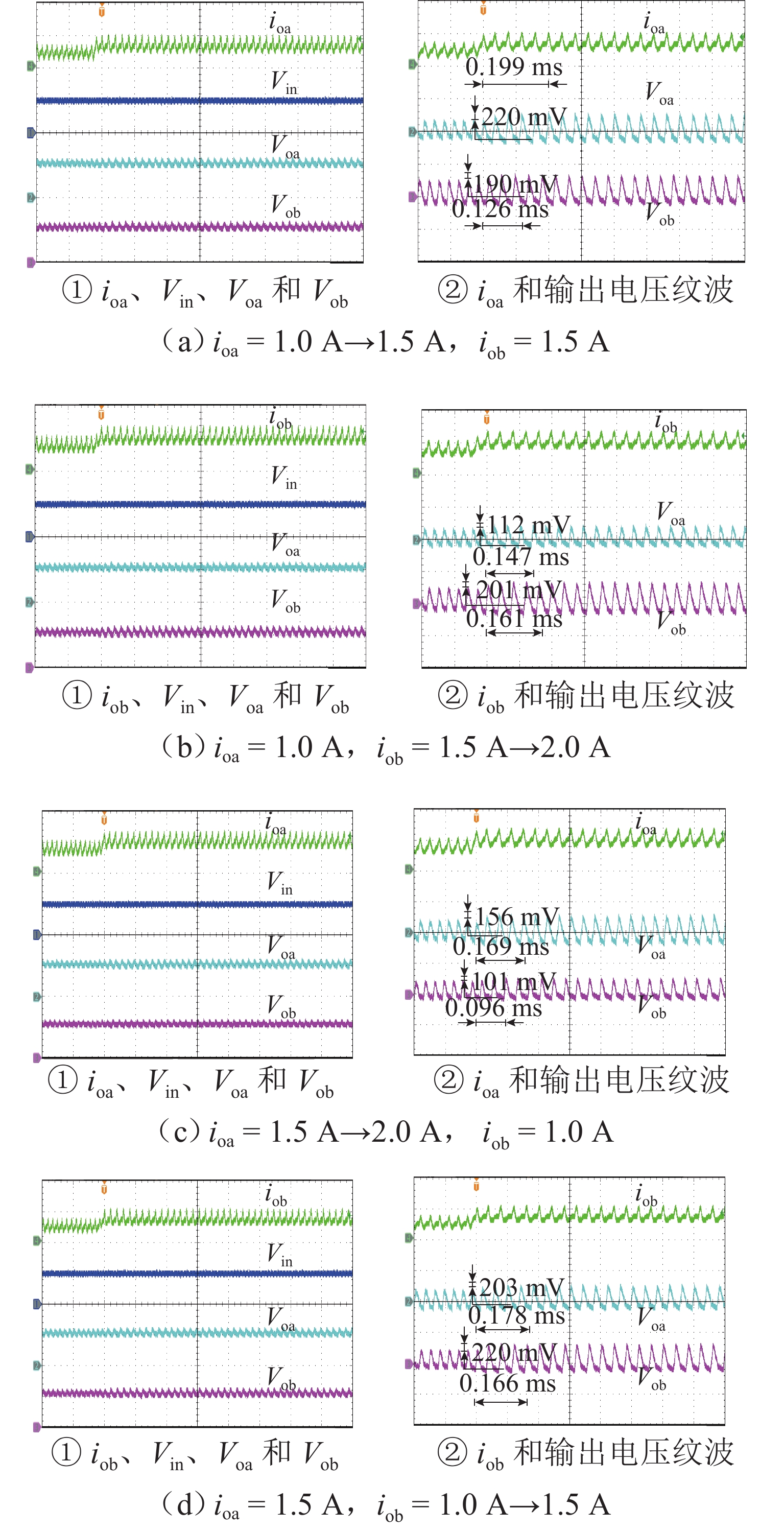
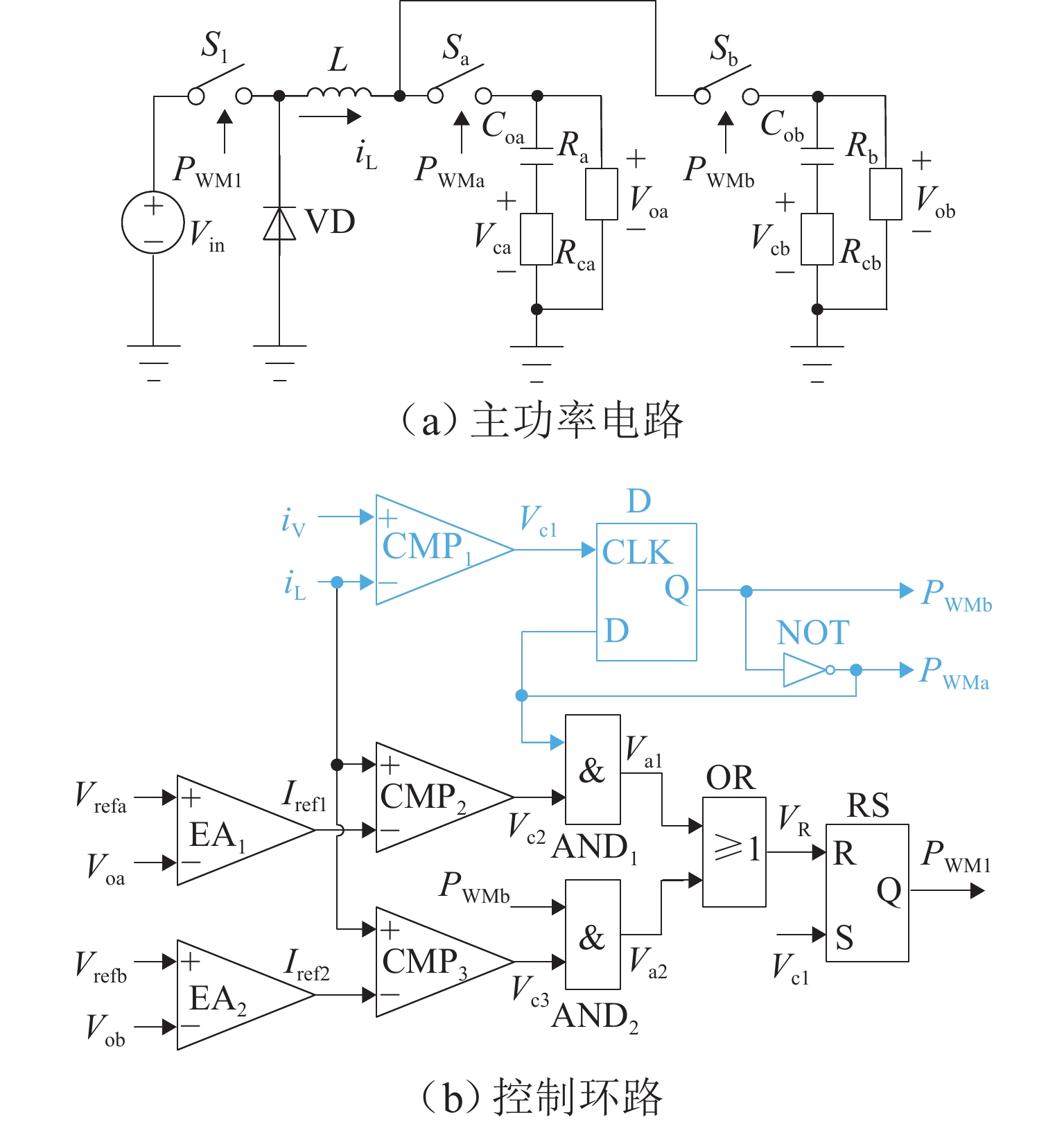
单电感双输出（single-inductor dual-output，SIDO）开关变换器工作在共享充放时序下存在电感电流纹波大、输出支路间交叉影响严重以及电路参数宽范围变化下控制电路不能正常工作等问题. 为此，提出一种独立充放时序电流型变频控制（current-mode variable frequency control，C-VF）技术. 首先，具体描述变换器在连续导电模式（continuous conduction mode，CCM）下的工作原理，并推导主电路开环传递函数；进一步构建闭环小信号模型，推导闭环交叉阻抗，详细分析不同输出电压及负载电流下变换器的交叉影响特性；最后，通过仿真和实验进行验证. 研究表明：相较于共享充放时序，独立充放时序C-VF CCM SIDO buck变换器减小了交叉影响，改善了负载瞬态响应性能；当两支路负载电压不等时，减轻某一支路负载可以降低该支路的交叉影响；当两支路输出电压相同但负载不同时，重载支路对轻载支路的交叉影响更小.
Abstract:Single-inductor dual-output (SIDO) switching converters with shared charge and discharge sequence have problems of the large inductor current ripple and cross-regulation between output branches, and the control circuit fails to work normally under the wide range of changes in circuit parameters. To solve these problems, a current-mode variable frequency control (C-VF) technique with an independent charge and discharge sequence was proposed. First, the working principle of the converter in continuous conduction mode (CCM) was specifically described, and the open-loop transfer function of the main circuit was derived. Furthermore, a closed-loop small signal model was constructed, and the closed-loop cross-regulation impedance transfer functions were derived. The cross-regulation characteristics of the converter with different output voltages and load currents were analyzed in detail. Finally, simulation and experimental verification were carried out. The results show that compared with the shared charge and discharge sequence, the C-VF CCM SIDO buck convert with independent charge and discharge sequence reduces the cross-regulation and improves the transient load response performance. When the load voltages of the two branches are different, decreasing the load of one branch can reduce the cross-regulation of this branch to another one. When the output voltages of the two branches are the same, but the loads are different, the branch with heavy loads has small cross-regulation on the branch with light load.
-
图 1 独立式充放时序C-VF CCM SIDO buck变换器
Figure 1. C-VF CCM SIDO buck converter with independent charge and discharge sequence
图 3 独立充放时序CCM SIDO buck变换器小信号等效电路
Figure 3. Small signal equivalent circuit of CCM SIDO buck converter with independent charge and discharge sequence
图 4 独立充放时序C-VF变换器电感电流波形
Figure 4. Inductor current waveforms of C-VF converter with independent charge and discharge sequence
图 5 独立充放时序C-VF小信号模型
Figure 5. Small signal model of C-VF with independent charge and discharge sequence
图 6 开关频率与谷值电流参考值的关系
Figure 6. Relationship between switching frequency and valley current reference value
图 7 负载不同时的闭环交叉影响阻抗Bode图
Figure 7. Bode diagrams of closed-loop cross-regulation impedance with different loads
图 8 独立充放时序C-VF CCM SIDO buck变换器实验装置
Figure 8. Experimental device of C-VF CCM SIDO buck converter with independent charge and discharge sequence
图 9 iV = 0.5, 1.1 A时稳态实验波形
Figure 9. Steady-state experimental waveforms with iV = 0.5, 1.1 A
图 10 负载不同、负载电压不等时ioa跳变的瞬态实验波形
Figure 10. Transient experimental waveforms with sudden variation of ioa under different loads and unequal load voltages
图 11 负载不同、负载电压不等时iob跳变的瞬态实验波形
Figure 11. Transient experimental waveforms with sudden sudden variation of iob with different loads and unequal load voltages
图 12 负载不同、负载电压相等时负载跳变的瞬态实验波形
Figure 12. Transient experimental waveforms with sudden variation of loads under different loads and equal load voltages
表 1 独立充放时序C-VF CCM SIDO buck变换器电路参数表
Table 1. Circuit parameters of C-VF CCM SIDO buck converter with independent charge and discharge sequence
参数 取值 参数 取值 Vin/V 20 Ioa/A 1 L/μH 22 Iob/A 1 Voa/V 12 Coa/μF 470 Vob/V 5 Cob/μF 470 
下载: 导出CSV
表 2 不同工况下闭环交叉影响
Table 2. Closed-loop cross-regulation under different working conditions
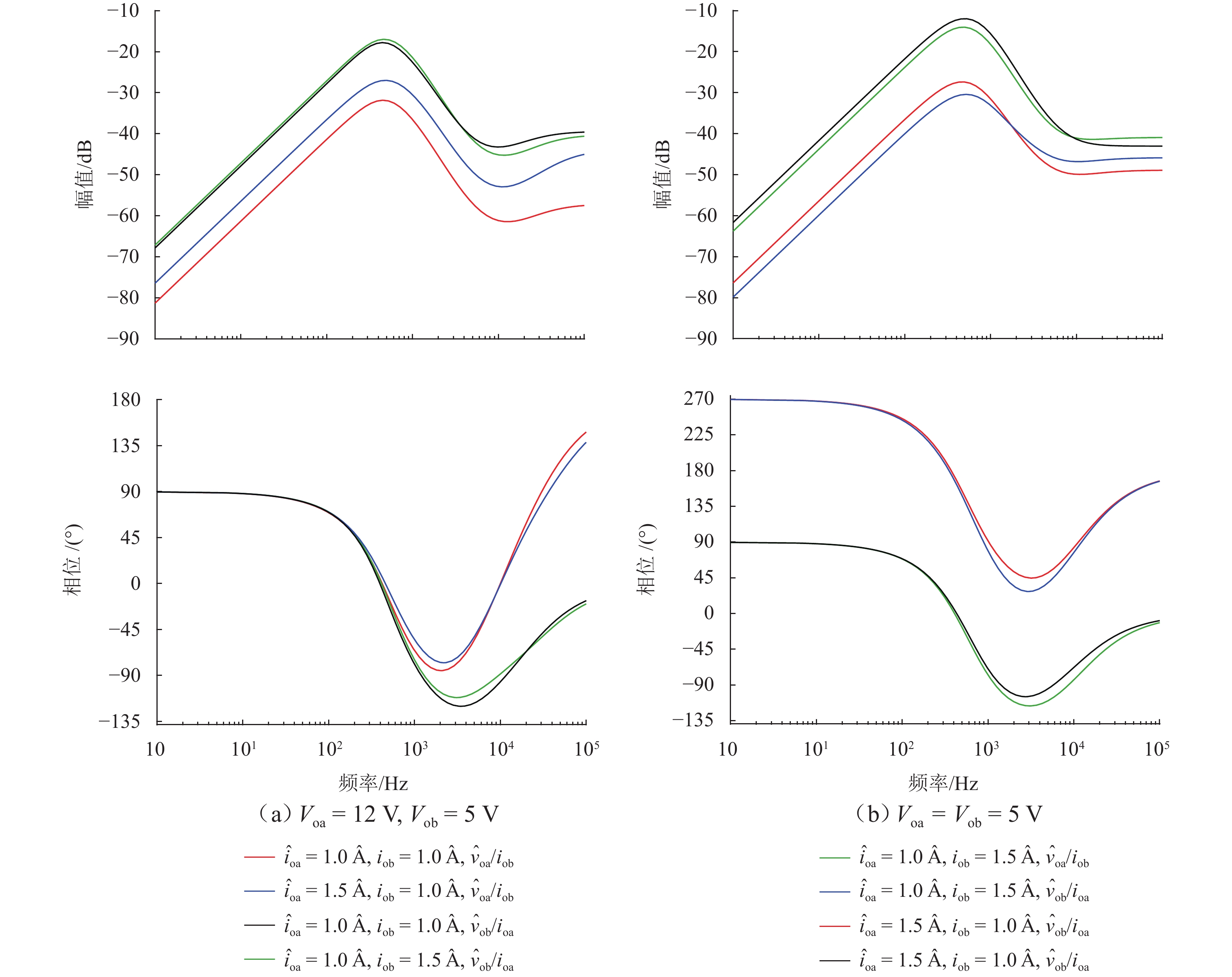
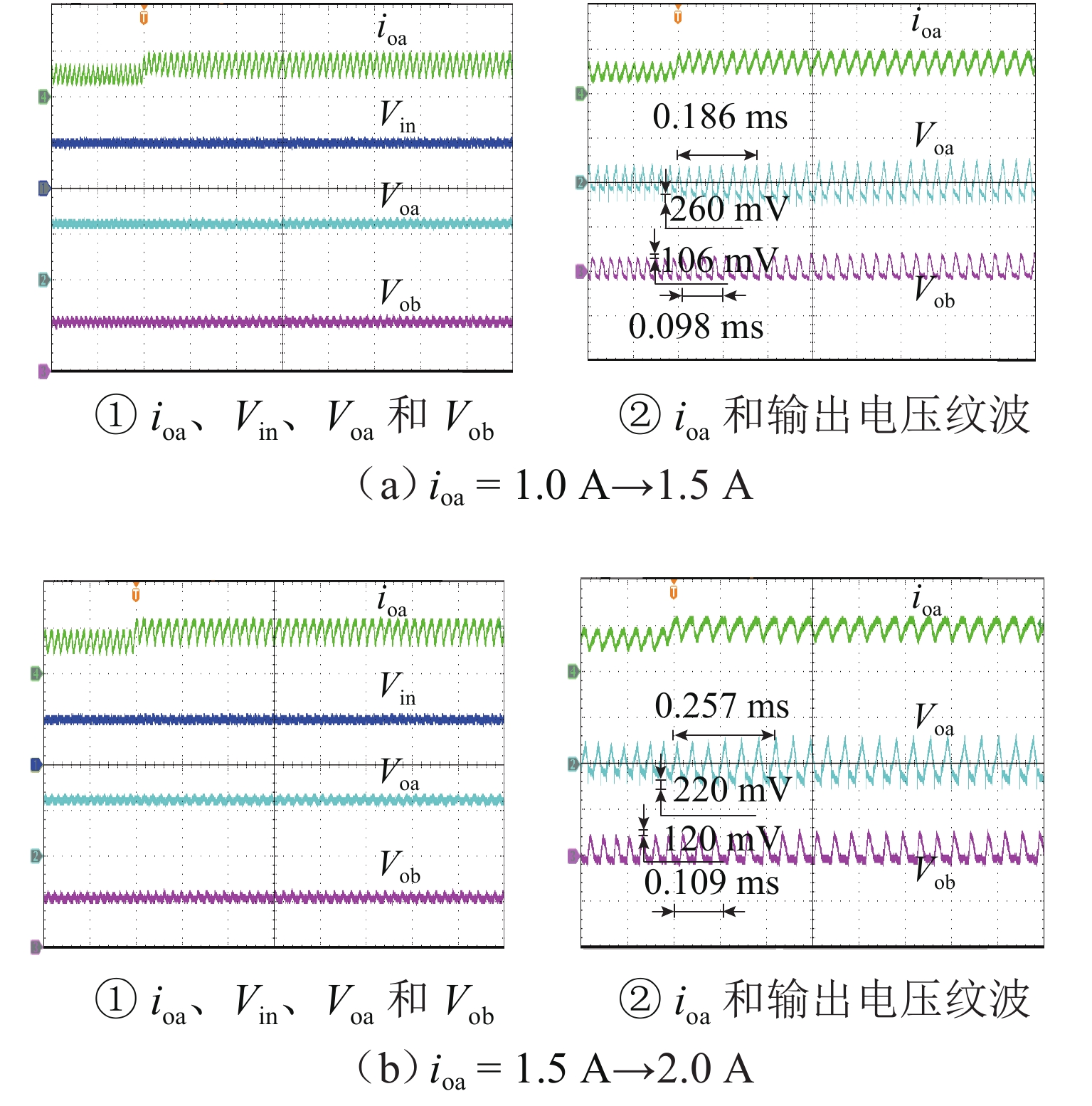
输出电压/V 负载电流/A 负载跳变/A Fa Voa=12，Vob=5 ioa=1.0，iob=1.0 ioa：1.0→1.5 0.0424 ioa=1.5，iob=1.0 ioa：1.5→2.0 0.0720 ioa=1.0，iob=1.0 iob：1.0→1.5 0.0173 ioa=1.0，iob=1.5 iob：1.5→2.0 0.0300 Voa=5，Vob=5 ioa=1.0，iob=1.5 ioa：1.0→1.5 0.0760 iob：1.5→2.0 0.0672 ioa=1.5，iob=1.0 ioa：1.5→2.0 0.0606 iob： 1.0→1.5 0.0812
下载: 导出CSV
表 3 不同SIDO变换器性能的对比
Table 3. Performance comparison of different SIDO converters
来源 工作模式 输入
电压/V输出电
容/μF输出
电压/V输出
功率/W电感/μH 开关
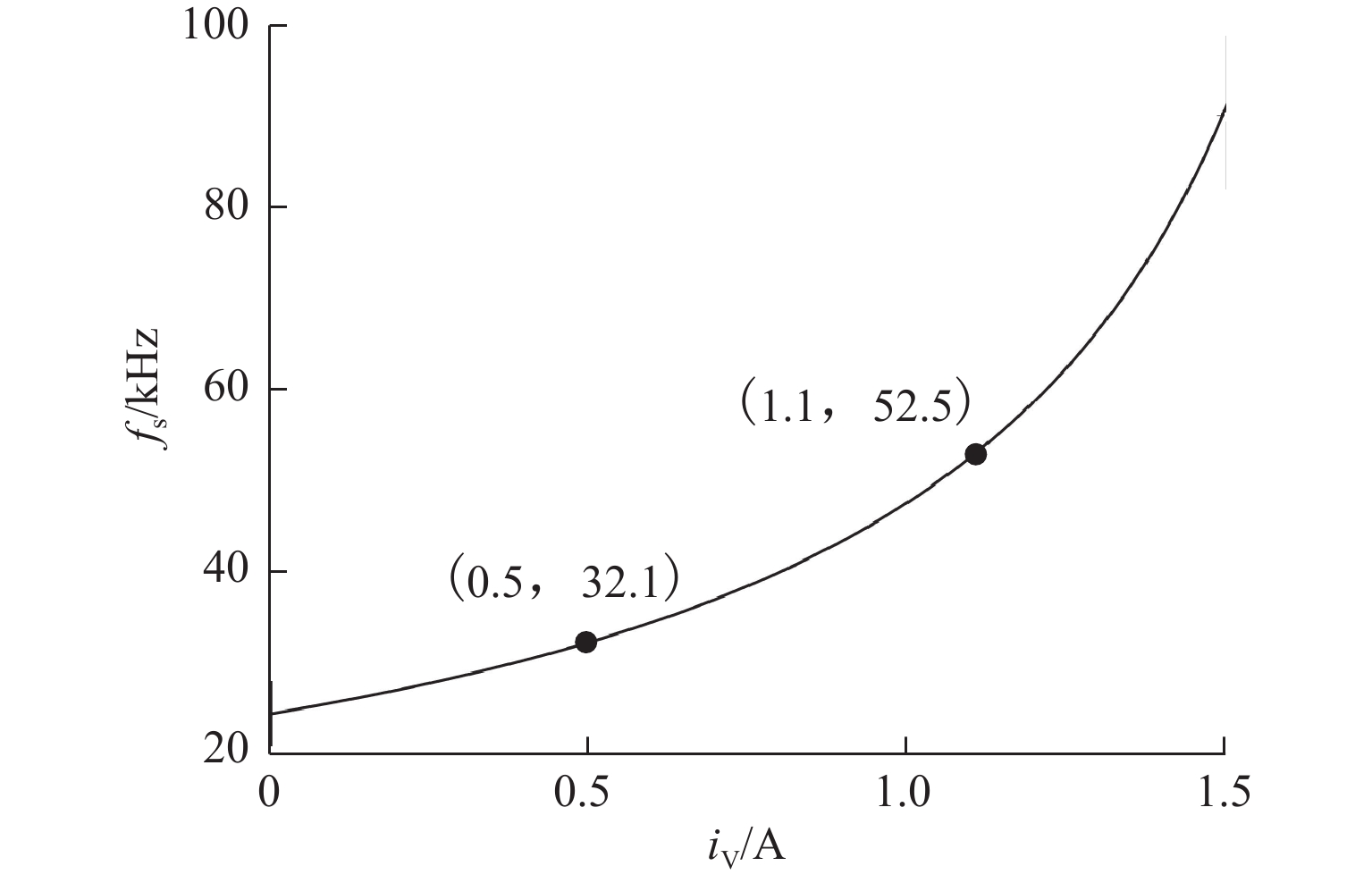
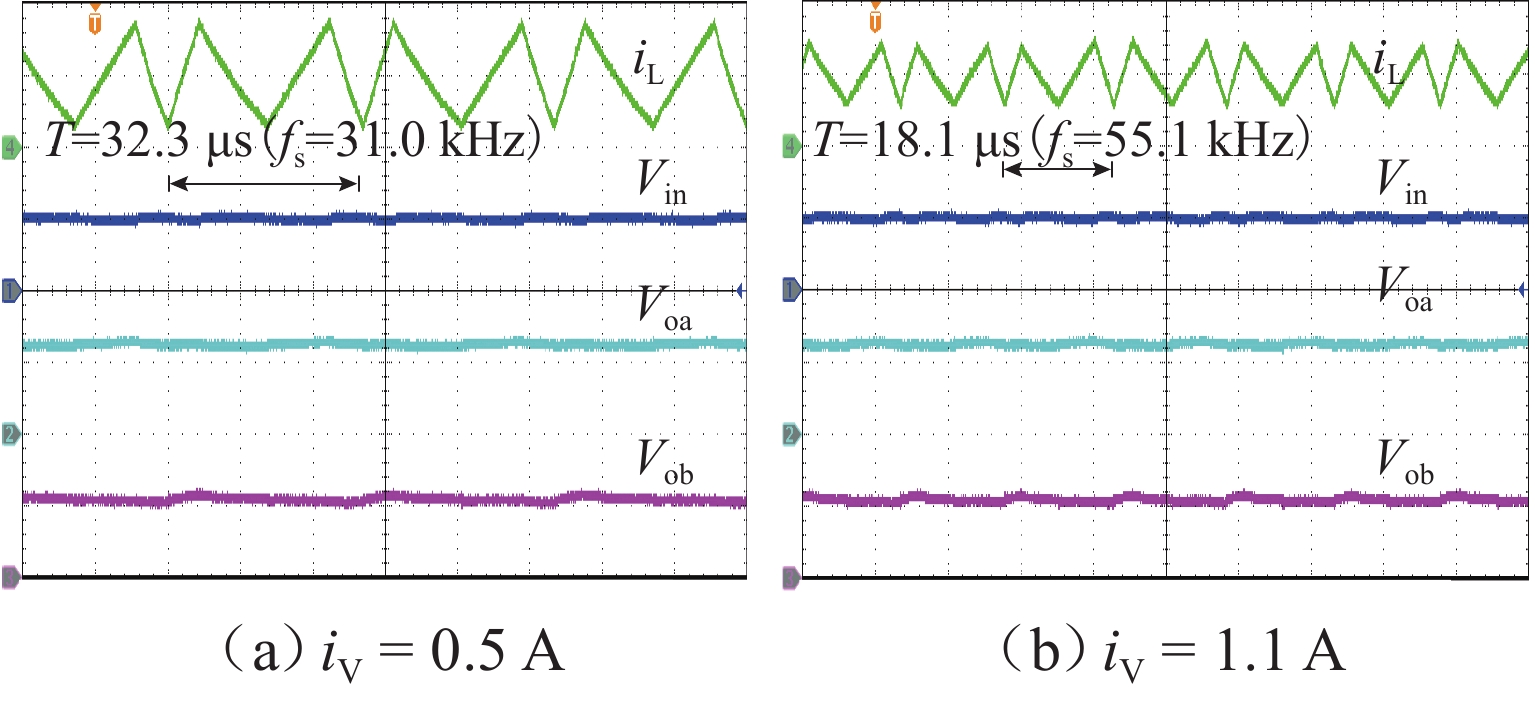
频率/kHz电感电流纹波率 交叉影响系数 负载瞬态响应 本文 CCM 20 470 12.0, 5.0 17.0 22 55.1 1.05 0.0128 7.0T 文献[12] CCM 12 100 24.0, 15.0 19.5 20 68.0 1.48 0.0146 142.8T 文献[13] CCM 12 470 24.0, 15.0 19.5 50 50.0 1.23 0.1240 215.0T 文献[14] CCM 10 470 3.3, 5.0 16.1 100 50.0 0.0800 28.0T
下载: 导出CSV
-
[1] XU J, WENG Z Y, JIANG H J, et al. A high efficiency single-inductor dual-output buck converter with adaptive freewheel current and hybrid mode control[C]//2016 IEEE International Symposium on Circuits and Systems (ISCAS). Montreal: IEEE, 2016: 1614-1617. [2] DONG Z, LI X L, TSE C K, et al. Derivation of single-input dual-output converters with simple control and no cross regulation[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 11930-11941. doi: 10.1109/TPEL.2020.2983618 [3] ZHENG Y Q, HO M, GUO J P, et al. A single-inductor multiple-output auto-buck-boost DC–DC converter with autophase allocation[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2296-2313. doi: 10.1109/TPEL.2015.2432040 [4] 杨利亚. 应用于航天器电源系统的多路输出变换器研究[D]. 哈尔滨: 哈尔滨工业大学, 2020. [5] 王瑶,陈玲,杨德鑫,等. I2控制单电感双输出buck LED驱动电源交叉影响分析[J]. 西南交通大学学报,2023,58(6): 1248-1256.WANG Yao, CHEN Ling, YANG Dexin, et al. Cross regulation analysis of I2-controlled single-inductor dual-output buck LED driver[J]. Journal of Southwest Jiaotong University, 2023, 58(6): 1248-1256. [6] ZHENG Y Q, GUO J P, LEUNG K N. A single-inductor multiple-output buck/boost DC–DC converter with duty-cycle and control-current predictor[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12022-12039. doi: 10.1109/TPEL.2020.2988940 [7] WANG Y, XU L M, ZHANG L Y, et al. Modeling and stablility analysis of peak-current-mode-controlled SIDO CCM buck converter[C]//2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA). Kristiansand: IEEE, 2020: 915-920. [8] JIN W J, LEE A T L, TAN S C, et al. Single-inductor multiple-output inverter with precise and independent output voltage regulation[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 11222-11234. doi: 10.1109/TPEL.2020.2979893 [9] DONG Z, LI Z, LI X L, et al. Single-inductor multiple-input multiple-output converter with common ground, high scalability, and no cross-regulation[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6750-6760. doi: 10.1109/TPEL.2020.3036704 [10] KWON D, RINCON-MORA G A. Single-inductor–multiple-output switching DC–DC converters[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2009, 56(8): 614-618. [11] WANG Y, XU J P, YIN G. Cross-regulation suppression and stability analysis of capacitor current ripple controlled SIDO CCM buck converter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1770-1780. doi: 10.1109/TIE.2018.2838103 [12] WANG B F, KANAMARLAPUDI V R K, XIAN L, et al. Model predictive voltage control for single-inductor multiple-output DC–DC converter with reduced cross regulation[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4187-4197. doi: 10.1109/TIE.2016.2532846 [13] 周国华,冉祥,周述晗,等. 恒定谷值电流型变频控制CCM单电感双输出Boost变换器建模与分析[J]. 中国电机工程学报,2018,38(23): 7015-7025,7135. doi: 10.13334/j.0258-8013.pcsee.172730ZHOU Guohua, RAN Xiang, ZHOU Shuhan, et al. Modeling and analysis of CCM single-inductor dual-output boost converter with fixed valley current mode variable frequency control[J]. Proceedings of the CSEE, 2018, 38(23): 7015-7025,7135. doi: 10.13334/j.0258-8013.pcsee.172730 [14] 冉祥,周国华,周述晗. 共模-差模电压型控制连续导电模式单电感双输出Boost变换器交叉影响特性分析[J]. 电工技术学报,2019,34(12): 2519-2528. doi: 10.19595/j.cnki.1000-6753.tces.180544RAN Xiang, ZHOU Guohua, ZHOU Shuhan. Cross-regulation characteristic of continuous conduction mode single-inductor dual-output boost converter with common-mode voltage and differential-mode voltage control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2519-2528. doi: 10.19595/j.cnki.1000-6753.tces.180544 [15] 王瑶. 电容电流-电容电压纹波控制单电感双输出CCM Buck变换器[J]. 中国电机工程学报,2020,40(10): 3280-3288.WANG Yao. Capacitor current and capacitor voltage ripple controlled single-inductor dual-output CCM buck converter[J]. Proceedings of the CSEE, 2020, 40(10): 3280-3288. [16] WANG B F, XIAN L, KANAMARLAPUDI V R K, et al. A digital method of power-sharing and cross-regulation suppression for single-inductor multiple-input multiple-output DC−DC converter[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 2836-2847. doi: 10.1109/TIE.2016.2631438 -
下载:
点击查看大图
计量
- 文章访问数: 253
- HTML全文浏览量: 89
- PDF下载量: 50
- 被引次数: 0