有砟轨道捣固作业起道方案的综合修正方法

张雨潇; 时瑾; 倪国华; 王英杰

doi:10.3969/j.issn.0258-2724.20220526

有砟轨道捣固作业起道方案的综合修正方法

doi: 10.3969/j.issn.0258-2724.20220526

1.
北京交通大学土木建筑工程学院，北京 100044
2.
中国铁路兰州局集团有限公司银川工务段，宁夏银川 750000

基金项目: 国家自然科学基金（52078035, 52178406）

详细信息

作者简介:
张雨潇（1996—），男，博士研究生，研究方向为轨道平顺性控制，E-mail：21115059@bjtu.edu.cn

通讯作者:
时瑾（1980—），男，教授，研究方向为铁路线路工程技术，E-mail：jshi@bjtu.edu.cn

中图分类号: U216.42
计量
- 文章访问数: 347
- HTML全文浏览量: 98
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-30
- 修回日期: 2022-11-28
- 网络出版日期: 2023-07-06
- 刊出日期: 2022-12-01

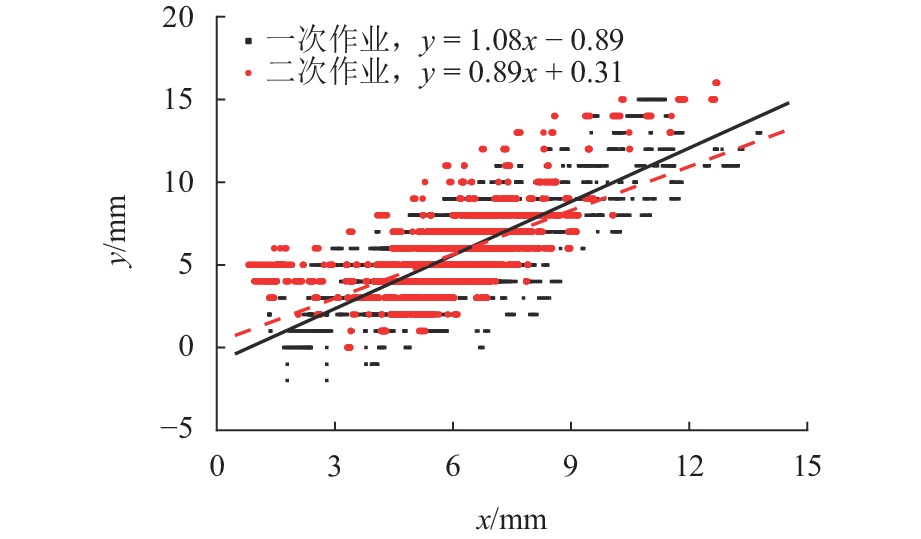
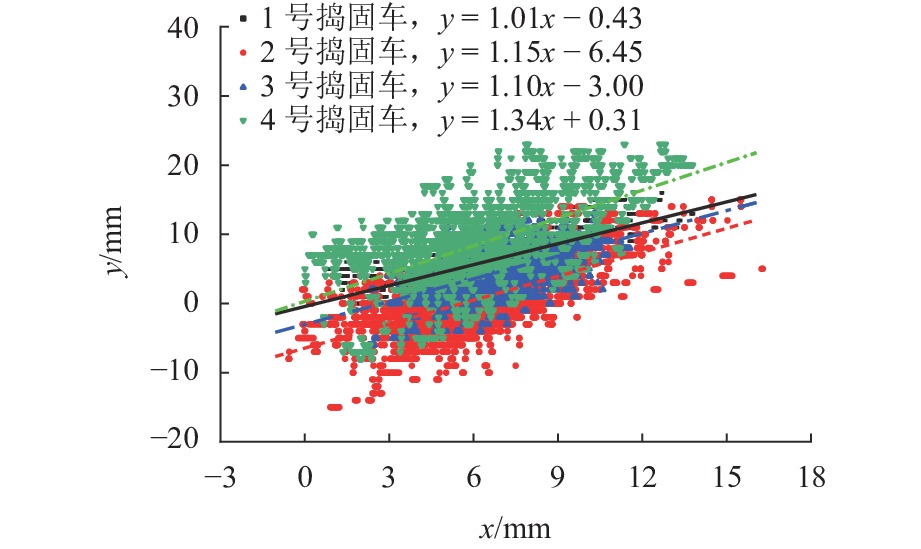
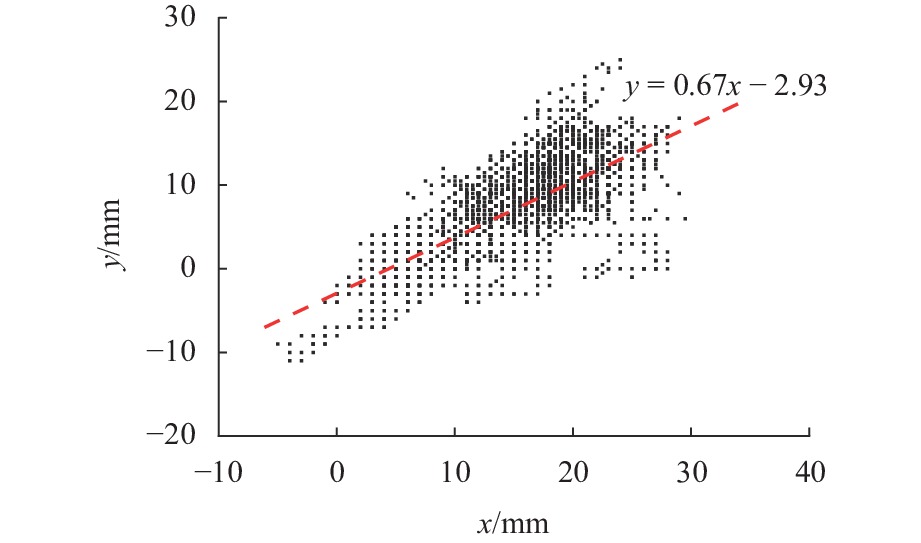
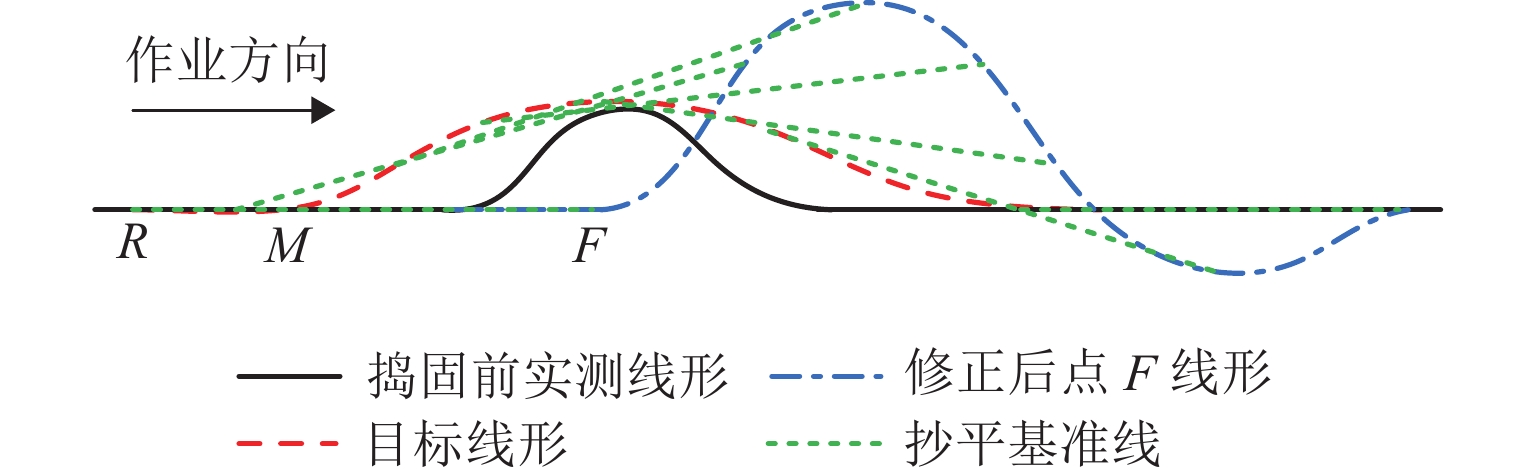
Comprehensive Correction Method of Lifting Scheme for Tamping Operation of Ballasted Track

1.
School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
2.
Yinchuan Track Maintenance Division, China Railway Lanzhou Group Co., Ltd., Yinchuan 750000, China

摘要

摘要:
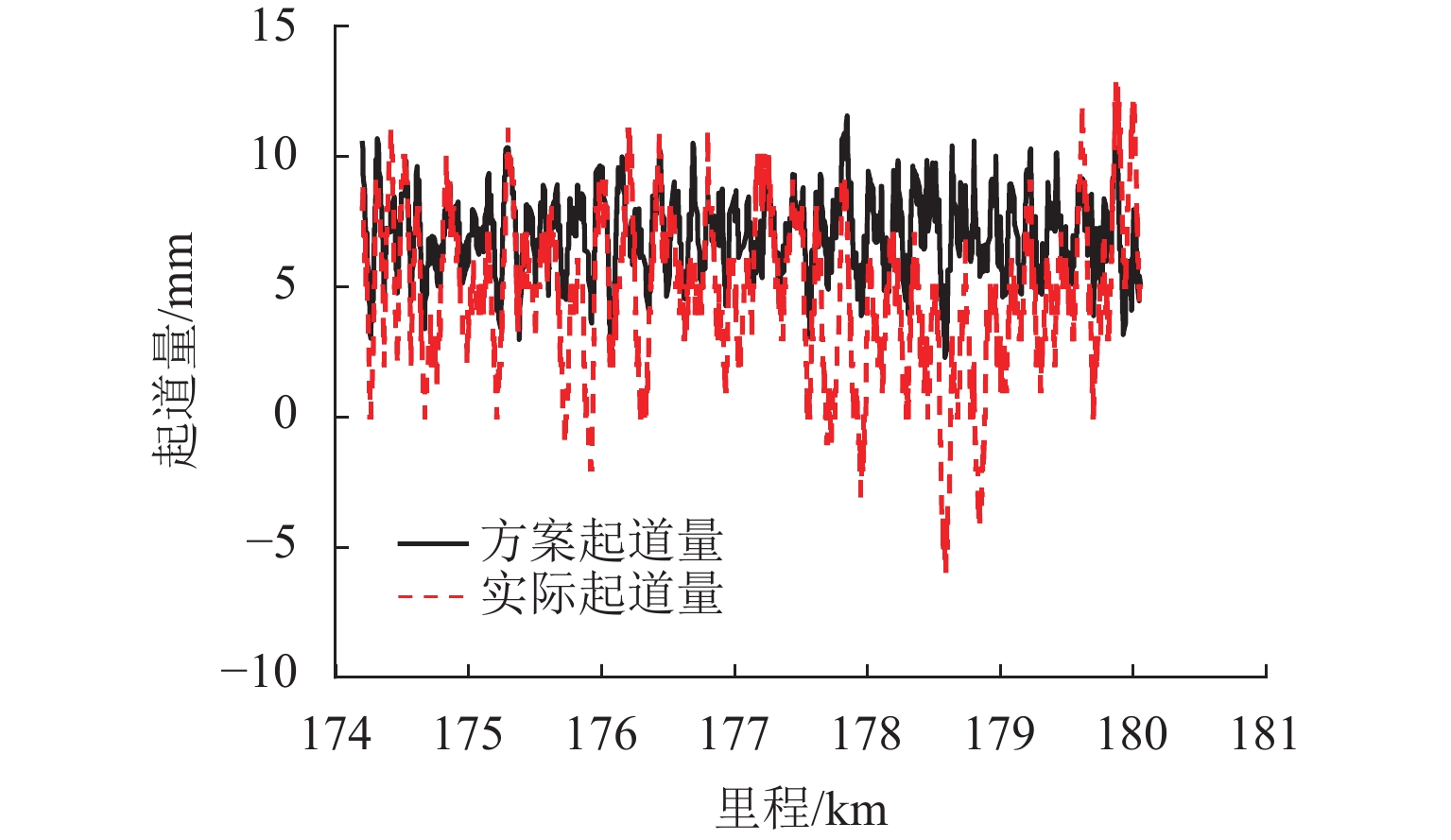
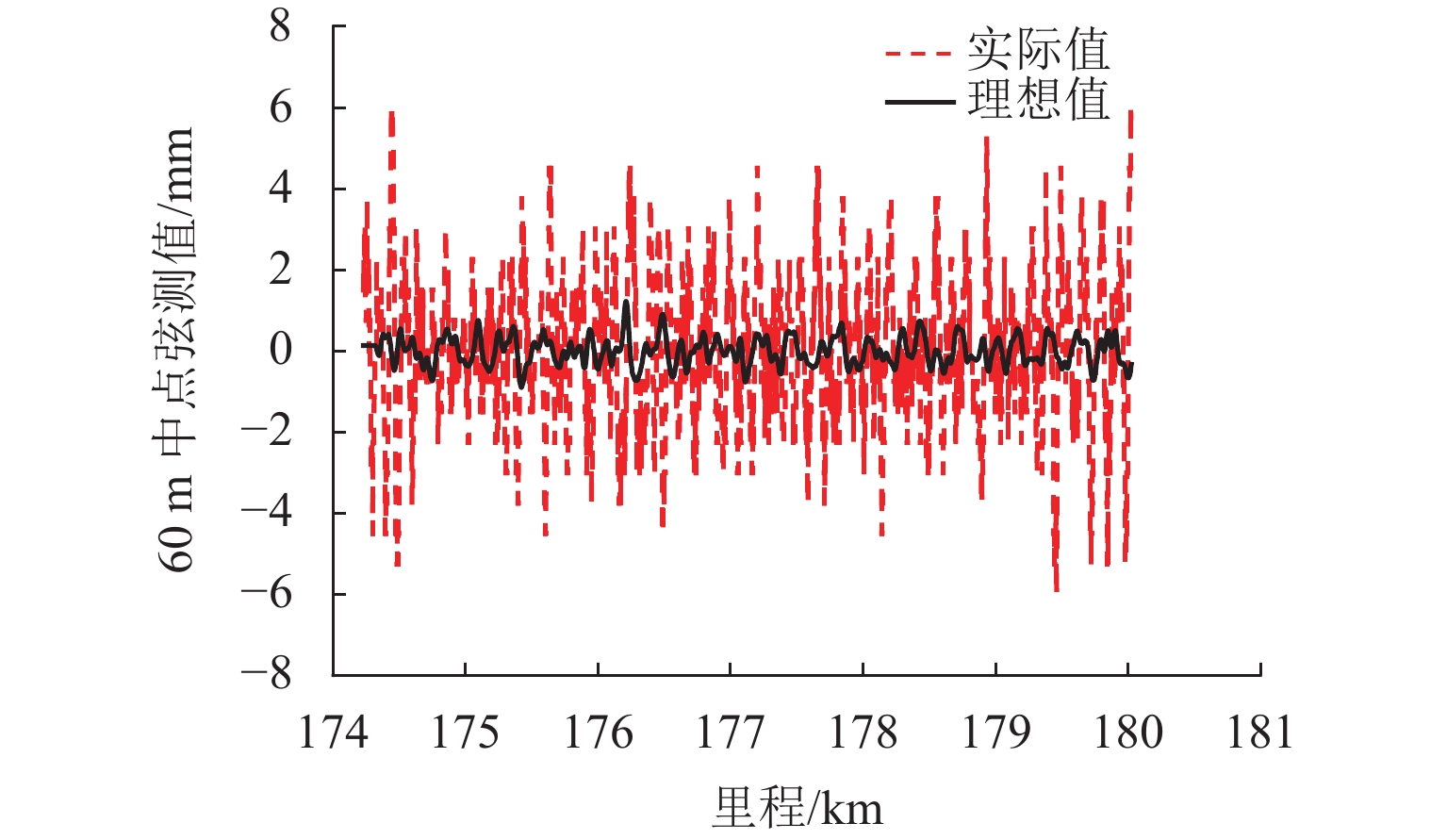
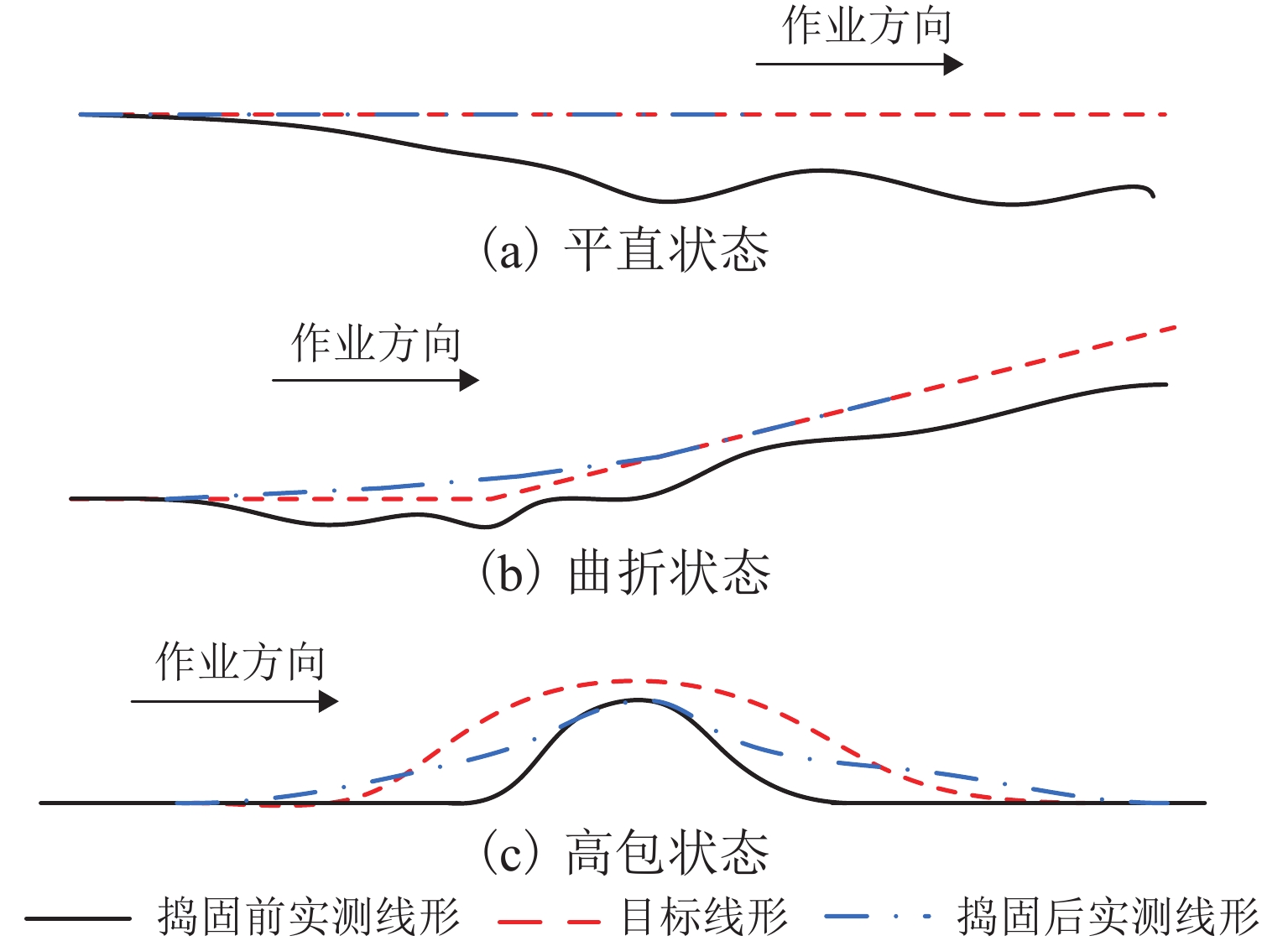
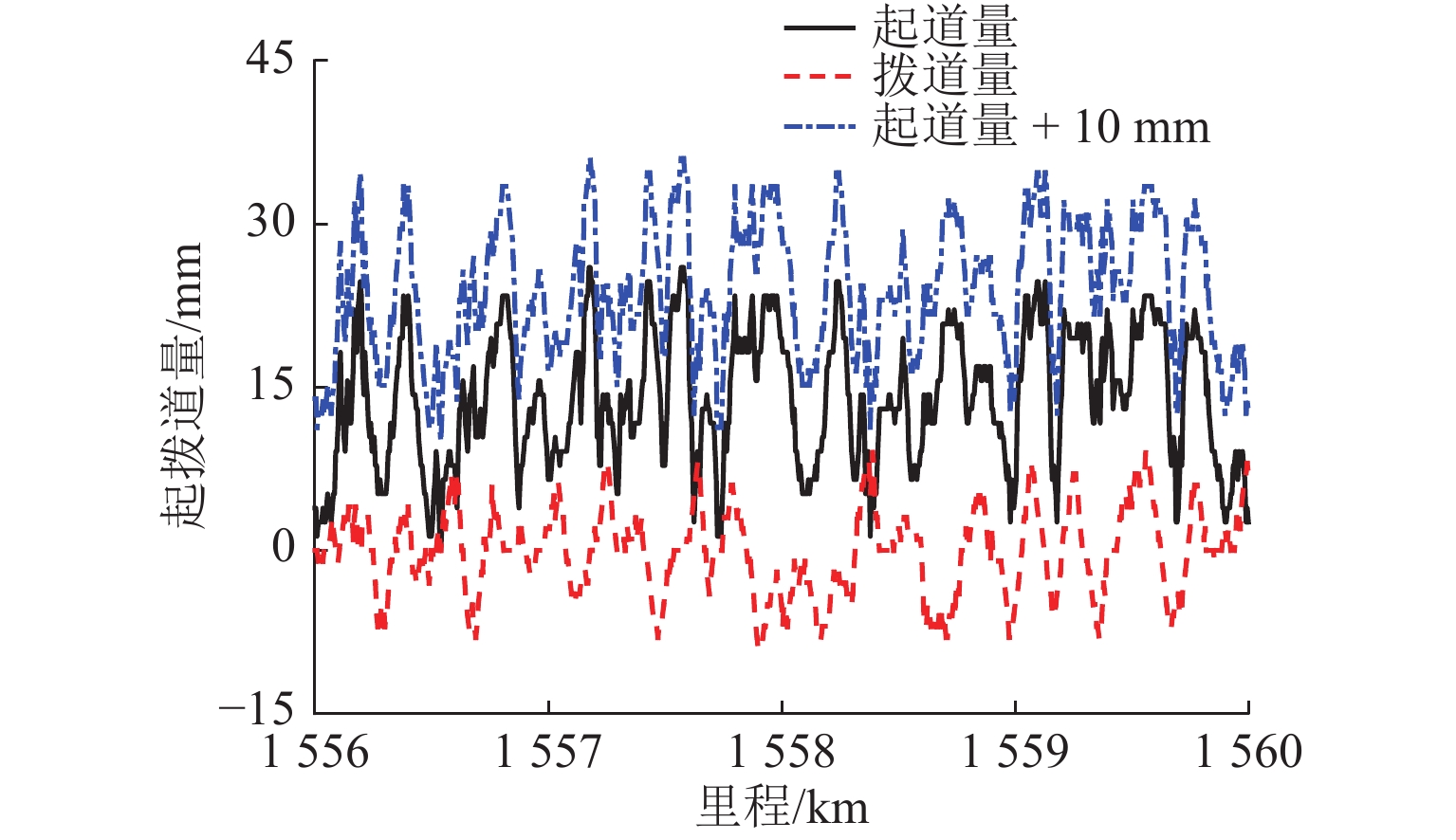
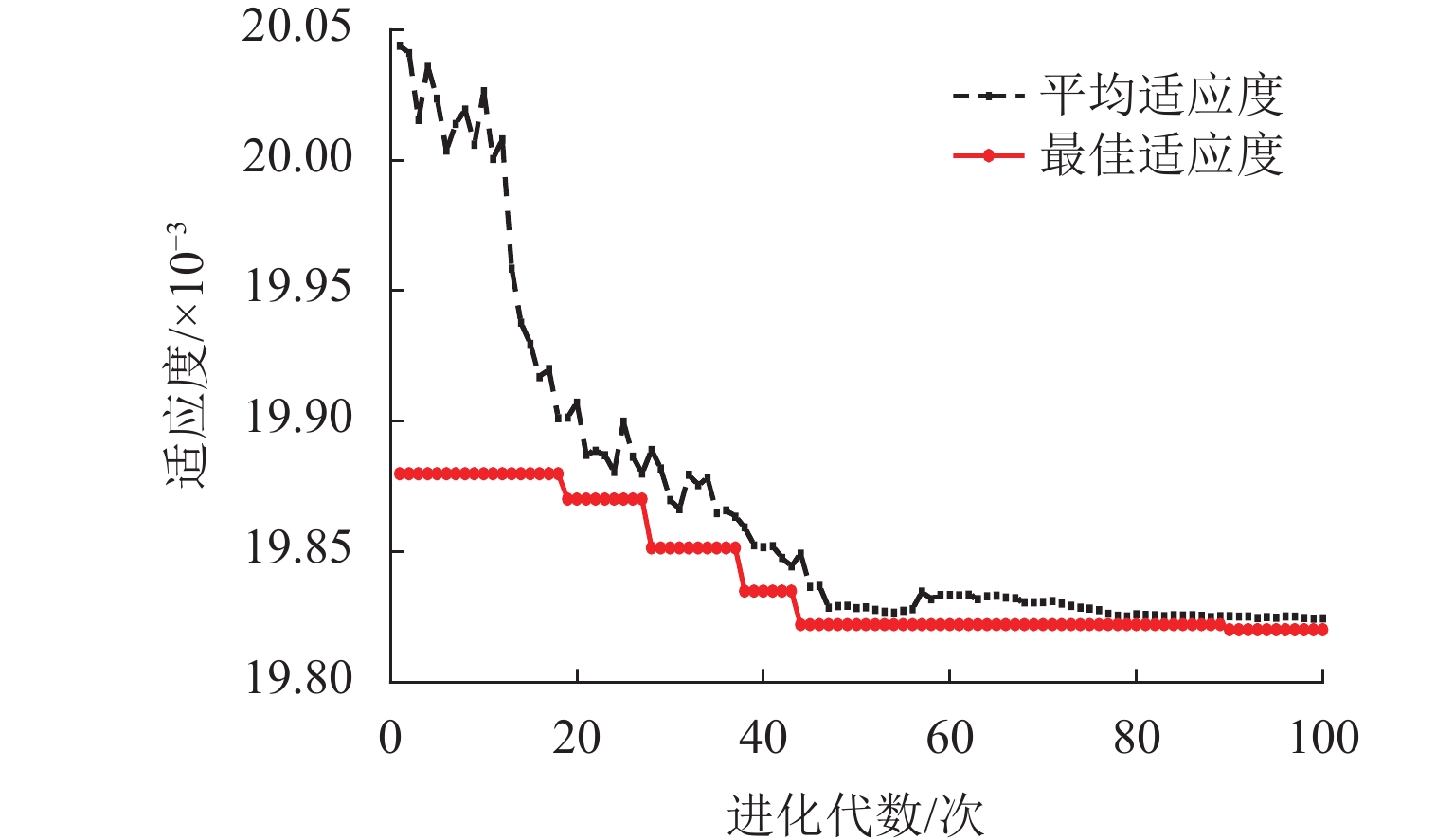
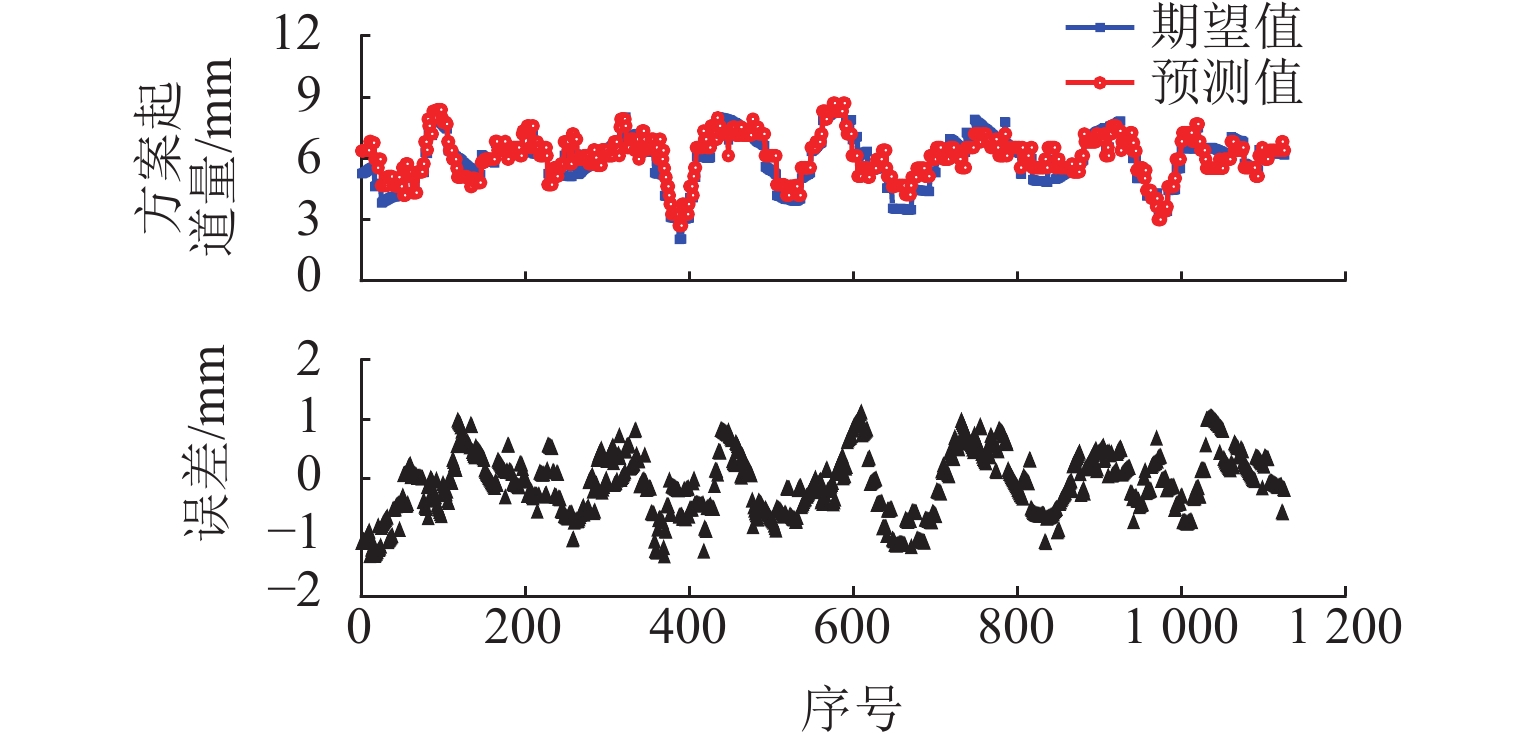
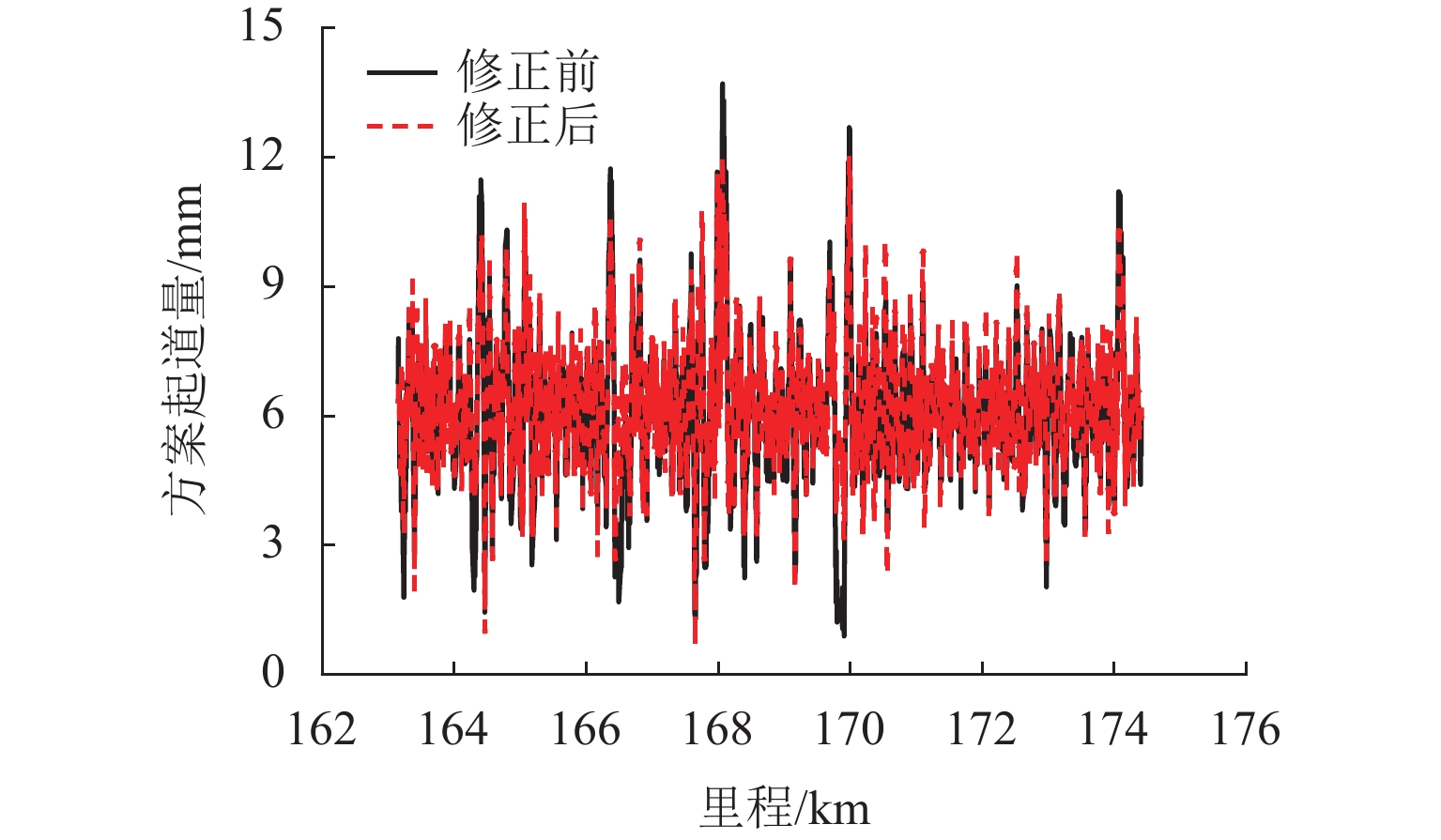
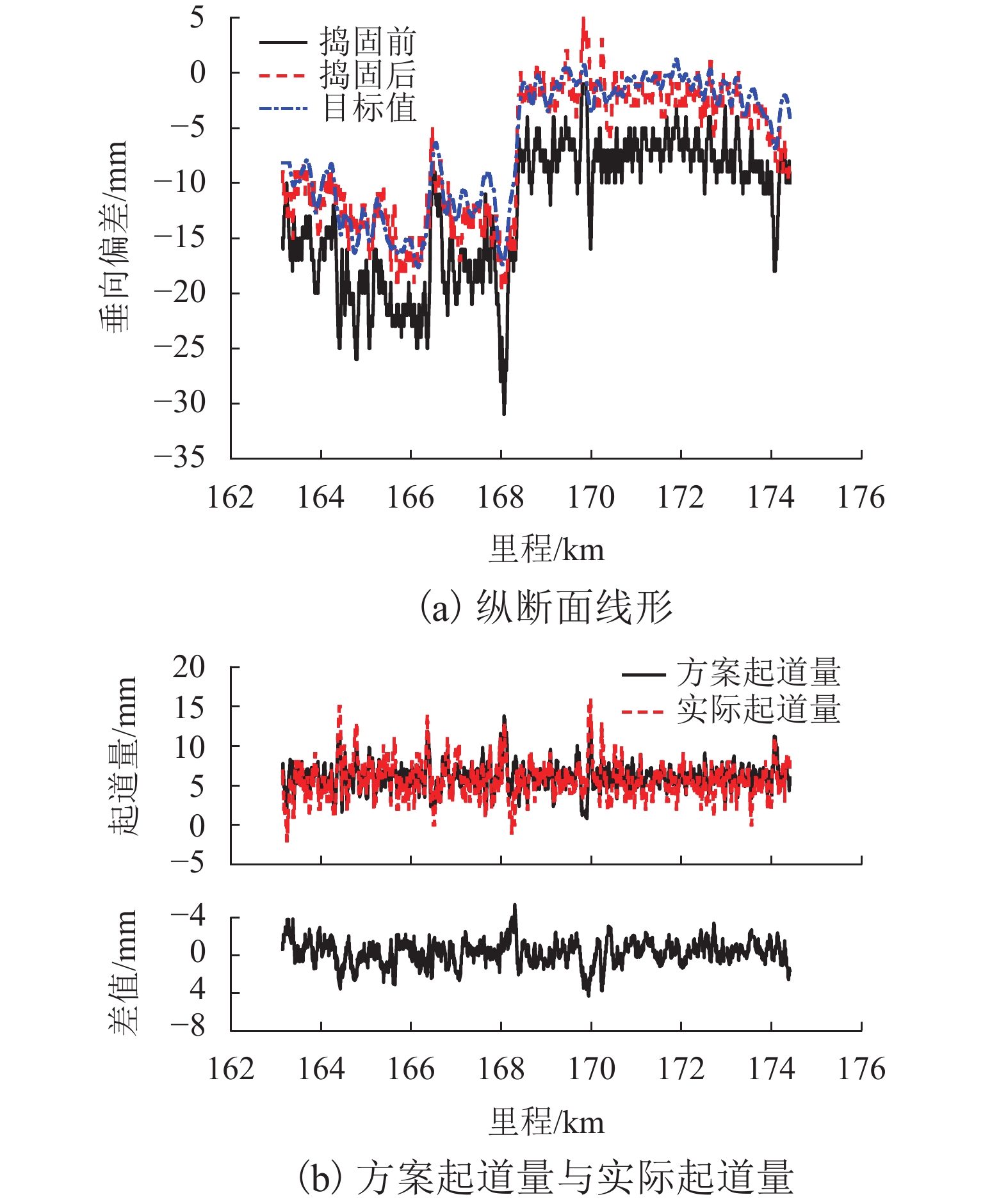
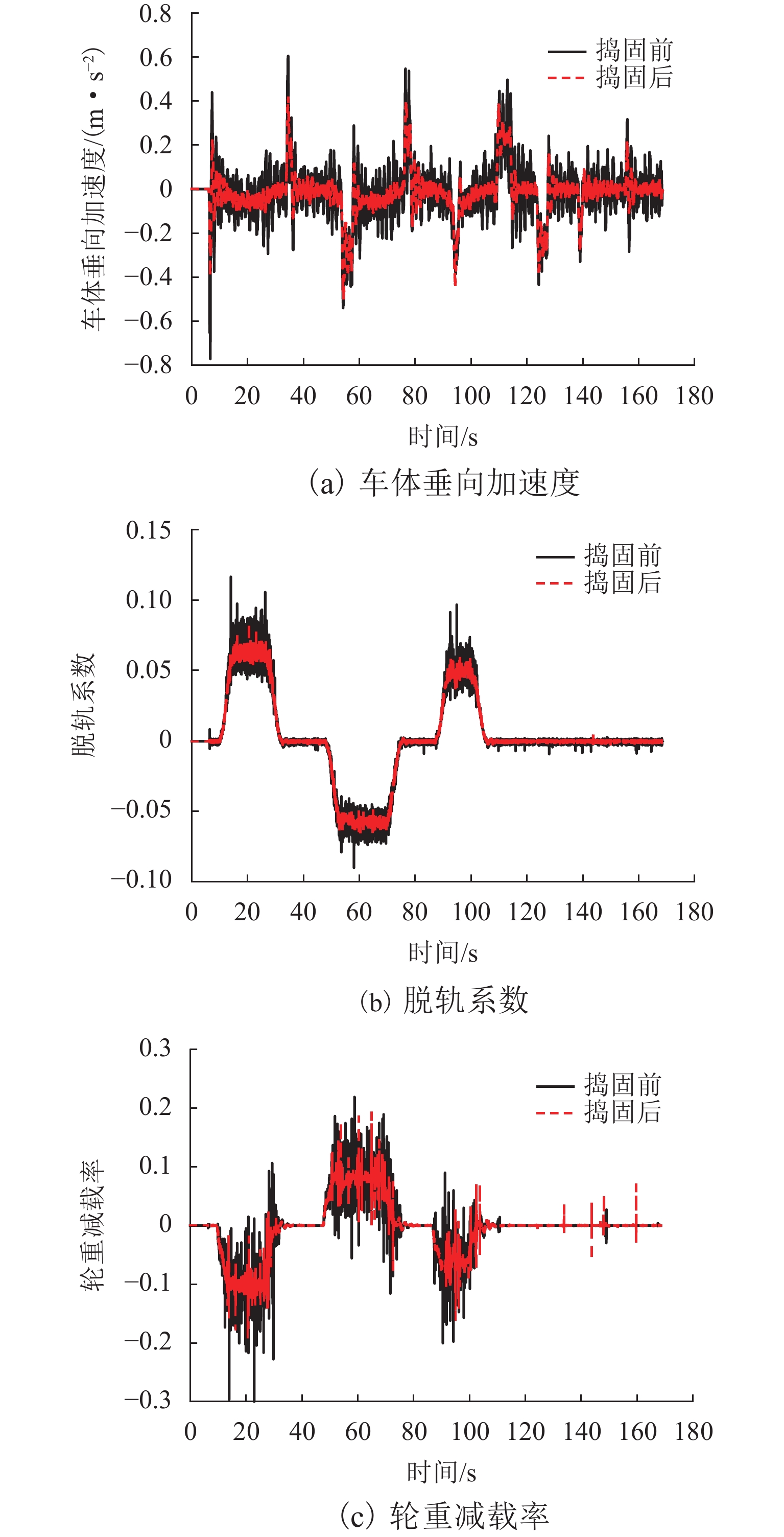
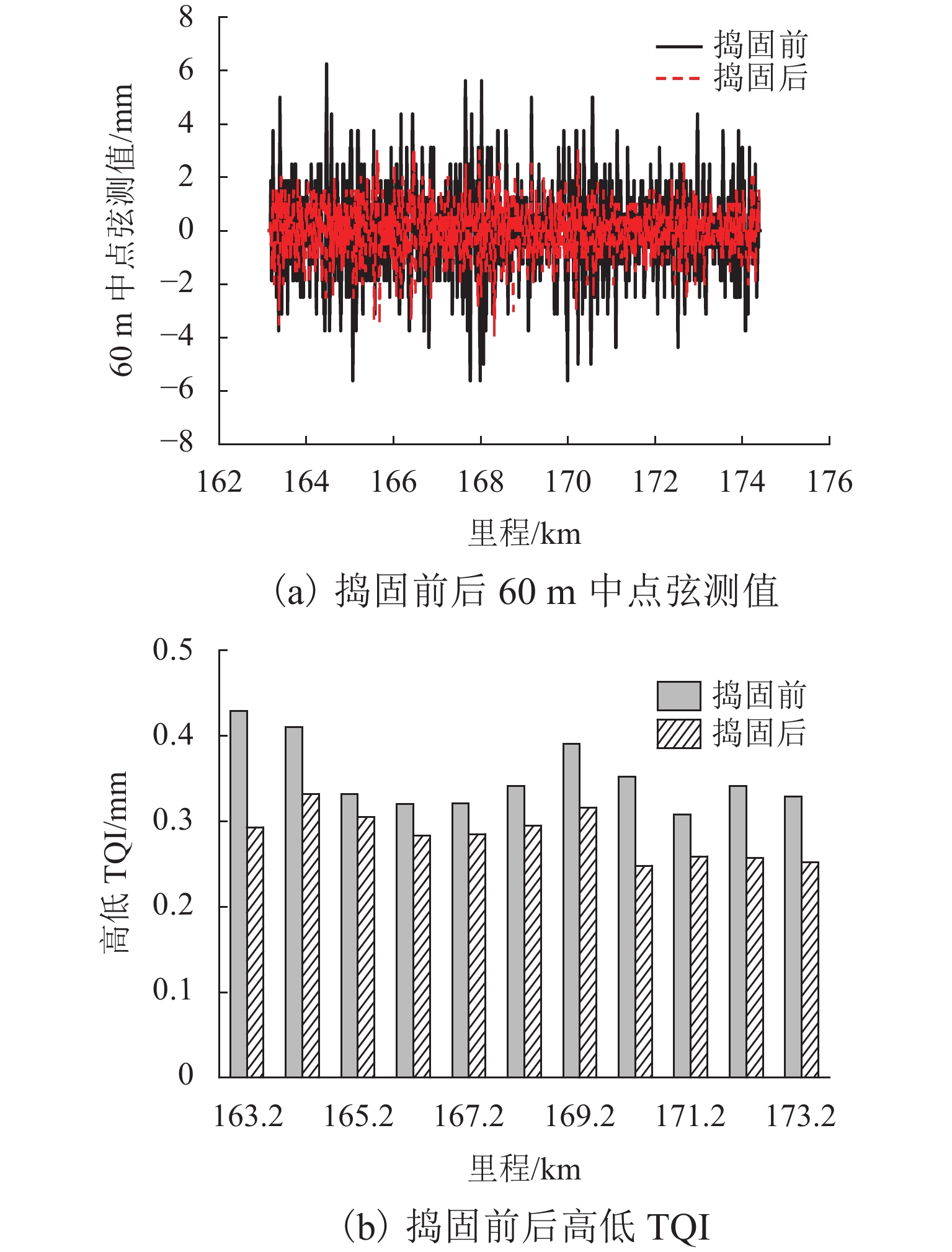
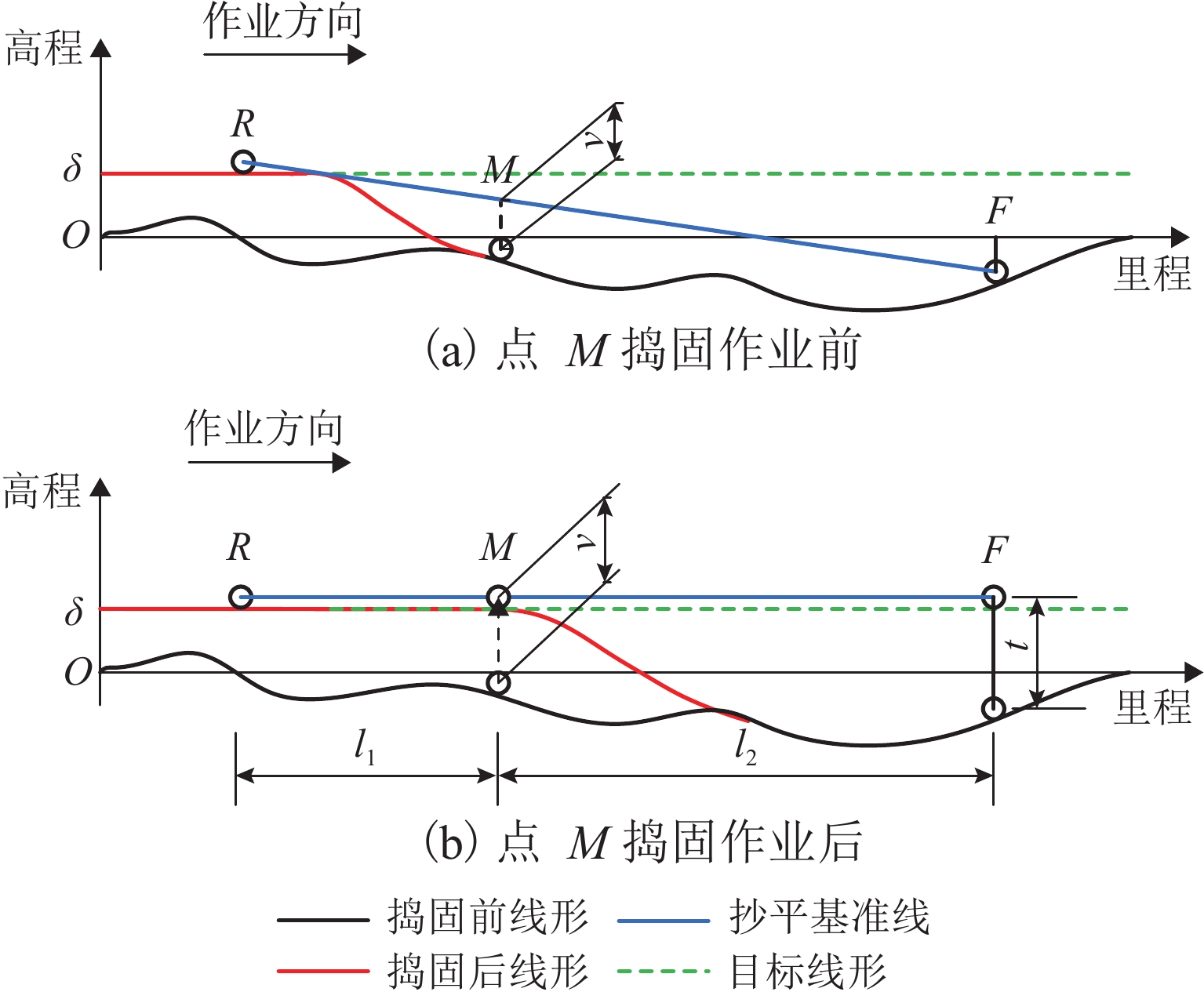
为保证捣固作业效果达到预期目标，需严格控制影响作业质量的不利因素，首先，以有砟轨道捣固作业数据为研究对象，分析影响作业质量的关键因素，探讨传统方法修正起道方案的基本原理；其次，将多因素约束条件纳入目标线形构造过程，并遵从历史作业规律，对起道量进行修正，构造一种用于提升轨道高低调整效果的起道方案综合修正方法；最后，以某高速铁路有砟轨道捣固作业为工程背景，验证综合修正方法的实施效果. 研究结果表明：在起道方案制定过程中施加针对性控制措施，有利于提高捣固作业对轨道不平顺的调整能力；捣固后，线形实测值与目标值之间决定系数高达0.92；方案起道量与实际起道量之间均方误差为1.8 mm；高低60 m中点弦测值降至4.0 mm，高低轨道质量指数降至0.28 mm.
- 捣固作业 /
- 起道量 /
- 有砟轨道 /
- 轨道不平顺 /
- 支持向量回归
Abstract:
In order to make the effect of tamping operation meet the expected goals, it is necessary to strictly control the unfavorable factors affecting the quality of the operation. Firstly, by taking the tamping operation data of ballasted track as the research object, the key factors affecting the operation quality were analyzed firstly, and the basic principles of the traditional methods to correct the lifting scheme were discussed. Secondly, by incorporating the multi-factor constraints into the target line construction process and correcting the lifting value according to the historical operation law, a comprehensive correction method of the lifting scheme for improving the adjustment effect of track height was constructed. Finally, by taking the ballasted track tamping operation of a high-speed railway as the engineering background, the implementation effect of the comprehensive correction method was verified. The results show that the application of targeted control measures in the process of lifting scheme formulation can improve the ability of the tamping operation to adjust the track irregularity. The coefficient of determination between the measured value and the target value of the alignment after tamping is as high as 0.92, and the mean square error between the planned lifting value and the actual lifting value is only 1.8 mm. The mid-chord value of 60 m is reduced to 4.0 mm, and the track quality index is reduced to 0.28 mm.
- tamping operation /
- lifting value /
- ballasted track /
- track irregularity /
- support vector regression (SVR)

HTML全文

图 1 纵向抄平作业原理

Figure 1. Principle of longitudinal leveling operation

下载: 全尺寸图片幻灯片

图 2 方案起道量与实际起道量

Figure 2. Planned and actual lifting values

下载: 全尺寸图片幻灯片

图 3 高低不平顺理想值与实际值

Figure 3. Ideal and actual values of track irregularity

下载: 全尺寸图片幻灯片

图 4 不同目标线形的捣固作业

Figure 4. Tamping operations with different target lines

下载: 全尺寸图片幻灯片

图 5 起、拨道方案

Figure 5. Schemes of lifting and lining

下载: 全尺寸图片幻灯片

图 6 捣固车重复性作业精度

Figure 6. Repetitive operation accuracy of tamping wagon

下载: 全尺寸图片幻灯片

图 7 不同捣固车作业精度

Figure 7. Operation accuracy of different tamping wagons

下载: 全尺寸图片幻灯片

图 8 起道量分布趋势

Figure 8. Distribution trend of lifting value

下载: 全尺寸图片幻灯片

图 9 目标线形修正示意

Figure 9. Target line correction

下载: 全尺寸图片幻灯片

图 10 目标线形构造及修正结果

Figure 10. Construction and correction of target line

下载: 全尺寸图片幻灯片

图 11 适应度曲线

Figure 11. Fit curve

下载: 全尺寸图片幻灯片

图 12 测试集数据预测效果

Figure 12. Prediction effect of test set data

下载: 全尺寸图片幻灯片

图 13 方案起道量修正结果

Figure 13. Correction results of planned lifting value

下载: 全尺寸图片幻灯片

图 14 捣固作业整体效果

Figure 14. Overall effect of tamping operation

下载: 全尺寸图片幻灯片

图 15 行车安全性和舒适性指标

Figure 15. Running safety and comfortability index

下载: 全尺寸图片幻灯片

图 16 轨道平顺性状态

Figure 16. Track regularity state

下载: 全尺寸图片幻灯片

表 1 高低不平顺改善效果

Table 1. Improvement effect of track irregularity

线路	60 m 中点弦测值/mm		改善率/%		方案起道量均值/ mm
线路	捣固前	捣固后	高低不平顺	TQI	方案起道量均值/ mm
线路 1	8.00	6.50	18.75	20.38	6.50
线路 2	18.00	12.30	31.67	37.50	14.36

下载: 导出CSV

表 2 建模典型数据

Table 2. Typical data for modeling

实际起道量/mm	高低 60 m 中点弦测值/mm	捣固车编号	方案起道量/mm
10.00	5.00	1	16.00
8.00	4.25	3	14.00
10.00	5.50	2	16.00
9.00	4.75	3	15.00
$\vdots $	$\vdots $	$\vdots $	$\vdots $
9.00	5.50	1	16.00

下载: 导出CSV

参考文献(21)

[1]	木东升,周宇,韩延彬,等. 轨道综合作业对高速铁路有砟轨道几何不平顺改善效果[J]. 交通运输工程学报,2018,18(5): 90-99. MU Dongsheng, ZHOU Yu, HAN Yanbin, et al. Effect of track comprehensive maintenance on geometry irregularity improvement of ballast track in high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 90-99.
[2]	王英杰,楚杭,时瑾,等. 有砟高铁大机捣固质量相关性及敏感波长研究[J]. 铁道工程学报,2021,38(1): 37-41,108. WANG Yingjie, CHU Hang, SHI Jin, et al. Research on the machine tamping quality correlation and sensitive wavelengths of high speed railway ballasted track[J]. Journal of Railway Engineering Society, 2021, 38(1): 37-41,108.
[3]	AINGARAN S, LE PEN L, ZERVOS A, et al. Modelling the effects of trafficking and tamping on scaled railway ballast in triaxial tests[J]. Transportation Geotechnics, 2018, 15: 84-90. doi: 10.1016/j.trgeo.2018.04.004
[4]	KUMARA J J, HAYANO K. Deformation characteristics of fresh and fouled ballasts subjected to tamping maintenance[J]. Soils and Foundations, 2016, 56(4): 652-663. doi: 10.1016/j.sandf.2016.07.006
[5]	王众保,许永贤,王红,等. 大型养路机械捣固作业参数对捣固效果影响规律的研究[J]. 铁道建筑,2020,60(1): 129-133. WANG Zhongbao, XU Yongxian, WANG Hong, et al. Study on influence laws of working parameters of heavy-duty maintenance machinery tamping on tamping effect[J]. Railway Engineering, 2020, 60(1): 129-133.
[6]	时瑾,张雨潇,楼梁伟,等. 新建高速铁路有砟轨道精捣作业环节改进及效果[J]. 中国铁道科学,2021,42(6): 8-17. SHI Jin, ZHANG Yuxiao, LOU Liangwei, et al. Optimization and effect of accurate tamping operation link for ballasted track in newly-built high-speed railway[J]. China Railway Science, 2021, 42(6): 8-17.
[7]	时瑾,张雨潇,陈云峰,等. 基于长波平顺性的提速线路精捣方案优化算法及应用[J]. 铁道学报,2022,44(2): 72-80. SHI Jin, ZHANG Yuxiao, CHEN Yunfeng, et al. Optimization algorithm and application of precise tamping for speed raising railway based on long-wave regularity[J]. Journal of the China Railway Society, 2022, 44(2): 72-80.
[8]	时瑾,张雨潇,陈云峰,等. 有砟高铁捣固作业轨向平顺性控制方法[J]. 交通运输工程学报,2022,22(2): 76-86. SHI Jin, ZHANG Yuxiao, CHEN Yunfeng, et al. Track alignment irregularity control method for tamping operation of ballasted high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2022, 22(2): 76-86.
[9]	李阳腾龙. 高速铁路轨道精测精调及其平顺性优化研究[J]. 测绘学报,2018,47(11): 15-62. LI Yangtenglong. Study on track precise inspection and adjustment as well as its regularity optimization for high-speed railways[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(11): 15-62.
[10]	李阳腾龙,岑敏仪,谭俊. 增加轨道扣件可调量和相邻点偏差约束的高铁轨道精调优化算法[J]. 铁道学报,2017,39(5): 90-98. LI Yangtenglong, CEN Minyi, TAN Jun. An optimization algorithm of track fine adjustment of high-speed railways with added constraints of remaining allowed adjustable values and differences in deviations of adjacent fasteners[J]. Journal of the China Railway Society, 2017, 39(5): 90-98.
[11]	魏晖,吴仕凤,朱洪涛. 基于相对测量调轨的高速铁路有砟线路整道技术研究[J]. 铁道标准设计,2013,57(8): 11-15. WEI Hui, WU Shifeng, ZHU Hongtao. Research on ballast trimming technology based on relative measurement method for ballast track of high-speed railway[J]. Railway Standard Design, 2013, 57(8): 11-15.
[12]	魏晖,朱洪涛,赵国堂,等. 基于中点弦测模型的无砟轨道精调量迭代求解[J]. 西南交通大学学报,2015,50(1): 131-136. WEI Hui, ZHU Hongtao, ZHAO Guotang, et al. Iterative algorithm of HSR ballastless track realignment calculation based on MCO model[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 131-136.
[13]	杨飞,孙宪夫,魏子龙,等. 基于动静态检测数据的轨道弹性状态评估及平顺性调整方法[J]. 铁道学报,2023,45(5): 82-90. YANG Fei, SUN Xianfu, TAN Shehui, et al. Evaluation difference of dynamic and static track irregularity and characteristics of dynamic chord measurement method[J]. Journal of Southwest Jiaotong University, 2023, 45(5): 82-90.
[14]	杨飞,孙宪夫,谭社会,等. 动静态轨道不平顺评价差异及动态弦测法特性[J]. 西南交通大学学报,2022,57(6): 1239-1249. YANG Fei, SUN Xianfu, TAN Shehui, et al. Evaluation difference of dynamic and static track irregularity and characteristics of dynamic chord measurement method[J]. Journal of Southwest Jiaotong University, 2022, 57(6): 1239-1249.
[15]	梁国栋. 道岔捣固车上的数字化精确捣固法运用[J]. 技术与市场,2020,27(2): 94-95.
[16]	江来伟,岑敏仪,赵栋. 新建有砟线路精测精捣起道量修正算法[J]. 铁道建筑,2019,59(6): 127-131. JIANG Laiwei, CEN Minyi, ZHAO Dong. Lifting correction algorithm of precise inspection and tamping for new-built railway[J]. Railway Engineering, 2019, 59(6): 127-131.
[17]	LEE J S, HWANG S H, CHOI I Y, et al. Deterioration prediction of track geometry using periodic measurement data and incremental support vector regression model[J]. Journal of Transportation Engineering, Part A: Systems, 2020, 146(1): 04019057.1-04019057.12.
[18]	YAN T H, CORMAN F. Assessing and extending track quality index for novel measurement techniques in railway systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2020, 2674(8): 24-36. doi: 10.1177/0361198120923661
[19]	BARBOUR W, MARTINEZ MORI J C, KUPPA S, et al. Prediction of arrival times of freight traffic on US railroads using support vector regression[J]. Transportation Research Part C: Emerging Technologies, 2018, 93: 211-227. doi: 10.1016/j.trc.2018.05.019
[20]	葛继科,邱玉辉,吴春明,等. 遗传算法研究综述[J]. 计算机应用研究,2008,25(10): 2911-2916. GE Jike, QIU YUhui, WU Chunming, et al. Summary of genetic algorithms research[J]. Application Research of Computers, 2008, 25(10): 2911-2916.
[21]	杨飞,赵文博,高芒芒,等. 运营期高速铁路轨道长波不平顺静态测量方法及控制标准[J]. 中国铁道科学,2020,41(3): 41-49. YANG Fei, ZHAO Wenbo, GAO Mangmang, et al. Static measurement method and control standard for long-wave irregularity of high-speed railway track during operation period[J]. China Railway Science, 2020, 41(3): 41-49.