Method of Splicing Constant Speed Signals with Short Signals During Wheelset Acceleration and Deceleration
-
摘要:
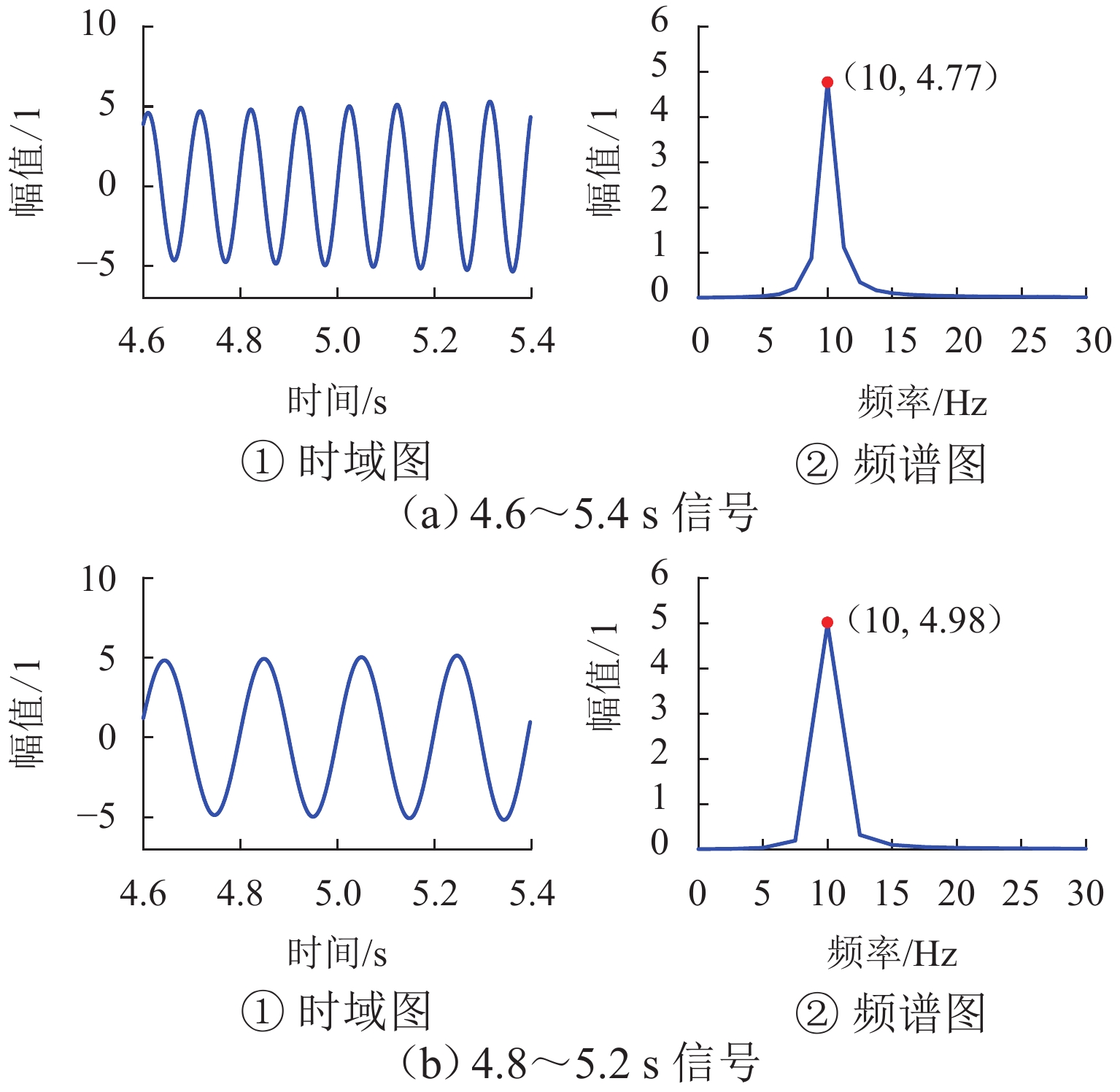
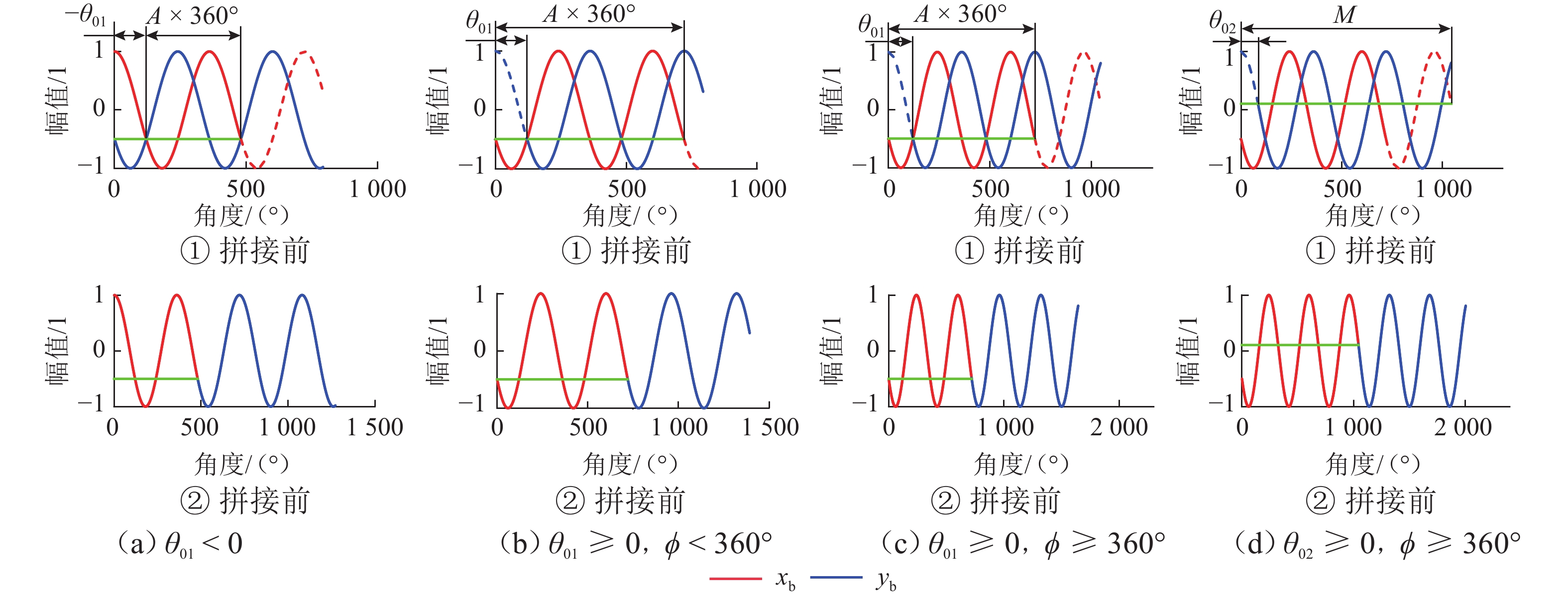
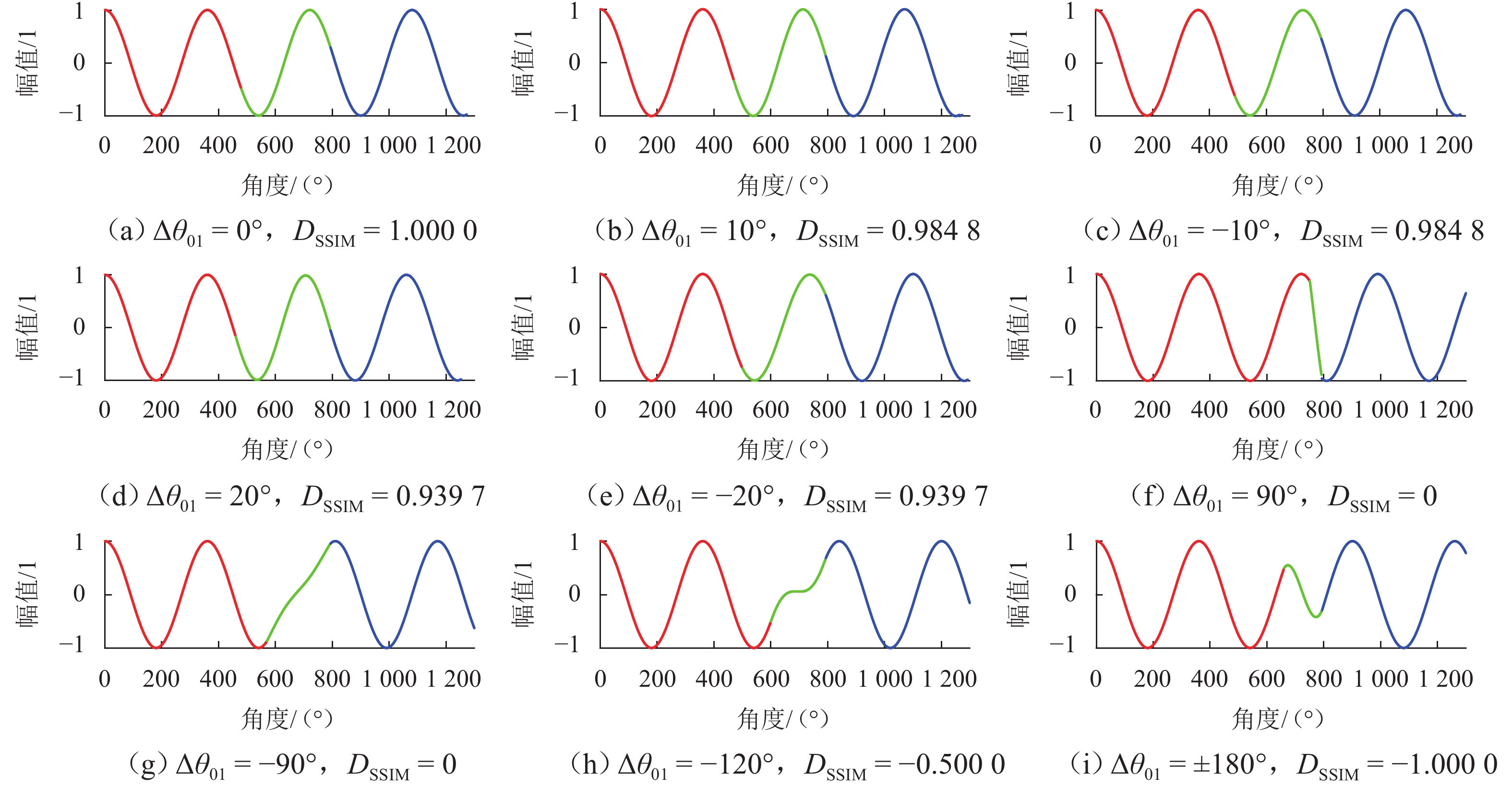
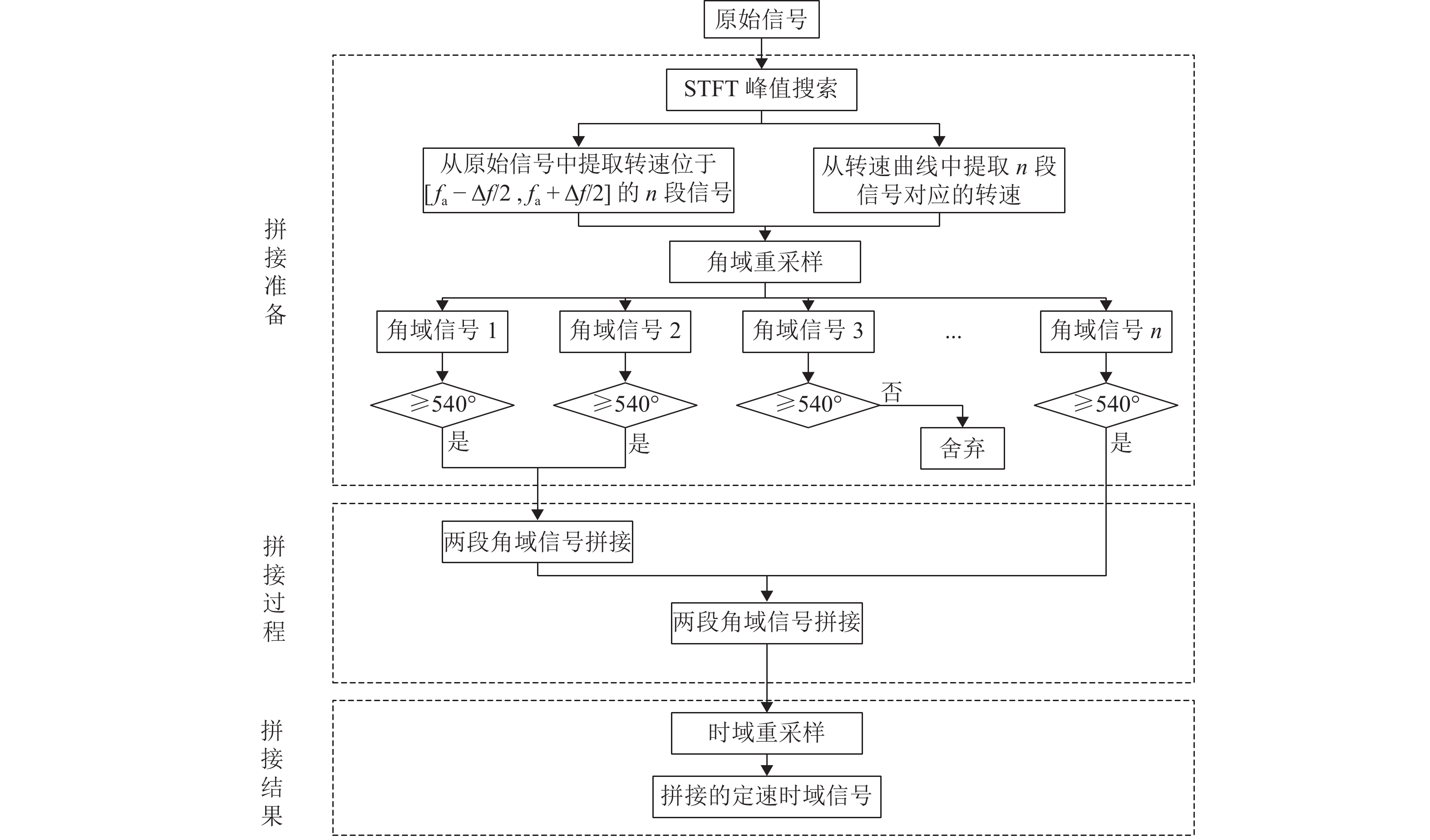
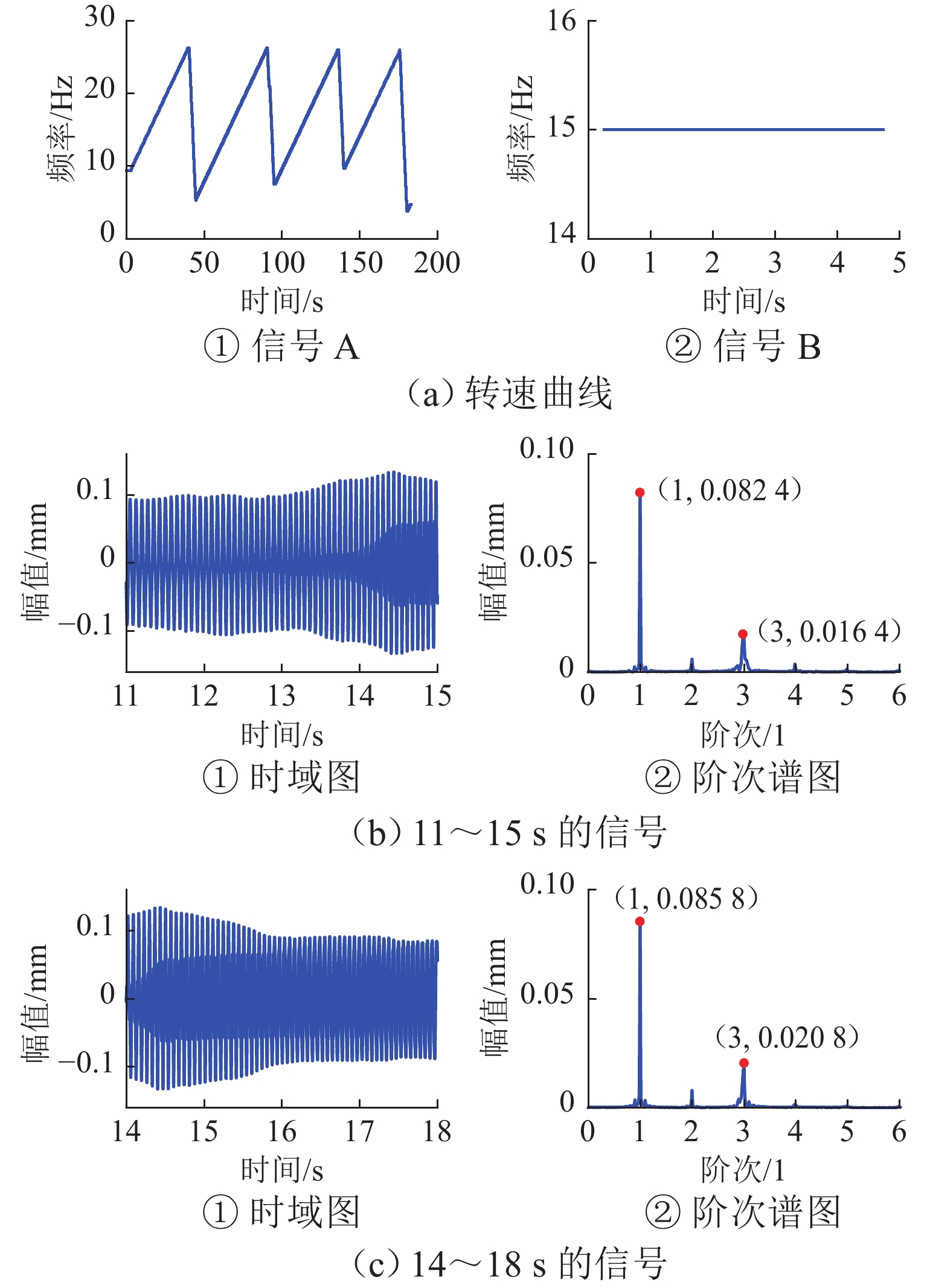
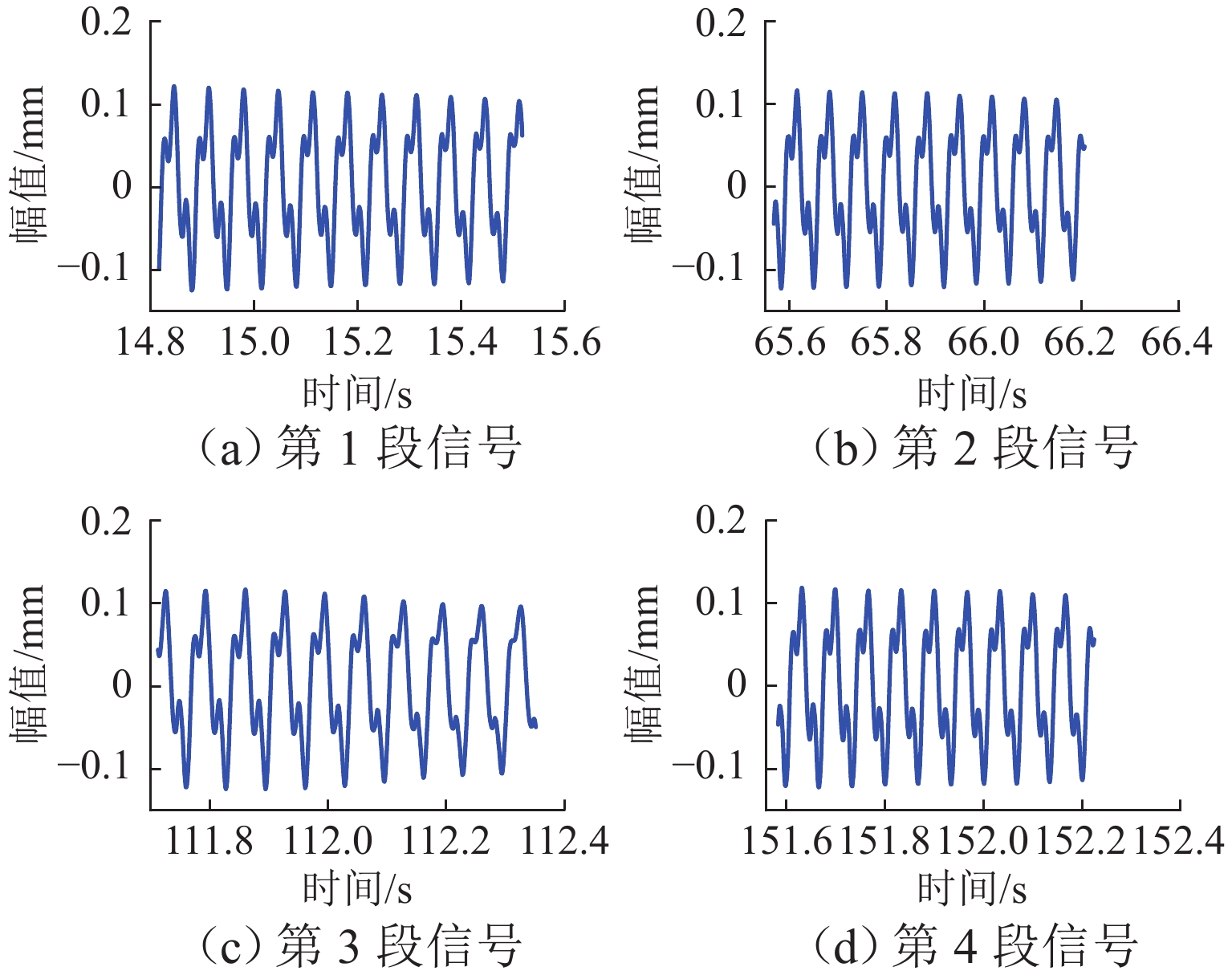
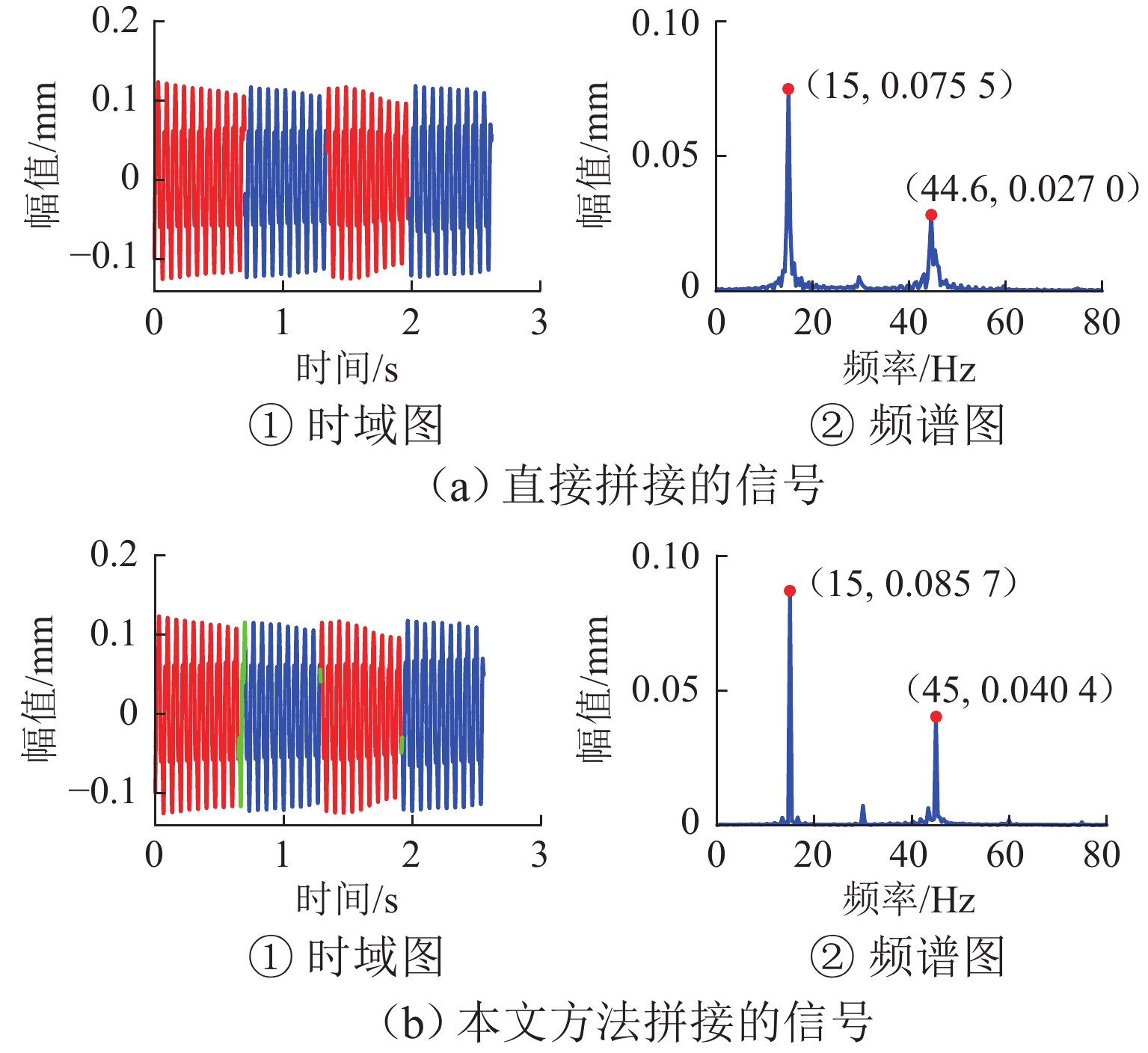
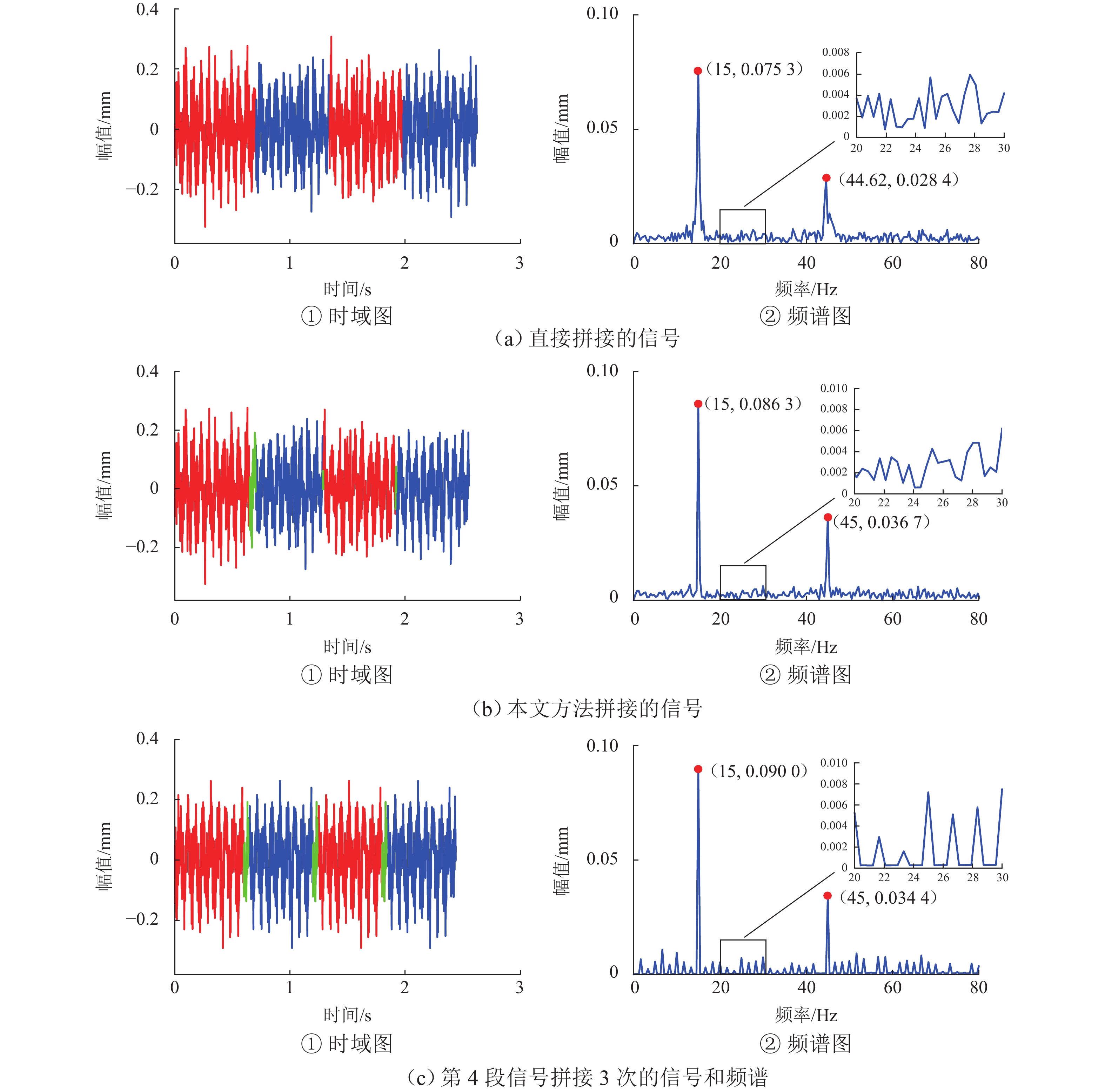
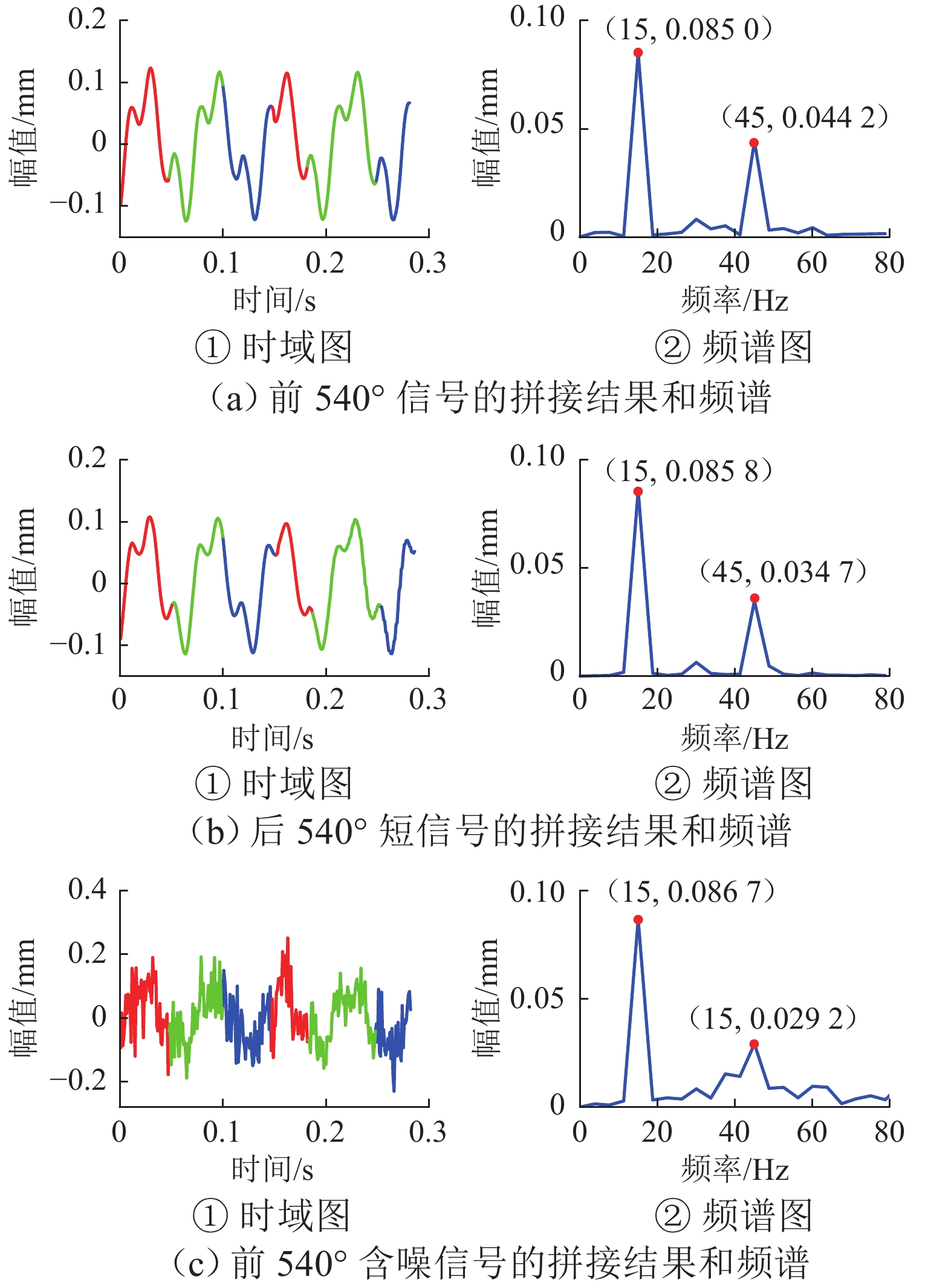
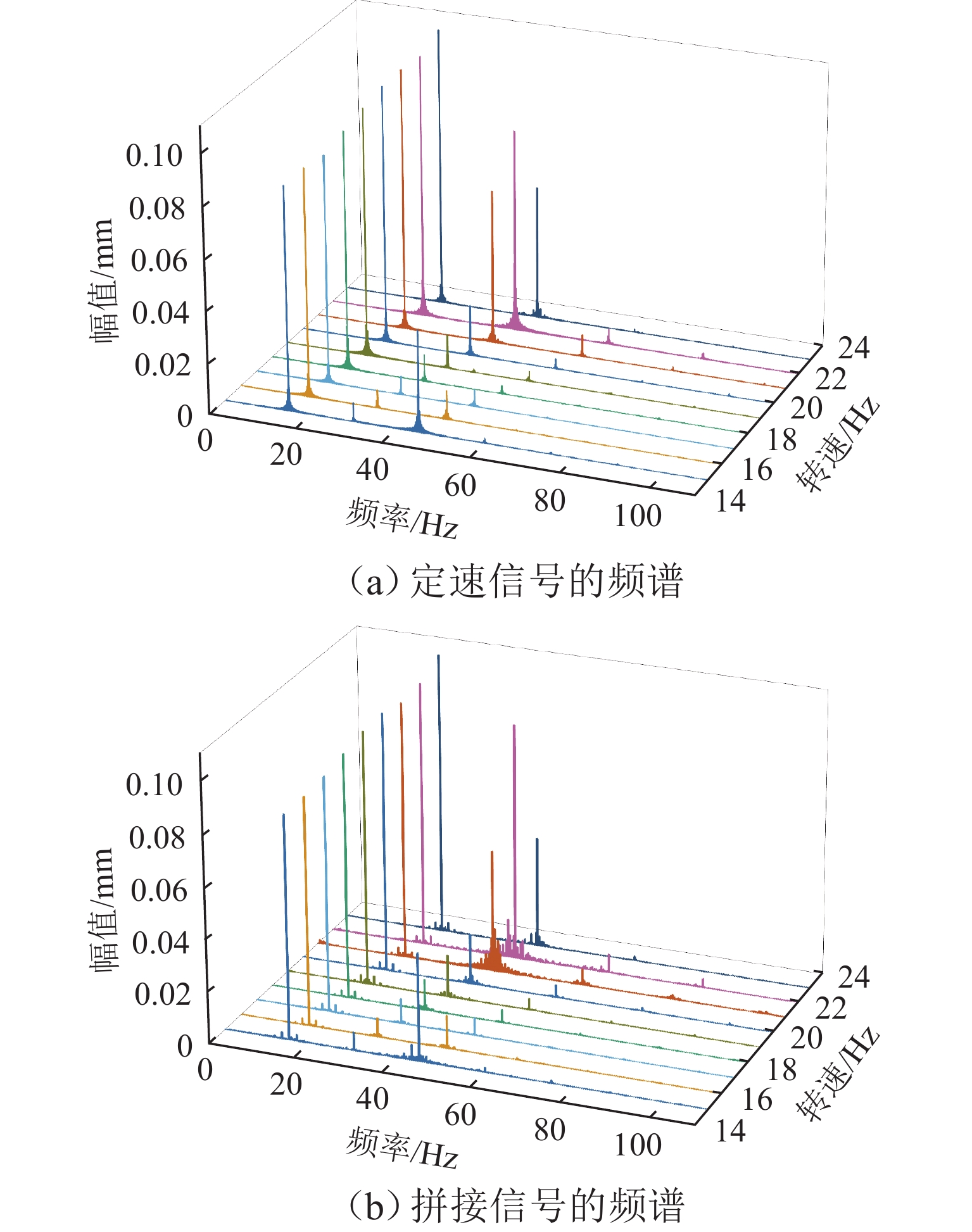
列车轮对的特征值与转速密切相关，进行轮对故障定量分析时需要采集某转速下一定长度的信号，而实际工作于变速工况的系统难以方便获得该信号，为满足定量分析的要求，提出一种不需要转速计的信号重构方法，该方法利用升降速工况下的短信号片段拼接成指定转速下的定速信号. 首先，采用STFT （short-time Fourier transform）峰值搜索方法获取转速曲线，并提取通过指定转速的多个信号片段；其次，将信号片段转换成角域信号，并通过互功率谱密度确定信号间的相位差，根据相位差和前信号的长度，得到信号间的拼接位置，并采用插值和融合技术保证拼接信号的连续性；最后，将拼接得到的角域信号恢复成时域信号. 经与轮对结构相似的转子实验台实验验证：某裂纹轴在升降速过程中，使用本方法获得的各转速拼接信号频谱和实验获得的定速信号频谱高度接近，其中15.0 Hz拼接信号与定速信号1
x 、3x 值（1x 和3x 表示转速的1倍频和3倍频）的相对误差仅为0.9%、1.0%，将待拼接信号加入噪声且缩短到1.5个周期后，拼接相位误差不超过10°.Abstract:The characteristic value of train wheelsets is closely related to the speed, and the quantitative analysis of wheelset faults requires signals with a certain length collected at a certain speed. However, such a signal is difficult to be obtained by the system working in the variable speed condition. Therefore, a signal reconstruction method that did not require any velocimeters was proposed to realize the above quantitative analysis. This method used short signal segments to splice the constant speed signals under the acceleration and deceleration conditions. Firstly, a short-time Fourier transform (STFT) peak search method was adopted to obtain the speed curve and extract multiple signal segments passing through a specified speed. Secondly, the signal segments were converted into an angular domain signal, and the phase difference between signals was determined by cross-power spectra density (CPSD). Then, according to the phase difference and the length of the front signal, the splicing position of signals was obtained, and interpolation and fusion techniques were used to ensure the continuity of spliced signals. Finally, the spliced angular domain signal was resampled into the time domain signal. A rotor test bench with a similar wheelset structure has verified that during acceleration and deceleration of a cracked shaft, the frequency spectrums of the spliced signals of each speed obtained by this method are highly close to the frequency spectrums of the constant speed signals obtained by the experiment. The relative errors of the 1
x and 3x values between the spliced signal of 15.0 Hz and the constant speed signal are only 0.9% and 1.0%, respectively. After adding noise to the signals to be spliced and shortening them to 1.5 cycles, the splicing phase error does not exceed 10°. -
光伏（photovoltaic，PV）阵列因建筑物、树木、云层等遮挡而处于局部阴影条件（partially shaded conditions，PSC），产生热斑效应[1]. 为避免热斑效应的产生，光伏组件两端通常并联旁路二极管，这将导致局部阴影条件下光伏阵列的功率-电压特性曲线呈现多峰特性. 扰动观察法、电导增量法等传统最大功率点跟踪（maximum power point tracking，MPPT）算法[2-3] 容易陷入局部最大功率点（local maximum power point，LMPP），造成能量损失，不适用于局部阴影条件. 为此，改进的MPPT技术被陆续提出，并促进了光伏发电技术的快速发展[4-17].
针对局部阴影条件下的MPPT可以分为硬件方法与软件方法两类. 硬件方法通过改变光伏发电系统的结构以减少局部阴影导致的能量损失. 文献[6-7]在光伏阵列与变换器之间引入可控的开关矩阵，实时改变阵列中光伏组件的组合方式以适应阴影条件；文献[8]通过增加直流变换器使光伏组件独立运行，且均工作在MPPT状态. 尽管硬件方法可有效解决传统MPPT算法在局部阴影条件下的误跟踪问题，但也增加了电路结构的复杂度和系统成本. 软件方法，又称全局最大功率点跟踪（global maximum power point tracking，GMPPT）算法，不需要额外增加硬件电路，即可识别多峰曲线的全局最大功率点（global maximum power point, GMPP） ，相较于硬件方法展现出明显的成本优势. GMPPT算法主要分为智能算法、快速功率线算法、基于传统搜索算法的改进型GMPPT算法等. 智能算法，如粒子群算法和模糊逻辑控制[9-10]，能够精确地从多个极值中找到最大值，实现优化目标，但算法较为复杂. 快速功率线算法则以Direct算法[11]和Fibonacci算法[12]较为常见，通过利用光伏阵列输出曲线的特征缩小搜索范围，快速定位GMPP，然而，若参数初始值设置不当，可能导致算法收敛到局部功率点. 基于传统搜索算法的改进型GMPPT算法原理简单，且易于实现. 文献[13]在已知光伏组件开路电压的情况下，控制算法扫描特定的电压点附近，有效缩短了扫描区间，但算法可靠性低；文献[14]分析光伏阵列中分段处的短路电流与峰值点电流的近似比例关系，提出基于光伏阵列电流特性的GMPPT算法，但不适用于曲线峰值点从左向右依次升高的情况；最大功率梯形算法[15] （maximum power trapezium，MPT）通过限制扫描电压的上下限，减少搜索范围，提高跟踪速度，但其扫描范围仍然偏大.
尽管改进型GMPPT算法在性能和成本上取得了较好的平衡，但其跟踪速度受限于扰动步长和扰动时间. 扰动时间一定时，扰动步长越小，算法的跟踪精度越高，但在扫描区间内的扰动次数增加，跟踪时间越长，跟踪速度越慢. 扰动步长一定时，扰动时间越小，跟踪时间越短，跟踪速度越快. 在电压闭环控制中，对于相同扰动步长，参考电压在电流-电压特性曲线恒流区所需的调整时间比恒压区要长[16-17]. 因此，现有算法多以恒流区为基准设计扰动时间.
为进一步提高局部阴影条件下光伏发电系统的跟踪速度，本文提出一种改进型快速GMPPT算法. 该算法通过在跟踪过程中跳过调整时间较长的恒流区，提高系统的跟踪速度. 本文通过仿真和实验验证所提算法的有效性，并将其与现有的MPT算法和全局扫描算法的跟踪效果进行对比.
1. 局部阴影条件下光伏组串的输出特性
光伏阵列由多个光伏组件组合而成，分为并联型光伏阵列、串联型光伏阵列与串并联型光伏阵列. 其中，并联型光伏阵列由于输出电压较低，不适用于光伏发电系统. 相比之下，串并联型光伏阵列可以实现较大的输出电流和较高的输出电压，但由于电压和电流之间相互影响，在局部阴影条件下其输出功率会显著降低. 而光伏组串作为串联型光伏阵列，输出电压可根据需求进行设置，在建筑集成光伏系统中应用广泛[18]. 图1为光伏组串的电路结构，图中，PV1、PV2和PVn为光伏组件，Ipv、Vpv分别为组串的电流和电压.
图2为光伏组件的输出特性. Ipv-Vpv 曲线从膝点（knee point，KP）处被划分为恒流区和恒压区. Ppv （组串功率）-Vpv 曲线表现出单峰特性，最大功率点（maximum power point，MPP）与KP相对应. MPP对应的电压VMPP和电流IMPP近似为[19]
{VMPP=0.76Voc,IMPP=0.9Isc, (1) 式中：Voc和Isc分别为同一条件下光伏组件的开路电压和短路电流.
光伏组件的短路电流近似与光照强度成正比，开路电压近似与光照强度的自然对数成正比，即光照强度改变，短路电流随之改变，而开路电压近似不变[20]. 因此，在任意光照条件下，VMPP近似为标准测试条件（光照强度S =
1000 W/m2，温度25 ℃）下组件开路电压Voc,STC,module的0.76倍，即恒流区的长度为0.76Voc,STC,module.图3为局部阴影条件下光伏组串的输出特性. 在Ipv-Vpv 曲线中，随着KP个数的增加，恒流区和恒压区也相应增加. Ppv-Vpv 曲线表现出多峰特性，峰值点中的最大值为GMPP，其他峰值点为LMPP，并与KP相对应. 在局部阴影条件下，第i个峰值点的电压VMPPi和电流IMPPi分别近似为[19]
{VMPPi=i−0.24nVoc,array,IMPPi=0.9Isci, (2) 式中：Voc,array为光伏阵列的开路电压，Isci为第i个组件的短路电流，i = 1, 2, …, n.
由于峰值点与膝点相对应，则第i个膝点电压满足式（2）. 在光伏组串中，每个组件对应的KP电压不变，恒流区长度近似不变.
2. 全局最大功率点跟踪
2.1 MPT算法
为缩短搜索范围，MPT算法根据GMPP的分布特点定义扫描电压的上限Vrange,max和下限Vrange,min分别为
{Vrange,max=0.9Voc,STC,array,Vrange,min=PGMPPIGMPP,STC,aray, (3) 式中：Voc,STC,array和IGMPP,STC,array分别为标准测试条件下光伏阵列的开路电压和GMPP处对应的输出电流，PGMPP为GMPP处的功率，即最大输出功率.
式（3）中，Voc,STC,array与IGMPP,STC,array均为常数. 因此，在搜索过程中，MPT算法的电压上限Vrange,max固定，而电压下限Vrange,min随着最大输出功率PGMPP的更新而增大，扫描区间相应减小，从而缩短跟踪时间.
图4为MPT算法的跟踪示例，其光伏组串由3个受光照强度不同（条件1～3）的组件串联构成. 图中，绿线为标准条件下MPT算法的功率边界，红线为扫描路径，阴影区域为恒流区，余图同；横坐标上变量为对应点的电压，点e对应的电压Ve = 0.9Voc,STC,array. 光照强度改变时，光伏组串的工作点由点b跳变为点c. MPT算法启动搜索过程，初始化点c为GMPP，且根据式（3）更新Vrange,min为点k对应的电压Vk；然后，MPT算法控制组串运行至Vrange,max工作在点e；再调节系统向左扫描至Vrange,min. 随着扫描过程中GMPP的更新，Vrange,min不断增大，扫描范围相应缩小，最终Vrange,min更新为点f对应的电压Vf. MPT算法的扫描路径为：c→d→e→f.
MPT算法通过限制搜索电压的动态上、下限，减少搜索区间的范围，有效提高跟踪速度. 但MPT算法仅是在开路电压范围内缩短了搜索区间，未在搜索区间内进一步减少搜索过程，搜索区间仍能进一步改善. 同时，光伏组串的GMPP所对应的输出电压较低或光照强度低导致其全局最大输出功率PGMPP较小时，MPT算法的电压下限Vrange,min小，搜索区间仍较大，跟踪时间长.
2.2 改进型快速GMPPT算法
基于传统搜索算法的改进型GMPPT算法通过缩短扰动时间和搜索范围来减少跟踪时间，提高能量的利用率. MPT算法正是通过限定扫描电压的上下限动态地减少搜索区间，缩短跟踪时间. 为避免误扰动，GMPPT算法扰动时间应大于电压扰动后的调整时间，以保证新一轮扰动在上一轮扰动稳定后进行. 但调整时间受光伏阵列的工作区域影响. 当电压扰动工作在恒流区时，其调整时间比电压扰动在恒压区时的调整时间长. 调整时间越长，扰动时间越长，跟踪时间相应增加，能量损失更严重. 本文提出基于MPT的改进型快速GMPPT算法，在MPT算法的动态搜索区间内进一步跳过调整时间较长的恒流区，缩短扫描区间.
图5为改进型快速GMPPT算法流程，主程序包含阴影检测和计数器溢出检测2个条件. 图中，Vold、Iold、Pold分别为初始化电压、电流、功率，V、I、P分别为当前周期检测电压、电流、功率，ΔV为电压步长，ΔP为当前周期与上一个周期的功率差，ILMPP为光伏阵列在峰值点的输出电流. 阴影检测利用功率差∆PGMPP与功率阈值Pthreshold的大小判断光照条件是否发生改变. 计数器溢出检测利用固定时间计数器定期执行GMPPT子程序，避免算法因未检测到光照变化而长时间运行在GMPP外，造成能量损失.
改进型快速GMPPT算法在MPT的电压上下限内扫描，在扫描过程中定位到峰值点时，跨越当前组件相对应的恒流区，其参考电压Vref为
Vref=VLMPP−VCCR, (4) 式中：VLMPP为光伏阵列在峰值点的输出电压；VCCR为恒流区的长度，近似为0.76Voc,STC,module.
受环境因素的影响，恒流区的范围有所波动. 为避免算法在跨越恒流区过程中错过GMPP，本文所取恒流区的长度为0.7Voc,STC,module. 另外，由式（1）和式（2）可知，峰值点电流近似为0.9倍的短路电流，且峰值点的左侧范围电流近似不变，视为恒流区. 因此，算法利用跨越前后的电流大小判断其是否可能错过GMPP. 若跨越恒流区后的当前电流I满足
I<ILMPP0.9, (5) 则算法仍处于恒流区；反之，算法可能错过峰值点，则在当前电压的基础上叠加VCCR/2，缩短跨越区间，并利用式（5）重新判断，以避免错过GMPP.
图6为改进型快速GMPPT算法的跟踪示例. 初始时，光伏阵列稳定工作于点b，光照强度突然改变，工作点由点b跳变为点c. 算法检测到光照条件变化，启动搜索过程. 其中，蓝色区间[0，Vf]、[Vj，Vh]和[Vg，Vd]为光照强度改变后光伏阵列输出特性曲线的恒流区.
图 6 改进型快速GMPPT算法的跟踪示例Figure 6. Tracking example of the improved and fast GMPPT algorithm改进型快速GMPPT算法的搜索过程分为以下3个阶段.
1） 初始化：初始化GMPP为点c，并更新电压下限Vrange,min为Vk；设置初始参考电压Vref为Vrange,max，调节光伏组串工作在点e，并根据点c、e的功率大小Pc、Pe，判断是否更新GMPP与Vrange,min.
2） 扫描与判断：减小参考电压Vref，调节光伏组串向左扫描至LMPP （点d）；比较点d与当前GMPP的功率大小，更新GMPP为点d，且电压下限Vrange,min更新为Vf.
3） 跨越：在扫描到LMPP后，跳过该组件的恒流区；即在Vd的基础上减去恒流区的电压范围，调节系统工作在点g.
在此基础上，不断重复上述过程，直到光伏阵列的输出电压小于最终的电压下限Vrange,min. 最后，设置Vref为最终的GMPP所对应电压，调节系统稳定运行于点d.
综上所述，改进型快速GMPPT算法的扫描路径为：e→d，g→h，j→f.
3. 仿真与实验
3.1 仿真分析
为验证算法的有效性，在MATLAB/Simulink中搭建了仿真模型. 光伏MPPT系统的主电路由光伏组串、变换器、负载电阻组成，如图7所示. 图中：D、D1~D3为二极管，Ci为输入电容，Co为输出电容，L为电感，S为开关管，R为电阻.
为与传统MPT算法[15]进行对比，本文选用了文献[15]中型号为Kyocera KC200GT的3个光伏组件进行串联，构成光伏组串，光照条件如表1所示. 组件参数为：最大功率点电压Vm=26.30 V，最大功率点电流Im=7.61 A，最大输出功率Pm=200.14 W，开路电压Voc=32.90 V，短路电流Isc=8.21 A. 变换器的参数为：Ci = 330 μF，L = 220 μH，Co = 330 μF，开关频率fs = 50 kHz，R = 200 Ω. 表1中列出的不同局部阴影条件下的光伏阵列输出特性如图8所示.
表 1 光伏阵列的输出参数Table 1. Output parameters of the PV array条件 光照强度/（W·m−2） 全局最大功率点 PV1 PV2 PV3 功率/W 电压/V 电流/A PSC1 120 210 400 90.13 54.60 1.65 PSC2 200 300 560 134.60 84.80 1.59 PSC3 150 270 750 143.60 25.20 5.70 
图 8 不同局部阴影条件下光伏阵列的输出特性Figure 8. Output characteristics of PV array under different PSCs图9为改进型快速GMPPT算法（算法1）、全局扫描算法（算法2）和MPT算法（算法3）的仿真波形. 图中，t为时间. 为对比算法的跟踪效果，3种算法的电压步长均为0.2 V，扰动时间为0.8 ms. 仿真跟踪性能对比结果如表2所示.
图 9 阴影改变时采用不同算法的光伏阵列仿真波形Figure 9. Simulation waveforms of the PV array with various algorithms when the shadow changes表 2 阴影条件变化下3种算法的仿真跟踪性能比较Table 2. Simulation tracking performance comparison of the three algorithms under shading variation光照条件 扫描时间/s 总路径的扫描电压/V 能量损失/J 算法 1 算法 2 算法 3 算法 1 算法 2 算法 3 算法 1 算法 2 算法 3 PSC1→PSC2 0.110 0.330 0.340 17.34 69.09 71.14 2.94 7.81 8.25 PSC2→PSC3 0.095 0.295 0.300 17.57 69.09 69.96 4.76 13.66 13.69 PSC3→PSC1 0.125 0.320 0.355 17.34 69.09 76.99 2.63 6.13 7.41 扫描时间为光照条件未突变前的稳定状态到突变后的稳定状态的跟踪时间. 光照条件在0.500 s时由PSC1变化为PSC2，改进型快速GMPPT算法在0.500 s时检测到光照变化，启动搜索过程，约在0.660 s时稳定，跟踪至突变后的GMPP，扫描时间为0.110 s；全局扫描算法约在0.830 s稳定，扫描时间为0.330 s； MPT算法则约在0.840 s稳定，扫描时间为0.340 s. 总路径的扫描电压是各算法通过电压步长进行扰动的电压区间总和. 其中，改进型快速GMPPT算法包含3个扫描区间，分别为从0.9Voc,STC,array （88.83 V）到最右侧峰值点（84.80 V）、从第一次跨越恒流区后的电压（61.77 V）到中间的峰值点（55.84 V）、从第二次跨越恒流区后的电压（32.81 V）到最左侧峰值点（25.43 V），总路径的扫描电压约为17.34 V. 全局扫描算法的扫描区间为[0.6Voc,STC,module, 0.9Voc,STC,array]，总路径的扫描电压为69.09 V. MPT算法的扫描区间为[PGMPP/IGMPP,STC,array, 0.9Voc,STC,array]，总路径的扫描电压为71.14 V. 综上，与全局扫描算法相比，所提算法在扫描时间、总路径的扫描电压、能量损失方面分别减少66.67%、74.86%和58.19%；与MPT算法相比，这些指标则分别减少67.65%、75.63%和62.31%.
当光照条件由PSC2改变为PSC3时，与全局扫描算法相比，所提算法在扫描时间、总路径的扫描电压、能量损失方面分别减少67.80%、74.57%和66.13%；与MPT算法相比，这些指标则分别减少68.33%、74.89%和66.14%.
当光照条件由PSC3突变为PSC1时，所提算法与全局扫描算法相比，扫描时间、总路径扫描电压、能量损失分别减少60.94%、74.57%和72.96%；与MPT算法相比，这些指标则分别减少64.79%、77.48%和76.91%.
3.2 实验结果
为验证改进型快速GMPPT算法的理论分析和仿真结果，本文搭建了由光伏模拟器、Boost变换器、电子负载、上位机、GMPPT数字控制器和示波器组成的实验平台，如图10所示. 其中，上位机控制光伏模拟器Chroma 63206A-600-420模拟表1的局部阴影条件. 图11为3种算法的实验波形，实验中各项参数保持一致，电压步长为1 V，扰动时间为0.4 s，其余硬件参数与仿真设置相同.
图 11 阴影改变时采用不同算法的光伏阵列实验波形Figure 11. Experiment waveforms of the PV array with various algorithms when the shadow changes由图11可知：当光照条件由PSC1改变为PSC2时，相较于全局扫描算法，所提算法的扫描时间、总路径扫描电压、能量损失分别减少68.25%、74.86%和58.19%；与MPT算法相比，分别减少68.00%、75.63%和62.31%. 当光照条件由PSC2改变为PSC3时，所提算法相比全局扫描算法的上述3项指标分别减少65.85%、74.57%和66.13%；与MPT算法相比，分别减少66.13%、74.89%和66.14%. 当光照条件由PSC3改变为PSC1时，所提算法与全局扫描算法相比，3项指标分别减少64.29%、74.57%和72.96%；与MPT算法相比，分别减少67.39%、77.48%和76.91%.
表3为3种算法的实验跟踪性能对比. 可以看出，这3种算法均能准确实现GMPPT；实验结果与仿真结果一致，进一步验证改进型快速GMPPT算法的有效性.
表 3 阴影变化下3种算法的实验跟踪性能比较Table 3. Experiment tracking performance comparison of the three algorithms under shading variation光照条件 扫描时间/s 总路径的扫描电压/V 能量损失/J 算法 1 算法 2 算法 3 算法 1 算法 2 算法 3 算法 1 算法 2 算法 3 PSC1→PSC2 4.0 12.6 12.5 17.34 69.09 71.14 98.19 234.86 260.49 PSC2→PSC3 4.2 12.3 12.4 17.57 69.09 69.96 158.23 467.10 467.35 PSC3→PSC1 4.5 12.6 13.8 17.34 69.09 76.99 72.00 266.25 311.85 4. 结 论
本文提出了一种适用于局部阴影条件下的改进型快速GMPPT算法，分析局部阴影条件下光伏阵列的输出特性，讨论了膝点与开路电压的关系；详细阐述了现有MPT算法与改进型快速GMPPT算法的工作原理，对比全局扫描算法、MPT算法以及本文算法在扫描时间、电压扫描路径与能量损失方面的表现. 通过理论分析、仿真与实验的验证，可得以下结论：
1） 改进型快速GMPPT算法无须增加额外硬件电路，节省了成本.
2） 与软件方法中的智能算法相比，本文算法更为简单，实现方便.
3） 相比于现有MPT算法和全局扫描算法，本文算法能够更快、更准确地跟踪到GMPP，缩短电压扫描路径，减少扫描时间，有效提高跟踪速度，降低能量损失，同时不增加算法复杂度，保持了算法的精确度和稳定性.
-
图 4 信号不同拼接误差的连接情况和DSSIM值
Figure 4. Signal connection and DSSIM value of different splicing errors
图 7 升降速信号和15 Hz定速信号的对比
Figure 7. Comparison of acceleration and deceleration signal and constant speed signal of 15 Hz
图 10 直接拼接和本文方法拼接结果对比
Figure 10. Comparison between direct splicing and the proposed method
图 11 加噪声后直接拼接和本文方法拼接的对比
Figure 11. Comparison of direct splicing and the proposed method after adding noise
图 12 缩短信号后本方法拼接的结果
Figure 12. Splicing results of the proposed method after shortening the signal
-
[1] 杨云帆,周青,巩磊,等. 轮对柔性对直线电机车辆动态响应的影响分析[J]. 西南交通大学学报,2020,55(6): 1313-1319.YANG Yunfan, ZHOU Qing, GONG Lei, et al. Influence of wheelset flexibility on dynamic response of linear induction motor vehicles[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1313-1319. [2] 宋志坤,岳仁法,胡晓依,等. 车轮多边形对车辆振动及轮轨力的影响[J]. 北京交通大学学报,2017,41(6): 88-93.SONG Zhikun, YUE Renfa, HU Xiaoyi, et al. Influence of wheel polygon on vehicle vibration and wheel/rail force[J]. Journal of Beijing Jiaotong University, 2017, 41(6): 88-93. [3] HASSAN M, BRUNI S. Experimental and numerical investigation of the possibilities for the structural health monitoring of railway axles based on acceleration measurements[J]. Structural Health Monitoring, 2019, 18(3): 902-919. doi: 10.1177/1475921718786427 [4] 黄采伦,陈春阳,樊晓平,等. 列车车轴裂纹的振动特性分析及在线监测方法[J]. 中国铁道科学,2007,28(5): 83-88.HUANG Cailun, CHEN Chunyang, FAN Xiaoping, et al. Vibration characteristic analysis of train axle crack and its on-line monitoring method[J]. China Railway Science, 2007, 28(5): 83-88. [5] 黄采伦,樊晓平,张剑,等. 机车走行部故障在线诊断的特征分析方法研究[J]. 仪器仪表学报,2007,28(6): 1007-1011.HUANG Cailun, FAN Xiaoping, ZHANG Jian, et al. Online fault diagnosis method for train running gear based on characteristic analysis[J]. Chinese Journal of Scientific Instrument, 2007, 28(6): 1007-1011. [6] WANG D Y, HUA C R, DONG D W, et al. Crack parameters identification based on a kriging surrogate model for operating rotors[J]. Shock and Vibration, 2018, 2018: 1-12. [7] 梅检民,肖云魁,贾继德,等. 基于改进阶比的变速器微弱故障特征提取[J]. 振动工程学报,2012,25(3): 317-322.MEI Jianmin, XIAO Yunkui, JIA Jide, et al. Weak fault characteristics extraction for automobile transmission based on improved order analysis[J]. Journal of Vibration Engineering, 2012, 25(3): 317-322. [8] 杨炯明,秦树人,季忠. 旋转机械阶比分析技术中阶比采样实现方式的研究[J]. 中国机械工程,2005,16(3): 249-253.YANG Jiongming, QIN Shuren, JI Zhong. Research on the methods to implement order sampling in rotating machinery order analysis technique[J]. China Mechanical Engineering, 2005, 16(3): 249-253. [9] 邓蕾,傅炜娜,董绍江,等. 无转速计的旋转机械Vold-Kalman阶比跟踪研究[J]. 振动与冲击,2011,30(3): 5-9.DENG Lei, FU Weina, DONG Shaojiang, et al. Tacholess Vold-Kalman order tracking of rotating machinery[J]. Journal of Vibration and Shock, 2011, 30(3): 5-9. [10] 陈向民,于德介,任凌志,等. 基于线调频小波路径追踪阶比能量解调的齿轮轮齿裂纹故障诊断[J]. 中国机械工程,2011,22(21): 2598-2603.CHEN Xiangmin, YU Dejie, REN Lingzhi, et al. Order energy demodulating approach based on chirplet path pursuit and its application to gear tooth crack fault diagnosis[J]. China Mechanical Engineering, 2011, 22(21): 2598-2603. [11] ZHAO M, LIN J, WANG X F, et al. A tacho-less order tracking technique for large speed variations[J]. Mechanical Systems and Signal Processing, 2013, 40(1): 76-90. doi: 10.1016/j.ymssp.2013.03.024 [12] 曲兴华,职广涛,张福民,等. 利用信号拼接提高调频连续波激光测距系统的分辨力[J]. 光学 精密工程,2015,23(1): 40-47. doi: 10.3788/OPE.20152301.0040QU Xinghua, ZHI Guangtao, ZHANG Fumin, et al. Improvement of resolution of frequency modulated continuous wave laser ranging system by signal splicing[J]. Optics and Precision Engineering, 2015, 23(1): 40-47. doi: 10.3788/OPE.20152301.0040 [13] 黄洋. 全景图像拼接算法研究[D]. 西安: 西安电子科技大学, 2013. [14] SZELISKI R. Video mosaics for virtual environments[J]. IEEE Computer Graphics and Applications, 1996, 16(2): 22-30. doi: 10.1109/38.486677 [15] SHUM H Y, SZELISKI R. Panoramic image mosaics[J]. Microsoft Research, 1997, 36(2): 101-130. [16] WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2004, 13(4): 600-612. doi: 10.1109/TIP.2003.819861 [17] PENNACCHI P, BACHSCHMID N, VANIA A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines[J]. Mechanical Systems and Signal Processing, 2006, 20(8): 2112-2147. doi: 10.1016/j.ymssp.2005.04.005 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 208
- HTML全文浏览量: 111
- PDF下载量: 56
- 被引次数: 0