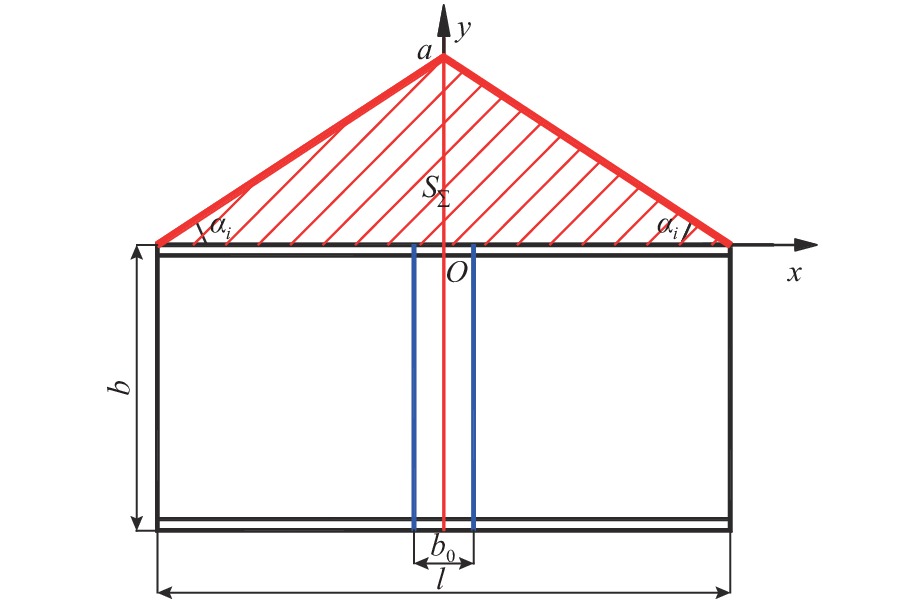
Dynamic Coordination Coefficient Method for Critical Buckling Load of Stiffened U-Shaped Steel Sheet Pile
-
摘要:
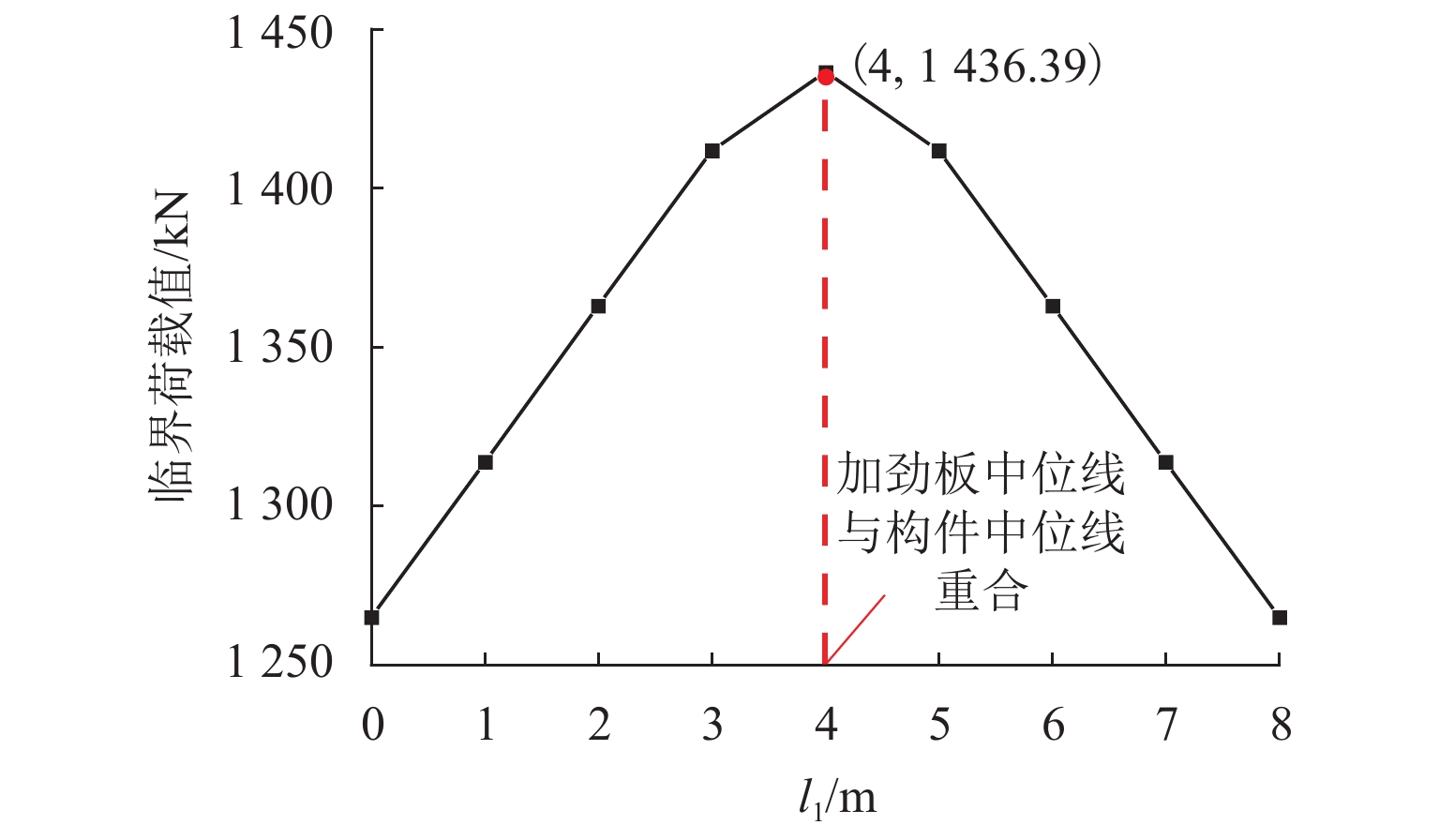
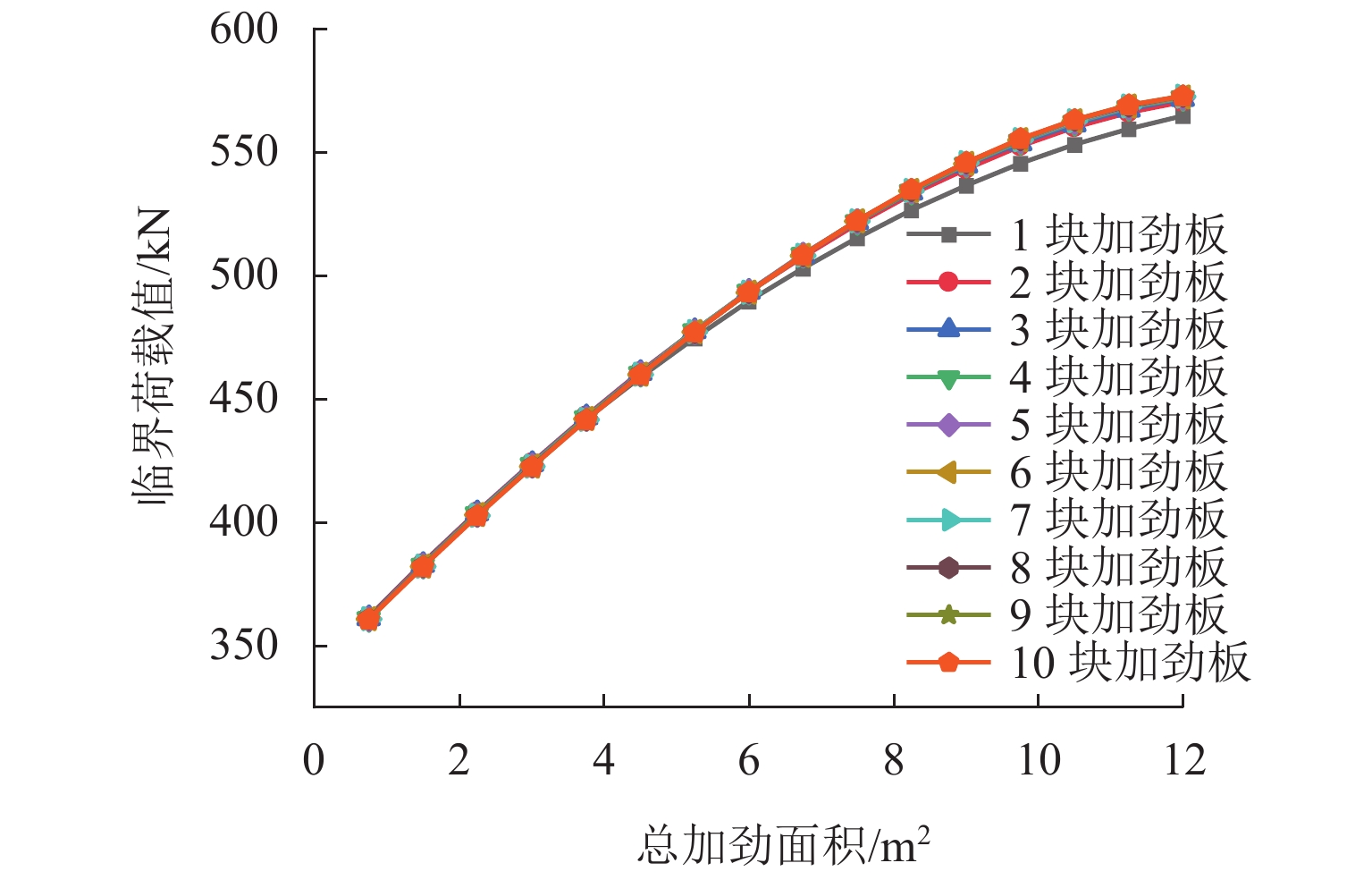
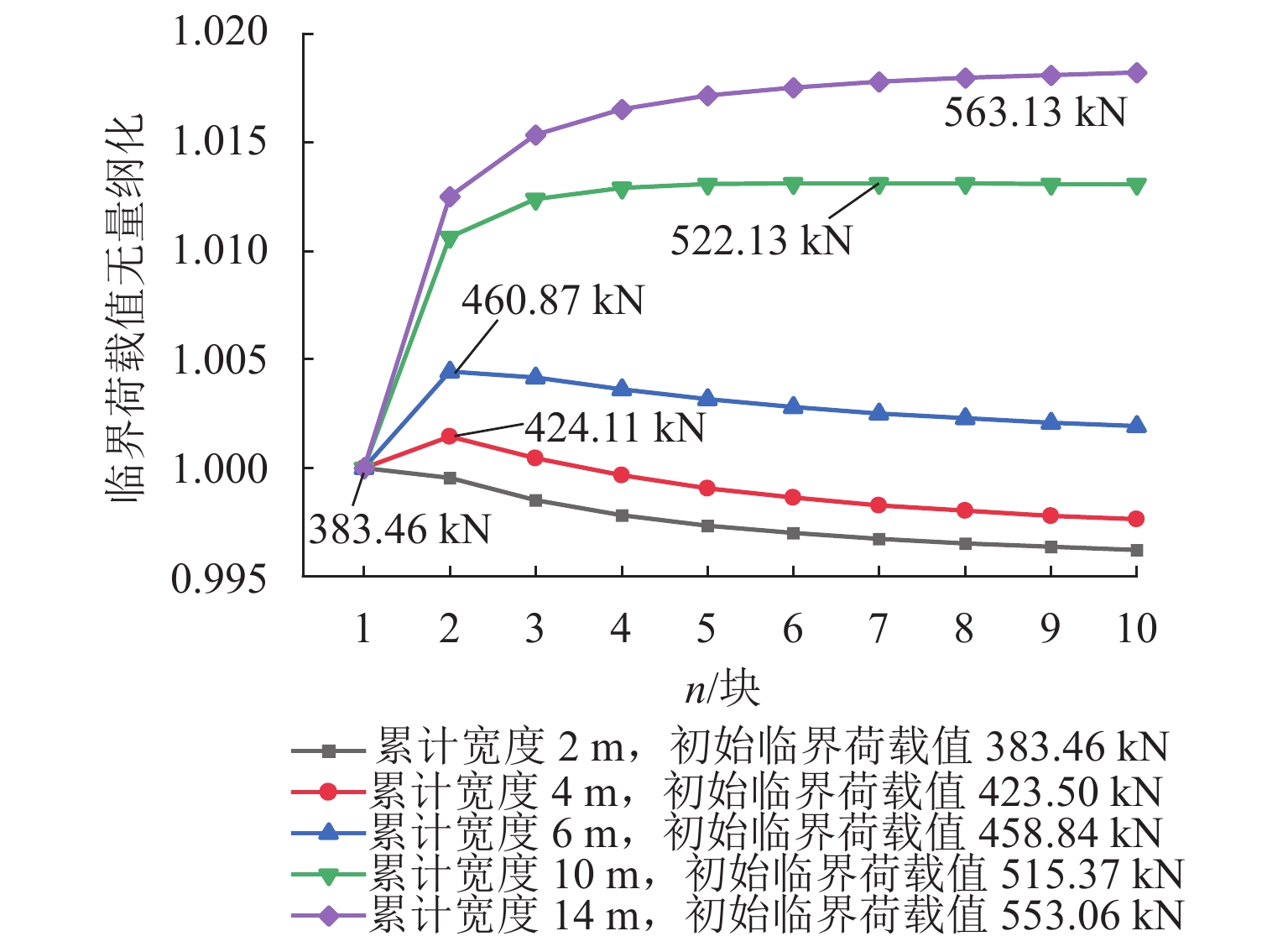
针对U型钢板桩插打容易发生屈曲的问题，提出 U型钢板桩局部加劲效应理论计算的“动态配位系数法”，建立了局部加劲U型钢板桩失稳临界荷载计算式，并分析了加劲面积、加劲位置、加劲板数量对加劲效应（即失稳临界荷载）的影响规律. 研究结果表明：加劲总面积（即加劲板累计宽度）一定时，对于长度确定的U型钢板桩，存在使构件临界荷载值最大化的加劲板布置方案，并揭示了块数太多时由于单块加劲板宽度太小而引起的局部失稳规律；以10 m长U型钢板桩为例，构件临界荷载值随单块加劲板布置位置的变化可提高13.55%，并求得20 m长的U型钢板桩不同加劲总面积对应的加劲板布置优化理论方案，为实际工程中U型板桩局部加劲方案设计提供了理论依据和参考.
Abstract:Since U-shaped steel sheet piles (USSSPs) are prone to buckle, a dynamic coordination coefficient method for theoretically calculating the local stiffening effect of USSSPs is proposed, and a formula for calculating the critical buckling load of locally stiffened USSSPs is established. The influence of different stiffening areas, stiffening positions, and number of stiffened plates on the stiffening effect (i.e., critical buckling load) is analyzed. The study shows that when the total stiffening area (i.e., cumulative width of stiffened plates) is constant, for the USSSP with determined length, there is a stiffened plate arrangement scheme to maximize the critical load value of the component, and the local buckling law caused by too small width of a single stiffened plate when the number of plates is too large is revealed. As an example, the critical load value of the component of the USSSP with a length of 10 m can be increased by 13.55% with the change of the position of the single stiffened plate, and the optimal theoretical scheme of stiffened plate arrangement corresponding to different total stiffening areas of the USSSP with a length of 20 m is obtained. This paper provides a theoretical basis and reference for the design of the local stiffening scheme of USSSPs in practical engineering.
-
图 8 第i块加劲板动态配位系数示意
Figure 8. Illustration of dynamic coordination coefficient of i-th stiffened plate
图 12 加劲面积与临界荷载值的关系
Figure 12. Relationship between stiffening area and critical load value
图 13 加劲板数量与临界荷载的无量纲化关系
Figure 13. Dimensionless relationship between number of stiffened plates and critical load
表 1 标准U型钢板桩及全长加劲下临界荷载
Table 1. Critical load of standard U-shaped steel sheet pile and U-shaped steel sheet pile under full-length stiffening
名称 l/m $\varphi $ Nmax/kN U 型钢板桩 10 0.502 1216.00 20 0.160 388.70 30 0.075 181.62 全长加劲 U 型钢板桩 10 0.480 1828.16 20 0.151 574.26 30 0.070 267.68 
下载: 导出CSV
表 2 20 m级构件临界荷载值最大化的加劲板布置优化方案
Table 2. Optimal arrangement of the number of stiffeners under different total stiffening areas for 20 m long members
加劲总面积/m2 单根加劲板宽度/m 最优加劲方案 构件临界荷载值/kN [0,2.03）∪[14.18,15.00] [0,2.7）∪[18.9,20.00] 纵向对称轴处布置 1 根加劲板 [388.70,435.42）∪[573.70,574.26] [2.03,5.03）∪[13.35,14.18） [2.7,6.7）∪[17.8,18.9） 等间距布置 2 根加劲板 [435.42,494.29）∪[574.22,574.26] [5.03,6.15）∪[13.13,13.35） [6.7,8.2）∪[17.5,17.8） 等间距布置 3 根加劲板 [494.29,513.11）∪[574.25,574.26] [6.15,6.83）∪[13.05,13.13） [8.2,9.1）∪[17.4,17.5） 等间距布置 4 根加劲板 [513.11,523.51）∪574.26 [6.83,7.28）∪[12.90,13.05） [9.1,9.7）∪[17.2,17.4） 等间距布置 5 根加劲板 [523.51,530.05）∪574.26 [7.28,7.43） [9.7,9.9） 等间距布置 6 根加劲板 [530.05,532.15） [7.43,7.58） [9.9,10.1） 等间距布置 7 根加劲板 [532.15,534.23） [7.58,7.88） [10.1,10.5） 等间距布置 8 根加劲板 [534.23,538.26） [7.88,12.90） [10.5,17.2） 等间距布置 10 根加劲板 [538.26,574.26]
下载: 导出CSV
-
[1] SCHAFER B W. Local, distortional, and Euler buckling of thin-walled columns[J]. Journal of Structural Engineering, 2002, 128(3): 289-299. doi: 10.1061/(ASCE)0733-9445(2002)128:3(289) [2] LAU S C W, HANCOCK G J. Distortional buckling formulas for channel columns[J]. Journal of Structural Engineering, 1987, 113(5): 1063-1078. doi: 10.1061/(ASCE)0733-9445(1987)113:5(1063) [3] CAMOTIM D, DINIS P B. Coupled instabilities with distortional buckling in cold-formed steel lipped channel columns[J]. Thin-Walled Structures, 2011, 49(5): 562-575. doi: 10.1016/j.tws.2010.09.003 [4] MUTHURAMAN M, ANURADHA R, AWOYERA P O, et al. Numerical simulation and specification provisions for buckling characteristics of a built-up steel column section subjected to axial loading[J]. Engineering Structures, 2020, 207: 110256.1-110256.8. [5] ZHANG L L, TAN K H, ZHAO O. Local stability of press-braked stainless steel angle and channel sections: testing, numerical modelling and design analysis[J]. Engineering Structures, 2020, 203: 109869.1-109869.18. [6] 吕蕴龙,郭兵. 支吊架用卷边槽钢轴压构件的稳定性研究[J]. 建筑结构,2021,51(7): 85-90. doi: 10.19701/j.jzjg.2021.07.013LÜ Yunlong, GUO Bing. Study on stability of cold-formed lipped channel steel axial compression members for supports and hangers[J]. Building Structure, 2021, 51(7): 85-90. doi: 10.19701/j.jzjg.2021.07.013 [7] 王春刚,张壮南,张耀春. 冷弯薄壁斜卷边槽钢轴压构件承载力计算的直接强度法研究[J]. 工程力学,2012,29(3): 75-82.WANG Chungang, ZHANG Zhuangnan, ZHANG Yaochun. Direct strength method study on bearing capacity calculation of channel columns with inclined simple edge stiffeners under axial compression[J]. Engineering Mechanics, 2012, 29(3): 75-82. [8] 王子龙. 腹板V形加劲的冷弯卷边槽钢轴压下局部和畸变屈曲分析[D]. 哈尔滨: 哈尔滨工业大学, 2006. [9] 姚永红. 腹板V形加劲冷弯薄壁卷边槽钢轴压柱稳定性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. [10] 胡启平,韩璐. 带缀板的开口薄壁钢构件整体稳定分析[J]. 江西建材,2015(9): 6-7. doi: 10.3969/j.issn.1006-2890.2015.09.005HU Qiping, HAN Lu. Overall stability analysis of open thin-walled steel members with battens[J]. Jiangxi Building Materials, 2015(9): 6-7. doi: 10.3969/j.issn.1006-2890.2015.09.005 [11] 王春刚,张壮南,张耀春. 中间加劲复杂卷边槽钢轴心受压构件承载力试验研究[J]. 工程力学,2013,30(1): 221-228,254. doi: 10.6052/j.issn.1000-4750.2011.05.0328WANG Chungang, ZHANG Zhuangnan, ZHANG Yaochun. Experimental investigation on channel columns with complex edge stiffeners and intermediate stiffeners under axial compression[J]. Engineering Mechanics, 2013, 30(1): 221-228,254. doi: 10.6052/j.issn.1000-4750.2011.05.0328 [12] 王春刚,张壮南,贾连光,等. 板件中间V形加劲复杂卷边槽钢轴压构件的稳定性能研究[J]. 工程力学,2012,29(增2): 113-116,121. doi: 10.6052/j.issn.1000-4750.2012.05.S022WANG Chungang, ZHANG Zhuangnan, JIA Lianguang, et al. Stability behavior research of channels with complex edge stiffeners and intermediate V type stiffeners under axial compression[J]. Engineering Mechanics, 2012, 29(S2): 113-116,121. doi: 10.6052/j.issn.1000-4750.2012.05.S022 [13] 王春刚, 徐子风, 刘泓, 等. 腹板加劲复杂卷边槽钢偏心受压构件稳定性分析[C]//第22届全国结构工程学术会议论文集第Ⅱ册. 乌鲁木齐: [出版者不详], 2013: 303-306. [14] 宋波,王连广,王春刚. 帽形加劲复杂卷边槽钢柱的稳定性能[J]. 东北大学学报(自然科学版),2018,39(1): 143-147. doi: 10.12068/j.issn.1005-3026.2018.01.029SONG Bo, WANG Lianguang, WANG Chungang. Stability behavior of channel columns with complex edge stiffeners and cap shaped stiffeners[J]. Journal of Northeastern University (Natural Science), 2018, 39(1): 143-147. doi: 10.12068/j.issn.1005-3026.2018.01.029 [15] 姜亦鑫. 支吊架用卷边槽钢压弯构件的整体稳定性计算[J]. 计算机辅助工程,2021,30(2): 50-55. doi: 10.13340/j.cae.2021.02.009JIANG Yixin. Global stability calculation on lipped channel compression flexural member for support and hanger[J]. Computer Aided Engineering, 2021, 30(2): 50-55. doi: 10.13340/j.cae.2021.02.009 [16] 陈明,周绪红,刘占科,等. 腹板加强型冷弯薄壁卷边槽钢柱受压性能试验研究[J]. 建筑结构学报,2017,38(2): 37-47. doi: 10.14006/j.jzjgxb.2017.02.005CHEN Ming, ZHOU Xuhong, LIU Zhanke, et al. Experimental investigation of web-stiffened cold-formed lipped channel columns[J]. Journal of Building Structures, 2017, 38(2): 37-47. doi: 10.14006/j.jzjgxb.2017.02.005 [17] 孙觅. 加隔板的冷弯薄壁卷边槽钢偏心受压性能试验研究与有限元分析[D]. 杭州: 浙江大学, 2008. [18] 杨文斌. 高强冷弯薄壁卷边槽钢轴心受压稳定性能研究[D]. 大连: 大连理工大学, 2020. [19] 顾建飞,姚谏,钱国桢. 冷弯薄壁槽钢柱畸变屈曲的有限元分析及一种控制措施[J]. 科技通报,2007,23(1): 111-115. doi: 10.3969/j.issn.1001-7119.2007.01.022GU Jianfei, YAO Jian, QIAN Guozhen. Finite element analysis and an effective measure to distortional buckling of cold-formed channel columns[J]. Bulletin of Science and Technology, 2007, 23(1): 111-115. doi: 10.3969/j.issn.1001-7119.2007.01.022 [20] 李元齐,刘翔,沈祖炎,等. 高强冷弯薄壁型钢卷边槽形截面轴压构件畸变屈曲控制试验研究[J]. 建筑结构学报,2010,31(11): 10-16. doi: 10.14006/j.jzjgxb.2010.11.002LI Yuanqi, LIU Xiang, SHEN Zuyan, et al. Experimental study on distortional buckling control for high-strength cold-formed thin-walled steel lipped channel columns subject to axial compression[J]. Journal of Building Structures, 2010, 31(11): 10-16. doi: 10.14006/j.jzjgxb.2010.11.002 [21] 中华人民共和国建设部. 钢结构设计规范: GB 50017—2003[S]. 北京: 中国计划出版社, 2003. [22] 欧领特. 钢板桩工程手册[M]. 北京: 人民交通出版社, 2011. -
下载:
点击查看大图
计量
- 文章访问数: 199
- HTML全文浏览量: 109
- PDF下载量: 19
- 被引次数: 0