含双向变流装置的城轨牵引供电系统协同供电潮流计算

刘炜; 曾佳欣; 马庆安; 张戬; 熊蓬; 戚贺

doi:10.3969/j.issn.0258-2724.20220494

含双向变流装置的城轨牵引供电系统协同供电潮流计算

doi: 10.3969/j.issn.0258-2724.20220494

西南交通大学电气工程学院，四川成都 610031

基金项目: 国家自然科学基金（51607148）

详细信息

作者简介:
刘炜（1982—），男，副教授，研究方向为牵引供电系统理论与仿真、杂散电流与钢轨电位和再生制动能量利用，E-mail：liuwei_8208@swjtu.cn

中图分类号: TM922.3
计量
- 文章访问数: 379
- HTML全文浏览量: 150
- PDF下载量: 48
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-13
- 修回日期: 2022-11-04
- 网络出版日期: 2023-04-21
- 刊出日期: 2022-11-11

Calculation of Collaborative Power Flow for Urban Rail Traction Power Supply System with Bidirectional Converter Device

School of Electric Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
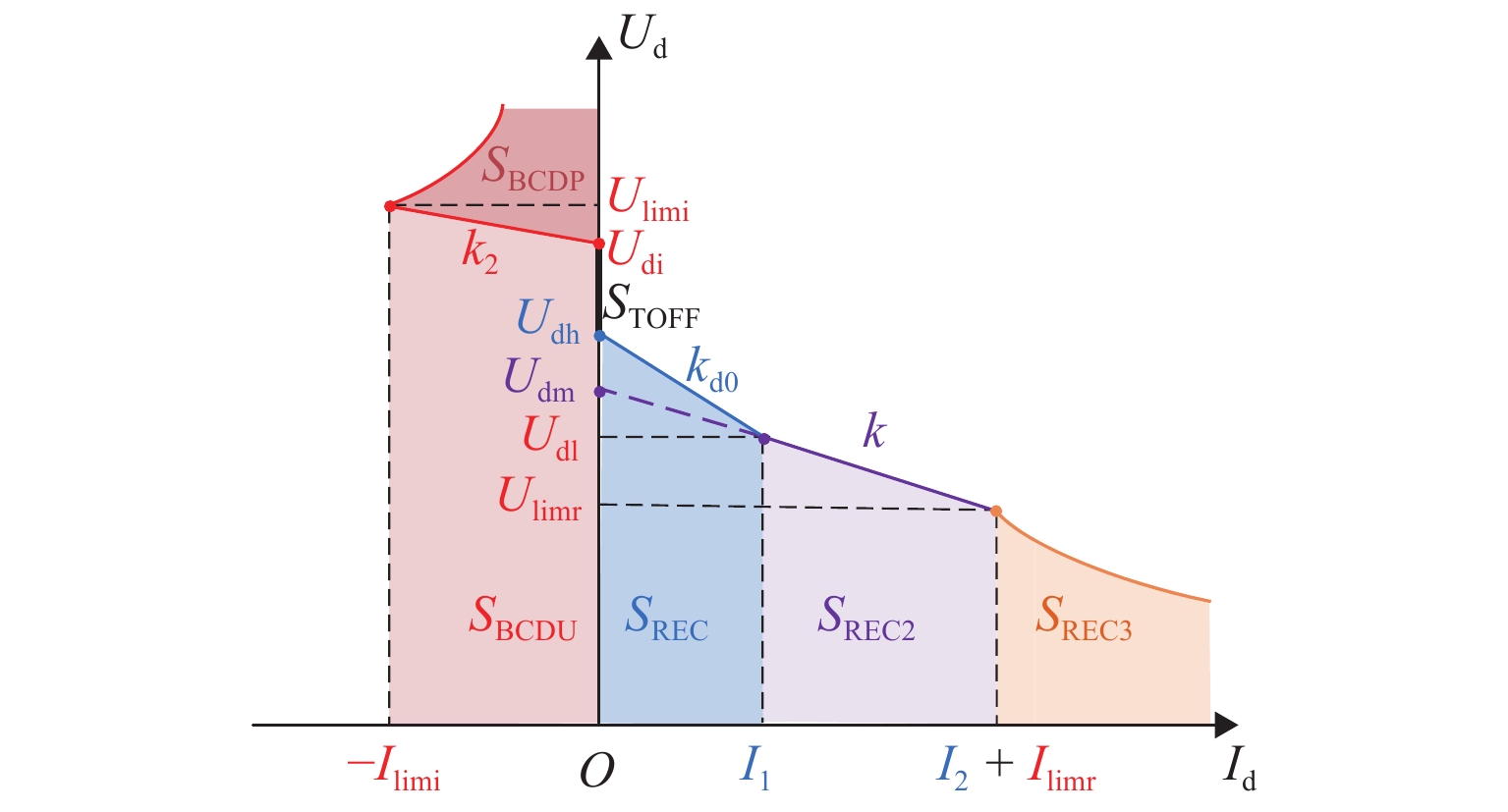
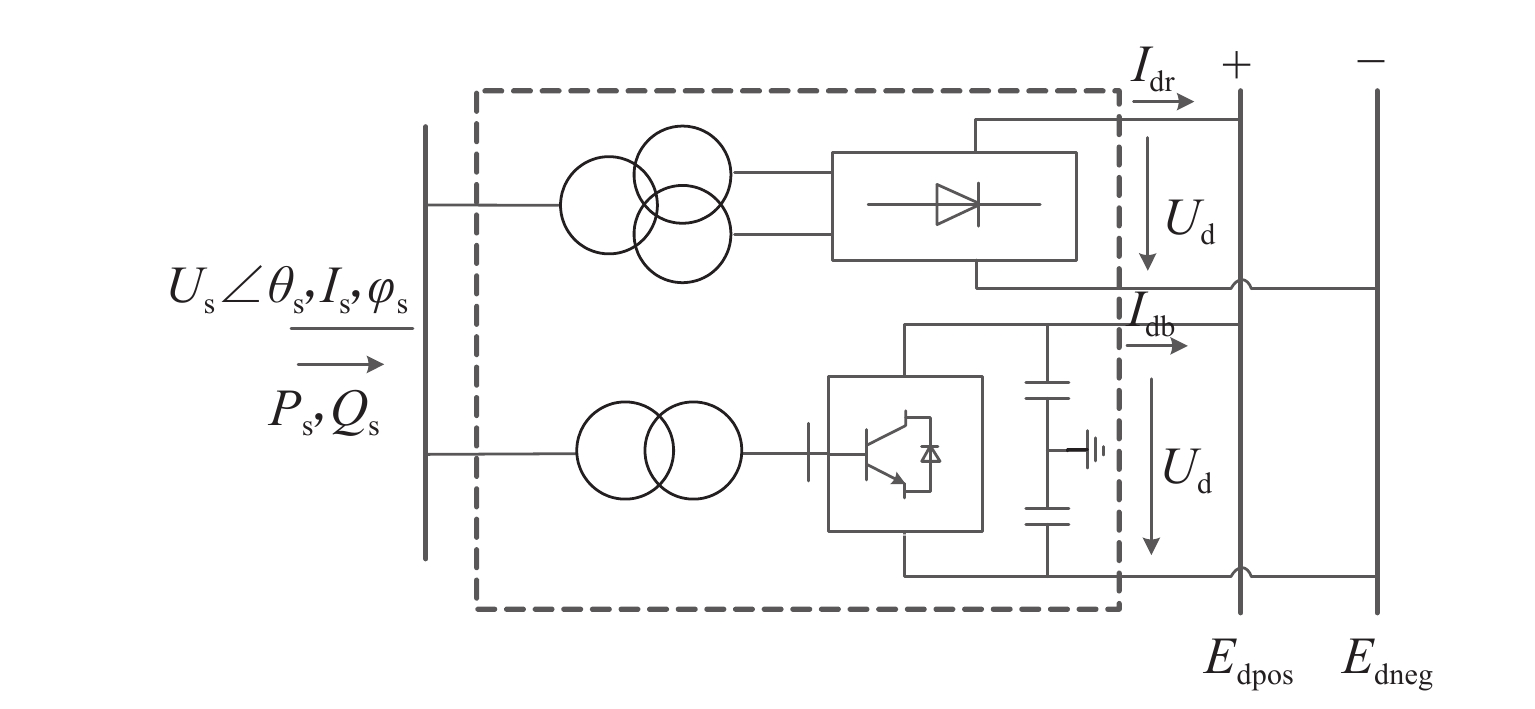
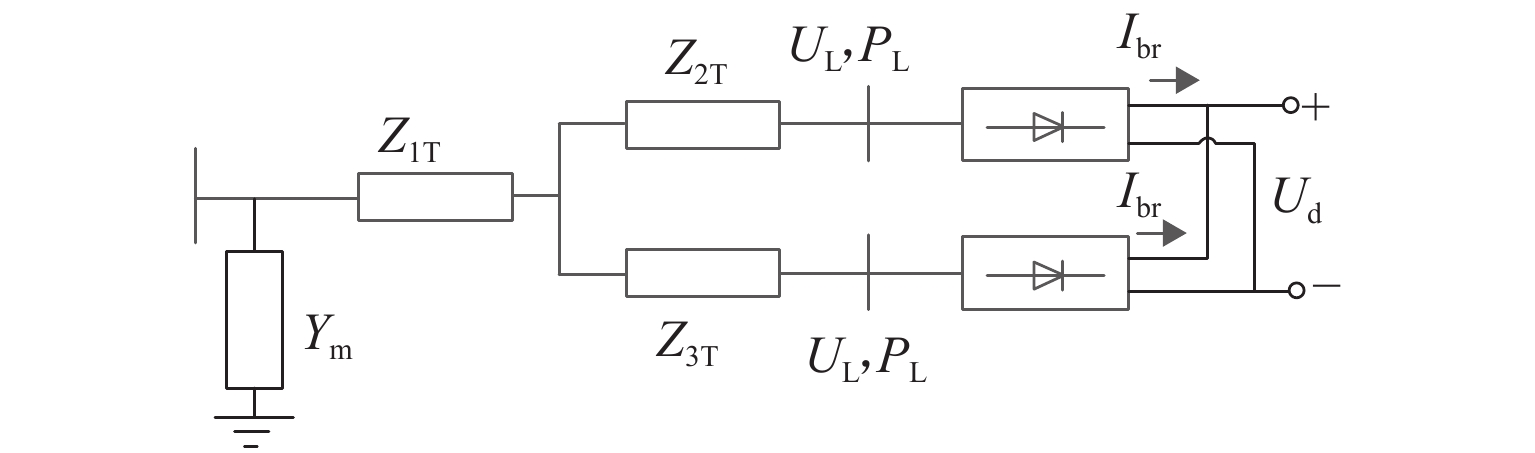
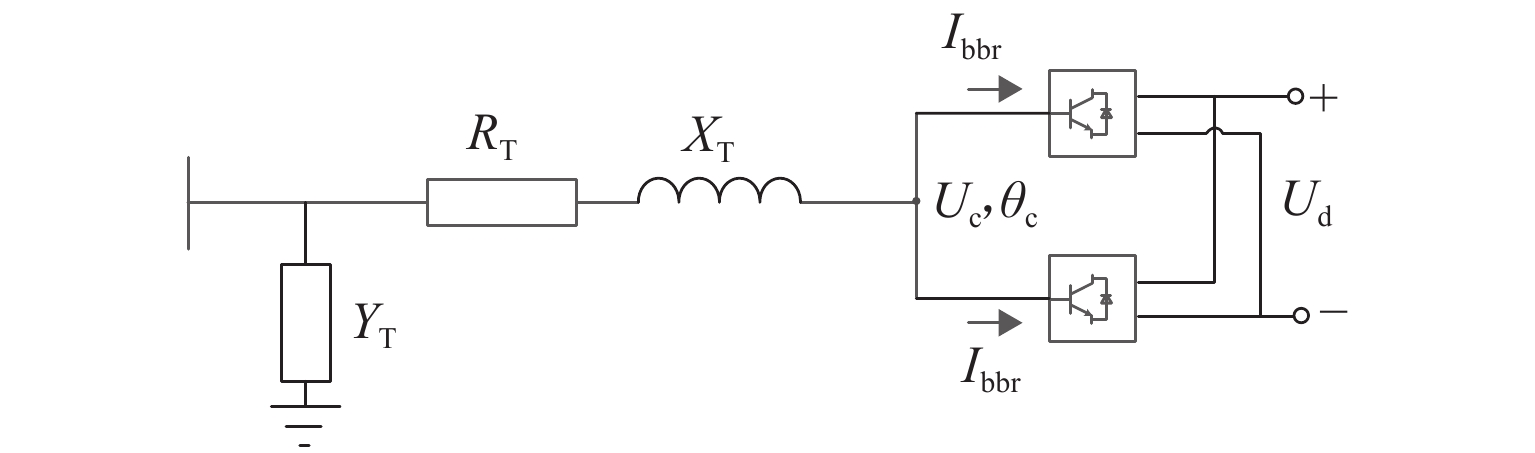
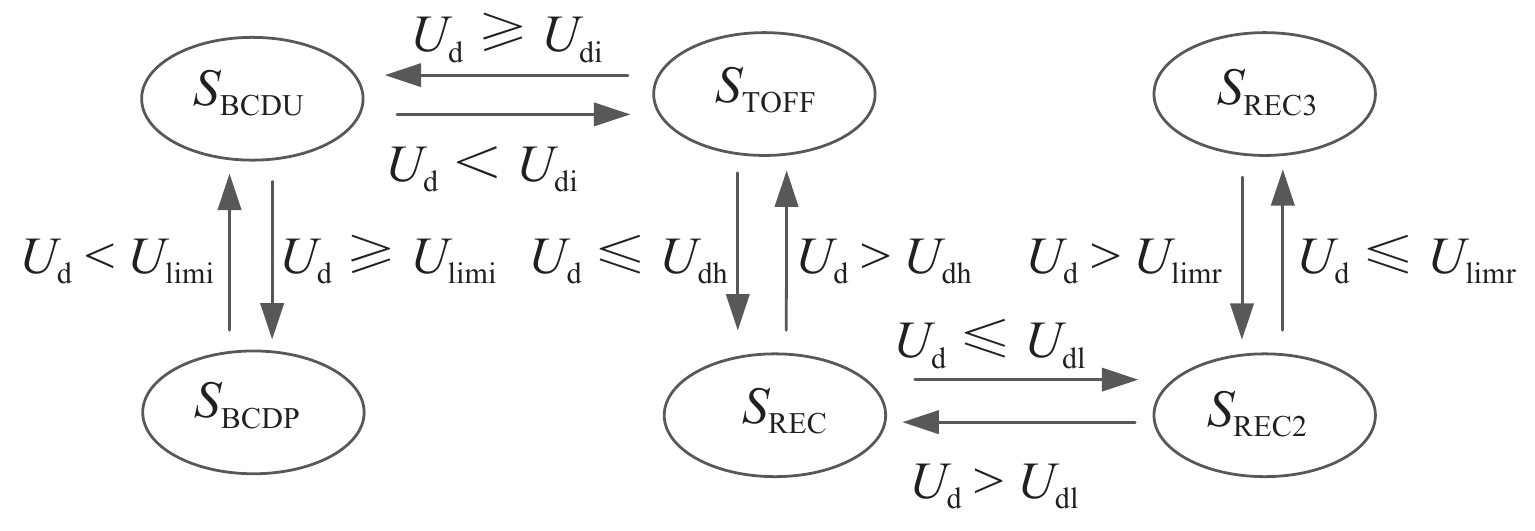
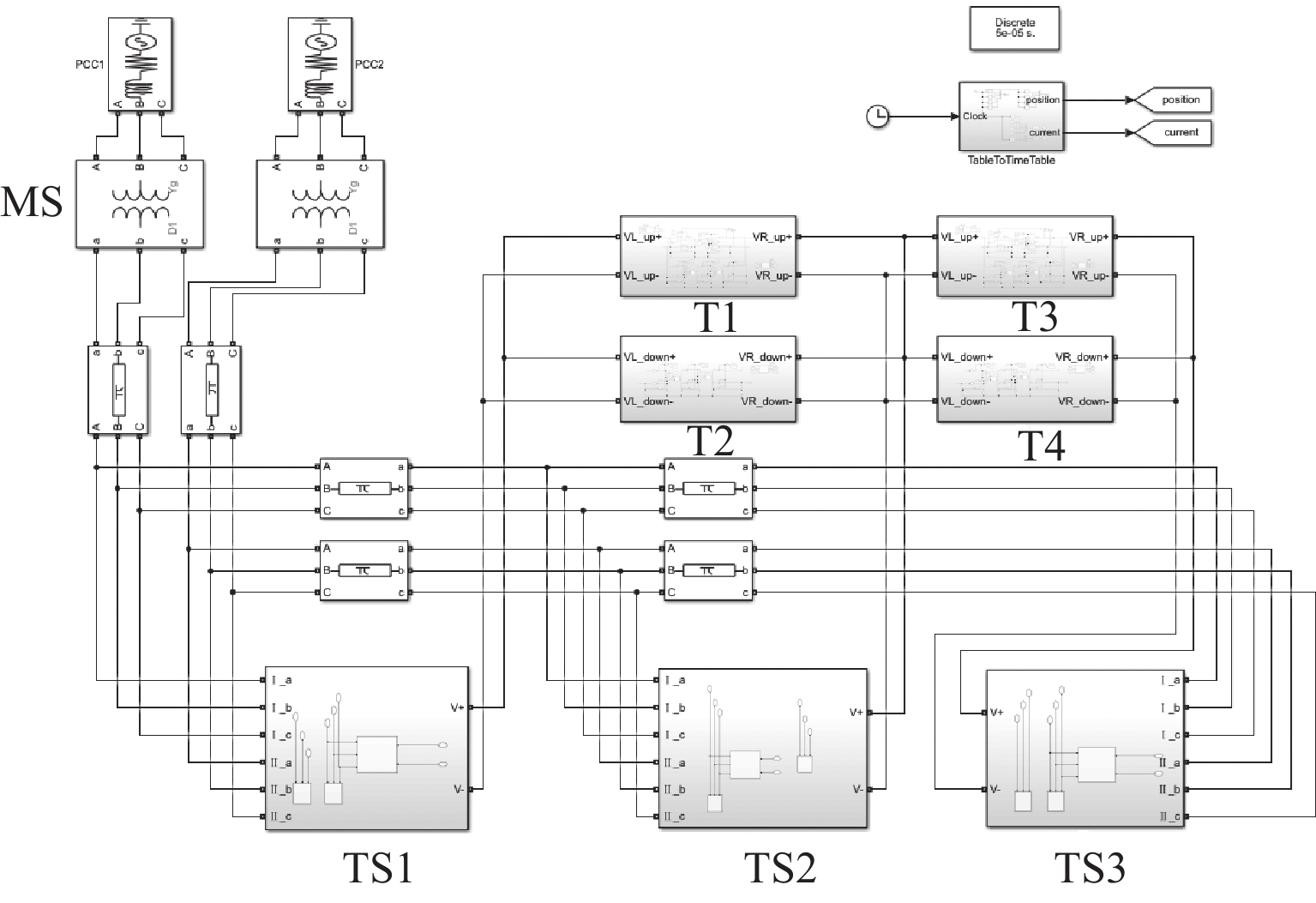
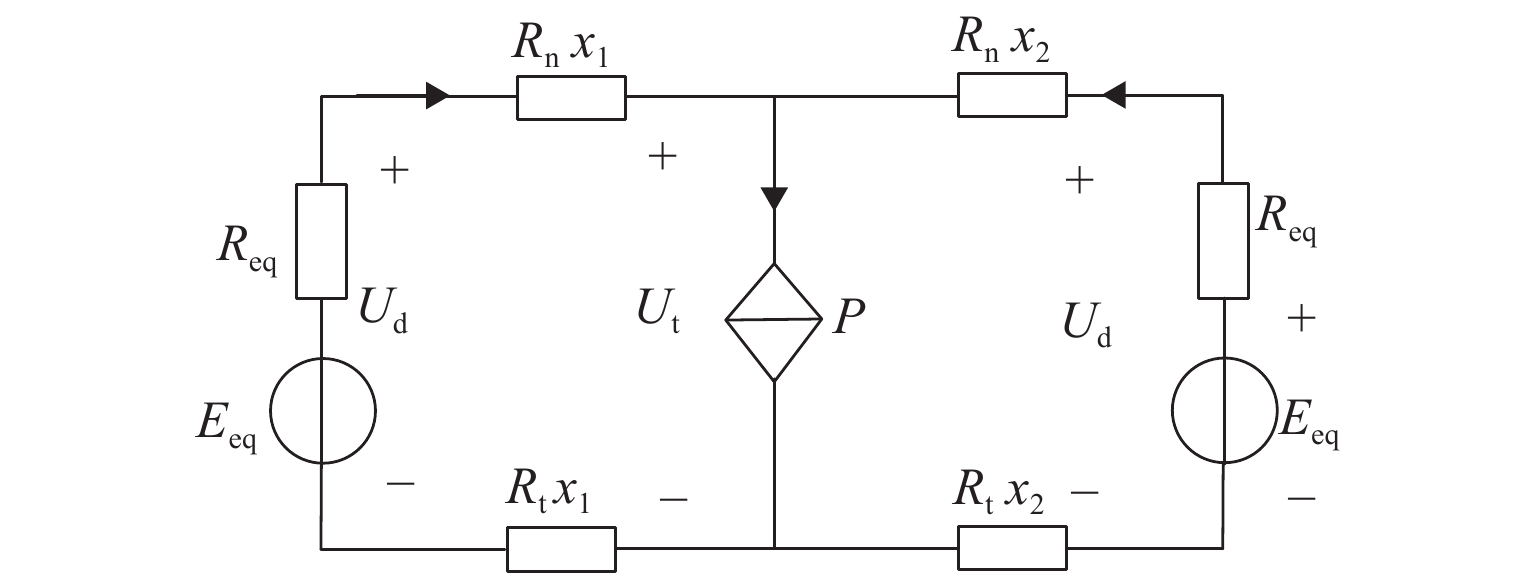
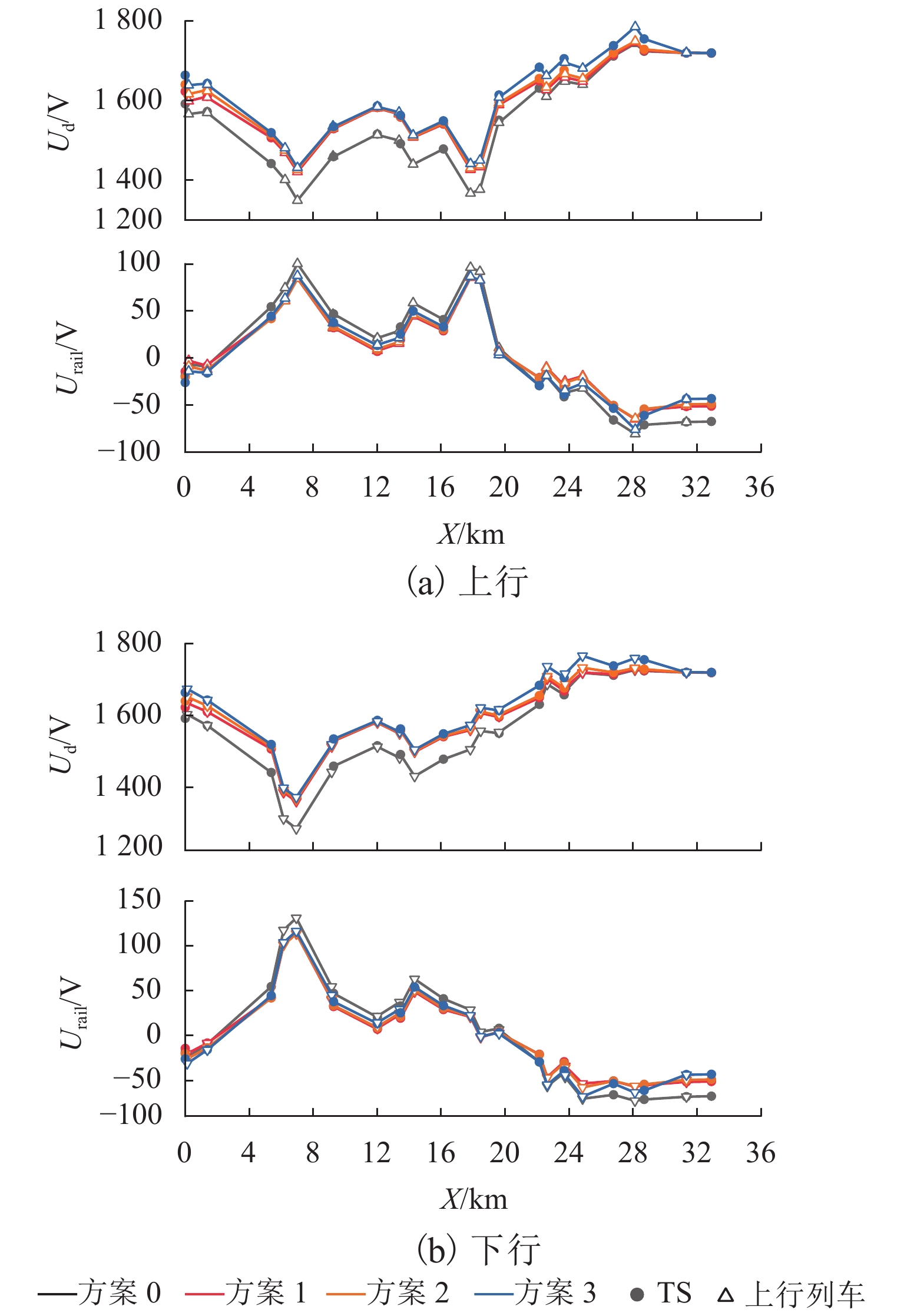
双向变流装置可以有效抑制牵引变电所直流侧网压的波动, 减小跨区间传输的电流，限制钢轨电位. 鉴于电双向变流装置与整流机组的协同控制策略会对城轨牵引供电系统潮流产生直接影响，提出双向变流装置与24 脉波整流机组协同供电的方案，分析该方案下牵引变电所的综合输出外特性；建立计及换流装置精确有功损耗的牵引变电所供电计算模型，并提出考虑滞环比较的多状态切换控制策略，实现含双向变流装置的城轨牵引供电系统协同供电潮流计算；通过与Simulink仿真结果对比，验证算法的有效性及准确性. 以某地铁工程为例进行仿真，仿真结果表明：协同供电方案下，牵引网网压上升，全线上、下行钢轨电位最大值分别降低12.6%～15.6%、14.7%～17.5%，直流牵引供电系统损耗、系统综合成本最多可分别降低9.7%、1.17%；随着双向变流装置整流启动电压增大，部分牵引变电所的整流/逆变功率增大，直流牵引供电系统损耗先升高后降低，但钢轨电位变化不大. 在实际工程中，双向变流装置的逆变启动电压一定时，适当提高其整流启动电压可以获得更佳的节能效果.
- 城市轨道交通 /
- 双向变流装置 /
- 输出外特性 /
- 潮流计算 /
- 协同控制策略
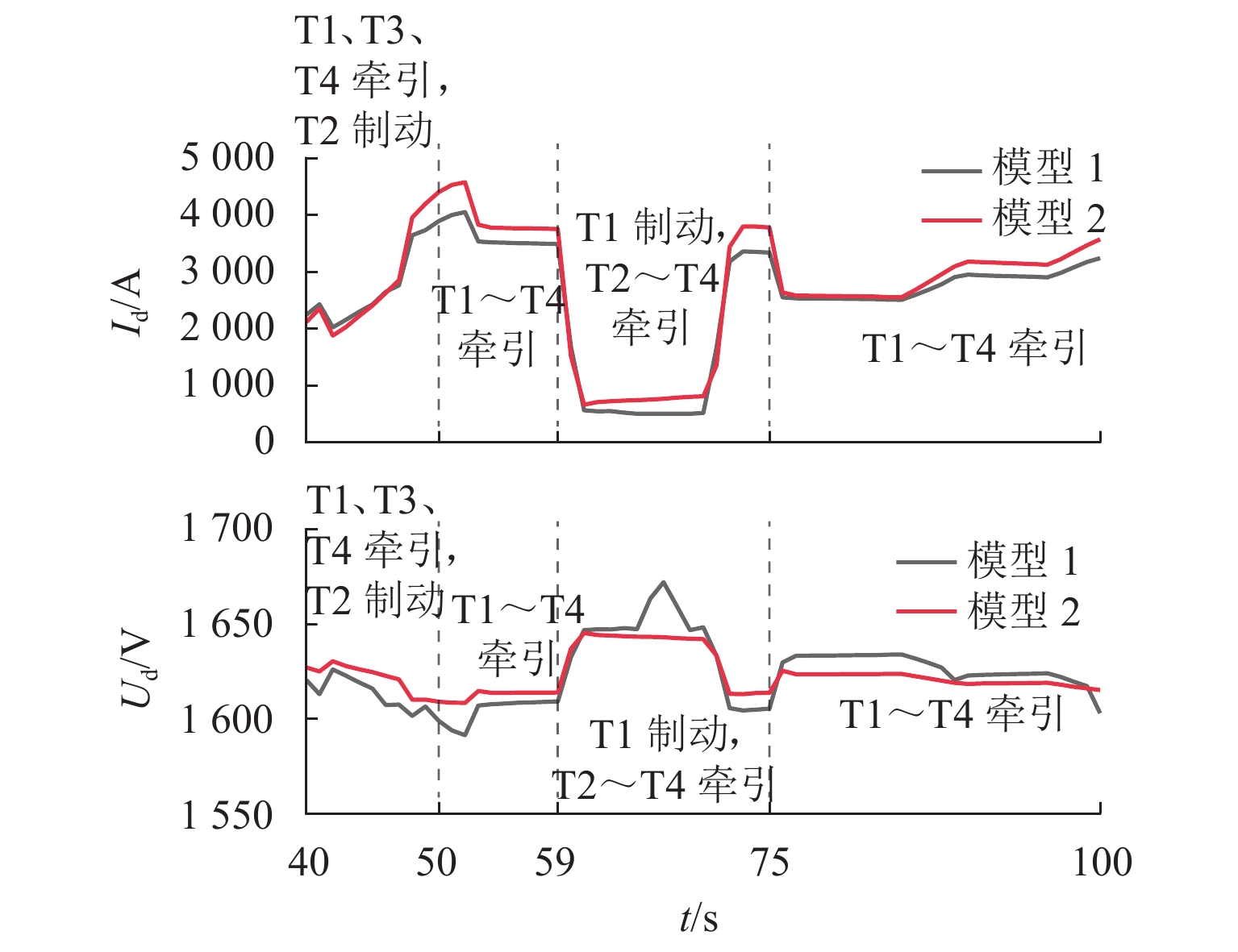
Abstract:
The bidirectional converter device can effectively inhibit the fluctuation of the DC-side grid voltage at traction substation, reduce the current transmitted between regions, and limit the rail potential. As the collaborative control strategy of the bidirectional converter and rectifier unit will directly affect the power flow of urban rail traction power supply system, a coordinated power supply scheme composed of a bidirectional converter device and a 24-pulse rectifier is proposed, and the comprehensive output characteristics of traction substation with this scheme are analyzed. The power supply calculation model of traction substation is established, allowing for the accurate active power loss of converter device, and a multi-state switching control strategy with hysteresis comparison is proposed to calculate the cooperative power flow for urban rail traction power supply system with a bidirectional converter device. Compared with Simulink simulation results, the effectiveness and accuracy of the algorithm are verified. In the simulation of a subway project, under the collaborative power supply scheme, when the traction network pressure increases, the maximum rail potential decreases by 12.6%–15.6% and 14.7%–17.5% up and down the whole line, respectively. The loss of DC traction power supply system and the overall cost of the system can be reduced by 9.7% and 1.17% at most. As the rectifier starting voltage of the bidirectional converter device increases, the rectifier/inverter power of some traction substations increases, and the loss of DC traction power supply system increases first and then decreases, but the rail potential changes little. In practice, when the inverter starting voltage of the bidirectional converter is fixed, increasing the rectifier starting voltage appropriately can achieve better energy saving.
- urban rail transit /
- bidirectional converter device /
- output external characteristics /
- power flow calculation /
- collaborative control strategy

HTML全文

图 1 BCD与整流机组下垂特性

Figure 1. Droop characteristics of bidirectional converter and rectifier unit

下载: 全尺寸图片幻灯片

图 2 牵引变电所综合输出外特性

Figure 2. Integrated output characteristics of traction substations

下载: 全尺寸图片幻灯片

图 3 牵引变电所交直流接口模型

Figure 3. AC–DC interface model of traction substations

下载: 全尺寸图片幻灯片

图 4 12脉波整流机组单相等值模型

Figure 4. Single phase equivalent model of 12-pulse rectifier unit

下载: 全尺寸图片幻灯片

图 5 双向变流装置单相等值模型

Figure 5. Single phase equivalent model of bidirectional converter

下载: 全尺寸图片幻灯片

图 6 牵引变电所运行状态确定法

Figure 6. Method of determining traction substation operation state

下载: 全尺寸图片幻灯片

图 7 3所4车供电系统结构

Figure 7. Power supply system structure of 3 stations and 4 vehicles

下载: 全尺寸图片幻灯片

图 8 TS2直流电流、网压对比

Figure 8. Comparison of TS2 DC and network voltage

下载: 全尺寸图片幻灯片

图 9 单车牵引等效电路

Figure 9. Equivalent circuit diagram of bicycle traction

下载: 全尺寸图片幻灯片

图 10 P_net随E_eq、x₁变化三维图

Figure 10. Three-dimensional diagram of P_net varied with E_eq and x₁

下载: 全尺寸图片幻灯片

图 11 某地铁工程线路

Figure 11. Subway line

下载: 全尺寸图片幻灯片

图 12 t = 155 s时全线钢轨电位、牵引网网压分布

Figure 12. Rail potential and traction network pressure distribution when t = 155 s

下载: 全尺寸图片幻灯片

图 13 t = 155 s时牵引变电所功率分布

Figure 13. Power distribution of traction substation when t = 155 s

下载: 全尺寸图片幻灯片

图 14 直流牵引供电系统平均每小时损耗电能

Figure 14. Average hourly power loss of DC traction power supply system

下载: 全尺寸图片幻灯片

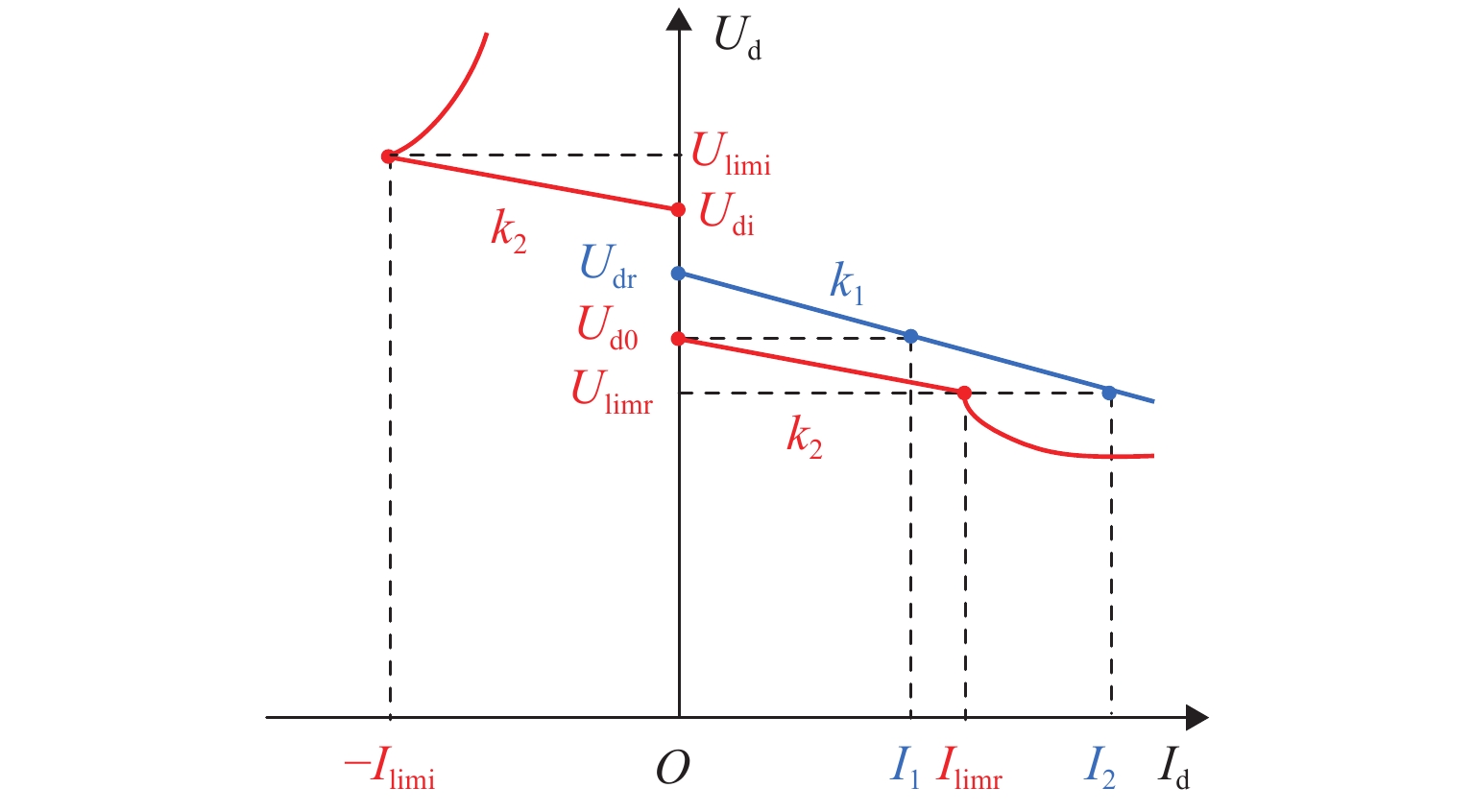
表 1 U_d0 与k₂选取

Table 1. Selection of U_d0 and k₂

k₂/k₁	U_d0/U_dr
k₂/k₁	1 − δ_V	1	1 + δ_V
1−δ_k	方案 1	方案 2	方案 3
1	方案 4	方案 5	方案 6
1 + δ_k	方案 7	方案 8	方案 9

下载: 导出CSV

表 2 仿真参数

Table 2. Simulation parameters

仿真参数	数值	仿真参数	数值
U_dr/V	1 664	n_b	6
U_di/V	1720	V_F/V	1.322
U_on /V	1790	R_n/（Ω·km⁻¹）	0.0172
S_B/kW	2 000	R_t/（Ω·km⁻¹）	0.02
S_R/kW	3 000	η_s	0.25
S_N/kW	1 000	n_p	4
V_N/V	1 500	n_s	1
δ_V/%	2	δ_k/%	40

下载: 导出CSV

表 3 变压器铭牌参数

Table 3. Nameplate parameters of transformer

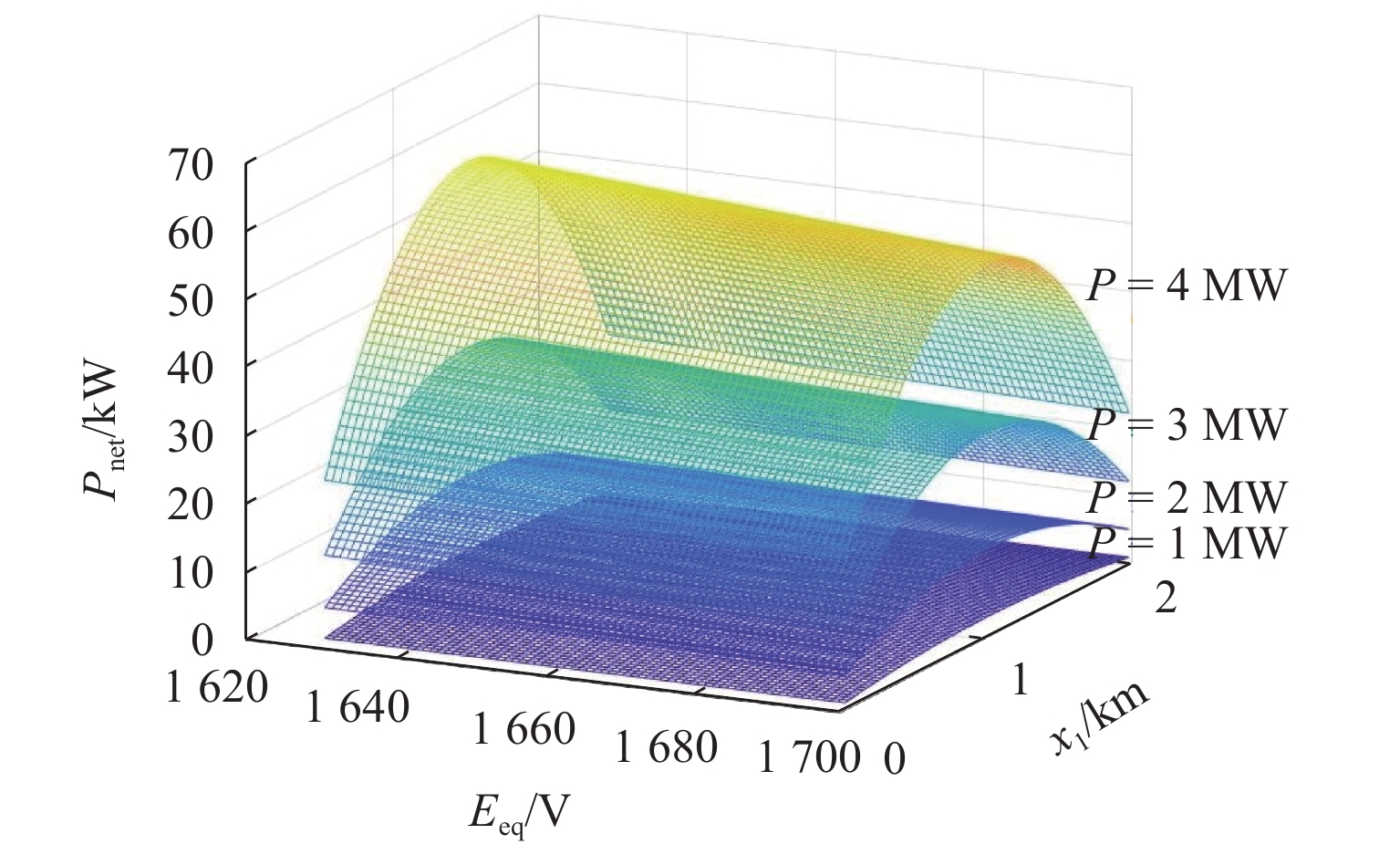
变压器	短路损耗/kW	空载损耗/kW	穿越阻抗/%	空载电流/%	额定容量/ （MV•A）	半穿越阻抗/%
整流变压器	21.544	4.407	7.67	0.256	3.0	6.38
BCD	27.000	6.670	6.00	0.300	2.5

下载: 导出CSV

表 4 P_net与P_device对比

Table 4. Comparison of P_net and P_device kW

控制方案	P_net		P_device
控制方案	模型 1	模型 2	模型 1	模型 2
方案 0	965.941	948.997	78.367	82.017
方案 1	839.404	858.485	129.585	140.863
方案 2	791.650	765.166	156.914	168.105
方案 3	763.240	740.965	186.323	194.123
方案 4	864.456	876.991	131.281	135.308
方案 5	795.564	801.213	147.300	147.922
方案 6	774.569	782.603	159.613	175.122
方案 7	881.667	867.185	127.999	134.818
方案 8	824.344	832.667	138.419	140.062
方案 9	790.304	784.278	152.234	156.016

下载: 导出CSV

表 5 工程算例行车组织

Table 5. Traffic organization of cases

发车对数/对	初期运营时每天持续时间/h	近期运营时每天持续时间/h
8	14	3
10	4	11
18 + 9	0	4

下载: 导出CSV

表 6 综合成本参数

Table 6. Overall cost parameters

参数	取值	参数	取值
BCD p_c/万元	80	EFS p_c/万元	40
c_mt/元	1000	Y/年	10
N/个	14	E_y/（元·（kW·h⁻¹）⁻¹）	0.75

下载: 导出CSV

表 7 算例综合成本

Table 7. Overall costs of cases 万元

控制方案	F（S_B,U_di,U_dh,k₂）	控制方案	F（S_B,U_di,U_dh,k₂）
方案 0	88234.25	方案 5	90123.28
方案 1	89834.89	方案 6	87200.14
方案 2	91338.15	方案 7	89812.72
方案 3	87969.00	方案 8	89235.79
方案 4	89815.68	方案 9	87446.19

下载: 导出CSV

参考文献(16)

[1]	刘洋. 城市轨道交通全自动运行模式下的车地无线综合通信网络方案分析[J]. 城市轨道交通研究,2019,22(12): 22-25. LIU Yang. Analysis of train/ground wireless communication under full automatic operation mode of urban rail transit[J]. Urban Mass Transit, 2019, 22(12): 22-25.
[2]	陈昕,杨立新,王财华,等. 双向变流技术在轨道交通牵引供电系统中的应用[J]. 城市轨道交通研究,2022,25(8): 145-148,152. CHEN Xin, YANG Lixin, WANG Caihua, et al. Engineering application of bidirectional converter technology in rail transit traction power supply system[J]. Urban Mass Transit, 2022, 25(8): 145-148,152.
[3]	SONG S Y, MCCANN R, JANG G S. Cost-based adaptive droop control strategy for VSC-MTDC system[J]. IEEE Transactions on Power Systems, 2021, 36(1): 659-669. doi: 10.1109/TPWRS.2020.3003589
[4]	吴红斌,杨超,陈煜,等. 基于电压源型换流器的多端直流配电网潮流计算[J]. 电力系统自动化,2018,42(11): 79-85,93. WU Hongbin, YANG Chao, CHEN Yu, et al. VSC based power flow calculation of multi-terminal DC distribution network[J]. Automation of Electric Power Systems, 2018, 42(11): 79-85,93.
[5]	王学奎,彭春华,孙惠娟. 考虑VSC控制策略的交直流混合电网潮流计算[J]. 中国电机工程学报,2023,43(10): 3731-3741. WANG Xuekui, PENG Chunhua, SUN Huijuan. Power flow calculation of AC/DC hybrid power grid considering VSC control strategy[J]. Proceedings of the CSEE, 2023, 43(10): 3731-3741.
[6]	ZHANG G, QIAN J L, ZHANG X Y. Application of a high-power reversible converter in a hybrid traction power supply system[J]. Applied Sciences, 2017, 7(3): 7030282.1-7030282.19.
[7]	徐金平,杜贵府,朱纪法,等. 城市轨道交通双向变流式牵引供电系统的应用[J]. 城市轨道交通研究,2020,23(1): 179-182. XV Jinping, DU Guifu, ZHU Jifa, et al. Application of bidirectional converter traction power supply system in urban rail transit[J]. Urban Mass Transit, 2020, 23(1): 179-182.
[8]	张戬,刘炜,周瑞兵,等. 基于双向变流装置的城市轨道牵引供电系统潮流计算[J]. 中国铁道科学,2020,41(1): 92-98. ZHANG Jian, LIU Wei, ZHOU Ruibing, et al. Power flow of traction power supply system for urban rail transit based on bidirectional converter device[J]. China Railway Science, 2020, 41(1): 92-98.
[9]	ZHANG J, LIU W, TIAN Z B, et al. Modelling, simulating and parameter designing for traction power system with bidirectional converter devices[J]. IET Generation, Transmission & Distribution, 2022, 16(1): 110-122.
[10]	HAO F J, ZHANG G, CHEN J, et al. Optimal voltage regulation and power sharing in traction power systems with reversible converters[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2726-2735. doi: 10.1109/TPWRS.2020.2968108
[11]	田胜利. 城轨1500 V 24脉波整流二极管配置分析[J]. 都市快轨交通,2005(1): 31-33.
[12]	刘飞,熊晓琪,查鹏程,等. 直流配电网网架结构与分布式光伏多目标协同优化[J]. 中国电机工程学报,2020,40(12): 3754-3765. LIU Fei, XIONG Xiaoqi, ZHA Pengcheng, et al. Multi-objective collaborative optimization for DC distribution network configuration and distributed photovoltaic[J]. Proceedings of the CSEE, 2020, 40(12): 3754-3765.
[13]	刘炜,张扬鑫,张戬,等. 考虑牵引所多运行状态的城轨交直流供电计算[J]. 西南交通大学学报,2020,55(6): 1163-1170. LIU Wei, ZHANG Yangxin, ZHANG Jian, et al. Calculation of urban rail AC/DC power supply with traction substation in multi-operation modes[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1163-1170.
[14]	刘炜,吴拓剑,禹皓元,等. 直流牵引供电系统地面储能装置建模与仿真分析[J]. 电工技术学报,2020,35(19): 4207-4215. LIU Wei, WU Tuojian, YU Haoyuan, et al. Modeling and simulation of way-side energy storage devices in DC traction power supply system[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4207-4215.
[15]	诸斐琴,杨中平,林飞,等. 城轨交通牵引供电系统参数与储能系统容量配置综合优化[J]. 电工技术学报,2019,34(3): 579-588. ZHU Feiqin, YANG Zhongping, LIN Fei, et al. Synthetic optimization of traction power parameters and energy storage systems in urban rail transit[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 579-588.
[16]	杜贵府,张栋梁,王崇林,等. 直流牵引供电系统电流跨区间传输对钢轨电位影响[J]. 电工技术学报,2016,31(11): 129-139. DU Guifu, ZHANG Dongliang, WANG Chonglin, et al. Effect of traction current transmission among power sections on rail potential in DC mass transit system[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 129-139.

施引文献

附加材料(0)

访问统计

点击查看大图

图(14) / 表(7)

计量

文章访问数: 379
HTML全文浏览量: 150
PDF下载量: 48
被引次数: 0

含双向变流装置的城轨牵引供电系统协同供电潮流计算

doi: 10.3969/j.issn.0258-2724.20220494

作者简介: 刘炜（1982—），男，副教授，研究方向为牵引供电系统理论与仿真、杂散电流与钢轨电位和再生制动能量利用，E-mail：liuwei_8208@swjtu.cn

计量

出版历程

Calculation of Collaborative Power Flow for Urban Rail Traction Power Supply System with Bidirectional Converter Device

计量

出版历程

目录

作者简介:
刘炜（1982—），男，副教授，研究方向为牵引供电系统理论与仿真、杂散电流与钢轨电位和再生制动能量利用，E-mail：liuwei_8208@swjtu.cn