连续排水边界下抽水引发的弱透水层固结解

江留慧; 李传勋; 吴文兵; 梅国雄

doi:10.3969/j.issn.0258-2724.20220473

连续排水边界下抽水引发的弱透水层固结解

doi: 10.3969/j.issn.0258-2724.20220473

1.
江苏大学土木工程与力学学院，江苏镇江 212013
2.
中国地质大学工程学院，湖北武汉 430074
3.
浙江大学海洋学院，浙江舟山 316021

基金项目: 国家自然科学基金项目（51878320）

详细信息

作者简介:
江留慧（1994—），女，实验师，硕士，研究方向为岩土工程，E-mail：jlh134606@163.com

通讯作者:
梅国雄（1975—），男，教授，博士，研究方向为岩土工程，E-mail：meiguox@163.com

中图分类号: TU46
计量
- 文章访问数: 186
- HTML全文浏览量: 83
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-05
- 修回日期: 2022-11-20
- 网络出版日期: 2023-12-04
- 刊出日期: 2022-11-25

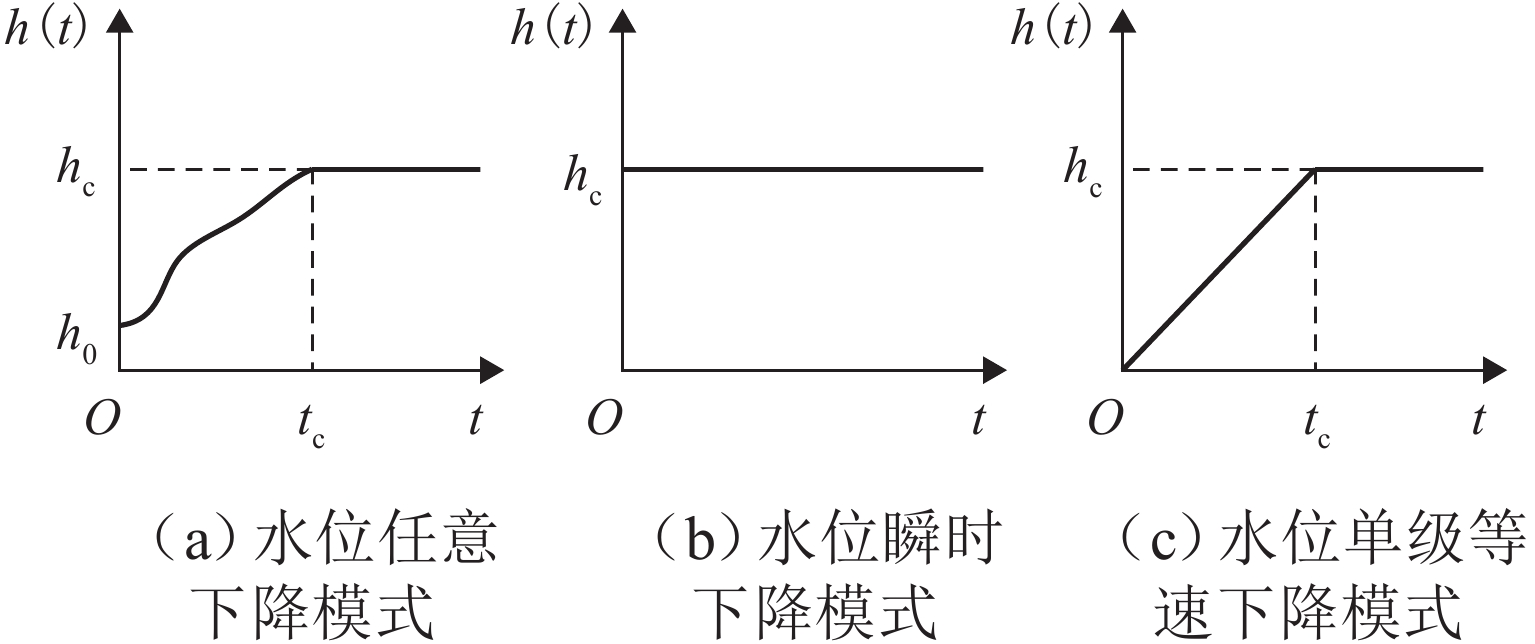
Consolidation Solution of Aquitard Induced by Dropping of Groundwater Table with Continuous Drainage Boundary

1.
Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China
2.
Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
3.
Ocean College, Zhejiang University, Zhoushan 316021, China

摘要

摘要:
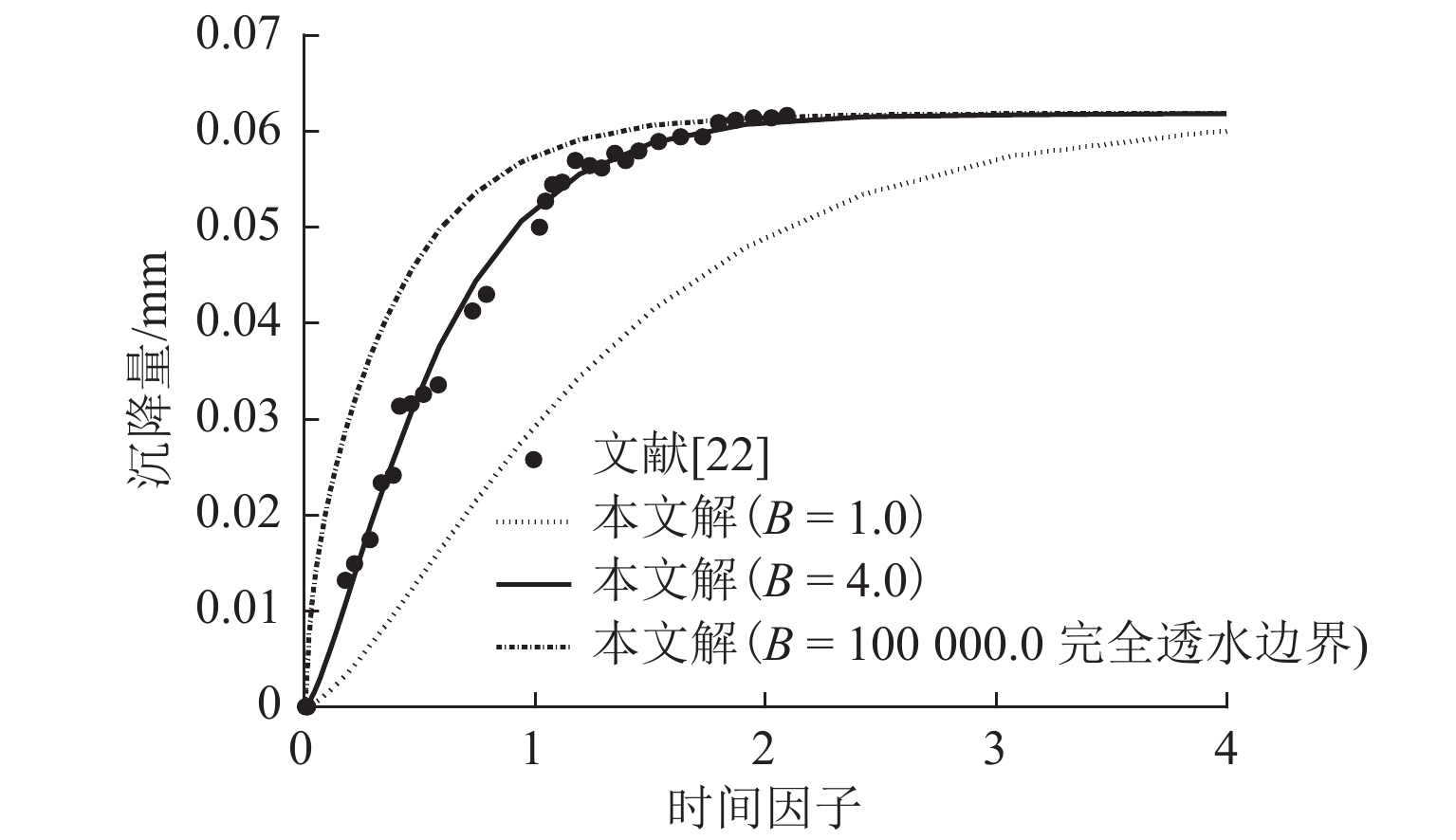
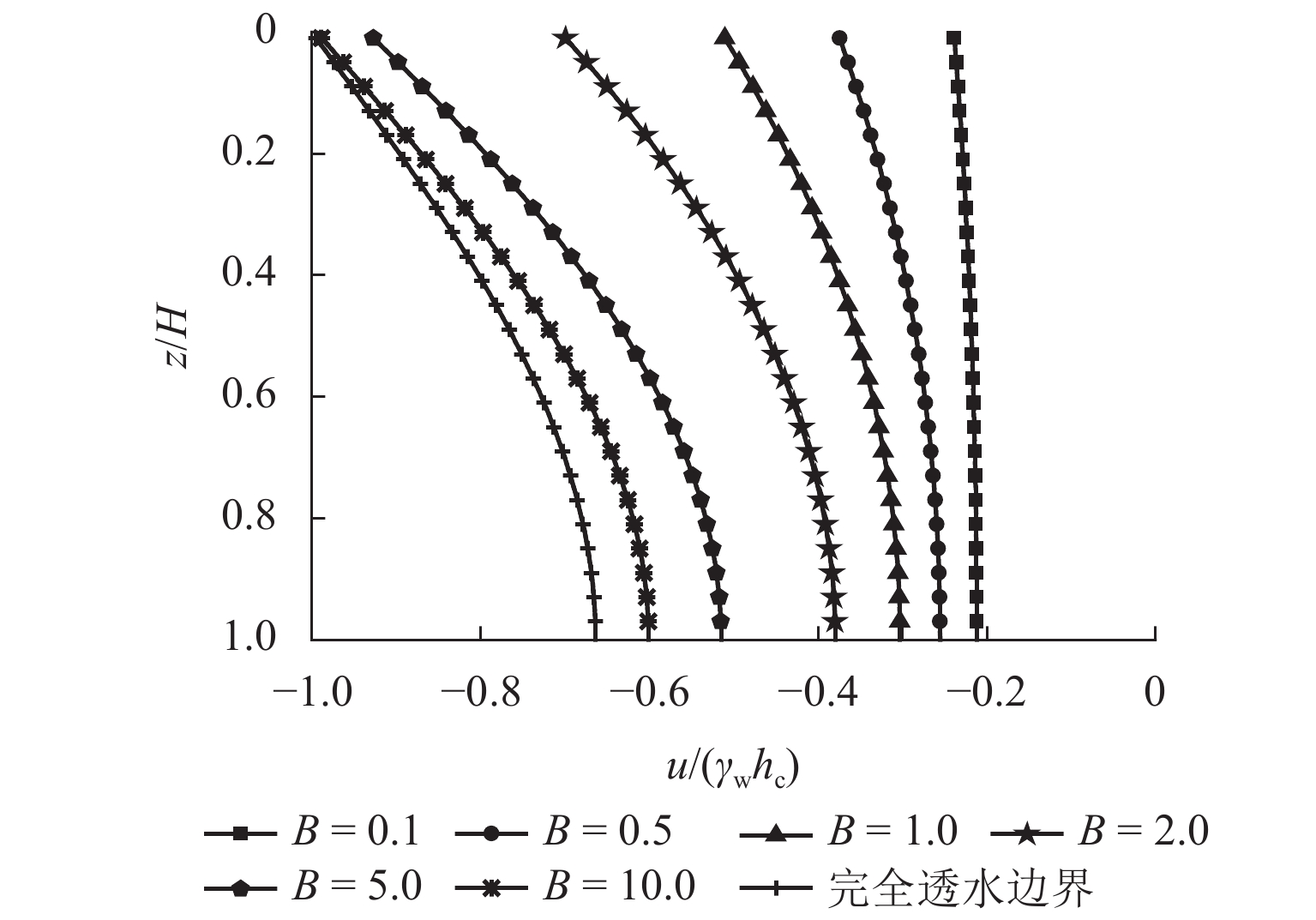
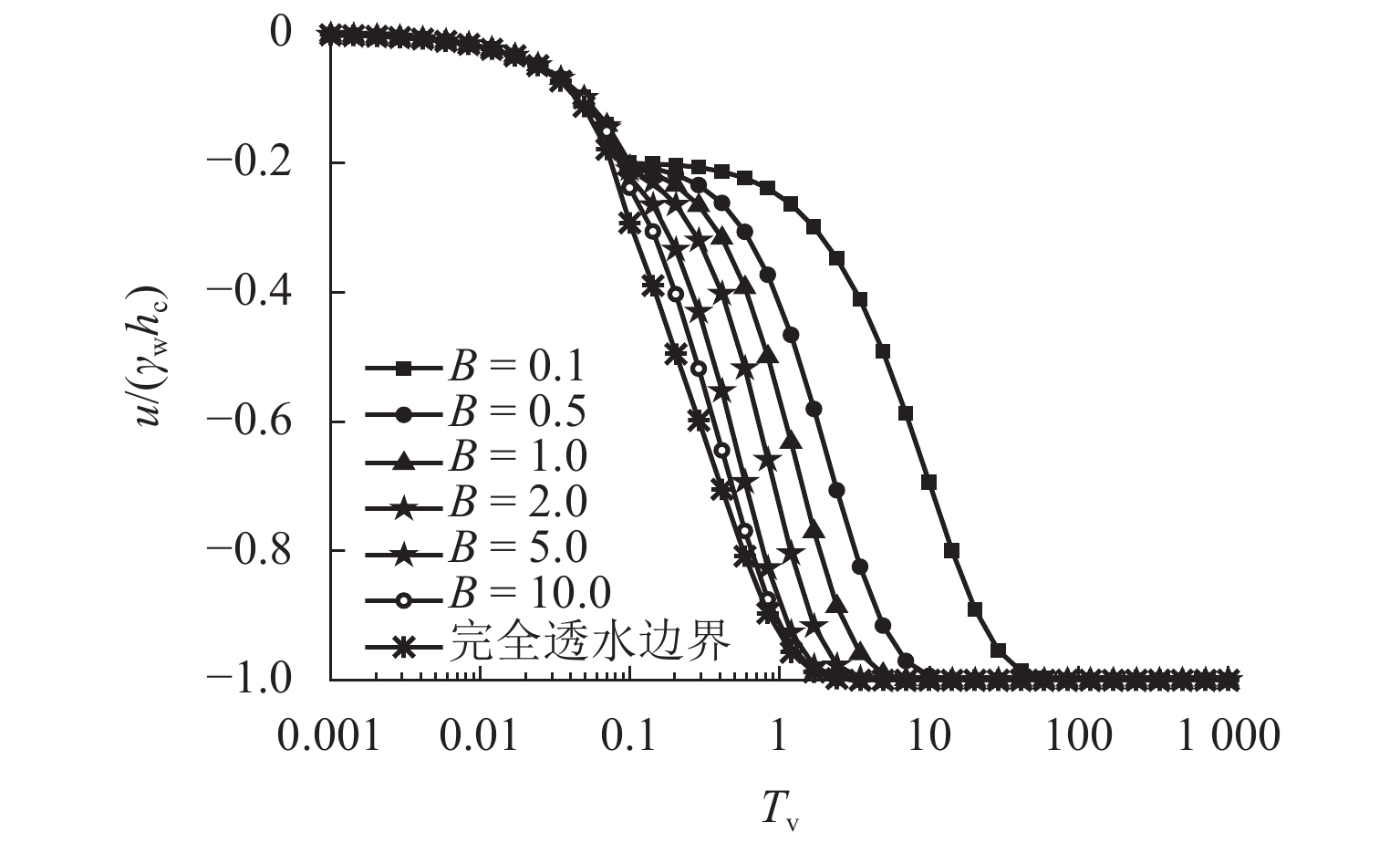
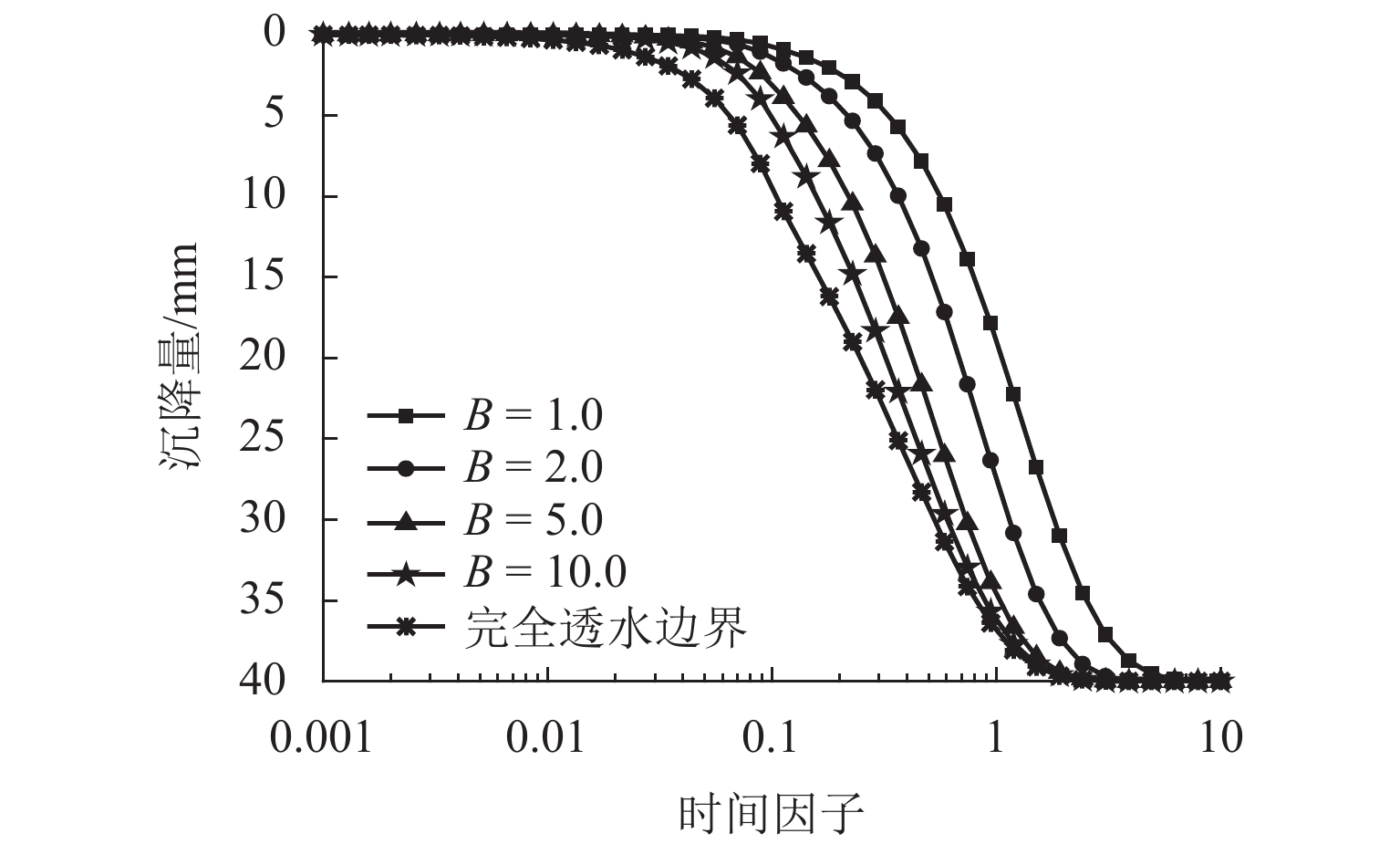
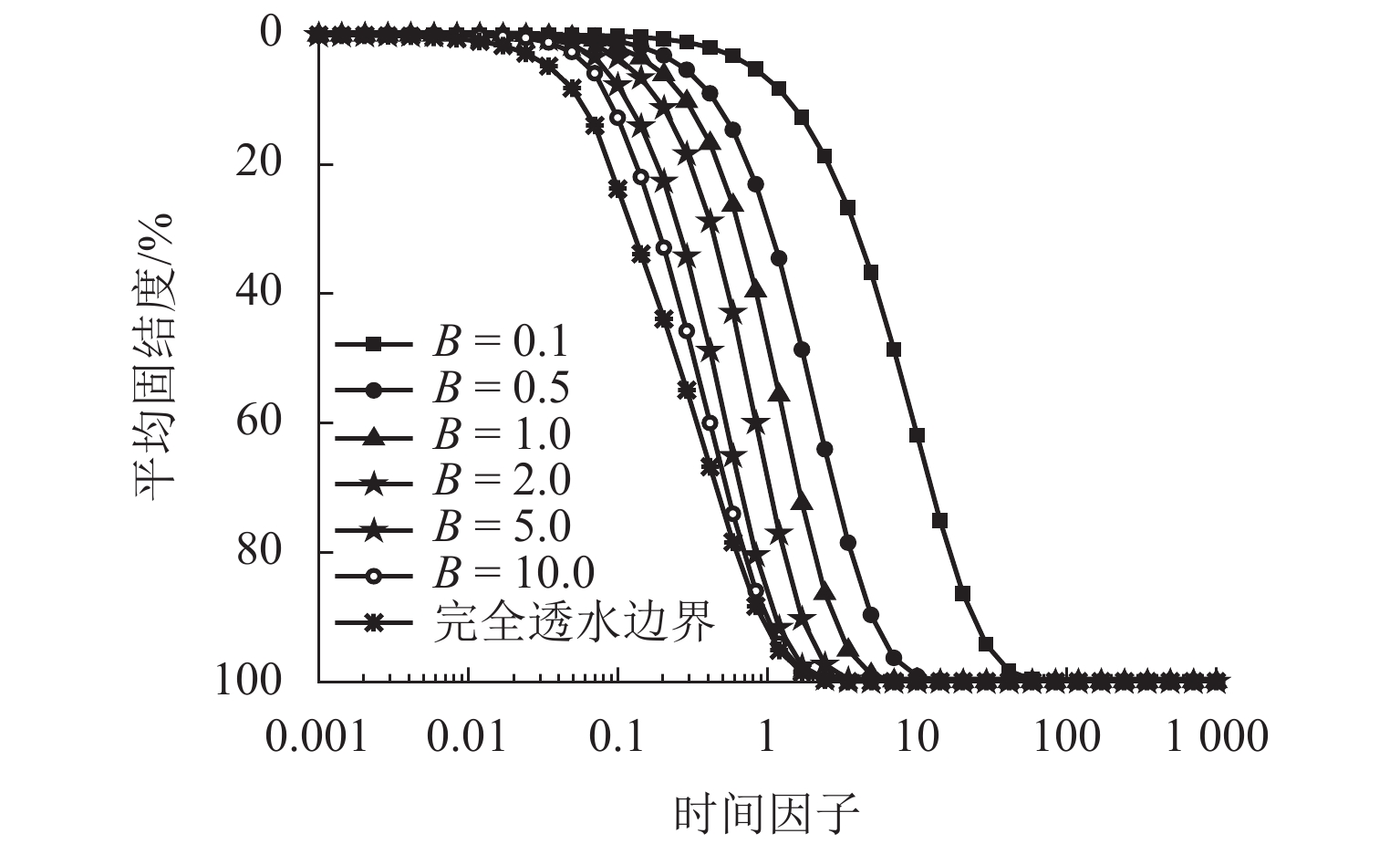
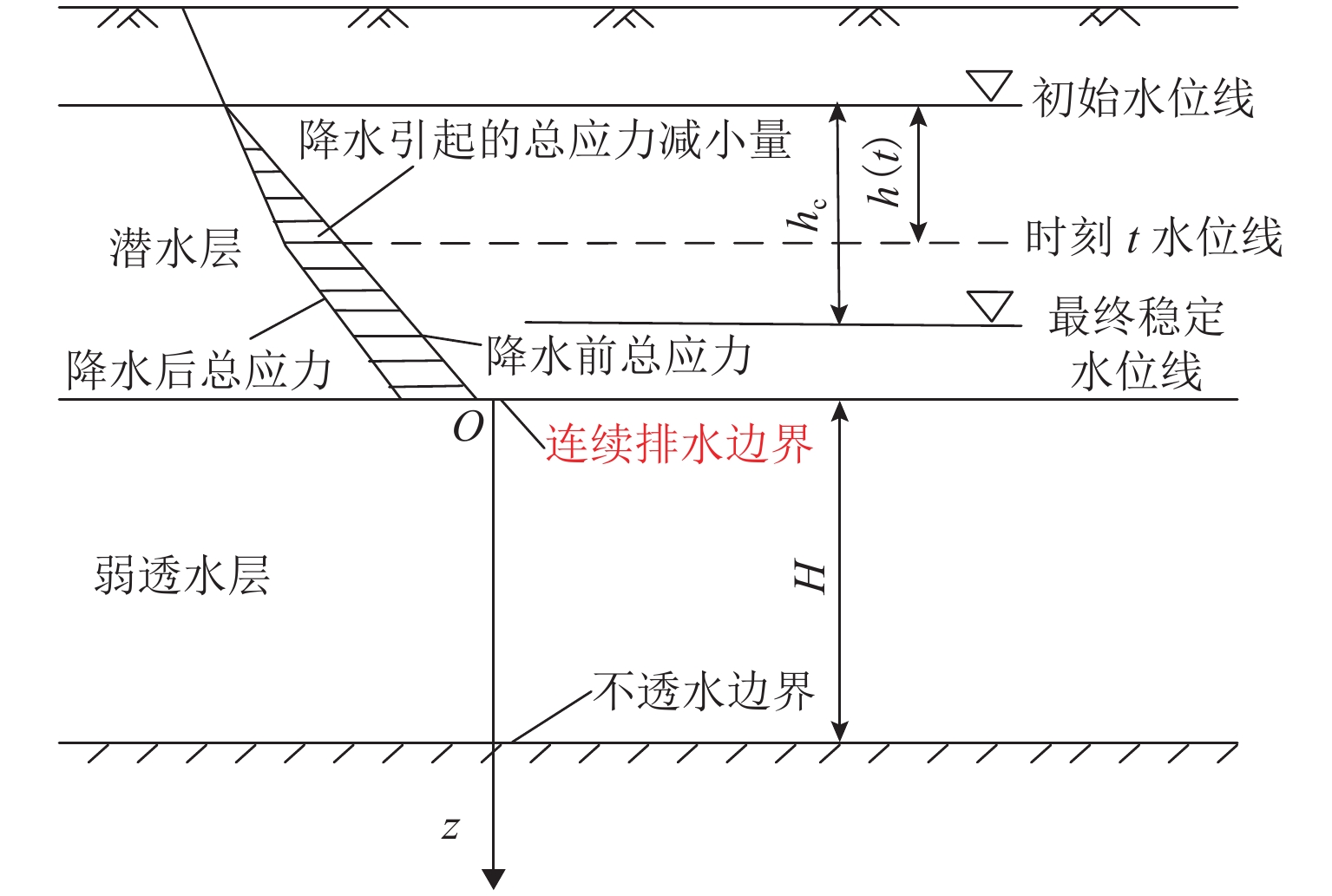
为探究更能反映实际透水能力的排水边界对超采地下水导致的地面沉降问题的影响，首先，通过引入孔压随时间指数衰减的连续排水边界，建立连续排水边界下潜水层水位变化引发的下卧弱透水层一维固结模型；其次，采用分离变量法获得其模型普遍解析解答以及水位瞬时下降和水位单极等速下降2种特殊降水模式的解析解；然后，通过特定条件下解析解的退化初步验证本文解析理论的正确性；最后，以水位单级等速下降为例，利用本文解计算不同界面参数下弱透水层的固结曲线，着重分析界面参数对固结性状的影响. 结果表明：理论计算的沉降曲线与室内试验沉降曲线对比，最大误差为13%，进一步说明连续排水边界更贴合实际透水边界；界面参数越大（排水边界透水性越好），孔压消散速率越快，固结速率越快，越早完成固结，但其并不影响最终固结状态.
- 水位下降 /
- 土力学 /
- 连续排水边界 /
- 界面参数 /
- 解析解
Abstract:
In order to investigate the influence of the drainage boundary, which can better reflect the actual permeability, on the land subsidence caused by over-exploitation of groundwater, firstly, a one-dimensional consolidation model of aquitard caused by the dropping of groundwater table in phreatic aquifer with continuous drainage boundary was established by introducing the continuous drainage boundary, where the pore pressure decayed exponentially with time. Secondly, the general analytical solutions of the model and the analytical solutions of two special dewatering models for the instantaneous dropping of the groundwater table and the single-stage and constant-rate dropping of the groundwater table were obtained by using the method of separate variables. Then, the correctness of the analytical theory in this paper was preliminarily verified by the degeneracy of the analytical solutions under certain conditions. Finally, the single-stage and constant-rate dropping of the groundwater table was taken as an example, and the consolidation curves of the aquitard under different interface parameters B were calculated based on the analytical solutions. In addition, the influence of interface parameter B on the consolidation behaviors was analyzed emphatically. The results show that the maximum error rate is 13% by comparing the theoretically calculated settlement curve with the experimental settlement curve, which further indicates that the continuous drainage boundary is closer to the actual permeable boundary. Furthermore, larger interface parameter B indicates (better water permeability of the drainage boundary) a faster pore pressure dissipation rate, faster consolidation rate, and shorter consolidation time, but the final consolidation state is not affected.
- dropping of groundwater table /
- soil mechanics /
- continuous drainage boundary /
- interface parameter /
- analytical solution

HTML全文

图 1 连续排水边界下潜水层降水引发的弱透水层一维固结示意

Figure 1. One-dimensional consolidation of aquitard caused by the dropping of groundwater table in phreatic aquifer with continuous drainage boundary

下载: 全尺寸图片幻灯片

图 2 水位下降值随时间变化示意

Figure 2. Variation of the dropping of groundwater table with time

下载: 全尺寸图片幻灯片

图 3 本文解与文献[22]试验结果的沉降对比

Figure 3. Comparison of settlement between solutions in this paper and experimental results in reference [22]

下载: 全尺寸图片幻灯片

图 4 B对超静孔压沿深度分布曲线的影响

Figure 4. Influence of B on distribution curves of excess pore pressure with depth

下载: 全尺寸图片幻灯片

图 5 B对超静孔压随时间发展曲线的影响

Figure 5. Influence of B on development curves of excess pore pressure with time

下载: 全尺寸图片幻灯片

图 6 B对沉降量的影响

Figure 6. Influence of B on settlement

下载: 全尺寸图片幻灯片

图 7 B对固结度的影响

Figure 7. Influence of B on consolidation degree

下载: 全尺寸图片幻灯片

表 1 固结性状分析采用的模型参数

Table 1. Model parameters adopted in consolidation behavior analysis

参数数值

γ_sat/（kN·m⁻³） 20
γ/（kN·m⁻³） 18
γ_w/（kN·m⁻³） 10
H/m 10
m_v/MPa⁻¹ 0.1
T_vc 0.1
h_c/m 5

下载: 导出CSV

参考文献(23)

[1]	CHEN C X, PEI S P, JIAO J. Land subsidence caused by groundwater exploitation in Suzhou City, China[J]. Hydrogeology Journal, 2003, 11(2): 275-287. doi: 10.1007/s10040-002-0225-5
[2]	YI L X, WANG J E, SHAO C Q, et al. Land subsidence disaster survey and its economic loss assessment in Tianjin, China[J]. Natural Hazards Review, 2010, 11(1): 35-41. doi: 10.1061/(ASCE)1527-6988(2010)11:1(35)
[3]	殷跃平,张作辰,张开军. 我国地面沉降现状及防治对策研究[J]. 中国地质灾害与防治学报,2005,16(2): 1-8. doi: 10.3969/j.issn.1003-8035.2005.02.001 YIN Yueping, ZHANG Zuochen, ZHANG Kaijun. Land subsidence and countermeasures for its prevention in China[J]. The Chinese Journal of Geological Hazard and Control, 2005, 16(2): 1-8. doi: 10.3969/j.issn.1003-8035.2005.02.001
[4]	张云,薛禹群. 抽水地面沉降数学模型的研究现状与展望[J]. 中国地质灾害与防治学报,2002,13(2): 1-6,24. ZHANG Yun, XUE Yuqun. Present sitution and prospect on the mathematical model of land subsidence due to pumping[J]. The Chinese Journal of Geological Hazard and Control, 2002, 13(2): 1-6,24.
[5]	骆冠勇,潘泓,曹洪,等. 承压水减压引起的沉降分析[J]. 岩土力学,2004,25(增2): 196-200. doi: 10.3969/j.issn.1000-7598.2004.z2.040 LUO Guanyong, PAN Hong, CAO Hong, et al. Analysis of settlements caused by decompression of confined water[J]. Rock and Soil Mechanics, 2004, 25(S2): 196-200. doi: 10.3969/j.issn.1000-7598.2004.z2.040
[6]	谢康和,陶立为,王玉林,等. 越流系统中弱透水层的一维固结解及分析[J]. 沈阳工业大学学报,2012,34(5): 581-585. XIE Kanghe, TAO Liwei, WANG Yulin, et al. One-dimensional consolidation solution and analysis for aquitard in leakage system[J]. Journal of Shenyang University of Technology, 2012, 34(5): 581-585.
[7]	黄大中. 水位变化引发的土层耦合固结变形理论研究[D]. 杭州: 浙江大学, 2014.
[8]	谢海澜,武强,赵增敏,等. 考虑非达西流的弱透水层固结计算[J]. 岩土力学,2007,28(5): 1061-1065. XIE Hailan, WU Qiang, ZHAO Zengmin, et al. Consolidation computation of aquitard considering non-Darcy flow[J]. Rock and Soil Mechanics, 2007, 28(5): 1061-1065.
[9]	张玮鹏,谢康和,吕文晓,等. 抽水引起的有起始比降饱和土固结解析解[J]. 中南大学学报(自然科学版),2016,47(3): 875-881. ZHANG Weipeng, XIE Kanghe, LÜ Wenxiao, et al. Analytical solution to one-dimensional consolidation of saturated soil with threshold gradient induced by groundwater pumping[J]. Journal of Central South University (Science and Technology), 2016, 47(3): 875-881.
[10]	晏凌晗. 水位下降引发的软土层一维流变固结解析与试验研究[D]. 杭州: 浙江大学, 2017.
[11]	吴浩,谢康和,黄大中. 第二类越流系统中结构性弱透水土层一维固结解析解[J]. 岩土工程学报,2014,36(9): 1688-1695. WU Hao, XIE Kanghe, HUANG Dazhong. Analytical solution for one-dimensional consolidation of structured aquitard soils in second kind of leakage system[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1688-1695.
[12]	夏长青. 成层结构性软土非线性大应变流变固结理论研究[D]. 杭州: 浙江大学, 2018.
[13]	李传勋,江留慧. 抽降水引发的弱透水层非线性固结解析解[J]. 工程科学与技术,2021,53(3): 106-114. LI Chuanxun, JIANG Liuhui. Analytical solutions for nonlinear consolidation of aquitard induced by the dropping of groundwater table[J]. Advanced Engineering Sciences, 2021, 53(3): 106-114.
[14]	梅国雄,夏君,梅岭. 基于不对称连续排水边界的太沙基一维固结方程及其解答[J]. 岩土工程学报,2011,33(1): 28-31. MEI Guoxiong, XIA Jun, MEI Ling. Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 28-31.
[15]	冯健雪,陈征,李勇义,等. 连续排水边界条件下线性加载地基一维固结解析解[J]. 工程力学,2019,36(6): 219-226. FENG Jianxue, CHEN Zheng, LI Yongyi, et al. Analytical solution for one-dimensional consolidation of soft clayey soil with a continuous drainage boundary under linear loading[J]. Engineering Mechanics, 2019, 36(6): 219-226.
[16]	宗梦繁,吴文兵,梅国雄,等. 连续排水边界条件下土体一维非线性固结解析解[J]. 岩石力学与工程学报,2018,37(12): 2829-2838. ZONG Mengfan, WU Wenbing, MEI Guoxiong, et al. An analytical solution for one-dimensional nonlinear consolidation of soils with continuous drainage boundary[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(12): 2829-2838.
[17]	宗梦繁,吴文兵,梅国雄,等. 连续排水边界条件下土体一维流变固结解析解[J]. 工程力学,2019,36(9): 79-88. ZONG Mengfan, WU Wenbing, MEI Guoxiong, et al. Analytical solution for one-dimensional rheological consolidation of soil based on continuous drainage boundary[J]. Engineering Mechanics, 2019, 36(9): 79-88.
[18]	陈余,李传勋. 连续排水边界下考虑起始坡降的软黏土固结解[J]. 工程力学,2021,38(9): 161-170. CHEN Yu, LI Chuanxun. Consolidation analysis of soft clay considering the threshold hydraulic gradient and a continuous drainage boundary[J]. Engineering Mechanics, 2021, 38(9): 161-170.
[19]	张云鹏,王宗琴,宗梦繁,等. 连续排水边界下成层陆域吹填地基一维固结解析解[J]. 地质科技通报,2023,42(3): 38-45. doi: 10.19509/j.cnki.dzkq.2022.0171 ZHANG Yunpeng, WANG Zongqin, ZONG Mengfan. et al. Closed-form solution for one-dimensional consolidation analysis in reclamation area based on continuous boundary conditions[J]. Bulletin of Geological Science and Technology, 2023, 42(3): 38-45. doi: 10.19509/j.cnki.dzkq.2022.0171
[20]	苗青,闻敏杰,宗梦繁,等. 连续排水边界下非线性饱和土体一维热固结解析解[J]. 哈尔滨工业大学学报,2023,55(2): 143-150. MIAO Qing, WEN Minjie, ZONG Mengfan, et al. Analytical solution for one-dimensional thermal consolidation of nonlinear saturated soils based on continuous drainage boundary[J]. Journal of Harbin Institute of Technology, 2023, 55(2): 143-150.
[21]	江留慧. 抽降水下既有建筑物基桩承载力性状分析[D]. 镇江: 江苏大学, 2020.
[22]	顾迪. 地下水位变化条件下黏土层变形的宏微观试验研究[D]. 南京: 南京大学, 2020.
[23]	张婧玮,梁杏,葛勤,等. 江汉平原第四系弱透水层渗透系数求算方法[J]. 地球科学,2017,42(5): 761-770. ZHANG Jingwei, LIANG Xing, GE Qin, et al. Calculation method about hydraulic conductivity of quaternary aquitard in Jianghan plain[J]. Earth Science, 2017, 42(5): 761-770.