Dynamic Characteristic Analysis of Constrained Damping Plate Based on Iterative Revised Modal Strain Energy Method
-
摘要:
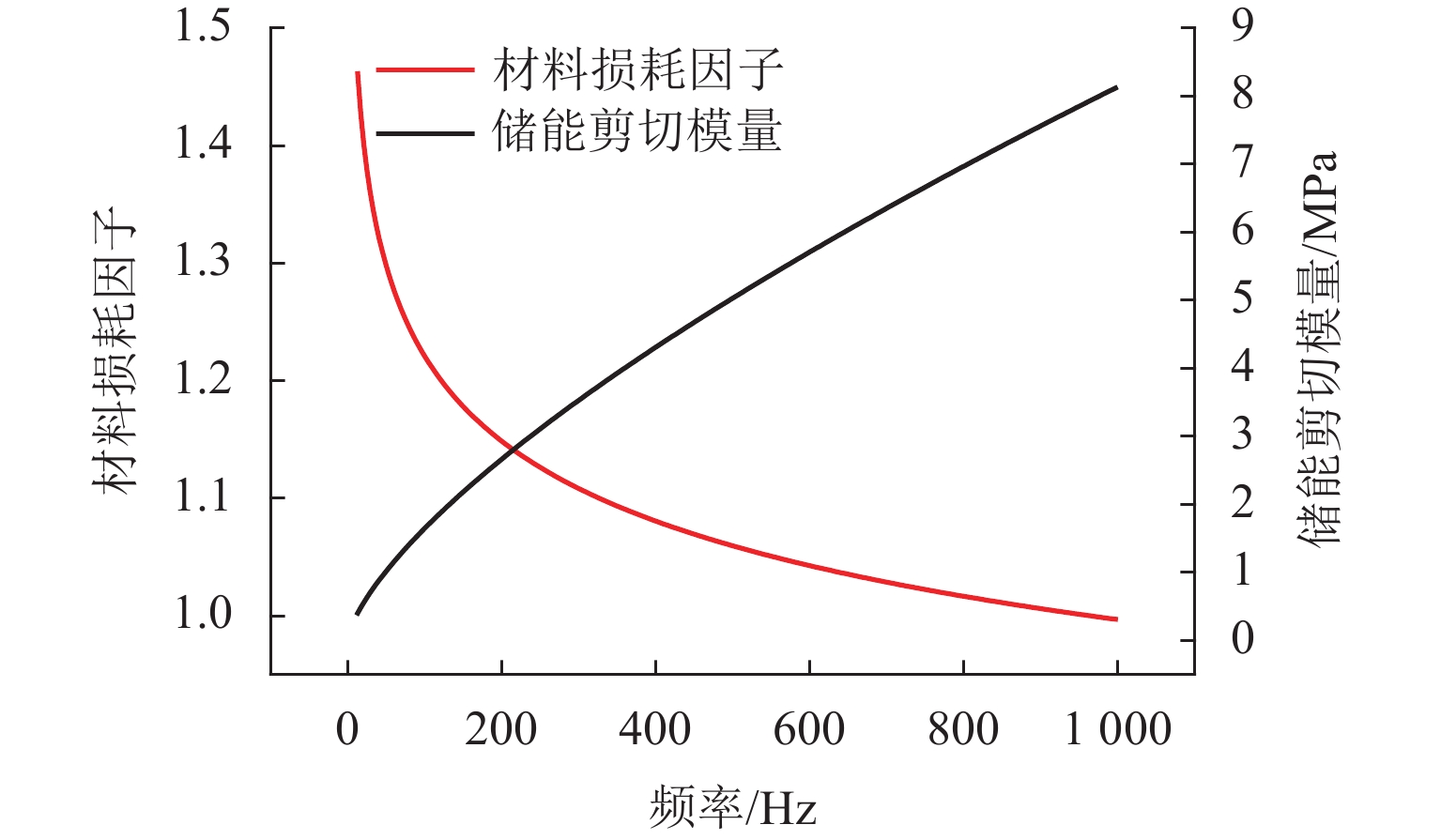
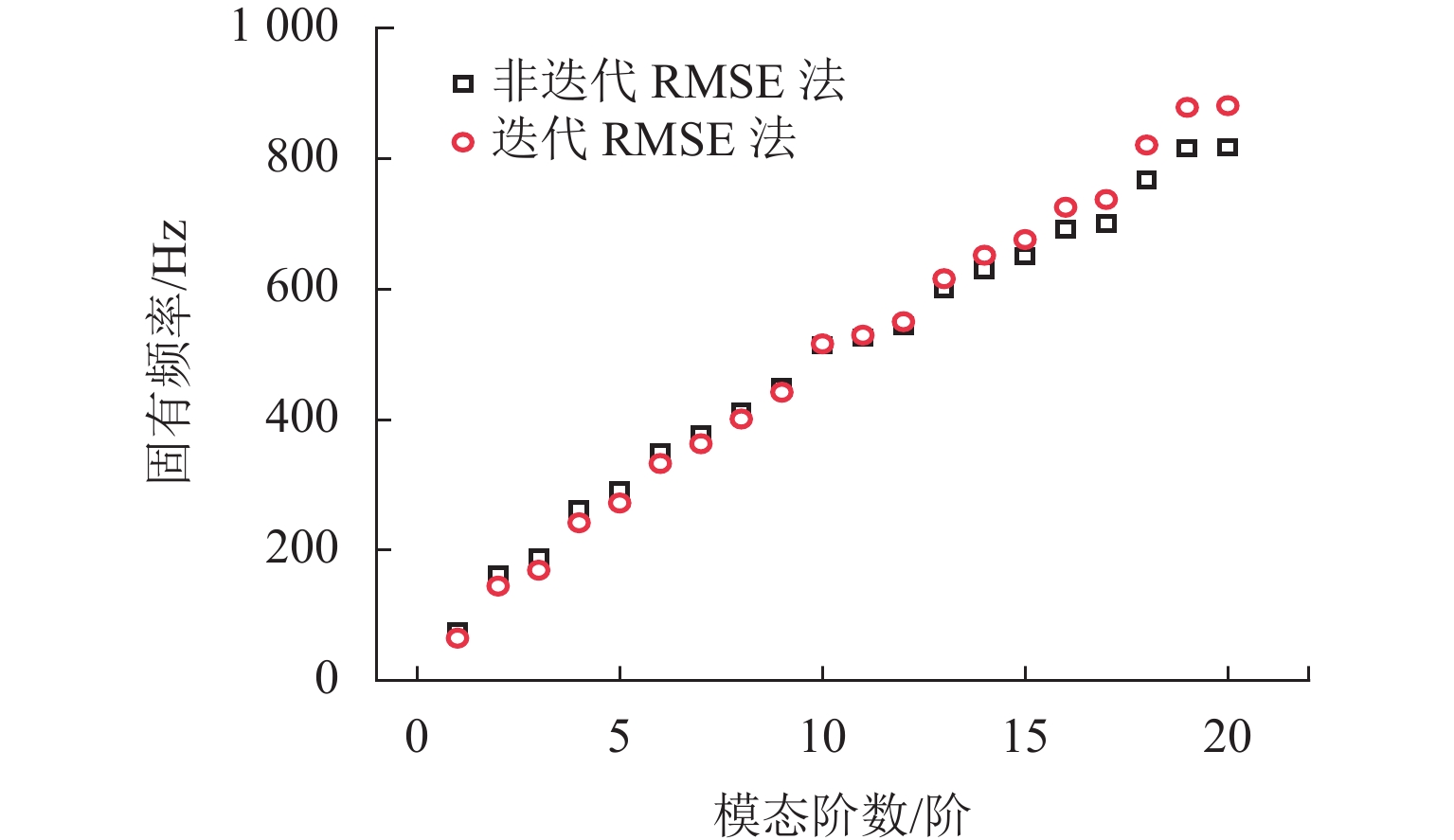
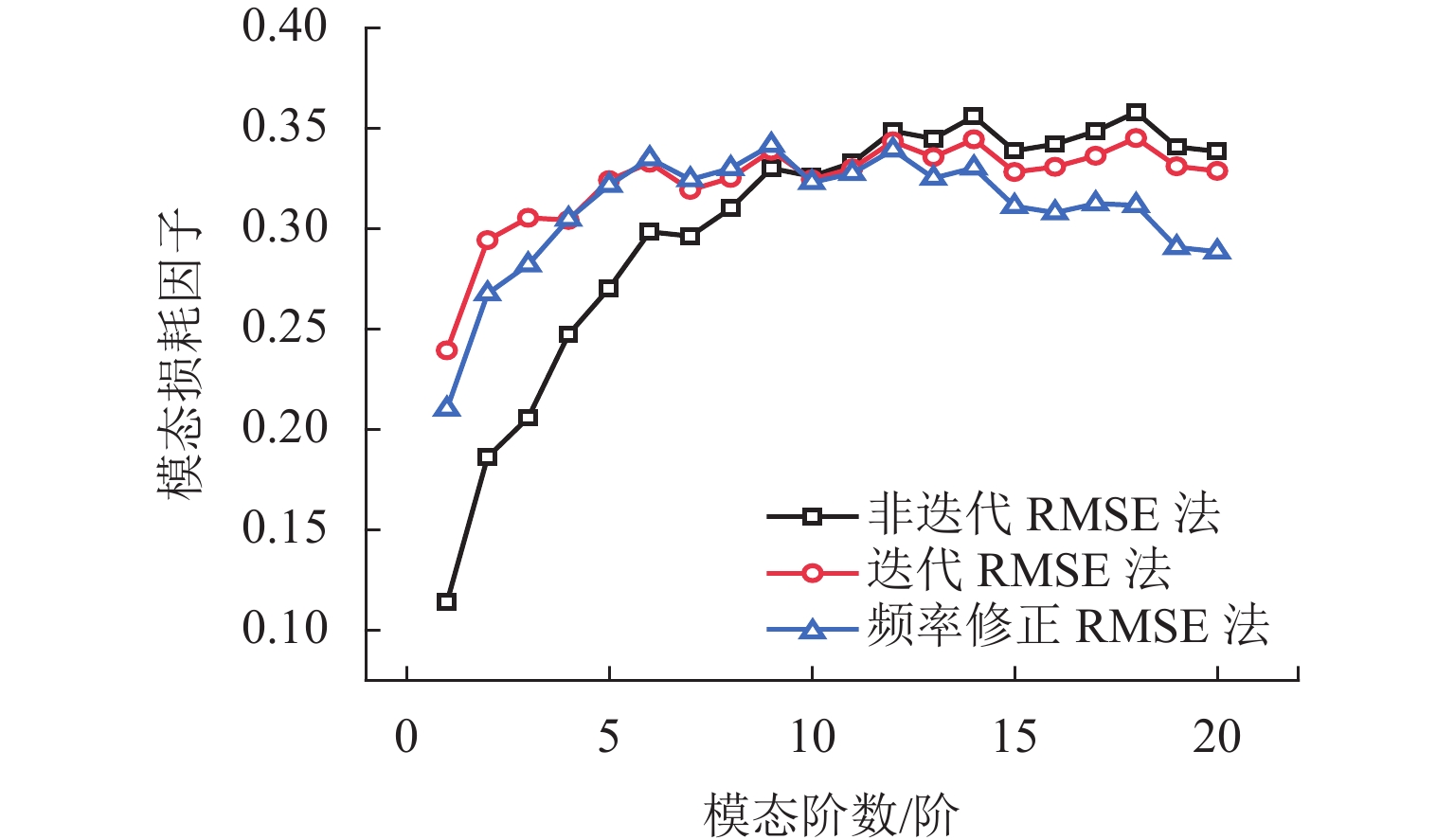
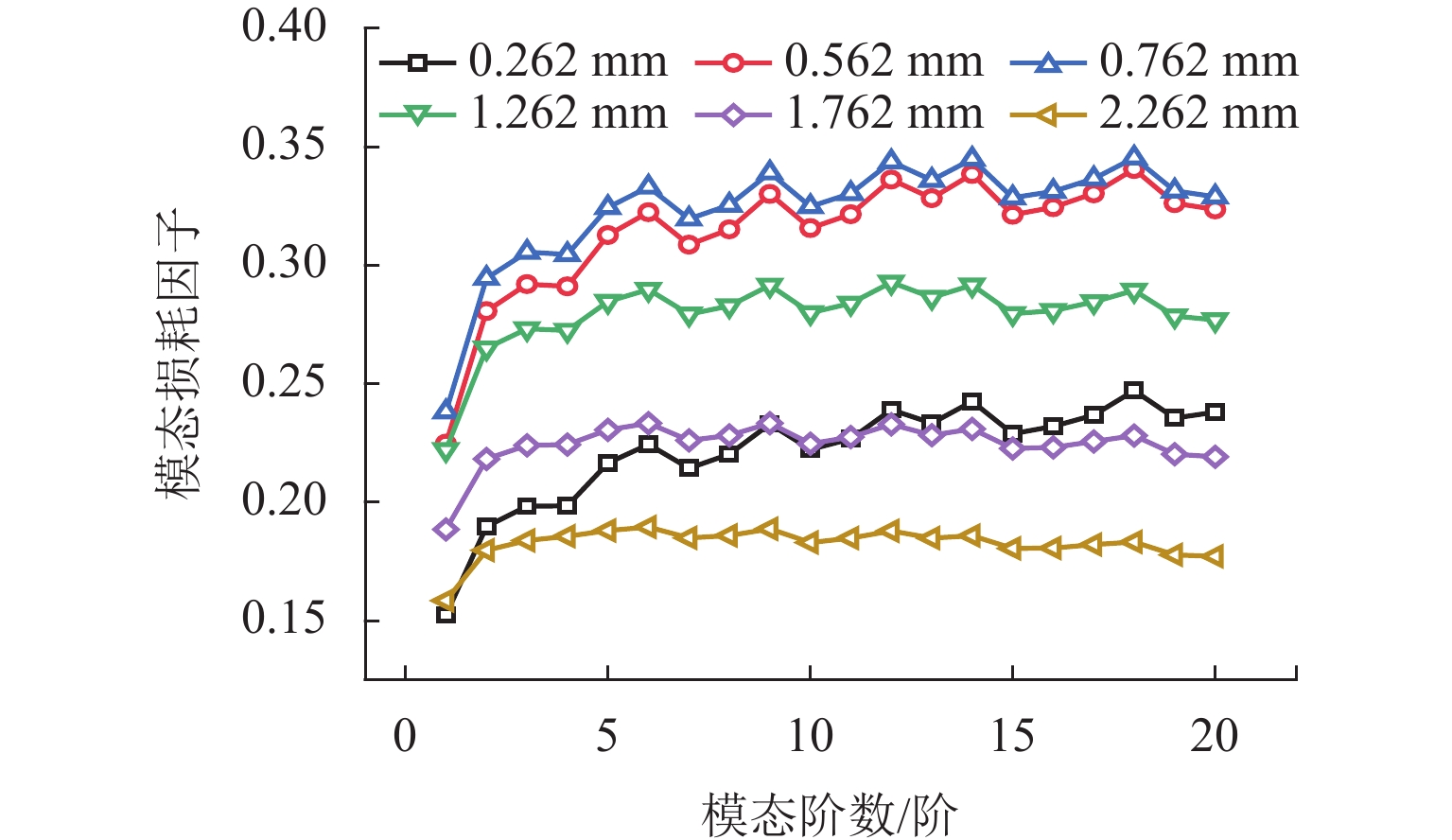
忽略约束阻尼结构阻尼层黏弹性材料虚刚度及参数频变特性会对计算该结构模态损耗因子带来误差. 本文在修正模态应变能法（RMSE法）的基础上，结合迭代算法，分析了黏弹性材料虚刚度及参数频变特性对约束阻尼板的振型、固有频率和模态损耗因子的影响，探讨了约束阻尼板阻尼层厚度和约束层厚度对结构模态损耗因子的影响规律. 分析结果表明：本文方法计算的固有频率和模态损耗因子与相关文献中的试验实测值吻合良好；不考虑黏弹性材料参数频变特性，各阶模态振型形状基本不变，但部分振型的相位相反；阻尼层剪切模量直接影响到结构固有频率，忽略其频变特性会导致在低阶时计算结果偏大17.2%，高阶时偏小7.6%；低阶模态时，忽略黏弹性材料频变特性的模态损耗因子误差最大可到56.0%；约束阻尼板模态损耗因子随阻尼层厚度增加而增大，随约束层厚度增加先增大后减小.
Abstract:The neglect of the imaginary stiffness and frequency-dependent characteristic of parameters of viscoelastic materials for the damping layer of the constrained damping structure will result in the error of the modal loss factor of the structure. The influence of the imaginary stiffness and frequency-dependent characteristic of parameters of viscoelastic materials on the modes of vibration, natural frequencies, and modal loss factors of the constrained damping plate was investigated by using the revised modal strain energy (RMSE) method and iterative algorithm. Moreover, the influence of the thickness of the damping layer and that of the constrained layer of the constrained damping plate on the modal loss factor of the structure was discussed. The results show that the natural frequency and modal loss factor calculated by the method in the paper are in good agreement with the experimentally measured values in the related literature. The modal shapes at all orders are not changed, but a reversal of the phase of several modes of vibration occurs if the frequency-dependent characteristic of parameters of viscoelastic materials is ignored. The shear modulus of the damping layer directly affects the natural frequency of the structure. If the frequency-dependent characteristic is ignored, the calculation results will be overestimated by 17.2% at the lower-order modal and underestimated by 7.6% at the higher-order modal. The maximum error of the modal loss factor is up to 56.0% at lower order modal when the frequency-dependent characteristic of the viscoelastic material is ignored. The modal loss factor of the constrained damping plate increases with the damping layer thickness and first goes up and then goes down with the constrained layer thickness.
-
Key words:
- constrained damping plate /
- iterative method /
- natural frequency /
- mode of vibration /
- modal loss factor
-
图 2 ISD-112阻尼材料频变特性
Figure 2. Frequency-dependent characteristics of damping material ISD-112
图 4 迭代前后各阶固有频率对比
Figure 4. Comparison of intrinsic frequencies before and after iteration
图 6 不同阻尼层厚度下CLD板模态损耗因子
Figure 6. Modal loss factors of CLD plate under various thicknesses of damping layer
图 7 不同约束层厚度下CLD板模态损耗因子
Figure 7. Modal loss factors of CLD plate under various thicknesses of constraint layer
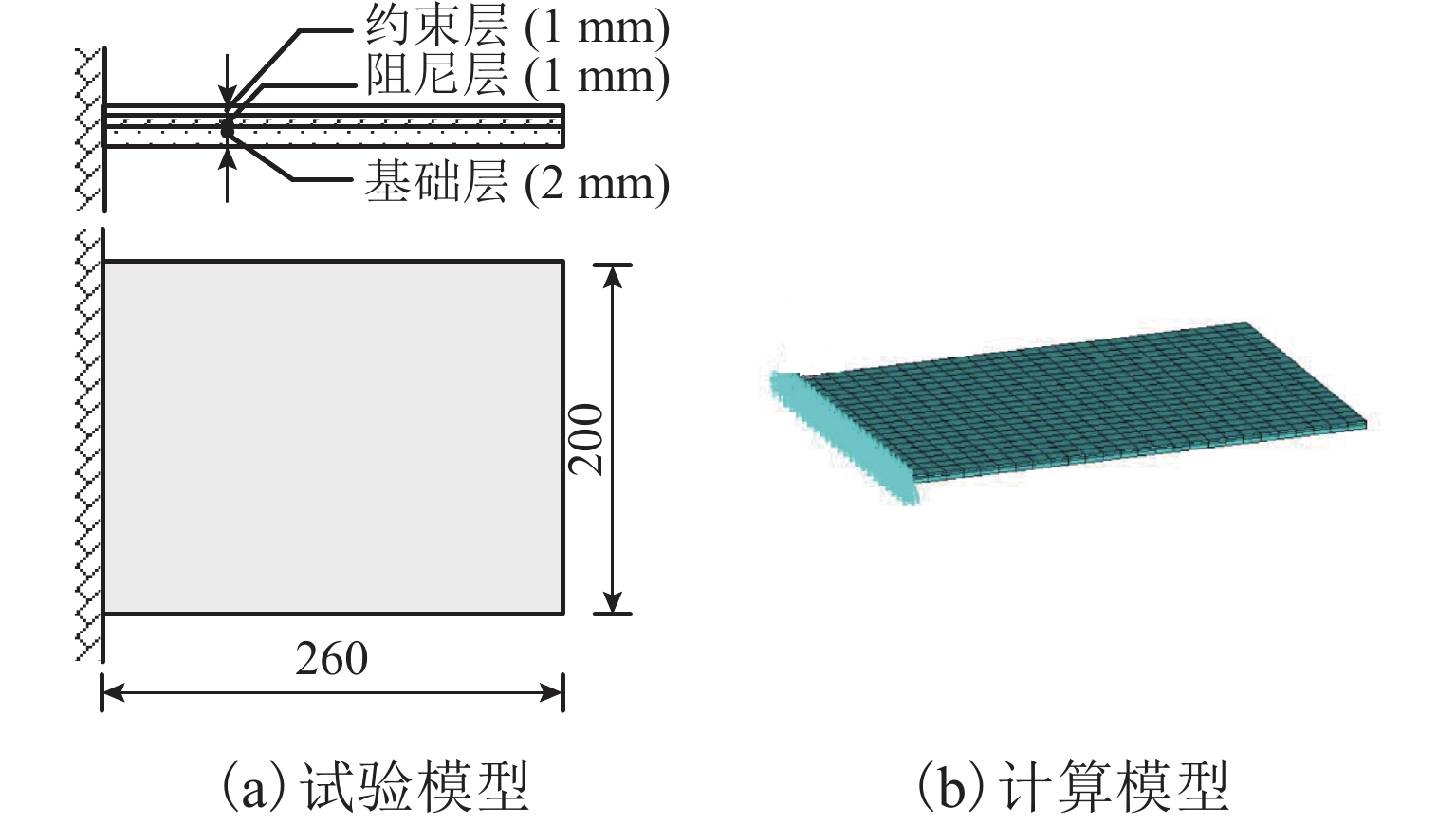
表 1 文献[23]模型参数
Table 1. Model parameters in reference [23]
项目 长度/
mm宽度/
mm厚度/
mm密度/
（kg•m−3）泊松比 基层 260 200 2 2800 0.33 阻尼层 260 200 1 999 0.49 约束层 260 200 1 2800 0.33 
下载: 导出CSV
表 2 试验与计算结果比较
Table 2. Comparison of experimental and calculated results
阶数 固有频率/Hz 模态损耗因子 试验
结果RMSE
迭代MSE
迭代试验
结果RMSE
迭代MSE
迭代1 23.1 24.0 24.0 0.21 0.15 0.15 2 90.6 86.6 80.2 0.28 0.29 0.37 3 191.9 187.4 170.6 0.31 0.31 0.44
下载: 导出CSV
表 3 模型参数
Table 3. Model parameters
项目 长度/
m宽度/
m厚度/
mm密度/
（kg•m−3）泊松比 基层 0.348 0.3048 0.762 2735 0.30 阻尼层 0.348 0.3048 0.254 1300 0.49 约束层 0.348 0.3048 0.762 2735 0.30
下载: 导出CSV
-
[1] 任志刚,卢哲安,楼梦麟. 复合夹层结构频率及损耗因子的计算[J]. 地震工程与工程振动,2004,24(2): 101-106. doi: 10.3969/j.issn.1000-1301.2004.02.018REN Zhigang, LU Zhean, LOU Menglin. Calculation of frequency and loss factor of composite sandwich structures[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(2): 101-106. doi: 10.3969/j.issn.1000-1301.2004.02.018 [2] 韦凯,赵泽明,王显,等. 浮置板轨道减振垫的刚度测试与评价[J]. 西南交通大学学报,2022,57(4): 848-854,925. doi: 10.3969/j.issn.0258-2724.20200190WEI Kai, ZHAO Zeming, WANG Xian, et al. Stiffness test and evaluation method of floating slab track damping pad[J]. Journal of Southwest Jiaotong University, 2022, 57(4): 848-854,925. doi: 10.3969/j.issn.0258-2724.20200190 [3] 赵才友,王平. 新型交叉式静音钢轨的理论与试验研究[J]. 西南交通大学学报,2013,48(2): 290-296. doi: 10.3969/j.issn.0258-2724.2013.02.016ZHAO Caiyou, WANG Ping. Theoretical analysis and experimental investigation on cross-legged silent rail[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 290-296. doi: 10.3969/j.issn.0258-2724.2013.02.016 [4] 冯梓鑫,韩峰,冯盟,等. 约束层阻尼对飞机壁板隔声特性的影响[J]. 噪声与振动控制,2016,36(3): 76-80.FENG Zixin, HAN Feng, FENG Meng, et al. Effects of constrained layer damping patches on the sound insulation characteristics of aircraft panels[J]. Noise and Vibration Control, 2016, 36(3): 76-80. [5] 戴光泽,夏燕,荒木荣敏. 粘弹性体的耗散效应与发展方程的系数矩阵[J]. 西南交通大学学报,2001,36(6): 604-608. doi: 10.3969/j.issn.0258-2724.2001.06.012DAI Guangze, XIA Yan, ARAKI Shigetoshi. Coefficient matrices of evolution equation and the dissipation effect of viscoelastic medium[J]. Journal of Southwest Jiaotong University, 2001, 36(6): 604-608. doi: 10.3969/j.issn.0258-2724.2001.06.012 [6] 宗福开. 带约束粘弹性阻尼层结构的动态模型[J]. 江苏化工学院学报,1989,1(3): 43-53.ZONG Fukai. Dynamical models of the structures with constrained viscoclastic damped layers[J]. Journal of Jiangsu Polytechnic University, 1989, 1(3): 43-53. [7] 王攀,鲁俊,邓兆祥,等. SCLD板模态控制模型及振动控制[J]. 西南交通大学学报,2015,50(4): 717-724. doi: 10.3969/j.issn.0258-2724.2015.04.022WANG Pan, LU Jun, DENG Zhaoxiang, et al. Modal control model and vibration control of SCLD plate[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 717-724. doi: 10.3969/j.issn.0258-2724.2015.04.022 [8] LUO H T, GUO S W, YU C S, et al. Vibration suppression analysis and experimental test of additional constrained damping layer in space science experiment cabinet[J]. Composites and Advanced Materials, 2021, 30: 2633366X2097865.1-2633366X2097865.12. [9] KERWIN E M Jr. Damping of flexural waves by a constrained viscoelastic layer[J]. The Journal of the Acoustical Society of America, 1959, 31(7): 952-962. doi: 10.1121/1.1907821 [10] 王金朝,王志强,徐宁,等. 约束阻尼板结构模态实验及阻尼特性研究[J]. 噪声与振动控制,2018,38(6): 205-208. doi: 10.3969/j.issn.1006-1355.2018.06.039WANG Jinzhao, WANG Zhiqiang, XU Ning, et al. Modal experiment and damping characteristics analysis of constrained damping plates[J]. Noise and Vibration Control, 2018, 38(6): 205-208. doi: 10.3969/j.issn.1006-1355.2018.06.039 [11] 郭中泽,罗景润,陈裕泽. 约束阻尼结构的模态损耗因子计算的一种修正方法[J]. 兵工学报,2006,27(6): 1064-1067. doi: 10.3321/j.issn:1000-1093.2006.06.025GUO Zhongze, LUO Jingrun, CHEN Yuze. An improved method of predicting the modal loss factors of constrained damping structure[J]. Acta Armamentarii, 2006, 27(6): 1064-1067. doi: 10.3321/j.issn:1000-1093.2006.06.025 [12] JOHNSON C D, KIENHOLZ D A. Finite element prediction of damping in structures with constrained viscoelastic layers[J]. AIAA Journal, 1982, 20(9): 1284-1290. doi: 10.2514/3.51190 [13] REN S H, ZHAO G Z. A four-node quadrilateral element for vibration and damping analysis of sandwich plates with viscoelastic core[J]. Journal of Sandwich Structures & Materials, 2019, 21(3): 1072-1118. [14] RAO V S, SANKAR B V, SUN C T. Constrained layer damping of initially stressed composite beams using finite elements[J]. Journal of Composite Materials, 1992, 26(12): 1752-1766. doi: 10.1177/002199839202601204 [15] RAVI S, KUNDRA T K, NAKRA B C. A response re-analysis of damped beams using eigenparameter perturbation[J]. Journal of Sound and Vibration, 1995, 179(3): 399-412. doi: 10.1006/jsvi.1995.0026 [16] PARK C H, BAZ A. Comparison between finite element formulations of active constrained layer damping using classical and layer-wise laminate theory[J]. Finite Elements in Analysis and Design, 2001, 37(1): 35-56. doi: 10.1016/S0168-874X(00)00017-2 [17] 王正兴,代会军. 粘弹性阻尼材料在板结构中的优化计算[J]. 噪声与振动控制,2000,20(6): 18-21,30. doi: 10.3969/j.issn.1006-1355.2000.06.004WANG Zhengxing, DAI Huijun. An optimized computation for damping-elastic plank structure[J]. Noise and Vibration Control, 2000, 20(6): 18-21,30. doi: 10.3969/j.issn.1006-1355.2000.06.004 [18] 刘全民,李小珍,刘林芽,等. 铁路钢板结合梁桥约束阻尼层减振降噪分析[J]. 中国科学:技术科学,2018,48(12): 1392-1400. doi: 10.1360/N092018-00361LIU Quanmin, LI Xiaozhen, LIU Linya, et al. Vibration and noise mitigation analysis of railway steel-concrete composite bridge using constrained layer damping[J]. Scientia Sinica (Technologica), 2018, 48(12): 1392-1400. doi: 10.1360/N092018-00361 [19] 刘天雄,华宏星,陈兆能,等. 约束层阻尼板的有限元建模研究[J]. 机械工程学报,2002,38(4): 108-114. doi: 10.3321/j.issn:0577-6686.2002.04.024LIU Tianxiong, HUA Hongxing, CHEN Zhaoneng, et al. Study on the model of finite element of constrained layer damping plate[J]. Chinese Journal of Mechanical Engineering, 2002, 38(4): 108-114. doi: 10.3321/j.issn:0577-6686.2002.04.024 [20] LIU Q M, LI X Z, ZHANG X, et al. Applying constrained layer damping to reduce vibration and noise from a steel-concrete composite bridge: an experimental and numerical investigation[J]. Journal of Sandwich Structures & Materials, 2020, 22(6): 1743-1769. [21] 刘全民, 李小珍, 张迅, 等. 钢桁结合梁桥约束阻尼层减振降噪方法研究[J]. 铁道学报, 2018, 40(12): 130-136.LIU Quanmin, LI Xiaozhen, ZHANG Xun, et al. Study on noise and vibration reduction of steel truss composite bridge using constrained layer damping[J]. Journal of the China Railway Society, 2018, 40(12): 130-136. [22] 李世其,张针粒,朱文革,等. 计算粘弹结构动力学参数的新模态应变能方法[J]. 噪声与振动控制,2011,31(6): 47-52. doi: 10.3969/j.issn.1006-1355-2011.06.011LI Shiqi, ZHANG Zhenli, ZHU Wenge, et al. A new modal strain energy method for analyzing dynamic parameters of viscoelastic structures[J]. Noise and Vibration Control, 2011, 31(6): 47-52. doi: 10.3969/j.issn.1006-1355-2011.06.011 [23] 罗忠,郭思伟,于长帅,等. 考虑频变特性的约束阻尼结构建模与试验研究[J]. 东北大学学报(自然科学版),2021,42(7): 966-971,979. doi: 10.12068/j.issn.1005-3026.2021.07.009LUO Zhong, GUO Siwei, YU Changshuai, et al. Modeling and experimental research of constrained damping structure considering frequency-dependent characteristics[J]. Journal of Northeastern University (Natural Science), 2021, 42(7): 966-971,979. doi: 10.12068/j.issn.1005-3026.2021.07.009 -
下载:
点击查看大图
计量
- 文章访问数: 216
- HTML全文浏览量: 74
- PDF下载量: 25
- 被引次数: 0