寒区隧道阳光棚温升效果与影响

孙克国; 魏勇; 贾敬龙; 孟庆余; 张弛; 秦晋行; 李世斌

doi:10.3969/j.issn.0258-2724.20220398

寒区隧道阳光棚温升效果与影响

doi: 10.3969/j.issn.0258-2724.20220398

1.
西南交通大学土木工程学院，四川成都 610031
2.
中国铁路设计集团有限公司，天津 300308

基金项目: 国家自然科学基金（52178396）

详细信息

作者简介:
孙克国（1981—），男，副教授，博士，博士生导师，研究方向为地下工程施工力学与灾害防治等，E-mail：sunkeg@126.com

中图分类号: U45
计量
- 文章访问数: 322
- HTML全文浏览量: 98
- PDF下载量: 45
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-07
- 修回日期: 2022-08-27
- 网络出版日期: 2023-04-10
- 刊出日期: 2022-09-22

Temperature Rise Effects and Impact of Solar Shed in Cold Region Tunnels

1.
College of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
China Railway Design Corporation, Tianjin 300308, China

摘要

摘要:
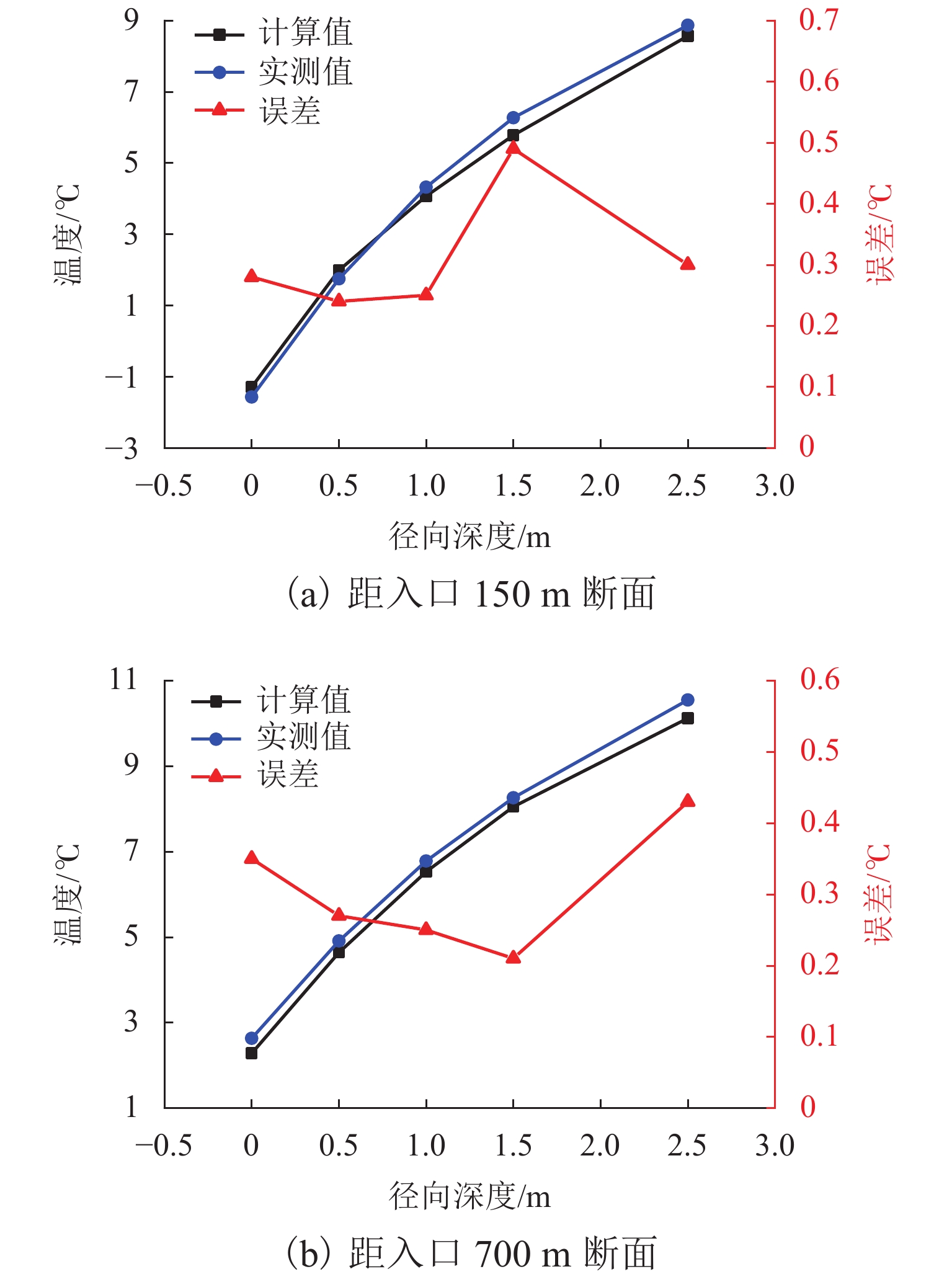
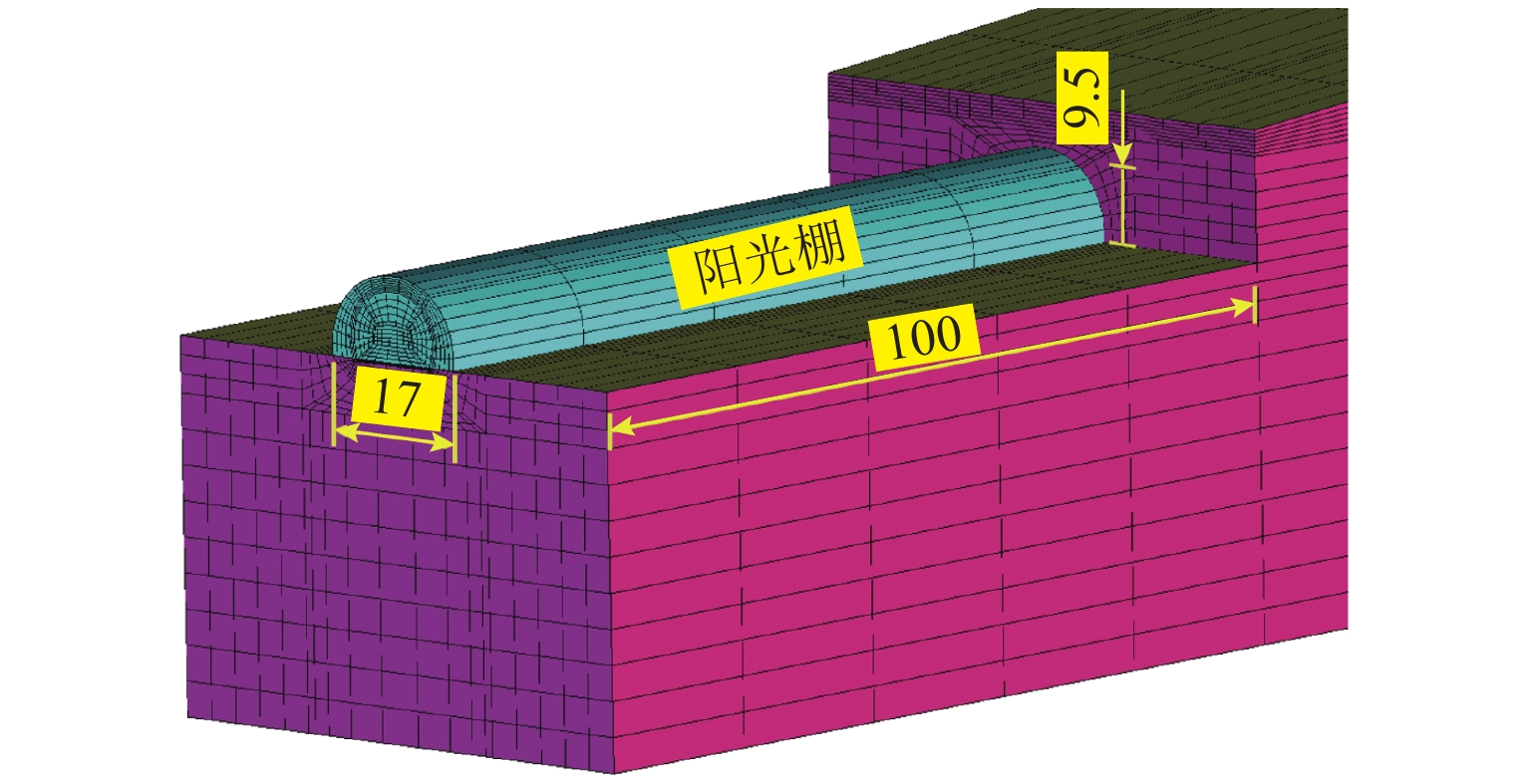
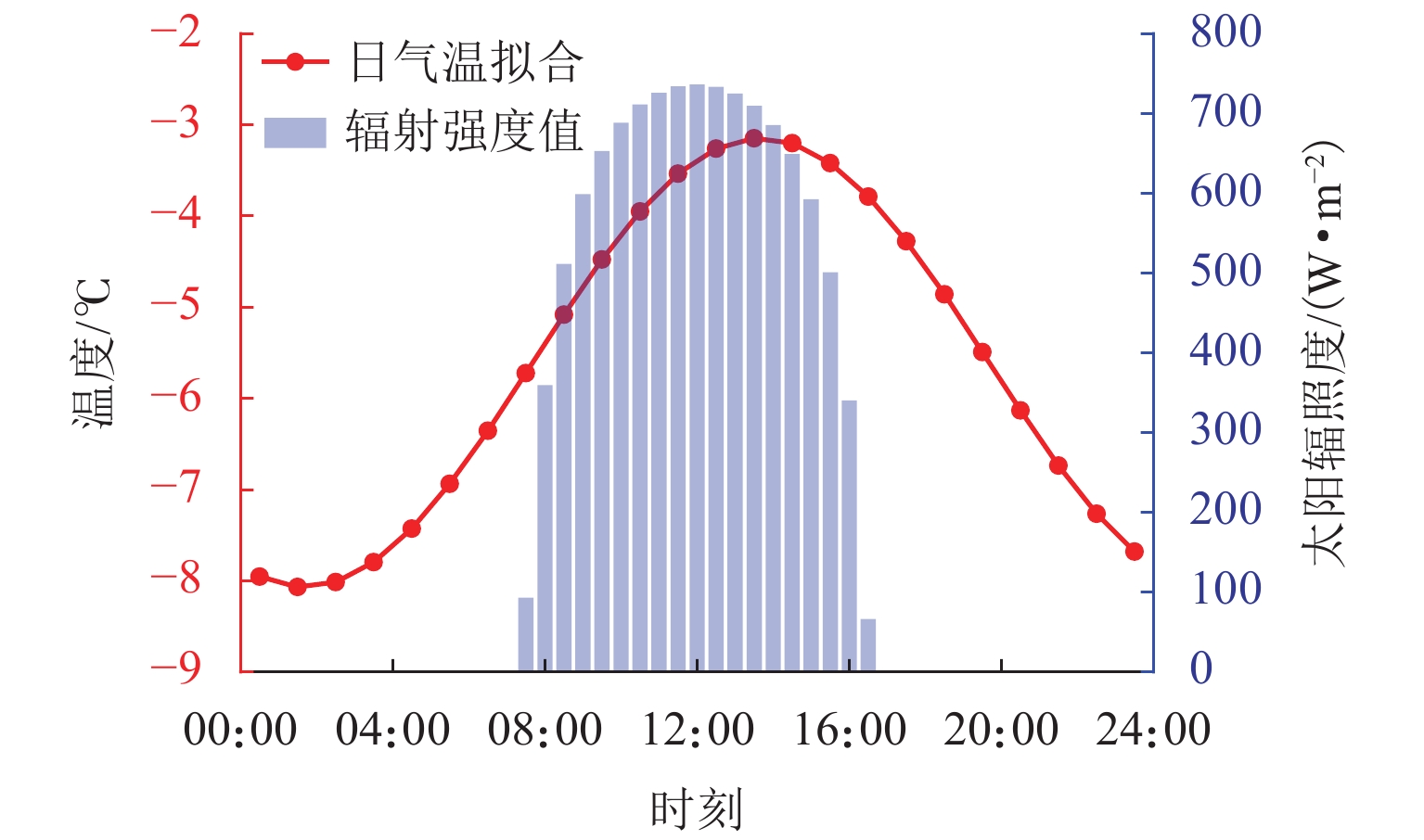
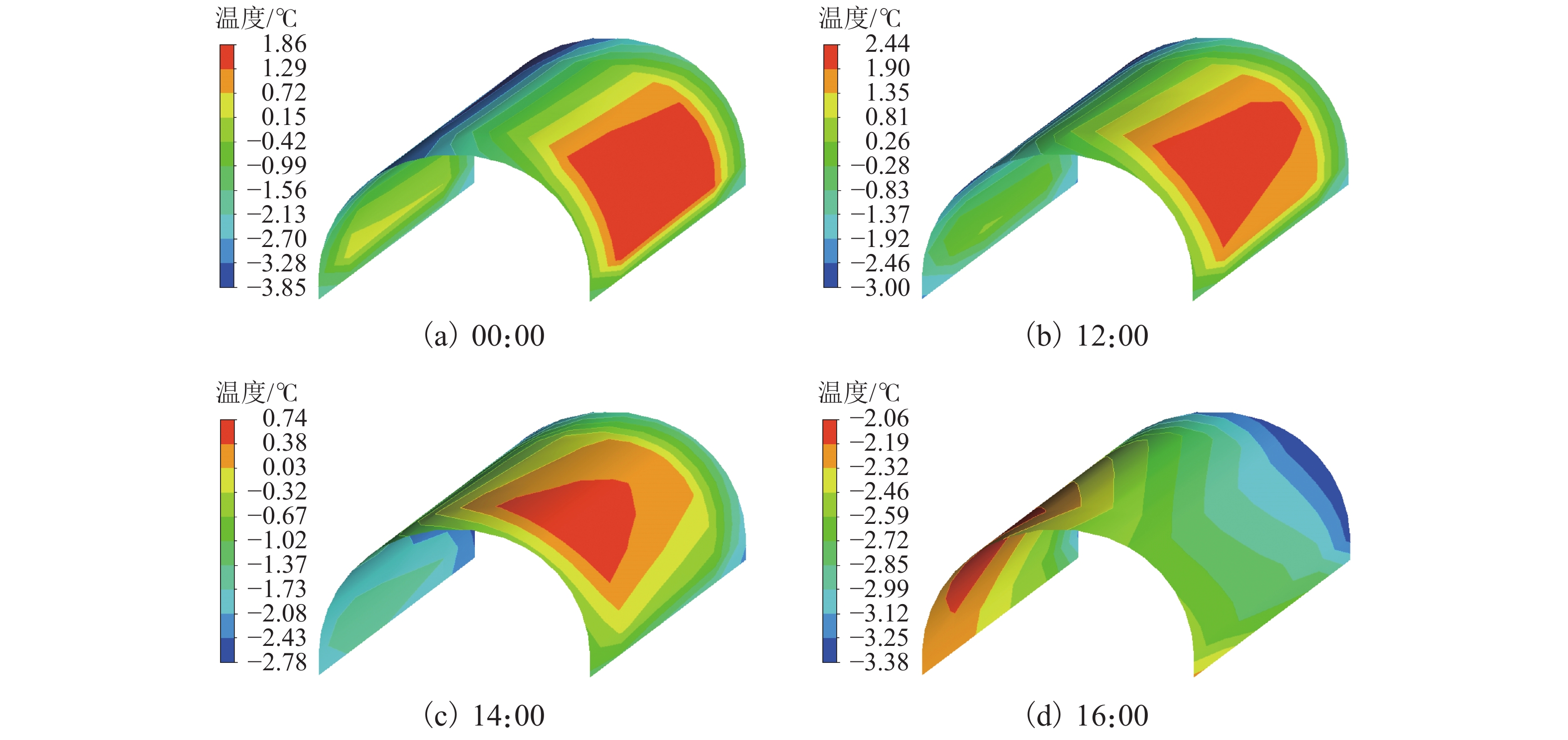
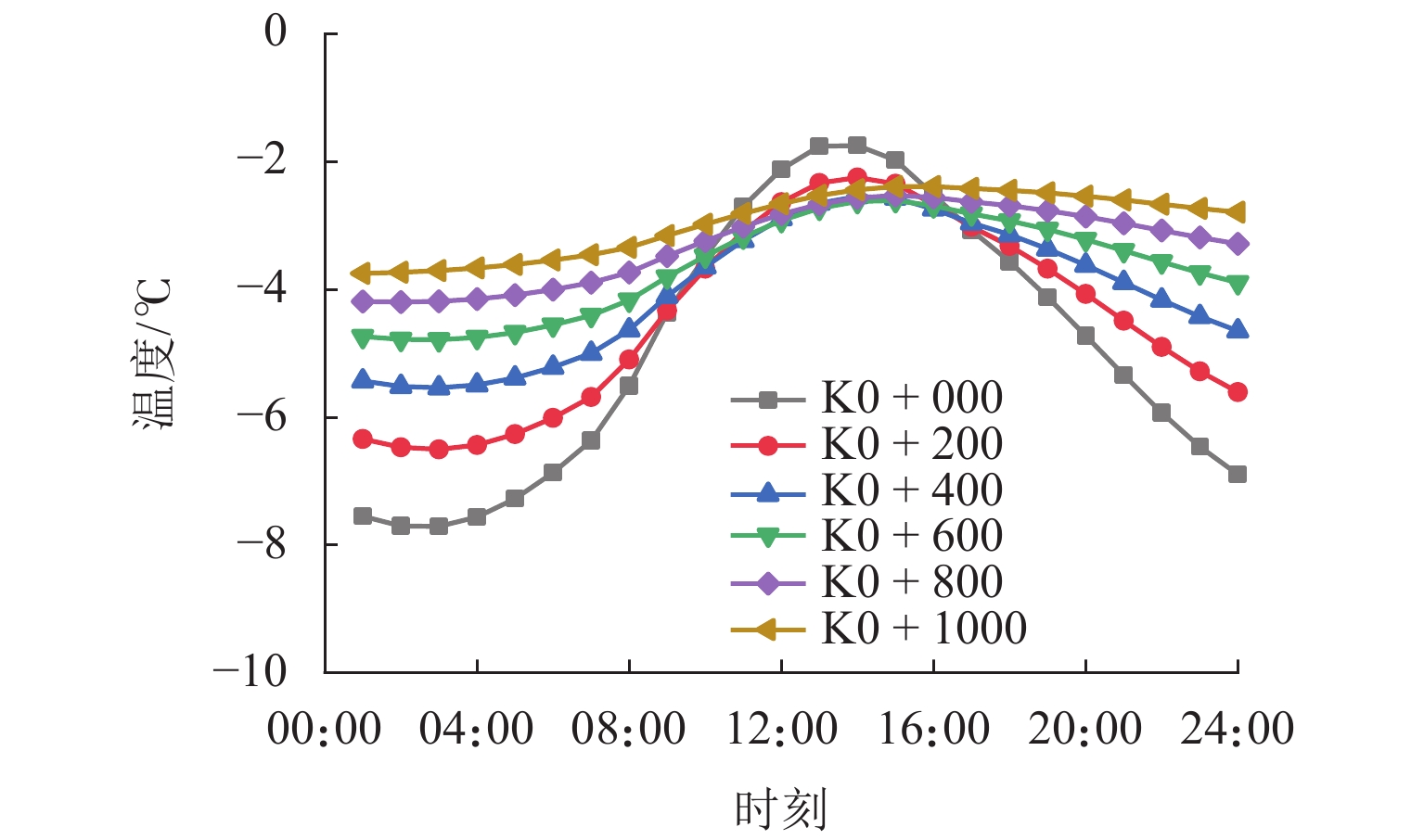
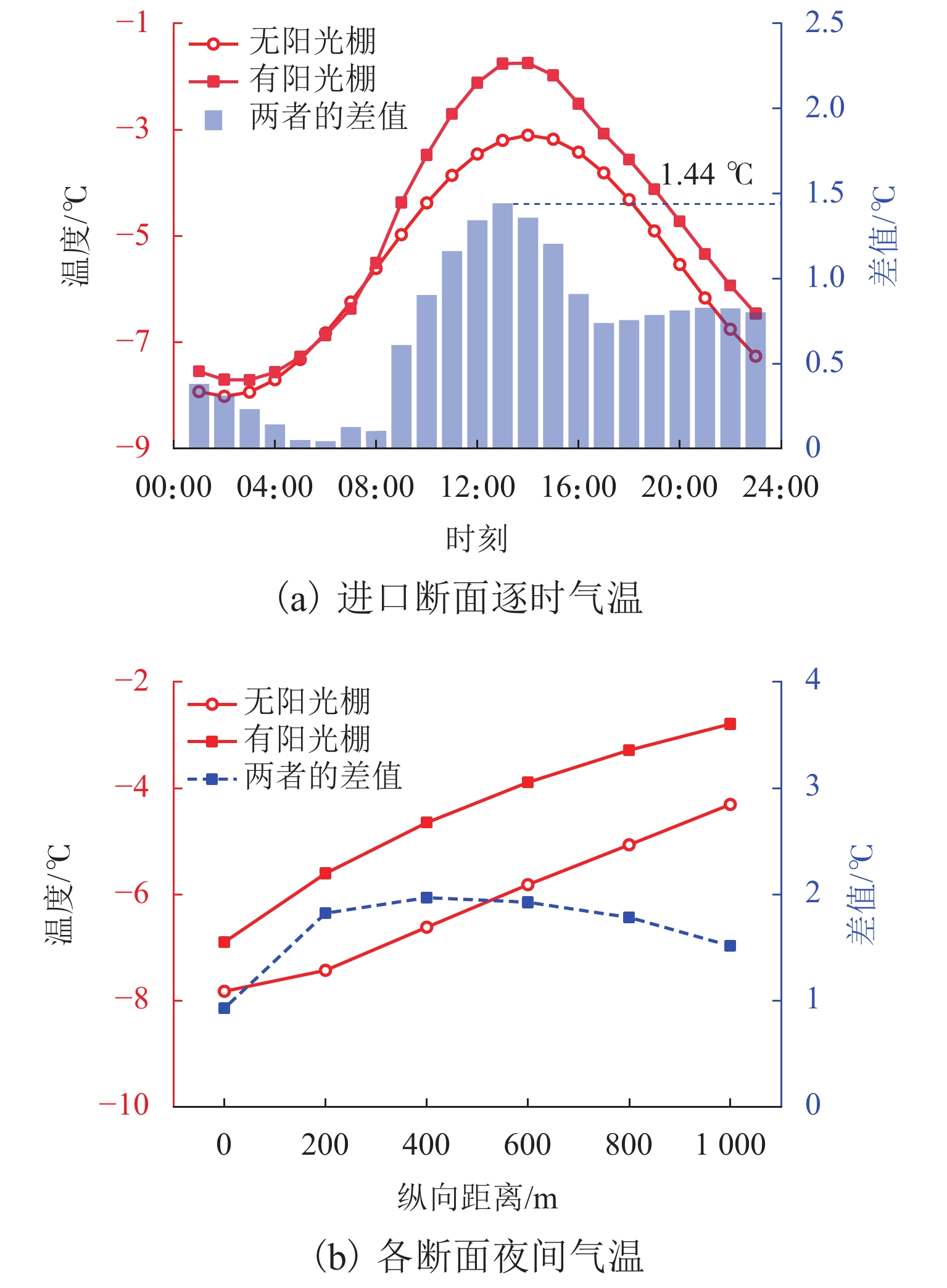
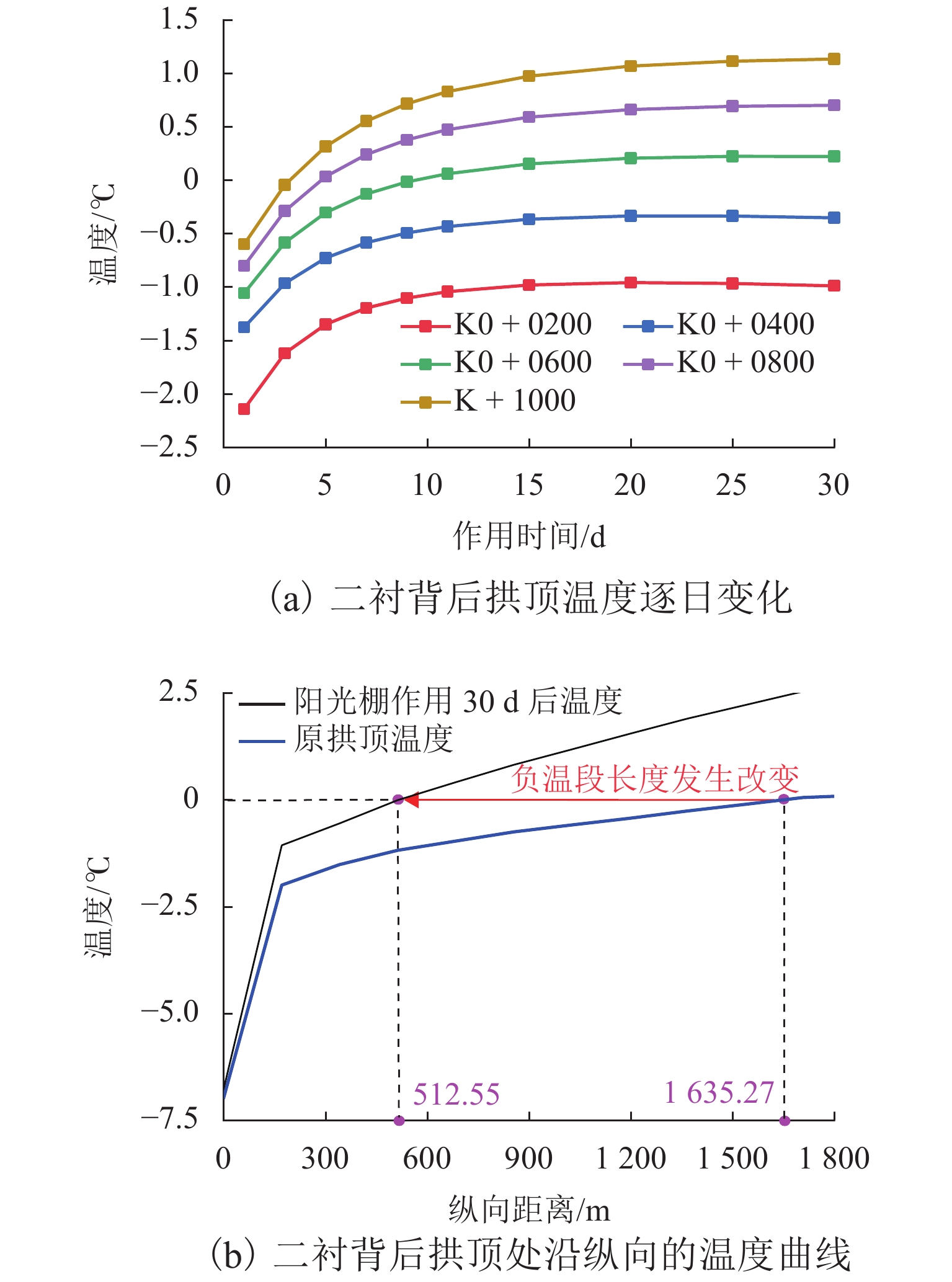
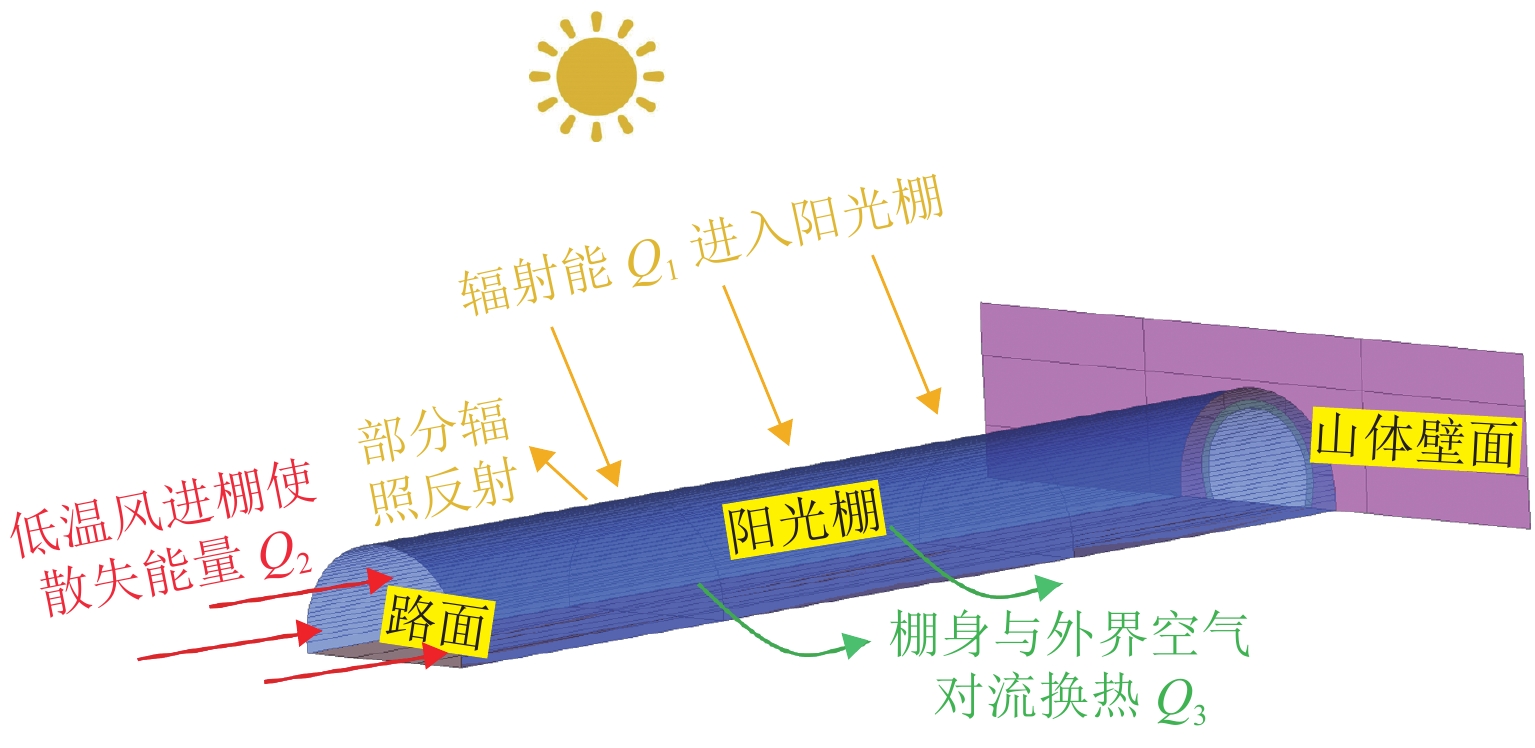
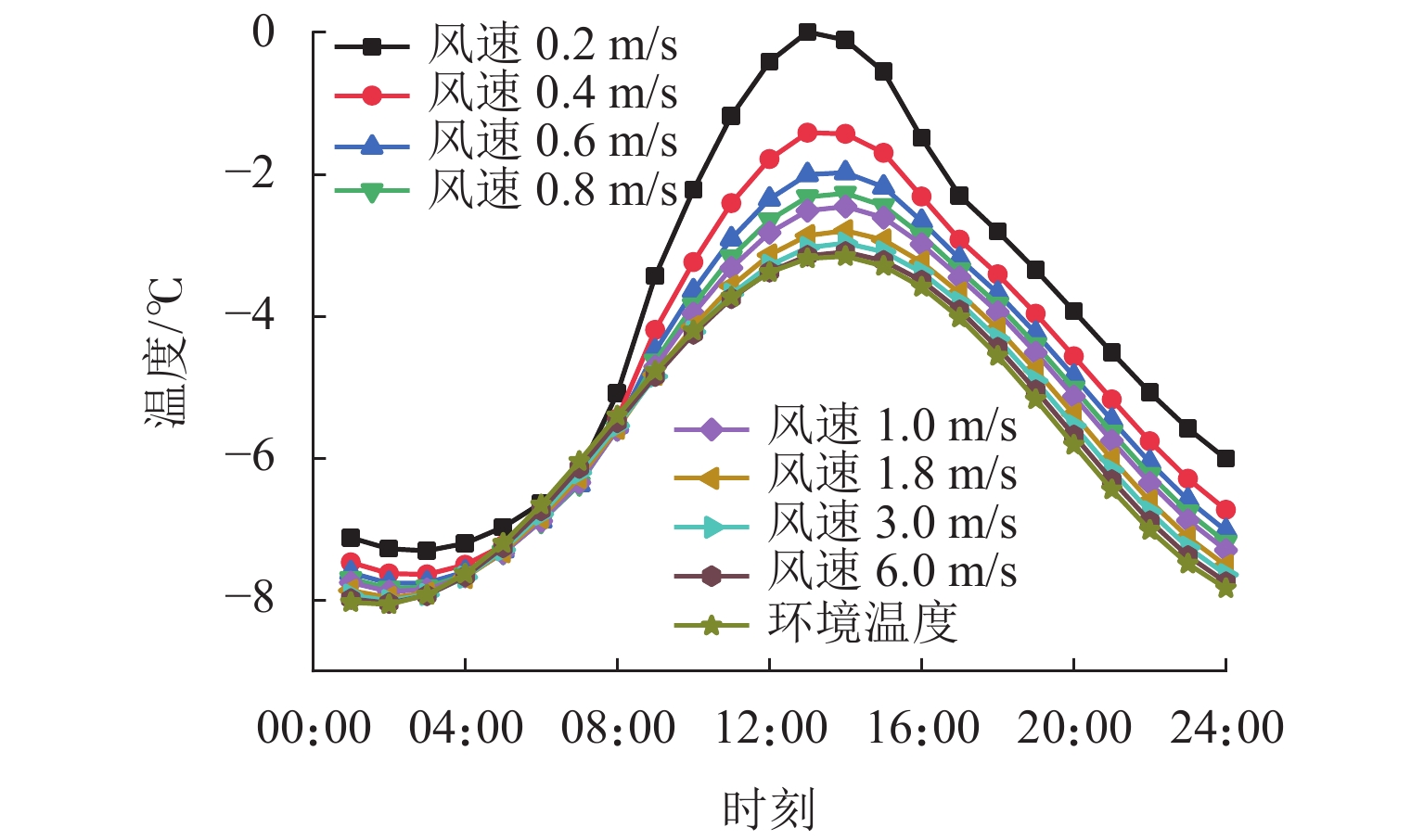
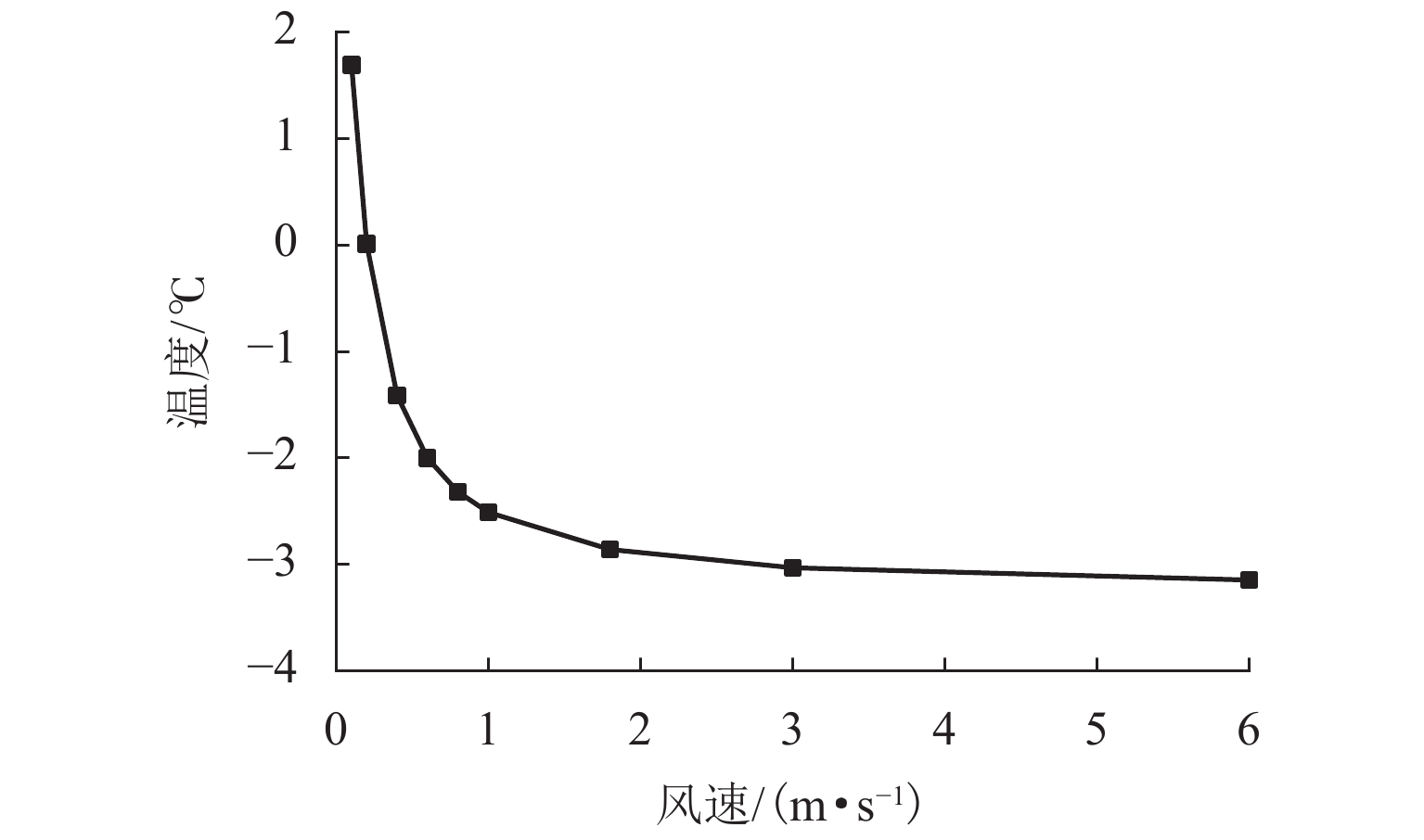
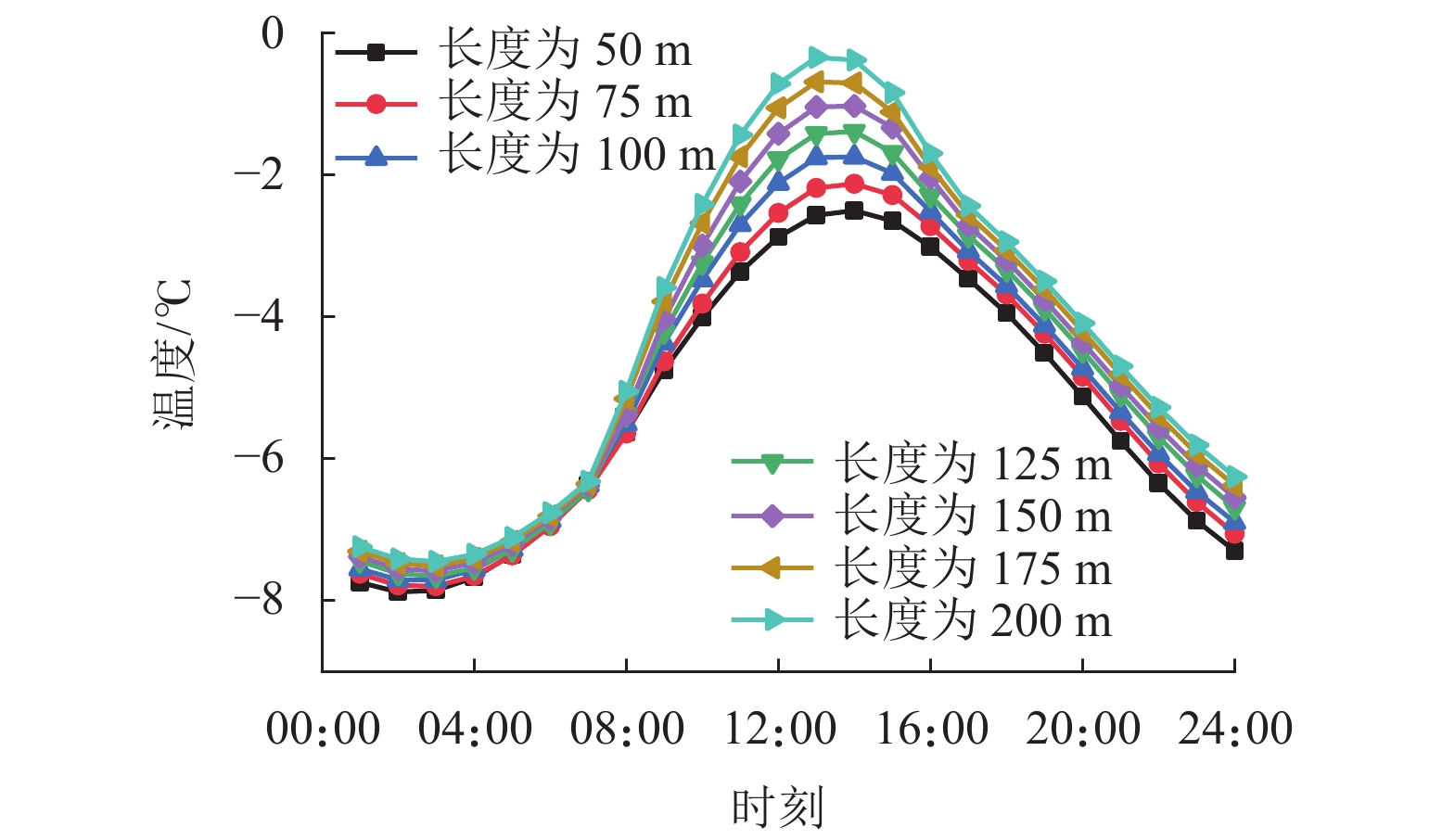
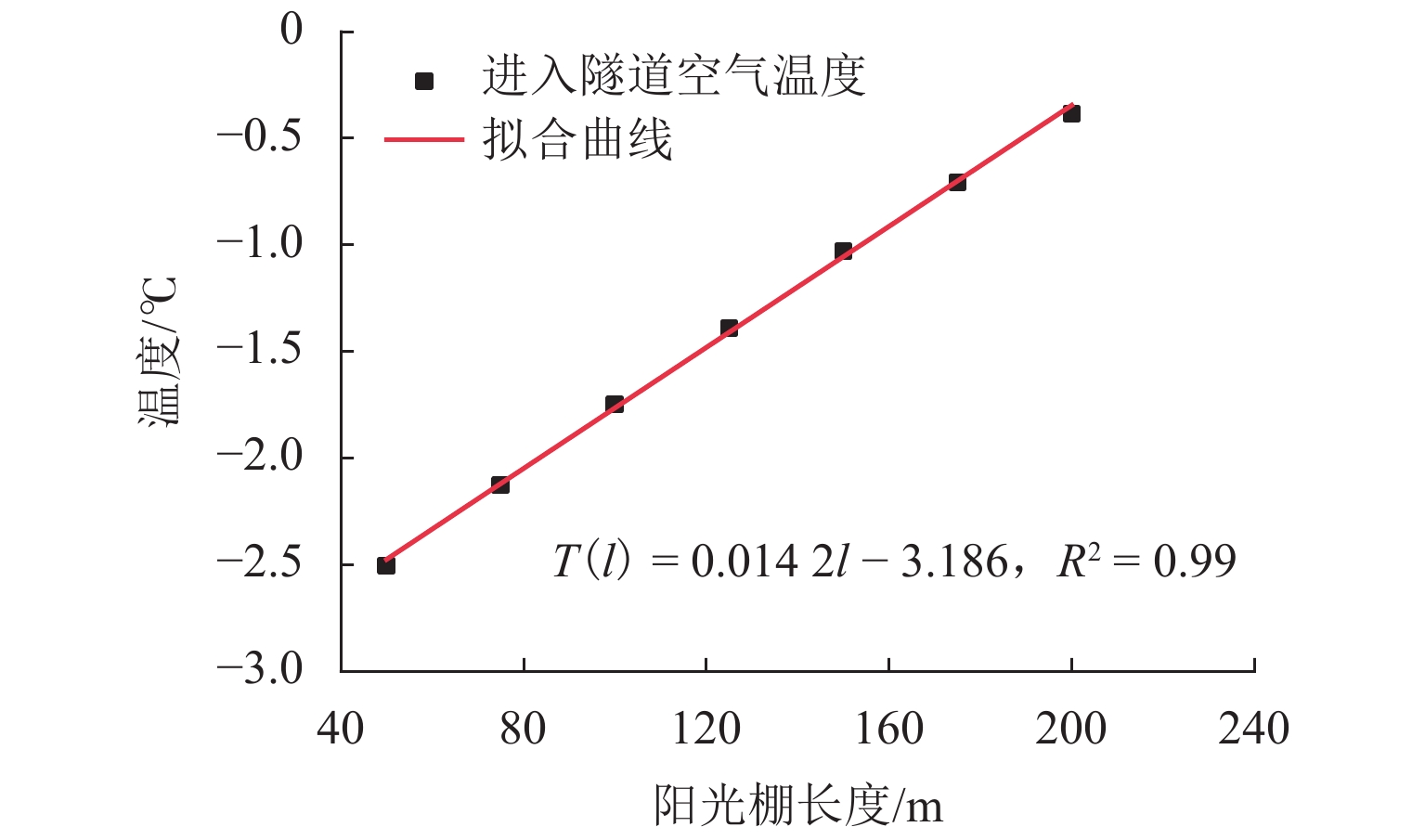
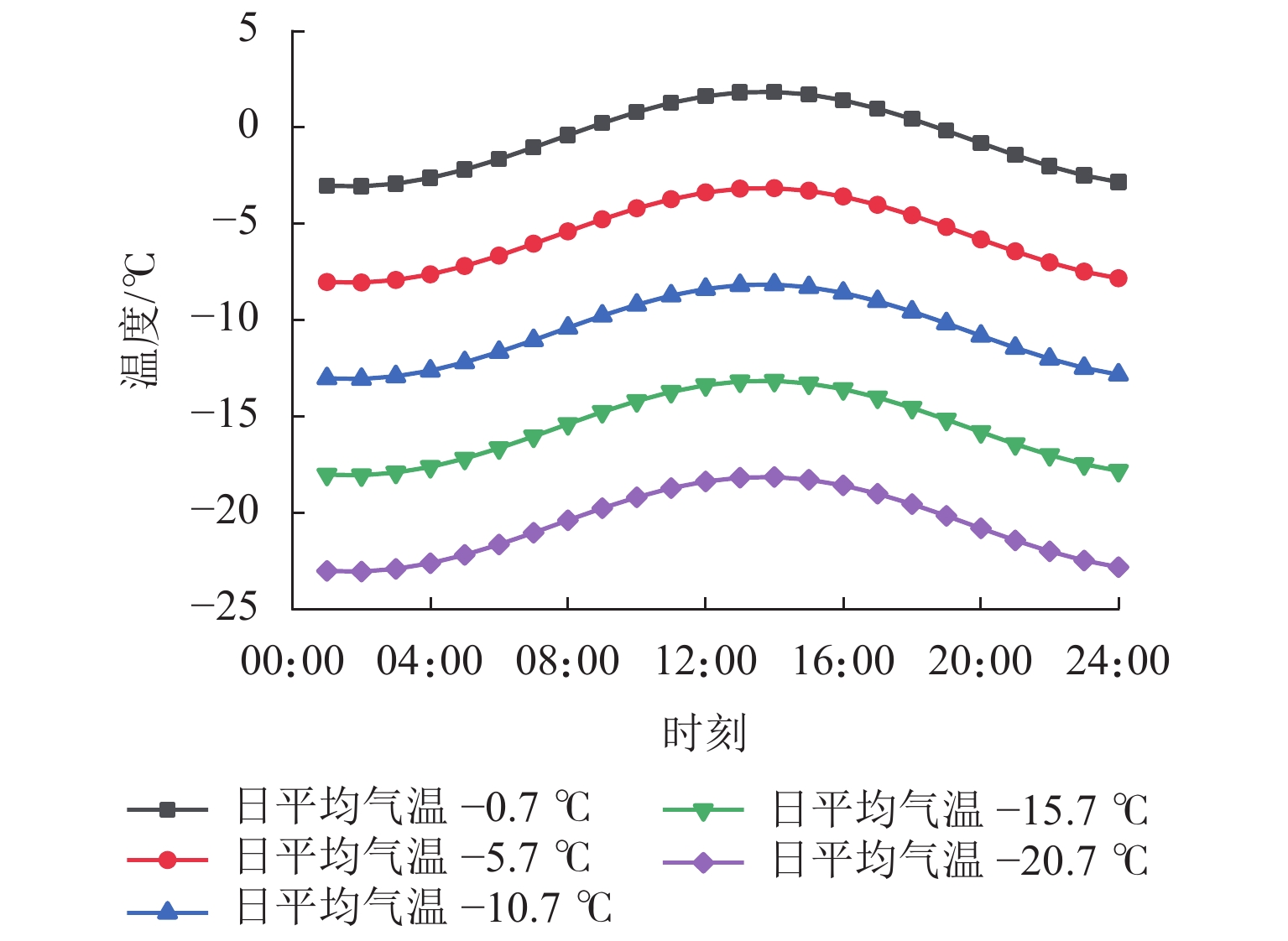
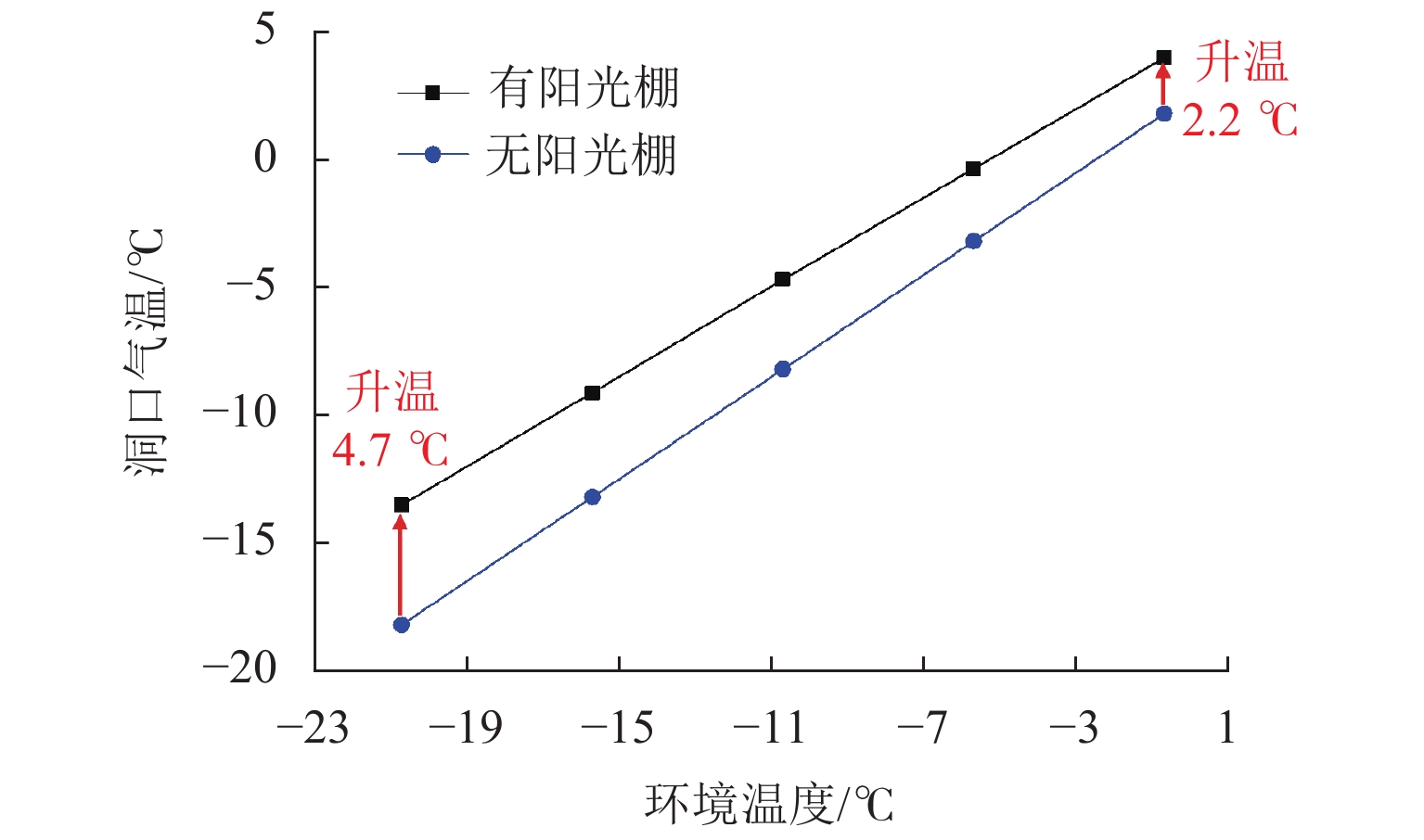
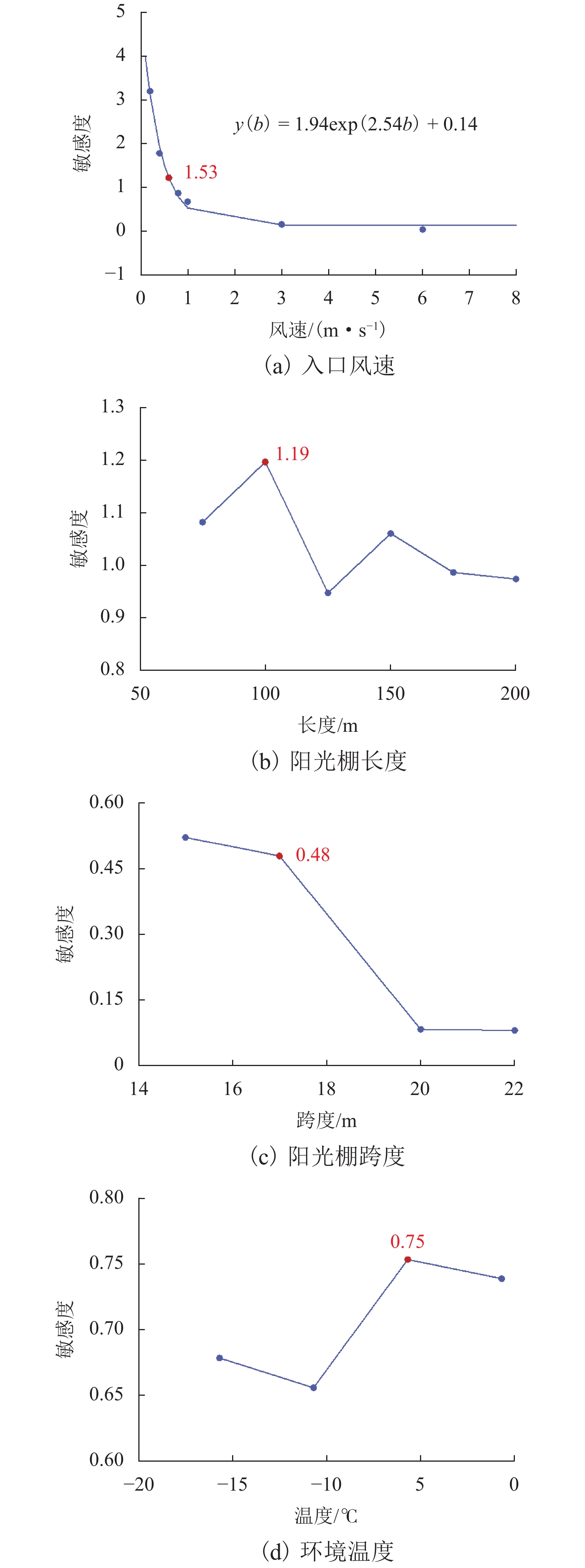
为避免寒区隧道冻害问题产生，引入新型阳光棚防寒措施. 首先，建立三维瞬态传热数值模型，获得自然通风条件下的隧道温度场，并通过现场温度监测验证数值计算模型的可靠性；然后，通过数值方法验证阳光棚的温升效果，并进一步探究阳光棚入口风速、长度、跨度及环境温度对温升效果的影响；最后，对各因素进行敏感性分析，研究其对温升效果的影响程度. 研究结果表明：入口风速低于1.0 m/s时，阳光棚发挥良好的温升效果. 风速与温升效果呈负相关；长度每延长50 m，隧道进口气温升高0.71 ℃；跨度对温升效果的影响不明显；温升效果随环境温度变低而愈显著. 上述因素对温升效果的敏感性排序为：入口风速（0.39） > 长度（0.30） > 环境温度（0.19） > 跨度（0.12），其中，入口风速为最敏感因素，应用时应着重考虑. 因此，对阳光棚的使用建议为：低风速、大长度、小跨度.
- 寒区隧道 /
- 冻害问题 /
- 阳光棚 /
- 温升效果 /
- 敏感性分析
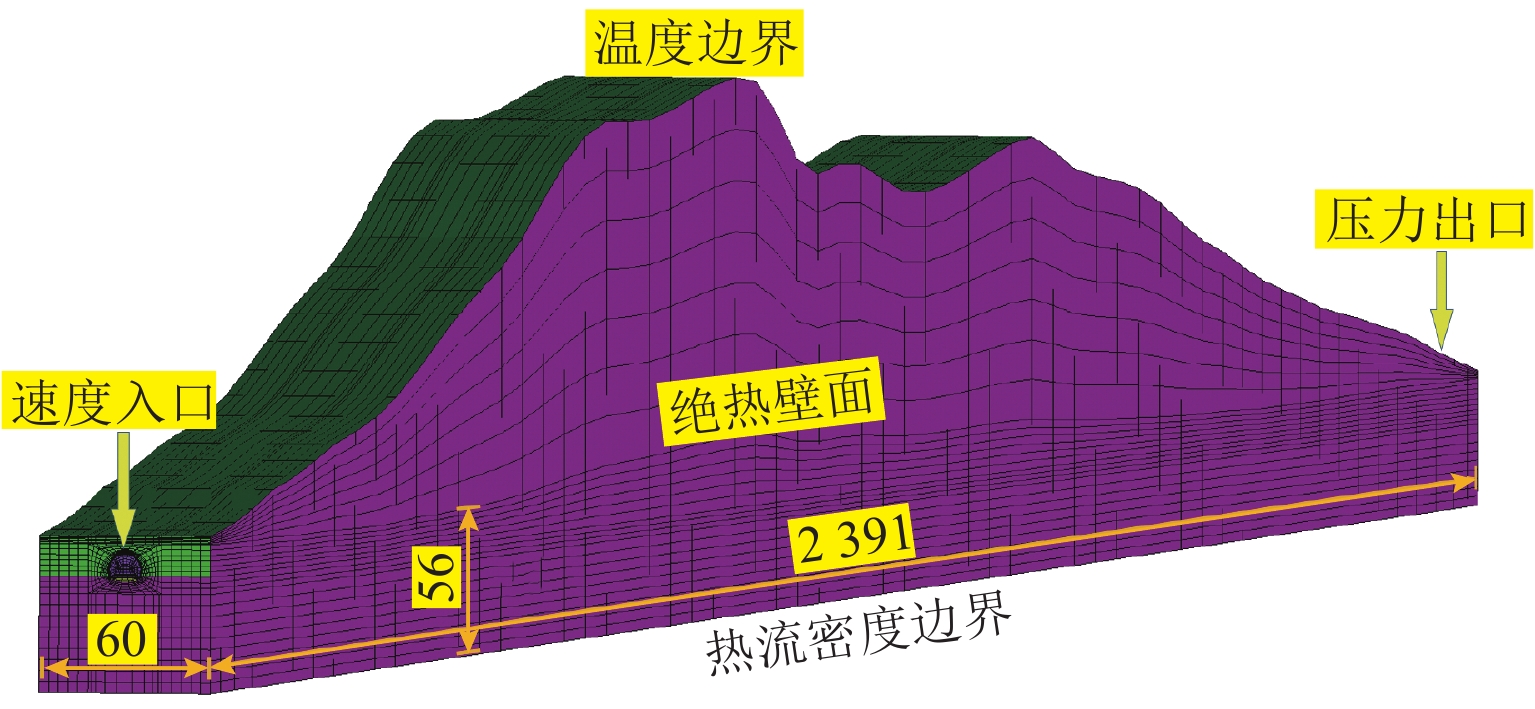
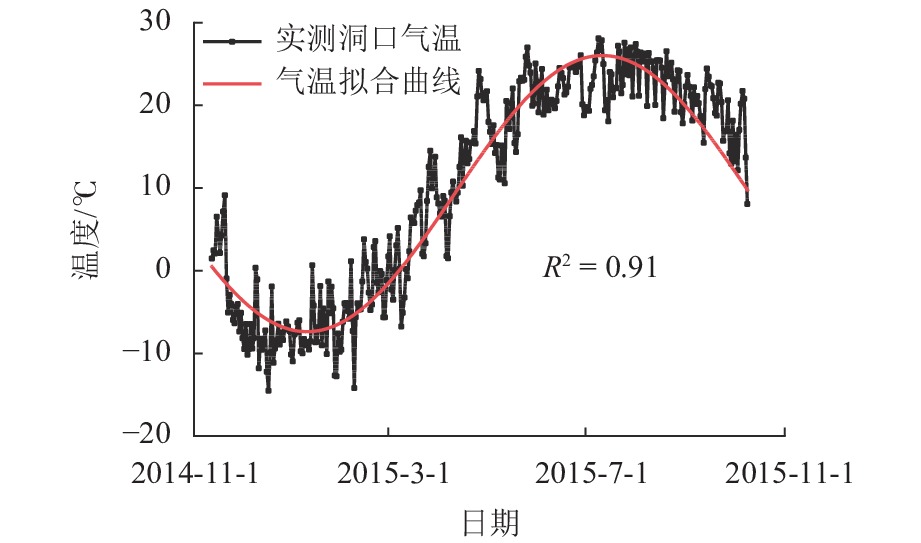
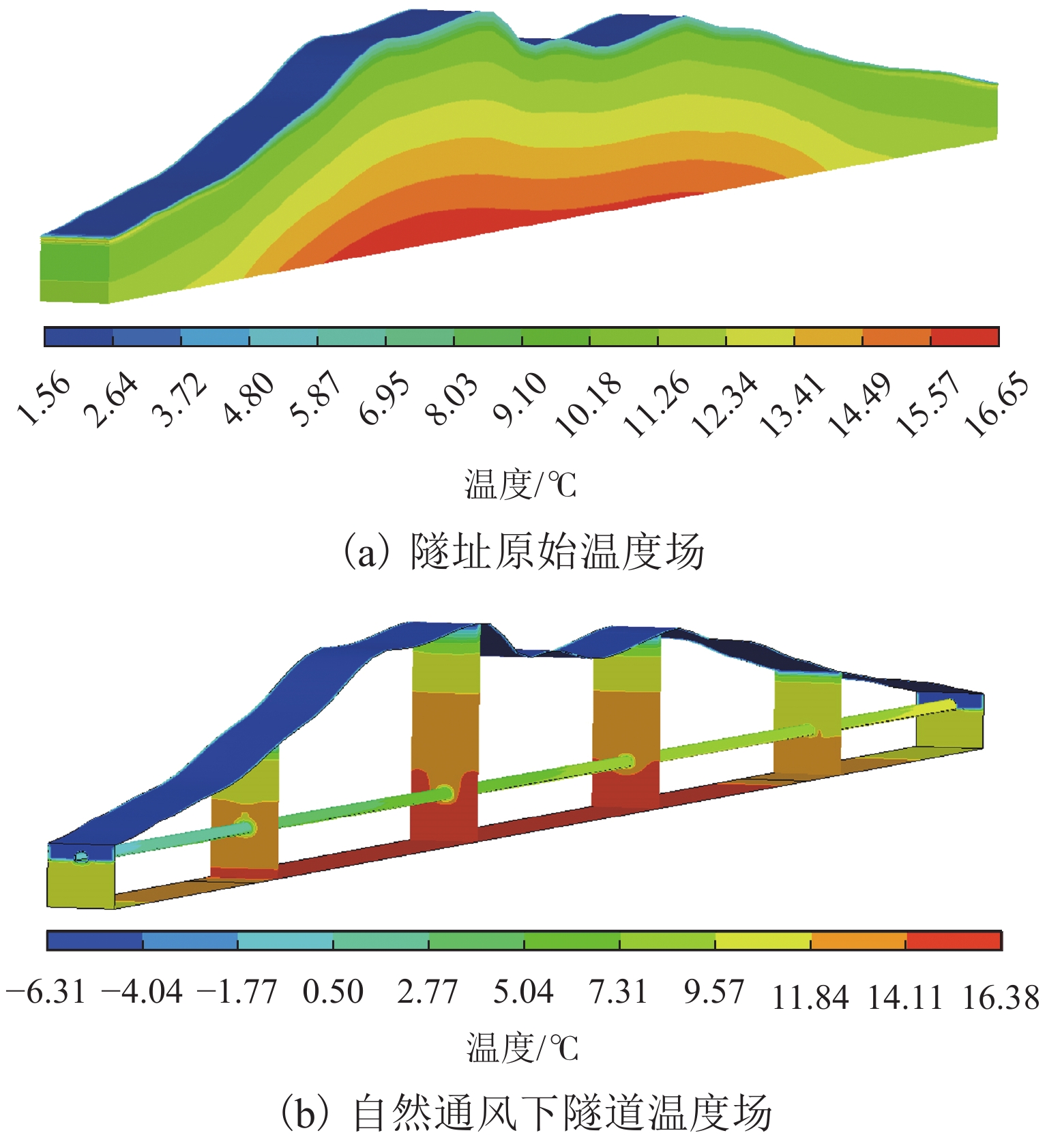
Abstract:
To avoid frost damage problems in cold regions tunnels, a solar shed was introduced as one of the insulation measures. First, a three-dimensional transient heat transfer numerical model was established to obtain the tunnel temperature field under natural ventilation, and the reliability of the numerical calculation model was verified through on-site temperature monitoring. Then, the temperature rise effects of the solar shed were demonstrated through numerical methods, and the effects of the solar shed’s speed, length, span, and ambient temperature on the temperature rise effects were further investigated. Finally, a sensitivity analysis was conducted on these factors to study their impact on temperature rise. The study results show that the solar shed has a good temperature rise effect when the wind speed is lower than 1.0 m/s. The wind speed was negatively related to the temperature rise effects. The air temperature at the tunnel entrance increases by 0.71 ℃ for every 50 m increase in length. The influence of the span on temperature rise effects is not obvious. The temperature rise effects become more and more significant as the ambient temperature becomes lower. The sensitivity of the above factors to temperature rise effects is ranked as follows: wind speed (0.39) > length (0.30) > ambient temperature (0.19) > span (0.12), of which the wind speed is the most sensitive factor and should be considered in the application. Therefore, the recommendation for the use of a solar shed is in environments with low wind speed, long tunnel lengths and small tunnel spans.
- tunnels in cold regions /
- freezing damage /
- solar shed /
- temperature-rising effects /
- sensitivity analysis

HTML全文

图 1 隧道横断面（单位：cm）

Figure 1. Cross-section of tunnel (unit: cm)

下载: 全尺寸图片幻灯片

图 2 地温测点布置（单位：cm）

Figure 2. Layout of ground temperature measuring points (unit: cm)

下载: 全尺寸图片幻灯片

图 3 数值计算模型（单位：m）

Figure 3. Numerical calculation model (unit: m)

下载: 全尺寸图片幻灯片

图 4 日平均气温正弦曲线拟合

Figure 4. Curve fitting of daily average temperature

下载: 全尺寸图片幻灯片

图 5 温度场分布

Figure 5. Temperature field distribution

下载: 全尺寸图片幻灯片

图 6 现场实测与数值模拟对比

Figure 6. Comparison between field measurement and numerical simulation

下载: 全尺寸图片幻灯片

图 7 阳光棚计算模型（单位：m）

Figure 7. Calculation model for solar shed (unit: m)

下载: 全尺寸图片幻灯片

图 8 气温和太阳辐照度逐时变化

Figure 8. Temporal variation of temperature and solar irradiance

下载: 全尺寸图片幻灯片

图 9 阳光棚表面温度分布

Figure 9. Temperature distribution on shed surface

下载: 全尺寸图片幻灯片

图 10 洞内气温逐时变化

Figure 10. Hourly variation of temperature in tunnel

下载: 全尺寸图片幻灯片

图 11 有、无阳光棚情况对比

Figure 11. Temperature comparison with and without solar shed

下载: 全尺寸图片幻灯片

图 12 阳光棚作用下拱顶温度变化

Figure 12. Temperature variation of vault wall with solar shed

下载: 全尺寸图片幻灯片

图 13 能量转移示意

Figure 13. Diagram of energy transfer

下载: 全尺寸图片幻灯片

图 14 进口气温随风速变化

Figure 14. Variation of air temperature with wind speed

下载: 全尺寸图片幻灯片

图 15 进口气温与风速的关系

Figure 15. Relationship between air temperature and wind speed

下载: 全尺寸图片幻灯片

图 16 进口气温随阳光棚长度变化

Figure 16. Variation of air temperature with shed length

下载: 全尺寸图片幻灯片

图 17 进口气温与阳光棚长度的关系

Figure 17. Relationship between air temperature and shed length

下载: 全尺寸图片幻灯片

图 18 进口气温随阳光棚跨度变化

Figure 18. Variation of air temperature with shed span

下载: 全尺寸图片幻灯片

图 19 环境温度计算工况

Figure 19. Calculation cases of ambient temperature

下载: 全尺寸图片幻灯片

图 20 温升效应随环境温度变化情况

Figure 20. Variation of temperature-rising with ambient temperature

下载: 全尺寸图片幻灯片

图 21 各参数敏感度曲线

Figure 21. Sensitivity curves under different parameters

下载: 全尺寸图片幻灯片

表 1 模型参数

Table 1. Parameters of the calculation model

名称密度/
（kg·m⁻³）比热容/
（J·kg⁻¹·K⁻¹）导热系数/
（W·m⁻¹·K⁻¹）

衬砌 2400 960 1.6
围岩 2025 1256 2.0

下载: 导出CSV

表 2 归一化后敏感度

Table 2. Sensitivity after normalization

因素入口风速阳光棚长度跨度环境温度

敏感度 0.39 0.30 0.12 0.19

下载: 导出CSV

参考文献(20)

[1]	陈仁升,康尔泗,吴立宗,等. 中国寒区分布探讨[J]. 冰川冻土,2005,27(4): 469-475. CHEN Rensheng, KANG Ersi, WU Lizong, et al. Cold regions in China[J]. Journal of Glaciology and Geocryology, 2005, 27(4): 469-475.
[2]	张学富,王成,喻文兵,等. 风火山隧道空气与围岩对流换热和围岩热传导耦合问题的三维非线性分析[J]. 岩土工程学报,2005,27(12): 1414-1420. ZHANG Xuefu, WANG Cheng, YU Wenbing, et al. Three-dimensional nonlinear analysis for coupled problem of heat transfer of surrounding rock and heat convection between air in Fenghuo Mountain tunnel and surrounding rock[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(12): 1414-1420.
[3]	张国柱,夏才初,殷卓. 寒区隧道轴向及径向温度分布理论解[J]. 同济大学学报(自然科学版),2010,38(8): 1117-1122,1160. doi: 10.3969/j.issn.0253-374x.2010.08.003 ZHANG Guozhu, XIA Caichu, YIN Zhuo. Analytical solution to axial and radial temperature of tunnel in cold region[J]. Journal of Tongji University (Natural Science), 2010, 38(8): 1117-1122,1160. doi: 10.3969/j.issn.0253-374x.2010.08.003
[4]	WU H, ZHONG Y J, XU W, et al. Experimental investigation of ground and air temperature fields of a cold-region road tunnel in NW China[J]. Advances in Civil Engineering, 2020, 6: 1-13.
[5]	WU Y M, XU P, LI W B, et al. Distribution rules and key features for the lining surface temperature of road tunnels in cold regions[J]. Cold Regions Science and Technology, 2020, 172: 102979.1-102979.18.
[6]	ZHAO P Y, CHEN J X, LUO Y B, et al. Field measurement of air temperature in a cold region tunnel in northeast China[J]. Cold Regions Science and Technology, 2020, 171: 102957.1-102957.10.
[7]	ZHANG HM, CAO HB, ZHANG MJ. Analysis of temperature field of the tunnel surrounding rock in cold regions[J]. Advanced Materials Research, 2013, 753/754/755: 745-749.
[8]	WANG T, ZHOU G Q, WANG J Z, et al. Stochastic analysis for the uncertain temperature field of tunnel in cold regions[J]. Tunnelling and Underground Space Technology, 2016, 59: 7-15. doi: 10.1016/j.tust.2016.06.009
[9]	YU Q Y, ZHANG C, DAI Z X, et al. Impact of tunnel temperature variations on surrounding rocks in cold regions[J]. Periodica Polytechnica Civil Engineering, 2019, 63(1): 160-167.
[10]	孙克国,李思,许炜萍,等. 导热系数对寒区隧道温度场时空分布的影响[J]. 西南交通大学学报,2020,55(2): 256-264,289. doi: 10.3969/j.issn.0258-2724.20180530 SUN Keguo, LI Si, XU Weiping, et al. Influence of thermal conductivity on temporal and spatial distributions of temperature filed in cold region tunnel[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 256-264,289. doi: 10.3969/j.issn.0258-2724.20180530
[11]	郑余朝,孙克国,司君岭,等. 气流作用下的季冻区隧道温度场及影响因素[J]. 中国铁道科学,2020,41(6): 81-90. ZHENG Yuchao, SUN Keguo, SI Junling, et al. Tunnel temperature field and its influencing factors in seasonal frozen region subjected to action of airflow[J]. China Railway Science, 2020, 41(6): 81-90.
[12]	王仁远,朱永全,高焱,等. 寒区隧道温度场模型试验及空气幕保温措施[J]. 中国铁道科学,2021,42(3): 70-82. doi: 10.3969/j.issn.1001-4632.2021.03.09 WANG Renyuan, ZHU Yongquan, GAO Yan, et al. Model test of temperature field of tunnel in cold region and air curtain insulation measures[J]. China Railway Science, 2021, 42(3): 70-82. doi: 10.3969/j.issn.1001-4632.2021.03.09
[13]	冯强,蒋斌松. 多层介质寒区公路隧道保温层厚度计算的一种解析方法[J]. 岩土工程学报,2014,36(10): 1879-1887. doi: 10.11779/CJGE201410016 FENG Qiang, JIANG Binsong. Analytical method for insulation layer thickness of highway tunnels with multilayer dielectric in cold regions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1879-1887. doi: 10.11779/CJGE201410016
[14]	ZHAO P Y, CHEN J X, LUO Y B, et al. Investigation of the insulation effect of thermal insulation layer in the seasonally frozen region tunnel: a case study in the zuomutai tunnel, China[J]. Advances in Civil Engineering, 2019, 2019(4): 1-14.
[15]	LAI JX, GONG CB, WANG YS. Model test study on insulator of cold-region tunnel in northeast China: a case study of Gaoling tunnel[J]. Applied Mechanics and Materials, 2011, 71/72/73/74/75/76/77/78: 1870-1874.
[16]	YAN Q X, LI B J, ZHANG Y Y, et al. Numerical investigation of heat-insulating layers in a cold region tunnel, taking into account airflow and heat transfer[J]. Applied Sciences, 2017, 7: 7070679.1-7070679.22.
[17]	成珂,马晓瑶,孙琦琦. 光伏温室大棚组件布置CFD模拟研究[J]. 太阳能学报,2021,42(8): 159-165. CHENG Ke, MA Xiaoyao, SUN Qiqi. CFD simulation study on module layout of photovoltaic greenhouse[J]. Acta Energiae Solaris Sinica, 2021, 42(8): 159-165.
[18]	孙克国,杨朋,仇文革,等. 寒区隧道温度场和排水沟埋置深度研究[J]. 铁道工程学报,2017,34(4): 51-57. SUN Keguo, YANG Peng, QIU Wenge, et al. Research on the temperature field and the buried depth of drains for tunnels in cold region[J]. Journal of Railway Engineering Society, 2017, 34(4): 51-57.
[19]	康德拉捷夫 К Я, 著. 太阳辐射能[M]. 李怀瑾, 译. 北京: 科学出版社, 1962.
[20]	蔡毅,邢岩,胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版),2008,44(1): 9-16. CAI Yi, XING Yan, HU Dan. On sensitivity analysis[J]. Journal of Beijing Normal University (Natural Science), 2008, 44(1): 9-16.