Stability Analysis and Evaluation of a Tunnel Entrance Slope Under Complex Disaster-Prone Environments
-
摘要:
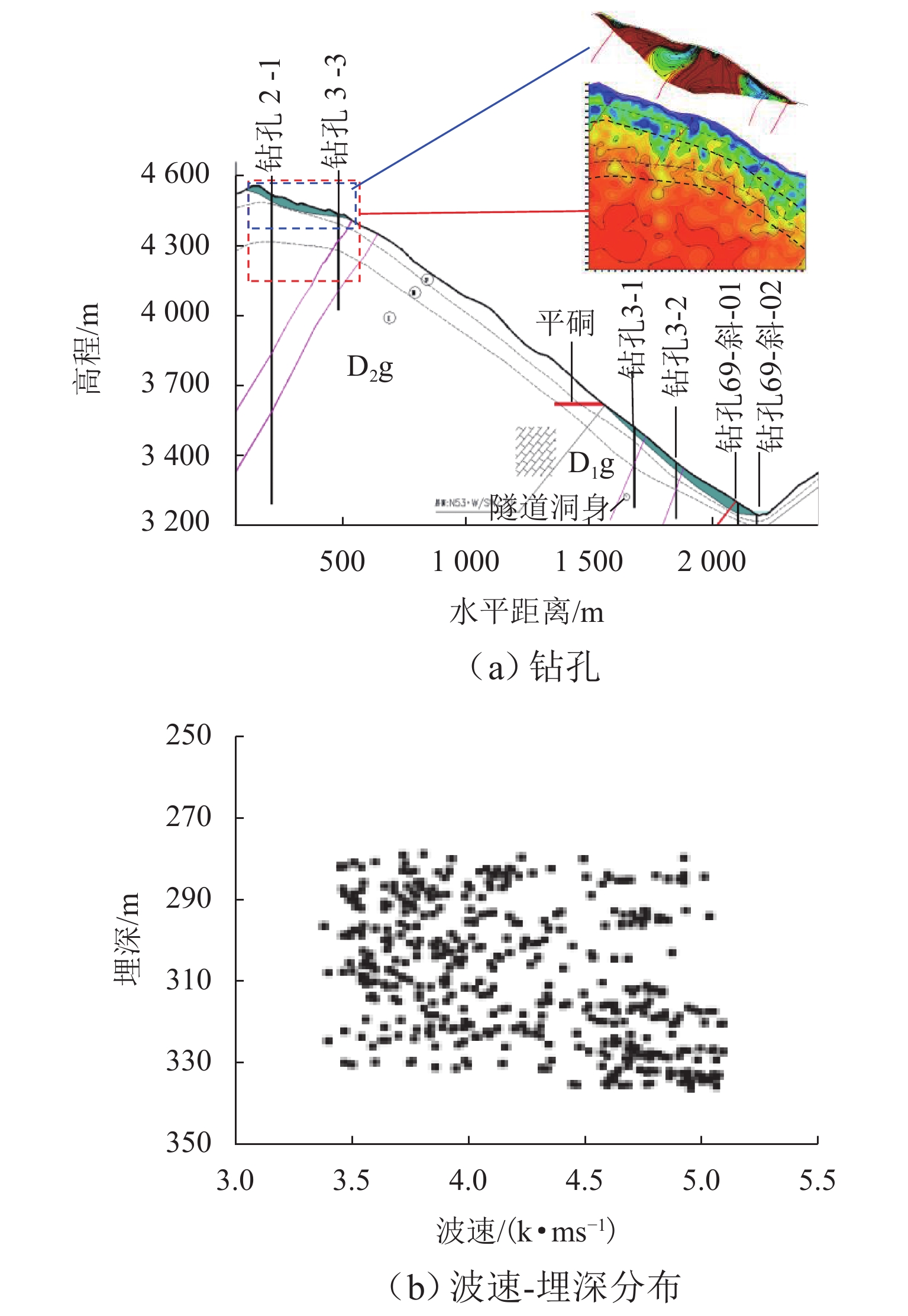
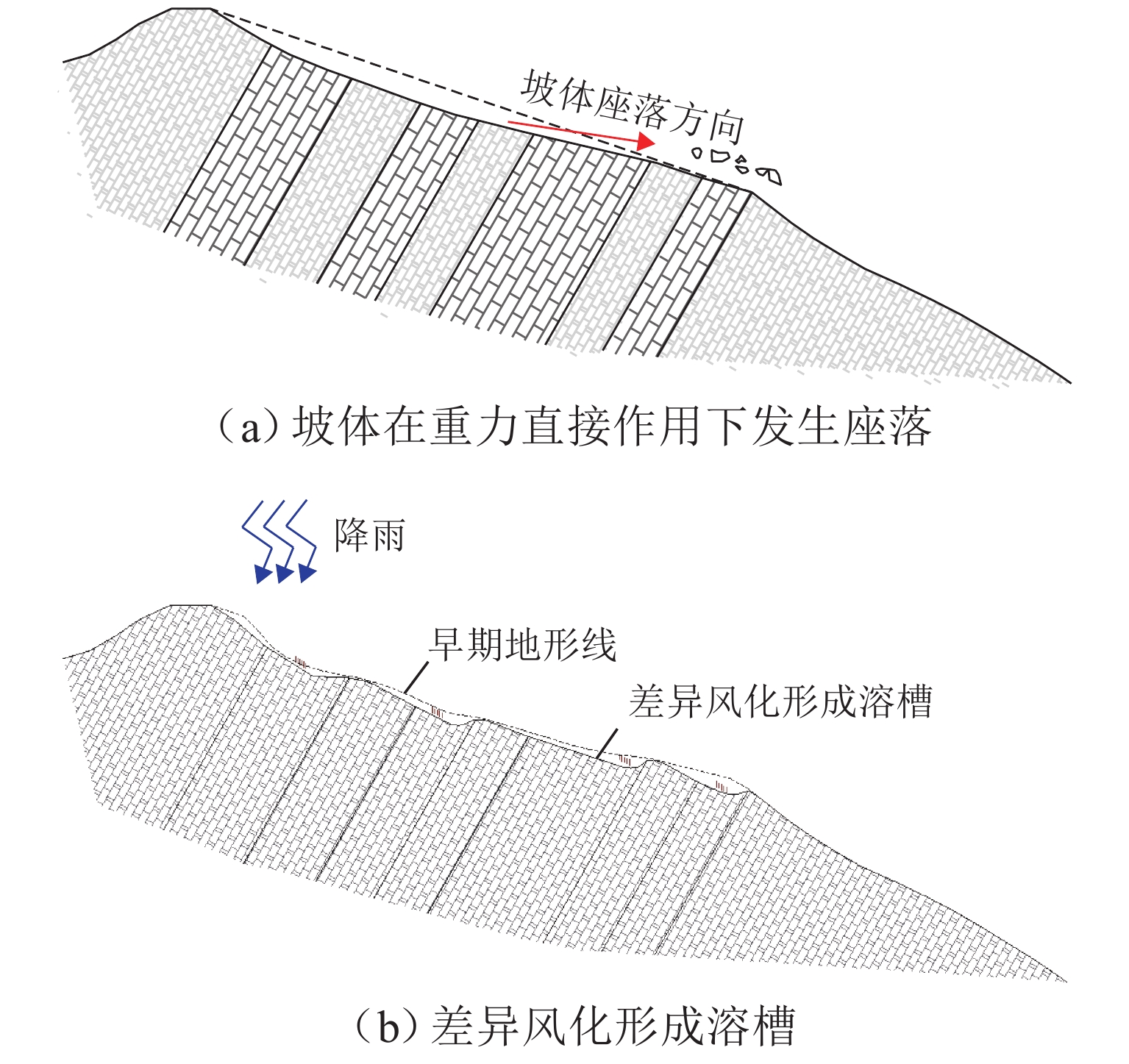
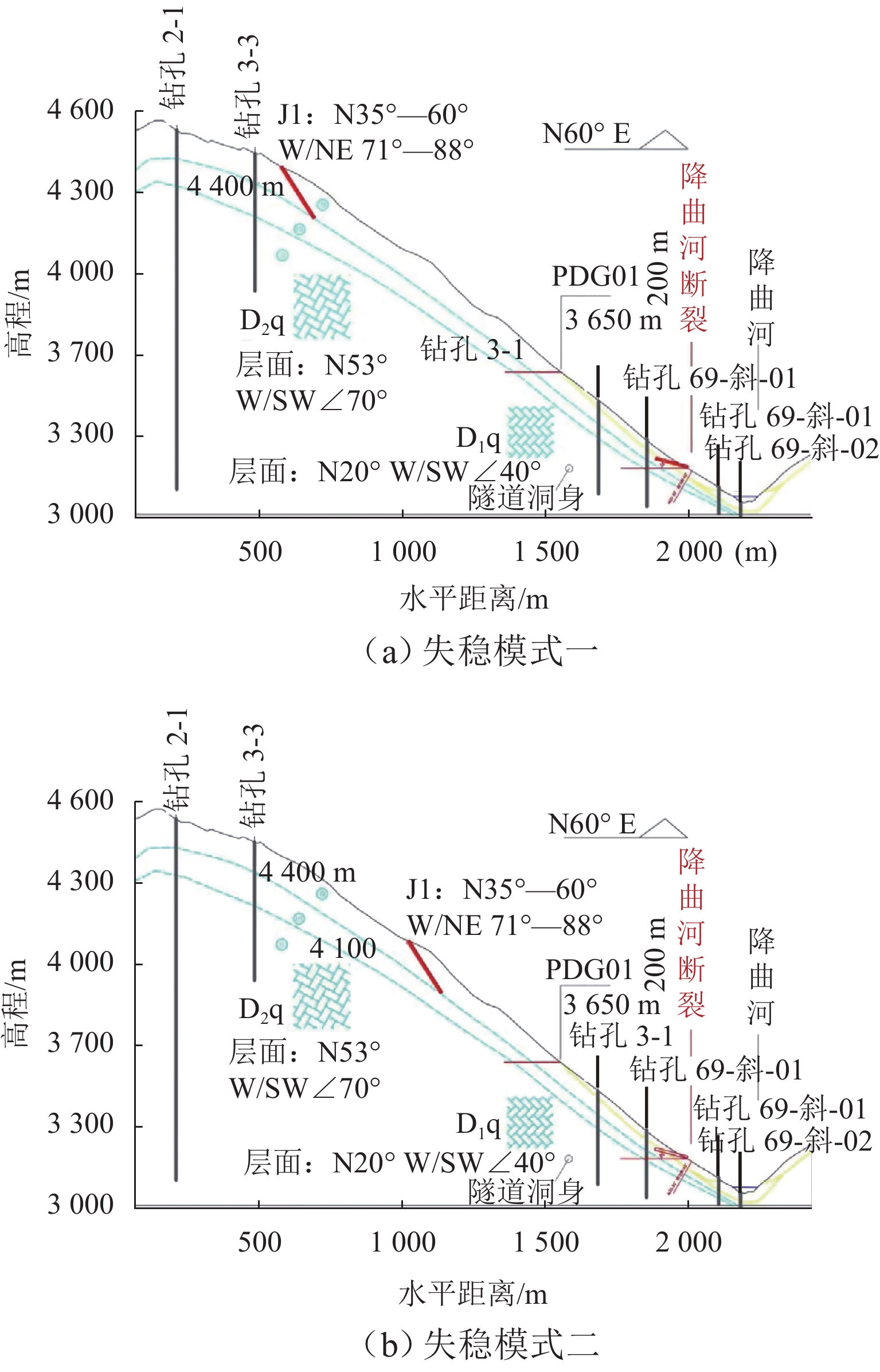
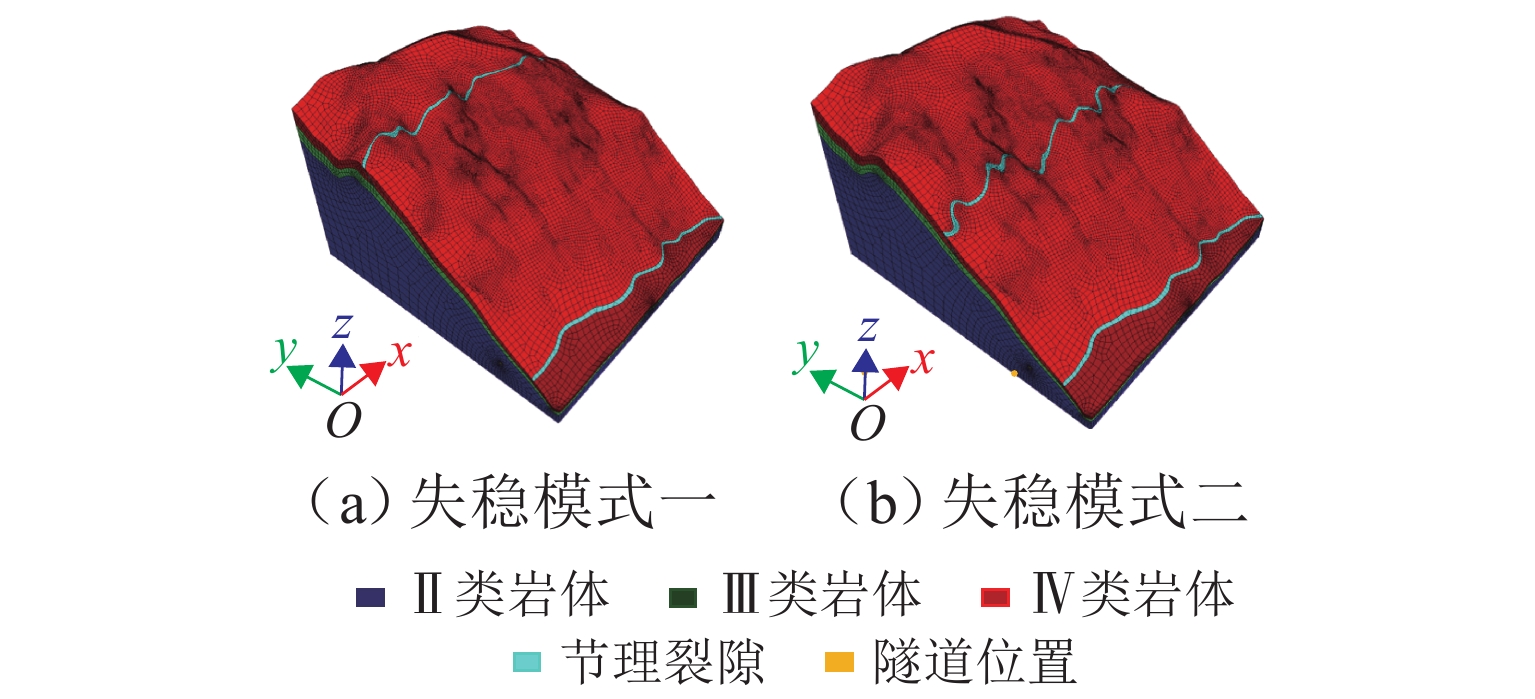
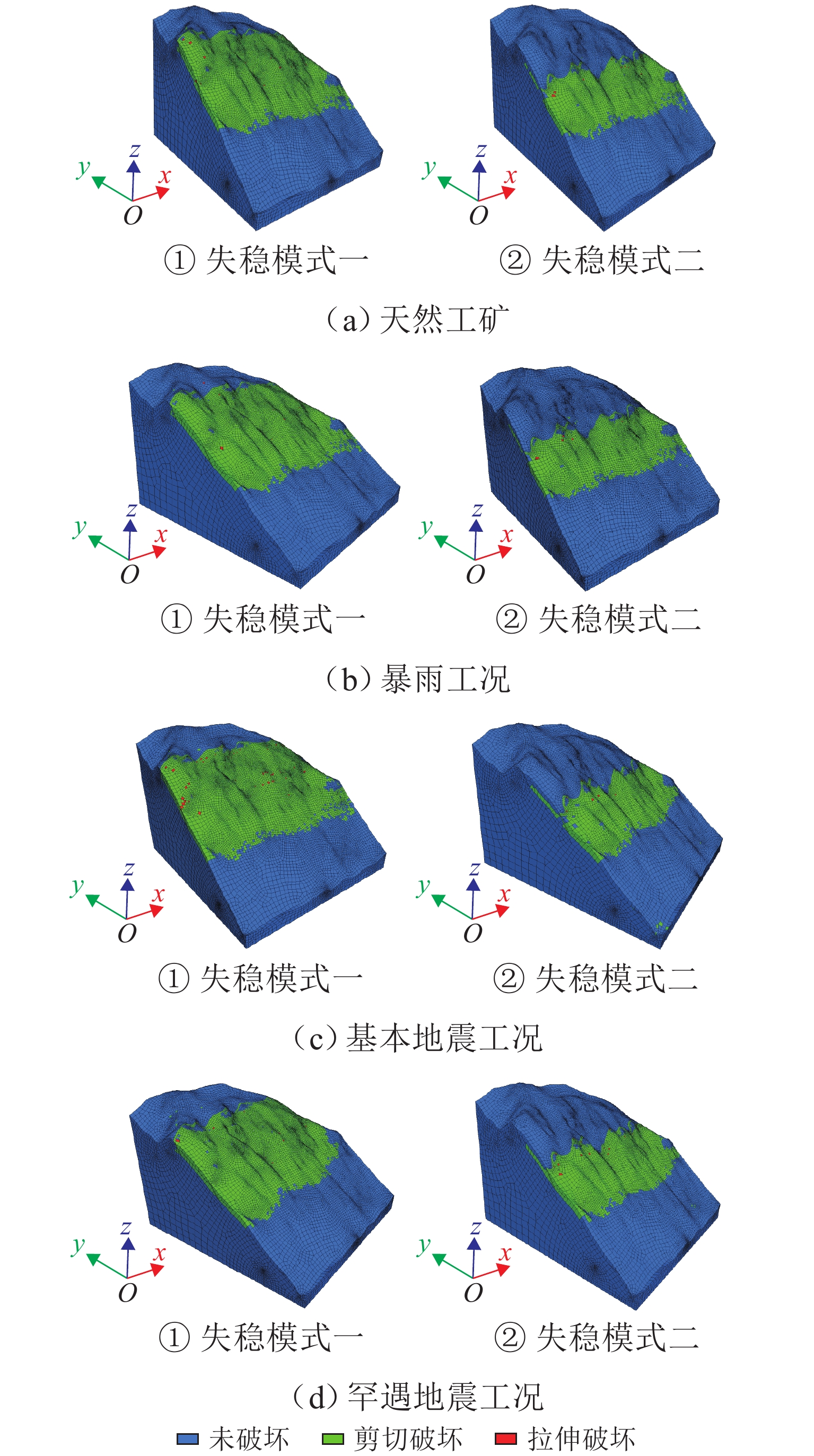
高地震烈度、高地应力、高陡、高寒等复杂孕灾环境下的隧道洞口斜坡，在降雨、强震或人类强烈工程活动影响下，极易发生崩塌、滑坡、泥石流等地质灾害. 为探究复杂孕灾环境下隧道进口斜坡在不同工况条件下的稳定性，以我国西南某加日山隧道为依托，通过无人机摄影、槽探、室内实验及洞探原位测试等“天空地”一体化勘察技术，实现斜坡工程地质信息精细获取，系统揭示斜坡典型破坏特征，讨论斜坡2种破坏成因与演化模式，在此基础上，利用极限平衡法与三维数值模拟方法，量化分析不同工况下的斜坡稳定性. 研究结果表明：加日山隧道进口斜坡在自然工况、暴雨工况、地震工况3种工况下稳定性系数均大于1.15，斜坡整体处于稳定状态，仅后缘表部存在局部变形失稳的可能，成果可为类似隧道的选线规划以及建设运营安全提供理论指导和技术支撑.
Abstract:Influenced by rainfall, strong earthquakes, and intensive engineering activities, the slope at the tunnel entrance may experience collapses, landslides, debris flows, and other geological disasters, especially under the complex conditions of violent earthquakes, high geostress, abrupt slopes, and extremely cold environments. To explore the stability of tunnel entrance slopes under different working conditions in complex disaster-prone environments, the Jiarishan tunnel in southwest China was taken as an example, and a “space-air-ground” integrated investigation technology combining unmanned aerial vehicle (UAV) photography, surface trenching, laboratory experiments, field tests, and cave surveys was employed to obtain accurate engineering geological information. Typical failure characteristics of the studied slope were systematically revealed, and the two failure causes and evolution models of the slope were discussed. In addition, the slope stability under different working conditions was qualitatively analyzed using the limit equilibrium method and three-dimensional numerical simulation. The results indicate that the stability factor of the slope at the Jiarishan tunnel entrance is always greater than 1.15 under natural, rainstorm, and earthquake working conditions. Overall, the slope is stable except for the local deformation and instability of the shallow horizon of the posterior margin. This research can provide theoretical guidance and technical support for similar tunnels in terms of siting, construction, and operation safety.
-
Key words:
- disaster-prone environment /
- slope deformation /
- evolution mode /
- stability analysis
-
20世纪80年代以来，世界各地发生了一系列破坏性地震，造成大量人员伤亡和工程结构破坏. 其中，1995年日本的神户大地震造成
6400 多人死亡，直接经济损失达1000 亿美元；1994年美国的北岭地震虽然只造成57人死亡，但因建筑物损坏造成的经济损失却高达170亿美元；1999年台湾的集集地震造成2405 人死亡，大约10万间房屋被毁，经济损失近100亿美元[1]；2008年我国的汶川大地震造成69227 人死亡，374643 人受伤，17923 人失踪，这是新中国成立以来破坏性最大的地震，也是唐山地震后伤亡最严重的一次地震，直接经济损失达8452 亿元[2]. 可以看出，地震的破坏性极大，会给社会带来巨大的经济损失和人员伤亡，人们也对结构的抗震性能提出了更高的要求.钢筋混凝土（RC）结构在土木工程领域的应用最为广泛，其抗震性能深受人们的重视. 在强震作用下，建筑以及桥梁结构中的墩柱在承受竖向力的同时还会受到往复作用的水平力，若构件的横向约束不足，即使外荷载较小，纵向钢筋也会发生明显的横向变形，即钢筋屈曲，将导致构件无法充分发挥钢材的抗压性能，从而使构件的承载力和延性显著降低. 因此，近些年，国内外对地震作用下钢筋混凝土墩柱的纵筋屈曲问题进行了大量研究，本文在此基础上，按照研究手段的不同分别对基于单筋直压试验的纵筋屈曲研究和基于RC短柱直压试验的纵筋屈曲研究进行总结. 同时，还对有关新材料/新构造对纵筋屈曲影响的研究进行讨论分析. 最后，总结现阶段纵筋屈曲研究存在的一些问题，并对今后的研究方向进行展望.
1. 基于单根钢筋直压试验的纵筋屈曲研究进展
基于单根钢筋直压试验的钢筋屈曲研究虽然不考虑混凝土保护层的约束作用以及核心混凝土膨胀作用等因素的影响，并认为箍筋能够提供充足的横向约束，即钢筋的两端完全固定，但方便获取钢筋的应力应变数据，是研究实际构件中纵筋屈曲的前提和基础. 因此，国内外学者对单根钢筋的屈曲行为做了大量研究，并提出相应的屈曲本构模型.
1.1 单根钢筋屈曲的试验研究
对于单根钢筋，影响其屈曲的因素主要有长细比、屈服强度、初始缺陷以及钢筋锈蚀等.
1.1.1 长细比
在钢筋屈曲问题的研究中，通常将长细比规定为钢筋的无约束长度L与钢筋直径D的比值. Montil等[3]通过试验发现，当长细比L/D高于某一临界值时，单根钢筋在较小的外荷载作用下就会发生屈曲，并且随着长细比的增大，钢筋应力-应变曲线表现出显著的应力软化现象. Dhakal等[4]通过对不同直径以及屈曲长度的钢筋进行试验发现，长细比越大，钢筋屈曲后的骨架曲线就越陡，如图1所示. 图中：$ \sigma $、$ \varepsilon $分别为钢筋的应力及对应的应变，$ {f}_{{\mathrm{y}}} $、$ \varepsilon_{{\mathrm{y}}} $分别为钢筋的屈服应力及对应的应变. Bae等[5]对162个钢筋试件进行单轴压缩试验发现：1） 对于给定的初始偏心，强度和延性随长细比的增大而减小；2） 对于L/D=4.0的钢筋，初始偏心率对构件承载能力的影响较小；3） 对于有高延性要求的柱或纵筋，为避免发生较大的塑性变形，应保证L/D＜6.0. Cosenza等[6]对不同长细比下光圆钢筋的压缩性能进行了试验研究，建立考虑长细比影响的压应力-应变关系. 并在研究中指出，长细比对钢筋屈曲的影响程度大致分为4个范围：1） 当L/D≤5.0时，钢筋在受压时延性较好，可以假定钢筋的受压性能与受拉性能一致；2） 当L/D=6.0～7.0时，受压钢筋在达到屈服平台之后会发生应变硬化，硬化阶段结束时对应的应变和应力可以通过试验得到；3） 当8.0≤L/D≤20.0时，受压钢筋会在屈服平台阶段发生应变软化，由屈服平台转为软化阶段的应变可通过试验确定；4） 当L/D＞20.0时，长细比不超过30的钢筋能够达到屈服强度，但会立刻发生屈曲，不会出现屈服平台，而长细比大于30的钢筋在达到屈服强度前就会发生屈曲. 陈昉健等[7]通过对不同长细比和屈服强度的热轧带肋钢筋进行单轴加载试验发现：1） 在高强钢筋的轴压过程中，抗压强度随着无约束长度的增加而逐渐降低，当无约束长度增至杆径的8倍时，抗压强度的值与屈服强度基本一致. 若无约束长度继续增大，抗压强度将低于钢筋未屈曲时的屈服强度. 2） 抗压强度受钢筋直径的影响，当无约束长度为杆径的6倍～8倍时，随着杆径的增大，屈曲后钢筋强度的退化加快.
1.1.2 屈服强度
Dhakal等[4]通过对不同强度的钢筋进行试验发现，当长细比一定时，屈服强度越高，钢筋在屈服点后的软化现象越显著. 同时还发现“长细比小于5的钢筋不会发生屈曲”这一结论不准确. 钢筋的屈曲应该是由长细比和$ f_{y} $ 2个因素共同决定的，通过试验对比分析，最终得出钢筋屈曲跟$ (L / D) \sqrt{f_{y}} $这一参数有关，如图2所示. 图中：参数C=(fy/100)0.5(L/D). Bae等[5]分别采用直径为8、10、20 mm的钢筋进行受压实验，3种钢筋的长细比相同，强屈比依次递减. 通过试验发现，强屈比对钢筋的屈曲行为也有较为显著的影响，强屈比大的钢筋能够表现出更好的稳定性，如图3所示.
Korentz[8]对不同几何参数、不同屈服强度的钢筋进行了数值分析，结果表明，钢筋屈曲不仅受其几何参数的影响，而且还受其屈服强度的影响. 对于长细比和材料应力-应变关系确定的受压杆件，临界力和平均屈曲应力随屈服强度的增加而减小. 相同强度的受压杆件在屈服后的受力性能实际上取决于参数$ f_{{\mathrm{y}}}(L / D)^{2} $，这一点与Dhakal等[4]的观点较为相似. Korentz等[9]对不同特性的钢筋进行数值分析后认为，钢筋屈服后的力学性能对屈曲有显著的影响. 当钢筋的长细比小于特定的极限值时，钢筋达到屈服极限后仍可在稳定平衡状态下工作. 对钢筋屈服后塑性平台长度、强屈比以及强化曲线形状等力学性能的描述对极限长细比有重要意义. 因此，要准确地模拟受压钢筋的屈曲行为，就需要了解整个材料的应力-应变曲线. 陈昉健等[7]通过试验发现，无论在何种长细比下，屈服强度越高，高强钢筋在屈曲后的强度退化越快. 因此，钢筋自身强度越高越需要重视抗压强度所受到的影响，在设计过程中应留有充分的安全储备.
1.1.3 初始缺陷
钢筋的初始缺陷主要包括材质不均匀和初始挠度. Bae等[5]将初始偏心率（e/D）作为钢筋初始缺陷的衡量标准，其中，e为钢筋的初始偏心距. 试验表明，对于给定的L/D，e/D的增大会导致钢筋的承载力和延性的降低. 但对于L/D=4.0的钢筋，无论e/D如何变化，试件的承载力在非弹性变形下均保持不变. Massone等[10]基于集中塑性模型建立一种考虑初始缺陷的钢筋屈曲模型，基于该屈曲模型的数值分析结果与试验结果吻合较好. 但对于大偏心距试样的峰值承载力与小长径比试样峰值承载力后的应力-应变关系，该模型适用性较差.
1.1.4 钢筋锈蚀
锈蚀是钢筋最常见的劣化类型之一，根据钢筋锈蚀外观特征的不同可以将其分为均匀锈蚀和非均匀锈蚀2种. 史庆轩等[11]通过对配有不同锈蚀程度纵筋的RC墩柱进行往复加载试验指出，钢筋锈蚀试件破坏时，外侧保护层会整块剥落，纵筋向外鼓曲并外露，使得试件到极限荷载后呈现明显的脆性性质. 但该试验中采用电化学方法使钢筋锈蚀，与钢筋自然锈蚀得到的产物有较大差别，在一定程度上对最终受力状态有影响. Kashani等[12-15]通过对多根锈蚀钢筋进行单调压缩以及循环加载试验，研究沿钢筋长度方向的不均匀锈蚀对钢筋屈曲的影响，考虑了锈蚀程度和长细比对钢筋拉压性能的影响，如图4所示. 研究发现，锈蚀会改变钢筋受压时的屈曲破坏机制，10%的质量损失可使锈蚀钢筋的抗屈曲能力降低约20%，并且坑蚀点沿锈蚀钢筋长度的分布是影响钢筋屈曲的重要参数. 此外，在发生屈曲时，长细比为5的钢筋受锈蚀作用的影响要大于长细比为10和15的钢筋. 陈武雄 [16]通过对锈蚀钢筋进行轴压试验，指出在锈蚀率较小的情况下钢筋也会因在坑蚀位置处产生应力集中而更容易发生屈曲，使得所能承受的最大应力有所下降. 同时，坑蚀点越靠近钢筋屈曲范围的中心位置，钢筋在受压过程中越容易发生屈曲. Imperatore等[17]基于不同长细比和锈蚀程度对46根锈蚀钢筋进行单调轴压试验，研究均匀腐蚀对受压钢筋应力-应变关系的影响，并提出了一个能够反映锈蚀钢筋屈曲行为的简化分析模型. 研究发现，锈蚀钢筋的峰值应力主要由锈蚀程度决定，峰值后屈曲行为主要由长细比决定，两者都是影响锈蚀钢筋屈曲行为的重要参数.
1.2 基于单根钢筋直拉试验的纵筋屈曲本构模型
结构在地震作用下往往会受到往复荷载作用，构件中的钢筋将处于拉压交替循环的受力状态. 因此，要想更好地通过数值分析来研究RC结构的受力状况，就需要一个能准确反映实际受力状态的钢筋本构模型. 合理的钢筋本构模型应该满足以下3点：1） 公式简洁，避免计算耗时过大. 2） 属于$ \sigma= f(\varepsilon ) $型（$ f$(·)为应力函数）. 便于在非线性程序中引入，将截面离散为单轴应力状态下的纤维几何组合. 3） 模型参数易于获得. 国内外很多学者在这方面进行深入研究，并提出了若干本构模型.
1.2.1 Montil-Nuti模型
Montil等[3]提出一种能考虑钢筋屈曲的本构模型，可适用于采用纤维离散化方法进行分析的有限元模型. 该本构模型具有4个可以通过试验确定的独立参数（屈服应力、弹性模量、强屈比和加权系数），采用了4种强化规则（随动强化、各向同性强化、记忆强化和饱和强化），并可以为加载分支使用$ \sigma=f(\varepsilon ) $和$ \varepsilon=f(\sigma) $中的任意一种关系，计算效率非常高. 本构模型的曲线如图5所示，其下降段和水平段可分别按式（1）、（2）进行计算. 图中：$\varepsilon_\infty $为极限应力值$f_\infty $对应的应变.
b−=Ep/E0=a((LD)cr−LD),LD>(LD)cr, (1) f∞≈6fyL/D, (2) 式中：$ b^{-} $为受压侧的应变强化率，随着长细比的增加而减小，且受拉侧应变强化率对其无影响；$ E_{{\mathrm{p}}} $为钢筋的后屈服模量；$ E_{0} $为钢筋的初始弹性模量；$ a $为斜率比；$ {\left(\dfrac{L}{D}\right)}_{\mathrm{c}\mathrm{r}} $为临界长细比，建议取值为5.
该模型在屈曲后引入L/D作为附加参数，能够较好地模拟对称和非对称循环加载过程. 但由于试验数据较少，拟合得到的加载刚度衰减规则适用范围较窄，该本构模型未得到广泛应用.
1.2.2 Dhakal-Maekawa模型
Dhakal等[4,18]通过试验研究钢筋屈曲与参数$ (L / D) \sqrt{f_{{\mathrm{y}}}} $的关系，并在此基础上对Giuffre-Menegotto-Pinto本构模型[19]的滞回规则进行了修正，建立可以考虑钢筋屈曲的本构模型，如图6所示. 该模型考虑了长细比和屈服强度的影响，函数形式简单，如式（3）.
{σ=Esε,ε⩽εy,σσl=1−(1−σ∗σ∗l)(ε−εyε∗−εy),εy<ε⩽ε∗,σ=σ∗−0.02Es(ε−ε∗),σ⩾0.2fy,ε>ε∗, (3) 式中：$ \varepsilon ^{*} $为钢筋屈曲起始点处的应变，如式（4）；$ \sigma^{*} $为钢筋屈曲起始点处的应力，如式（5）；$ {\sigma }_{\mathrm{l}} $为钢筋受拉曲线上的应力；$ \sigma_{{\mathrm{l}}}^{*} $为屈曲起始点对应的未屈曲曲线上的应力.
ε∗εy=55−2.3√fy100LD,ε∗εy⩾7, (4) σ∗σ∗l=α(1.1−0.016√fy100LD),σ∗⩾0.2fy, (5) α=0.75+εu−εsh300εy,α⩽fu1.5fy,0.75⩽α⩽1.0, (6) 式中：$\alpha $为考虑钢筋应力-应变关系的参数，理想弹塑性时取0.75 ，完全线性强化时取1；$ \varepsilon_{{\mathrm{u}}} $为钢筋极限应变；$ \varepsilon _{{\mathrm{sh}}} $为钢筋强化起始点的应变；$ f_{{\mathrm{u}}} $为钢筋的极限应力.
1.2.3 Bae模型
Bae等[5]对162个钢筋试件进行了单调压缩试验，研究钢筋的长细比、初始偏心率和强屈比对钢筋屈曲的影响. 结果表明，钢筋的平均轴向应变主要由轴向变形引起的轴向应变和横向位移引起的轴向应变组成，并提出可模拟钢筋屈曲行为的本构模型. 该本构模型的应力-应变关系可通过如下5个步骤确定：
步骤1 当钢筋应力$ f_{{\mathrm{s}}}\leqslant f_{{\mathrm{y}}} $时，钢筋处于弹性阶段.
步骤2 当$ f_{{\mathrm{s}}}>f_{{\mathrm{y}}} $时，认为钢筋开始发生屈曲. 对于位移控制法，可以假定一个初始的横向位移，然后通过经验公式计算相应的轴力.
步骤3 根据轴力，又可以通过经验公式计算对应的轴向应变$ \varepsilon _{{\mathrm{s}}}. $
步骤4 最后根据轴向应变与横向位移的关系，得到横向位移引起的轴向应变$ \varepsilon _{{\mathrm{tra}}}. $
步骤5 重复步骤2～4，得到完整的应力-应变关系曲线.
1.2.4 钢筋锈蚀本构模型
Kashani等[15]基于Dhakal-Maekawa模型建立一个考虑无屈服平台的高强度钢筋屈曲行为的本构模型，通过对未锈蚀钢筋和锈蚀钢筋的试验验证了该本构模型的有效性，并在OpenSees中成功实现. 该模型与Dhakal-Maekawa模型的主要区别是在参数$ (L / D) \sqrt{f_{{\mathrm{y}}}} $的计算中考虑了锈蚀对钢筋的影响，具体公式如下：
λp1=√σyc1100LDcorr, (7) σyc1=σy(1−βψ), (8) 式中：$ \lambda_{{\mathrm{p1}}} $为考虑钢筋锈蚀的一个无量纲参数，$ \sigma_{{\mathrm{yc1}}} $为锈蚀钢筋的屈服强度，$ D_{ {{\mathrm{corr}} }} $为考虑质量损失的锈蚀钢筋直径（如式（9）），$\;\beta $为反映非均匀锈蚀影响的参数，$ \psi $为锈蚀钢筋的质量损失百分比（如式（10）），$\; \beta $可通过表1选取.
表 1 参数$\; \beta $的选取Table 1. Selection of parameter $\;\beta$条件 $ L / D \leqslant 5 $ $ 5<L / D \leqslant 10 $ $ L / D>10 $ 取值 0.0050 0.0065 0.0125 Dcorr=D0√1−γ, (9) ψ=100γ, (10) γ=m0−mm0, (11) 式中：$ D_{0} $为未锈蚀钢筋直径，$ \gamma $为锈蚀钢筋的质量损失比，$ m_{0} $为原始钢筋单位长度质量，$ m $为锈蚀后钢筋单位长度质量.
该本构模型仍存在一些不足：1） 由于局部锈蚀的复杂性和高度不确定性，难以准确模拟严重的局部锈蚀；2） 所提出的本构模型是基于单根钢筋的试验数据和数值模拟建立的，需要进一步的研究来验证该模型是否适用于模拟RC柱中的纵筋. 此外，Limbert等[20]还对不锈钢钢筋的屈曲行为进行了研究，不锈钢钢筋是解决RC结构耐久性和可持续性问题的一个有效方法. 在不依赖混凝土高碱性及保护层的情况下，仍能很大程度上抵抗氯离子的侵蚀. 同时，还对不锈钢钢筋进行了拉伸及压缩试验，且将试验结果与数值模拟相结合提出不锈钢钢筋在非弹性屈曲作用下的应力-应变关系，并基于OpenSees平台对这一模型进行了开发. 目前，有关不锈钢钢筋的研究较少，该模型的准确性有待进一步探讨.
综上所述，本节对国内外学者基于单根钢筋的直压试验，分析长细比、屈服强度、初始缺陷、钢筋锈蚀等因素对纵筋屈曲行为的影响，并提出相应的纵筋屈曲本构模型. 然而，基于单根钢筋直拉试验的纵筋屈曲研究忽略了外部因素对钢筋的影响，并假设箍筋对钢筋的约束作用充分，因此与实际情况存在一定差异，但这为研究RC结构中纵筋屈曲行为打下坚实基础.
2. 基于RC短柱直压试验的纵筋屈曲研究进展
国内外学者最初主要基于单筋直压试验对纵筋的屈曲问题进行研究，主要是因为：1） 影响RC柱中纵筋屈曲的因素多且复杂，对纵筋屈曲发生的状态以及区域不好确定，难以进行直接观察；2） 相比于单根钢筋的直压试验，RC柱中纵筋屈曲的试验方法更为复杂，尚且处于不断完善阶段，存在诸多难点有待解决. 但为更好地描述纵筋的屈曲问题，反映材料间相互作用对纵筋屈曲的影响，不少国内外学者也基于RC短柱的直压试验对纵筋的屈曲问题进行了分析. 因此，本文结合国内外学者的研究对可能影响RC柱中纵筋屈曲的因素进行了总结和分析.
2.1 混凝土的影响
混凝土对纵筋屈曲的影响主要体现在核心混凝土的侧向膨胀和混凝土保护层的剥落2个方面[21].
对于核心混凝土与纵筋的相互作用，一般认为核心区混凝土在轴压作用下会产生侧向膨胀，纵筋会对混凝土有一定的约束作用，而混凝土则会对纵筋产生侧向推力，从而导致纵筋发生屈曲. Pantazopoulou[22]基于一个包含300多项梁柱试验结果的数据库，研究了RC构件中纵筋的屈曲力学行为，指出纵筋的稳定性设计应考虑箍筋的有效性、核心混凝土的变形能力以及长细比等因素. Bayrak等[23]对56根钢筋进行单轴压缩实验，并结合以往RC柱试验数据，指出核心混凝土对纵筋有外推作用，使其向外变形，不仅降低了纵筋受压时的延性，还降低了纵筋能够达到的最大强度.
对于混凝土保护层与纵筋的相互作用，Dhakal等[24]通过试验发现，随着压应变的增加，混凝土保护层开始产生一些竖向裂缝，横向抗拉能力降低，而纵筋屈曲产生的横向变形使竖向裂缝进一步发展，最终使混凝土保护层丧失抗拉能力，并使混凝土保护层与核心混凝土分离. Hilson等[25]也通过试验发现混凝土保护层表面沿纵筋方向会产生竖向裂缝，并最终导致混凝土保护层发生剥落. 以上研究均认为，纵筋屈曲会受到混凝土保护层的抑制作用，即混凝土保护层会因纵筋的外突鼓曲而剥落. Fragiadakis等[26]的试验结果表明，即使保护层发生剥落，纵筋仍会受到箍筋的横向约束作用，只有变形足够大时，纵筋才开始屈曲，也就是说，保护层的剥落会先于纵筋屈曲，其对抑制纵筋屈曲的作用有限.
2.2 箍筋的影响
根据RC柱破坏形式可以将纵筋屈曲分为局部屈曲和整体屈曲. 局部屈曲是指纵筋屈曲发生在相邻的两箍筋之间，而整体屈曲则是指纵筋的屈曲行为发生在多根箍筋之间（如图7所示）. 图中，s为箍筋间距. 国内外研究大多集中于局部屈曲，将相邻箍筋间距定义为纵筋的屈曲长度. Mander等[27]通过试验指出：在普通RC构件发生破坏时，对于长细比≤6的情形，纵筋应力可达到或者超过极限强度并具有良好的延性；对于长细比≤8的情形，纵筋应力可达到屈服强度并有一定延性；对于长细比＞8的情形，纵筋应力虽然可达到屈服强度，但应力随后会急剧下降，延性较差. Dhakal等[24]通过试验指出，造成局部屈曲的原因主要有箍筋间距较大、箍筋约束刚度较大以及纵筋直径较小，并基于能量原理提出一种简单可靠的方法来预测纵向纵筋的屈曲长度以及混凝土保护层剥落时纵筋的侧向变形. 研究还指出，合理配置箍筋能够有效地抑制纵筋屈曲，提高结构延性. 并改进横向箍筋的设计方法，以避免纵筋过早屈曲. Zong 等[28-29]提出了RC柱的“full-column”模型，并通过对比研究指出，基于“full-column”的有限元模型能够合理地预测纵筋、箍筋和核心混凝土之间的相互作用，并能获得与试验结果一致的屈曲形状. 为提高计算效率，该文还采用简化梁-弹簧模型来模拟箍筋对纵筋屈曲的影响. 邓宗才等[30]分别对配有高强箍筋和普通箍筋的UHPC柱进行轴压试验发现，箍筋的横向约束主要与体积配箍率和箍筋强度有关，并且体积配箍率相较于箍筋强度对轴压性能的影响更大. 该研究还指出，提高高强箍筋的配筋率可以有效抑制屈曲，延迟保护层的剥落，显著提高构件延性；纵筋微曲会削弱高强箍筋对核心UHPC的约束效果，建议将高强纵筋与高强箍筋进行组合配置.
Massone等[10,31]利用塑性铰的概念并基于纤维模型，研究纵向钢筋的整体屈曲. 该模型最初用于局部屈曲的验证，在考虑了截面加固和核心混凝土膨胀的影响后，将其推广到整体屈曲，并将预测的失稳模式与数据库中实验测试结果进行比较，验证了所提模型的有效性. 可以看出，目前国内外有关RC柱中纵筋整体屈曲的研究较少，这主要是因为纵向钢筋整体屈曲的范围难以确定，试验的实施和观测存在较大困难.
2.3 纵筋锈蚀的影响
纵筋锈蚀是RC结构最常见的劣化类型之一. 许多研究表明[32-33]，RC柱内纵筋在发生锈蚀后，屈服强度、极限伸长率、极限强度等一系列力学性能均出现退化，屈服平台逐步缩短甚至消失，塑性性能下降，而引起锈蚀纵筋力学性能变化的主要原因是纵筋截面面积的减少. 史庆轩等[11]通过对7根带有锈蚀纵筋的RC方柱进行循环往复加载试验指出，对纵筋锈蚀试件，纵筋屈服后沿纵筋方向的裂缝继续开展加宽成为主裂缝，而水平受力裂缝稀疏，当混凝土保护层发生破坏时，纵筋屈曲外露，使试件在达到极限荷载后出现明显的脆性. Ma等[34]通过对13根纵筋锈蚀的RC圆柱进行循环往复加载试验发现，纵筋屈服后，随着构件变形的增大，纵筋锈蚀引起的初始纵向裂缝会不断延伸扩大，最终在构件端部引发保护层的剥落，随后纵向纵筋发生屈曲，核心混凝土被压碎，这与史庆轩等的观点一致. Lavorato等[35]通过对3种不同截面尺寸且带有锈蚀纵筋的RC柱进行循环加载试验指出，锈蚀会减小箍筋及纵筋的截面面积，使得箍筋与纵筋之间产生空隙，从而增大了纵筋的无约束长度，使其过早发生屈曲. 同时，由于箍筋的保护层厚度小于纵筋，因此，箍筋的腐蚀程度要高于纵筋，在高锈蚀率的情况下甚至可能导致箍筋断裂，并基于试验结果提出能体现箍筋与纵筋空隙的表达式，但这一公式还需通过试验和数值模拟来进一步验证.
2.4 加载历程的影响
Suda等[36]通过试验测定了低周往复荷载作用下RC柱中纵筋的应力和应变，指出纵筋屈曲通常发生在反向受力阶段，并且很大程度上依赖于反向受力前的最大拉应变. Rodriguez等[37]对不同长细比的单根纵筋进了循环轴向加载，也得到了与Suda等类似的结果. Moyer等[38]通过对圆形截面纵筋混凝土墩柱进行往复加载试验，进一步研究了加载历程对纵筋屈曲的影响. 试验结果表明，由于受拉侧的混凝土会发生开裂，该侧的纵筋在反向加载时会首先单独受力，从而使该侧纵筋更容易发生屈曲，并且屈曲起始点的位置还与纵筋拉应变的积累相关. Zong等[39]通过建立“full-column”有限元模型分析发现，初始张拉应变确实会影响杆件屈曲的发生，而且初始拉应变越大，纵筋就越早发生屈曲，这一点与之前研究[36-38]得出的结论一致.
2.5 防止普通RC柱纵筋屈曲的相关规定
目前，国内外有关RC结构的设计规范大多未考虑纵筋屈曲行为对结构的影响，主要通过箍筋配置数量、间距以及构造措施来控制纵筋屈曲.
2.5.1 箍筋配置数量
1） 欧洲规范 EN 1998[40]规定，按式（12）来确定箍筋的最小数量.
min{AtsT}=fys∑At1.6fyt, (12) 式中：$ A_{{\mathrm{t}}} $为单肢箍筋的截面面积（mm2），$ s_{\mathrm{T}} $为箍筋间距（m），$ A_{{\mathrm{t}}} $为受箍筋约束的纵向纵筋面积（mm2），$ f_{{\mathrm{yt}}} $为箍筋的屈服强度，$ f_{\mathrm{ys}} $为纵向纵筋的屈服强度.
2） 新西兰混凝土结构标准NZS 3101[41]为了防止纵筋屈曲，对箍筋配置进行了如下规定：
① 对于环形箍筋：
ρs⩾Ast155d1fyfyt1db, (13) 式中：$ \rho_{{\mathrm{s}}} $为体积配箍率，$ A_{{\mathrm{st}}} $为纵筋面积，$ d_1 $为核心混凝土区高度，$d_{\mathrm{b}} $为纵筋直径强度.
② 对于矩形箍筋：
Ate⩾fy∑Ab135fytshdb, (14) 式中：$ A_{{\mathrm{te}}} $为单肢箍筋的截面面积；$ A_{{\mathrm{b}}} $为与箍筋相接的纵筋面积；$ s_{{\mathrm{h}}} $为箍筋间距；$ f_{{\mathrm{yt}}} $为箍筋的屈服强度，取值不得大于800 MPa.
3） 我国《建筑抗震设计规范》（GB 50011—2010）[42]规定，对于框架柱，在地震作用组合下处于小偏心受拉状态时，柱中实际配筋面积应在计算值基础上增加25%，并明确指出是为了避免纵筋在往复荷载作用下先受拉再受压而最终引起屈曲.
2.5.2 箍筋间距
1） 欧洲规范 EN 1998[40]规定，可通过箍筋来限制纵向纵筋发生屈曲，且箍筋应垂直于纵向纵筋布置，间距$ s_{\mathrm{L}} $不超过$ \delta d_{\text {bL }} $，其中：$ d_{\mathrm{bL}} $为纵向纵筋的直径，$ \delta $为与箍筋抗拉强度$ f_{{\mathrm{tk}}} $与屈服强度$ f_{{\mathrm{yk}}} $相关的系数，按式（15）取值.
5⩽δ=2.5(ftk/fyk)+2.25⩽6. (15) 2） 新西兰混凝土结构标准NZS 3101[41]规定，在满足其他设计要求的同时，箍筋间距不应超过6倍的纵筋直径，以防止纵筋屈曲.
3） 美国规范ACI 318R-05[43]规定，横向纵筋的间距不能超过6倍的纵筋直径，用来抑制混凝土剥落后的纵筋屈曲.
4） 我国《建筑抗震设计规范》（GB 50011—2010）[42]对小偏心受拉的框架柱有明确规定，为避免柱中受拉纵筋在屈服后发生屈曲，当抗震等级为一级时，柱密配区箍筋间距不应大于纵筋直径的6倍，抗震等级为二级、三级和四级时，箍筋间距不应大于纵筋直径的8倍. 条文说明中明确指出该规定参考了以往的震害调查经验，当箍筋间距小于8D时，纵筋通常不会在混凝土被压溃前发生屈曲
我国《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）[44]规定，为避免受压纵筋屈曲行为的出现，螺旋箍和矩形箍不应设置过大间距，建议箍筋间距应满足以下条件：
s⩽[3+6(fufy−1)]ds, (16) 式中：$ f_{{\mathrm{u}}} $为纵筋的极限强度，$d_{\mathrm{s}} $为纵筋的直径.
2.5.3 构造措施
1） 欧洲规范 EN 1998[40]规定，沿着直形截面边界，应通过2种方式实现对纵向纵筋的限制：① 箍筋应在一端设有135° 弯钩，在另一端设有135° 或者90° 弯钩. 两边设有135° 弯钩的箍筋可以采用两端搭接形式进行锚固. 若轴压比大于0.3，箍筋不允许使用90° 弯钩. 对于设有不同角度弯钩的箍筋，这些弯钩应在水平向和竖向彼此交错排列. 当截面尺寸较大时，箍筋应该采用弯钩形式锚固并保证足够的搭接长度. ② 采用封闭箍筋局部重叠的方式进行配置，以确保每根纵筋都能受到有效的横向约束. 箍筋的横向（纵向）间距不应超过200 mm.
2） 新西兰混凝土结构标准NZS 3101规定，为抑制纵筋发生屈曲，箍筋应设置90° 弯钩.
2.5.4 对比总结
依据各国规范的相关规定，本文对比了控制钢筋屈曲的措施规定，如表2所示.
表 2 各国规范对比Table 2. Comparison of norms among different countries规定 箍筋
最小数量箍筋间距 构造措施 欧洲规范
EN 1998√ √ √ 新西兰规范
NZS3101 √ √ √ 美国规范
ACI 318—05√ 我国规范 √ √ 尽管目前各国设计规范中对纵筋屈曲的控制以保守为主，尚未真正将纵筋屈曲纳入设计中，但这方面的研究已经相继展开，RC结构的设计正从基于简单预防的极限状态设计思想向基于主动控制屈曲程度或屈曲易损性的概率设计方法发展，这与基于性能的结构抗震设计思想是相一致的[45].
2.6 基于RC柱试验修正的纵筋屈曲本构模型
2.6.1 Gomes-Appleton模型
Gomes等[46]在Giuffre-Menegotto-Pinto模型的基础上，依据塑性铰原理提出纵筋屈曲后软化段的应力-应变关系，假定相邻箍筋之间的纵筋只在屈曲段中部及两端的塑性铰处发生弯曲变形，从而得到软化段的应力-应变关系，并分析考虑和不考虑轴力和弯矩相互影响的纵筋应力-应变. 通过对比指出：当应变较小时，二者得到的应力-应变曲线具有较大差别；当应变较大时，二者的曲线基本相同. 为减轻计算量，忽略轴力与弯矩间相互作用，给出了纵筋的屈曲模型，如图8（a）所示. 图8（b）为按该模型计算得到的纵筋单调受压应力-应变关系. 仇建磊等[45]认为，该模型在一定程度上低估了纵筋屈曲后的承载力，当长细比≤5时，利用该模型计算得到的结果与试验结果出现显著差异，纵筋仍会出现明显的应力退化.
定义加载段曲线AB （加载规则采用Giuffré-Menegotto-Pinto模型）和屈曲曲线CD的交点为P，即为屈曲的开始点. 纵筋屈服后的应力-应变关系为
fs=√2×0.424fyL/D1√εs−ε0, (17) Ω=fsfy=√2×0.424L/D1√εs−ε0, (18) 式中：$ \varepsilon _{{\mathrm{s}}}$为纵筋的应变；$ \varepsilon _{0} $为纵筋应力为0时对应的应变，如图8（a）所示；$ \varOmega $为G-A模型的比例系数.
2.6.2 修正的Gomes-Appleton模型
G-A模型理论简单，程序实现也较为容易，但其模拟结果与试验结果相差较大，如图8（b）所示. 故Brown等[47]对其进行了修正，并将其应用在Opensees平台上的ReinforcingSteel材料本构模型中，如图9所示. 修正后的模型引入了$ \beta、 r、 \gamma $ 3 个参数. 用户可以通过放大因子$\beta_{\mathrm{G}} $来缩放屈曲曲线，并可调整屈曲曲线与未屈曲曲线分岔点（即屈曲起始点）的位置；参数r用于调整屈曲程度，取值范围为0～1，0代表纵筋完全屈曲，1代表未发生屈曲；参数$ \gamma_{\mathrm{G}} $用来调节受压到受拉的过渡曲线与纵轴交点的位置，用来避免在曲线中出现扭结，取值范围为0～1. 具体如式（19）、（20）.
Ωb=βG√323πL/D√εs−ε0, (19) σb=γGfu−Ωb+γG1+γG(γGfu−σ), (20) 式中：$ {{\varOmega }}_{\mathrm{b}} $为修正后G-A模型的比例系数，$ {\sigma }_{\mathrm{b}} $为屈曲后的纵筋应力，$ f_{{\mathrm{u}}} $为纵筋的极限拉应力.
2.6.3 Fragiadakis-Pinho模型
Fragiadakis等[26]认为，结构在地震作用下往往会发生部分卸载再加载的情况，而一些传统模型可能会大大高估结构相应的承载力，并基于Giuffre-Menegotto-Pinto模型和Monti-Nuti模型提出一种能够合理描述纵筋在地震作用下屈曲行为的本构模型，该模型引入了附加记忆规则来解决传统模型的缺陷. 通过悬臂梁和剪力墙结构对该模型进行了验证，发现与试验结果较为一致.
综上所述，本节讨论了不同因素对RC柱中纵筋屈曲行为的影响，并对相关本构模型进行了总结. 但由于观测难度较大、相互作用复杂，使得基于RC短柱直压试验的纵筋屈曲研究在试验结果以及理论分析上都与基于单根纵筋直压试验的纵筋屈曲研究有着很大的差别，有待进一步深入探讨. 此外，通过对比分析可以看出，各国规范对纵筋屈曲的规定仍较为保守，无法满足基于性能的抗震设计需求.
3. 新材料/新构造对纵筋屈曲影响的研究进展
3.1 新材料对纵筋屈曲的影响
随着社会的飞速发展，传统混凝土材料已经无法满足实际工程需求. 力学性能更优越的新材料被广泛应用在实际工程中. 这些新材料在墩柱中的应用会对纵筋的屈曲产生一定影响，本文就目前常见的几种新型材料对纵筋屈曲的影响进行了总结.
3.1.1 FRP材料对纵筋屈曲的影响
FRP （ fiber reinforced polymer）是一种纤维增强复合材料，具有轻质高强、耐腐蚀、耐久性能好、施工便捷等性能特点，广泛用于结构加固中. 不少学者通过试验发现[48-49]，在传统RC柱中，纵向纵筋屈曲加速了混凝土保护层的剥落，从而进一步导致纵向纵筋的横向约束力降低. 而对于有FRP约束的RC柱，混凝土保护层因为受到FRP的约束，使其延性得到很大的提升，也有效延缓了纵筋屈曲的发生. 此外，由于FRP的约束作用，纵筋在荷载作用下发生屈曲后，仍能承受很大的压缩荷载，处于压缩过载状态，继而引发截面内力重分布，将原本由纵筋承担的荷载转移至核心混凝土，提高了构件的承载力和延性.
根据上述研究可知，纵筋的屈曲不可能通过FRP套管完全消除，特别是非圆形截面. 同时，由于FRP的弹性模量较小且层间剪切强度低，在纵筋屈曲以及构件横向变形后，纤维布容易发生破裂，较大地降低其使用性能. 因此，为准确地预测FRP约束RC柱在地震荷载作用下的强度，了解纵筋与FRP套管在受力全过程中的相互作用机制是非常重要的. Sato等[50]通过对墩底使用FRP约束的RC柱进行低周往复加载试验，建立了考虑FRP约束的纵筋屈曲模型，虽然该模型考虑了FRP约束作用对混凝土保护层剥落和纵筋屈曲的影响，但模型中包含了大量的经验公式和系数，使得模型难以使用. Bai等[49,51-52]通过试验指出FRP约束RC柱的纵筋屈曲行为主要取决于纵筋的长细比、屈服应力及侧向约束刚度. 通过对上述影响因素的参数敏感性分析，给出单调轴压作用下考虑FRP约束作用的纵筋应力-应变关系. 在此基础上，结合Menegotto-Pinto模型中的滞回规则建立可考虑FRP约束作用对纵筋屈曲影响的纵筋本构模型，并基于OpenSees软件平台对该本构模型的有效性进行了验证，所得的数值模拟结果与试验结果吻合较好. 然而，该本构模型仅适用于FRP约束力分布均匀的圆形截面RC柱，对于FRP约束力分布不均匀的矩形截面RC柱是否适用还有待进一步验证. 此外，还需注意的是，该模型只考虑了纵筋发生局部屈曲的情形，并未考虑纵筋发生整体屈曲的情形.
3.1.2 TRM材料对纵筋屈曲的影响
Bournas等[53]通过对FRP约束以及TRM约束RC柱进行轴压试验发现，纤维编织网增强砂浆又称纤维编织网增强精细混凝土（TRM），可以有效地延缓RC柱中纵筋的屈曲，提高构件延性，但在强化构件方面，TRM相较于等强度和刚度的FRP较弱. 随后，Bournas等[47,54-55]又通过13根足尺墩柱的循环往复加载试验对TRM加固RC柱进行了研究，指出纵筋开始屈曲的临界轴向应变取决于纵筋的长细比. 此外，对于采用不同加固方式的RC柱，纵筋屈曲的初始轴向应变值都很接近，约为0.7%. 与未加固RC柱相比，TRM加固RC柱中纵筋的屈曲延后了3～7次循环加载. 与同等强度和刚度的FRP相比，TRM加固RC柱的变形能力提高了50%，而使用光圆纵筋的TRM加固RC柱的变形能力基本不变. 此外，纵筋屈曲后TRM加固RC柱的力学行为仍与加固层的刚度相关，这一点与FRP相似. 然而，由于TRM在耐久性、耐高温性以及经济性等方面均有优于FRP的表现，且能在潮湿等复杂环境下完成修复加固，因此，TRM加固同样被认为是一种极具发展前景的结构加固方式.
3.1.3 FRC材料对纵筋屈曲的影响
纤维增强混凝土（FRC）是掺加一定量短切纤维的混凝土，目前常见的有UHPC （ultra high performance concrete） 和ECC （engineered cementitious composite） 2种.
Hung等[56]通过试验研究了加筋UHPC短柱的抗压性能. 研究发现，当体积纤维含量大于0.75%时，钢纤维可以有效抑制混凝土保护层的剥落和裂缝的扩大，提高UHPC柱的轴向承载力，而当体积纤维含量大于1.5%时，钢纤维能够替代部分箍筋的作用，防止纵筋在轴向荷载作用下过早屈曲. 胡锐等[57]对5根UHPC足尺柱试件进行了低周往复加载试验，研究发现，钢纤维掺量的提高能够有效提高UHPC柱的抗震性能. 随着钢纤维掺量的提高，混凝土的整体性得到加强，有效延缓了混凝土的压溃破坏，限制了裂缝的发展，对受压纵筋屈曲行为起到了抑制作用，从而提高了构件的延性. Li等[58]对4根墩柱进行了低周往复加载试验并进行了数值模拟，其中包括一根常规RC柱和3根塑性铰区使用ECC套管的RC组合柱，研究发现，由于ECC具有多重细密开裂和损伤容限较大的特性，故塑性铰区域的ECC套管在结构发生破坏时不会剥落，能够持续提供有效的侧向约束力，不但可以减轻纵筋的累积损伤，还对纵筋屈曲有明显的抑制作用. 从上述研究可以看出，2种FRC材料都有利于延缓纵筋发生屈曲，但FRC材料对纵筋屈曲的影响仍缺乏试验研究和理论分析，还未建立相应的纵筋屈曲模型.
3.2 新构造对纵筋屈曲的影响
为提高RC柱的抗震性能，国内外学者还提出了一些防止塑性铰区纵筋屈曲的新构造. Ruangrassamee等[59]设计了一套可以有效减缓纵筋屈曲行为的约束套管装置，该约束套管与纵筋之间没有任何浆体材料，并开展了基于约束套管的单根纵筋轴压试验以及RC桥墩循环往复加载试验. Lukkunaprasit等[60]、伍云天等[61]先后基于内部填充砂浆的约束套管，对RC柱进行了循环往复加载试验，研究发现：1） 该屈曲约束装置能够在纵筋承受高轴压时有效抑制屈曲失稳破坏的发生；2） 采用的屈曲约束套管的外表面是光滑的，虽然对柱轴向承载力并没有产生明显影响，但降低了纵筋与混凝土间的黏结效应，且不利于裂缝控制；3） 要使受屈曲约束的纵筋充分发挥作用，须保证有效传递柱中轴向荷载；4） 该装置能够产生类似于箍筋的横向约束作用，但箍筋用量能否相应减少，尚需进一步研究. 如图10所示，张文涛等[62]提出了一种相类似的屈曲约束装置，内部采用泡沫填充，并通过一系列试验对比研究了该装置的力学性能与壁厚、套管长度及纵筋与套筒间隙等因素的关系，如图11所示. 通过试验发现：尽管该装置无法完全避免屈曲行为的发生，纵筋在试件破坏后仍会发生局部屈曲，但相较于无套管约束纵筋，纵筋屈曲得到明显改善；该装置能够在不影响纵筋拉伸性能的情况下提高纵筋抵抗横向变形的能力，是一种能够有效提升RC构件延性性能的措施.
4. 结束语
本文针对RC结构中常见的纵筋屈曲行为，对国内外学者的相关研究进行了概括总结. 虽然有关纵筋屈曲的研究取得了较为丰硕的成果，但仍有问题需要进一步研究.
1） 基于RC短柱直压试验的纵筋屈曲研究仍缺乏科学、有效的方法，目前对纵筋屈曲方向、屈曲范围的判断大多是经验性的，缺少相关的理论支持.
2） 既有研究大都集中于箍筋间距较大、箍筋约束充足条件下的纵筋局部屈曲，即纵筋屈曲行为发生在相邻两箍筋之间. 而在实际工程中，构件往往会出现整体屈曲的情况，此类屈曲的受力情况更为复杂，屈曲范围更难控制和观察，有待进一步研究.
3） 国内外学者基于单根纵筋的直拉试验和RC短柱的直拉试验，提出一些与试验数据吻合良好的纵筋屈曲本构模型，但对新型RC结构（即采用新材料和新构造）中的纵筋屈曲行为缺乏系统性的研究.
4） 目前大多数本构模型的参数化研究对象都集中在长细比、屈服强度等因素，对锈蚀、加载历程以及截面形式（圆形、方形、矩形等）等参数的研究相对较少. 此外，RC结构中纵筋的屈曲行为十分复杂，不仅跟纵筋自身的力学特性息息相关，核心混凝土、箍筋、混凝土保护层等其他组成材料的力学特性及其与纵筋的相互作用对纵筋的屈曲行为也有一定影响. 因此，有待提出更为全面的纵筋屈曲本构模型.
5） 各国规范中对控制纵筋屈曲的措施相对保守，主要集中在控制箍筋方面（数量、间距、构造等），对其他可能影响纵筋屈曲行为的因素考虑较少，且大多尚都只是定性、保守的控制，无法满足基于性能的抗震设计需求.
-
图 1 石林、石墙、石丛地貌及石墙走向
Figure 1. Morphologies of stone forest, stone wall, stone cluster, and direction of stone wall
图 3 多手段获取的斜坡岩体卸荷特征
Figure 3. Unloading characteristics of slope obtained using various methods
图 4 坡面小型溶洞沿构造线分布示意
Figure 4. Distribution of small caves of slope along structural lines
图 7 某隧道进口斜坡推测潜在失稳模式
Figure 7. Potential instability patterns of slope at tunnel entrance
表 1 斜坡岩体力学参数建议值
Table 1. Suggested mechanical parameters of slope rock masses
岩体质量等级 干密度 ρd/（g·cm−3） 变形模量 E0/GPa 泊松比 μ 抗剪断强度 摩擦系数 黏聚力/MPa Ⅱ 类 2.52～2.58 (10, 20] [0.25, 0.29] (1.20, 1.40] (1.50～2.00] Ⅲ 类 2.30～2.50 (5, 10] (0.29, 0.33] (0.80, 1.20] (0.70～1.50] Ⅳ 类 2.10～2.40 [2, 5) (0.33, 0.37] [0.55, 0.80] [0.30～0.70] 
下载: 导出CSV
表 2 结构面强度试验成果
Table 2. Test results of structural surface strength
试验编号 试验位置/m 抗剪断强度 抗剪强度 地质特征 摩擦系数 黏聚力/MPa 摩擦系数 黏聚力/MPa 1-1 PDG01 洞 0+150 m 1.09 1.33 0.87 0.20 主要为压碎带弱风化大理岩，但剪切主要沿压碎带及其影响带剪断 1-2 PDG01 洞 0+71 m 0.81 1.34 0.70 0.51 弱风化大理岩，碎裂结构，岩级为 Ⅳ 岩体
下载: 导出CSV
-
[1] 王振涛. 青藏高原的地质特征与形成演化[J]. 科技导报,2017,35(6): 51-58.WANG Zhentao. Geological features, the formation and the evolution of the Qinghai—Tibetan Plateau[J]. Science & Technology Review, 2017, 35(6): 51-58. [2] 刘刚,燕云鹏,刘建宇. 青藏高原西部地质灾害分布特征及背景分析[J]. 中国地质调查,2017,4(3): 37-45.LIU Gang, YAN Yunpeng, LIU Jianyu. Analysis of distribution character and background of geological hazards in western Qinghai—Tibet Plateau[J]. Geological Survey of China, 2017, 4(3): 37-45. [3] ZHAO S Y, HE Z L, DENG J H, et al. Giant river-blocking landslide dams with multiple failure sources in the Nu River and the impact on transient landscape evolution in southeastern Tibet[J]. Geomorphology, 2022, 413: 108357.0-108357.16. [4] CUI Y L, DENG J H, HU W Y, et al. 36Cl exposure dating of the Mahu Giant landslide (Sichuan Province, China)[J]. Engineering Geology, 2021, 285: 106039.1-106039.11. [5] 杨帆. 西部山区大型滑坡分类及识别图谱初步研究[D]. 成都: 成都理工大学, 2017. [6] 陈帆,刘立,陆海空,等. 岩质高陡边坡稳定性分析[J]. 西华大学学报(自然科学版),2010,29(3): 54-55,94.CHEN Fan, LIU Li, LU Haikong, et al. Stability analysis of high and steep rock slope[J]. Journal of Xihua University (Natural Science Edition), 2010, 29(3): 54-55,94. [7] 雷远见,王水林. 基于离散元的强度折减法分析岩质边坡稳定性[J]. 岩土力学,2006,27(10): 1693-1698.LEI Yuanjian, WANG Shuilin. Stability analysis of jointed rock slope by strength reduction method based on UDEC[J]. Rock and Soil Mechanics, 2006, 27(10): 1693-1698. [8] 邓建辉,高云建,余志球,等. 堰塞金沙江上游的白格滑坡形成机制与过程分析[J]. 工程科学与技术,2019,51(1): 9-16.DENG Jianhui, GAO Yunjian, YU Zhiqiu, et al. Analysis on the formation mechanism and process of baige landslides damming the upper reach of Jinsha River, China[J]. Advanced Engineering Sciences, 2019, 51(1): 9-16. [9] GAO Y J, ZHAO S Y, DENG J H, et al. Flood assessment and early warning of the reoccurrence of river blockage at the Baige landslide[J]. Journal of Geographical Sciences, 2021, 31(11): 1694-1712. doi: 10.1007/s11442-021-1918-9 [10] CHEN F, GAO Y J, ZHAO S Y, et al. Kinematic process and mechanism of the two slope failures at Baige Village in the upper reaches of the Jinsha River, China[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(4): 3475-3493. doi: 10.1007/s10064-021-02146-0 [11] YANG Z K, WEI J B, DENG J H, et al. Mapping outburst floods using a collaborative learning method based on temporally dense optical and SAR data: a case study with the baige landslide dam on the Jinsha River, Tibet[J]. Remote Sensing, 2021, 13(11): 2205.1-2205.21. [12] 朱赛楠,殷跃平,王猛,等. 金沙江结合带高位远程滑坡失稳机理及减灾对策研究——以金沙江色拉滑坡为例[J]. 岩土工程学报,2020,43(4): 688-697.ZHU Sainan, YIN Yueping, WANG Meng, et al. Instability mechanism and disaster mitigation measures of long-distance landslide at high location in Jinsha River junction zone: case study of Sela landslide in Jinsha River, Tibet[J]. Chinese Journal of Geotechnical Engineering, 2020, 43(4): 688-697. [13] ZHANG S L, YIN Y P, HU X W, et al. Geo-structures and deformation-failure characteristics of rockslide areas near the Baige landslide scar in the Jinsha River tectonic suture zone[J]. Landslides, 2021, 18(11): 3577-3597. doi: 10.1007/s10346-021-01741-2 [14] 刘文,王猛,朱赛楠,等. 基于光学遥感技术的高山极高山区高位地质灾害链式特征分析——以金沙江上游典型堵江滑坡为例[J]. 中国地质灾害与防治学报,2021,32(5): 29-39.LIU Wen, WANG Meng, ZHU Sainan, et al. An analysis on chain characteristics of highstand geological disasters in high mountains and extremely high mountains based on optical remote sensing technology: a case study of representative large landslides in upper reach of Jinsha River[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(5): 29-39. [15] YAO X, LI L J, ZHANG Y S, et al. Types and characteristics of slow-moving slope geo-hazards recognized by TS-InSAR along Xianshuihe active fault in the eastern Tibet Plateau[J]. Natural Hazards, 2017, 88(3): 1727-1740. doi: 10.1007/s11069-017-2943-y [16] 郭长宝,吴瑞安,李雪,等. 川西日扎潜在巨型岩质滑坡发育特征与形成机理研究[J]. 工程地质学报,2020,28(4): 772-783.GUO Changbao, WU Ruian, LI Xue, et al. Developmental characteristics and formation mechanism of the rizha potential giant rock landslide, western Sichuan Province, China[J]. Journal of Engineering Geology, 2020, 28(4): 772-783. [17] 谭明健, 周春梅, 孙东, 等. 软硬互层顺层岩质边坡破坏试验[J]. 地质科技通报, 2022, 41(2): 274-281, 324.TAN Mingjian, ZHOU Chunmei, SUN Dong, et al. Failure experiment of soft-hard interlayer bedding rock slope, 2022, 41(2): 274-281, 324. [18] 黄少平,晏鄂川,尹晓萌,等. 不同临空条件的层状反倾岩质边坡倾倒变形几何特征参数影响规律[J]. 地质科技通报,2021,40(1): 159-165.HUANG Shaoping, YAN Echuan, YIN Xiaomeng, et al. Action law of geometrical characteristic parameters in the anti-dip rock slopes under different free face conditio[J]. Bulletin of Geological Science and Technology, 2021, 40(1): 159-165. [19] 伍保祥. 金沙江上游波罗水电站库区滑坡发育规律及岸坡稳定性风险分析[D]. 成都: 成都理工大学, 2008. [20] 帅正阳. 叶巴滩水电站坝区右岸深部变形破裂成因模拟研究[D]. 成都: 成都理工大学, 2017. [21] 朱吉龙. 溪洛渡库区滑坡地质灾害风险评价研究[D]. 成都: 西南石油大学, 2019. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 319
- HTML全文浏览量: 165
- PDF下载量: 80
- 被引次数: 0