基于机器学习算法的智能编组站5G天线参数规划

陈建译; 闫连山; 郭兴海; 钟章队

doi:10.3969/j.issn.0258-2724.20220329

基于机器学习算法的智能编组站5G天线参数规划

doi: 10.3969/j.issn.0258-2724.20220329

陈建译^{1, 2,},
闫连山^1, ,,
郭兴海³,
钟章队^{3, 4}

1.
西南交通大学信息科学与技术学院，四川成都 611756
2.
中国铁路广州局集团有限公司，广东广州 510008
3.
北京交通大学轨道交通控制与安全国家重点实验室，北京 100044
4.
北京交通大学宽带移动信息通信铁路行业重点实验室，北京 100044

基金项目: 国家自然科学基金重点项目（61735015）；中国国家铁路集团有限公司重大科研课题（K2018G053，N2021S003）；四川省科技计划项目（2019ZDZX0007）；

详细信息

作者简介:
陈建译（1964—），男，正高级工程师，研究方向为轨道交通通信信号，E-mail：cjy45220@126.com

通讯作者:
闫连山(1971—)，男，教授，博士，研究方向为信息光子与通信，E-mail：lsyan@home.swjtu.edu.cn

中图分类号: O454
计量
- 文章访问数: 95
- HTML全文浏览量: 29
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-13
- 修回日期: 2022-08-02
- 网络出版日期: 2024-12-16

5G Antenna Parameter Planning for Intelligent Marshalling Station Based on Machine Learning Algorithm

CHEN Jianyi^{1, 2
,},
YAN Lianshan^{1
, ,},
GUO Xinghai³,
ZHONG Zhangdui^{3, 4}

1.
School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756, China
2.
China Railway Guangzhou Bureau Co. Ltd., Guangzhou 510088, China
3.
State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China
4.
Key Laboratory of Railway Industry of Broadband Mobile Information Communications, Beijing Jiaotong University, Beijing 100044, China

摘要

摘要:
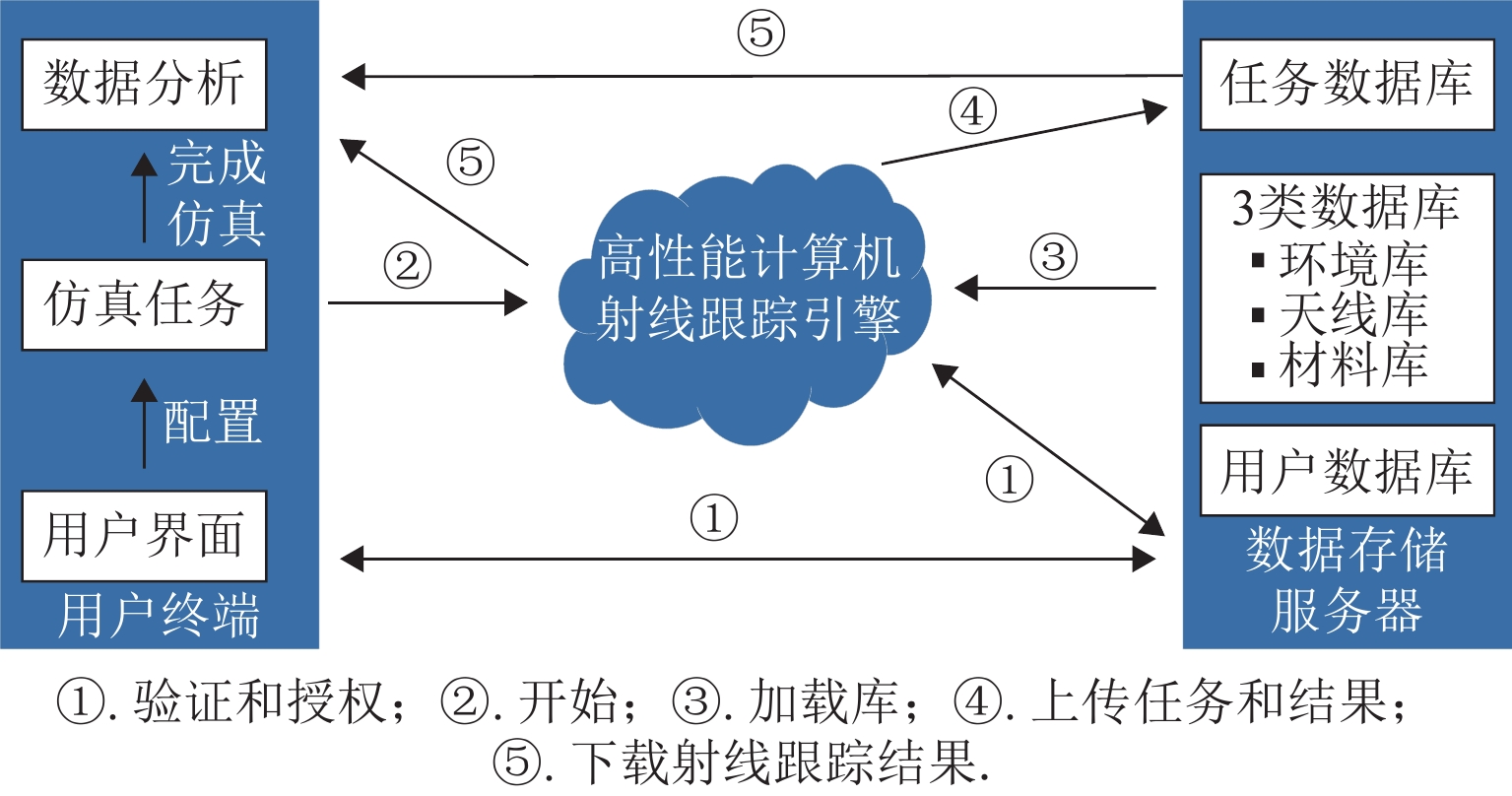
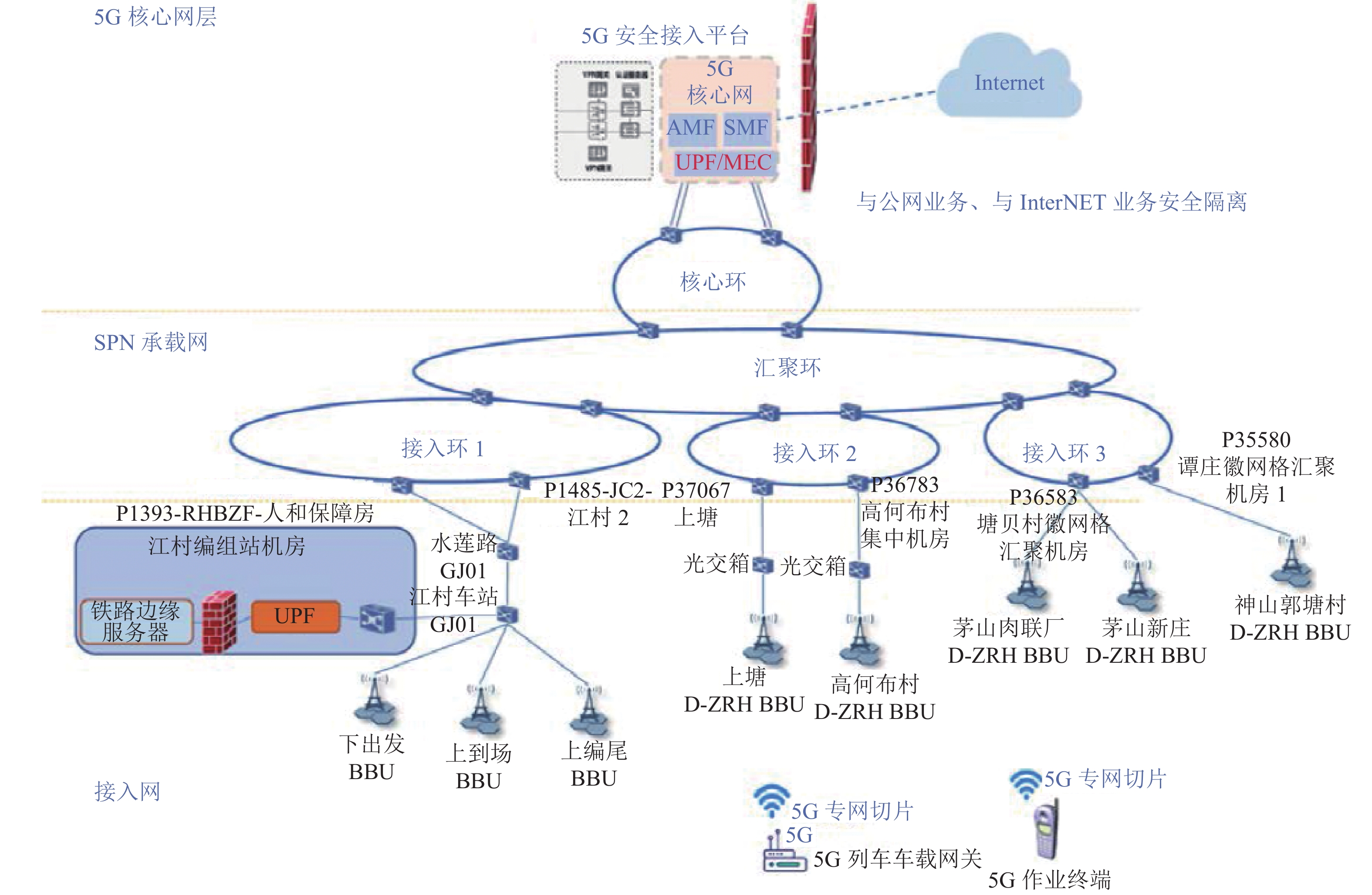
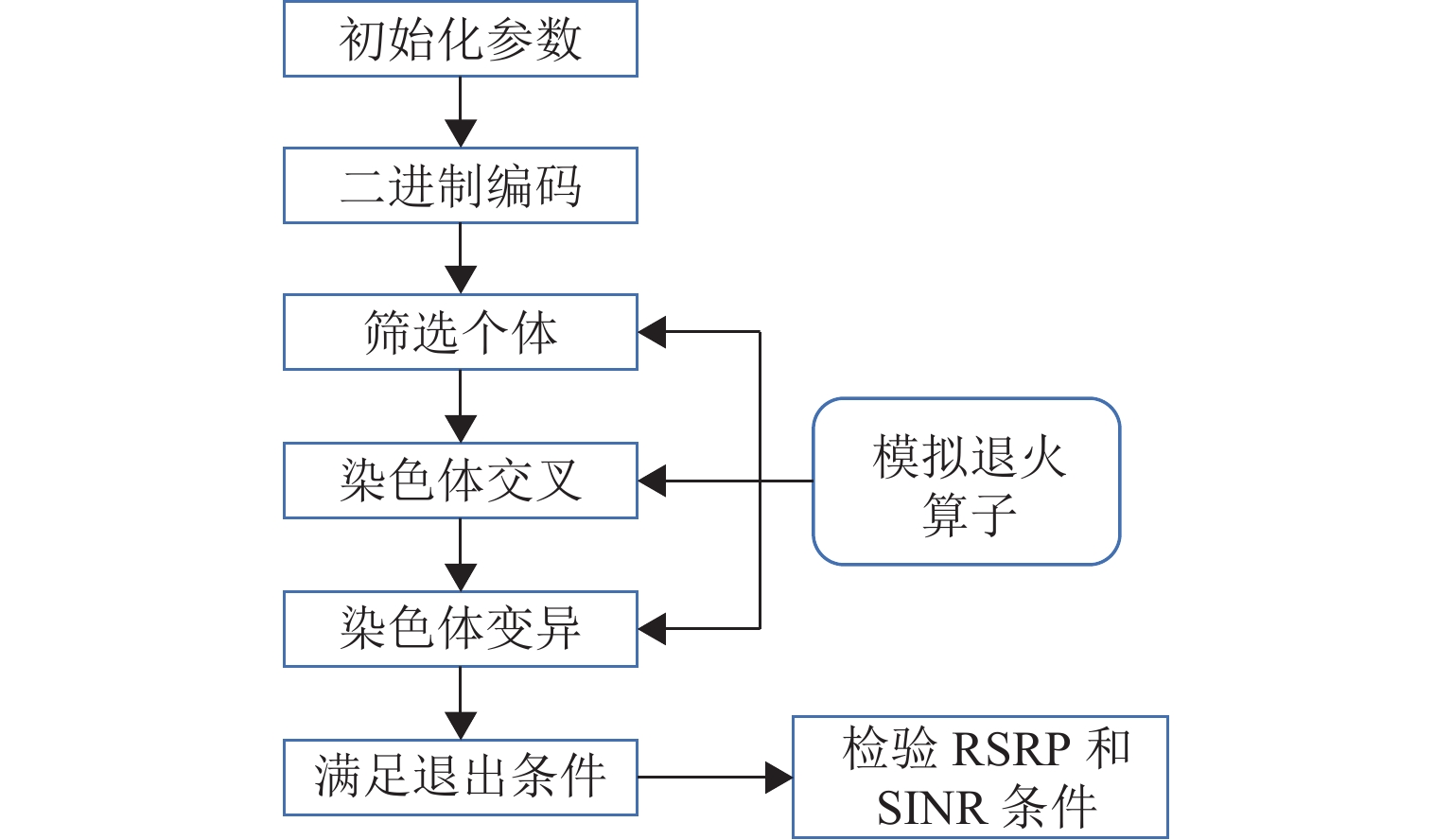
第5代移动通信技术（5G）具有连接速率高与系统容量大等优势，是编组站通信系统向未来演进的重要支撑，为解决所涉及天线参数规划技术面临计算量大、效率和准确性难以兼顾的难题，基于CloudRT射线跟踪平台仿真场景信号覆盖情况，综合考虑通信基站天线角度选取及功率优化问题，提出一种基于机器学习算法的规划方法. 首先，基于重叠复杂度和聚类算法对天线角度参数聚类，并对聚类结果进行评估；其次，根据天线增益与角度的关系设计优化算法，简化天线角度参数组合的筛选过程；最后，在遗传算法中引入模拟退火算子求解最优功率组合，以江村编组站为场景进行验证. 研究结果表明：本文方法所得总功率比遍历算法高5.6 dB，所用时间为遍历算法的13.5%，同时实现了准确性和高效性，有望应用到未来高铁和编组站的5G系统中.
- 5G /
- 编组站 /
- 机器学习 /
- 聚类算法 /
- 混合遗传算法
Abstract:
The 5th generation mobile communication technology (5G) has advantages such as a high connection rate and large system capacity, which can support the development of marshalling station communication systems. However, the 5G antenna parameter planning is challenging due to the large amount of calculation, and it is difficult to achieve both high efficiency and accuracy simultaneously. Therefore, Based on the CloudRT ray-tracing (RT) platform, the signal coverage scenario was simulated. By considering the problem of angle selection and power optimization of communication base station antenna, a planning method based on a machine learning algorithm was proposed. Firstly, based on the overlap complexity and the clustering algorithm, the antenna angle parameters were clustered, and the clustering results were evaluated. Secondly, according to the relationship between antenna gain and angle, the optimization algorithm was designed to simplify the selection process of antenna angle parameter combinations. Finally, the simulated annealing operator was introduced into the genetic algorithm to solve the optimal power combination, and Jiangcun Marshalling Station was taken as the scenario for verification. The results indicate that the total power derived by the proposed method is 5.6 dB higher than that of the traversal algorithm, and the time required is only 13.5% of the traversal algorithm. It achieves high efficiency and accuracy simultaneously, which is expected to be applied to the 5G system of high-speed railways and marshalling stations.
- 5G /
- marshalling station /
- machine learning /
- clustering algorithm /
- hybrid genetic algorithm

HTML全文

图 1 混合遗传算法流程

Figure 1. Hybrid genetic algorithm flow

下载: 全尺寸图片幻灯片

图 2 CloudRT使用流程

Figure 2. Application of CloudRT

下载: 全尺寸图片幻灯片

图 3 江村编组站布局示意与俯视图

Figure 3. Layout and top view of Jiangcun Marshalling Station

下载: 全尺寸图片幻灯片

图 4 对数欧氏距离排序

Figure 4. Ranking for logarithmic euclidean distance

下载: 全尺寸图片幻灯片

图 5 层次聚类树

Figure 5. Hierarchical clustering tree

下载: 全尺寸图片幻灯片

图 6 江村编组站5G网络组

Figure 6. 5G network of Jiangcun Marshalling Station

下载: 全尺寸图片幻灯片

图 8 江村编组站RSRP

Figure 8. RSRP of Jiangcun Marshalling Station

下载: 全尺寸图片幻灯片

图 9 江村编组站SINR

Figure 9. SINR of Jiangcun Marshalling Station

下载: 全尺寸图片幻灯片

图 7 江村编组站5G服务基站位置分布

Figure 7. Location of 5G service base stations at Jiangcun Marshalling Station

下载: 全尺寸图片幻灯片

表 1 基站和天线配置

Table 1. Configuration of base stations and antennas

参数	配置
中心频率/GHz	2.1
天线增益/dBi	19
基站高度/m	15
车载接收天线位置	沿部分铁轨间隔20 m撒点
车载接收天线高度/m	4.57
子载波带宽/kHz	15

下载: 导出CSV

表 2 2.1 GHz材料电磁参数

Table 2. Electromagnetic parameters of materials at 2.1 GHz

材料	介电常数实部	损耗角正切
金属	1.00	1000000.00
地砖	1.83	0.31
红砖	1.44	0.11
木材	1.28	0.01

下载: 导出CSV

表 3 各聚类方法结果对比

Table 3. Comparison of results of each clustering algorithm

聚类方法	聚类簇数	Calinski-Harabaz指数
KNA-DBSCAN	19	2.0077 × 10⁷
K-means + +	27	1.5512 × 10⁷
层次聚类	23	2.1164 × 10⁶

下载: 导出CSV

表 4 功率优化初始化参数取值

Table 4. Initialized parameter configuration for power optimization

参数	取值
N_S	216
T_d	200
p_m	0.4
p_c	0.03
t	100

下载: 导出CSV

表 5 混合遗传算法和遍历算法得出的天线参数

Table 5. Antenna parameters derived from hybrid genetic algorithm and traversal algorithm

组数	1号天线		2号天线		3号天线		总功率/dBm
组数	角度组合	发射功率	角度组合	发射功率	角度组合	发射功率	总功率/dBm
1	（0°,4°）	−4 dBm	（180°,5°）	18 dBm	（120°,3°）	2 dBm	18.1
2	（0°,4°）	−11 dBm	（180°,5°）	18 dBm	（120°,2°）	−7 dBm	20.0
3	（0°,5°）	1 dBm	（60°,5°）	22 dBm	（60°,1°）	7 dBm	22.2
4	（0°,4°）	−3 dBm	（180°,5°）	18 dBm	（300°,1°）	−8 dBm	18.0
5	（0°,4°）	−8 dBm	（180°,5°）	18 dBm	（300°,2°）	0 dBm	18.1
6	（0°,5°）	8 dBm	（60°,5°）	22 dBm	（60°,1°）	4 dBm	22.2
7	（0°,4°）	−9 dBm	（180°,5°）	18 dBm	（60°,1°）	0 dBm	18.1
8	（0°,5°）	0 dBm	（60°,5°）	22 dBm	（60°,1°）	4 dBm	22.1
9	（0°,4°）	−3 dBm	（180°,5°）	18 dBm	（300°,1°）	−8 dBm	18.0
10	（0°,4°）	−6 dBm	（180°,5°）	24 dBm	（120°,2°）	−5 dBm	24.0
遍历算法	（240°,5°）	−6 dBm	（300°,5°）	16 dBm	（180°,1°）	−6 dBm	16.1

下载: 导出CSV

表 6 本文方法所需时间表

Table 6. Time required for proposed algorithm

算法	本文方法所需时间
K-means + + 算法	1 h 52 min
层次聚类算法	1 h 15 min
DBSCAN算法	20 min
求R值算法	< 1 min
基于R值的筛选	< 1 min
混合遗传算法	6 h 29 min
总时间	9 h 56 min

下载: 导出CSV

表 7 江村编组站5G基站信息表

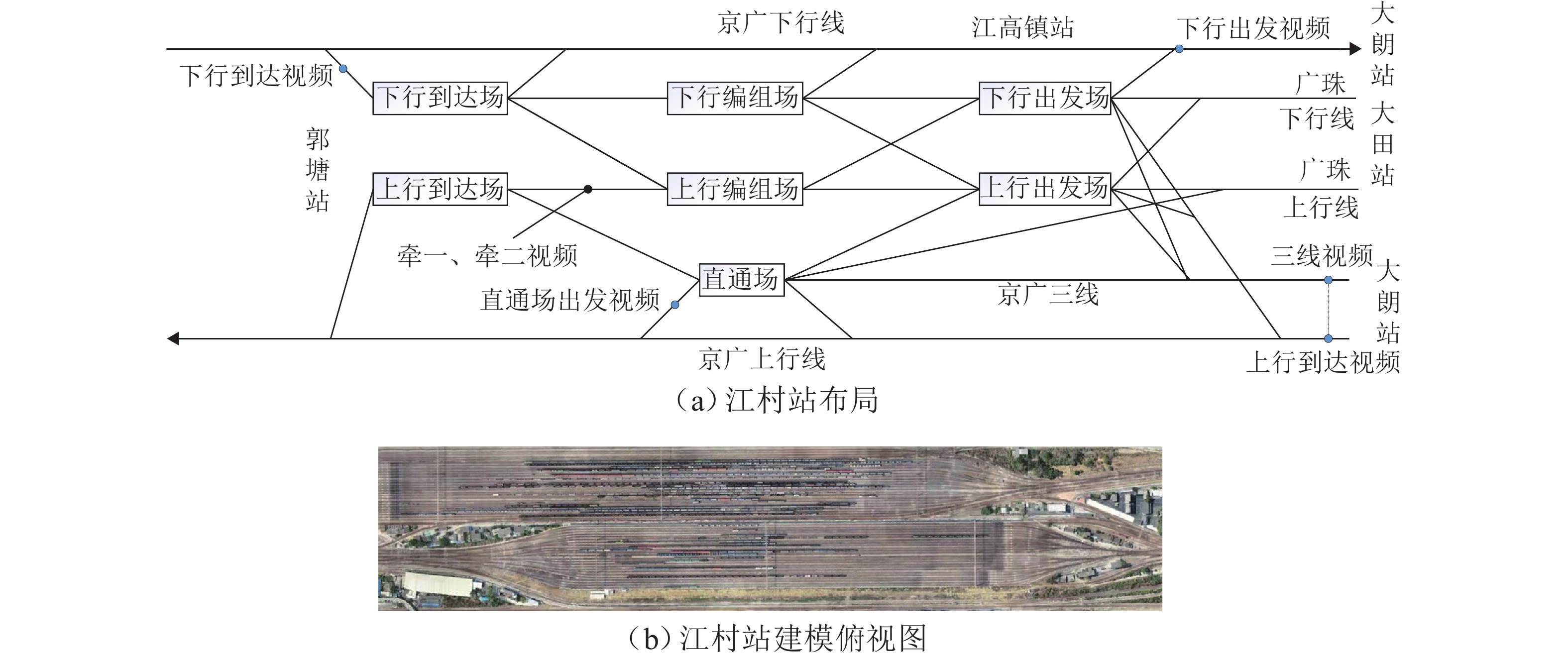
Table 7. Configurations of 5G base stations at Jiangcun Marshalling Station

站点名称	小区名称	高度/ （°）	水平角/ （°）	俯仰角/ （°）
广州白云区江村车站上编尾	D-ZRH-1	39	80	6
	D-ZRH-2	39	190	6
	D-ZRH-3	39	320	6
广州白云区江村车站下出发	D-ZRH-1	24	30	6
	D-ZRH-2	24	130	6
	D-ZRH-3	24	240	6
	D-ZRH-4	24	320	6
广州白云区江村车站上到场	D-ZRH-1	21	60	3
	D-ZRH-2	21	190	3
	D-ZRH-3	21	290	6

下载: 导出CSV

表 8 覆盖情况

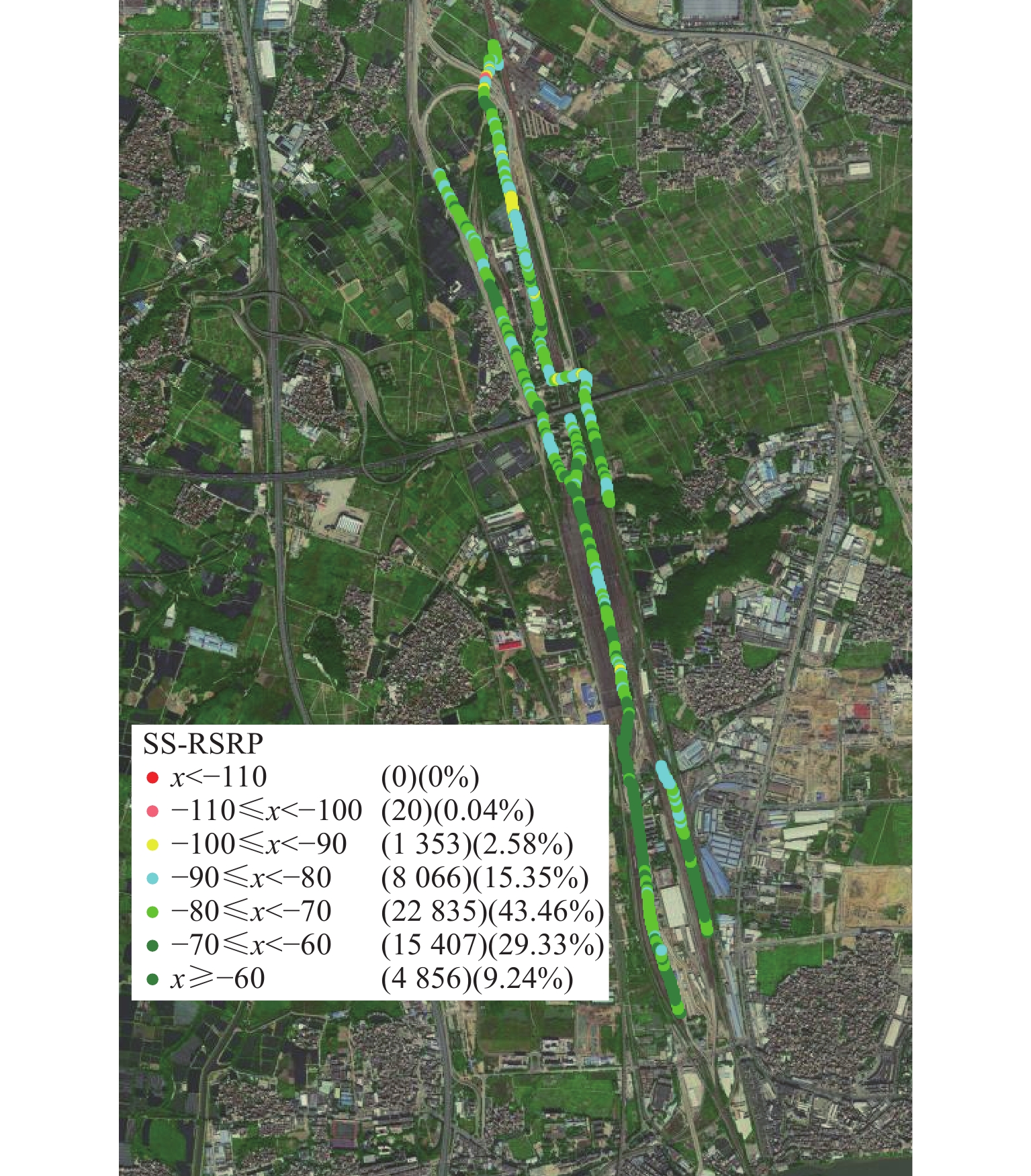
Table 8. Coverage situation

参数	配置
覆盖率/%	98.87
平均RSRP/dBm	−73.36
平均SINR/dB	12.43

下载: 导出CSV

参考文献(17)

[1]	AI B, MOLISCH A F, RUPP M, et al. 5G key technologies for smart railways[J]. Proceedings of the IEEE, 2020, 108(6): 856-893. doi: 10.1109/JPROC.2020.2988595
[2]	HE R S, AI B, WANG G P, et al. High-speed railway communications: from GSM-R to LTE-R[J]. IEEE Vehicular Technology Magazine, 2016, 11(3): 49-58. doi: 10.1109/MVT.2016.2564446
[3]	中国国家铁路集团. 新时代交通强国铁路先行规划纲要:铁发改[2020]129号[A/OL]. (2020-08-13)[2022-04-12]. http://www.china-railway.com.cn/xwzx/rdzt/ghgy/gyqw/202008/t20200812_107636.html.
[4]	熊嘉阳,沈志云. 中国高铁永葆工程领跑[J]. 西南交通大学学报,2023,58(4): 711-719. XIONG Jiayang, SHEN Zhiyun. Permanent world-leading position of high-speed railways in China in Engineering [J]. Journal of Southwest Jiaotong University, 2023, 58(4):711-719.
[5]	杨焱,钟章队. 铁路编组站GSM-R分层覆盖系统及其干扰共存分析[J]. 铁道学报,2014,36(12): 40-45. doi: 10.3969/j.issn.1001-8360.2014.12.007 YANG Yan, ZHONG Zhangdui. Analysis on interference co-existence of GSM-R hierarchical coverage system in marshalling yards[J]. Journal of the China Railway Society, 2014, 36(12): 40-45. doi: 10.3969/j.issn.1001-8360.2014.12.007
[6]	KASEM F, HASKOU A, DAWY Z. On antenna parameters self optimization in LTE cellular networks[C]//2013 Third International Conference on Communications and Information Technology (ICCIT). Beirut: IEEE, 2013: 44-48.
[7]	朱思峰,陈国强,张新刚,等. 多目标优化量子免疫算法求解基站选址问题[J]. 华中科技大学学报(自然科学版),2012,40(1): 49-53. ZHU Sifeng, CHEN Guoqiang, ZHANG Xingang, et al. Multi-objective optimization quantum immune algorithm for solving base stations location planning problem[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(1): 49-53.
[8]	蔡佳祺,万海斌,孙友明,等. 基于人工蜂群算法的基站天线方位角与下倾角自优化方法[J]. 电信科学,2021,37(1): 69-75. doi: 10.11959/j.issn.1000-0801.2021006 CAI Jiaqi, WAN Haibin, SUN Youming, et al. Artificial bee colony algorithm based self-optimization of base station antenna azimuth and down-tilt angles[J]. Telecommunications Science, 2021, 37(1): 69-75. doi: 10.11959/j.issn.1000-0801.2021006
[9]	ZHU F S, CAI W W, WANG Z G, et al. AI-empowered propagation prediction and optimization for reconfigurable wireless networks[J]. Wireless Communications and Mobile Computing, 2022, 2022: 9901960.1-9901960.10.
[10]	胡津铭. 基于能效的无线通信网络资源分配算法研究[D]. 南京: 东南大学,2018.
[11]	田春明,杨安,叶乐,等. 基于贝叶斯算法的天线端到端优化[J]. 系统工程与电子技术,2021,43(12): 3413-3419. doi: 10.12305/j.issn.1001-506X.2021.12.01 TIAN Chunming, YANG An, YE Le, et al. End-to-end antenna optimization based on Bayesian optimization algorithm[J]. Systems Engineering and Electronics, 2021, 43(12): 3413-3419. doi: 10.12305/j.issn.1001-506X.2021.12.01
[12]	RAJ N. Indoor RSSI Prediction using machine learning for wireless networks[C]//2021 International Conference on COMmunication Systems & NETworkS (COMSNETS). Bangalore: IEEE, 2021: 9352852.1-9352852.3.
[13]	唐苏文,陈明. 基于改进粒子群算法的分布式天线系统跨层功率分配方案[J]. 高技术通讯,2010,20(2): 138-142.
[14]	侯雄文. 浅析DBSCAN算法中参数设置问题的研究[J]. 科教导刊-电子版(下旬),2017(10): 266,277.
[15]	北京乾径科技有限公司. CloudRT高性能云计算射线跟踪仿真平台[EB/OL].[2021-09-23]. http://cn.raytracer.cloud
[16]	HE D P, AI B, GUAN K, et al. The design and applications of high-performance ray-tracing simulation platform for 5G and beyond wireless communications: a tutorial[J]. IEEE Communications Surveys & Tutorials, 2019, 21(1): 10-27.
[17]	中国移动通信. 4G网络高速铁路覆盖技术需求[EB/OL]. (2016-06-03)[2022-02-13]. https://max.book118.com/html/2016/0603/44748063.shtm