Vehicle Trajectory Reconstruction Model of Signalized Intersection in Connected Automated Environments
-
摘要:
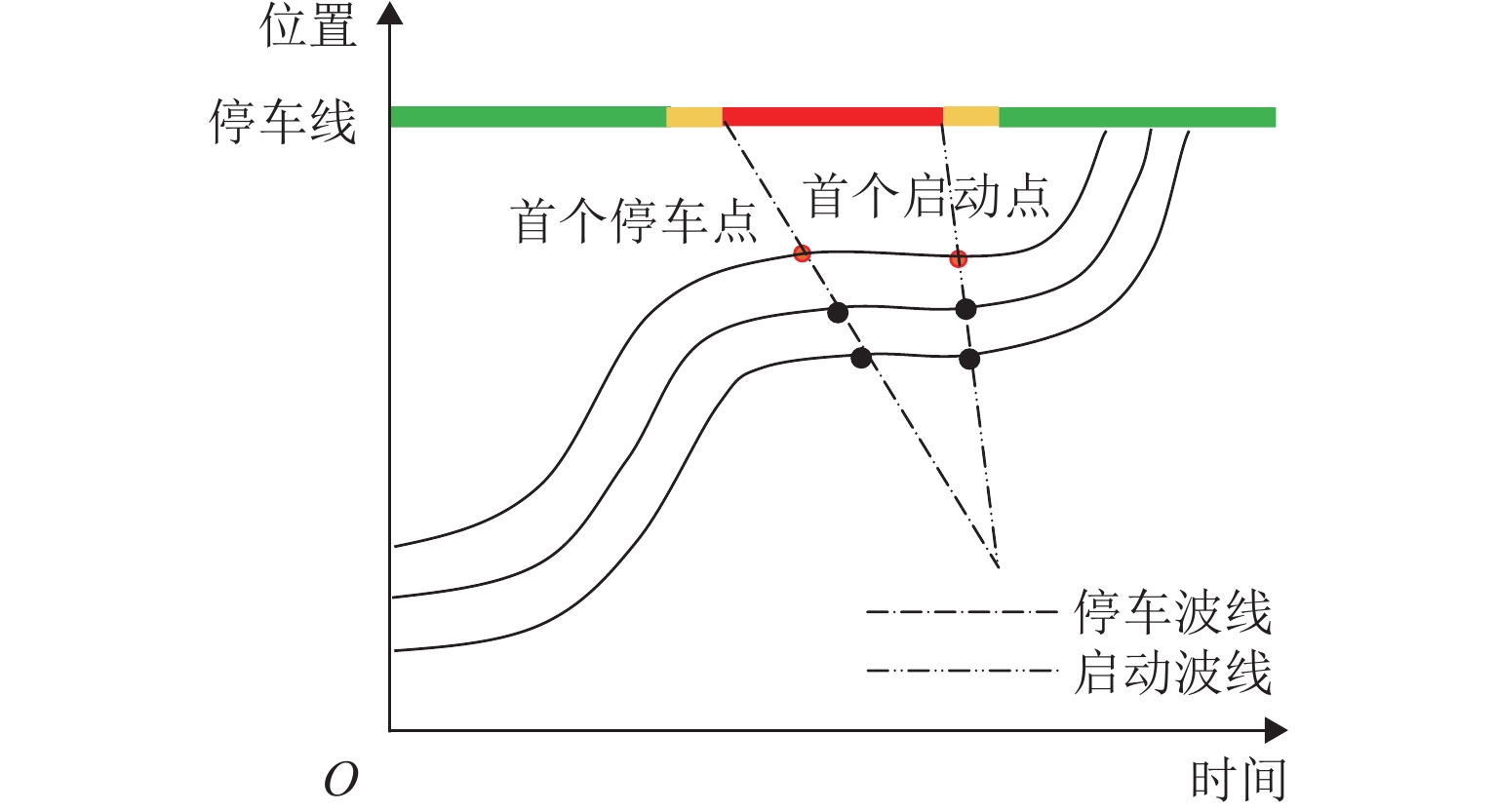
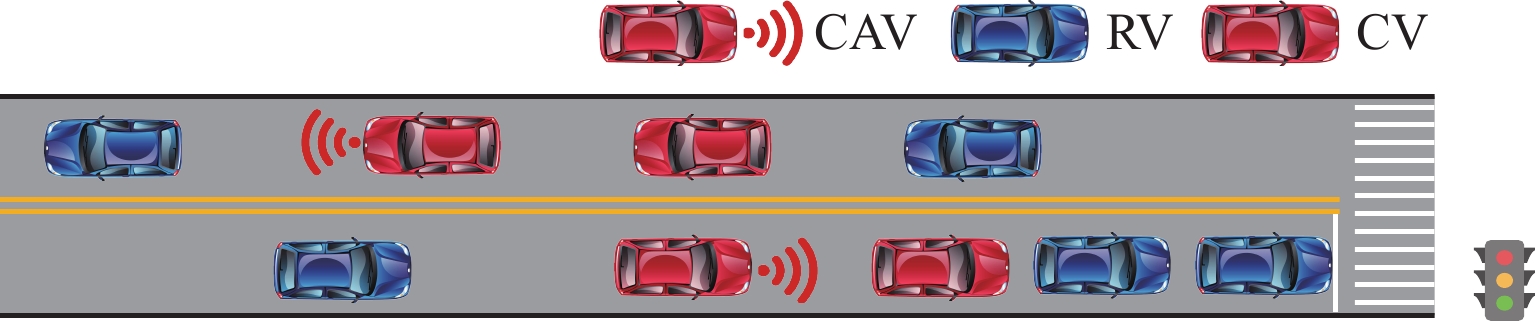
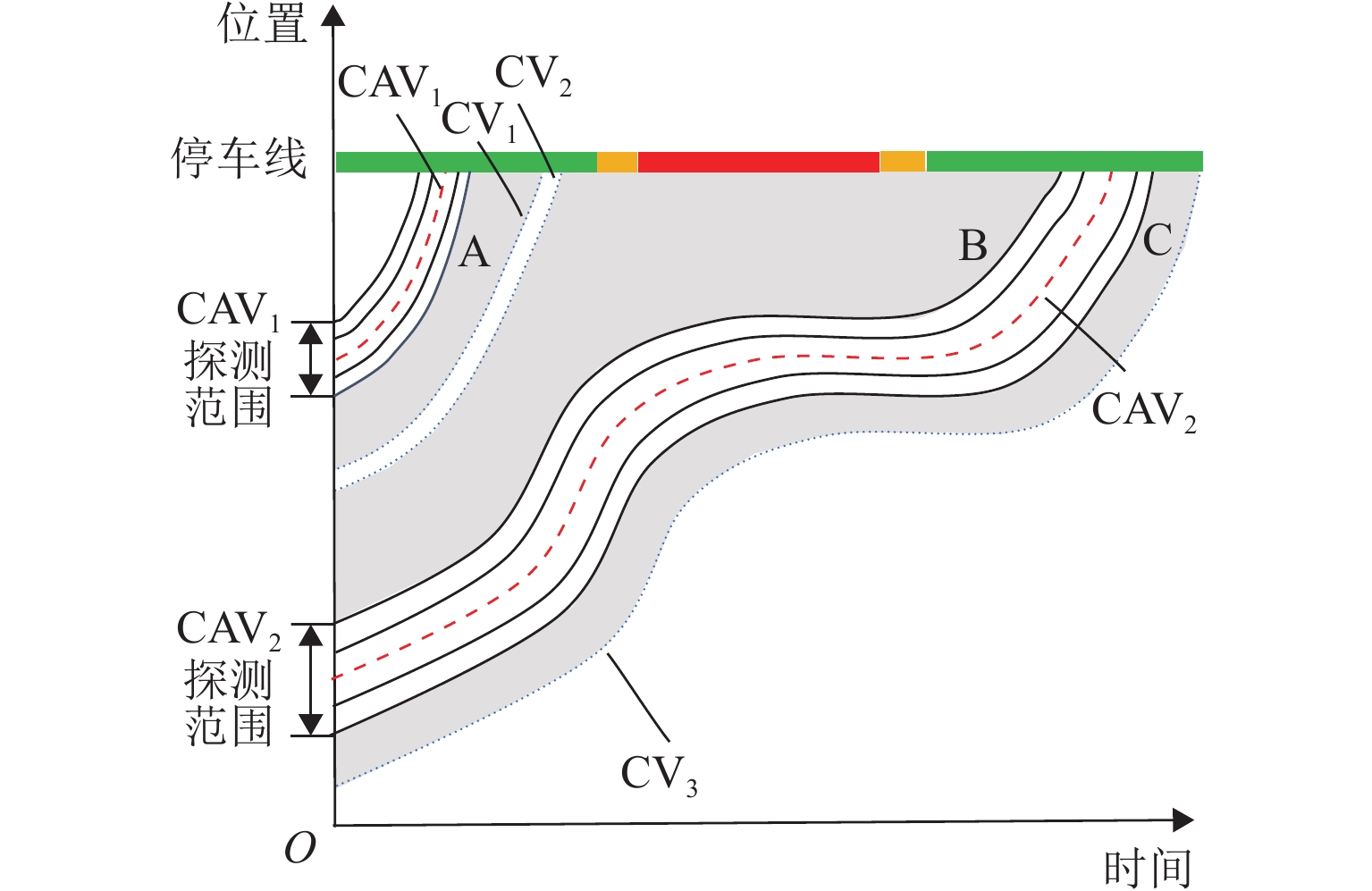
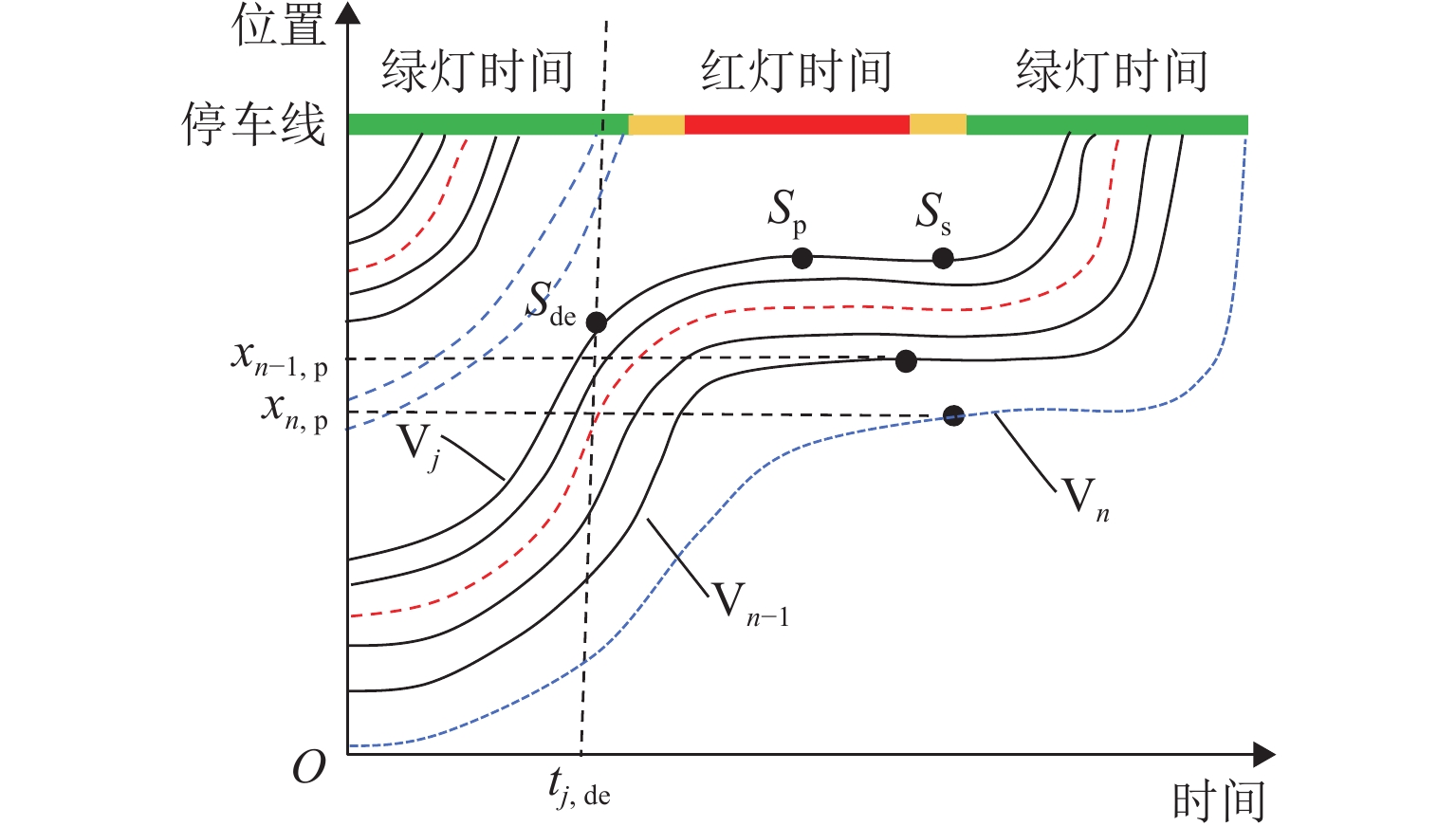
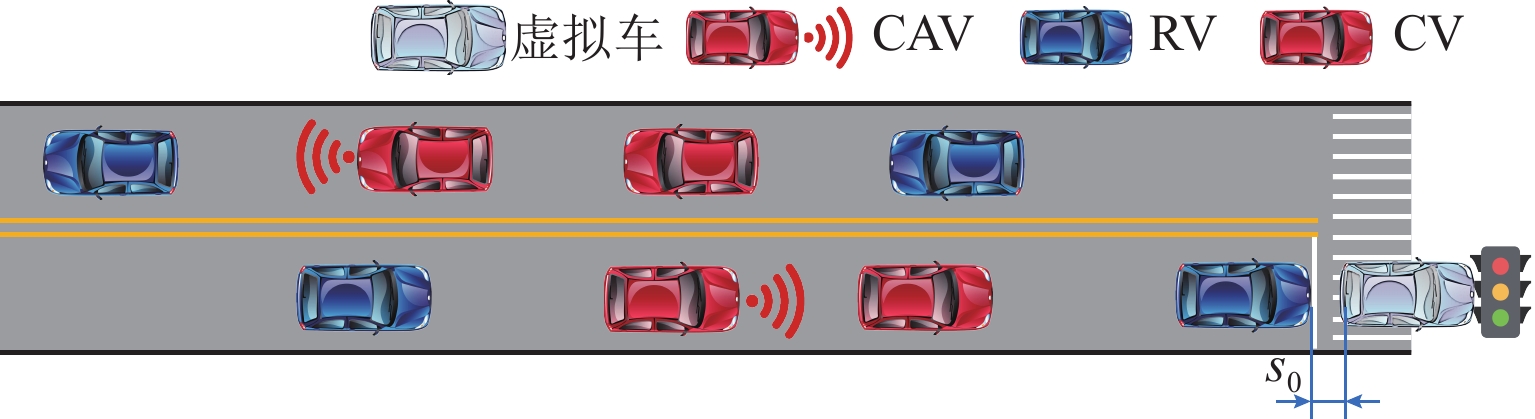
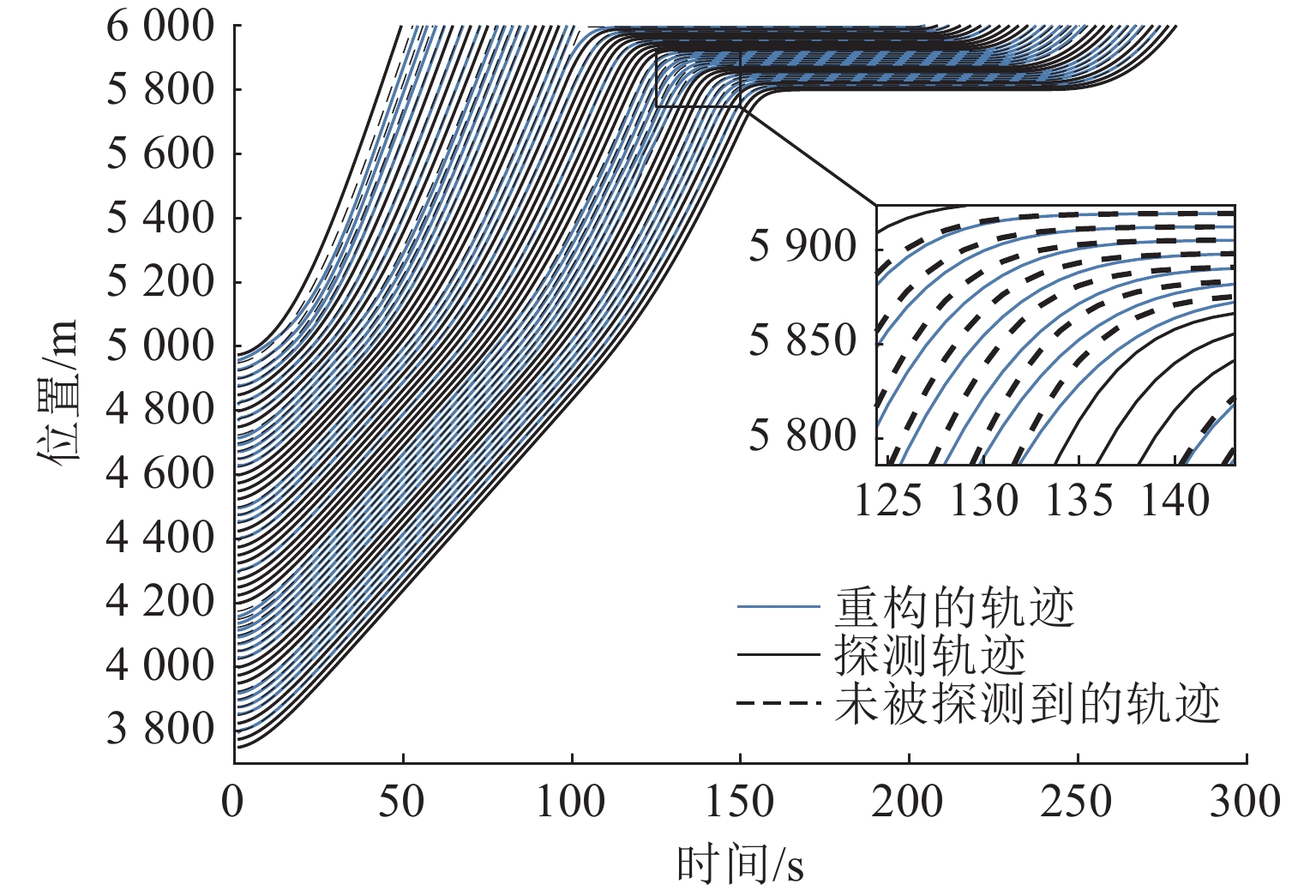
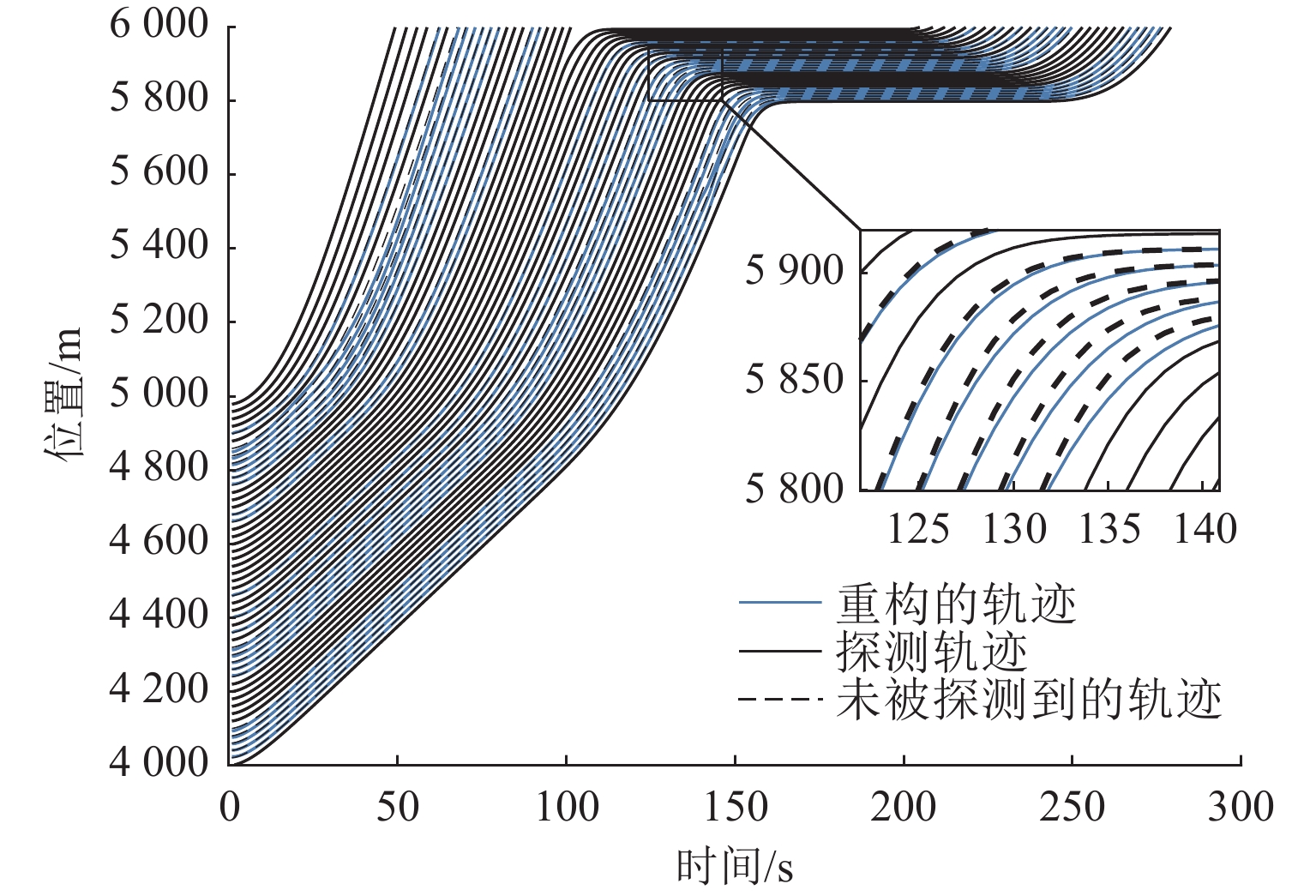
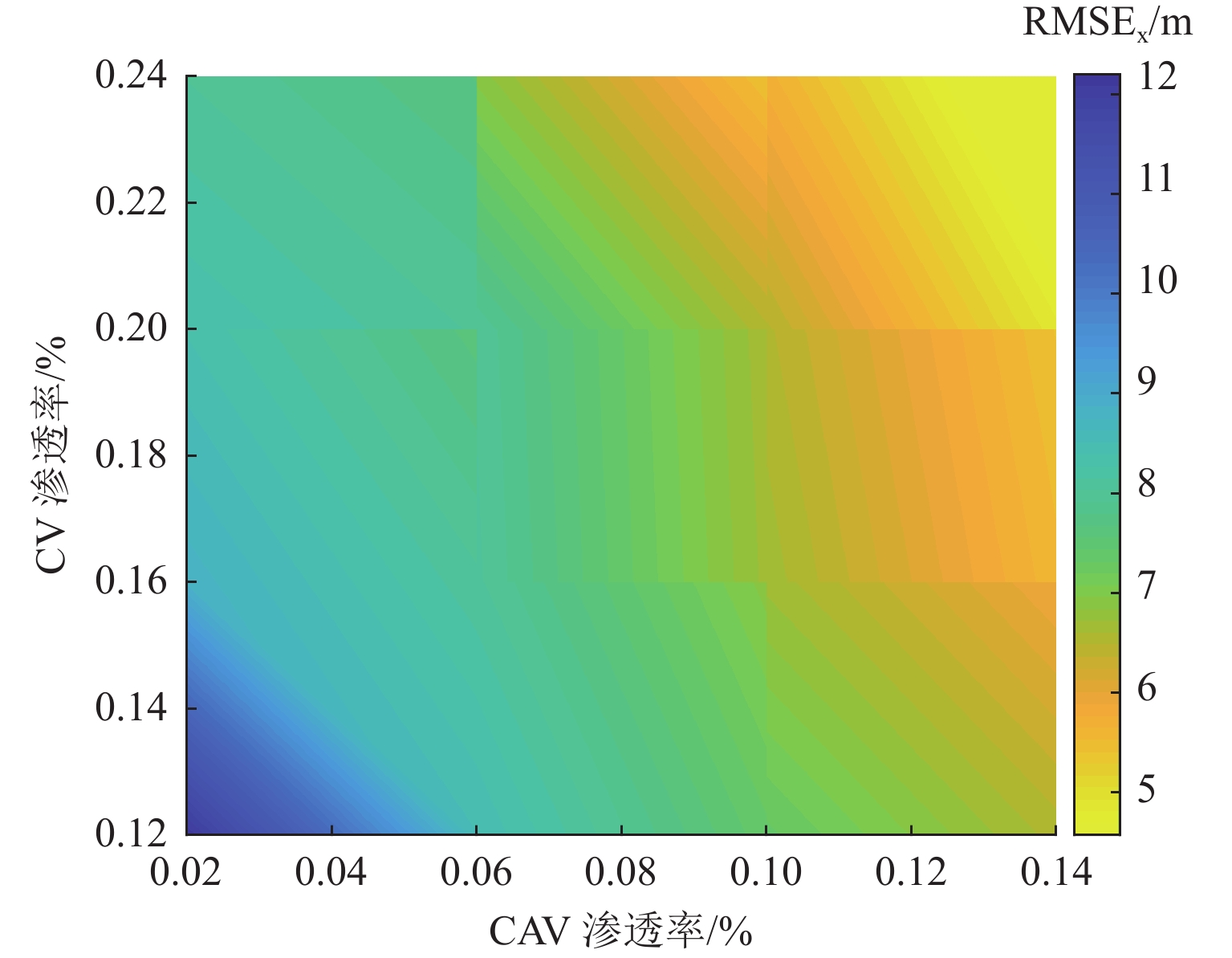
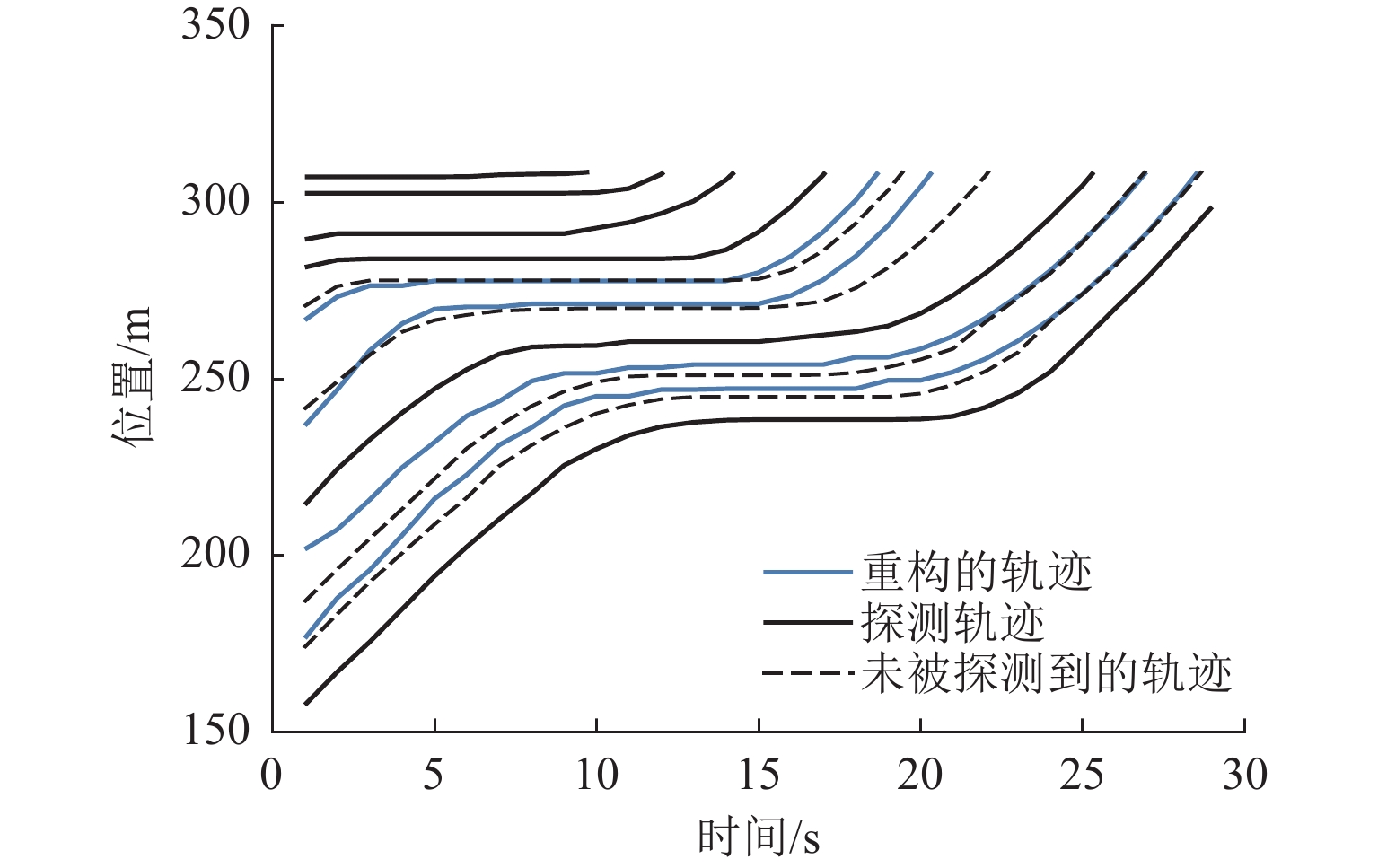
车辆轨迹数据提供了大量的时空交通流信息，可用于各类交通研究. 传统车辆轨迹模型多以人工驾驶环境为研究对象，普遍未考虑由常规车（RV）、网联人工驾驶车（CV）以及智能网联车（CAV）组成的混合交通流的影响. 为解决该问题，构建智能网联环境下信号交叉口全样本车辆轨迹重构模型. 首先，介绍并分析智能网联环境下城市道路交叉口处车辆组成及排队通过情况；然后，构建城市道路混合交通流轨迹数量估计模型，并针对前后车的排队情况提出虚拟车的概念，用于估计不同车辆的交通状态；最后，设计数值仿真实验分析交通流密度和网联车渗透率对模型的影响，并基于NGSIM数据进行实例验证. 结果表明：轨迹重构模型的数量误差和位置误差均随着交通流密度和网联车渗透率的增大而减小，如交通流密度由20 veh/km增大至50 veh/km的过程中，模型数量误差和位置误差均呈现下降趋势，且最大误差分别不超过6.88%和8.02 m；与网联人工驾驶车渗透率相比，智能网联车的渗透率对模型结果影响更大.
Abstract:Vehicle trajectory data provides abundant spatial-temporal traffic flow information, which can be used for traffic research. Traditional vehicle trajectory models mostly focus on the artificial driving environment and fail to consider the impact of mixed traffic flows composed of regular vehicles (RVs), connected vehicles (CVs), and connected automated vehicles (CAVs). To solve this problem, a full sample vehicle trajectory reconstruction model of signalized intersections in connected automated environments was proposed. Firstly, the composition of vehicles at signalized intersections of urban roads and the passage of queues in connected automated environments were analyzed. Secondly, a model for estimating the number of trajectories of mixed traffic flows on urban roads was constructed, and the concept of virtual vehicles was further proposed to estimate the traffic status of different vehicles according to the queuing of front and rear vehicles. Finally, a numerical simulation test was designed to analyze the influence of traffic flow density and penetration rate of CAVs and CVs on the model, and the model was verified by NGSIM data. The results show that the error of the number and position of the model decreases with the increase in traffic flow density and the penetration rate of CAVs and CVs. For example, when the traffic flow density increases from 20 veh/km to 50 veh/km, both the error of the number and position of the model shows a decreasing trend, and the maximum error is no more than 6.88% and 8.02 m. Compared with that of CVs, the penetration rate of CAVs has a greater impact on the model results.
-
随着三维扫描仪等硬件设备的成本降低和市场增长，其应用越来越广泛. 在三维扫描应用场景中，由于每个摄像头或扫描仪在其自身的空间中生成点云，而并非在对象空间中，所以2个点云模型之间没有对应关系，使点云的数据融合[1]、交叉纹理映射[2]、三维人体扫描[3]、即时定位与高精度地图构建[4]等后处理过程面临巨大挑战. 因此，构建点云模型之间的对应关系成为一个亟待解决的问题，特别是构建非刚性模型间的对应关系更具挑战性. 非刚性模型发生的局部形变会导致模型间特征差异过大. 此外，离散的点云模型缺少几何先验知识，使得无监督学习在计算对应关系时很难实现，在实际应用中，往往需要大量的带标注数据. 因此，如何采用无监督学习准确构建非刚性三维点云模型间密集的对应关系是一个极具挑战性的问题.
近年来，主流的三维模型对应关系计算方法主要有2类：基于模型的方法[5-8]和数据驱动的方法[9-10]. 基于模型的方法使用人工制作的特征描述符作为输入，优化预定义的函数映射；而基于数据驱动的方法使用大规模数据集训练神经网络来预测对应关系. 近期的研究表明，数据驱动方法计算精度明显高于基于模型的方法[9]. 但数据驱动方法需要大量的标注数据和使用模型中顶点之间的连接信息（例如三角网格模型）. 研究者通过计算模型在拉普拉斯-贝尔特拉米算子特征基[9-11]上的投影，来实现三角网格模型间对应关系映射，该方法已被广泛使用，且证明是高效的.
研究者致力于非刚性模型的密集对应关系研究，其目的是计算发生非刚性形变的三维模型间逐点对应关系. 其中，针对于三角网格模型对应关系计算的一个重要方法是函数映射法. 该方法使用简化后的基函数将模型的特征描述符表示为函数映射矩阵，将模型间对应关系计算问题转化为求解相应的函数映射矩阵问题[8,12]. 文献[13]结合局部函数映射和局部流形谐波算子计算三维模型特征描述符，并构建模型间对应关系. 文献[14]提出同时计算完整模型与多个发生非刚性形变残缺模型的对应关系计算方法，并且对带有噪声的模型得到更准确的匹配结果. 该类方法的优点是使用函数映射进行结构化对应预测. 然而，频谱基的计算需要较高的算力和预处理时间，并且需要点之间的连通性信息. 文献[15]提出一种点云频谱匹配方法，利用神经网络学习模型基函数，从而避免对拉普拉斯算子进行特征分解的计算. 文献[16]提出基于上采样细化和全频谱特征值对齐的方法，提高了非刚性残缺模型对应关系结果的平滑度和准确性，对带有拓扑噪声的三维模型也具有较好的鲁棒性，但是该方法需要大量特征值来定位正则化项. 文献[17]提出三维模型之间的基矩阵校准方法，通过尖端点遍历匹配即可获取较优的对应关系结果. 这些方法在谱域计算模型拉普拉斯-贝尔特拉米算子特征基的预处理过程中非常耗时，占用过多计算资源. 此外，拉普拉斯-贝尔特拉米算子的计算需要模型顶点之间连通性信息，但当数据来源于三维扫描设备时，点云模型采样点之间是离散的.
为解决上述问题，研究者提出了多种三维点云模型对应关系计算方法[18-20]，这些方法通常采用编码器-解码器结构. 文献[18]使用给定的模板模型以重建不同的输入点云，解码器返回每个点的坐标，并根据重建模型与模板的最近邻点确定对应关系；但是该方法严重依赖人工设计的参数化模板质量. 文献[20]使用交叉重建的方式摒弃了参数化模板，但是非刚性模型中对应点特征差别较大，其使用最近邻搜索寻找匹配特征的方法泛化能力较差. 文献[21]提出利用特征序列匹配的思想来预测2个点云模型的刚性变换，但该方法无法计算非刚性模型的对应关系.
综上所述，目前针对三维点云模型对应关系计算的研究中，由于离散的点云模型缺少几何先验知识，难以实现无监督学习；此外，当模型发生非刚性形变时，现有的特征提取方法难以获得唯一且具有丰富的局部与全局信息的三维点云模型本征描述符，导致对应关系计算准确率不高. 为此，本文提出一种基于特征序列注意力机制和结构化构造的无监督三维点云模型对应关系计算方法.
1. 序列到序列的无监督点云模型对应关系计算
设输入的三维点云源模型和目标模型分别为${\mathcal X} $,$ {{\mathcal Y}} \in {\mathbb{R}}^{n \times 3} $，其中，n为点的个数. 本文的目标是在源模型和目标模型之间寻找一个映射，即在目标模型$ {\mathcal{Y}} $中寻找与点$ {x_i} \in {\mathcal X} $的对应点$ {y_j} \in {\mathcal{Y}} $，$ 1 \leqslant i,j \leqslant n $. 为此，构建如图1所示的神经网络架构，主要由特征提取模块、Transformer模块、对应关系预测模块和点云重构模块构成. 图中：$ {{\boldsymbol{F}}_{\mathcal X}} $、$ {{\boldsymbol{F}}_{\mathcal{Y}}} $为点云特征，$ {\hat{\boldsymbol{ F}}_{\mathcal X} } $、$ {\hat{\boldsymbol{ F}}_{\mathcal Y}} $为施加了注意力的点云特征，$ {{\boldsymbol{S}}_{ \mathcal{XY}}} $、$ {{\boldsymbol{S}}_{\mathcal{YX}}} $为软映射矩阵，$ {\hat {\mathcal X}_{\mathcal Y}} $、$ {\hat {\mathcal{Y}}_ {\mathcal X}} $为重建点云. 首先，使用特征提取模块提取三维点云模型特征，通过Transformer模块对源模型和目标模型的特征序列施加注意力机制；然后，通过对应关系预测模块得到软映射矩阵；最后，通过软映射矩阵确定目标点及其邻域，并对目标点邻域加权融合，以进行点云重构.
1.1 特征提取模块
本文的核心任务是寻找2个模型间相匹配的特征，所以获取点云模型准确的局部特征尤为重要. 为获得较好的点云模型局部特征，使用具有多个边缘卷积层[22]的动态图卷积网络，将源模型$ \mathcal X $和目标模型$ {\mathcal{Y}} $嵌入到高维特征空间中. 具体来说，对于点云中第i个点，首先计算该点特征到其最近邻特征集合$ \varOmega _{i,l} $中各特征的欧氏距离，其中，l为边缘卷积层的序号. 然后，把该点特征$ {\boldsymbol{f}}_{i,l} $和该点特征到最近邻特征的距离$ \{ {\boldsymbol{f}}_{j,l} - {\boldsymbol{f}}_{i,l}|{\boldsymbol{f}}_{j,l} \in \varOmega _{i,l}\} $相拼接（$ {\boldsymbol{f}}_{i,l} $,$ {\boldsymbol{f}}_{j,l} \in {\mathbb{R}^{1 \times d}，} $d为特征维度，$ i \ne j $），通过多层感知机和最大池化获得新的特征表示：
fi,l+1=Γ(Ml(fi,l,fj,l−fi,l)),fj,l∈Ωi,l, (1) 式中：$ \varGamma $(•)为最大池化操作，Ml (•)为第l个边缘卷积中的多层感知机.
边缘卷积中使用的最近邻域特征聚合操作可以使得$ {\boldsymbol {f}}_{i,l + 1} $更好地捕捉点云的局部几何信息.
1.2 Transformer模块
由特征提取模块得到的逐点特征虽然在一定程度上可以较好地表征其局部特征，但是在非刚性模型中，局部特征差异较大，难以获得较好的匹配结果. 本文使用Transformer模块中的注意力机制[23]完成特征序列到特征序列的学习，从而优化非刚性模型间的特征匹配. 经特征提取模块获得的模型$ {\mathcal X} $、$ {\mathcal {Y}} $的特征序列$ {{\boldsymbol{F}}_ {\mathcal X}} $,$ {{\boldsymbol{F}}_{\mathcal Y}} \in {\mathbb{R}^{n \times d}} $. 对应关系可以通过神经网络在目标模型$ {\mathcal {Y}} $中预测一个与源模型$ {\mathcal X} $中一个点对应的点来构建，此时可以利用注意力机制使$ {{\boldsymbol{F}}_{\mathcal Y}} $对$ {{\boldsymbol{F}}_ {\mathcal X}} $施加注意力，得到兼顾模型$ {\mathcal {Y}} $的模型$ {\mathcal X} $的特征信息；同理，也可得到兼顾模型$ {\mathcal X} $的模型$ {\mathcal {Y}} $的特征信息.
Transformer模块的任务是学习一个函数$ g:{\mathbb{R}^{n \times P}} \times {\mathbb{R}^{n \times P}} \to {\mathbb{R}^{n \times P}} $，P为特征嵌入的维度，并由函数g(·)得到点云新的特征嵌入，具体过程可表示为
{ˆFX=FX+g(FX,FY),ˆFY=FY+g(FY,FX). (2) 如图2所示，Transformer模块为编码器-解码器结构. 前后传播模块由1个线性层和1个ReLu激活函数层组成. 编码器的功能为：输入特征序列$ {{\boldsymbol{F}}_ {\mathcal X}} $，经过自注意力机制和共享多层感知机将其编码并嵌入到特征空间中. 解码器分为两部分：第一部分输入另一个特征序列$ {{\boldsymbol{F}}_{\mathcal Y}} $，并以与编码器相同的方式对其进行编码；第二部分使用交叉注意力机制关联2个嵌入的特征序列. 具体而言，注意力机制将输入的线性编码表示分别建模为查询向量$ {\boldsymbol{Q}} \in {\mathbb{R}^{n \times P}} $、关键向量$ {\boldsymbol{K}} \in {\mathbb{R}^{n \times P}} $和值向量$ {\boldsymbol{V}} \in {\mathbb{R}^{n \times P}} $，从而可以计算出注意力得分矩阵W=Softmax(QKTd−0.5)，最终得到输出特征$ \hat{\boldsymbol{ F}} = {\boldsymbol{WV}} $. 其中，Softmax(·)可以将输出值转换为0～1且和为1的概率分布. 图2中，编码器和解码器的输入分别为$ {{\boldsymbol{F}}_ {\mathcal X}} $和$ {{\boldsymbol{F}}_{\mathcal Y}} $，可得到点云模型$ {\mathcal X} $的新特征$ {\hat{\boldsymbol{ F}}_ {\mathcal X}} $；同理，若将$ {{\boldsymbol{F}}_ {\mathcal X}} $和$ {{\boldsymbol{F}}_{\mathcal Y}} $调换输入位置（即编码器的输入为$ {{\boldsymbol{F}}_{\mathcal Y}} $，解码器的输入为$ {{\boldsymbol{F}}_ {\mathcal X}} $），可得到点云模型$ {\mathcal {Y}} $的新特征$ {\hat{\boldsymbol{ F}}_{\mathcal Y}} $. 因此，输出的特征序列$ {\hat{\boldsymbol{ F}}_ {\mathcal X}} $和$ {\hat{\boldsymbol{ F}}_{\mathcal Y}} $具有来自于2个特征序列（$ {{\boldsymbol{F}}_ {\mathcal X}} $和$ {{\boldsymbol{F}}_{\mathcal Y}} $）的上下文信息.
1.3 对应关系预测模块
在大多数特征匹配的任务中，直接使用特征最近邻搜索即可得到对应关系，但是在网络训练之初，预测结果远未达到较好效果的时候，这种方法容易使神经网络模型陷入局部最优. 为解决这个问题，本文使用概率来定位对应点，即生成从一组特征序列到另一组特征序列的概率映射矩阵，称为软映射矩阵. 软映射定义为源模型的特征嵌入和目标模型的特征嵌入之间的相似度，所以，软映射矩阵明确了源模型上任一点与目标模型上任一点之间的相似度. 软映射矩阵由式（3）求出.
{SXY=Softmax(ˆFXˆFTY),SYX = Softmax(ˆFYˆFTX), (3) 式中：$ {{\boldsymbol{S}}_{ {\mathcal X}{\mathcal Y}}} $,$ {{\boldsymbol{S}}_{{\mathcal Y} {\mathcal X}}} \in {\mathbb{R}^{n \times n}} $，矩阵中第i行第j列的元素${S_{ij}} \in \left[ {0,1} \right]$，表示$ {\mathcal X} $中点i和$ {\mathcal {Y}} $中点j的对应概率.
本文最终的对应关系由软映射矩阵中最大对应概率确定. 但由于使用的是无连接信息的点云模型，所以采用重建的方式构造损失函数来监督训练，从而优化软映射矩阵.
1.4 点云重构模块
在使用谱方法计算三角网格模型的对应关系时，可以根据三角网格模型自身的几何拓扑结构应用无监督学习方法，但是本文算法以点云模型作为输入，采样点之间不具有连接信息，很难应用自身几何性质完成无监督训练. 为了在没有真实对应关系的情况下学习点云模型的特征，设计一个点云重构模块，通过重构输入点云，并利用重构模型与输入模型的相似度来间接监督训练.
早期针对点云模型的对应关系计算方法是通过模板和解码器完成三维重建，利用最近邻搜索进行无监督训练，但是需要大量训练数据，并且难以在跨数据集评估中推广. 本文使用特征序列相似性和输入坐标来重构点云并确定对应关系，以取代使用坐标回归的解码器模块.
如图3所示，首先，k近邻特征搜索模块接收2组三维点云模型和软映射矩阵作为输入，寻找点云模型$ {\mathcal {Y}} $上与模型$ {\mathcal X} $上第i个点对应的概率最大k个点，可以表示为$ {\{ {y_i}\} _{i \in [1,k]}} $. 其次，根据软映射矩阵计算出$ {\mathcal X} $上第i个点与点集{yi}中各点的对应概率Sij，并使用Softmax进行归一化处理再求和，得到权重集合{wij}，如式（4）所示.
wij=eSij/∑h∈N(xi)eSih, (4) 式中：$ N({x_i}) $为软映射矩阵中点云模型$ {\mathcal {Y}} $上与模型$ {\mathcal X} $上第i个点对应的概率最大k个点的序号.
最后，根据得到的权重集合{wij}和点集{yi}计算重构后的点$ {\hat y_{{x_i}}} $如式（5）所示.
ˆyxi=∑h∈N(xi)wihyh. (5) 同理，根据对应概率将模型$ {\mathcal X} $上与模型$ {\mathcal {Y}} $上第i个点对应的k个点$ {\{ {x_i}\} _{i \in [1,k]}} $和$ {\mathcal {Y}} $上第i个点与{xi}的对应概率集合{Sij}使用式（4）得到权重集合{wij}，根据式（5）得到重构后的点$ {\hat x_{{y_i}}} $. 此时，式（4）、（5）中的N(xi)需修改为软映射矩阵中模型$ {\mathcal X} $上与模型$ {\mathcal {Y}} $上第i个点对应的概率最大k个点的序号.
点云模型$ {\mathcal X} $和$ {\mathcal {Y}} $上所有点经过重构模块后得到重构点云$ {\hat {{\mathcal Y}}_ {\mathcal X}} $,$ {\hat { {\mathcal X}}_{\mathcal Y}} \in {\mathbb{R}^{M \times 3}} $，且$ {\hat y_{{x_i}}} \in {\hat {{\mathcal Y}}_ {\mathcal X}} $，$ {\hat x_{{y_i}}} \in {\hat { {\mathcal X}}_{\mathcal Y}} $.
1.5 损失函数
在对应关系计算任务中，有监督训练依赖于人工标注的点对点真实对应关系来监督特征匹配结果. 而无监督训练则在未知真实点对点对应关系的情况下进行，通过利用模型数据自身的几何性质进行监督，从而节约人工标注成本.
定义损失函数为
L=λ1LCD+λ2LSC+λ3LNC, (6) 式中：$ {\lambda _1} $、$ {\lambda _2} $和$ {\lambda _3} $为系数，依次取为1、10和1，LCD、LSC和LNC分别为倒角距离损失函数、促进特征平滑的正则化项和相邻点对应的正则化项.
输入点云模型经过重构点云步骤，$ {\mathcal X} $和$ {\hat { {\mathcal X}}_{\mathcal Y}} $、$ {\mathcal {Y}} $和$ {\hat {{\mathcal Y}}_ {\mathcal X}} $2组点云应分别保持近似一致，所以使用$ {\mathcal X} $与$ {\hat { {\mathcal X}}_{\mathcal Y}} $、$ {\mathcal {Y}} $与$ {\hat {{\mathcal Y}}_ {\mathcal X}} $之间的倒角距离作为损失函数，如式（7）所示.
LCD=C(X,ˆXY)+C(Y,ˆYX), (7) C(X,Y)=1|X|∑x∈Xminy∈Y‖x−y‖22+1|Y|∑y∈Yminx∈X‖y−x‖22, (8) 式中：C(·)为倒角距离，||·||2为两点间欧式距离.
为使特征提取模块和Transformer模块得到的特征更平滑，即使得相邻点的特征更加相似，本文利用点云重构模块将$ {\mathcal X} $和$ {\mathcal {Y}} $分别根据其自身进行重构，得到重构模型$ {\hat { {\mathcal X}}_ {\mathcal X}} $和$ {\hat {{\mathcal Y}}_{\mathcal Y}} $，并由此计算正则化项LSC（式（9））. 如果重建结果与自身相似度较大，则模型上的点到其邻域点的对应概率较大. 因为采用了特征匹配的思想，对应概率大意味着特征相似度高.
LSC=C(Y,ˆYY)+C(X,ˆXX). (9) 此处的重构模型是通过点云重构模块，根据模型自身及其自身到自身的软映射矩阵计算得到的. 其自身到自身的软映射矩阵为
{SXX=Softmax(ˆFXˆFTX),SYY=Softmax(ˆFYˆFTY). (10) 将点云$ {\mathcal X} $和对应的软映射矩阵$ {{\boldsymbol{S}}_{ {\mathcal X} {\mathcal X}}} $输入重构模块后，由式（11）即可求得模型$ {\mathcal X} $的重构模型$ {\hat { {\mathcal X}}_ {\mathcal X}} $.
ˆxi=∑h∈N(xi)wc,ihxh, (11) 式中：$ {\hat x_i} \in {\hat { {\mathcal X}}_ {\mathcal X}} $，为模型$ {\mathcal X} $中第i个点的重构点；wc,ih为第i个点到N(xi)中各点对应分配的权重，由式（4）计算得到.
同理，$ {\hat {{\mathcal Y}}_{\mathcal Y}} $也可根据点云$ {\mathcal {Y}} $和软映射矩阵$ {{\boldsymbol{S}}_{{\mathcal Y}{\mathcal Y}}} \in {\mathbb{R}^{M \times M}} $求出.
为了使源点的邻点与源点对应的目标点的邻点相对应，本文设置了正则化项LNC，如式（12）所示. 该正则化项通过源模型中一点到其邻域点的距离对预测对应点到其邻域点的距离进行加权，从而促使源模型中相邻点在目标模型中也保持相邻.
LNC=1nk∑i∑h∈NX(xi)vih‖ˆyxi−ˆyxh‖22, (12) 式中：$ {N_ {\mathcal X}}({x_i}) $为点云模型$ {\mathcal X} $中与xi相邻点的集合； $ {v_{ih}} = {{\mathrm{e}}^{{{ - \left\| {{x_i} - {x_h}} \right\|_2^2} / \alpha }}} $，为根据邻域内各点到中心点的距离所计算的权重，$\alpha $=8.
2. 实验结果与分析
2.1 实验数据集与评估标准
2.1.1 数据集
在人体和非人体数据集上对本文方法进行测试. 对于人体模型，训练时采用从参数化人体模型SMPL[24]生成的Surreal数据集，共包含
230000 个训练模型. 将数据集划分为115000 对，按对输入网络模型进行训练；测试时，使用FAUST数据集[3]和SHREC’19数据集[25]. FAUST数据集包含10个真人扫描模型，每个人体模型包含10个不同姿态. SHREC’19数据集包含44个真人扫描模型，共有430个带标签的测试对，模型间具有较大的非刚性形变. 因此，对应关系可分为同一个人体不同姿态的模型间对应关系（类内）和不同人体模型之间的对应关系（类间）.对于非人体模型，采用SMAL数据集[26]进行训练和评估. SMAL包含猫、狗、牛、马和河马的动物模型. 本文使用其提供的模板为每种动物类型创建
2000 个不同姿态的模型，获得包含共10000 个模型的数据集，每个类别又分别生成40个测试模型. 在训练时，从同一动物类别中随机选择模型对作为神经网络的输入；在测试时，将测试数据中同类的两两模型组成一对，形成一个100对的测试集.实验从每个模型中随机抽取
1024 个点，随机排列点的顺序，创建用于训练和测试的点云模型.2.1.2 定量评估标准
模型对应的通用评估指标是平均测地误差[27]，但是计算测地误差时需要已知模型中点的连接信息. 由于本文使用的是点云数据，采样点之间缺少连接信息，因此，需要使用欧氏距离来代替测地距离，构建对应误差进行评估.
给定源模型$ {\mathcal X} $和目标模型$ {\mathcal {Y}} $，对应误差为
e=1n∑x∈X,ygt∈Y‖φ(x)−ygt‖2, (13) 式中：$ {y_{{\mathrm{gt}}}} \in {{\mathcal Y}} $，为点$ x $的真实对应点；$ \varphi (x) $为点$ x $根据计算对应关系映射到模型$ {\mathcal {Y}} $上的一个点，即$ \varphi (x) \in {{\mathcal Y}} $.
为进一步评估对应关系的计算准确率，使用式（14）计算在不同的对应误差容忍度量下对应关系精度.
a=1n∑x∈X,ygt∈Yξ(‖φ(x)−ygt‖2⩽ε), (14) 式中：$ \xi $(·)为指示器函数，$ \varepsilon $为对应误差容忍度量.
2.2 实验结果与分析
将本文方法与最新的针对点云模型的对应关系计算方法进行定性和定量对比，包括3D-CODED[18]、Elementary Structures[19]和CorrNet3D[20]，其中，3D-CODED和Elementary Structures为不使用点之间连接信息的有监督方法.
2.2.1 定性实验
为测试本文方法的跨数据集泛化能力，在FAUST数据集上测试，可视化对比结果如表1所示. 表中，源模型点的颜色是根据点的空间坐标值设定的，此外，根据真实对应关系和各算法计算得到的对应关系，将源模型点的颜色映射到Ground-truth和其余4种方法的模型上. 其中，Ground-truth为对应关系的真值. 可以看出，由于3D-CODED的重建模型在躯干伸展的方向和源模型之间存在角度误差，所以在手部和腿部产生错误的对应关系；Elementary Structures在手部、脚部和头部存在较多错误对应，这是因为在特征提取阶段没有强制施加特征平滑措施；CorrNet3D依赖于解码器网络来回归重建模型坐标，所以模型的手部、腹部和腿部均存在较多错误的对应关系. 与上述方法相比，本文方法既不需要使用模板，也不需要使用解码器重建，而是借助于Transformer完成点云的序列到序列对应，并实现了结构化重建，获得更好的对应关系结果.
表 1 FAUST数据集上各方法的实验结果对比Table 1. Comparison of experimental results of methods onFAUST dataset示例 源模型 Groud-truth 3D-CODED Elementary Structures CorrNet3D 本文算法 1 
2 
为更好地测试本文方法的跨数据集泛化能力和在非刚性模型上对应关系的构建能力，在SHREC’19数据集上进行了实验，可视化对比结果如表2所示. 3D-CODED和Elementary Structures都依赖于模板分析源点云模型和目标点云模型的变形来构建他们之间的对应关系，但是当模型发生较大的非刚性形变时，由解码器得到的重建模型效果较差，使得计算的对应关系准确率下降，如图中人体模型的腿部和手部的错误对应；CorrNet3D依赖于解码器网络回归重建模型坐标，没有对特征进行平滑处理，所以泛化能力弱，且在计算软映射矩阵时容易产生错误对应. 以上3种方法均需要使用模型的全局特征进行重建，这导致其跨数据集的泛化能力较差，而本文方法既不需要使用模型的全局特征，也不需要使用解码器重建，而是借助于Transformer模块完成点云的序列到序列对应和结构化重建，提高了非刚性模型间对应关系计算的准确度和跨数据集的泛化能力.
表 2 SHREC’19数据集上各方法的实验结果对比Table 2. Comparison of experimental results of methods on SHREC’19 dataset示例 源模型 Groud-truth 3D-CODED Elementary Structures CorrNet3D 本文算法 3 
4 
表1和表2的实验都是在人体模型数据集上进行的，为进一步评估本文方法的灵活性和准确性，在SMAL动物数据集上进行训练和测试，可视化对比结果见表3. 3D-CODED和Elementary Structures算法结果存在较多错误的对应点，因为他们都依赖于模板对源模型和目标模型进行变形来预测对应关系. 相比之下，CorrNet3D在这方面有一定改进，但由于依赖训练解码器网络来重建模型，在多种尺度混合数据集中表现不佳. 而本文方法采用对应的最近邻点加权融合的重建方法，增强了算法的健壮性和对多尺度数据集的适应能力.
表 3 SMAL数据集上各方法的实验结果对比Table 3. Comparison of experimental results of methods on SMAL dataset示例 源模型 Groud-truth 3D-CODED Elementary Structures CorrNet3D 本文算法 5 
6 
7 
2.2.2 定量实验
为进一步评估本文方法的有效性，对不同方法的对应误差变化曲线进行计算，结果如图4所示. 由图可知：1） 在SHREC’19数据集上，本文方法有14.1%的对应关系没有对应误差，而3D-CODED、Elementary Structures和CorrNet3D在没有对应误差时的对应关系准确率明显低于本文方法；且在对应误差增大时，本文方法的对应关系准确率始终高于这3种方法. 2） 在FAUST数据集上，本文方法有24.6%的对应关系没有对应误差，高于其他3种方法；且在对应误差为0.04时，CorrNet3D和本文方法的对应关系准确率接近100%，结果优于3D-CODED和Elementary Structures. 3） 在SMAL数据集上，本文方法有20.2%的对应关系没有对应误差，高于其他3种方法的结果；且在对应误差为0.03时，本文方法的对应关系准确率接近100%，3D-CODED、Elementary Structures和CorrNet3D均未能达到100%. 这主要归功于基于注意力的特征序列对应和提取到的平滑特征，使本文方法取得了更好的结果.
实验进一步计算测试集中的平均对应误差，对比结果如表4所示. 可以看出，本文方法在数据集SGREC’19、FAUST 和SMAL上均取得了更低的平均对应误差，尤其是在非刚性变形程度较大的SHREC’19数据集中平均对应误差下降幅度更大.
表 4 不同方法平均对应误差Table 4. Average correspondence errors of different methods数据集 3D-
CODEDElementary
StructuresCorrNet
3D本文
算法FAUST 7.2 6.6 5.3 5.1 SHREC’19 8.1 7.6 6.9 5.8 SMAL 6.8 6.4 5.7 5.4 2.2.3 消融实验
通过设置有Transformer模块和无Transformer模块两组实验，验证本文方法中Transformer模块的作用，在数据集FAUST、SHREC’19和SMAL上的对比结果如表5所示. 可以看出，有Transformer模块的网络平均对应误差低于无Transformer模块的网络，进一步验证了本文提出的特征序列匹配思想可以显著提升对应关系准确率.
表 5 Transformer模块消融实验误差Table 5. Errors of ablation experiment on Transformer module数据集 无 Transformer 模块 有 Transformer 模块 FAUST 5.6 5.1 SHREC’19 6.1 5.8 SMAL 7.6 5.4 此外，设置2两组实验验证对应关系预测模块的有效性，结果如表6所示，其中，无对应关系预测模块实验中使用最近邻搜索策略进行特征匹配. 可以看出，有对应关系预测模块的网络平均对应误差均低于无对应关系预测模块的网络. 所以，基于概率的方法可以显著提升对应关系准确率，且在当模型发生较大尺度非刚性变形时表现更好.
表 6 对应关系预测模块消融实验误差Table 6. Errors of ablation experiment on correspondence prediction module数据集 无对应关系
预测模块有对应关系
预测模块FAUST 6.1 5.1 SHREC’19 7.3 5.8 SMAL 8.0 5.4 3. 结束语
本文结合注意力机制，使用特征序列注意力匹配的方法生成软映射矩阵，有效提高了无监督深度学习方法计算三维点云模型间稠密对应关系的准确率，在多个数据集上表现出较好的泛化能力. 然而，本文方法也存在需要改进的地方，如使用Transformer模块导致了网络参数增加；与针对三角网格模型的对应关系计算结果相比，仍有一定的提升空间；离散点云模型目前必须借助于重建才能实现无监督训练等，这些都是今后需要继续研究的方向.
致谢： 兰州交通大学天佑创新团队项目（TY202002）的资助.
-
图 4 混合交通流下信号交叉口处时空轨迹
Figure 4. Spatial-temporal trajectories at signalized intersection under mixed traffic flow
图 7 交通流密度为40 veh/km时重构轨迹
Figure 7. Trajectory reconstruction with a traffic flow density of 40 veh/km
图 8 智能网联车渗透率为14%时重构轨迹
Figure 8. Trajectory reconstruction with a CAV penetration rate of 14%
图 10 Lankershim Boulevard街道重构轨迹
Figure 10. Trajectory reconstruction of Lankershim Boulevard Street
表 1 车辆速度与视野和注视距离关系
Table 1. Relationship among vehicle speed, horizon, and gaze distance
车辆速度/（km·h−1） 视野/（°） 注视距离/m 0 170 80 40 100 180 60 86 355 80 60 377 100 40 564 120 22 710 
下载: 导出CSV
表 2 IDM跟驰模型参数
Table 2. Parameters of IDM car-following model
模型 An/ （m·s−2） bn/ （m·s−2） vf/ （m·s−1) Tn/s s0/m IDM 1.00 2.00 33.30 1.50 2.00 虚拟 IDM 2.00 1.68 28.92 1.45 2.00
下载: 导出CSV
表 3 不同交通流密度条件下轨迹重构结果
Table 3. Trajectory reconstruction results under different traffic density conditions
交通流
密度/
（veh·km−1）插入 RV 的数量 插入 RV 的位置 实际车
辆/vehMAEm/
vehMAPEm/
%MAEx/
mRMSEx/
m20 29.05 2.00 6.88 4.15 8.02 30 29.09 1.85 6.36 3.18 7.45 40 29.00 1.82 6.27 2.93 7.06 50 23.50 1.33 5.67 2.88 6.61
下载: 导出CSV
表 4 不同CAV渗透率条件下轨迹重构结果
Table 4. Trajectory reconstruction results under different CAV penetration rates
CAV 渗透率/
%CAV 数量/
veh插入 RV 的数量 插入 RV 的位置 实际车辆/veh MAEm/
vehMAPEm/
%MAEx/
mRMSEx/
m2 1 34.04 2.41 7.07 3.46 8.37 4 2 29.85 2.04 6.83 3.01 7.63 6 3 28.03 2.00 7.14 3.31 8.01 8 4 23.50 1.33 5.67 2.88 6.61 10 5 22.05 1.18 5.37 2.80 6.51 12 6 18.93 0.67 3.54 2.21 5.04 14 7 16.48 0.58 3.52 2.19 4.85
下载: 导出CSV
表 5 不同CV渗透率条件下轨迹重构结果
Table 5. Trajectory reconstruction results under different CV penetration rates
CV 渗透率/% CV 辆数/veh 插入 RV 的数量 插入 RV 的位置 实际车辆/veh MAEm/
vehMAPEm/
%MAEx/
mRMSEx/
m8 4 27.33 2.25 8.23 3.74 8.72 12 6 26.61 1.74 6.54 3.55 8.23 16 8 24.86 1.57 6.32 3.07 6.96 20 10 23.50 1.33 5.67 2.88 6.61 24 12 23.30 1.23 5.26 2.71 6.43 28 14 21.41 0.91 4.26 2.49 6.06
下载: 导出CSV
表 6 Lankershim Boulevard街道轨迹重构误差
Table 6. Trajectory reconstruction errors of Lankershim Boulevard Street
插入 RV 的数量 插入 RV 的位置 本文方法 已有方法 实际车
辆/vehMAEm/
vehMAPEm/
%MAEx/
mRMSEx/
mMAEx/
mRMSEx/
m5.63 0.38 6.75 4.35 5.94 6.53 7.60
下载: 导出CSV
-
[1] SHI X W, LI X P. Constructing a fundamental diagram for traffic flow with automated vehicles: methodology and demonstration[J]. Transportation Research Part B: Methodological, 2021, 150: 279-292. doi: 10.1016/j.trb.2021.06.011 [2] 冉斌,谭华春,张健,等. 智能网联交通技术发展现状及趋势[J]. 汽车安全与节能学报,2018,9(2): 119-130. doi: 10.3969/j.issn.1674-8484.2018.02.001RAN Bin, TAN Huachun, ZHANG Jian, et al. Development status and trend of connected automated vehicle highway system[J]. Journal of Automotive Safety and Energy, 2018, 9(2): 119-130. doi: 10.3969/j.issn.1674-8484.2018.02.001 [3] HU X W, SUN J. Trajectory optimization of connected and autonomous vehicles at a multilane freeway merging area[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 111-125. doi: 10.1016/j.trc.2019.02.016 [4] LU G Y, NIE Y, LIU X B, et al. Trajectory-based traffic management inside an autonomous vehicle zone[J]. Transportation Research Part B: Methodological, 2019, 120: 76-98. doi: 10.1016/j.trb.2018.12.012 [5] 张惠玲,刘晓晓,许裕东. 基于车辆轨迹重构的信号交叉口延误提取研究[J]. 交通运输系统工程与信息,2020,20(2): 237-243. doi: 10.16097/j.cnki.1009-6744.2020.02.035ZHANG Huiling, LIU Xiaoxiao, XU Yudong. Delay extraction based on vehicle’s trajectory reconstruction at signalized intersection[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(2): 237-243. doi: 10.16097/j.cnki.1009-6744.2020.02.035 [6] PUNZO V, BORZACCHIELLO M T, CIUFFO B. On the assessment of vehicle trajectory data accuracy and application to the next generation simulation (NGSIM) program data[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(6): 1243-1262. doi: 10.1016/j.trc.2010.12.007 [7] COIFMAN B. Estimating travel times and vehicle trajectories on freeways using dual loop detectors[J]. Transportation Research Part A: Policy and Practice, 2002, 36(4): 351-364. doi: 10.1016/S0965-8564(01)00007-6 [8] MU J T, HAN Y, ZHANG C, et al. An unscented Kalman filter-based method for reconstructing vehicle trajectories at signalized intersections[J]. Journal of Advanced Transportation, 2021, 2021: 1-12. [9] WANG Y P, WEI L, CHEN P. Trajectory reconstruction for freeway traffic mixed with human-driven vehicles and connected and automated vehicles[J]. Transportation Research Part C: Emerging Technologies, 2020, 111: 135-155. doi: 10.1016/j.trc.2019.12.002 [10] HAN X, MA R, ZHANG H M. Energy-aware trajectory optimization of CAV platoons through a signalized intersection[J/OL]. Transportation Research Part C: Emerging Technologies, 2020, 118: 102652.1- 102652.16. [11] 蒋阳升,刘梦,王思琛,等. 基于跟驰特性的智能网联车混合交通流轨迹重构[J]. 西南交通大学学报,2021,56(6): 1135-1142,1132.JIANG Yangsheng, LIU Meng, WANG Sichen, et al. Trajectory reconstruction for traffic flow mixed with connected automated vehicles based on car-following characteristics[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1135-1142,1132. [12] OSAMA O A, BAKHIT P R, ISHAK S. Analysis of queue estimation process at signalized intersections under low connected vehicle penetration rates[J]. Canadian Journal of Civil Engineering, 2021, 48(10): 1398-1408. doi: 10.1139/cjce-2020-0366 [13] 张驰,杨少伟,潘兵宏,等. 交通仿真中驾驶人空间视野感知模型[J]. 交通运输工程学报,2010,10(4): 115-120. doi: 10.3969/j.issn.1671-1637.2010.04.019ZHANG Chi, YANG Shaowei, PAN Binghong, et al. Perception model of driver spatial vision in traffic simulation[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 115-120. doi: 10.3969/j.issn.1671-1637.2010.04.019 [14] 潘兵宏,赵一飞,梁孝忠. 动视觉原理在公路线形设计中的应用[J]. 长安大学学报(自然科学版),2004,24(6): 20-24. doi: 10.19721/j.cnki.1671-8879.2004.06.005PAN Binghong, ZHAO Yifei, LIANG Xiaozhong. Application of dynamic vision theory in highway alignment design[J]. Journal of Chang’an University (Natural Science Edition), 2004, 24(6): 20-24. doi: 10.19721/j.cnki.1671-8879.2004.06.005 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 490
- HTML全文浏览量: 238
- PDF下载量: 83
- 被引次数: 0