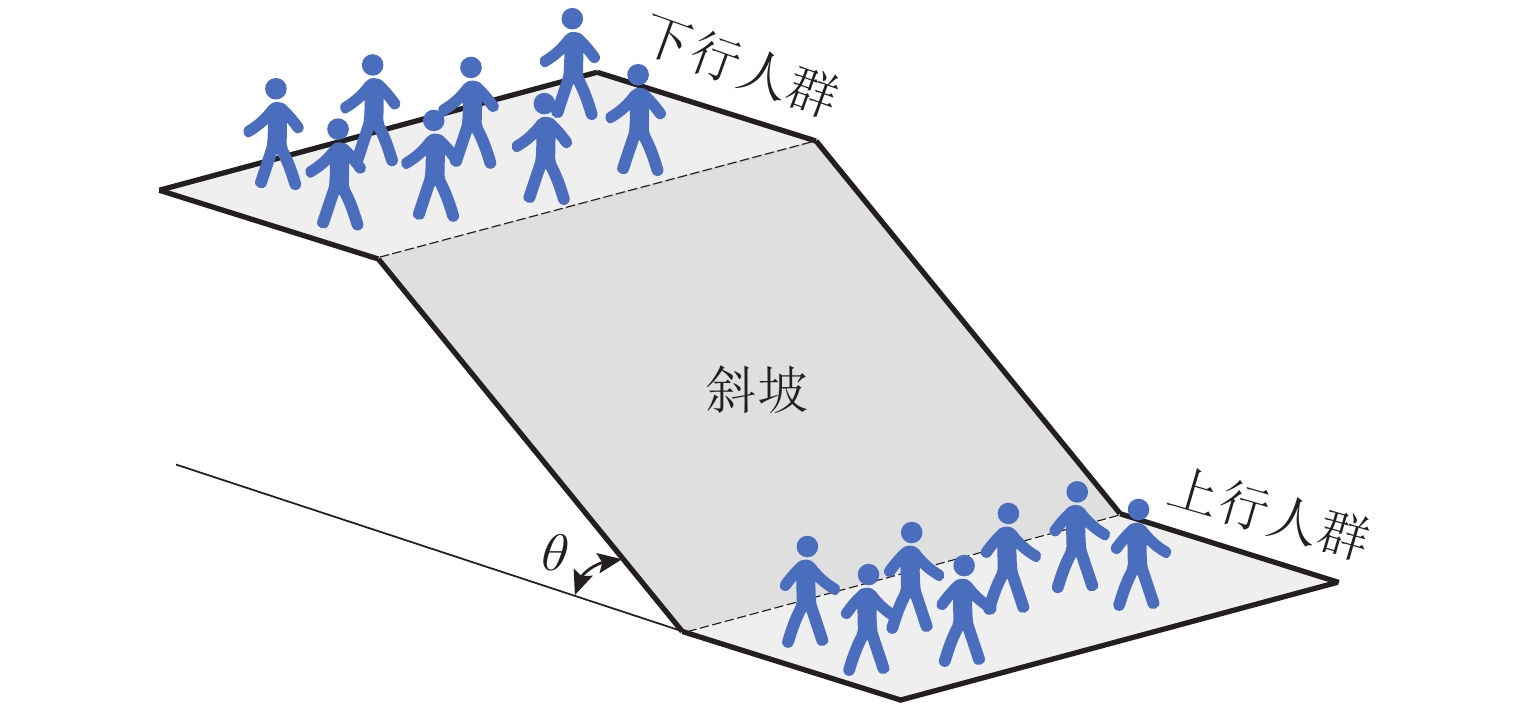
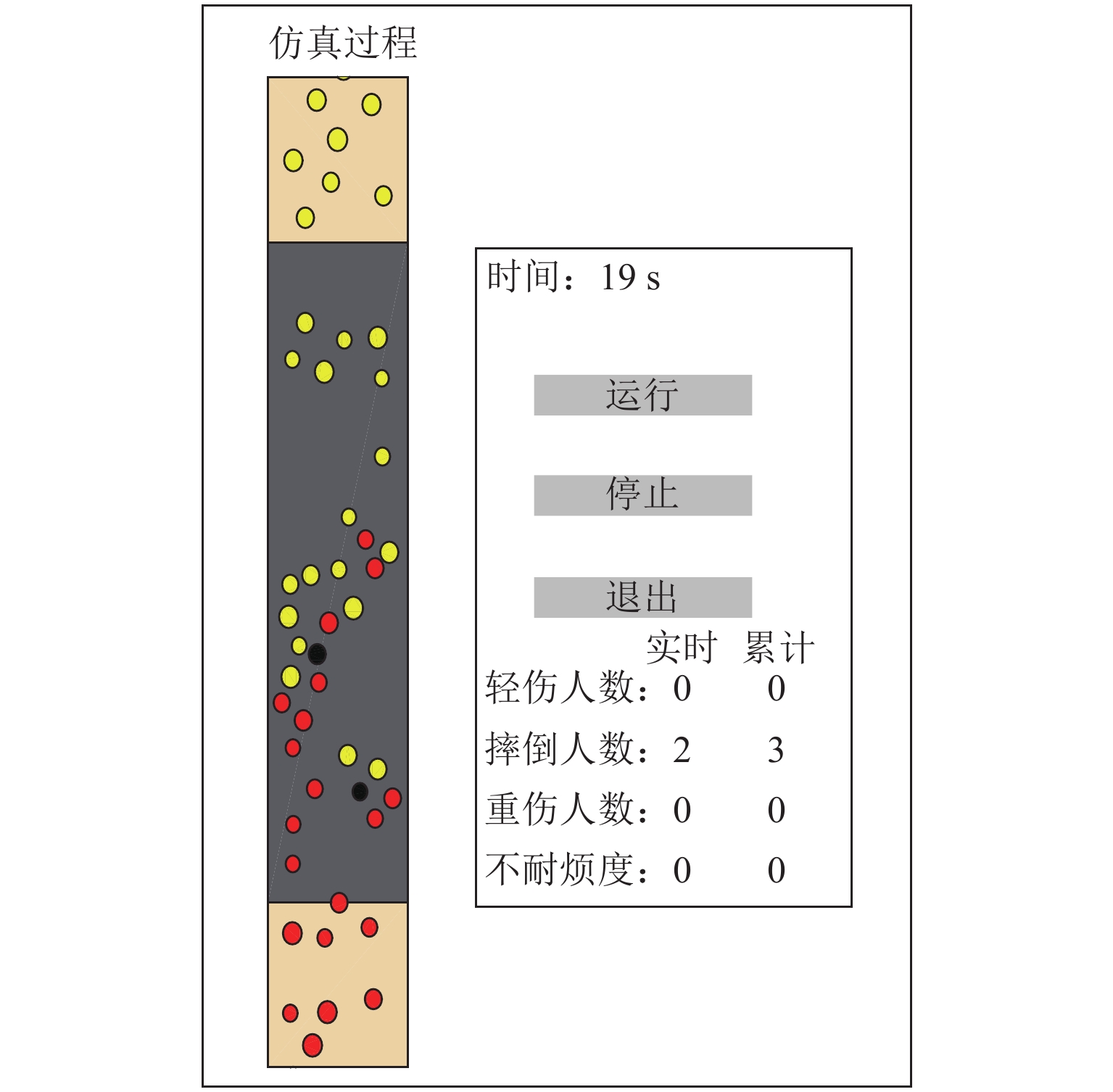
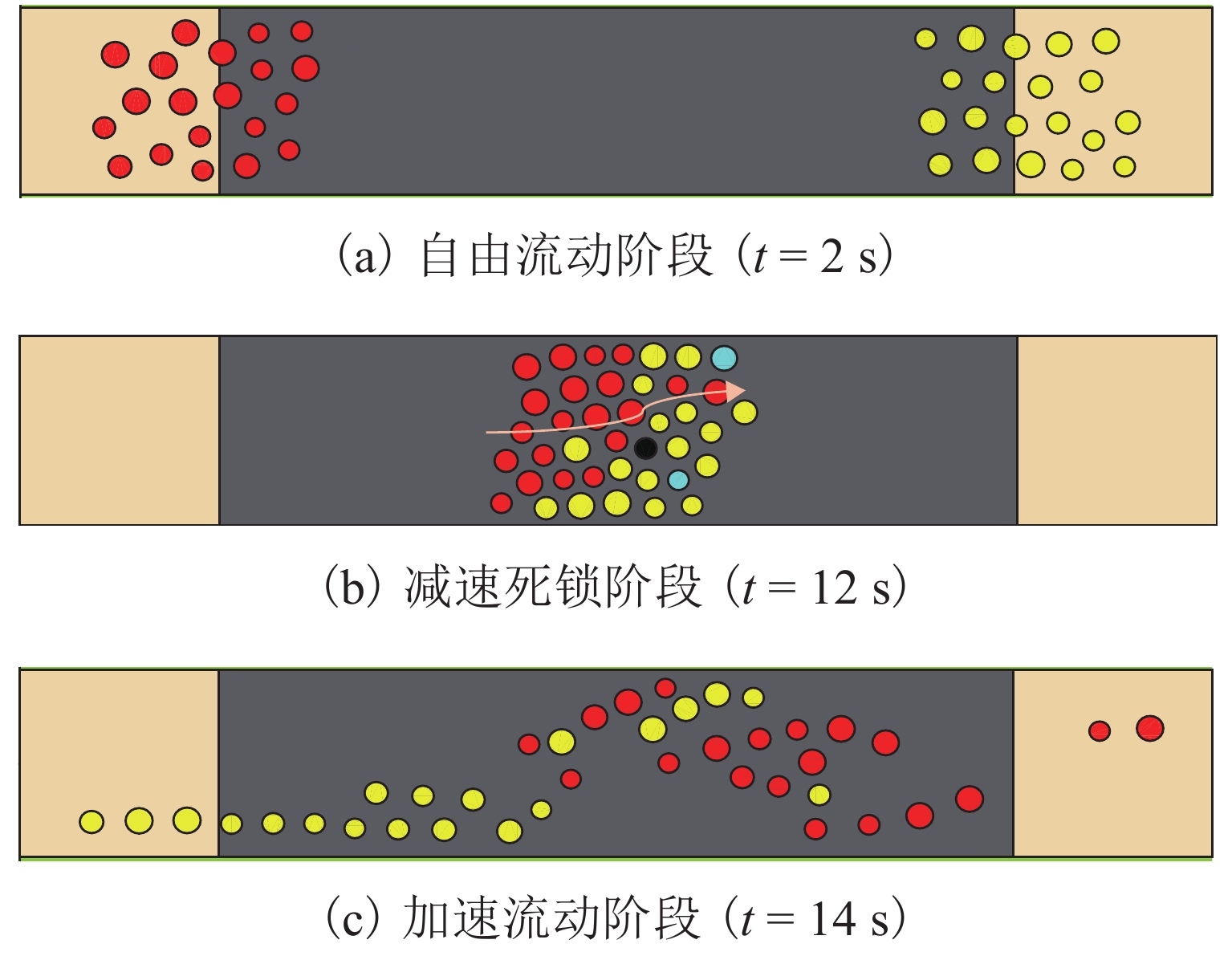
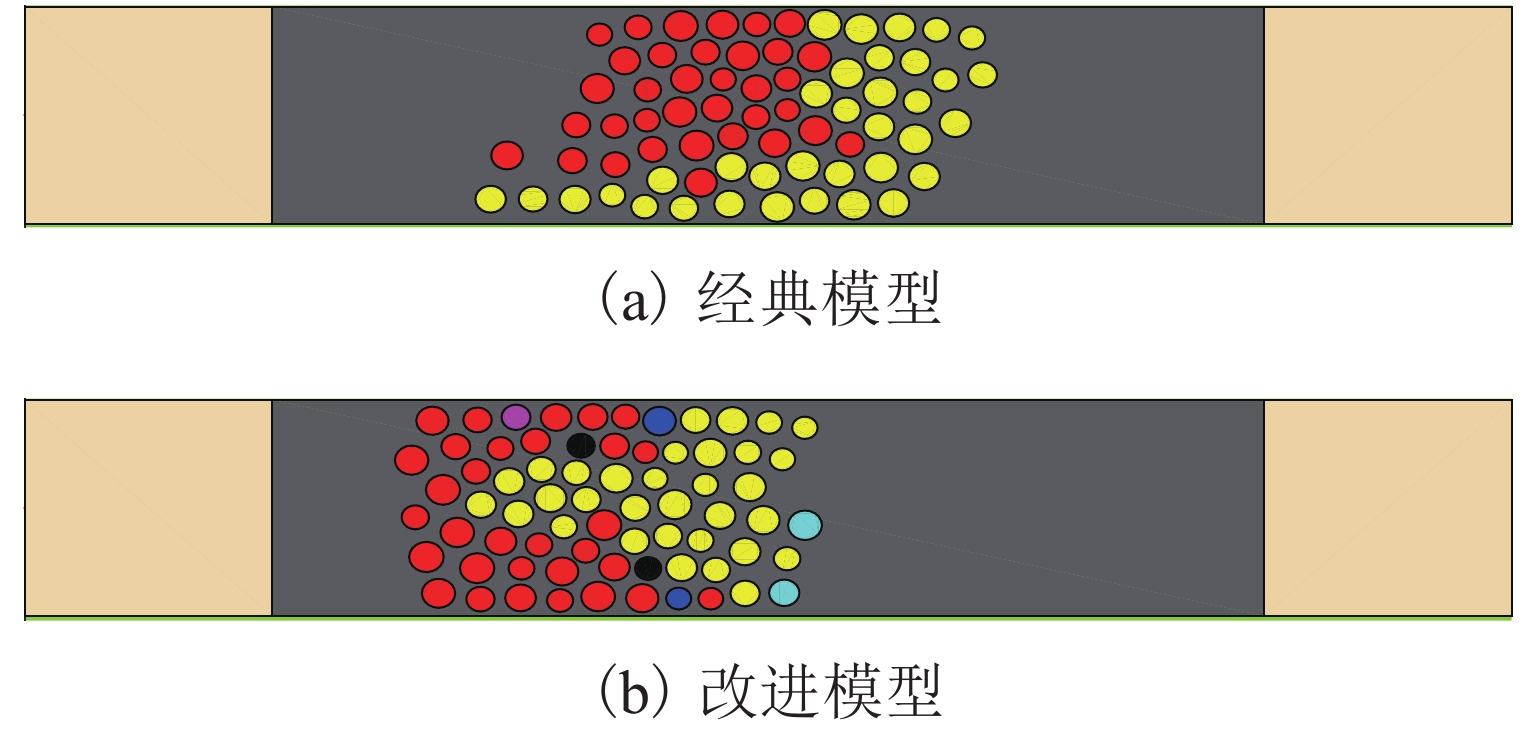
A Social Force Model Considering Falls and Injuries of Pedestrian Counterflow on Slopes
-
摘要:
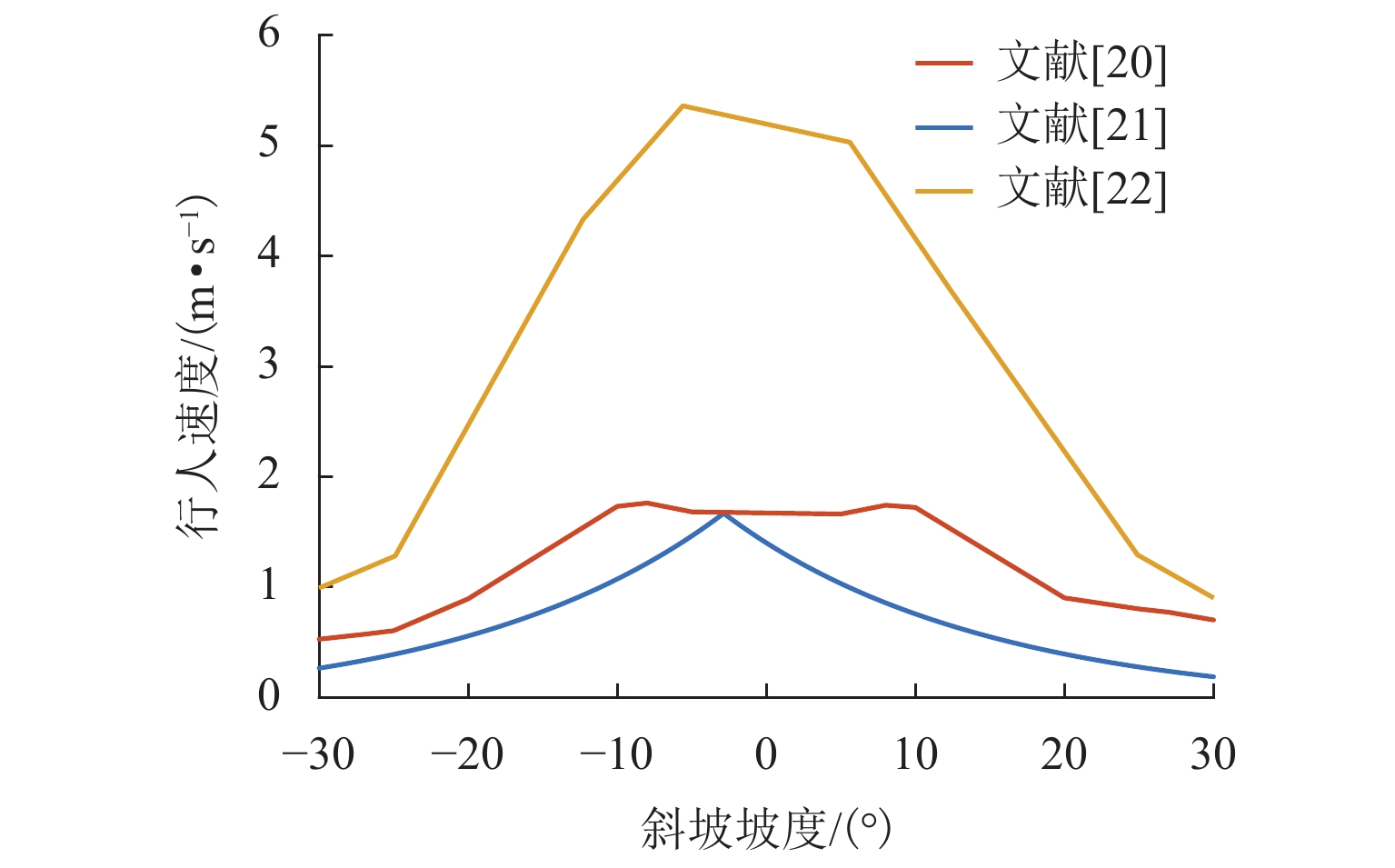
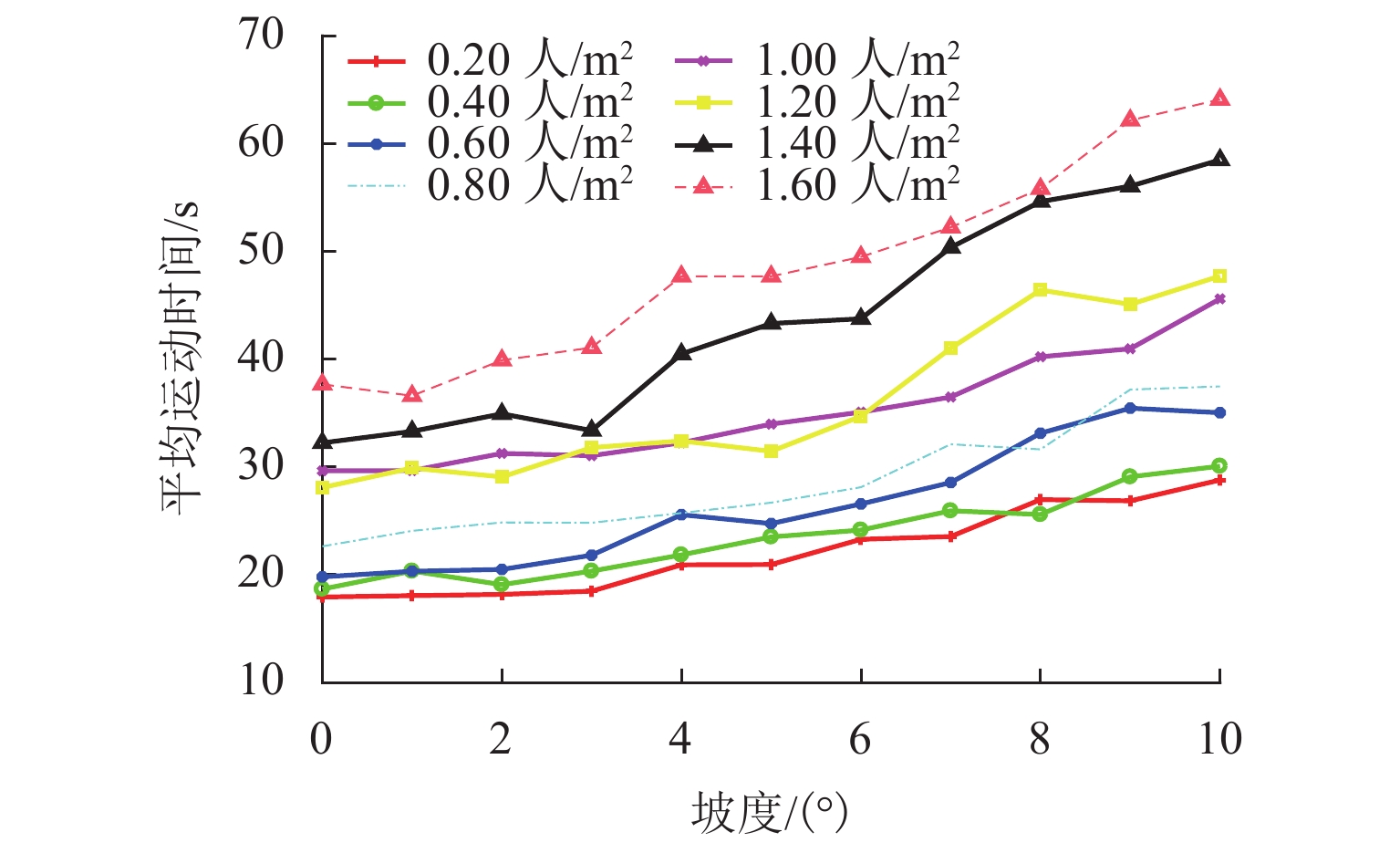
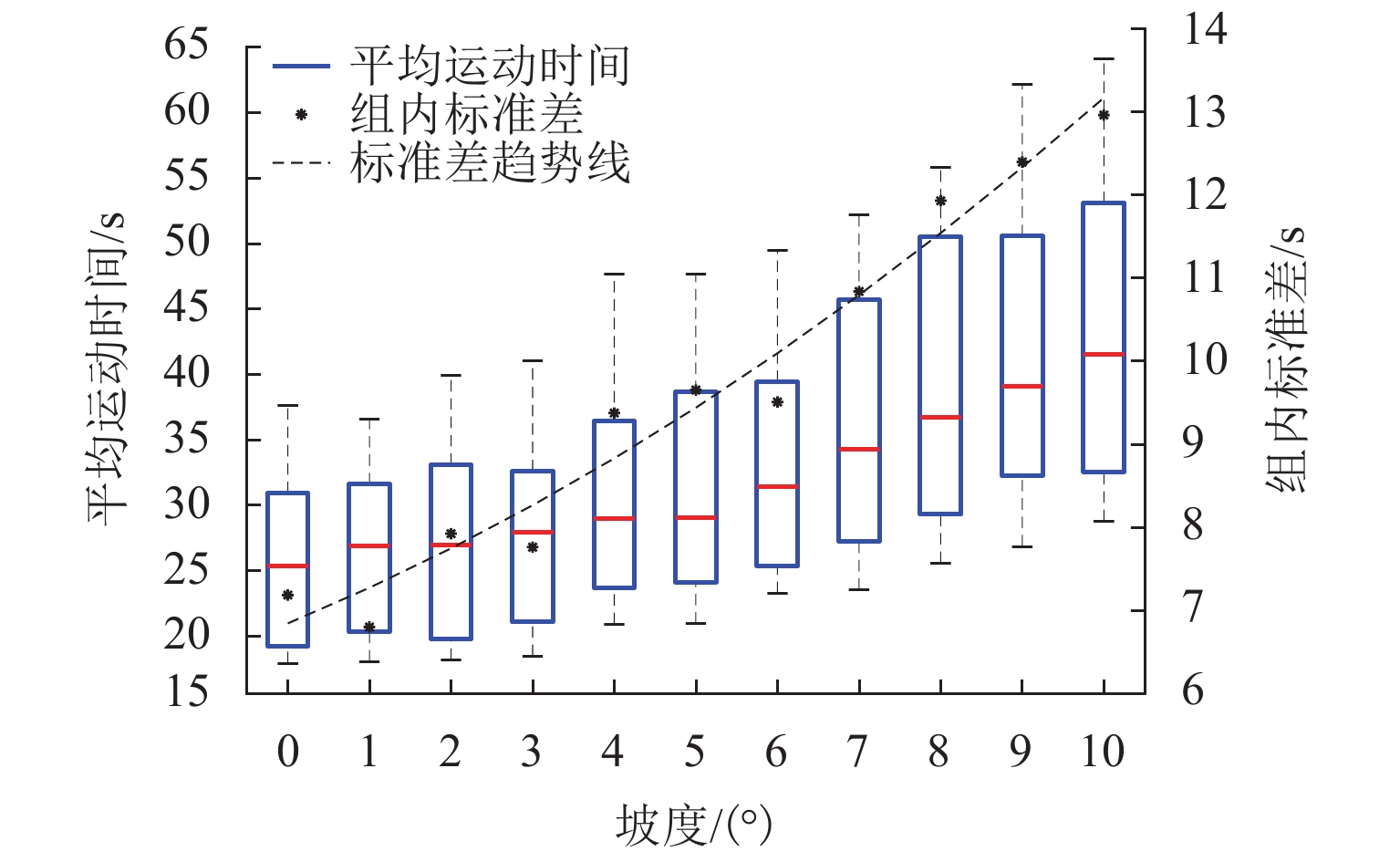
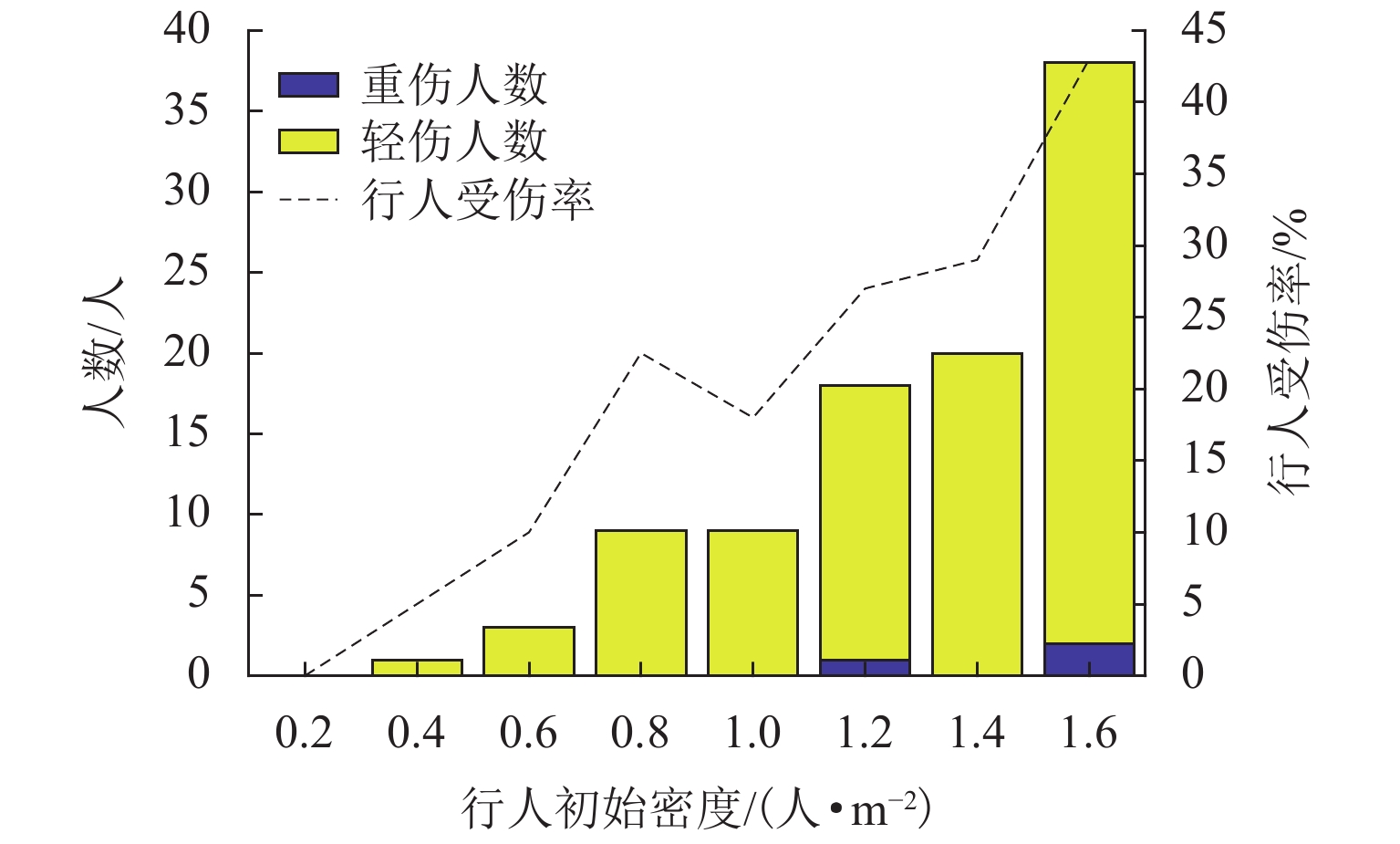
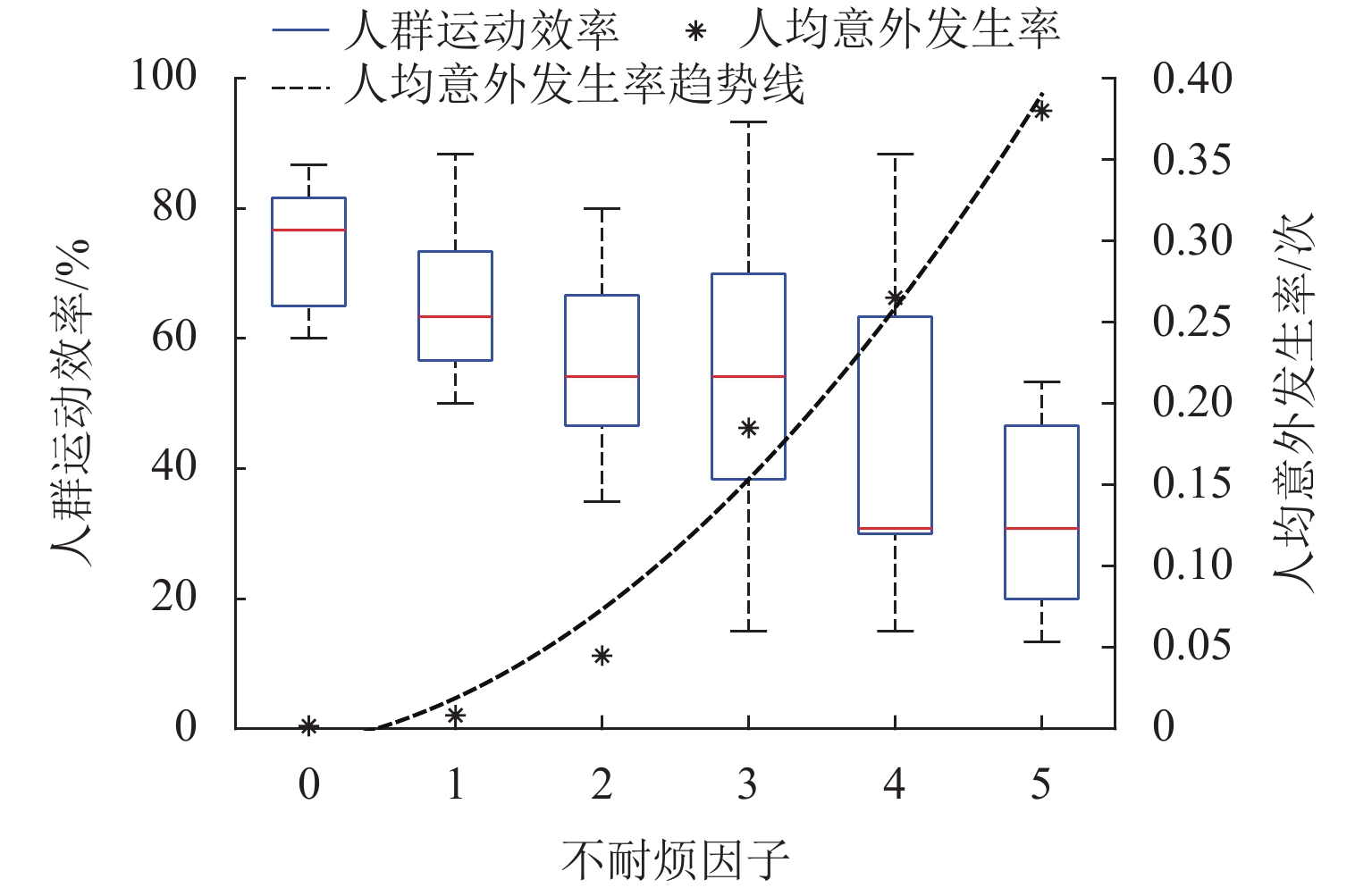
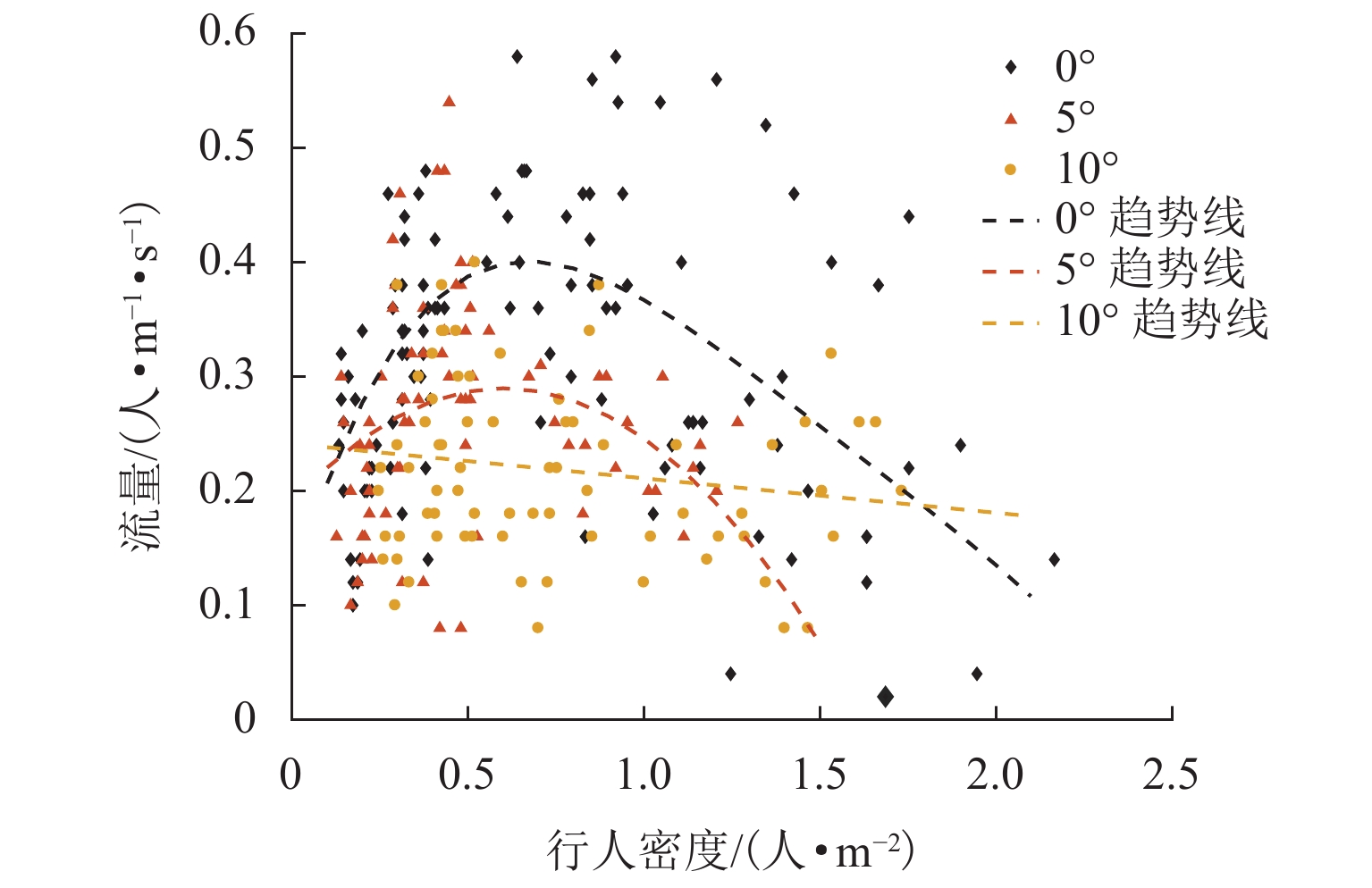
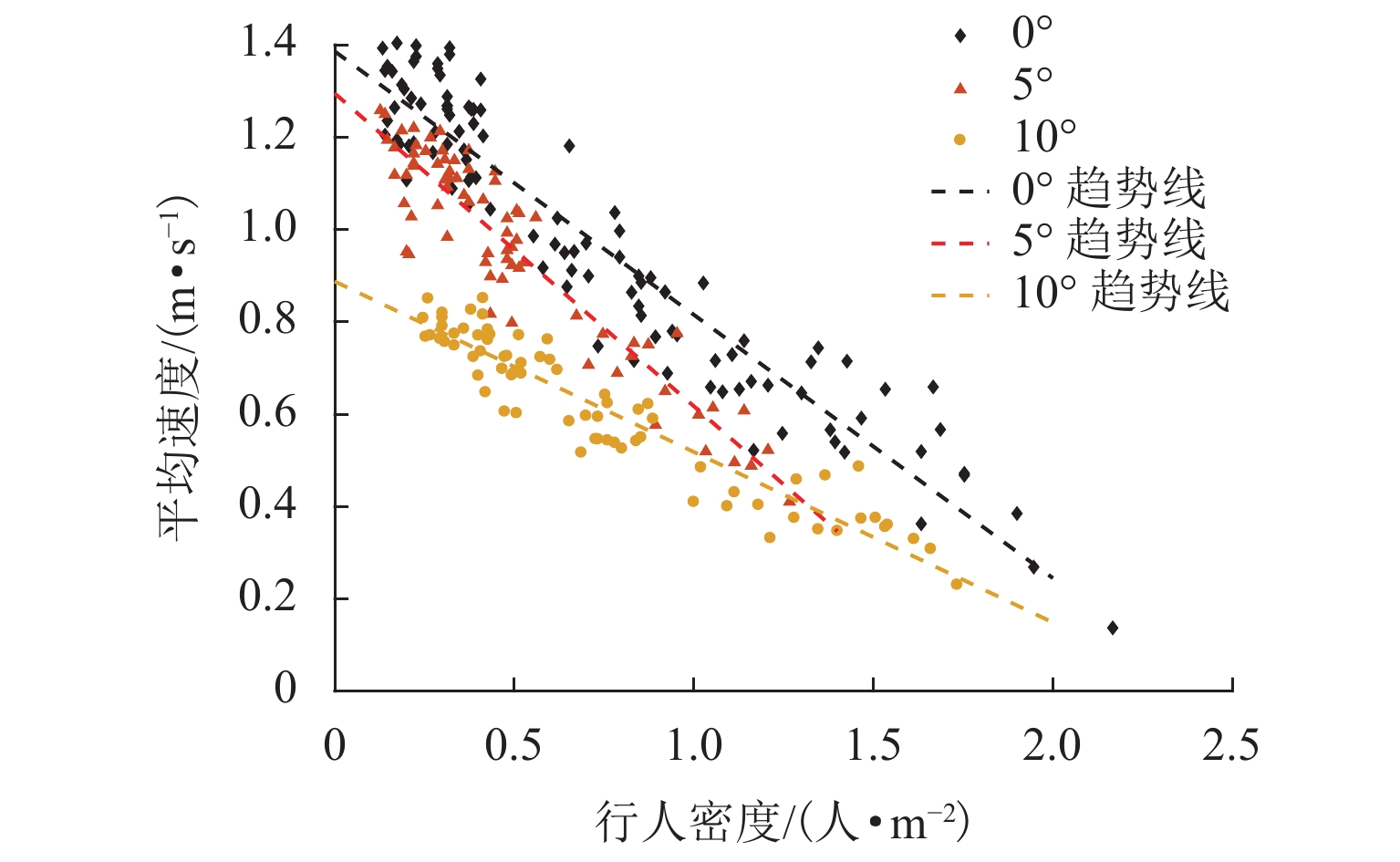
行人在斜坡上运动时，其受力情况、运动速度及心理状态均与在平地运动时不同，难以应用现有社会力模型进行有效仿真. 为此，考虑斜坡上行人的运动特征，提出一个改进的社会力模型，此模型基于过往实证数据对行人在斜坡上的期望速度进行了校准，并提出了推搡行为下行人摔倒的概率计算方法，同时，结合行人体重、运动加速度、承受压力及等待时间等实时状态实现了对行人摔倒、受伤及不耐烦心理的模拟. 斜坡相向行人流场景仿真结果表明：坡度、行人初始密度的升高会延长人群运动时间，使人均意外发生率上升最高至38.0%；不耐烦心理有助于车道效应的形成，但会降低人群运动效率；行人流基本图中，高坡度下流量-密度关系趋势不如平地明显，各坡度行人平均速度比较接近.
Abstract:When pedestrians move on the slope, their force condition, speed, and mental states are different from those on the flat road, so it is difficult to apply the existing social force model for effective simulation. Therefore, the social force model was improved by considering the movement characteristics of pedestrians on slopes. The improved model calibrated pedestrian speed on slopes based on previous empirical data to a desired value, and the probability calculation method of pedestrian falls under the pushing behavior was proposed. Meanwhile, pedestrian falls, injuries, and impatience were simulated according to their weight, acceleration, body pressure, and waiting time in real time. The simulation results of pedestrian counterflow on slopes show that the increase in slope gradient and initial pedestrian density prolongs the movement time and increases the per capita accident rate of the crowd to 38.0%. Pedestrian impatience contributes to the formation of lane effects but reduces the movement efficiency of the crowd. In the fundamental pedestrian flow diagram, the trend of the flow-density relationship under high slopes is not as obvious as that under a flat road, and the average speed of pedestrians under different slopes is relatively close.
-
Key words:
- slopes /
- pedestrian counterflow /
- social force model /
- falls and injuries /
- impatience
-
电动汽车由于其能量利用率高、行驶零排放，成为解决能源和环境问题的重要手段，是我国重点支持的战略性新兴产业[1]. 目前，电动汽车能源补充方式主要是充电和换电2种模式. 由于受到自身参数特性、用户行为等随机性因素的影响[2-3]，电动汽车负荷，特别是充电负荷，具有很强的不确定性. 大规模电动汽车的充换电行为势必会加大电网的负荷峰谷差[4]，降低电能质量[5]，威胁电网安全稳定运行.
在“碳达峰、碳中和”大背景下，具有不确定性的可再生能源和电动汽车接入电网规模不断扩大，给电网规划与运行带来巨大挑战. 其中，储能技术是应对该挑战全面可控的解决方案[6]，可用于削峰填谷、平抑波动，实现电网的调峰、调频、调压、黑启动电源、备用电源等功能[7]. 储能电站和电动汽车换电站具有相似的获利方式：储能电站通过“低储高发”，实现峰谷套利；电动汽车换电站获取换电电价和充电电价差收益. 因此，二者可以进行优化整合. 近年来，随着电动汽车换电模式的兴起和电力一体化趋势的加强，同时具有电动汽车换电功能和储能电站功能的储换一体站受到高度关注[8-10]. 电动汽车储换一体站（EVSS-IS）提供换电服务，具有传统储能电站调峰调频、黑启动等功能，还能减小电动汽车负荷对电网造成的不利影响，提供进一步的供电支撑，发挥协调互济能力，对电动汽车行业的发展和配电网安全稳定运行具有重要意义.
目前，对于电动汽车充换电站和储能电站规划，主要集中在充换电站和储能电站作为独立个体的单一规划[11-14]或协同规划[15-17]，一体站规划研究较少[8,18-21]，尤其对储换一体站的容量规划鲜有报道. 文献[8]引入了充换储一体站模型，并在模型预测控制框架下，优化微网的调度运行，但缺少对一体站的容量配置和经济性分析；文献[10]分析了一体化电站不同运行状态和接入位置对电网供电能力的影响，没有涉及到具体的一体站规划模型；文献[19]建立了充换放储一体站的选址定容规划模型，以一体站经济性和电动汽车（EV）行驶路径最短为目标，但没有考虑到一体站的收益，同时缺少一体站对接入配电网的影响分析；文献[20]建立了考虑用户、一体站和电网三方因素的两步选址定容模型，但只考虑了规划结果由综合成本确定，缺少收益分析；文献[21]提出一种计及光储快充一体站的配电网随机-鲁棒混合优化调度方法，但主要针对微网能量优化，缺少换电站模式.
为此，本文对储换一体站的运行模式和容量规划问题进行了建模分析. 首先，结合电动汽车换电站和储能电站，构建储换一体站的结构，并对其能量流动关系进行分析. 其次，结合用户出行行为特性建立电动汽车用户换电需求预测模型，并采用K-medoids算法削减换电需求场景. 然后，建立储换一体站容量规划双层模型，内、外层分别以储换一体站年综合收益最大和对电网的支撑能力为目标. 规划模型中，同时考虑运行过程中电池的寿命衰减，从而使规划更具有实际意义. 最后，在IEEE33节点算例上，采用改进的粒子群算法进行仿真验证.
1. 储换一体站运行模式
1.1 运行方式
储换一体站主要由换电电池系统（EVSS）、储能电池系统（ESS）和功率变换系统（PCS）等组成，如图1所示. EVSS和ESS均可以实现“削峰填谷”和峰谷差电价获利：EVSS含若干换电服务电池（TB），主要提供电动汽车换电服务，在满足电动汽车用户需求且电量有冗余时，可以支撑电网；ESS包含一定容量储能服务电池（ESB），主要负责支撑电网，同时，在电网高负荷阶段按需向换电服务电池输电. 因此，储换一体站工作模式有5种：模式Ⅰ是电网为TB和ESB充电；模式Ⅱ是TB为电动汽车提供满电电池，并收回亏电电池；模式Ⅲ表示ESB按照放电策略向电网输电以支撑电网；模式Ⅳ表示在负荷高峰时冗余的TB向电网输电，支撑电网；模式Ⅴ表示在换电服务电池不足以满足换电需求，且电网处于高负荷或故障时，ESB向TB充电. 不同的能量流动方向受电价、电池特性、电网电能质量等多方面因素的影响.
1.2 运行模型
储换一体站采取基于分时电价的能量管理策略，以利润最大化决定储换一体站的最佳充放电策略. 以1 d为一个循环周期，按电价水平可以分为3个阶段：谷时段、平时段和峰时段，并将每个周期按时间划分为24个时间段.
对于储换一体站，作如下假设：
1） 储换一体站作为运营主体，承担所有电池和变流器设备的购置、运行维护费用；
2） 在任意一个时间段内，TB和ESB仅存在3种状态：充电状态、放电状态和不动作状态，且在任意时刻只存在一种状态；
3） 对于TB，充放电操作总是发生在t时段开始时刻，充电的TB在t时段结束时（t + Δt时段开始时）充到满电状态，在t时段内换下的电池在下一时段之后充电.
在每个时间段内，可能存在的能量流动关系如图2所示.
假设t时段起始时满电的TB数量为$ {N_{{\text{TB}}}}\left( t \right) $，则t + Δt时段开始时满电的TB数量可表示为
NTB(t+Δt)=NTB(t)+NTB,+(t)−NTB,−(t)−NSD(t), (1) 式中：${N_{{\text{TB,+}}}}\left( t \right)$、$ {N_{{\rm{TB, - }}}}\left( t \right) $、$ {N_{{\text{SD}}}}\left( t \right) $分别为 t 时段内充电TB、放电TB和换电需求量.
假设 t 时刻ESB可用剩余容量为$ {C_{{\text{ESB}}}}\left( t \right) $，则t+ Δt时段开始时可用剩余容量可表示为
CESB(t+Δt)=CESB(t)+CESB,+(t)−CESB,−(t), (2) 式中：$ {C_{{\text{ESB,+}}}}\left( t \right) $、$ {C_{{\rm{ESB, - }}}}\left( t \right) $分别为 t 时段内ESB充电容量、放电容量.
在电价谷时段，储换一体站中ESB和亏电的TB集中从电网充电. 如果此时段发生换电需求，换下的亏电TB立即进行充电，即式（1）中$ {N_{{\rm{TB, - }}}}\left( t \right) $和式（2）中$ {C_{{\rm{ESB, - }}}}\left( t \right) $为0.
在电价平时段，储换一体站中TB参与换电服务. 对于ESB和换下的亏电TB存在2种可能的状态：如果剩余的满电状态的TB不足以满足剩余时间的换电需求，则ESB或电网对亏电的TB进行充电；否则，二者均不动作，即式（1）中${N_{{\text{TB,+}}}}\left( t \right)$和式（2）中$ {C_{{\text{ESB,+}}}}\left( t \right) $为0.
在电价峰时段，满电的TB参与换电服务；ESB向电网放电以支撑电网，即式（2）中$ {C_{{\text{ESB,+}}}}\left( t \right) $=0. 如果满电的TB不足以满足剩余时间的换电需求，则ESB对亏电的TB进行充电，即式（1）中$ {N_{{\rm{TB, - }}}}\left( t \right) $=0；否则，TB向电网放电，辅助ESB支撑电网，即式（1）中$ {N_{{\text{TB,+}}}}\left( t \right) $=0.
2. 电动汽车换电需求预测模型
电动汽车换电需求涉及的因素相当复杂，受到电动汽车行驶特性、电池充放电特性、用户行为习惯以及政策时间天气等因素的综合影响. 本文仅考虑影响电动汽车换电需求的3种主要因素：用户出行开始时间、出行结束时间和电动汽车日行驶里程，进行换电需求预测. 预测过程分为4个步骤.
步骤1 初始化出行参数
基于美国家用汽车调查2009 年车辆出行统计数据[22-23]，用户出行开始时间和出行结束时间近似拟合为正态分布函数，电动汽车日行驶里程近似拟合为对数正态分布函数，其概率密度函数依次为
fs={1√2πσsexp(−(t−μs)22σ2s),0<t⩽μs+12，1√2πσsexp(−(t−24−μs)22σ2s),μs+12<t⩽24, (3) fe={1√2πσeexp(−(t+24−μe)22σ2e),0<t⩽μe−12,1√2πσeexp(−(t−μe)22σ2e),μe−12<t⩽24, (4) fd=1d√2πσdexp(−(lnd−μd)22σ2d), (5) 式中：${\mu _{\text{s}}}$、${\mu _{\text{e}}}$、${\mu _{\text{d}}}$和${\sigma _{\text{s}}}$、${\sigma _{\text{e}}}$、${\sigma _{\text{d}}}$分别为用户出行开始时间、出行结束时间、电动汽车日行驶里程的均值和方差，${\mu _{\text{s}}} = 8.92$，${\sigma _{\text{s}}} = 3.24$，${\mu _{\text{e}}} = 17.47$，${\sigma _{\text{e}}} = 3.41$，${\mu _{\text{d}}} = 3.00$，${\sigma _{\text{d}}} = 0.91$；d为电动汽车日行驶里程.
步骤2 计算各时间段起始时刻电动汽车荷电状态（SOC）
在用户出行起始时间、结束时间和电动汽车日行驶里程的基础上，根据统计得到电动汽车单位时间出行距离与总路程的比例，如图3所示，可近似得到各时段电动汽车耗电量和对应时间的SOC. t + Δt时段开始时，第i辆电动汽车的SOC为
oi(t+Δt)=oi(t)−Eumdp(t)/p(t)EumdEbatEbat, (6) 式中： $ {E_{{\text{um}}}} $= 0.25 kW/km，为电动汽车单位里程耗电量；$ p\left( t \right) $为t时段内出行距离与总路程之比； $ {E_{{\text{bat}}}} $为电池额定容量.
步骤3 电动汽车用户换电决策
由于换电电价包含换电电量电价和换电服务费，高于居民充电电价，用户在电动汽车剩余电量不允许时接受换电服务，以保证用户经济性. 因此，电动汽车用户的换电决策根据以下2条规则确定：1） 若剩余电量无法满足用户出行，则选择换电；2） 换电时，电池荷电状态值ost为正态分布产生的随机数，即ost～N(0.3, 0.03). 因此，t时段开始时第k辆车的换电需求$ {N_{{\text{SD}},k}}\left( t \right) $为
NSD,k(t)={1，ok(t)⩽ok,r(t),ok(t)⩽ost，0,其他， (7) 式中：$ {o_{k,{\text{r}}}}\left( t \right) $为第k辆车t时段开始时剩余路程对应所需的最小SOC.
步骤4 生成电动汽车换电需求典型场景
对每一辆电动汽车重复步骤1～3，可模拟生成规模化电动汽车换电需求场景集. t时段内总的换电需求$ {N_{{\text{SD}}}}\left( t \right) $及1 d内总的换电需求NSD,a （参与换电的汽车数量）分别为
{NSD(t)=K∑k=1NSD,k(t)，NSD,a=T∑t=1NSD(t)， (8) 式中：T为划分的时间区间数；K为电动汽车数量.
在实际规划中，受计算复杂性的限制，对每一个换电需求场景进行计算是不切实际的. 为降低计算复杂度，同时保证需求场景的准确性，本文采用K-medoids算法削减换电需求场景.
3. 规划模型
在实际工程应用中，系统的经济性和安全性在很多情况下是需要统一协调的. 在储换一体站的运行模式中，储换一体站获取收益的方式有2种：提供换电服务收益和基于分时电价的“高放低储”收益. 而电网的安全运行又与电池组的充放电功率密切相关. 为保证电网和储换一体站安全经济运行，以全寿命周期内的净收益为外层规划目标，同时，在内层优化中考虑一体站对电网的支撑能力，建立储换一体站双层规划模型.
3.1 外层规划模型
为评价储换一体站项目全寿命周期的经济可行性，外层规划以储换一体站寿命周期内收益最大为目标，表示为
maxS=SS+SEV+SG−SIN−SOM−SD−SB， (9) 式中：S为储换一体站年均利润；$ {S_{\text{S}}} $、$ {S_{{\text{EV}}}} $、${S_{\text{G}}}$、${S_{{\text{IN}}}}$、${S_{{\text{OM}}}}$、${S_{\text{D}}}$、${S_{\text{B}}}$分别为储换一体站年均支撑电网收益、换电服务收益、补贴收益、投资建设成本、运维成本、电池衰减成本和购电成本.
1） 支撑电网收益
SS=∑s∈ΩsY∑y=1T∑t=1[PES,ds,y(t)+NTB,−(t)∑i=1PEV,ds,y,i(t)]psηdD(t)Δt， (10) 式中：s为换电需求场景；${\varOmega _s}$为换电需求场景集合；Y为年运行总天数；${p_s}$为场景s的发生概率；$ P_{s,y}^{{\text{ES,d}}}\left( t \right) $、$ P_{s,y,i}^{{\text{EV,d}}}\left( t \right) $分别为场景s下第y天t时段内ESB向电网放电功率、第i块TB向电网放电功率；$ {\eta _{\text{d}}} $为放电效率；$ D\left( t \right) $为t时段电网电价.
2） 换电服务收益
SEV=∑s∈ΩsY∑y=1T∑t=1NSD,s(t)∑i=1(EEVs,y,i(t)−EEV,res,y,i(t))DEVps+∑s∈ΩsNSD,a,sDrtps， (11) 式中：$ E_{s,y,i}^{{\text{EV}}}\left( t \right) $为场景s下第y天t时段一体站为第i辆车提供的换电电池电量；$ E_{s,y,i}^{{\text{EV,re}}}\left( t \right) $为场景s下第y天t时段一体站从第i辆车收回的换电电池电量；${N_{{\text{SD}},s}}\left( t \right)$、${N_{{\text{SD}},{\text{a}},s}}$分别为场景s下t时段换电需求、1 d 节点内总换电需求；$ {D_{{\text{EV}}}} $为换电价格；$ {D_{{\text{rt}}}} $为电池年租赁价格.
3） 补贴收益
SG=∑s∈ΩsY∑y=1T∑t=1NSD,s(t)∑i=1PEV,ds,y,i(t)DEV,bpsΔt+∑s∈ΩsY∑y=1T∑t=1PES,ds,y(t)DES,bpsΔt， (12) 式中： $ {D_{{\text{ES,b}}}} $、$ {D_{{\text{EV,b}}}} $分别为储能服务补贴单价、换电服务补贴单价.
4） 投资建设成本
采用等值年成本表示一体站投资建设成本：
SIN=[CEV,EEEV,B+CES,EEES,B+CP(PEV+PES)]×r(1+r)N(1+r)N−1， (13) 式中：$ {C}_{\text{EV,E}}、{C}_{\text{ES,E}}、{C}_{\text{P}} $分别为TB容量单价、ESB容量单价、PCS功率单价；$ {P}_{\text{EV}}、{P}_{\text{ES}} $分别为PCS 1和PCS 2的额定功率；r为贴现率；N为一体站运行周期.
5） 运维成本
SOM=COM(PEV+PES)， (14) 式中：$ {C_{{\text{OM}}}} $为运行维护费用单价.
6） 电池衰减成本
SD=CES,EEES,BlES/(YcES)+NTB,tol∑i=1CEV,EEEV,BlEV,i/(YcEV,i)， (15) 式中：$ {l}_{\text{ES}}、{l}_{\text{EV},i} $分别为ESB循环寿命、第i块TB循环寿命[24]；$ {c}_{\text{ES}}、{c}_{\text{EV},i} $分别为ESB日循环次数、第i块TB日循环次数；NTB,tol为一体站配置换电电池数量.
7） 购电成本
SB=∑s∈ΩsY∑y=1T∑t=1[PES,cs,y(t)+NTB,+(t)∑i=1PEV,cs,y,i(t)]D(t)psΔt/D(t)psΔtηcηc, (16) 式中：$ P_{s,y}^{{\text{ES,c}}}\left( t \right) $、$ P_{s,y,i}^{{\text{EV,c}}}\left( t \right) $分别为场景s下第y天t时段内ESB的充电功率、第i块TB的充电功率；$ {\eta _{\text{c}}} $为充电效率.
3.2 内层规划模型
储换一体站的容量初步确定，为保证电网和储换一体站的安全运行，内层规划以支撑电网、提高电网电能质量为目标，进行充放电优化. 以电压日方差f表示储换一体站对电网的支撑能力，内层规划模型目标函数为
minf=1TJ∑j=1T∑t=1(uj(t)−ˉuj)2, (17) 式中：${u_j}\left( t \right)$为t时段内节点j的电压；$ {\bar u_j} $为1 d内节点j的电压均值；J为系统节点总数.
3.3 约束条件
1） 潮流约束
{Pn=UnJ∑j=1Uj(Gnjcosθnj+Bnjsinθnj)，Qn=UnJ∑j=1Uj(Gnjsinθnj−Bnjcosθnj)， (18) 式中：$ {P_n} $、$ {Q_n} $分别为节点n注入的有功功率、无功功率；$ {\theta _{nj}} $为节点n与节点j间的电压相角差；$ {G_{nj}} $、$ {B_{nj}} $分别为节点n、j间支路的电导、电纳.
2） 节点电压约束
为保证电网的安全可靠运行，各节点电压幅值应保持在可接受的范围内：
Unmin⩽Un⩽Unmax， (19) 式中：${U_{n\max }}$、${U_{n\min }}$分别为节点n电压的上限、下限.
3） 电动汽车换电需求约束
任意时刻，一体站能够满足换电需求，即
{NSD(t)+NTB,+(t)−NTB,−(t)⩽NTB(t)，NTB(t)⩽NTB,tol. (20) 4） 充放电功率约束
任意时刻，一体站需满足功率上下限约束，即
{0⩽NTB， + (t)∑i=1PEV,ci(t)⩽PEV，0⩽NTB.−(t)∑i=1PEV,di(t)⩽PEV，0⩽PES,c(t)⩽PES，0⩽PES,d(t)⩽PES， (21) 式中：${P}_{i}^{\text{EV,c}} (t)$、${P}_{i}^{\text{EV,d}} (t)$分别为第i块换电服务电池充电、放电功率.
5） 荷电状态约束
任一时刻，一体站内TB和ESB均满足：
{omin⩽o(t)⩽omax，o(t+1)=o(t)+ηcPc(t)ΔtEbat−Pd(t)ΔtηdEbat， (22) 式中：o(t)为TB和ESB在t时段内的SOC；omin、omax分别为SOC的下限、上限；Ebat为TB和ESB额定容量；Pc(t)、Pd(t)分别为充电、放电功率.
3.4 求解算法
由于本文为双层规划模型，规模较大且涉及潮流计算，难以转化为传统的线性规划法、非线性规划法求解问题，而粒子群算法较为成熟，具有简单易行、收敛速度快、优化效率高、鲁棒性好等特点，因此，采用粒子群算法进行规划结果求解，流程如图4所示.
步骤1 对换电需求预测建模，利用蒙特卡洛模拟建立随机预测场景，并利用K-medoids算法削减换电需求场景，生成典型场景并计算相应概率；
步骤2 初始化粒子位置和速度，即储能电池、换电电池容量配置，作为外层规划的输入；
步骤3 以外层规划配置的电池总容量作为内层规划输入参数，在内层规划中采用粒子群算法优化各时段变流器功率、电池充放电功率，并反馈到外层规划；
步骤4 外层规划接收内层各时段变流器功率、电池充放电功率结果，计算储换一体站寿命周期内收益，并更新粒子个体最优值和群体最优值；
步骤5 判断是否满足终止条件，若满足终止条件则算法结束，输出储换一体站规划结果；否则，更新粒子种群位置和速度，重复步骤1～5.
4. 算例分析
4.1 测试参数设置
为验证所提方法在配电网中的有效性，以IEEE33节点测试系统为例进行规划分析；通过某地10 kV系统典型日负荷曲线模拟负荷节点的日负荷变化，分时电价参照该地标准，如图5所示；算例优化收敛曲线如图6所示，外层在种群规模为30时迭代约30次得到最优解，内层在种群规模为25时迭代约15次得到最优解. 为保证算法的收敛性，粒子群算法内、外层种群规模分别为25、30，迭代次数分别设置为30、50次，其他参数如表1所示.
图 5 某地10 kV系统典型日负荷曲线及分时电价Figure 5. Typical daily load curve of a 10 kV system and a time-of-use tariff4.2 换电需求预测分析
假设储换一体站服务于1 000辆电动汽车，且电动汽车出发时电池已经充满. 根据所构建的换电需求预测模型，电动汽车部分换电需求预测分布结果如图7所示. 根据结果统计，存在换电需求的车辆平均值为29辆. 由于本文设置的电动汽车电池容量为100 kW·h，续航里程能够满足大部分用户的出行需求，电动汽车换电需求较低，所以，预测换电需求数量是合理的. 通常电动汽车换电需求发生在出行途中，并且在换电行为发生前，用户已经行驶较长时间，换电时间集中在下午. 如图7所示，电动汽车换电需求存在明显的波峰，高峰时刻分布在10：00—19：00，这是由于多数电动汽车用户在午间选择充电所致；与图5中的分时电价曲线相比，换电需求集中发生于电价平时段和峰时段. 同时，从仿真结果中还可以看出，不同场景下的换电需求相差较大，这在一定程度上反映了换电需求的随机性.
表 1 储换一体站参数表Table 1. Parameters of EVSS-IS参数 数值 参数 数值 Ebat/（kW·h） 100 CES,E/（元·（kW·h）−1） 1800 CEV,E/（元·（kW·h）−1） 1280 CP/（元·kW−1） 2400 COM/（元·（kW·年）−1） 155 DEV/（元·（kW·h）−1） 1.47 DES,b/（元·（kW·h）−1） 0.15 DEV,b/（元·（kW·h）−1） 0.1 Drt/（元·年−1） 10800 $ {\eta _{\text{c}}}{\text{, }}{\eta _{\text{d}}} $ 0.9 r/% 5 N/a 15 在上述10 000个日换电需求场景的基础上，采用K-medoids聚类算法进行场景缩减，并根据Davies-Bouldin（DB）指标确定最佳聚类数，DB指标随聚类数变化关系如图8所示，可以看出，在聚类数为5个时存在明显拐点. 为平衡模型的准确性和计算的复杂性，本文选择聚类数为5个. 将随机得到的10000个换电需求场景压缩成5个典型场景，得到的换电需求典型场景如图9所示，其统计结果见表2.
表 2 换电需求典型聚类场景统计结果Table 2. Statistical results of demands for battery swapping on typical clustering scenarios场景编号 总需求/次 概率 1 20 0.0785 2 25 0.4189 3 30 0.3265 4 35 0.1397 5 40 0.0364 4.3 储换一体站容量规划分析
为验证所提的储换一体站模式的效果，设计4种配置方案，分别为方案2～5. 方案1是配置储换一体站模型，方案2是仅配置储能系统，方案3是仅配置换电站，方案4是分别配置储能系统和换电站，方案5是不配置储能系统或换电站. 5种方案下的规划结果如表3所示，从表中可以看出：
表 3 接入节点为11、18时不同情景下的规划结果Table 3. Optimization results for different scenarios with the accessing 11th, 18th nodes接入
节点方案
编号储能容
量/（MW·h）储能功
率/MW换电容
量/（MW·h）换电功
率/MW年均净
利润/万元电压日
方差年均成
本/万元11 1 10 2.00 3.5 0.60 60.590 6.0303 598.61 2 13.5 2.70 0 0 42.961 5.3699 534.91 3 0 0 3.5 0.61 17.016 5.9595 216.55 4 10.0 2.00 3.5 0.60 53.510 5.6288 621.68 5 7.6981 18 1 2.7 0.54 3.5 0.71 26.159 5.7167 320.57 2 6.2 1.26 0 0 19.885 5.6637 245.51 3 0 0 3.5 0.73 16.318 5.9594 214.94 4 2.7 0.54 3.5 0.71 25.440 5.6904 336.27 5 7.6981 1） 在配置容量方面，相同的测试系统能够接入的储能电池和换电电池容量之和是确定的. 一体站接入节点为11时，总容量为13.5 kW·h；接入节点为18时，总容量为6.2 kW·h，均为本文双层规划模型下的最大接纳容量.
2） 在配置经济性方面，根据本文设置的参数条件和充换电策略，前4种方案中的储能电站、换电站和储换一体站模式均可以获得收益. 当一体站接入点为11时，其投资收益率为10.13%；与方案2单独储能系统相比，方案1的年均净利润高17.629万元，投资收益率约高2.10%；与方案3单独的换电站相比，方案1的年均净利润、投资收益率分别高于单独的换电站43.572万元、2.15%；与方案4单独成站的储能系统相比，二者的配置相同，但方案1的年均净利润高7.075万元、投资收益率高1.52%. 当接入节点为18时，方案1的投资收益率为8.26%，年均净利润分别比方案2～4依次多6.274万、9.841万、0.719万元，投资收益率分别高2.09%、2.26%、1.51%. 因此，本文提出的储换一体站模式更具经济性.
3） 在电网支撑方面，与方案5不配置储能系统或者换电站相比，测试系统的电压日方差均有一定程度的降低. 在本文选择的2个接入节点上，电力系统的电压日方差降低值均在20%以上，这表明本文基于双层规划的储换一体站容量配置对系统电压水平具有一定程度的支撑能力.
综上所述，本文的储换一体站在满足电动汽车换电需求的同时，兼具低储高发获利和对电网电压支撑作用. 在本文的储换一体站运行模式中，储能系统和电动汽车换电站协调互济，在整个运行周期内，谷时段为一体站充电、峰时段向电网馈电，提高了经济效益，也有助于电网电压稳定，实现电动汽车用户、一体站运营者和电网“三赢”.
4.4 场景和接入点对储换一体站容量影响
4.4.1 不同场景下储换一体站规划分析
为进一步分析储换一体站模式在不同换电需求下的经济性和对配电网的支撑能力，按照4.3节储换一体站配置结果：在节点11处ESB 10.0 MW·h/2.00 MW（即容量为10.0 MW·h，功率为2.00 MW，下同）、TB 3.5 MW·h/0.60 MW；节点18处ESB 2.7 MW·h/0.54 MW、TB 3.5 MW·h/0.71 MW，对不同场景进行验证分析，结果如图10所示.
图 10 不同换电场景下规划结果Figure 10. Optimization results under different demand scenarios for battery swapping由表3和图10可以看出，年均净利润、电压日方差以及年均成本与换电需求呈现出正相关关系. 在场景1～3中，换电需求均小于储换一体站中配置的换电服务电池数，冗余的换电服务电池协助储能服务电池，向电网放电；而在场景4中，换电需求恰好等于储换一体站中配置的换电服务电池数，换电服务电池只提供换电服务；与前4种场景相比，场景5中的换电需求大于储换一体站中配置的换电服务电池数，为满足换电需求，换电服务电池需要从储能服务电池中充电. 在上述场景中，换电服务电池和储能服务电池所提供的总能量是相同的，由于单位电量换电服务收益大于储能服务收益，因此，在相同配置下，随着换电需求的增加，年均净利润呈现增加趋势；但是电压日方差整体上差别不大，对电网支撑能力影响较小.
4.4.2 储换一体站接入节点影响分析
接入节点分别为11和18时的储换一体站配置结果及各部分收益和成本如图11所示. 由图可知，在满足相同的换电需求时，不同节点的配置结果在储能系统的容量上存在差别，二者的收益差距主要来自于储能系统.
测试系统在典型日负荷曲线下各节点电压标幺值取值范围如图12所示，在本文中储换一体站充电时作为负荷节点，放电时为电压控制节点. 若储换一体站接入点接近平衡节点，则放电时会强制降低接入节点电压，使末端节点电压水平降低；若接入节点处于线路末端，则充电时会加重负荷，造成电压降落较大. 与节点11相比，节点18位于线路末端，为保证各节点电压在允许范围内，只能接纳较小的充电功率. 因此，对储换一体站的容量配置较小，总收益也较低. 综上所述，为保持较高的收益和电网电压水平，储换一体站应接入接近系统电压的节点.
5. 结 论
本文分析了电动汽车换电站和储能电站一体站的运行模式，提出一种考虑全寿命周期经济性和电网支撑能力的储换一体站容量规划模型，结论如下：
1） 建立的电动汽车换电需求预测模型，通过模拟电动汽车用户的出行特性，进而得到换电需求，客观反映电动汽车换电需求时间特性，对提高一体站容量规划的合理性具有一定的实用性；
2） 建立的储换一体站容量双层规划模型，既考虑了一体站设施投资运行的经济性，为一体站带来较高的经济收益，又能充分考虑一体站接入后对电网的支撑作用，降低电压波动；
3） 储换一体站模式，能够协调储能服务和换电服务，与储能电站或换电站单独接入电力系统相比，系统经济性更优.
-
图 2 不同文献斜坡行人速率对比
Figure 2. Comparison of pedestrian speeds on slopes in different literature
图 9 经典模型与改进模型对比（t=18 s）
Figure 9. Comparison of traditional model and improved model (t=18 s)
图 10 不同密度、不同坡度下的行人平均运动时间
Figure 10. Average movement time of pedestrians under different densities and slopes
图 11 不同坡度下的行人平均运动时间统计
Figure 11. Average movement time of pedestrians under different slopes
图 12 不同行人初始密度下的受伤情况统计
Figure 12. Injured pedestrians under different initial densities
图 13 各不耐烦因子下的人群运动效率及人均意外发生率
Figure 13. Movement efficiency and per capita accident rate of the crowd under different impatience factors
表 1 模型各参数取值
Table 1. Parameter values of the model
参数 取值 τi/s 0.5 Ai/N 2 × 103 Bi/m 0.08 σ1 0.1 σ2 0 vi0 根据式（5）取值 k/（kg•s−2） 1.2 × 105 κ/（kg•m−1•s−1） 2.4 × 105 mi [50,80] ri 根据式（6）取值 Ts/s 2 Tim/s 2 Pi 根据式（7）取值 Qi 根据式（9）取值 kim 1 qs 0.8 
下载: 导出CSV
表 2 分析指标及含义
Table 2. Analysis indicators and meanings
分析指标 含义 行人初始密度 仿真开始时刻在坡顶和坡底平台下的行人密度 平均运动时间 每个行人离开斜坡的平均时长 轻伤人数 运动过程中受轻伤的人数 重伤人数 运动过程中受重伤的人数 人群运动效率 30 s 内完成离开斜坡人数占总人数的比例 人均意外发生率 运动过程中人均受伤或摔倒次数，摔倒并受伤按 2 次意外计
下载: 导出CSV
-
[1] 马剑,王若成,邱谦谦. 紧急情况下城市轨道隧道客流疏散配流模型研究[J]. 铁道学报,2016,38(6): 8-14. doi: 10.3969/j.issn.1001-8360.2016.06.003MA Jian, WANG Ruocheng, QIU Qianqian. Passenger assignment model for emergency evacuation in metro rail tunnels[J]. Journal of the China Railway Society, 2016, 38(6): 8-14. doi: 10.3969/j.issn.1001-8360.2016.06.003 [2] MA J A, SHI D D, LI T, et al. Experimental study of single-file pedestrian movement with height constraints[J]. Journal of Statistical Mechanics: Theory and Experiment, 2020, 2020(7): 073409.1-073409.17. [3] KAWAMURA K, TOKUHIRO A, TAKECHI H. Gait analysis of slope walking: a study on step length, stride width, time factors and deviation in the center of pressure[J]. Acta Medica Okayama, 1991, 45(3): 179-184. [4] SUN J, WALTERS M, SVENSSON N, et al. The influence of surface slope on human gait characteristics: a study of urban pedestrians walking on an inclined surface[J]. Ergonomics, 1996, 39(4): 677-692. doi: 10.1080/00140139608964489 [5] MCINTOSH A S, BEATTY K T, DWAN L N, et al. Gait dynamics on an inclined walkway[J]. Journal of Biomechanics, 2006, 39(13): 2491-2502. doi: 10.1016/j.jbiomech.2005.07.025 [6] FINNIS K K, WALTON D. Field observations to determine the influence of population size, location and individual factors on pedestrian walking speeds[J]. Ergonomics, 2008, 51(6): 827-842. doi: 10.1080/00140130701812147 [7] PINGEL T J. Modeling slope as a contributor to route selection in mountainous areas[J]. Cartography and Geographic Information Science, 2010, 37(2): 137-148. doi: 10.1559/152304010791232163 [8] WALL-SCHEFFLER C M. Sex differences in incline-walking among humans[J]. Integrative and Comparative Biology, 2015, 55(6): 1155-1165. [9] SHEEHAN R C, GOTTSCHALL J S. At similar angles, slope walking has a greater fall risk than stair walking[J]. Applied Ergonomics, 2012, 43(3): 473-478. doi: 10.1016/j.apergo.2011.07.004 [10] MEEDER M, AEBI T, WEIDMANN U. The influence of slope on walking activity and the pedestrian modal share[J]. Transportation Research Procedia, 2017, 27: 141-147. doi: 10.1016/j.trpro.2017.12.095 [11] BROACH J, DILL J. Pedestrian route choice model estimated from revealed preference GPS data[C]//Proceedings of Transportation Research Board 94th Annual Meeting. Washington D. C.: Transportation Research Board, 2015: 3669.1-3669.13 [12] 殷路伟,杜志刚,罗正宇,等. 城市人行过街天桥局部通行能力分析研究[J]. 武汉理工大学学报(交通科学与工程版),2015,39(5): 996-1000.YIN Luwei, DU Zhigang, LUO Zhengyu, et al. Analysis of local capacity for urban pedestrian overcrossing[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2015, 39(5): 996-1000. [13] HENDERSON L F. The statistics of crowd fluids[J]. Nature, 1971, 229(5284): 381-383. doi: 10.1038/229381a0 [14] HENDERSON L F. On the fluid mechanics of human crowd motion[J]. Transportation Research, 1974, 8(6): 509-515. doi: 10.1016/0041-1647(74)90027-6 [15] YUE F R, CHEN J, MA J, et al. Cellular automaton modeling of pedestrian movement behavior on an escalator[J]. Chinese Physics B, 2018, 27(12): 124501.1-124501.6. [16] FU Z J, XIA L A, YANG H T, et al. Simulation study of overtaking in pedestrian flow using floor field cellular automaton model[J]. International Journal of Modern Physics C, 2017, 28(5): 1750059.1-1750059.17. [17] 李芳,狄月,陈绍宽,等. 考虑客流引导和小群体行为的地铁车站疏散模型[J]. 西南交通大学学报,2019,54(3): 587-594. doi: 10.3969/j.issn.0258-2724.20170668LI Fang, DI Yue, CHEN Shaokuan, et al. Modelling passenger evacuation from metro platforms considering passenger flow guidance and small group behaviour[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 587-594. doi: 10.3969/j.issn.0258-2724.20170668 [18] 菅肖霞,张小宁. 斜坡通道双向行人流安全疏散行为研究[J]. 系统工程理论与实践,2017,37(10): 2715-2726. doi: 10.12011/1000-6788(2017)10-2715-12JIAN Xiaoxia, ZHANG Xiaoning. Study on safety evacuation behavior for counter flow on an inclined tunnel[J]. Systems Engineering−Theory & Practice, 2017, 37(10): 2715-2726. doi: 10.12011/1000-6788(2017)10-2715-12 [19] SARMADY S, HARON F, TALIB A Z. Simulation of pedestrian movements on slope using fine grid cellular automata[EB/OL]. (2020-10-07)[2022-04-20]. https://doi.org/10.48550/arXiv.2010.03387 [20] 王丽,刘茂,孟博,等. 开放空间复杂地形人员疏散模拟研究[J]. 中国安全科学学报,2012,22(1): 29-33. doi: 10.3969/j.issn.1003-3033.2012.01.005WANG Li, LIU Mao, MENG Bo, et al. Simulation study on pedestrian evacuation in open space under complicated topographic condition[J]. China Safety Science Journal, 2012, 22(1): 29-33. doi: 10.3969/j.issn.1003-3033.2012.01.005 [21] TOBLER W. Non-isotropic geographic modeling[R]. Santa Barbara: National Center for Geograpgic Information and Analysis, 1993. [22] 汤雪飞,季经纬,谢信亮,等. 坡度对疏散影响的试验研究[J]. 消防科学与技术,2017,36(11): 1508-1511. doi: 10.3969/j.issn.1009-0029.2017.11.008TANG Xuefei, JI Jingwei, XIE Xinliang, et al. The experimental studies on influence of slope on evacuation[J]. Fire Science and Technology, 2017, 36(11): 1508-1511. doi: 10.3969/j.issn.1009-0029.2017.11.008 [23] FUJIYAMA T, TYLER N. Predicting the walking speed of pedestrians on stairs[J]. Transportation Planning and Technology, 2010, 33(2): 177-202. doi: 10.1080/03081061003643770 [24] FRUIN J J. Designing for pedestrians: a level of service concept[J]. Highway Research Record, 1971, 1971(35): 1-15. [25] FRUIN J J. Pedestrian planning and design[J]. Metropolitan Association of Urban Designers and Environmental Planners, 1971, 77(4): 556-561. [26] HELBING D, FARKAS I, VICSEK T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(6803): 487-490. doi: 10.1038/35035023 [27] CHEN X, TREIBER M, KANAGARAJ V, et al. Social force models for pedestrian traffic−state of the art[J]. Transport Reviews, 2018, 38(5): 625-653. doi: 10.1080/01441647.2017.1396265 [28] 纪仲秋,赵盼超,姜桂萍,等. 人体在向后滑倒时平衡调节能力的生物力学研究[J]. 北京师范大学学报(自然科学版),2018,54(2): 269-276. doi: 10.16360/j.cnki.jbnuns.2018.02.019JI Zhongqiu, ZHAO Panchao, JIANG Guiping, et al. Biomechanic of balancing and adjusting the human body in backward slip[J]. Journal of Beijing Normal University (Natural Science), 2018, 54(2): 269-276. doi: 10.16360/j.cnki.jbnuns.2018.02.019 [29] KHOW K S F, VISVANATHAN R. Falls in the aging population[J]. Clinics in Geriatric Medicine, 2017, 33(3): 357-368. doi: 10.1016/j.cger.2017.03.002 [30] ELVIK R, BJØRNSKAU T. Risk of pedestrian falls in Oslo, Norway: relation to age, gender and walking surface condition[J]. Journal of Transport & Health, 2019, 12: 359-370. [31] HELBING D, MUKERJI P. Crowd disasters as systemic failures: analysis of the Love Parade disaster[J]. EPJ Data Science, 2012, 1(1): 1-40. doi: 10.1140/epjds1 [32] LIANG H Y, DU J, WONG S C. A continuum model for pedestrian flow with explicit consideration of crowd force and panic effects[J]. Transportation Research Part B: Methodological, 2021, 149: 100-117. doi: 10.1016/j.trb.2021.05.006 [33] HELBING D, BUZNA L, JOHANSSON A, et al. Self-organized pedestrian crowd dynamics: experiments, simulations, and design solutions[J]. Transportation Science, 2005, 39(1): 1-24. doi: 10.1287/trsc.1040.0108 [34] LEE J, KIM T, CHUNG J H, et al. Modeling lane formation in pedestrian counter flow and its effect on capacity[J]. KSCE Journal of Civil Engineering, 2016, 20(3): 1099-1108. doi: 10.1007/s12205-016-0741-9 [35] 张琦,渠静. 基于前摄效应的不耐烦行为建模与双向行人流动态[J]. 物理学报,2022,71(7): 070502.1-070502.13.ZHANG Qi, QU Jing. Impatient behavior modelling and simulation of bidirectional pedestrian flow dynamics based on proactive effect[J]. Acta Physica Sinica, 2022, 71(7): 070502.1-070502.13. [36] 中华人民共和国住房和城乡建设部. 地铁设计规范: GB 50157—2013[S]. 北京: 中国建筑工业出版社, 2014. [37] VANUMU L D, RAMACHANDRA RAO K, TIWARI G. Fundamental diagrams of pedestrian flow characteristics: a review[J]. European Transport Research Review, 2017, 9(4): 49.1-49.13. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 418
- HTML全文浏览量: 185
- PDF下载量: 42
- 被引次数: 0