Short-Circuit Characteristics Analysis of New Continuous Cable Traction Power Supply System
-
摘要:
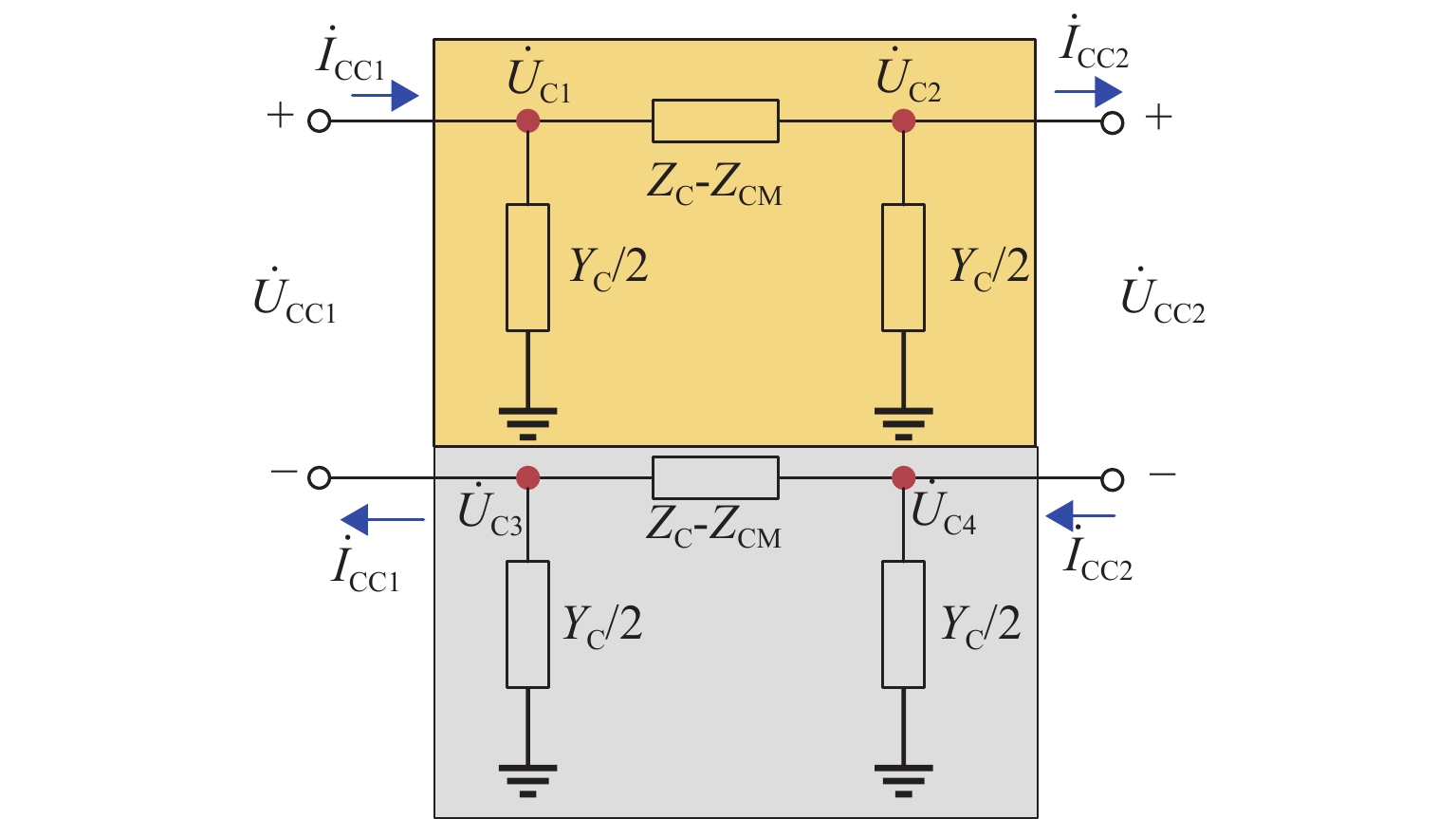
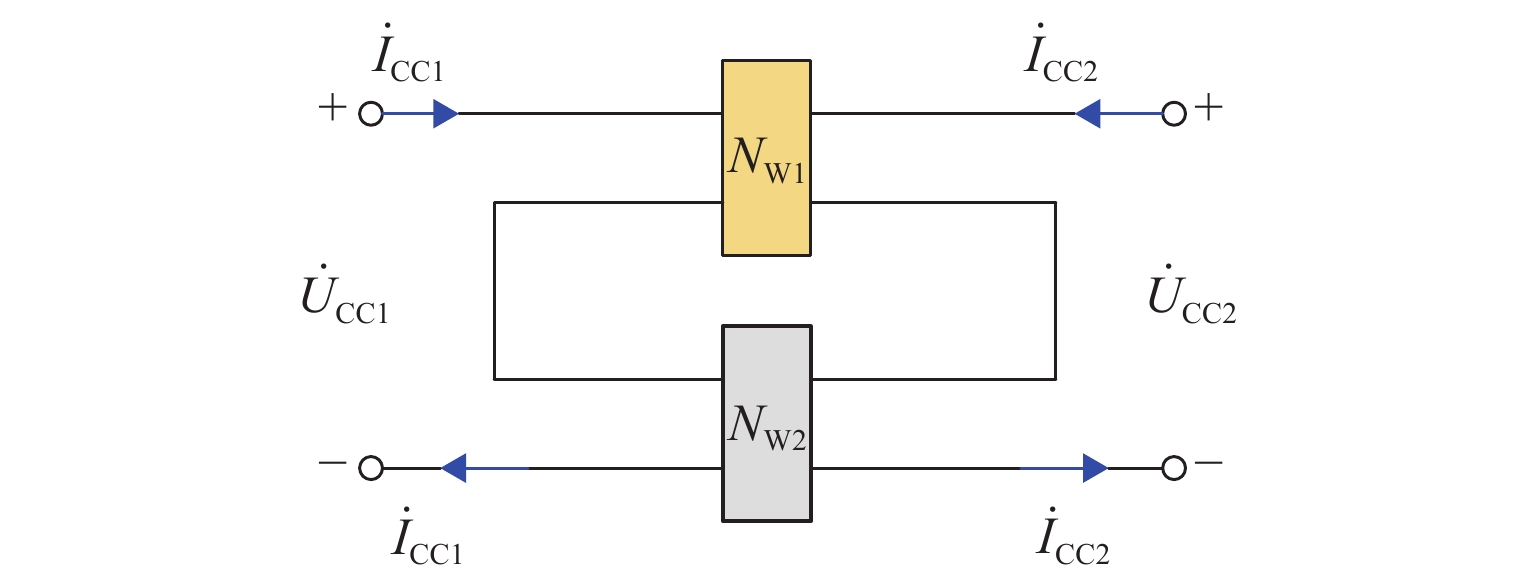
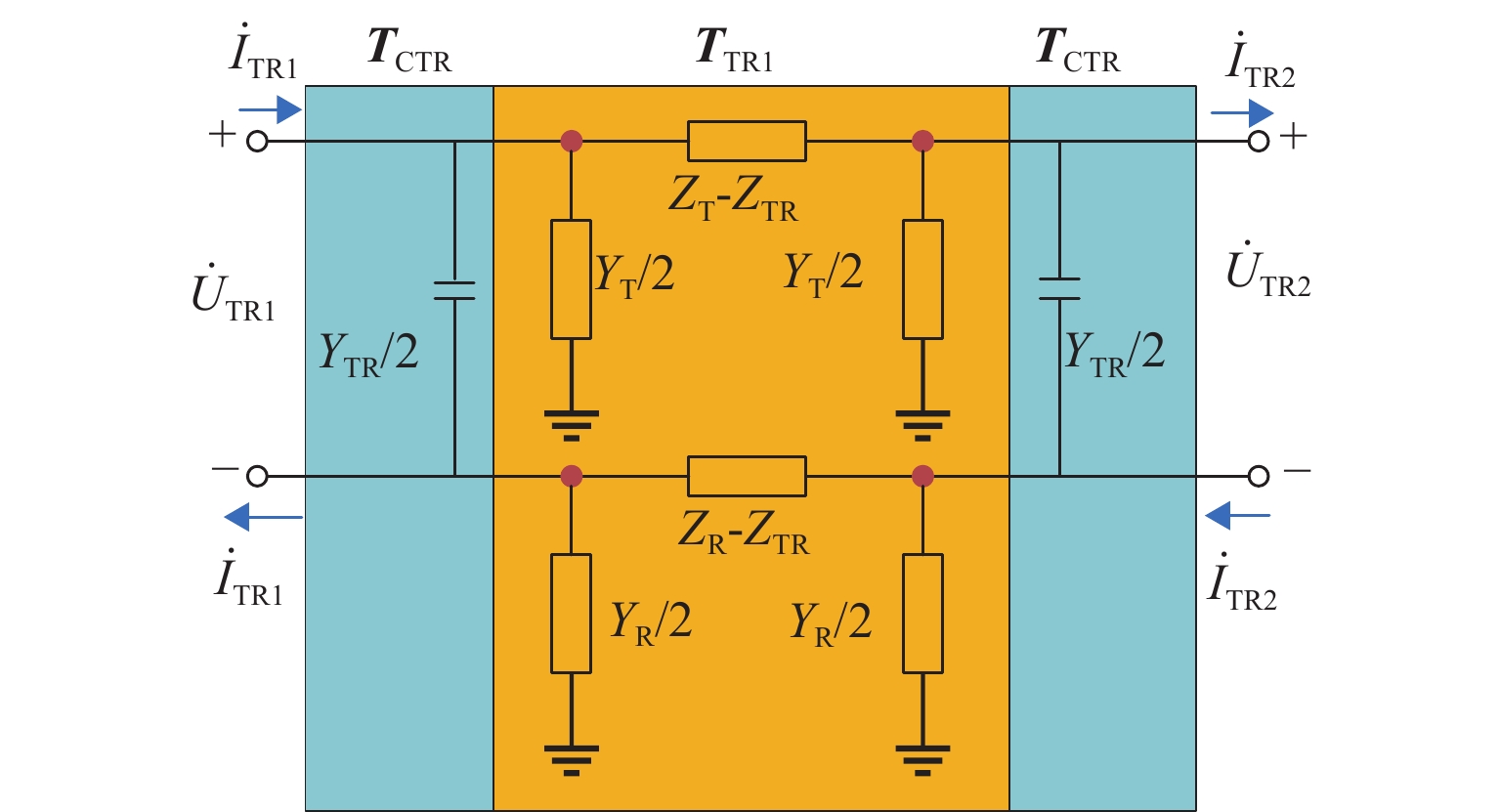
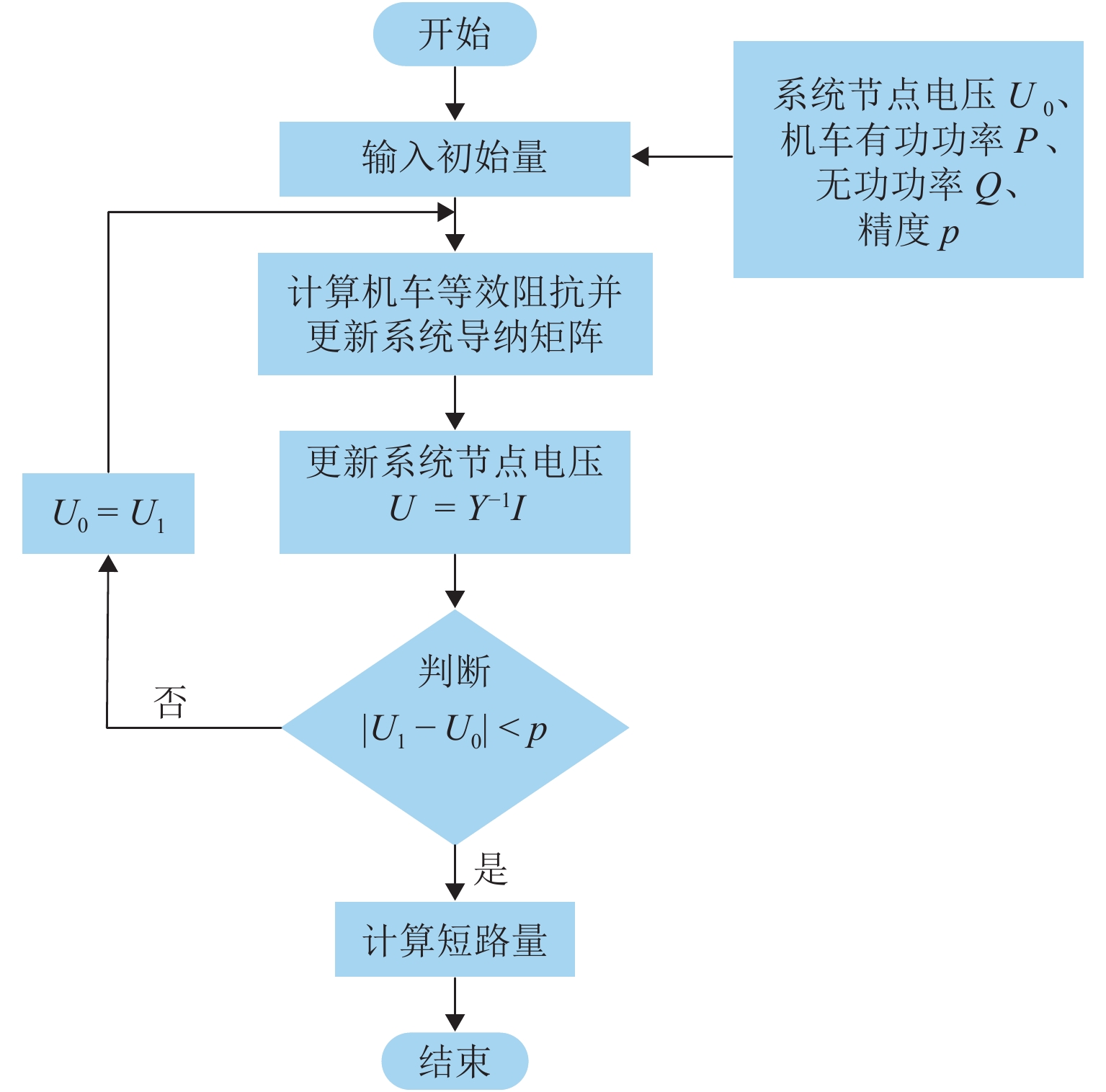
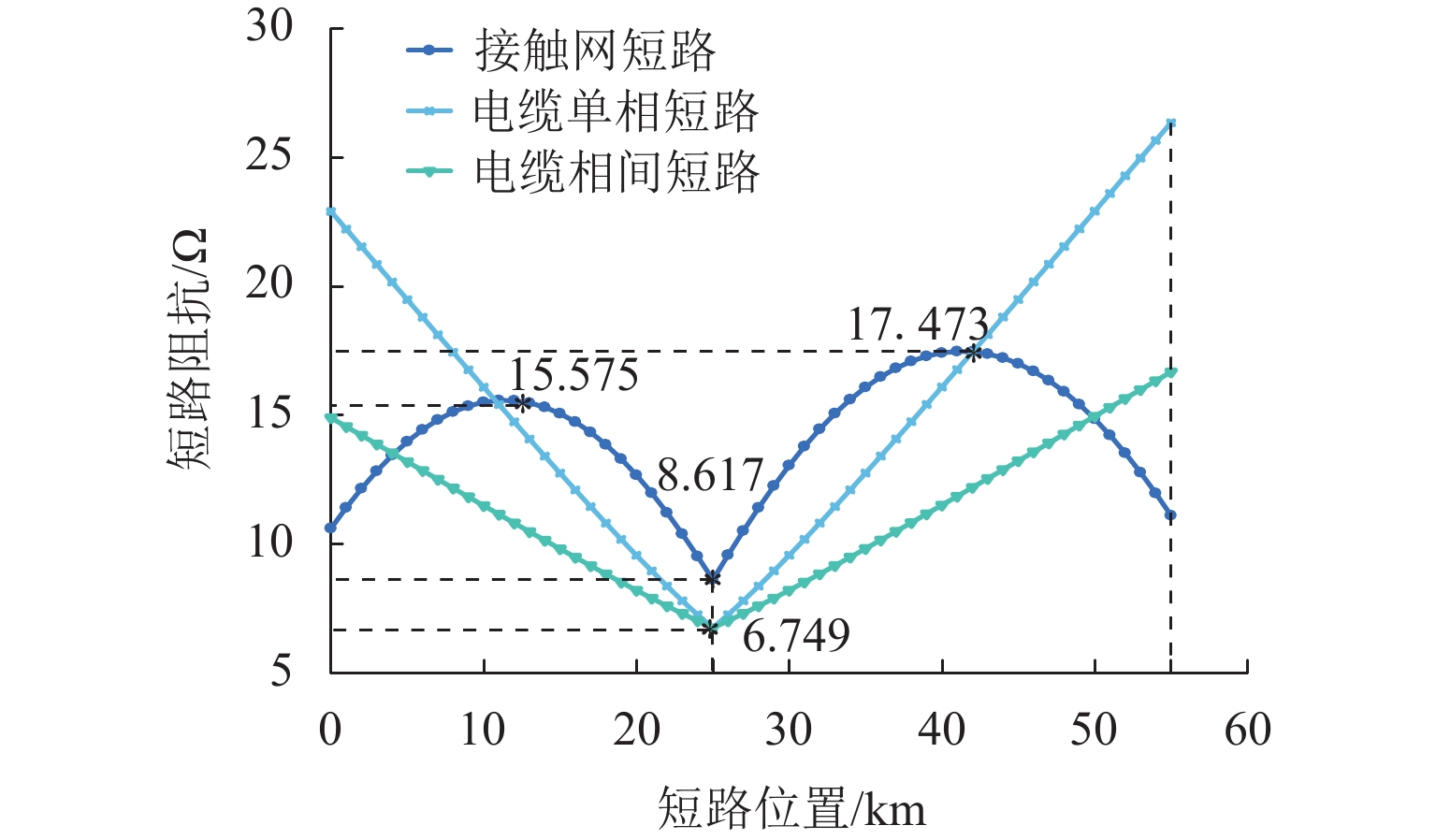
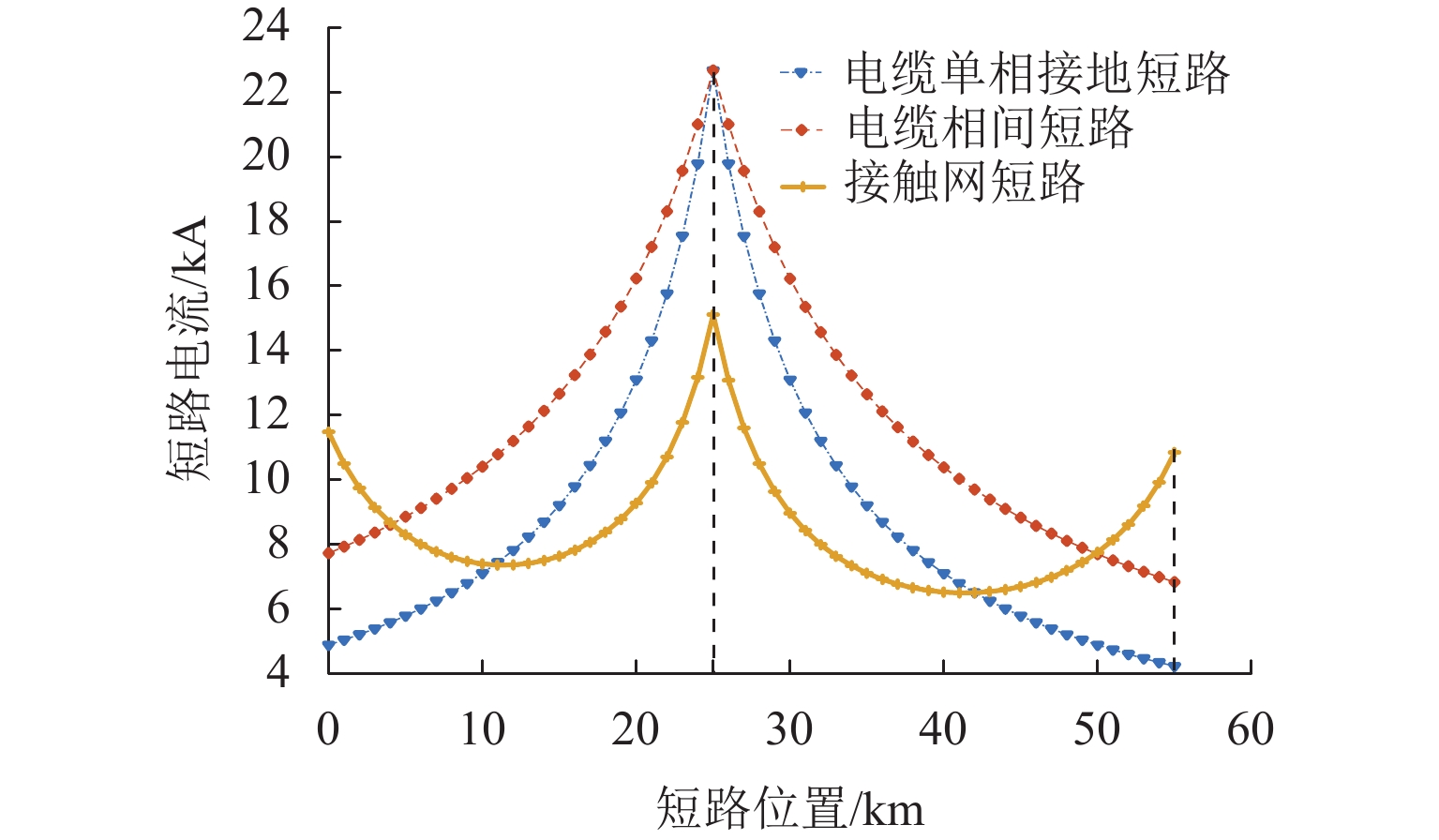
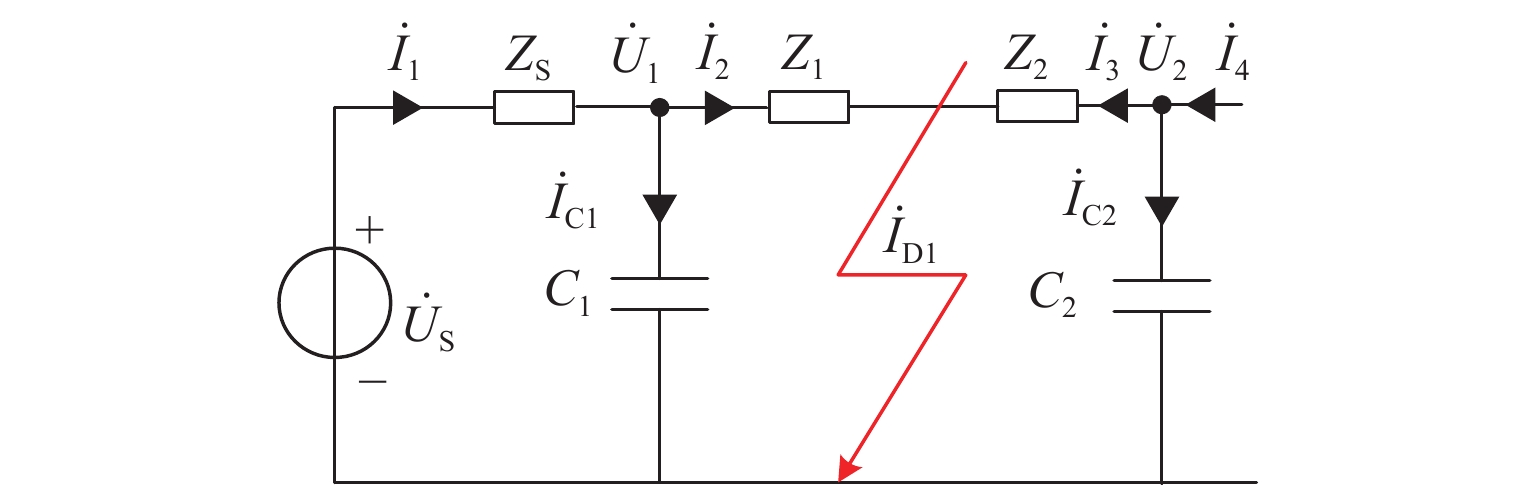
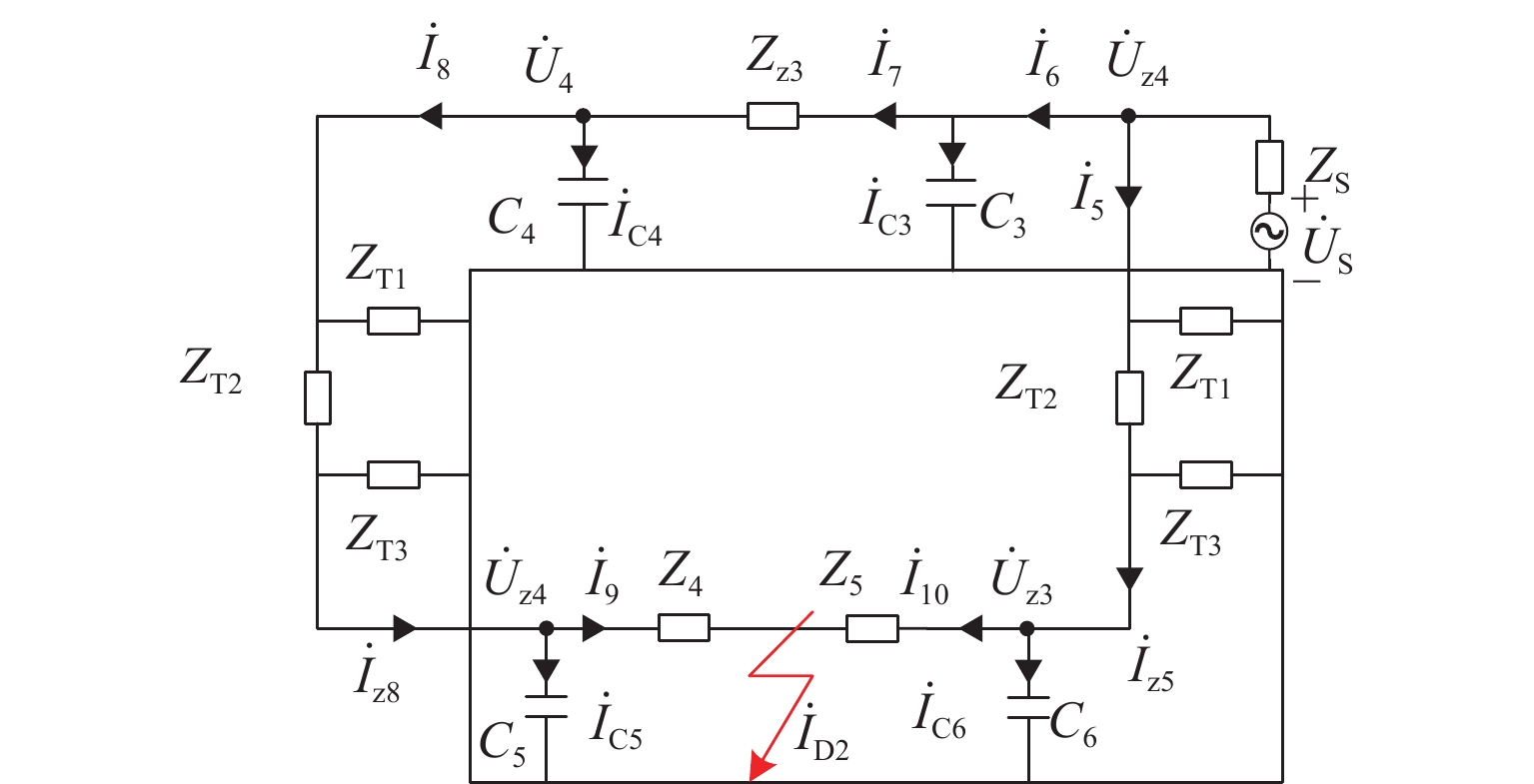
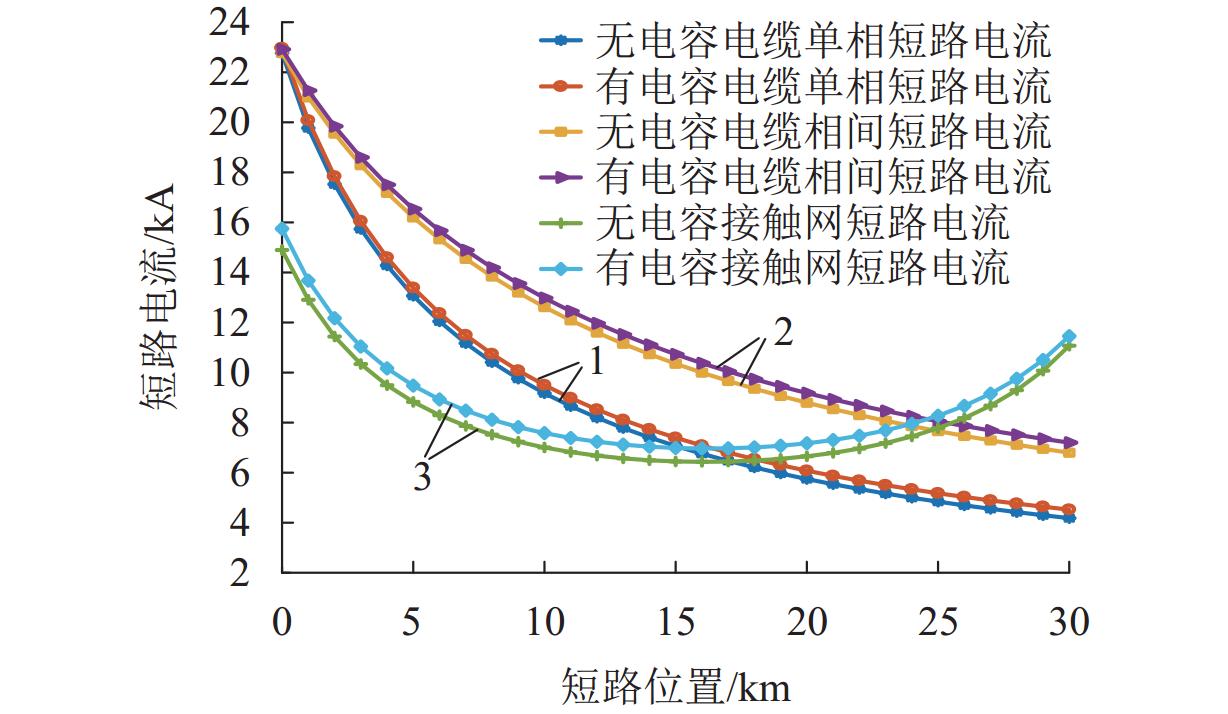
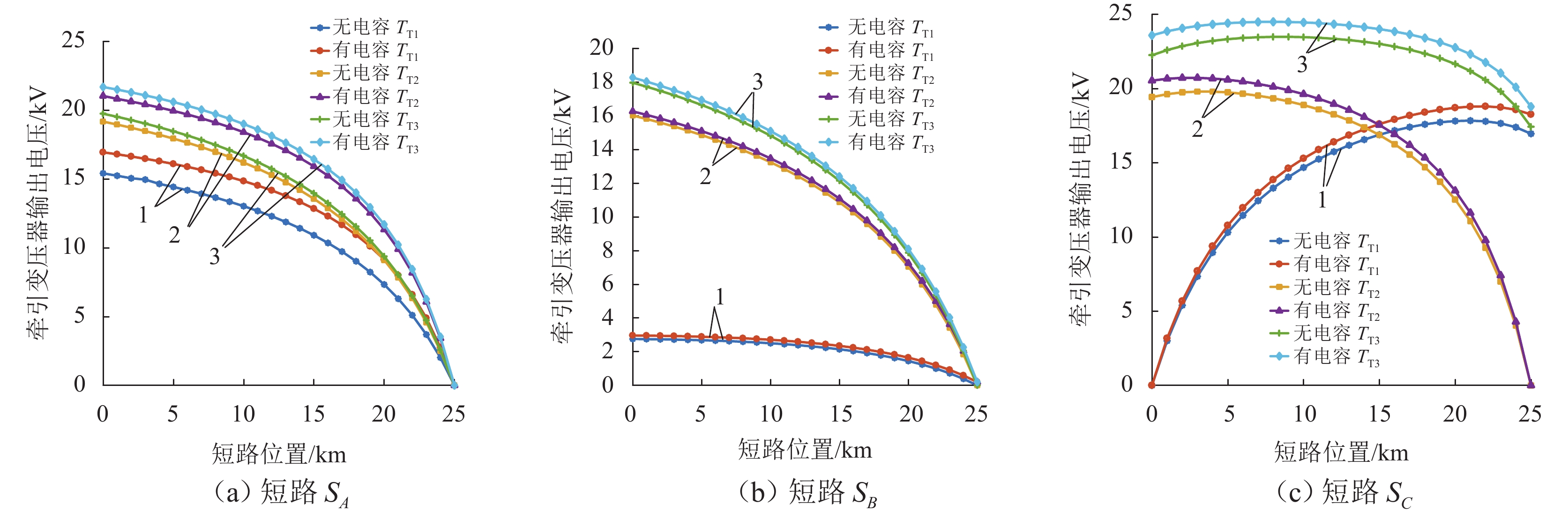
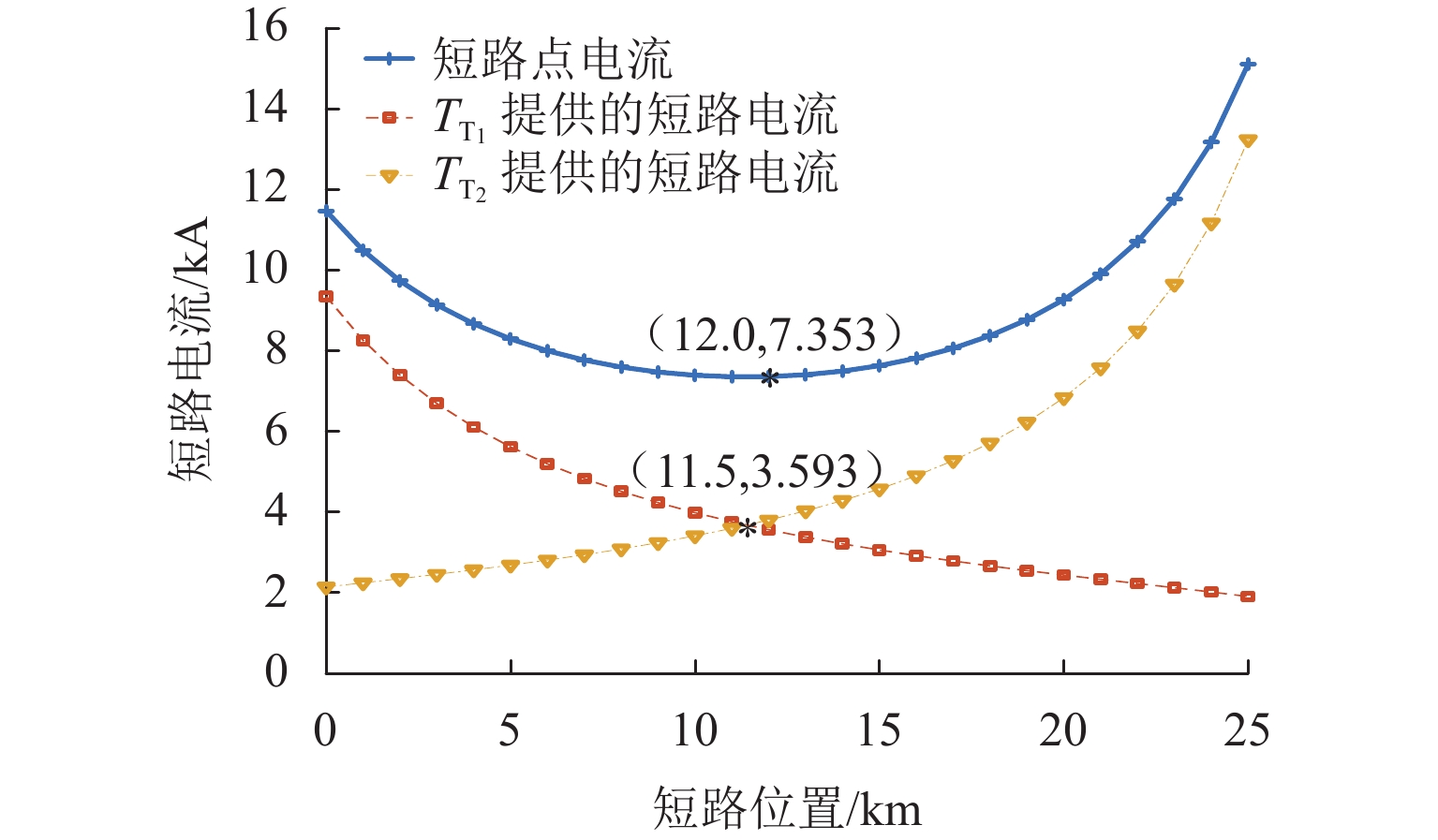
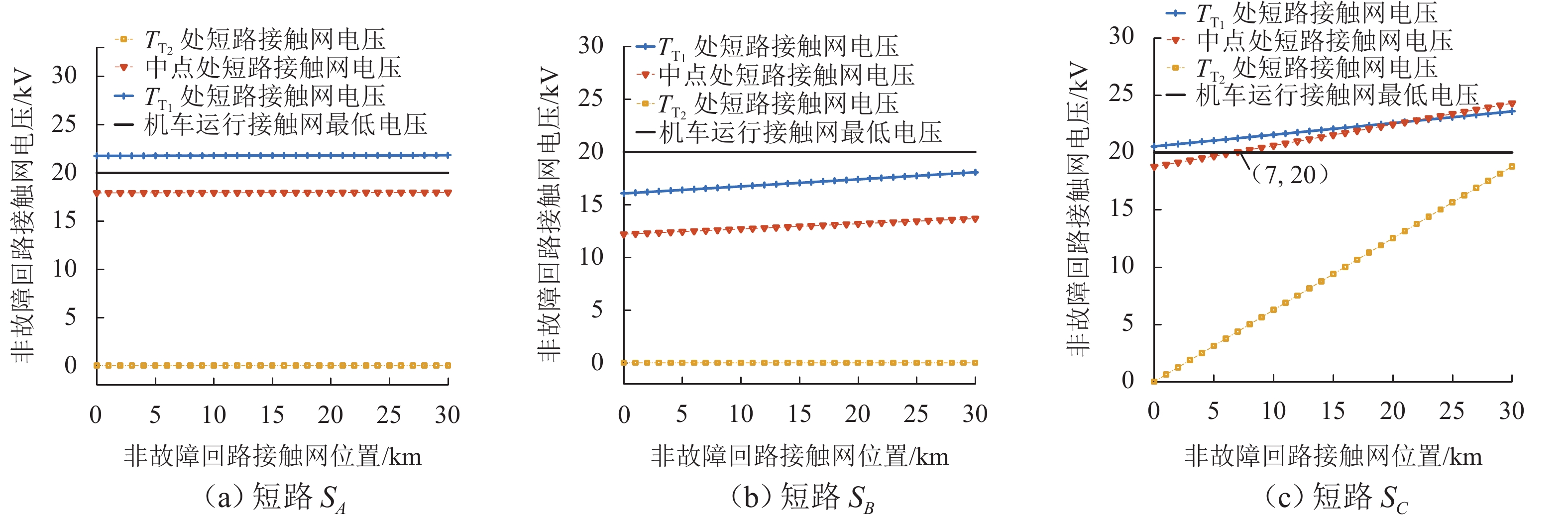
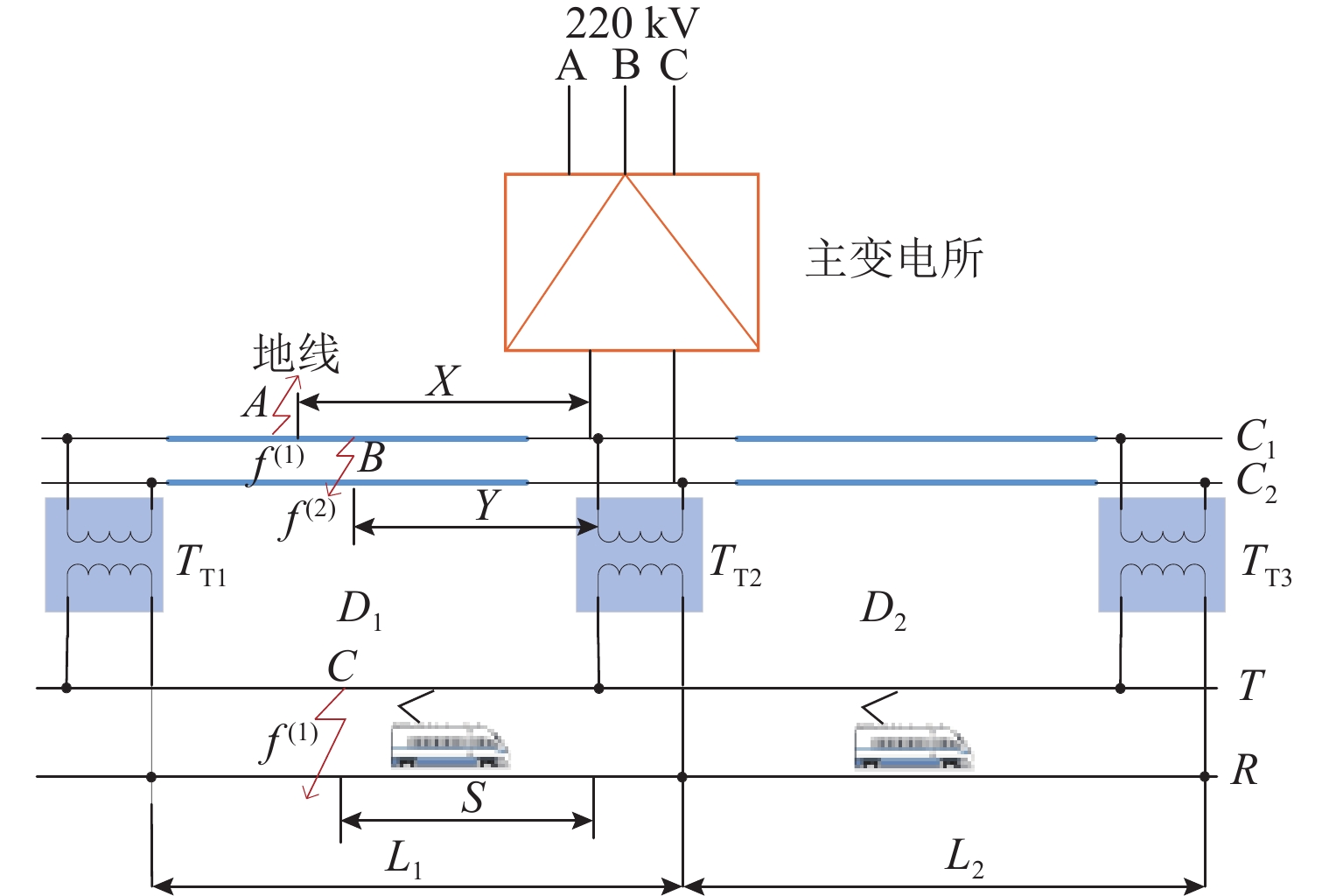
新型电缆贯通供电系统能够实现长距离输电、减少电分相数目，但两级供电模式将导致该系统结构复杂. 为研究电缆贯通供电系统短路特性，首先，建立单位长度的牵引电缆和接触网-钢轨的二端口网络参数，将各个子网络级联等效成1个二端口网络，进而转化为Ⅱ型电路，实现牵引电缆和接触网-钢轨任意长度的分布参数建模；由于接触网短路后导致机车电压下降，基于车网耦合关系采用迭代计算求解短路电流电压，仿真验证计算方法的准确性. 最后，解析不同短路类型的电气特性，重点分析分布电容对短路电流、电压的影响. 研究结果表明：分布电容会引起短路电流增大，且在不同短路情况下均造成牵引变压器输出电压增加；接触网短路电流由两侧牵引变压器共同提供，距短路点越远提供的电流越少；电缆相间短路对非故障回路机车运行影响最大.
-
关键词:
- 新型电缆贯通供电系统 /
- 分布电容 /
- 二端口网络 /
- 接触网 /
- 短路分析
Abstract:New continuous cable traction power supply system (CCTPSS) can achieve long-distance transmission and reduce the number of electric phases. However, the two-stage power supply mode leads to the complex structure of the system. In order to reveal the short-circuit characteristics of CCTPSS, the two-port network parameters of traction cable and catenary-rail of unit length were established. Each sub-network was cascaded and equated with a two-port network, which was then transformed into a Ⅱ-type circuit for modeling the distribution parameters of the traction cable and catenary-rail of any length. The locomotive voltage drops after short circuit of catenary. Therefore, considering the coupling relationship between the train and the network, the short-circuit current and voltage were solved by iterative calculation. The accuracy of the calculation method was validated by simulation. Finally, the electrical characteristics of different short-circuit types were analyzed, with emphasis placed on the influence of distributed capacitance on short-circuit current and voltage. The results show that the distributed capacitance can increase the short-circuit current and, under different short-circuit conditions, the output voltage of traction transformer. The short-circuit current of catenary is jointly provided by traction transformers on both sides, and the farther away from the short-circuit point is, the less current is provided. The cable phase-to-phase short circuit has the greatest impact on the operation of the non-fault-circuit locomotive.
-
图 17 3种短路非故障回路接触网电压
Figure 17. Voltage of non-fault-circuit catenary under three kinds of short-circuit conditions
表 1 3种短路情况短路电流
Table 1. Short-circuit current of three short-circuit conditions
结果与误差 电缆单相接地短路 电缆相间短路 接触网−钢轨短路 模值/A 角度/（°） 模值值/A 角度/（°） 模值/A 角度/（°） 仿真结果 5763.89 −83.54 8849.90 −78.71 8291.06 −79.53 本文计算结果 5771.46 −83.31 8850.04 −78.66 8291.52 −79.48 文献[11]结果 5409.47 −83.22 8542.94 −78.59 7846.05 −78.34 本文误差 7.57 0.23 0.14 0.05 0.46 0.05 文献[11]误差 354.42 0.33 306.96 0.12 445.01 1.19 
下载: 导出CSV
表 2 回路D1、D2电缆首末端电流
Table 2. Head and end currents of D1- and D2-circuit cables
回路 电缆首端 电缆尾端 $ \mathrm{\mathit{T}}_{\mathrm{T}1} $ 中点 $ \mathit{\mathrm{\mathit{T}}}_{\mathrm{T}2} $ $ \mathrm{\mathit{T}}_{\mathrm{T}1} $ 中点 $ \mathrm{\mathit{T}}_{\mathrm{T}2} $ D1 161.2 406.0 869.00 265.8 523.5 1967 D2 346.0 49.5 30.21 409.0 107.3 58
下载: 导出CSV
-
[1] MA F J, LUO A, XU X Y, et al. A simplified power conditioner based on half-bridge converter for high-speed railway system[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 728-738. doi: 10.1109/TIE.2012.2206358 [2] CHEN M W, LI Q Z, ROBERTS C, et al. Modelling and performance analysis of advanced combined co-phase traction power supply system in electrified railway[J]. IET Generation, Transmission & Distribution, 2016, 10(4): 906-916. [3] 李群湛. 城市轨道交通交流牵引供电系统及其关键技术[J]. 西南交通大学学报,2015,50(2): 199-207. doi: 10.3969/j.issn.0258-2724.2015.02.001LI Qunzhan. Industrial frequency single-phase AC traction power supply system and its key technologies for urban rail transit[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 199-207. doi: 10.3969/j.issn.0258-2724.2015.02.001 [4] 周婷,解绍锋. 电气化铁路新型电缆供电方案[J]. 电力自动化设备,2018,38(7): 189-195,206.ZHOU Ting, XIE Shaofeng. New-type cable traction power supply scheme of electric railroad[J]. Electric Power Automation Equipment, 2018, 38(7): 189-195,206. [5] ZHANG L Y, LIANG S W, LI X, et al. Modelling on novel cable traction power supply system and power distribution analysis[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 745-754. doi: 10.1109/TPWRD.2021.3069980 [6] 郭鑫鑫,李群湛,解绍锋,等. 电气化铁路高压电缆牵引网电气特性研究[J]. 电力自动化设备,2015,35(12): 132-137.GUO Xinxin, LI Qunzhan, XIE Shaofeng, et al. Electrical characteristic of cable traction network for electrified railway[J]. Electric Power Automation Equipment, 2015, 35(12): 132-137. [7] 张丽艳,梁世文,李鑫,等. 新型电缆贯通供电系统载流机制[J]. 西南交通大学学报,2021,56(3): 650-658.ZHANG Liyan, LIANG Shiwen, LI Xin, et al. Current-carrying mechanism of new continuous cable traction power supply system[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 650-658. [8] ZHANG L Y, LIANG S W, LI X. Research on the harmonic in new continuous cable traction power supply system and its transmission characteristic[J]. IET Generation, Transmission & Distribution, 2020, 14(14): 2710-2718. [9] 张丽艳,梁世文,李鑫,等. 新型电缆贯通供电系统运行特性分析[J]. 中国电机工程学报,2020,40(16): 5229-5238.ZHANG Liyan, LIANG Shiwen, LI Xin, et al. Operation characteristic analysis on new continuous cable power supply system[J]. Proceedings of the CSEE, 2020, 40(16): 5229-5238. [10] 郭鑫鑫,解绍锋,易东,等. 高压电缆牵引网短路特性分析[J]. 电力系统及其自动化学报,2017,29(8): 15-21,42.GUO Xinxin, XIE Shaofeng, YI Dong, et al. Analysis of short-circuit characteristics for high-voltage cable traction network[J]. Proceedings of the CSU-EPSA, 2017, 29(8): 15-21,42. [11] 郭鑫鑫. 电气化铁路电缆牵引网研究[D]. 成都:西南交通大学,2016. [12] 范芳芳. 电气化铁路新型电缆牵引供电方式继电保护方案研究[D]. 成都:西南交通大学,2016. [13] 谭永霞. 电路分析[M]. 2版. 成都:西南交通大学出版社,2009. [14] 胡海涛,何正友,王江峰,等. 基于车网耦合的高速铁路牵引网潮流计算[J]. 中国电机工程学报,2012,32(19): 101-108.HU Haitao, HE Zhengyou, WANG Jiangfeng, et al. Power flow calculation of high-speed railway traction network based on train-network coupling systems[J]. Proceedings of the CSEE, 2012, 32(19): 101-108. [15] MA Qingan, DONG Zhaode, GUO Kai. Calculation of short circuit current of electrified railway traction network [C]//Proceedings of 2017 Annual Meeting and New Technology Seminar of Electrification Committee of China Railway Society, 2017: 125-129. -
下载:
点击查看大图
计量
- 文章访问数: 199
- HTML全文浏览量: 61
- PDF下载量: 47
- 被引次数: 0