Rail Corrugation Measurement Method Based on Vibration-Noise Fusion in Metro System
-
摘要:
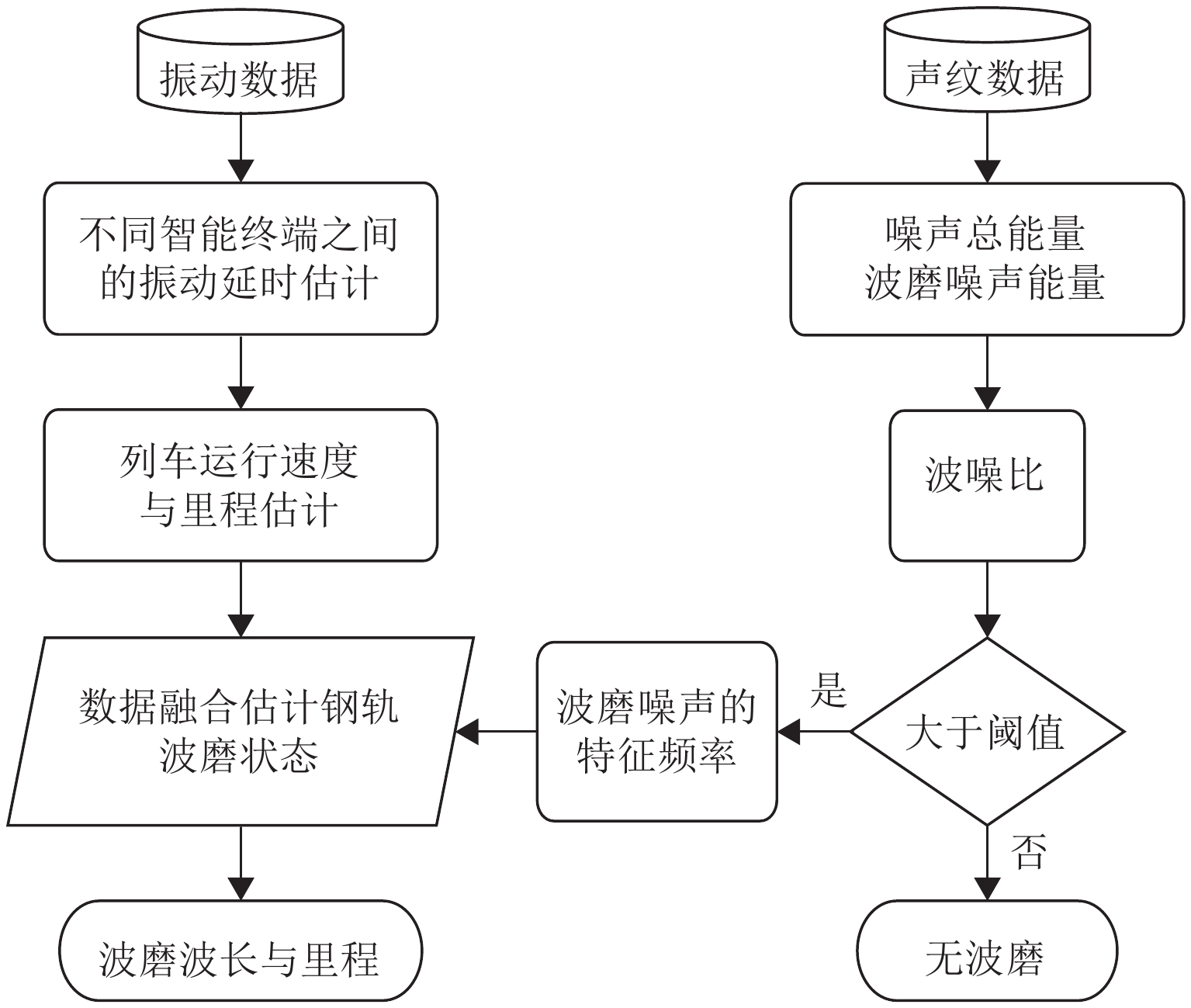
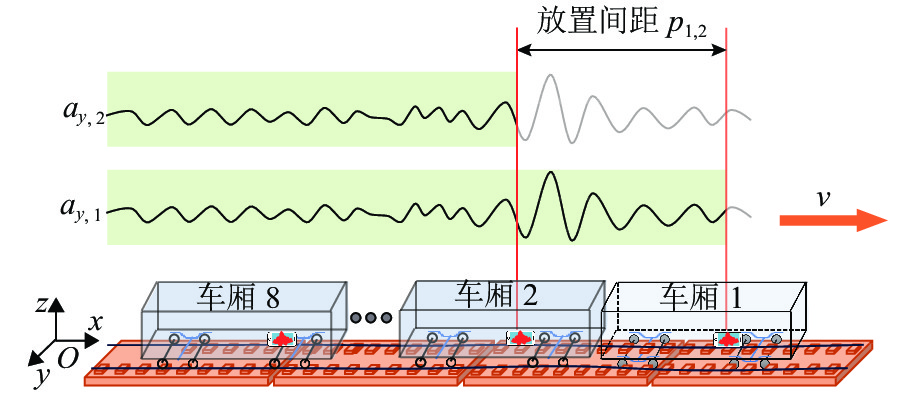
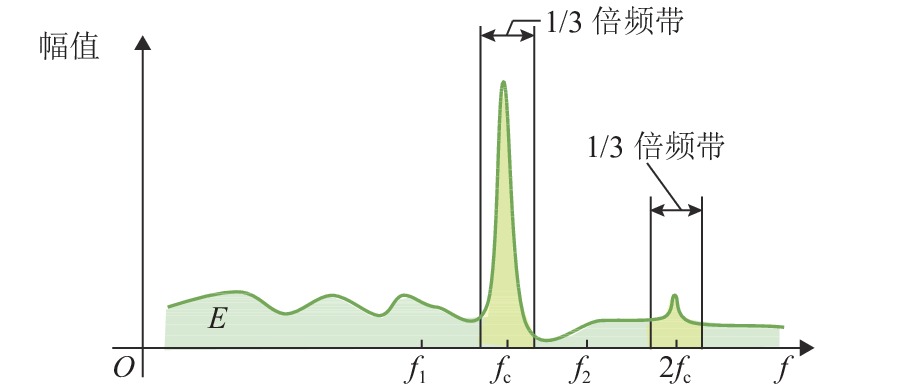
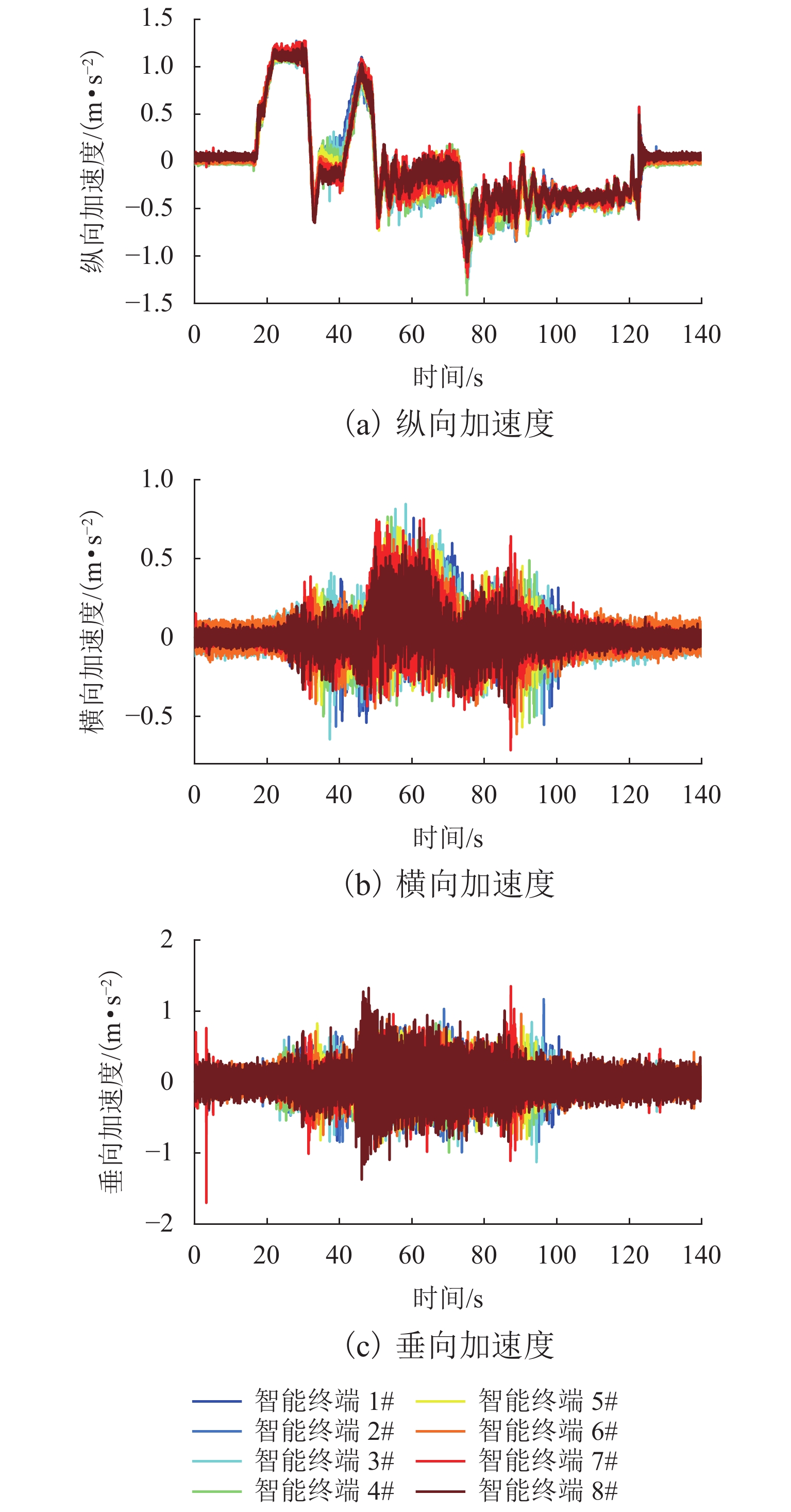
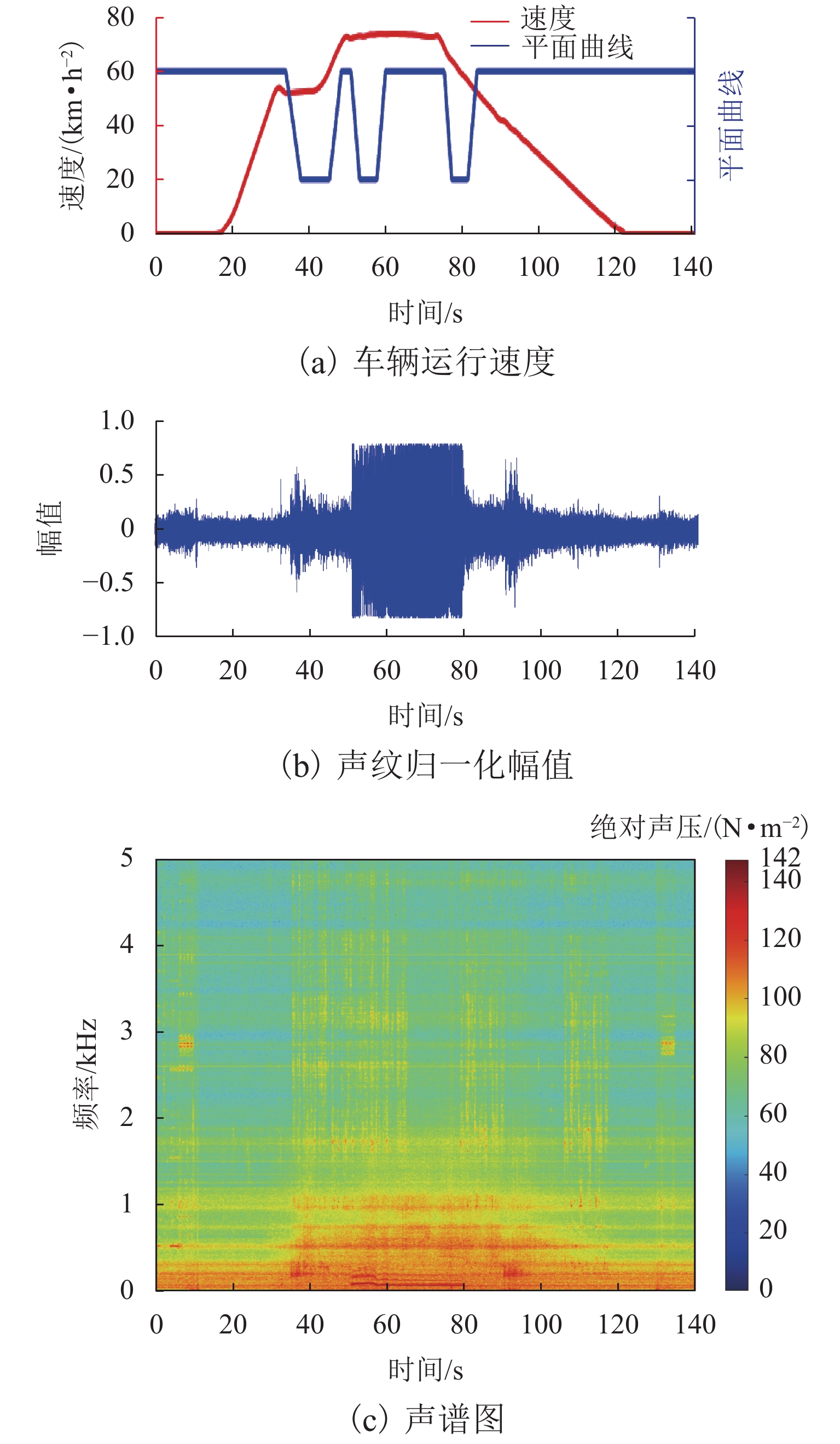
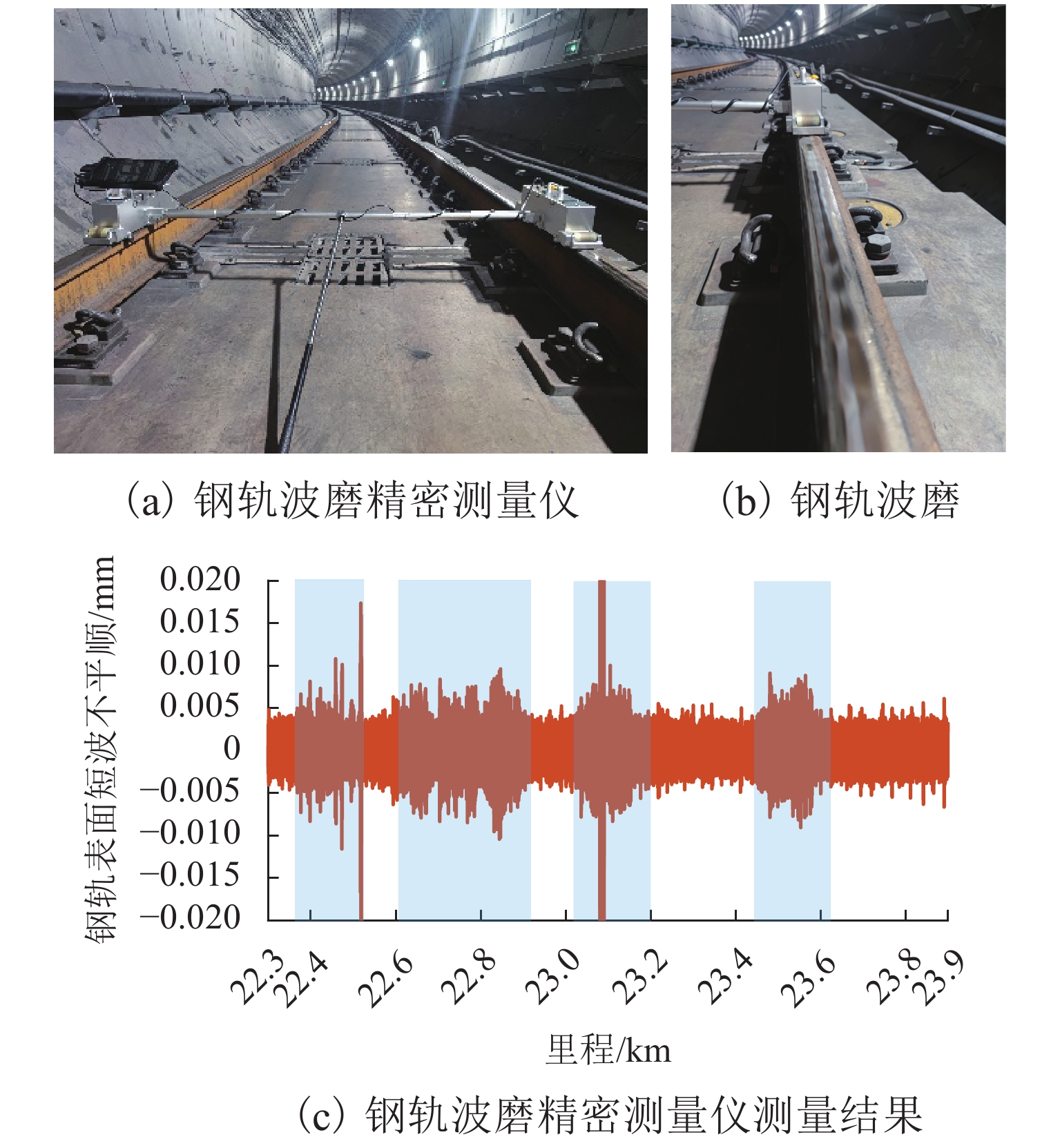
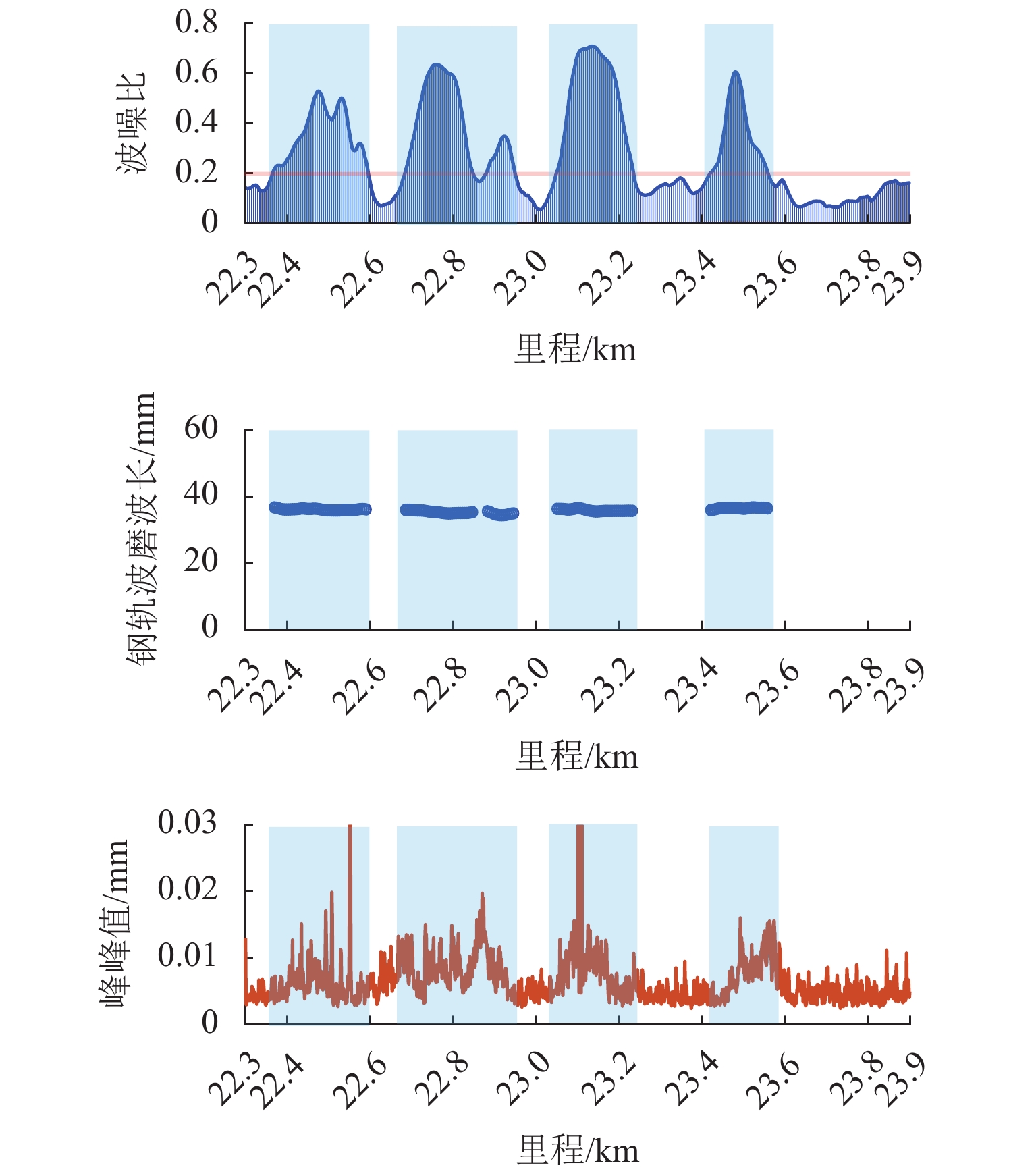
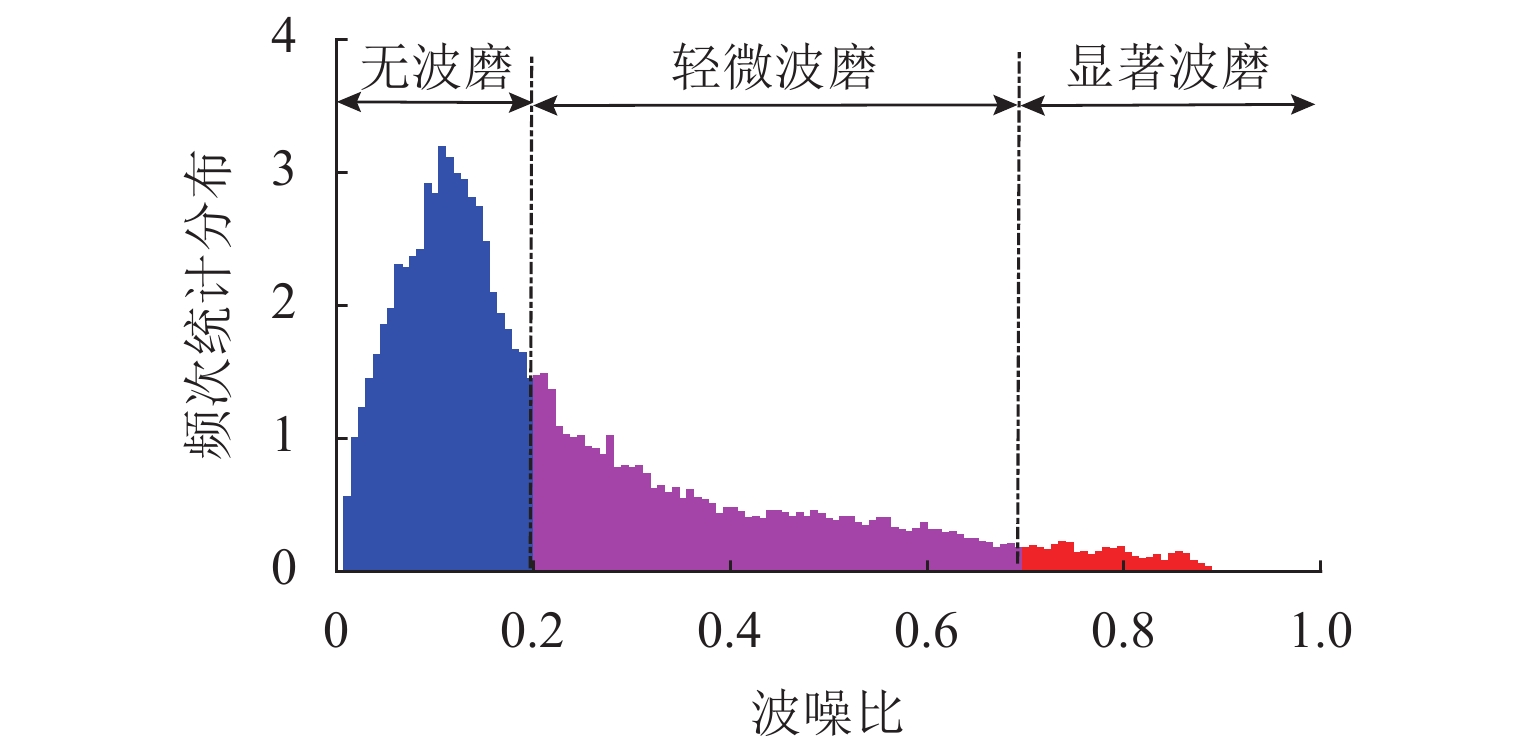
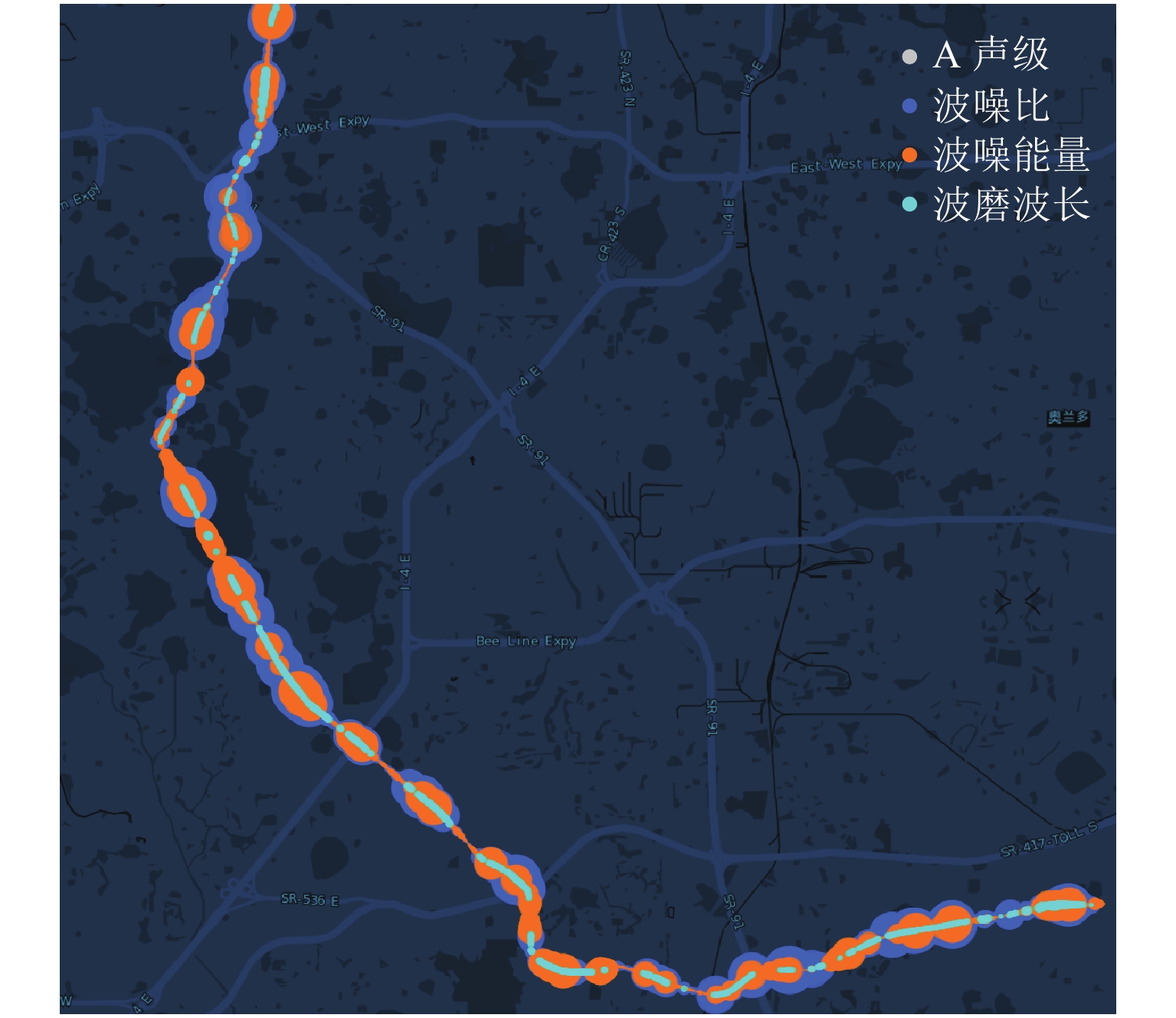
为实现数据驱动的钢轨波磨状态修，提出一种时-空密集型的钢轨波磨测量方法. 首先，采用智能终端检测列车编组车体振动和车厢噪声，对列车编组不同车体三向加速度进行波形匹配，得到延时估计值，修正列车运行速度和里程估计误差；其次，基于声纹谱能量法分析车厢声纹数据，并定义“波噪比”指标，量化钢轨波磨噪声能量及其高阶谐波能量占噪声总能量的比值，作为钢轨波磨自动识别的依据；最后，建立列车响应到钢轨波磨状态的反向映射关系，获取波噪比超限时的钢轨波磨波长和里程信息，以地铁某区间实测为例，采用钢轨波磨仪测量1.6 km范围的轨面短波不平顺，将测量结果 [0,50] mm波长范围的波深峰峰值与车厢声纹波噪比进行对比. 结果表明：当波噪比阈值取为0.2时，基于声纹数据识别的钢轨波磨与线路分布一致，验证了该方法可为钢轨波磨状态评估提供数据支撑.
Abstract:To realize the condition-based maintenance of rail corrugation in a data-driven way, a time-space intensive measurement method of rail corrugation is proposed. First, the intelligent terminal is used to detect vibration and noise at a car body of the train formation, the acceleration waveforms in three directions of different car bodies were matched to obtain the estimated time delay, and the error of the train speed and mileage estimation was corrected. Second, the car voiceprint data is analyzed with the voiceprint spectrum energy method, and the corrugation-noise ratio index is defined to quantify the ratio of rail corrugation noise energy and its high-order harmonic energy to the total noise energy, as the basis for automatic identification of rail corrugation. Finally, the inverse mapping relationship between the train response and rail corrugation sate is established to obtain the rail corrugation wavelength and mileage information when the corrugation-noise ratio exceeds the limit. The field test in metro line is taken as an example, where a rail corrugation measurement trolley was used to measure the shortwave irregularity of the rail surface on 1.6 km rail, and the measured peak-to-peak value in the wavelength range of [0,50] mm was compared to the corrugation-noise ratio of voiceprint data. The results show that, when the threshold of the corrugation-noise ratio is set as 0.2, the rail corrugation identified by the voiceprint data is consistent with the line distribution, which verifies that this method can enhance data evidence in evaluating rail corrugation state.
-
钢轨波磨是地铁线路较为常见的轮轨接触疲劳和轨面磨耗不均匀病害[1]，其不仅激发车辆-轨道系统的高频振动，长期波磨将导致轮轨系统关键功能件疲劳失效[2]，威胁车辆运行安全，也是导致轮轨辐射噪声超限的重要原因之一，降低车辆乘坐舒适性[3]. 钢轨打磨是一种快速、经济、有效的减振降噪控制措施[4]，而关于钢轨波磨打磨阈值及最佳打磨期选取等相关研究较少. 现场对钢轨波磨的个性化管理需求较突出，探索一种时-空密集的钢轨波磨快速测量方法，为不同地铁线路实现数据驱动的钢轨波磨状态修提供技术支撑.
目前，地铁钢轨打磨依据线路总运量进行计划性打磨，大约每半年打磨一次，平均成本为2万元/ km[5]，辅以因钢轨波磨引起的扣件弹条飞断及轮轨噪声超限等情况下的临时打磨[6]. 钢轨波磨测量是打磨作业的重要前提，按照测量原理分为弦测法和惯性基准法[7-10]. 相比于定长直尺测量方法，基于弦测法研制的移动式钢轨波磨测量仪效率明显提升，且测量精度高. 王源等[8-13]基于不同的弦测配置，设计相应的逆系统反演钢轨表面短波几何不平顺，最大测量速度接近3 m/s. Grassie等[7]基于惯性基准法研制了波磨测量小车，但存在测量效率和测量范围难以满足时-空密集的波磨状态测量需求. 为使得里程覆盖式的波磨测量成为可能，Tanaka等[14-18]研制了车载式惯性基准测量装置，监测列车轴箱加速度实现钢轨波磨测量与评估，但需要大型轨道检测设备，造价与使用成本高.
实现数据驱动的钢轨波磨状态修需要一种时-空密集型检测方法，高效测量不同通过总重或运营时间对应的钢轨波磨状态. Han等[4]实测了轮轨噪音与车厢噪音间的传递函数，结合轮轨有限元模型，研究车厢噪声限值下的钢轨波磨在不同波长域的粗糙度限值；Tanaka等[19]测量了地铁不同通过总重对应的钢轨波磨数据，拟合钢轨波磨幅值的生长曲线模型，并利用该模型实现有效且经济的钢轨打磨策略；Thompson等[20]研究发现，轮轨粗糙度与滚动噪声之间存在线性映射关系. 上述研究表明，钢轨波磨与车厢噪声存在正向映射关系.
本文提出地铁系统无GPS环境下振噪融合的钢轨波磨快速检测方法. 首先，采用智能传感终端监测列车车体振动与车厢噪声，融合不同车厢位置的智能终端振动数据，估计任意时刻的列车运行速度与里程位置；接着，基于车厢噪声数据进行频域转换，采用频率采样法提取钢轨波磨特征噪声频率成分，计算其频带能量及高阶谐波能量占噪声总能量的比值来识别钢轨波磨；最后，建立列车响应到钢轨波磨状态的反向映射关系，获取波噪比超限时的钢轨波磨波长和里程信息，并与传统钢轨波磨仪测试结果进行对比，验证该检测方法的有效性，对实现数据驱动的钢轨波磨状态修具有重要意义.
1. 钢轨波磨快速测量技术方案
基于车厢噪声到钢轨波磨状态的反向映射关系，钢轨波磨波长
${\lambda }_{{\rm{c}}}$ 可表示为λc=vfc， (1) 式中：
$ v $ 为车辆运行速度；${f}_{{\rm{c}}}$ 为车厢噪声主频.智能终端采集列车车体加速度与车厢噪声数据，其中，车体加速度数据用于车速和里程估计，噪声数据用于声纹谱分析提取噪声主频.
智能终端放置在列车编组各节车厢内，依据待测列车的行车组织计划，设置智能终端工作时间范围，其连续工作时长可覆盖地铁列车单个上、下行运营周期，测量过程无需人员操作，实现自启动、自停止等基本测量操作，是一种非侵入式的测量方法，如图1所示. 采用的智能传感终端集成了惯性测量单元（IMU）、麦克风、锂电池等，用于监测运营车辆的车体振动和车厢噪声.
图 1 多智能终端监测列车振动-声纹Figure 1. Multi-intelligent terminal monitoring train vibration-voiceprint数据处理算法涉及振动、声纹数据的离线处理，输出结果包括钢轨波磨波长和分布里程信息，如图2所示. 算法中车辆运行速度和里程的估计精度决定了钢轨波磨波长和定位的精度. 车辆纵向加速度积分误差可融合多智能终端振动数据进行修正，保障了速度估计精度，具体过程见第2节；接着，对车厢噪声数据进行短时傅里叶分析，通过波磨噪声能量与车厢噪声能量的比值（波噪比）来判断是否存在波磨，若波噪比大于阈值，进一步提取波磨噪声特征频率，结合式（1）输出钢轨波磨波长和里程信息；若小于阈值，则无波磨.
通过实例分析，采用钢轨波磨测量仪复核振噪融合识别的钢轨波磨结果，验证该算法输出的钢轨波磨波长和里程位置的正确性，并完成地铁线路钢轨波磨分布可视化.
2. 振动/声纹数据的里程标定
振动/声纹数据的里程定位涉及一种无GPS环境下地铁列车运行速度与里程估计 [21]，该方法原理如图3所示，图中：
$ {p}_{\mathrm{1,2}} $ 为智能终端1、2的放置间距；${a}_{{y},1}$ 、${a}_{{y},2}$ 分别为智能终端1、2的横向加速度. 首先，采用惯性积分法对车体纵向加速度进行一次积分获取车辆运行速度，受传感器性能（信噪比、噪声等因素）影响，存在积分误差；接着，不同车辆驶经线路曲线、坡度、竖曲线时，各智能终端检测的垂向加速度${a}_{z}$ 、横向加速度${a}_{y}$ 波形之间存在时间延迟，通过波形匹配估计不同智能终端间的时间延迟量，结合多智能终端间的放置间距进行速度估计，修正对应时刻惯性积分速度；最后，对修正后的车辆运行速度曲线进行积分得到精度较高的车辆运行里程信息.对纵向加速度
${a}_{{x}}\left(t\right)$ 积分，得到时刻$ t\in \left[{t}_{1},{t}_{2}\right] $ 的初始估计速度$ v\left(t\right) $ ，如式（2）所示.v(t)=∫t2t1ax(t)dt, (2) 式中：
${t}_{1}、{t}_{2}$ 分别为列车驶出站时刻、列车进入下一站停靠时刻.对
${a}_{x}\left(t\right)$ 进行二次积分，可获取车辆里程初始估计值$S \left(t\right)$ 为S(t)=S(t1)+∫t2t1v(t)dt=S(t1)+(t−t1)v(t1)+∫t2t1∫t2t1ax(t)dtdt. (3) 通过纵向加速度积分直接获取的列车运行速度和里程信息与真实值偏差较大，为降低与真实值的偏差量，采用数据融合方法修正加速度积分误差项，具体步骤如下：
步骤1 别对智能终端i、j检测的车体垂向加速度
${a}_{z}$ 和横向加速度${a}_{{y}}$ 进行波形匹配，$ i,j=\mathrm{1,2},\cdots , n $ ，$ n $ 为列车编组长度. 以${a}_{y}$ 的波形匹配为例，获取时刻t智能终端i、j之间的信号时间延迟量$ {\delta }_{ij,t} $ 为δij,t=argmax(cov(ayi,t,l,ayj,t+τ,l)), (4) 式中：
$ \tau $ 为时间偏差；${a}_{{y}i,t,l}$ 为智能终端 i以时刻t为中心截取长度l的横向加速度.步骤2 最大协方差值
$ {\delta }_{ij,t} $ 对应最优时间偏差$ {\tau }_{ij,t} $ ，结合已知的智能终端i、j之间的放置距离$ {p}_{i,j} $ ，获取时刻t智能终端i、j的列车运行速度$ {v}_{i,j,t} $ 为vi,j,t=1δij,t(pi,j−∫t+τij,tt∫t+τij,ttaxi(t)dtdt), (5) 式中：
${a}_{xi}\left(t\right)$ 为智能终端i的纵向加速度.对任意两个智能终端的横向加速度进行波形匹配均可得到时间延迟
$ {\tau }_{ij,t}\;\left(i\ne j\right) $ ，则智能终端i相对智能终端j得到的列车运行速度估计值$ {\boldsymbol{v}}_{\boldsymbol{i}} $ 可表示为{vi=(vi,1,vi,2,⋯,vi,j−1,0,vi,j+1,⋯,vi,n),v=(vT1,vT2,⋯,vTi,⋯,vTn), (6) 式中：
$\boldsymbol{v}$ 为智能终端i、j间的速度估计矩阵.融合各智能终端估计的列车运行速度，列车速度的最优估计向量可表示为
${\boldsymbol{v}}^{\boldsymbol{*}}$ ，优化公式为minv∗{12(v∗−v)Tdiag(W)(v∗−v)}， (7) 式中：
$ \boldsymbol{W} $ 为权重矩阵，可由时间延迟$ {\tau }_{ij,t} $ 进行加速度波形匹配得到，如式（9）所示.{W=(wT1,wT2,⋯,wTi,⋯,wTn),wi=(wi,1,wi,2,⋯,wi,n),wi,j={0,i=j或ρi,j<ρ0,ρi,j,i≠j和ρi,j>ρ0,ρi,j=corr(ayi,t,l,ayj,t+τij,t,l), (9) 式中：
$ {\rho }_{0} $ 为波形相似度阈值；$ {\boldsymbol{w}}_{\boldsymbol{i}} $ 为智能终端i对应的权重向量；$ {\rho }_{i,j} $ 为波形相似度系数.则时刻t的最优速度估计
$ {\boldsymbol{v}}^{*}\left(t\right) $ 为{\boldsymbol{v}}^{*}\left(t\right)=\frac{1}{‖\boldsymbol{W}‖}{\boldsymbol{W}}^{{\rm{T}}}\boldsymbol{v}, (8) 步骤3 基于智能终端i积分获取的车体速度初始估计
$\boldsymbol{v}\left({t}\right)$ ，与满足$ {\rho }_{i,j} > {\rho }_{0} $ 条件下的离散时刻$\boldsymbol{T}=\left({T}_{0},{T}_{1},{T}_{2},\cdots ,{T}_{e}\right)$ 对应的最优速度估计${\boldsymbol{v}}^{*}\left(t\right)$ 进行作差，得到修正量$ \Delta \boldsymbol{v} $ 为\begin{split} &\Delta \boldsymbol{v}=\left({\boldsymbol{v}}^{*}\left({T}_{0}\right)-\boldsymbol{v}\left({T}_{0}\right),{\boldsymbol{v}}^{*}\left({T}_{1}\right)-\boldsymbol{v}\left({T}_{1}\right),{\boldsymbol{v}}^{*}\left({T}_{2}\right)- \right.\\ &\quad \left. \boldsymbol{v}\left({T}_{2}\right),\cdots,{\boldsymbol{v}}^{*}\left({T}_{e}\right)-\boldsymbol{v}\left({T}_{e}\right)\right), \end{split} (10) 式中：
$ {T}_{e} $ 为波形匹配过程满足$ {\rho }_{i,j} > {\rho }_{0} $ 条件下的最后时刻.为获取以等间隔
$\Delta {t}$ 离散的列车速度修正值$\Delta {{\boldsymbol{v}}}^{*}$ ，对离散时刻T的$\Delta {{\boldsymbol{v}}}$ 进行线性插值方法，获取等间隔$ \Delta t $ 对应的速度修正量，如式（11）所示.\left\{ \begin{aligned} &\Delta {{\boldsymbol{v}}}^{\boldsymbol{*}}=D\left(\boldsymbol{T},\Delta {{\boldsymbol{v}}},t\right),\quad t \in \left\{0,\Delta t,2\Delta t,\cdots ,N\Delta t\right\},\\ &\Delta t=\frac{{t}_{2}-{t}_{1}}{N + 1},\end{aligned} \right. (11) 式中：
$D\left( {\text{•}} \right)$ 为线性插值函数；$ \Delta t $ = 0.01 s；$ N $ 为时间分割份数.数据融合得到列车速度
${{{\boldsymbol{v}}}}_{\rm{f}{u}{s}{e}}$ 为{{{\boldsymbol{v}}}}_{\rm{{f}{u}{s}{e}}}={{\boldsymbol{v}}} + \Delta {{{\boldsymbol{v}}}}^{\boldsymbol{*}}. (12) 3. 声纹谱分析与波噪比的定义
3.1 声纹谱
列车噪声主要由轮轨噪声、气动噪声及牵引噪声等组成，通过车体结构与空气传至车厢内部，不同车速下车厢噪声的频谱主要分布在低频（100 Hz以下）和中频（300～800 Hz），其频率分布与钢轨波磨的波长、车速等因素有关，且车厢噪声频率和幅值随车速的增大有明显的提升.
采用频谱能量法实现噪音信号特征提取，是借助短时傅里叶变换对时序信号进行频谱转码的特征映射方法，以不同频带的信号能量值作为信号的特征向量. 最小移动窗长
${t}_{{\rm{win}}}$ 为{t}_{\rm win}=\frac{{f}_{\rm u}}{{F}_{\rm s}} , (13) 式中：
${f}_{\rm u}$ 为待分析频率上限，取值1600 Hz （钢轨波磨声纹中频段800 Hz的2倍）；${F}_{\rm s}$ 为声纹采样频率，一般为44 kHz.由式（13）可知
${t}_{\rm win}\geqslant$ 36 ms，窗长$L={t}_{\rm win} F _{\rm{s}}$ ，且相邻移动窗重叠率为$ r $ ，则车厢噪声数据可分割成M等份（式（14）），M为移动窗个数.M={\rm{ent}}\left(\frac{N-L + 1}{rF_{\rm{s}}}\right). (14) 各移动窗下噪声的傅里叶变换为
{X}\left[k\right]=\sum _{s=0}^{L-1}w\left[s\right]{x}[s]{{\rm{e}}}^{-\tfrac{{\text{i2π}} ks}{L}}, \quad k=\mathrm{0,1},\cdots ,d-1, (15) 式中：
${x}[s]$ 为移动窗下第$ s $ 个噪声数据点；$ d $ 为频率范围$\left[0,F_{\rm{s}}/2\right]$ 的等份数；$w\left[s\right]$ 为Hanning窗单位冲击响应.3.2 波噪比的定义
调研地铁线路钢轨波磨典型波长范围
$ \left[{\lambda }_{1},{\lambda }_{2}\right] $ mm，波磨区段的车辆运行速度为$ {v}_{1} $ ，则钢轨波磨噪声频带的下限$ {f}_{1} $ 和上限$ {f}_{2} $ 为\left\{ \begin{aligned} &{f}_{1}=\frac{{v}_{1}}{{\lambda }_{2}},\\ &{f}_{2}=\frac{{v}_{1}}{{\lambda }_{1}}.\end{aligned} \right. (16) 钢轨波磨引起的声纹特征频率为
{f}_{{\rm{c}}}=A\left(\mathrm{max}\left\{\boldsymbol{X}\right\}\right), (17) 式中：
$A\left({{\rm{max}}}\left\{\boldsymbol{X}\right\} \right)$ 为输出频带$ \left[{f}_{1},{f}_{2}\right] $ 内声纹幅值X最大值对应的特征频率${f}_{{\rm{c}}}$ 的函数，其对应的二次谐波特征频率为$2{f}_{{\rm{c}}}$ ，如图4所示.移动窗声纹数据总能量为
E=\sum\nolimits _{s=1}^{L}{|x\left[s\right]}|^{2} =\sum\nolimits _{k=1}^{d-1}{|X|}^{2} . (18) fc、f2c对应的1/3倍频频带分别为
$\left[{2}^{-\tfrac{1}{6}}{f}_{{\rm{c}}},{2}^{\tfrac{1}{6}}{f}_{{\rm{c}}}\right]$ 和$\left[{{2}^{\tfrac{5}{6}}f}_{{\rm{c}}},{{2}^{\tfrac{7}{6}}f}_{{\rm{c}}}\right]$ ，结合频率采样法设计带通滤波器${f}_{{\rm{c}}}\left[\text{•} \right]$ 和${f}_{2{\rm{c}}}\left[\ {\text{•}} \right]$ ，获取移动窗下钢轨波磨引起的声纹成分如式（19）所示.\left\{ \begin{aligned} &{x}_{\mathrm{c}}\left[s\right]=\sum\nolimits _{k=1}^{m}{h}_{{\rm{c}}}\left[k\right]x\left[s-k\right],\\ &{x}_{2\mathrm{c}}\left[s\right]=\sum\nolimits _{k=1}^{m}{h}_{{\rm{2c}}}\left[k\right]x\left[s-k\right],\end{aligned} \right. (19) 式中：
${x}_{{\rm{c}}}\left[s\right]$ 、${x}_{{\rm{2c}}}\left[s\right]$ 分别为fc、f2c 1/3倍频对应的时域数据；$ m $ 为带通滤波器${h}_{{\rm{c}}}\left[\text{•} \right]$ 和${h}_{{\rm{2}}c}\left[\text{•} \right]$ 的长度.声纹数据含有钢轨波磨引起的特征频率成分，通过引入波噪比Rc进行钢轨波磨识别，即钢轨波磨激发的声纹特征频率和二次谐波的1/3倍频能量占噪声总能量的比值，计算式为
{R}_{{\rm{c}}}=\frac{\displaystyle\sum\nolimits _{s=1}^{m}(|{x}_{{\rm{c}}}\left[s\right]|^2+|{x}_{{\rm{2c}}}\left[s\right]|^2)}{E}. (20) 4. 实例分析
4.1 列车车体振动与车厢声纹测量
智能终端内置加速度传感器采样频率为400 Hz，量程2 g，麦克风采样频率为44 kHz，满足地铁车体振动和车厢噪声测量要求. 为避免测量过程乘客触碰干扰，保证车体振动与车厢噪声测量精度，智能终端放置在客车车厢B09电磁阀箱体内.
以国内某地铁线路测试为例，全线共设车站23座，上、下行共计57.28 km，44个区间，8个智能传感终端分别布置于8节车厢内，全程测试时间为2 h.
4.2 列车运行速度与里程估计
列车运行速度与里程的计算完全通过多智能终端的数据融合实现，不依赖任何线路射频标签、线路信标、列车系统等提供的速度与里程信息.
以某运行区间的智能终端检测数据为例，积分获取列车速度与里程定位的纵向加速度数据，如图5（a）所示，可知8节车辆在牵引-匀速-制动阶段加速度响应一致. 用于数据融合的横向与垂向加速度幅值大小和波形相似（图5（b）、（c）），仅存在微小的时间延迟，这是由列车各节车厢通过曲线等特殊路段时刻不一致引起（见图3）.
图 5 某区间车载智能终端振动测量数据Figure 5. Vibration data of on-board intelligent terminal in one section各智能终端横向和垂向加速度数据作为车辆运行速度与里程估计模型的输入，经时间延迟估计、最优速度估计和速度修正3个阶段处理，得到列车运行速度如图6所示.
4.3 钢轨波磨识别与复核
如图6所示，列车匀速通过半径大小分别为450、700、1000 m的3个曲线地段，速度分别为52、72、52 km/h；声纹数据明显存在钢轨波磨激发的特征噪声成分，特别在 [50,80] s内；车厢声纹谱图表明声纹能量主要集中在1200 Hz，其中车体结构特征噪声频率为 [20,200] Hz，提取曲线地段钢轨波磨激发的 [450,800]、[1000,1200] Hz的频率成分，并计算移动窗下的声纹谱主频及二次谐波对应的波噪比.
为验证振噪融合的钢轨波磨快速测量方法的准确性，复核输出的钢轨波磨波长和里程信息能否与现场一一对应，采用钢轨波磨精密测量仪测量里程22.3～23.9 km的轨面短波不平顺，现场测试及轨面波磨状态如图7（a）、（b）所示. 钢轨波磨精密测量仪最大测量速度可达3 m/s，有效波长范围 [10,3000] mm，空间采样间隔1 mm[22]. 依据现场钢轨波磨波长范围，设计高通滤波器提取 [0,50] mm波长的钢轨波磨成分，如图7（c）所示，现场波磨分布区段标记为浅蓝色.
图 7 某区段钢轨短波不平顺现场测量Figure 7. Field test of shortwave irregularity for rail in certain section对比里程范围对应的车厢声纹数据波噪比和实测波磨峰峰值，如图8. 当波噪比限值为0.2时，识别的钢轨波磨分布里程范围与实测波磨分布范围一致，对应的车辆运行速度为40～74 km/h，钢轨波磨激励频率为 [450,800] Hz，振噪融合估计的特征波长约36 mm.
图 8 基于波噪比的钢轨波磨识别效果Figure 8. Identification results of rail corrugation based on corrugation-noise ratio全线声纹数据波噪比的统计概率分布如图9所示，依据声纹数据分析可知，
${R}_{{\rm{c}}} < 0.2$ 的区段占全线长度约61.97%，为无波磨；当$0.2\leqslant {R}_{{\rm{c}}} < 0.7$ 时，从声纹数据中人耳可清晰分辨出钢轨波磨引起的特征频率噪声，长度约占34.46%，为轻微波磨；当${R}_{{\rm{c}}} > 0.7$ 时，声纹数据中存在刺耳的轮轨噪声，长度约占3.57%，为显著波磨.
图 9 全线波噪比统计概率分布Figure 9. Statistical probability distribution of corrugation-noise ratio for metro line对全线测试数据以10 m等间隔离散获取沿线波噪比结果，借助百度地铁API接口输入全线钢轨波磨评估结果，包括波噪比、波噪能量、波磨波长，可视化效果如图10所示，圆点半径越大，表示钢轨波磨现象越严重，受不同里程位置平面线型、轨道结构型式、车辆运行速度等存在差异，全线不同里程位置的钢轨波磨状态多样化.
图 10 全线钢轨波磨状态分布地图Figure 10. Distribution map of rail corrugation state along metro line5. 结 论
1） 采用波噪比指标可实现基于声纹数据的钢轨波磨自动识别，即通过声纹谱能量法分析钢轨波磨相关的频带噪声能量及其高阶谐波能量占噪声总能量的比值.
2） 列车不同车辆在通过线路平面曲线与竖曲线时，车体横向与垂向加速度存在频率低且幅值大的振动成分，通过波形相关系数估计不同车体间响应时间延迟，获得列车最佳速度估计，插值修正纵向加速度积分速度曲线.
3） 实例分析表明，依据某区间车辆运行速度和波磨特征噪声频带，计算得到钢轨波磨波长估计值为36 mm，与钢轨波磨精密测量仪测量结果一致，且自动识别的钢轨波磨里程与现场分布里程一致，验证了该方法的准确性.
基于振噪融合的钢轨波磨测量方法具备测量效率高、精度高、成本低等特点，可实现线路钢轨波磨状态时间密集型、空间覆盖式测量，可跟踪、高频次测量，并统计不同里程位置处钢轨波磨状态演变过程的声纹数据，为实现钢轨波磨状态修提供数据支撑. 但该方法仅提供钢轨波磨的波长和里程信息，后续将结合钢轨波磨仪大量测试数据进行波磨幅值与噪声能量关系的定量估计.
-
图 1 多智能终端监测列车振动-声纹
Figure 1. Multi-intelligent terminal monitoring train vibration-voiceprint
图 5 某区间车载智能终端振动测量数据
Figure 5. Vibration data of on-board intelligent terminal in one section
图 7 某区段钢轨短波不平顺现场测量
Figure 7. Field test of shortwave irregularity for rail in certain section
图 8 基于波噪比的钢轨波磨识别效果
Figure 8. Identification results of rail corrugation based on corrugation-noise ratio
图 9 全线波噪比统计概率分布
Figure 9. Statistical probability distribution of corrugation-noise ratio for metro line
-
[1] 关庆华,张斌,熊嘉阳,等. 地铁钢轨波磨的基本特征、形成机理和治理措施综述[J]. 交通运输工程学报,2021,21(1): 316-337. doi: 10.19818/j.cnki.1671-1637.2021.01.015GUAN Qinghua, ZHANG Bin, XIONG Jiayang, et al. Review on basic characteristics, formation mechanisms, and treatment measures of rail corrugation in metro systems[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 316-337. doi: 10.19818/j.cnki.1671-1637.2021.01.015 [2] 吴越,韩健,左齐宇,等. 钢轨波磨对高速列车车轮多边形磨耗产生与发展的影响[J]. 机械工程学报,2020,56(17): 198-208. doi: 10.3901/JME.2020.17.198WU Yue, HAN Jian, ZUO Qiyu, et al. Effect of rail corrugation on initiation and development of polygonal wear on high-speed train wheels[J]. Journal of Mechanical Engineering, 2020, 56(17): 198-208. doi: 10.3901/JME.2020.17.198 [3] 郭建强,朱雷威,刘晓龙,等. 地铁司机室噪声与钢轨波磨关系的试验与仿真研究[J]. 机械工程学报,2019,55(16): 141-147. doi: 10.3901/JME.2019.16.141GUO Jianqiang, ZHU Leiwei, LIU Xiaolong, et al. Experimental and simulation study on the relationship between interior noise of metro cab and rail corrugation[J]. Journal of Mechanical Engineering, 2019, 55(16): 141-147. doi: 10.3901/JME.2019.16.141 [4] HAN J, XIAO X B, WU Y, et al. Effect of rail corrugation on metro interior noise and its control[J]. Applied Acoustics, 2018, 130: 63-70. doi: 10.1016/j.apacoust.2017.09.007 [5] SONG X L, QIAN Y, WANG K Y, et al. Effect of rail pad stiffness on vehicle-track dynamic interaction excited by rail corrugation in metro[J]. Transportation Research Record: Journal of the Transportation Research Board, 2020, 2674(6): 225-243. doi: 10.1177/0361198120918584 [6] 朱海燕,袁遥,肖乾,等. 钢轨波磨研究进展[J]. 交通运输工程学报,2021,21(3): 110-133. doi: 10.19818/j.cnki.1671-1637.2021.03.006ZHU Haiyan, YUAN Yao, XIAO Qian, et al. Research progress on rail corrugation[J]. Journal of Traffic and Transportation Engineering, 2021, 21(3): 110-133. doi: 10.19818/j.cnki.1671-1637.2021.03.006 [7] GRASSIE S L. Rail irregularities, corrugation and acoustic roughness: characteristics, significance and effects of reprofiling[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2012, 226(5): 542-557. doi: 10.1177/0954409712443492 [8] WANG Y, TANG H Y, WANG P, et al. Multipoint chord reference system for track irregularity: part Ⅰ–theory and methodology[J]. Measurement, 2019, 138: 240-255. doi: 10.1016/j.measurement.2019.01.080 [9] WANG Y, TANG H Y, WANG P, et al. Multipoint chord reference system for track irregularity: part Ⅱ–numerical analysis[J]. Measurement, 2019, 138: 194-205. doi: 10.1016/j.measurement.2019.01.081 [10] 王源,李帅,陈嵘,等. 基于逆滤波的轨道不平顺测评误差分析及滤波参数优化[J]. 铁道学报,2017,39(10): 102-109. doi: 10.3969/j.issn.1001-8360.2017.10.014WANG Yuan, LI Shuai, CHEN Rong, et al. Error analysis of track irregularity measuring and filter parameters optimization based on inverse filtering method[J]. Journal of the China Railway Society, 2017, 39(10): 102-109. doi: 10.3969/j.issn.1001-8360.2017.10.014 [11] GRASSIE S L, KALOUSEK J. Rail corrugation: characteristics, causes and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 57-68. doi: 10.1243/PIME_PROC_1993_207_227_02 [12] 殷华,朱洪涛,魏晖,等. 基于中点弦测模型的钢轨波磨量值估计[J]. 振动•测试与诊断,2016,36(5): 954-959,1027.YIN Hua, ZHU Hongtao, WEI Hui, et al. Discussion on estimate rail corrugation amplitude based upon midpoint chord model[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(5): 954-959,1027. [13] 陶捷, 朱洪涛, 殷华. 基于多中点弦同步测量的轨道波浪形磨耗快速检测方法: CN105128888A[P]. 2017-06-09. [14] TANAKA H, MATSUMOTO M, HARADA Y. Application of axle-box acceleration to track condition monitoring for rail corrugation management[C]//7th IET Conference on Railway Condition Monitoring 2016 (RCM 2016). Birmingham: IET, 2016: 1-7. [15] BOCCIOLONE M, CAPRIOLI A, CIGADA A, et al. A measurement system for quick rail inspection and effective track maintenance strategy[J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1242-1254. doi: 10.1016/j.ymssp.2006.02.007 [16] MOLODOVA M, LI ZL, DOLLEVOET R. Axle box acceleration: measurement and simulation for detection of short track defects[J]. Wear, 2011, 271(1/2): 349-356. [17] 刘金朝,陈东生,赵钢,等. 评判高铁轨道短波不平顺病害的轨道冲击指数法[J]. 中国铁道科学,2016,37(4): 34-41. doi: 10.3969/j.issn.1001-4632.2016.04.06LIU Jinzhao, CHEN Dongsheng, ZHAO Gang, et al. Track impact index method for evaluating track short wave irregularity of high speed railway[J]. China Railway Science, 2016, 37(4): 34-41. doi: 10.3969/j.issn.1001-4632.2016.04.06 [18] 牛留斌,刘金朝,孙善超,等. 钢轨波磨指数与轨道短波不平顺关系研究[J]. 中国铁道科学,2020,41(5): 46-55. doi: 10.3969/j.issn.1001-4632.2020.05.06NIU Liubin, LIU Jinzhao, SUN Shanchao, et al. Relationship between rail corrugation index and track short wave irregularity[J]. China Railway Science, 2020, 41(5): 46-55. doi: 10.3969/j.issn.1001-4632.2020.05.06 [19] TANAKA H, MIWA M. Modeling the development of rail corrugation to schedule a more economical rail grinding[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(4): 370-380. doi: 10.1177/0954409719894833 [20] THOMPSON D, JONES C. Noise and vibration from the wheel-rail interface[M]//Wheel-rail interface handbook. Amsterdam: Elsevier, 2009: 477-509. [21] WANG Y, CONG JL, WANG P, et al. A data-fusion approach for speed estimation and location calibration of a metro train based on low-cost sensors in smartphones[J]. IEEE Sensors Journal, 2019, 19(22): 10744-10752. doi: 10.1109/JSEN.2019.2933638 [22] CONG J L, TANG H Y, WANG Y, et al. Experimental and numerical investigations of asymmetric chord-reference system regarding track geometry measurement[J]. Measurement, 2021, 182: 109743.1-109743.15. doi: 10.1016/j.measurement.2021.109743 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 661
- HTML全文浏览量: 144
- PDF下载量: 78
- 被引次数: 0