Rail Corrugation Suppressing Method on Braking Sections of High-Speed Trains
-
摘要:
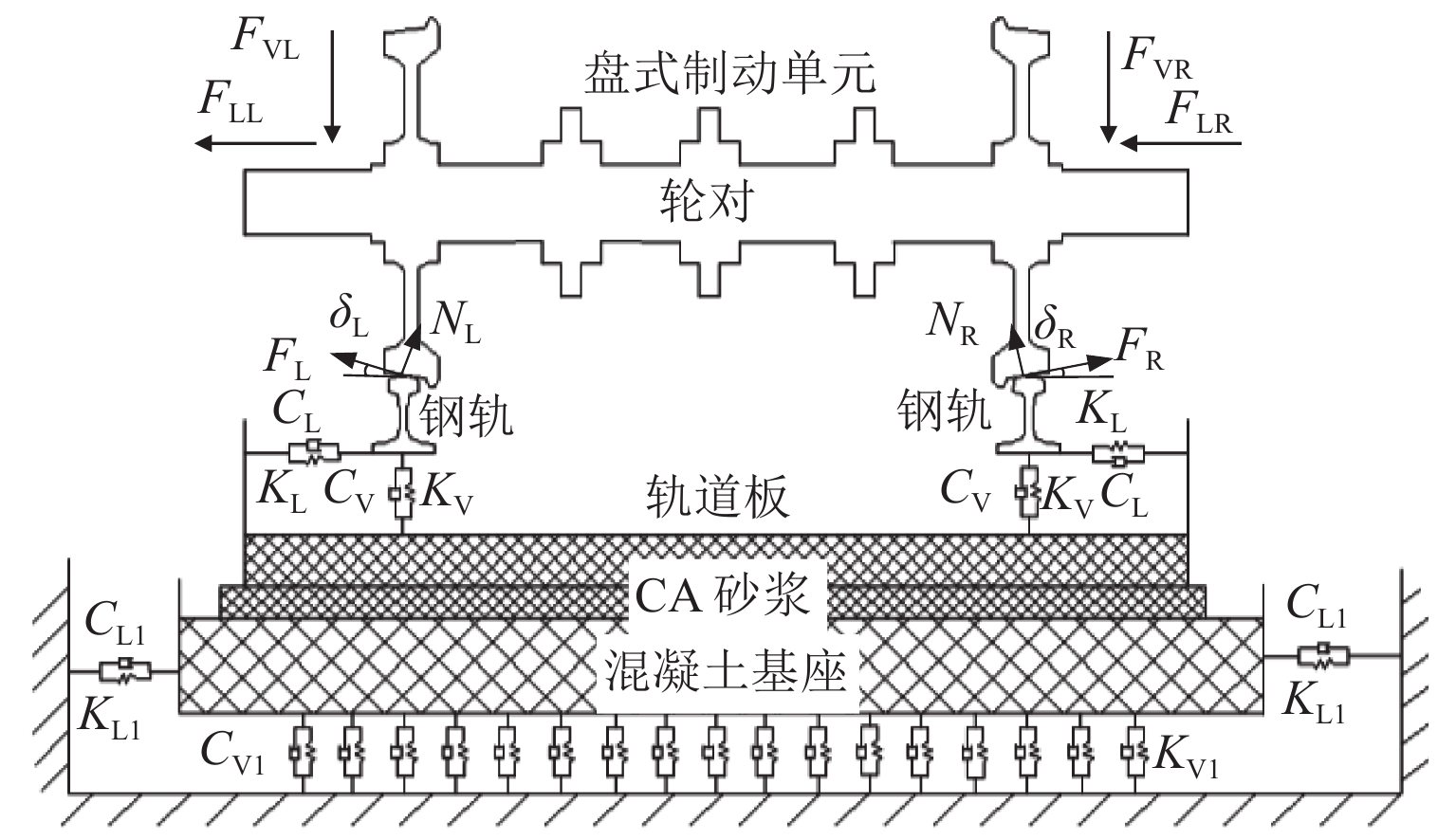
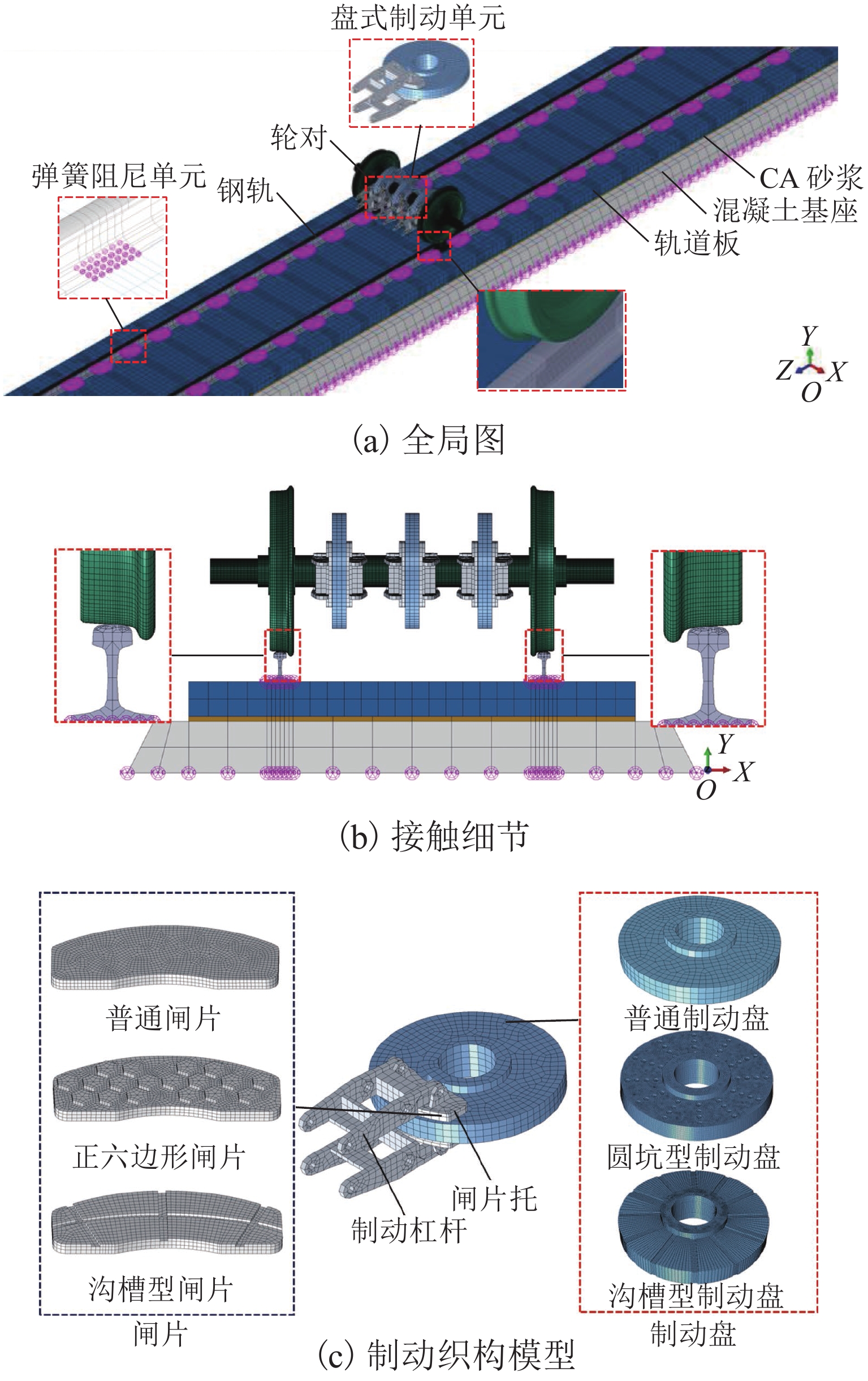
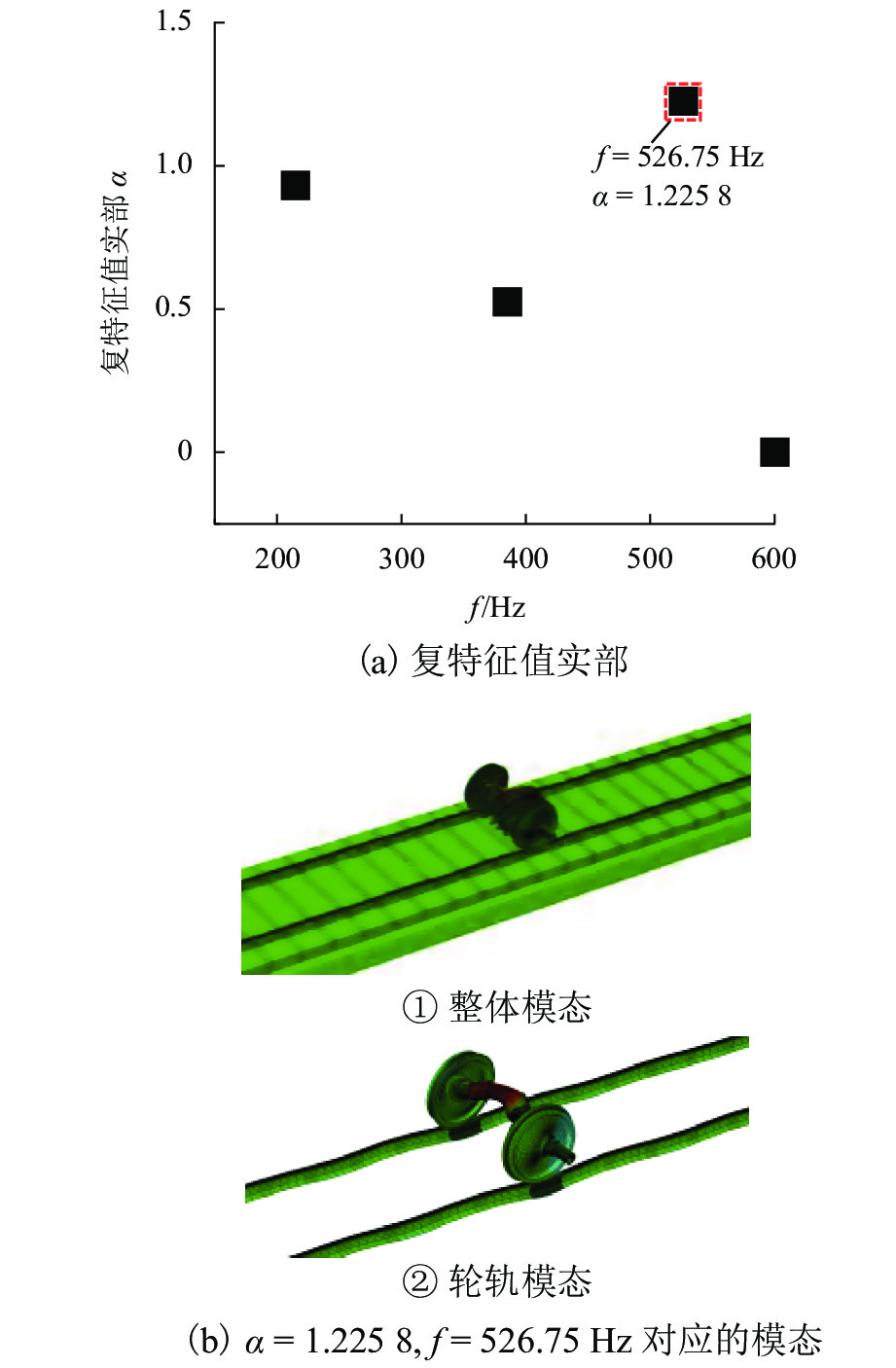
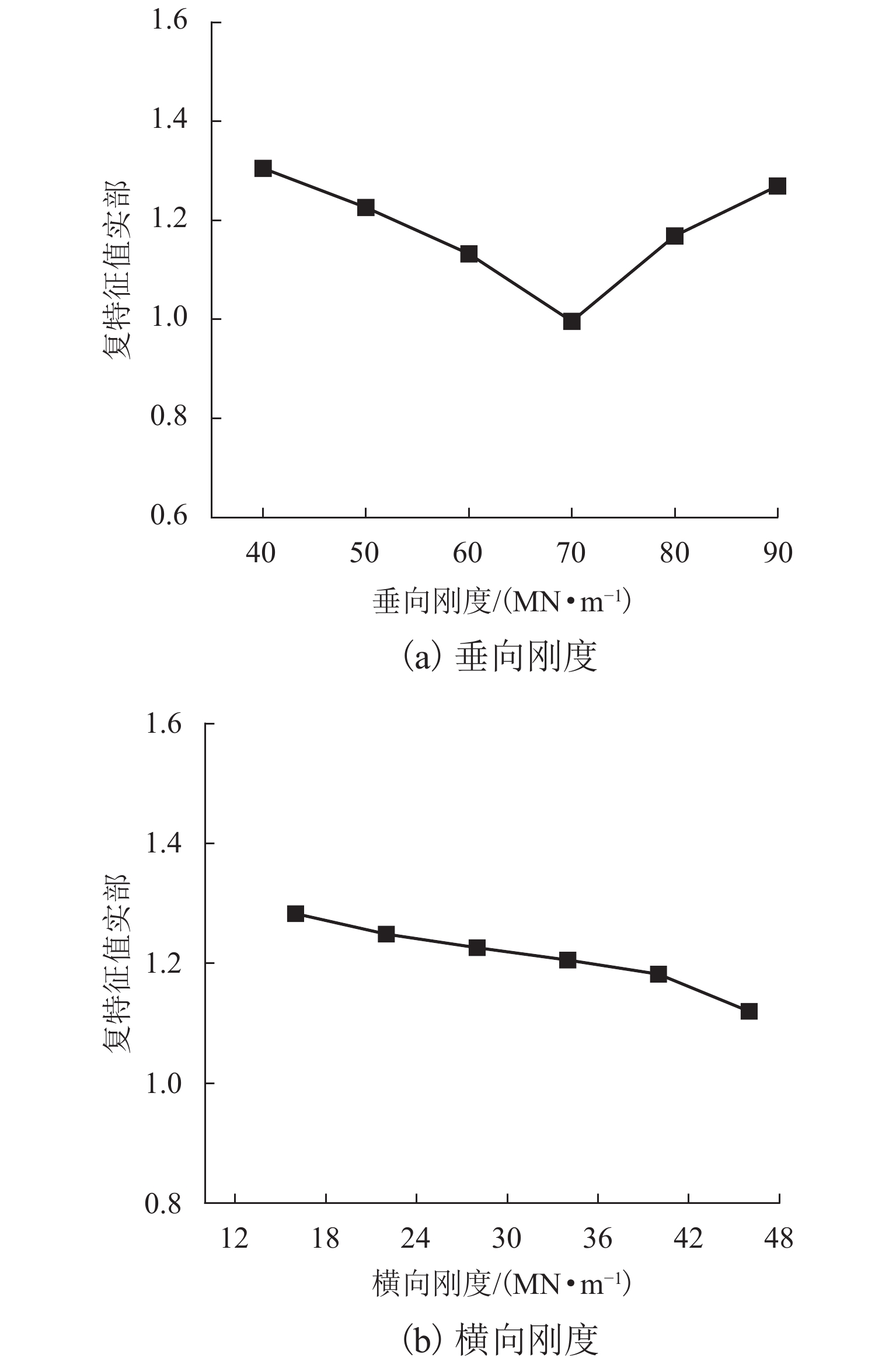
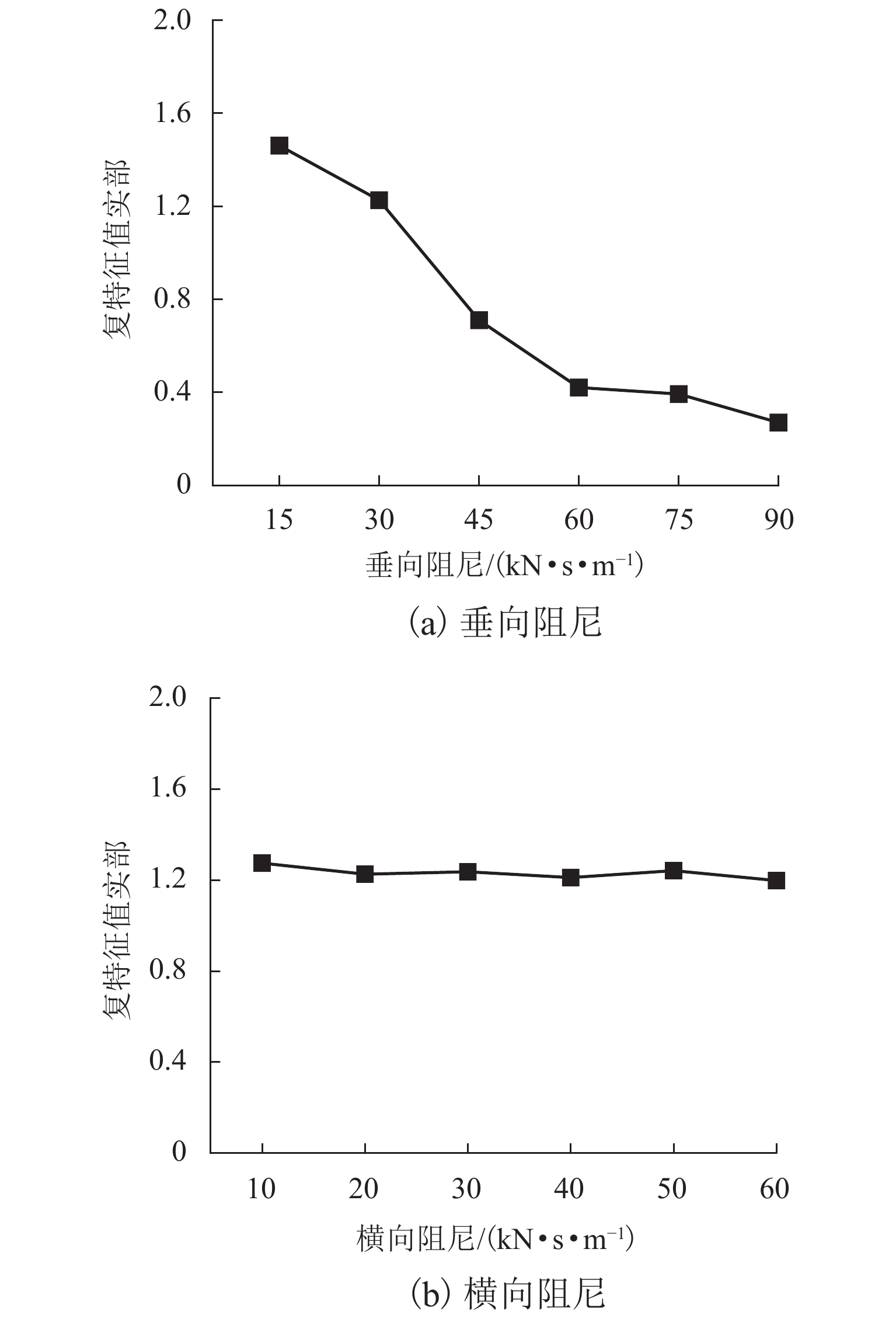
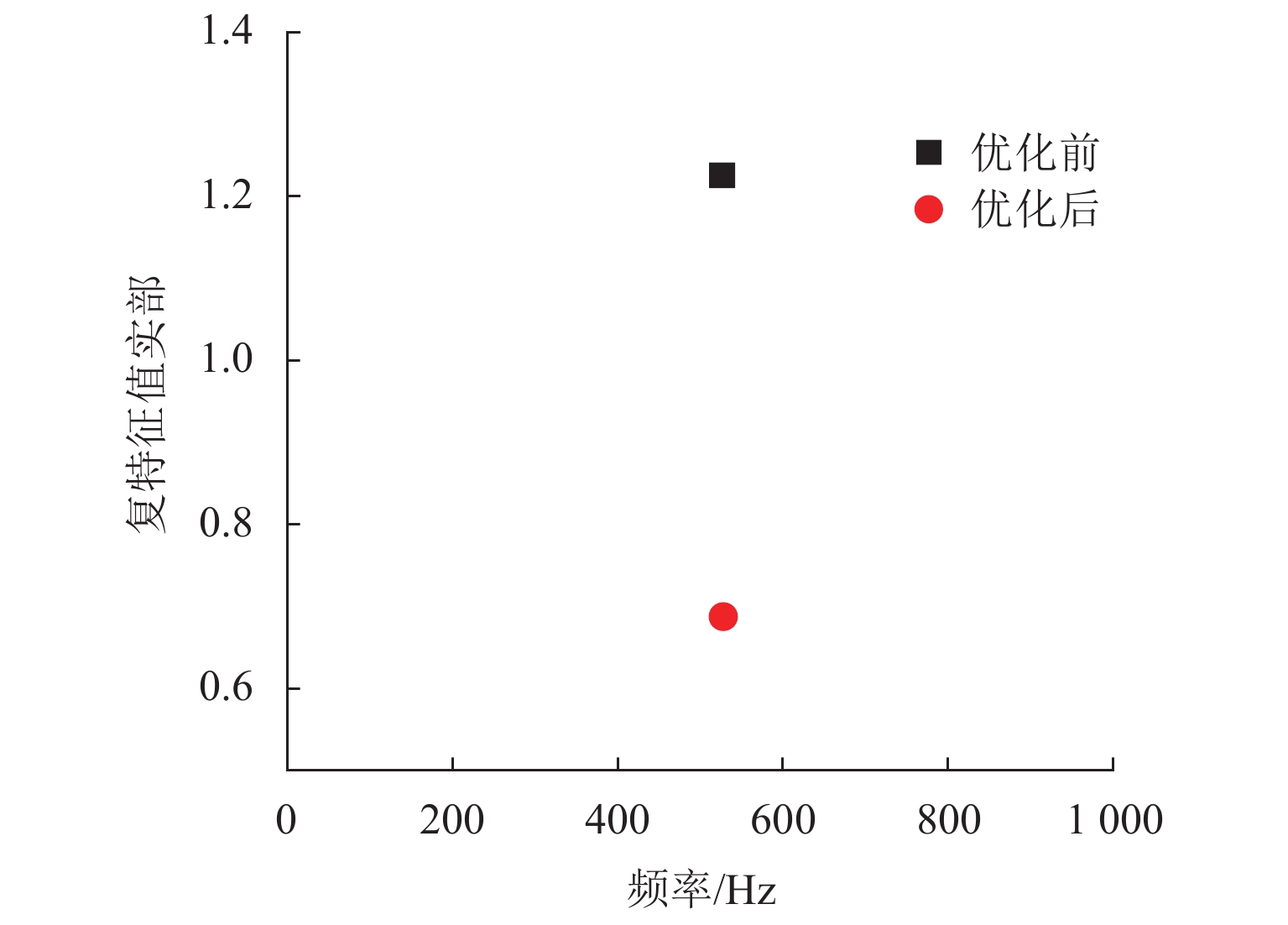
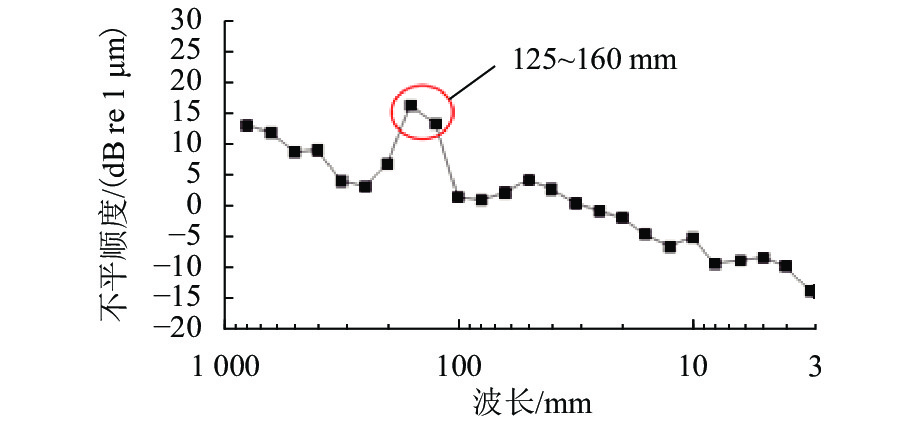
为研究高速列车制动区段制动结构/轨道结构对轮对-轨道-制动系统摩擦自激振动的影响，首先，结合现场调研，建立CRH3高速列车轮对-轨道-制动系统有限元模型；然后，采用复特征值法研究考虑轮轨粘滑和制动滚滑作用下的轮对-轨道-制动系统的摩擦自激振动特性；进而探究制动结构中表面织构对整个系统摩擦自激振动特性的影响；最后，对轨道结构中扣件参数进行参数化分析，并采用最小二乘法和粒子群算法求得抑制钢轨波磨的扣件参数的最优解. 研究结果表明：高速列车在制动区段时，轮轨粘滑和制动滚滑作用导致的轮对-轨道-制动系统摩擦自激振动的主要频率为526.75 Hz，与现场波磨特征频率接近，说明轮对-轨道-制动系统的摩擦自激振动可能是该区段钢轨波磨的主要诱因；采用具有表面织构的闸片或制动盘能有效抑制制动区段的钢轨波磨，其中沟槽型闸片的抑制效果最佳；当扣件的垂向刚度为65.5 MN/m，横向刚度为46.0 MN/m，垂向阻尼为84.0 kN·s/m和横向阻尼为23.5 kN·s/m时，可以抑制高速列车制动区段的钢轨波磨.
Abstract:To explore the influence of the braking structure/track structure on the frictional self-excited vibration of the wheelset−track−brake system on braking sections of high-speed trains, firstly, combined with on-site investigation, the finite element model of the wheelset−track−brake system of CRH3 high-speed trains is established. Then, the frictional self-excited vibration characteristics of the wheelset–track–brake system under the effects of wheel-rail stick-slip and brake roll-slip are analyzed with the complex eigenvalue method. Furthermore, the influence of the surface texture in the braking structure on the frictional self-excited vibration of the whole system is examined. The parameters of the fasteners in the track structure are parametrically analyzed. The least squares method and the particle swarm optimization algorithm are used to obtain the optimal solution of the fasteners parameters to suppress the rail corrugation. The results show that the main frequency in the frictional self-excited vibration of the wheelset–track–brake system caused by wheel-rail stick-slip and braking roll-slip is 526.75 Hz on the braking section, which is close to the characteristic frequency of the on-site corrugation. The frictional self-excited vibration of the whole system may be the main cause of rail corrugation. The rail corrugation on the braking section can be effectively suppressed by the brake pads or brake discs with surface texture, and the grooved brake pads have the best suppression effect. When the vertical stiffness of the fastener is 65.5 MN/m, the lateral stiffness is 46.0 MN/m, the vertical damping is 84.0 kN·s/m, and the lateral damping is 23.5 kN·s/m, the rail corrugation on the braking section of high-speed trains can be effectively suppressed.
-
高层建筑作为典型的风敏结构，建筑上的风荷载与其气动外形密切相关[1-2]. 随着建造技术的发展，越来越多的辅助构件，如阳台、外伸板、粗糙条[3-4]等被安装在高层建筑外立面. 这些附属物的存在不仅影响建筑的气动外形，也会改变建筑表面风压分布、风荷载及周围风环境. 因此，弄清附属物对建筑风效应的影响十分必要.
部分学者通过风洞试验探索了附属物对风压和风荷载的影响. 阳台可以显著改变迎风面上部的平均和峰值风压分布[5-6]，建筑物表面风压降低约30%[7]. 不同布置形式的肋板对风荷载的影响不同[8]，连续水平板会略微增加顺风向平均基底弯矩，而间隔水平板能降低横风向脉动基底弯矩[9]. 迎风面边缘附近的竖向肋板会增加迎风角区域的吸力[10]，同时，还会显著降低表面脉动风压，最大降幅约为57%[11].
虽然试验证明了附属物能减弱结构上的风荷载，但其抗风工作机理尚不清楚. 因此，为阐明附属物的流场修正机理，一些学者尝试利用流动可视化 技术（PIV）和LES （large eddy simulation）研究附属物对建筑周围流场特征的影响. Ai等[12]发现带栏杆的水平阳台能显著抑制迎风面和背风面附近的竖向流，但同时增强了近壁湍流脉动. Zheng等[13]认为相邻阳台间的局部旋涡是影响风速和风压分布的重要因素. 建筑边缘附近的阳台能有效抑制流动分离，并破坏涡脱过程[14].
除水平附属物外，Liu等[15]发现竖向肋板能显著降低侧风面附近湍流脉动，并将高湍流区推离侧风面；Liu等[16-17]认为迎风角竖向肋板附近形成的局部涡旋可以明显改变模型周围的流场结构；Hui等[18]发现不同位置的肋板对流场结构的影响明显不同，迎风面肋板抗风作用最明显，而侧风面和背风面肋板对流场结构的影响较弱.
尽管部分学者探究了外伸肋板的流场修正机理，但由于肋板布置的复杂性，水平肋板的抗风工作机理仍需进行系统的研究.
本文采用LES方法研究大气边界层来流（ABL）下水平肋板密度和布置形式对高层建筑流场和气动特性的影响，并详细分析肋板对风场特征的影响，如近壁流、涡结构和竖向流等，借助流场信息阐明肋板的抗风工作机理，为实际高层建筑外辅助构件的抗风设计和布置提供参考.
1. 数值方法
1.1 模型信息
以刚性模型为目标高层建筑，模型长、宽、高（D、B、H）的比例为1∶1∶4. 模型缩尺比为1∶200，模型高度和对应实际建筑高度分别为0.4 m和80 m. 外伸肋板安装在模型的外立面，如图1所示. 图中：d为外伸长度，b、h分别为2个相邻板间的水平和垂直距离, α为风向角. 模型1～3研究肋板密度的影响，模型2～5研究肋板布局的影响. 外伸肋板主要有3个参数， d固定为0.06D （实际尺寸为1.2 m），该尺寸与阳台的尺寸相似[6]. 肋板的具体尺寸信息如表1所示.
表 1 肋板尺寸信息Table 1. Dimension information of ribs模型编号 d/D/% b/D//% h/D//% 1 6 50.0 2 6 25.0 3 6 12.5 4 6 20 25.0 5 6 60 25.0 1.2 控制方程及求解策略
本次模拟选择LES湍流模型，亚格子尺度模型为标准SGS （subgrid scale）模型，Smagorinsky常数Cs取值为0.13，Cs在0.10～0.14范围内模拟结果较好[19]. 不可压缩流滤波后的N-S方程为
∂¯ui∂t+∂(¯ui¯uj)∂xj=−1ρ∂¯p∂xi+ν∂2¯ui∂xj∂xj−∂τij∂xj, (1) τij = −2νt¯Sij+13τkkδij, (2) ¯Sij = 12(∂¯ui∂xj+∂¯uj∂xi), (3) ∂¯ui∂xi=0, (4) 式中：xi （xj）为笛卡尔坐标系中x、y、z 3个方向的坐标值，${\overline u}_i\left(u_j\right) $为x、y、z 3个方向的速度，${\overline p}$为滤波后的压力，ρ、ν分别为空气密度和运动黏度，τij为SGS亚格子应力张量，νt为SGS涡黏性系数，${\overline S}_{ij} $为滤波后的应变率张量，t为时间.
利用开源软件OpenFOAM进行瞬态模拟，求解器选择PimpleFoam. 在控制方程的求解中，数值模型离散格式选择如下：二阶后向差分方案用于时间离散，控制方程中的扩散项和对流项分别采用二阶中心差分格式和线性迎风稳定输运格式（LUST）. PIMPLE算法用于解决压力-速度耦合问题. 几何代数多重网格（GAMG）和预处理双共轭梯度（PBiCG）求解器用于计算迭代过程中的压力和速度[20]. 本次模拟的时间步长设置为5 × 10−5，模拟中的平均库郎数（CFL）为0.008，最大库郎数小于1.200. 每个工况的总模拟时长为9 s.
1.3 网格信息和边界条件
计算域和网格信息如图2所示. 图中：①～④ 为加密区. 计算域入口处施加湍流来流（ABL），出口为自由流条件，侧壁和计算域顶部为滑移边界条件，建筑物表面和地面为无滑移边界条件，阻塞率为0.6%.
利用网格生成工具snappyHexMesh生成网格系统. 本次模拟采用4个加密区实现网格的逐级加密（图2（a）、（b）），加密区 ①～④ 尺寸分别为9H × 3.5H × 2H、1.75H × 1.75H × 1.5H、0.75H × 0.75H × 1.1H、0.04H × 0.04H × 1.03H. 计算域内主要采用结构化网格，非结构化网格只出现在加密区的交界处. 3种不同的网格布局用于检查网格无关性，如表2所示. 网格2的近壁首层网格在水平方向上高度为1/125D. 建筑物附近竖直方向的网格尺寸远小于水平方向的网格尺寸，近地面的网格尺寸为1/600D，网格2的数量约为7百万.
表 2 网格信息Table 2. Mesh information网格 最小网格 最大网格 数量/百万 x/y z x/y z 网格 1 1/62.5D 1/300D 0.6D 1D 3.7 网格 2 1/125.0D 1/600D 0.6D 1D 7.2 网格 3 1/250.0D 1/ 1200 D0.6D 1D 13.6 使用一致离散随机流生成（CDRFG）方法[21]生成入口的脉动风速时程. 该方法基于速度功率谱的离散化和合成技术，可以很好地保持湍流能量和速度相干性，也可以准确评估作用在建筑物上的风荷载[21]. 顺流向平均风速U、湍流强度Iu剖面[22-23]及顺风向脉动风速功率谱如图3所示：速度剖面指数为1/6，建筑物屋顶处的顺风向平均风速UH为8 m/s，对应的雷诺数Re=5.5 × 104，建筑物高度处的湍流积分尺度LuH为0.24 m. 目标建筑物处的风场特性决定结构上的风荷载. 由图3可知，平均风速和湍流强度剖面与已有文献[22-23]结果吻合较好，但由于LES自身的数值耗散，模型位置处的湍流强度相比入口处有一定程度的减小；顺风向脉动风速谱也与von Karma谱[20]一致，表明CDRFG方法生成的来流湍流是可靠的.
1.4 气动力定义和结果验证
无量纲风压系数Cp、阻力系数Cd和升力系数Cl定义如下：
Cp=Δp1/2ρU2H， (5) Cd=Fd1/2ρU2HA, (6) Cl=Fl1/122ρU2HA， (7) 式中：Δp为压差，Fd、Fl分别为总阻力和总升力，A为投影面积.
大涡模拟的结果验证如图4[22-23]和表3所示. 图中：a、b、c、d表示模型边缘. 表中：AR为高宽比，${\overline C}_{\mathrm{d}} $、${C}_{{\mathrm{d}}1} $为阻力的时均值和均方根值，Cl1为升力的均方根值. 可以看出，本次LES得到的平均风压系数${\overline C}_{\mathrm{P}} $的分布与已有研究结果接近[22-23]，但LES得到的脉动风压均方根${C}_{{\mathrm{p}}1} $与已有结果略微差异，可能因为湍流生成方法、数值方案和网格分辨率等方面的差异造成的. 风压的差异会导致模型上风荷载不同（如表3所示）. 与已有研究结果相比，本次模拟结果在合理范围内，表明本次模拟结果是可靠的. 网格1会高估脉动风压均方根，网格2、3的结果更接近已有研究结果. 因此，本研究采用网格2方案来平衡计算成本和结果精度.
表 3 参考方柱LES结果及验证Table 3. LES results of square column and verification方法 文献 Re/104 AR ${\overline C}_{\mathrm{d}} $ ${C}_{{\mathrm{d}}1} $ ${C}_{{\mathrm{l}}1} $ St LES 网格 1 5.5 4 1.220 0.09 0.330 0.100 网格 2 5.5 4 1.147 0.10 0.300 0.096 网格 3 5.5 4 1.156 0.11 0.310 0.094 试验 文献 [22] 5.5 4 1.200 0.410 0.100 文献 [23] 5.0 4 1.280 0.13 0.320 0.085 文献 [24] 6.0 4 1.270 0.08 0.296 0.097 文献 [25] 7.3 3 1.290 0.102 文献 [11] 5.5 5 0.930 0.350 0.100 文献 [10] 5.5 5 1.080 2. 外伸板对流场结构的影响
2.1 平均流场结构
大气边界层来流下的建筑物周围会产生明显的三维流动结构，不同高度处的平均流场如图5所示. 可以看出：不同高度处的旋涡大小差异明显；相比模型1～3，在z=0.52H高度处，参考模型的尾涡相对较短，尺寸较小，表明肋板能拉长尾涡；模型顶部自由端效应导致建筑物屋顶附近尾涡缺失（z=0.95 H）.
图 5 不同高度处水平截面上的平均流线和平均流速Figure 5. Mean streamlines and mean flow velocity on horizontal sections at different heights图6所示为竖直中心面（y=0D）上的顺风向平均风速和平均流线，以阐明水平肋板对竖向流动的影响. 对于参考模型，来流在迎风面0.73H高度附近停滞. 当模型上安装水平肋板时，迎风面上的驻点相比参考模型无明显变化，肋板附近形成小尺寸局部旋涡.
图 6 竖直截面上（y = 0D）的平均流线和平均流速Figure 6. Mean streamlines and mean flow velocity on vertical sections （y = 0D）肋板密度会明显改变尾流区鞍点高度，鞍点高度随密度增加而减小，模型2、3的尾部鞍点高度分别为1.17D和1.23D（图6（c）、（d）），远低于参考模型的高度（1.50D）. 对比图6（c）、（d）的结果可以发现，沿建筑物高度的肋板密度较大时，肋板对尾部鞍点影响较小. 图6（c）中的点F表示流动再附点，局部旋涡再附在模型迎风面上.
另外，本节还研究了肋板水平间距（模型4和模型5）对平均流场的影响. 对比模型2、4、5的结果可以看出，随着水平间隙的增加，尾涡逐渐变小，尾部鞍点的高度明显变高（图6（c）、（e）～（f）），说明外伸板随着水平距离的增大，其对尾涡的影响逐渐变弱.
3. 外伸板对风压和风荷载的影响
3.1 外伸板密度影响
流场结构的变化会影响模型壁面风压分布（图7）. 由图7（a）可知，参考模型中心线上的${\overline C }_{\mathrm{P}}$沿竖向平滑变化，${\overline C }_{\mathrm{P}} $最大值出现在0.8H左右. 当模型上安装外伸板时，${\overline C }_{\mathrm{P}} $分布变化明显，模型1～3的${\overline C }_{\mathrm{P}} $呈“之”字形分布，肋板附近出现${\overline C }_{\mathrm{P}} $的局部最大值和最小值. Hui等[9]也发现了迎风面和背风面${\overline C }_{\mathrm{P}} $的“之”字形模式. 这种结果可用图6所示的近壁流场来解释，因为肋板上、下形成的局部旋涡会导致局部压力的出现. 靠近模型自由端（0.8H～1.0H）或模型底部（0～0.3H）时，压力变化更显著（图7（a）），因为上、下部肋板附近形成的旋涡尺寸相对较大，大尺寸旋涡对${\overline C}_{\mathrm{P}} $的影响更大. ${\overline C }_{\mathrm{p}} $的变化幅度随着肋板密度的增加而减小，因为密集的肋板明显影响近壁流并减小肋板附近局部旋涡的尺寸（图6（b）～（d）中的区域L）. 较大的局部旋涡将导致模型1上出现较大${C}_{{\mathrm{p}}1} $. 对于迎风面，${C}_{{\mathrm{p}}1} $的变化也随着肋板密度的增加而减小，如图7（b）所示.
在z=0.52H处，侧壁面上的风压分布如图8所示. 图中：A、B为侧风面边缘. 4个模型在0.52H处的风压系数在前缘和后缘处基本保持不变，（图8（a）），但模型边缘附近风压系数因流动分离和次级涡的影响而发生突变. 外伸板能明显降低侧壁面风压，相比参考模型，模型1～3在0.52H处的${\overline C }_{\mathrm{P}} $和${C}_{{\mathrm{p}}1} $小于参考模型，${\overline C }_{\mathrm{P}} $和${C}_{{\mathrm{p}}1} $的最大降幅分别为20%和17%.
带板和无板光面模型的平均阻力系数${\overline C}_{\mathrm{d}}$、${C}_{{\mathrm{d}}1} $和${C}_{{\mathrm{l}}1} $如表4所示，脉动力是荷载系数的标准差. 由表可知，外伸板虽然影响迎风面的压力分布，但其对阻力无明显影响，然而，带板模型1～3的${C}_{{\mathrm{l}}1} $明显较小，减幅约为27%，是因为模型1～3侧壁面风压较小（图8）.
表 4 参考方柱和模型1～3的风荷载系数Table 4. Wind load coefficients for square column and models 1–3名称 ${\overline C}_{\mathrm{d}} $ ${ C}_{{\mathrm{d}}1} $ ${ C}_{{\mathrm{l}}1} $ 方柱 1.147 0.100 0.300 模型 1 0.146 0.102 0.232 模型 2 0.149 0.102 0.219 模型 3 0.145 0.101 0.218 3.2 外伸板布置形式的影响
图9为不同布置形式肋板模型的平均压力分布. 由图可知：连续和间断布置形式明显影响压力的分布；对于迎风面，肋板的存在使带板模型上的${\overline C}_{\mathrm{P}} $间断分布，模型4、5的${\overline C}_{\mathrm{P}} $表面压力分布特征逐渐消失；模型2中的连续肋板明显增加了模型迎风面顶部的${\overline C}_{\mathrm{P}} $；肋板显著降低整个侧壁面上的${\overline C}_{\mathrm{P}} $，尤其侧壁面底部，相比参考模型，${\overline C}_{\mathrm{P}} $最大减小22%.
模型2、4、5的风荷载如表5所示. 由表可知，3个模型的阻力相似，但脉动升力从模型2到模型5逐渐增加，模型5的升力最大，这说明仅在模型角部布置水平板对升力影响较小.
表 5 模型2、4、5的风荷载Table 5. Wind loads of models 2, 4, 5名称 ${\overline C}_{\mathrm{d}} $ ${C}_{{\mathrm{d}}1} $ ${C}_{{\mathrm{l}}1} $ 模型 2 1.149 0.102 0.219 模型 4 1.156 0.106 0.229 模型 5 1.153 0.103 0.261 4. 结 论
本文采用LES方法评估大气边界层流下外伸肋板对高层建筑气动特性的影响. 详细阐述了肋板密度和布置形式对模型流场特征的影响，如近壁流、涡结构和竖向流等，并借助流场信息阐明了壁面风压和整体风荷载的变化，以评估不同肋板的抗风性能，阐明湍流来流下外伸板的流场机理. 得到以下结论：
1） 水平板明显影响尾涡尺寸和尾部鞍点，水平板能明显拉长尾涡. 尾部鞍点高度随着肋板密度的增加而减小，沿建筑物高度的肋板密度过大时，尾部鞍点无明显变化. 外伸板随着水平间距的增大，其对尾涡的影响逐渐变弱.
2） 水平板可以有效抑制建筑立面附近的竖向流动，导致近壁流动形式明显变化. 连续竖直板明显影响近壁流，而间隔肋板对近壁流的影响相对较弱.
3） 流场的变化会改变壁面风压分布. 水平板使迎风面的平均风压${\overline C}_{\mathrm{P}} $呈“之”字形分布. 水平板可以明显降低侧壁面上平均和脉动风压，最大降幅分别约为20%和17%.
4） 水平板不改变模型的平均阻力${\overline C}_{\mathrm{d}} $，但会明显降低模型上的${ C}_{{\mathrm{l}}1} $，最大减幅为27%. 连续肋板相比间隔肋板能更明显的降低模型上的气动力.
5） 连续布置且密度适中的水平肋板对高层建筑周围的流场结构和建筑上的风荷载影响更显著，因此，实际高层建筑外辅助构件的设计和布置时应采用连续水平肋板，肋板布置密度适中即可.
致谢：中国电建集团成都院科技项目（P49321，PA2202）
-
图 1 制动区段钢轨波磨现场调查分析
Figure 1. On-site investigation and analysis of rail corrugation on braking section
图 2 CRH3高速列车轮对-轨道-制动系统的接触模型
Figure 2. Contact model of wheelset–track–brake system of CRH3 high-speed train
图 3 CRH3高速列车轮对-轨道-制动系统有限元模型
Figure 3. Finite element model of wheelset–track–brake system of CRH3 high-speed train
图 4 轮对-轨道-制动系统摩擦自激振动实部分布及模态
Figure 4. Real part distribution and modes of frictional self-excited vibration in wheelset–track–brake system
图 5 不同表面织构下轮对-轨道-制动系统摩擦自激振动实部分布及闸片接触应力
Figure 5. Real part distribution of frictional self-excited vibration of wheelset–track–brake system and contact stress of brake pads under different surface textures
图 6 扣件刚度对整个系统摩擦自激振动的影响
Figure 6. Influence of fastener stiffness on frictional self-excited vibration of overall system
图 7 扣件阻尼对整个系统摩擦自激振动的影响规律
Figure 7. Influence of fastener damping on frictional self-excited vibration of overall system
图 9 优化前、后复特征值实部结果对比
Figure 9. Comparison of real part results of complex eigenvalues before and after optimization
表 1 有限元模型材料参数
Table 1. Material parameters of finite element model
部件参数 密度/（k•gm−3） 弹性模量/MPa 泊松比 轮对 7800 210000 0.30 钢轨 7800 210000 0.30 制动盘 7300 207000 0.30 制动闸片 2500 8100 0.30 闸片托 5600 100000 0.30 制动杠杆 7000 190000 0.30 轨道板 2400 29500 0.25 CA 砂浆层 2600 32500 0.20 混凝土底座 2400 22500 0.20 
下载: 导出CSV
表 2 有限元模型连接参数
Table 2. Connection parameters of finite element model
方向 扣件刚度/
（MN·m−1）扣件阻尼/
（kN·s·m−1）地基支撑刚度/（MN·m−1） 地基支撑阻
尼/（kN·s·m−1）垂向 50 30 190 30 横向 28 20 纵向 28 20
下载: 导出CSV
-
[1] 金学松,李霞,李伟,等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报,2016,51(2): 264-273. doi: 10.3969/j.issn.0258-2724.2016.02.006JIN Xuesong, LI Xia, LI Wei, et al. Review of rail corrugation progress[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 264-273. doi: 10.3969/j.issn.0258-2724.2016.02.006 [2] 林凤涛,黄琴,张海,等. CRH3高速列车多边形磨耗车轮通过钢轨波磨区段的轮轨力研究[J]. 铁道科学与工程学报,2021,18(7): 1706-1714.LIN Fengtao, HUANG Qin, ZHANG Hai, et al. Study on wheel-rail force of CRH3 high speed train with wheel polygon when passing corrugation rail[J]. Journal of Railway Science and Engineering, 2021, 18(7): 1706-1714. [3] GRASSI E S. Rail irregularities, corrugation and acoustic roughness: characteristics, significance and effects of reprofiling[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail and Rapid Transit, 2012, 226(5): 542-557. doi: 10.1177/0954409712443492 [4] EI BESHBICHI O, WAN C, BRUNI S, et al. Complex eigenvalue analysis and parameters analysis to investigate the formation of railhead corrugation in sharp curves[J]. Wear, 2020, 450/451: 203150.1-203150.10. [5] 陈光雄,金学松,邬平波,等. 车轮多边形磨耗机理的有限元研究[J]. 铁道学报,2011,33(1): 14-18. doi: 10.3969/j.issn.1001-8360.2011.01.003CHEN Guangxiong, JIN Xuesong, WU Pingbo, et al. Finite element study on the generation mechanism of polygonal wear of railway wheels[J]. Journal of the China Railway Society, 2011, 33(1): 14-18. doi: 10.3969/j.issn.1001-8360.2011.01.003 [6] WANG Z Q, LEI Z Y. Analysis of rail corrugation characteristics on high-speed rail based on transient finite element method[J]. The International Journal of Acoustics and Vibration, 2021, 26(3): 231-239. doi: 10.20855/ijav.2021.26.31778 [7] 王立乾. 高速铁路钢轨波浪型磨耗研究及其防治建议[J]. 石家庄铁道大学学报(自然科学版),2013,26(4): 83-86, 90. doi: 10.13319/j.cnki.sjztddxxbzrb.2013.04.010WANG Liqian. Research on high-speed railway rail corrugated wear and tear[J]. Journal of Shijiazhuang Tiedao University (Natural Science), 2013, 26(4): 83-86, 90. doi: 10.13319/j.cnki.sjztddxxbzrb.2013.04.010 [8] CORREA N, OYARZABAL O, VADILLO E G, et al. Rail corrugation development in high speed lines[J]. Wear, 2011, 271(9/10): 2438-2447. doi: 10.1016/j.wear.2010.12.028 [9] 司道林,李伟,杜香刚,等. 减缓高速铁路钢轨波磨的仿真分析[J]. 中国铁道科学,2014,35(6): 79-83. doi: 10.3969/j.issn.1001-4632.2014.06.12SI Daolin, LI Wei, DU Xianggang, et al. Simulation analysis on mitigating rail corrugation for high speed railway[J]. China Railway Science, 2014, 35(6): 79-83. doi: 10.3969/j.issn.1001-4632.2014.06.12 [10] 姜子清,司道林,李伟,等. 高速铁路钢轨波磨研究[J]. 中国铁道科学,2014,35(4): 9-14. doi: 10.3969/j.issn.1001-4632.2014.04.02JIANG Ziqing, SI Daolin, LI Wei, et al. Research on rail corrugation of high-speed railway[J]. China Railway Science, 2014, 35(4): 9-14. doi: 10.3969/j.issn.1001-4632.2014.04.02 [11] CUI X L, LI T, BAO P Y, et al. Research on the dynamic cause of rail corrugation in the braking section of high-speed railways under multiple vibration inducements[J]. Journal of Vibration Engineering & Technologies, 2023, 11(7): 71-83. [12] 吴波文. 制动对车轮多边形磨耗和钢轨波磨影响的研究[D]. 成都: 西南交通大学, 2020. [13] 崔晓璐,包鹏羽,陈佳欣,等. 高速铁路制动区间钢轨摩擦自激振动研究[J]. 西南交通大学学报,2023,58(1): 141-149.CUI Xiaolu, BAO Pengyu, CHEN Jiaxin, et al. Rail friction self-excited vibration in braking section of high-speed railway[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 141-149. [14] BAO P Y, CUI X L, DING H H, et al. Influences of friction self-excited vibration characteristics of various types of high-speed trains on rail corrugations in braking sections[J]. Engineering Failure Analysis, 2022, 134: 106087.1-106087.10. [15] CHEN G X, ZHOU Z R, OUYANG H, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset-track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011 [16] 陈光雄,钱韦吉,莫继良,等. 轮轨摩擦自激振动引起小半径曲线钢轨波磨的瞬态动力学[J]. 机械工程学报,2014,50(9): 71-76. doi: 10.3901/JME.2014.09.071CHEN Guangxiong, QIAN Weiji, MO Jiliang, et al. A transient dynamics study on wear-type rail corrugation on a tight curve due to the friction-induced self-excited vibration of a wheelset-track system[J]. Journal of Mechanical Engineering, 2014, 50(9): 71-76. doi: 10.3901/JME.2014.09.071 [17] NIELSEN J C O, LUNDÉN R, JOHANSSON A, et al. Train-track interaction and mechanisms of irregular wear on wheel and rail surfaces[J]. Vehicle System Dynamics, 2003, 40(1/2/3): 3-54. [18] PALIWAL M, MAHAJAN A, DON J, et al. Noise and vibration analysis of a disc-brake system using a stick-slip friction model involving coupling stiffness[J]. Journal of Sound and Vibration, 2005, 282(3): 1273-1284. [19] WU B W, QIAO Q F, CHEN G X. et al. Effect of the unstable vibration of the disc brake system of high-speed trains on wheel polygonalization[J]. Proceedings of the Institution of Mechanical Engineers, 2020, 234(1): 80-95. doi: 10.1177/0954409719833787 [20] ABUBAKAR A R, OUYANG H J. Complex eigenvalue analysis and dynamic transient analysis in predicting disc brake squeal[J]. International Journal of Vehicle Noise and Vibration, 2006, 2(2): 143-155. doi: 10.1504/IJVNV.2006.011051 [21] ZHU, Q, CHEN, G. X, WU, B. W, et al. Effect of the material parameter and shape of brake pads on friction-induced disc brake squeal of a railway vehicle[J]. Tribology Transactions, 2021, 64(4): 744-752. doi: 10.1080/10402004.2021.1914254 [22] 胡利鸿,莫继良,王东伟,等. 沟槽和圆坑织构抑制摩擦尖叫噪声研究[J]. 中国机械工程,2016,27(9): 1158-1164. doi: 10.3969/j.issn.1004-132X.2016.09.004HU Lihong, MO Jiliang, WANG Dongwei, et al. Groove-textured and pit-textured surfaces to suppress friction-induced squeal noise[J]. China Mechanical Engineering, 2016, 27(9): 1158-1164. doi: 10.3969/j.issn.1004-132X.2016.09.004 [23] 王东伟. 沟槽型织构化表面调控界面摩擦振动噪声行为的研究[D]. 成都: 西南交通大学, 2019. [24] 张青,崔晓璐,陈光雄,等. 沟槽织构对盘形制动噪声的影响[J]. 机械设计,2017,34(2): 62-67.ZHANG Qing, CUI Xiaolu, CHEN Guangxiong, et al. Effect of groove-texture on disc braking noise[J]. Journal of Machine Design, 2017, 34(2): 62-67. [25] 陈光雄,崔晓璐,王科. 高速列车车轮踏面非圆磨耗机理[J]. 西南交通大学学报,2016,51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004CHEN Guangxiong, CUI Xiaolu, WANG Ke. Generation mechanism for plolygonalization of wheel treads of high-speed trains[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 244-250. doi: 10.3969/j.issn.0258-2724.2016.02.004 [26] ZHAO H Y, JENG D S. Accumulated pore pressures around submarine pipeline buried in trench layer with partial backfills[J]. Journal of Engineering Mechanics, 2016, 142(7): 04016042.1-04016042.15. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 445
- HTML全文浏览量: 149
- PDF下载量: 42
- 被引次数: 0