Simulation Study of Influence of Structural Parameters on Entrainment Coefficient of Ejector Based on Response Surface Method
-
摘要:
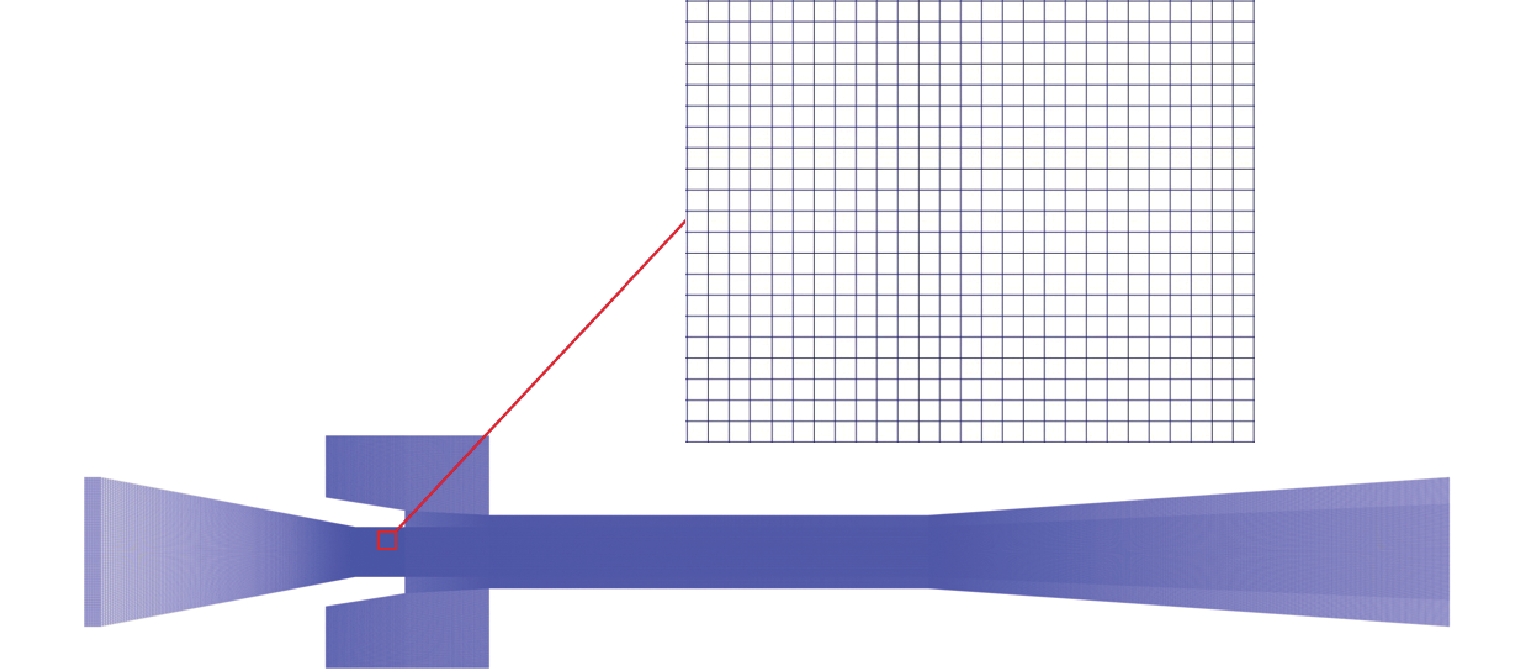
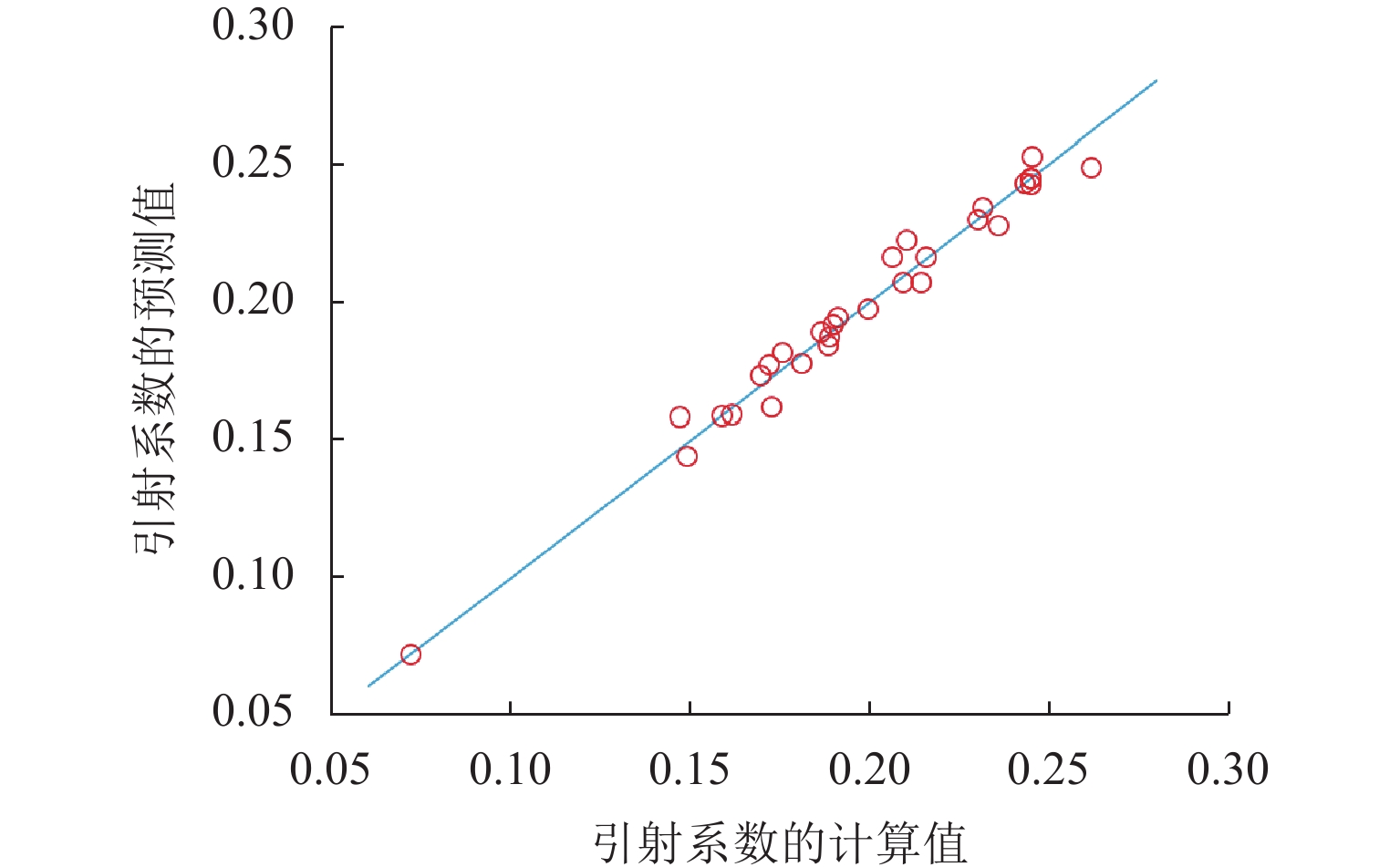
为分析引射器引射系数的显著影响因素，建立以空气为介质的引射器二维可压缩流动数值模型，基于实验数据完成了引射器模型计算准确性的校核验证. 采用D最优实验设计方法设计计算矩阵，基于最小二乘法构建二阶形式的引射系数响应面预测模型，并基于响应面预测模型开展了引射系数显著参数及参数交互作用的仿真分析. 研究结果表明：引射系数预测值和计算值的吻合性证明了响应面预测模型的准确性；扩压段长度、混合段长度、混合段直径和喷嘴出口到混合段入口距离的交互、混合段直径和混合段长度的交互、混合段长度和扩压段扩散角的交互是引射器引射系数的关键影响因素，因其对引射系数影响的
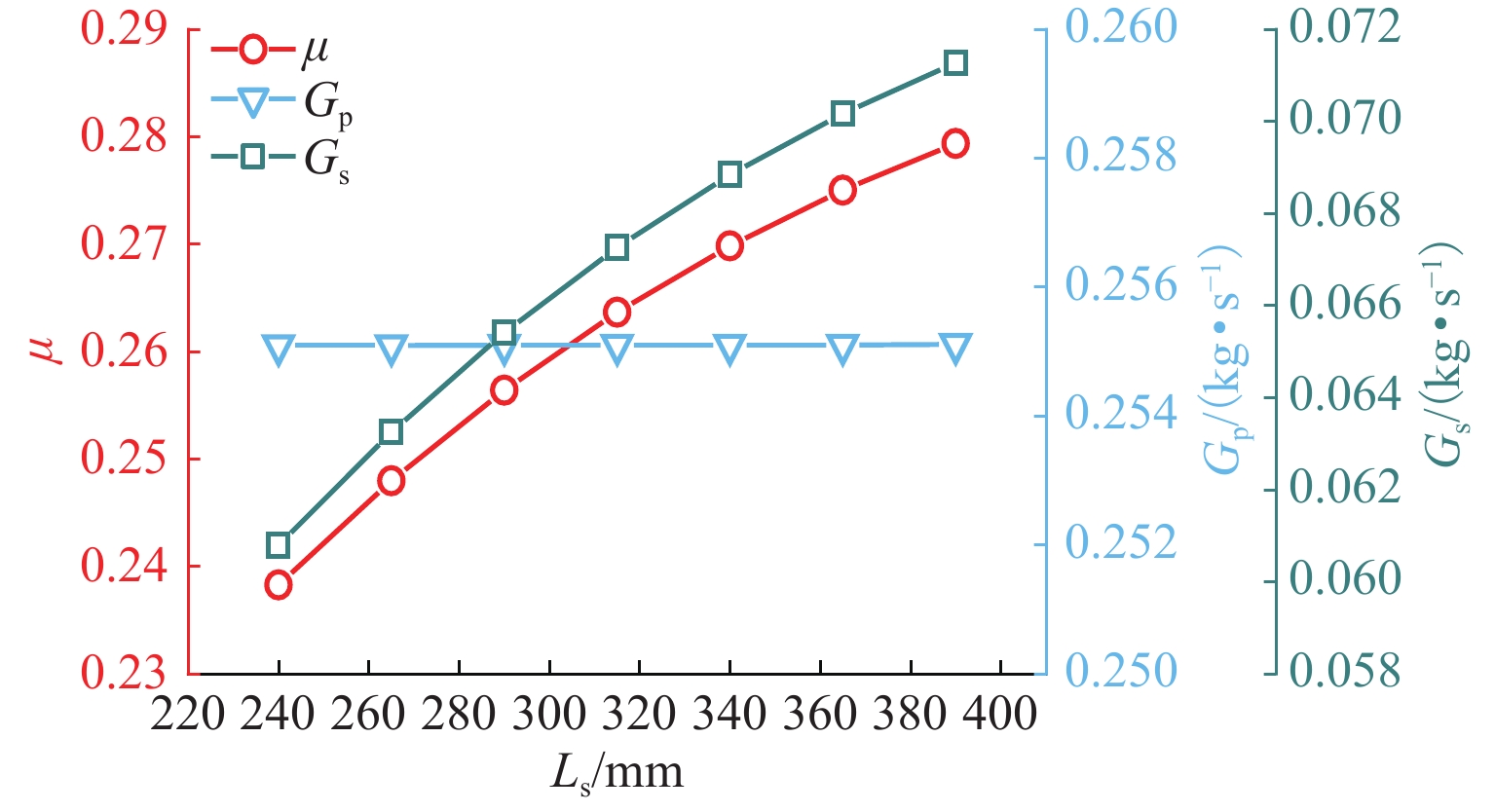
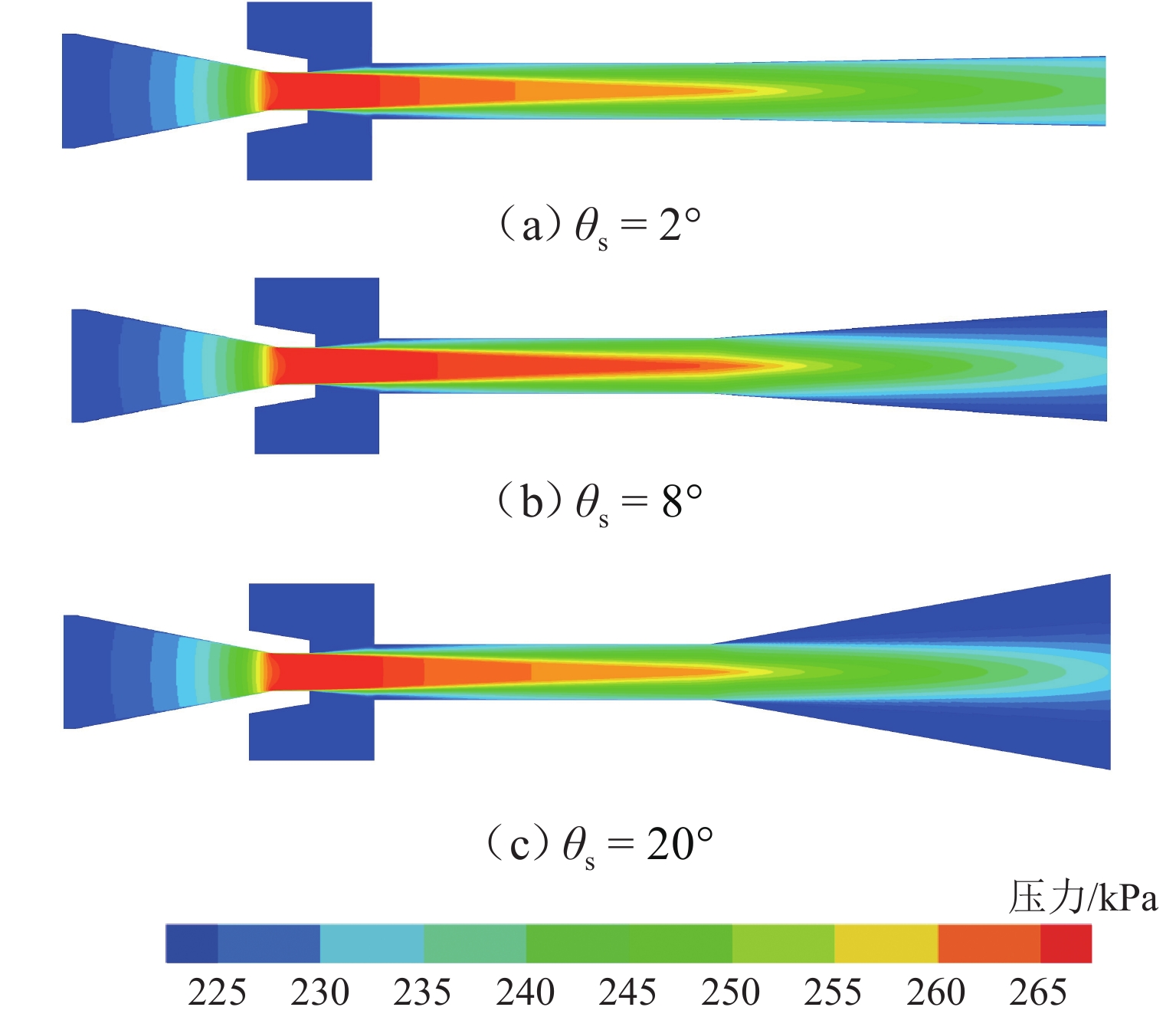
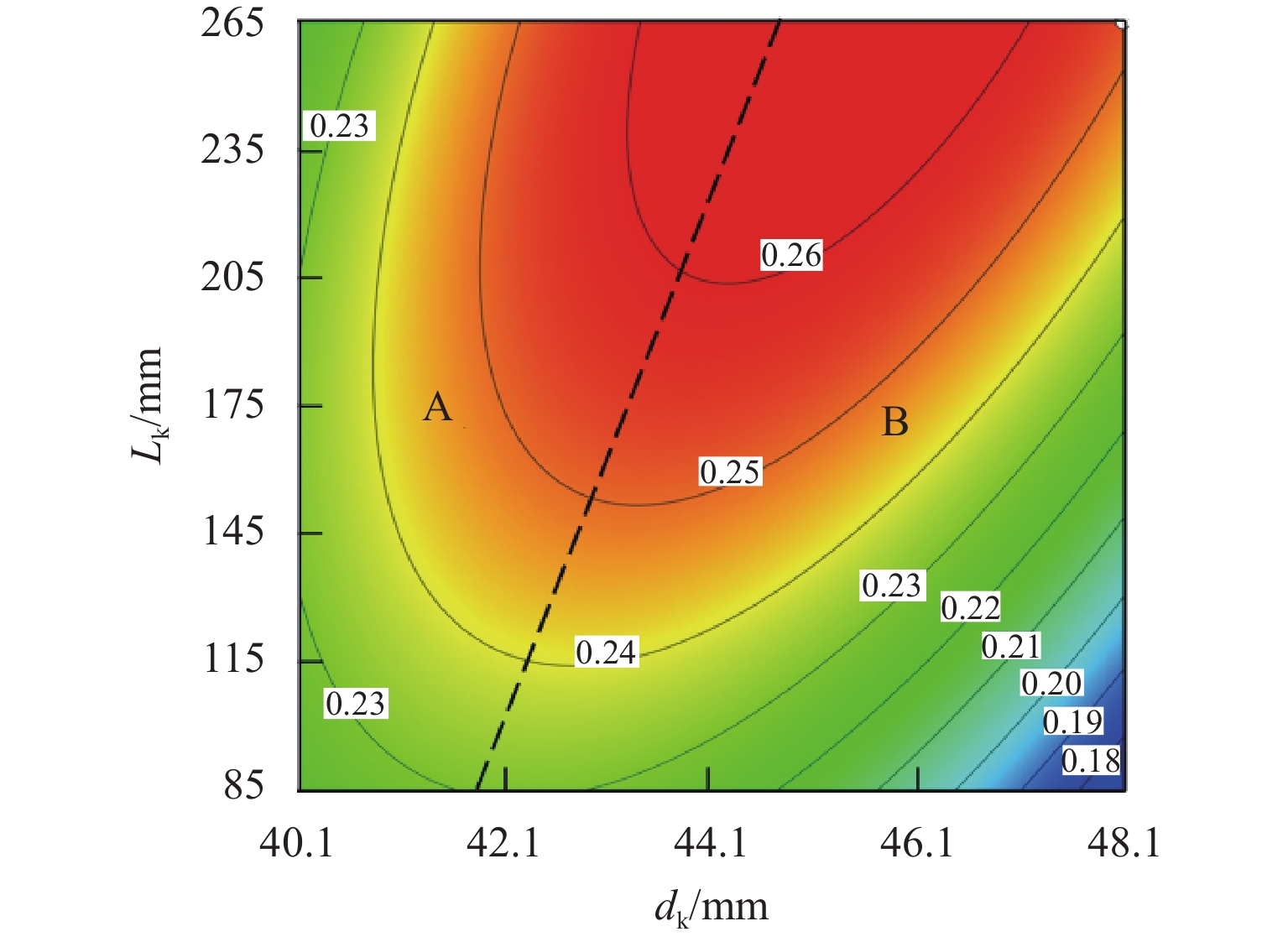
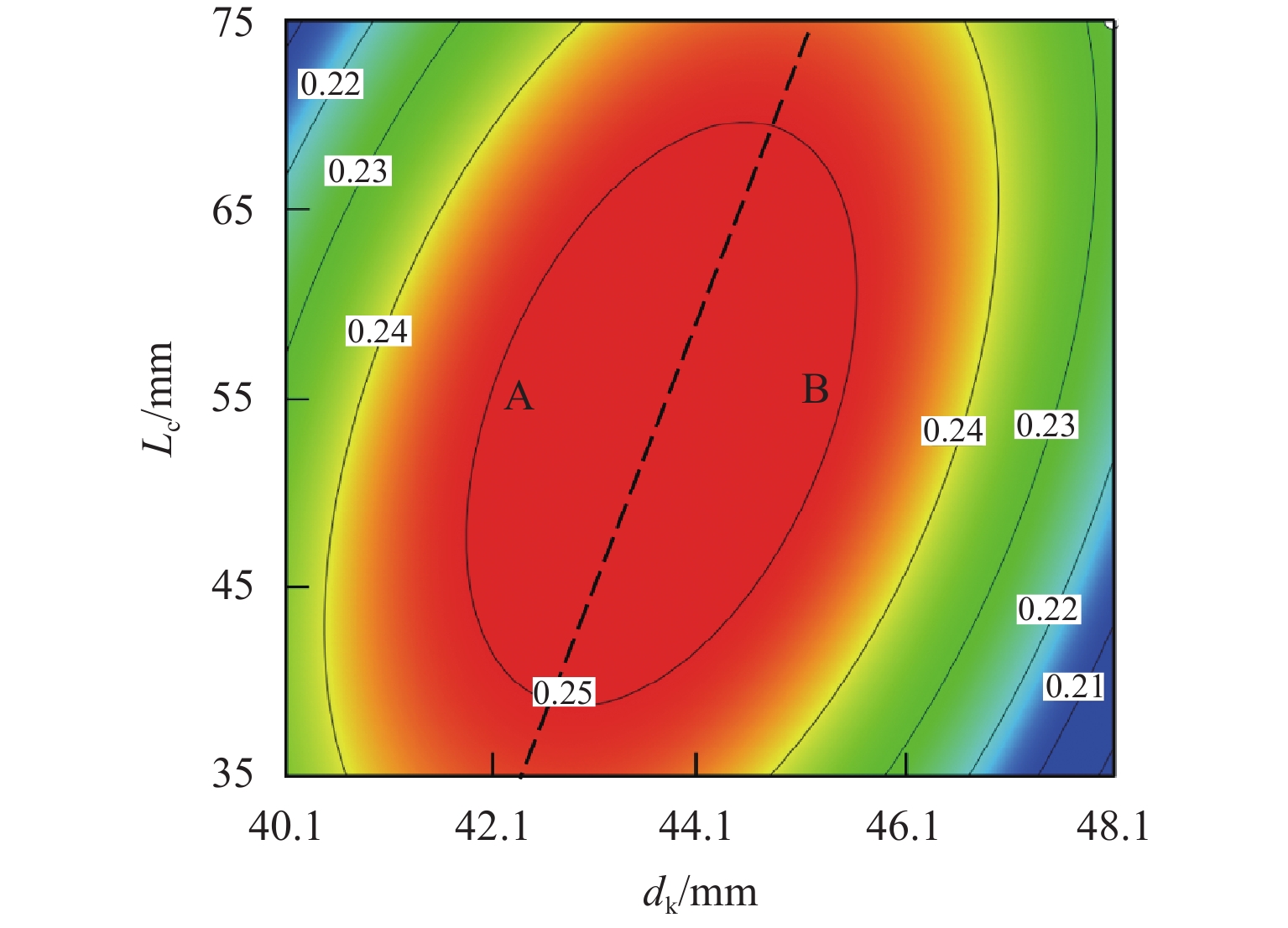
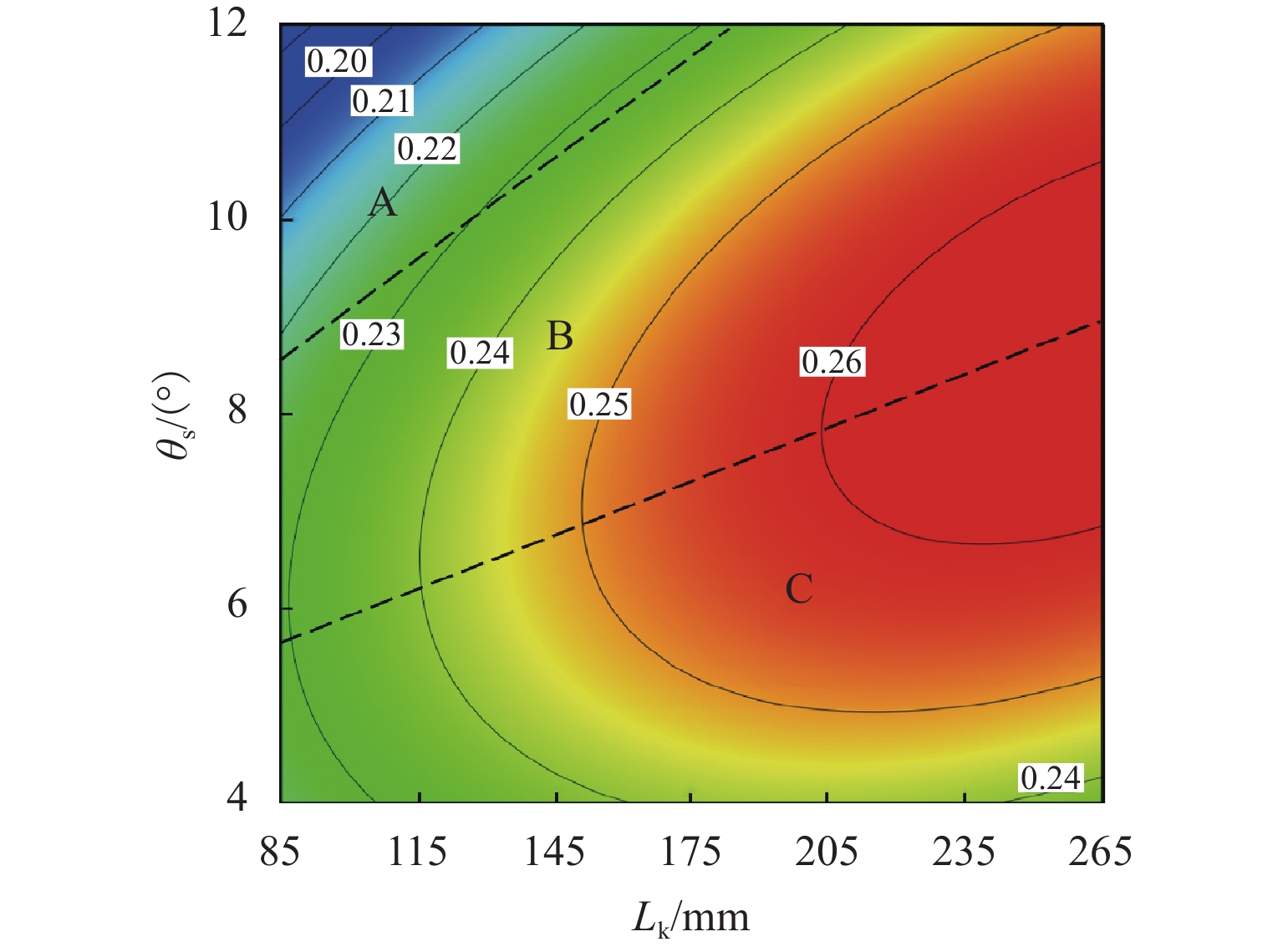
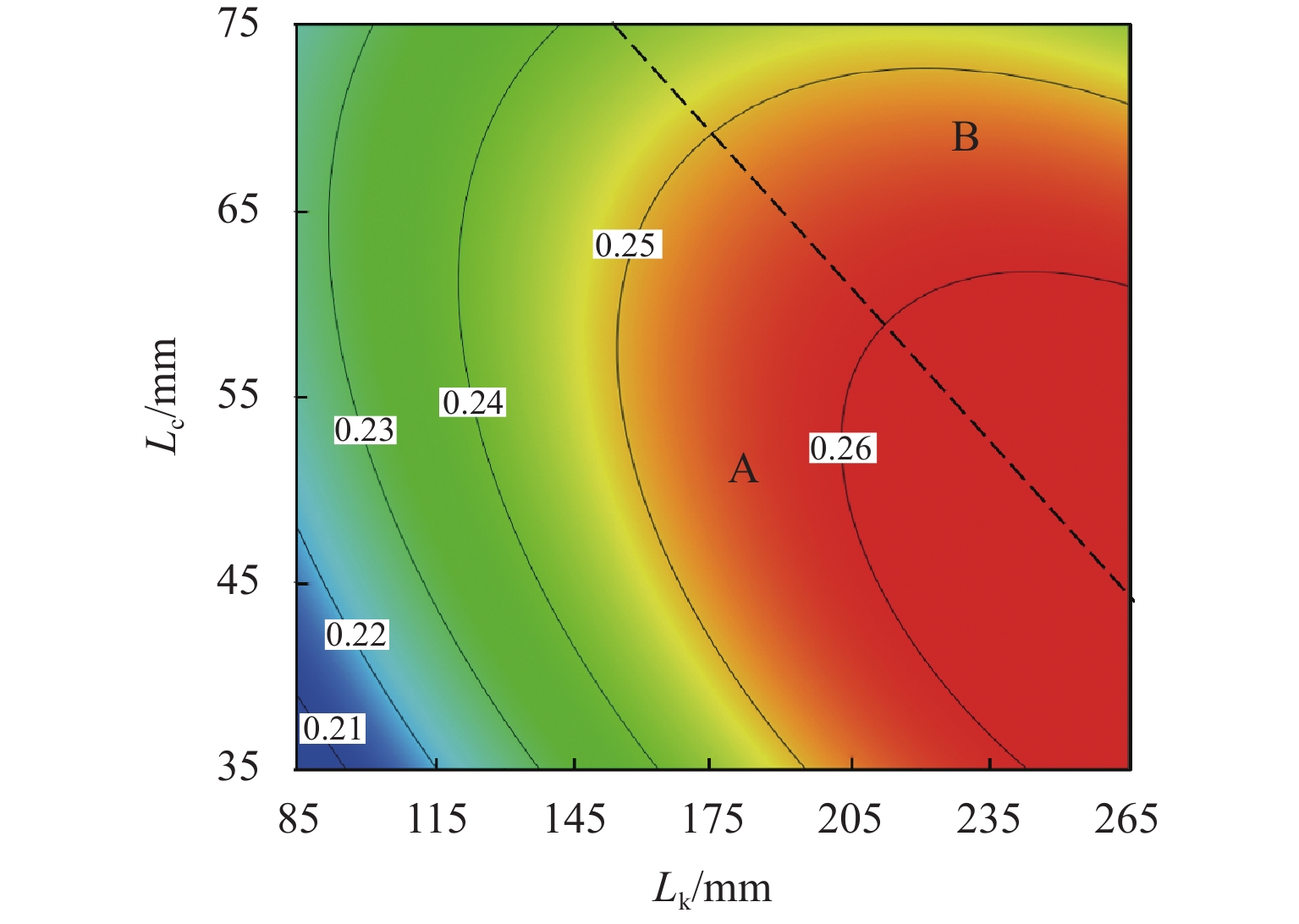
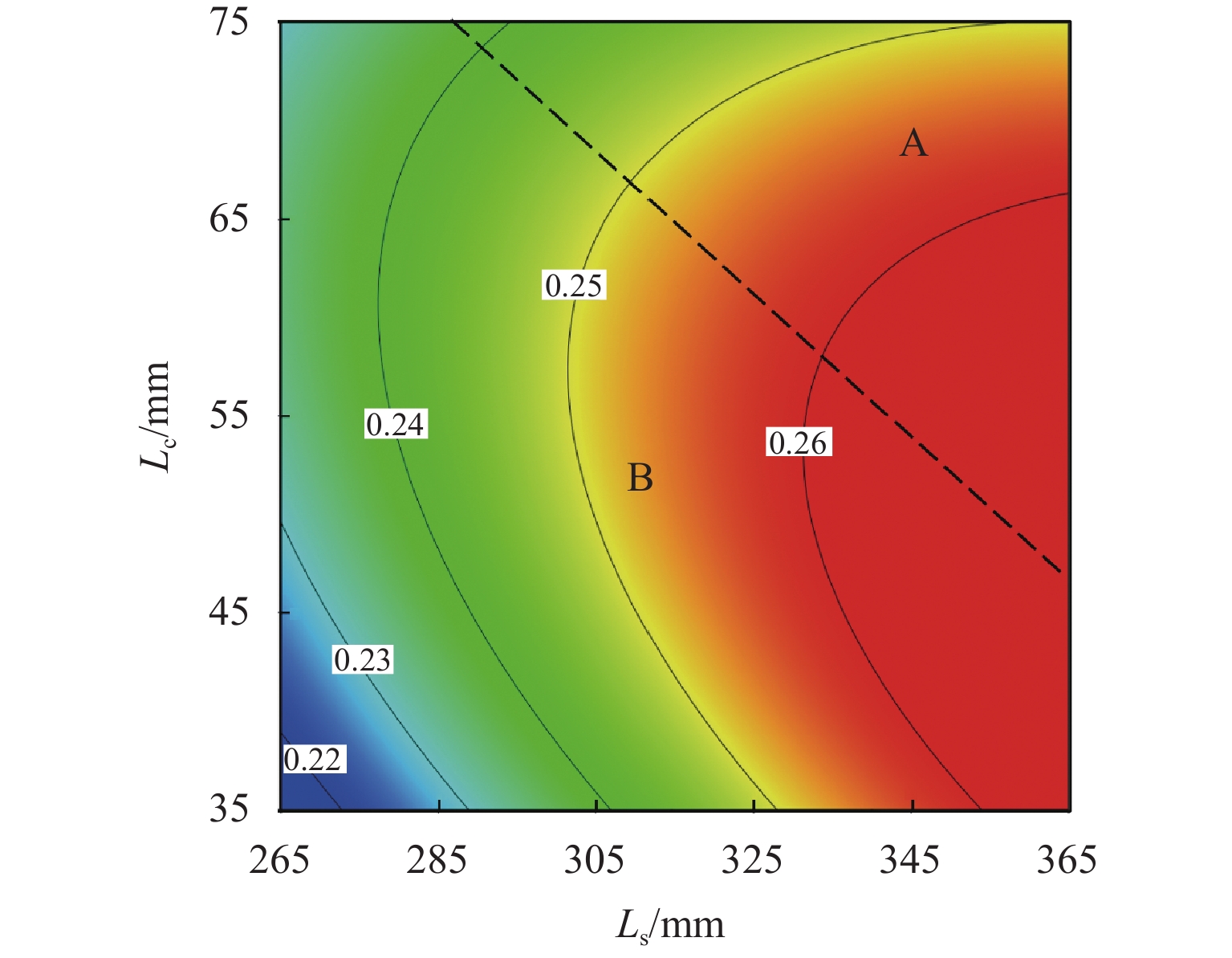
P 值小于0.001；扩压段扩散角、喷嘴出口到混合段距离和扩压段长度的交互、混合段长度和喷嘴出口到混合段距离的交互对引射系数具有重要的影响，是引射系数影响的主要参数；在参数显著交互作用中，影响引射系数的显著因素是变化的，取决于显著交互作用双参数的取值范围.Abstract:To analyze the significant influencing factors of the entrainment coefficient of the ejector, a two-dimensional numerical model of the compressible flow of the ejector with air as the working medium was established, and its calculation accuracy was validated by the experimental data. Meanwhile, the calculation matrix was designed by utilizing the D-optimal experimental design method. Based on the least-squares method, the response surface prediction model of the entrainment coefficient with a second-order form was constructed, and the significant parameters of the ejection coefficient and their interaction were simulated based on the constructed model. The research results show that the coincidence between the predicted and calculated values of the entrainment coefficients proves the accuracy of the response surface prediction model; the interaction between the length of the diffuser section, the mixing section length, the diameter of the mixing section, and the distance from the nozzle outlet to the inlet of the mixing section, the interaction between the mixing section diameter and mixing section length, and the interaction between the mixing section length and the diffusion angle of the diffuser section are the key factors affecting the entrainment coefficient because their
P -values are less than 0.001. Meanwhile, the interaction of the diffusion angle of the diffuser section, the distance from the nozzle outlet to the inlet of the mixing section and the length of the diffuser section, and the interaction between the length of the mixing section and the distance from the nozzle outlet to the inlet of the mixing section have an important influence on the entrainment coefficient. Therefore, they are the main parameters affecting the entrainment coefficient. In addition, it is found that among the significant interaction of parameters, the significant factors affecting the entrainment coefficient will change with the value range of the two parameters with significant interaction. -
图 3 引射系数随网格数量的变化
Figure 3. Variation of entrainment coefficient with the number of grids
图 4 模型计算结果与实验数据的对比
Figure 4. Comparison between calculated values and experimental data of the model
图 5 引射系数的预测值与计算值对比
Figure 5. Comparison between predicted values and calculated values of entrainment coefficient
图 7 不同Ls下压力、流体速度分布云图
Figure 7. Pressure and velocity distribution of the flow under different Ls
图 9 不同Lk下压力、流体速度分布云图
Figure 9. Pressure and velocity distribution of the flow under different Ls
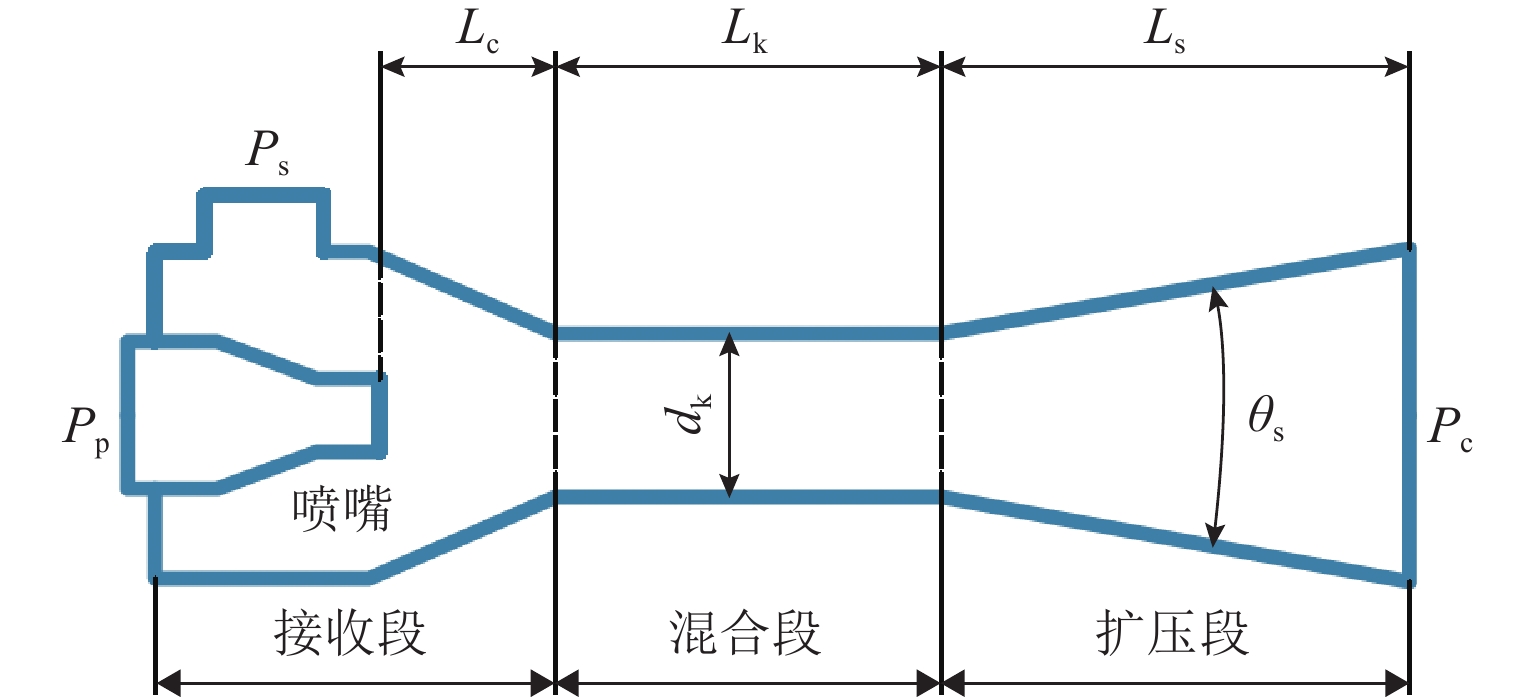
表 1 引射器主要结构参数
Table 1. Main structural parameters of the ejector
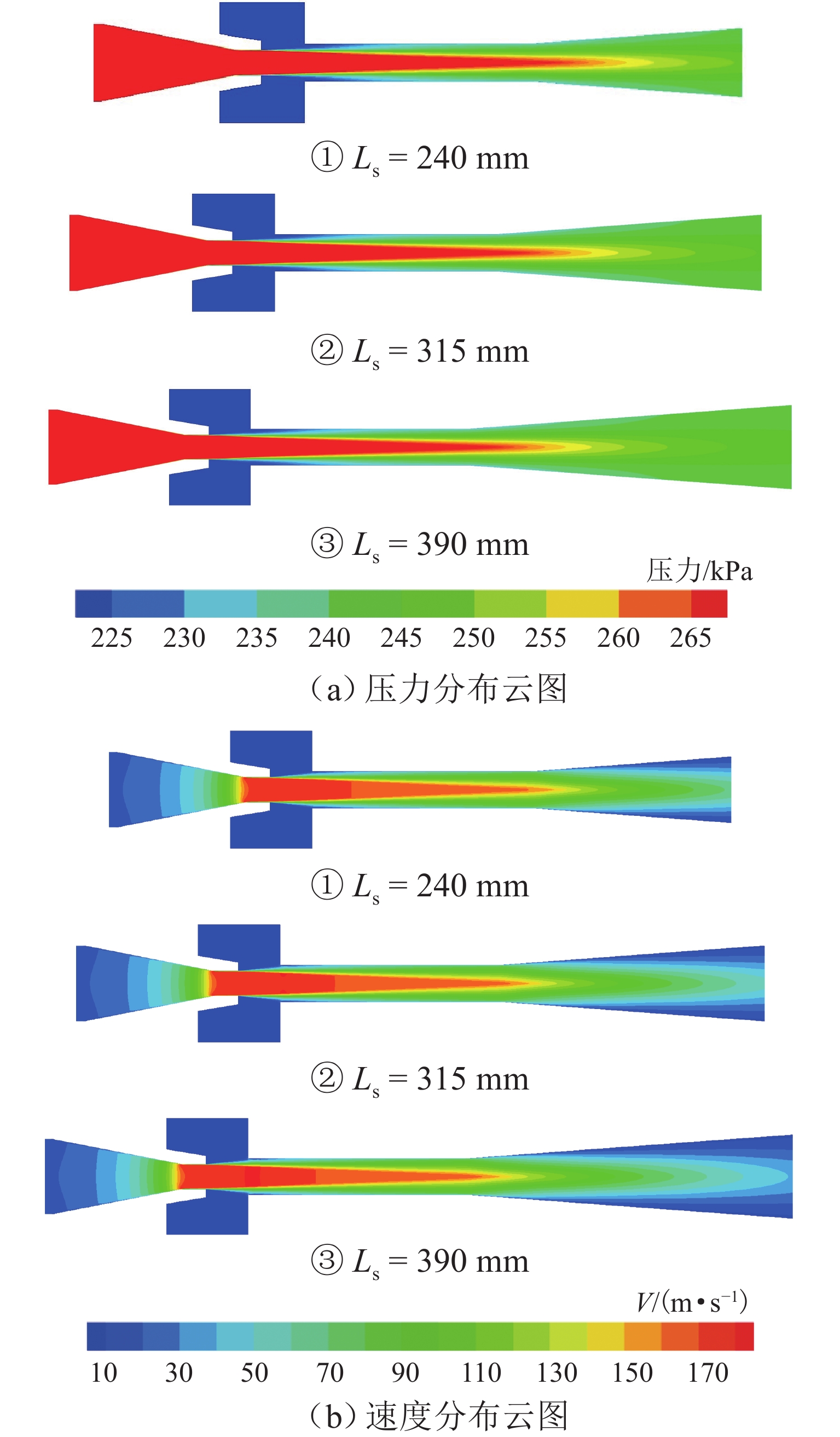
参数 数值 混合段直径 dk/mm 44.1 喷嘴出口到混合段入口距离 Lc/mm 51 混合段长度 Lk/mm 265 扩压段长度 Ls/mm 315 扩压段扩散角 θs/（°） 8 
下载: 导出CSV
表 2 不同压力下引射器实验结果[8]（Pc=1100.1 kPa）
Table 2. Experimental results of the ejector under different pressures [8] （Pc = 1100.1 kPa）
组别 Pp/kPa Ps/kPa Gp/（g·ms−1） Gs/（g·ms−1） A1 300 85.1 130.7 40.2 A2 300 90.0 130.8 176.3 A3 300 95.0 130.9 272.1 A4 300 97.5 130.9 337.9 A5 301 99.9 130.8 389.0
下载: 导出CSV
表 3 引射器结构参数的变化范围
Table 3. Variation range of structural parameters of ejector
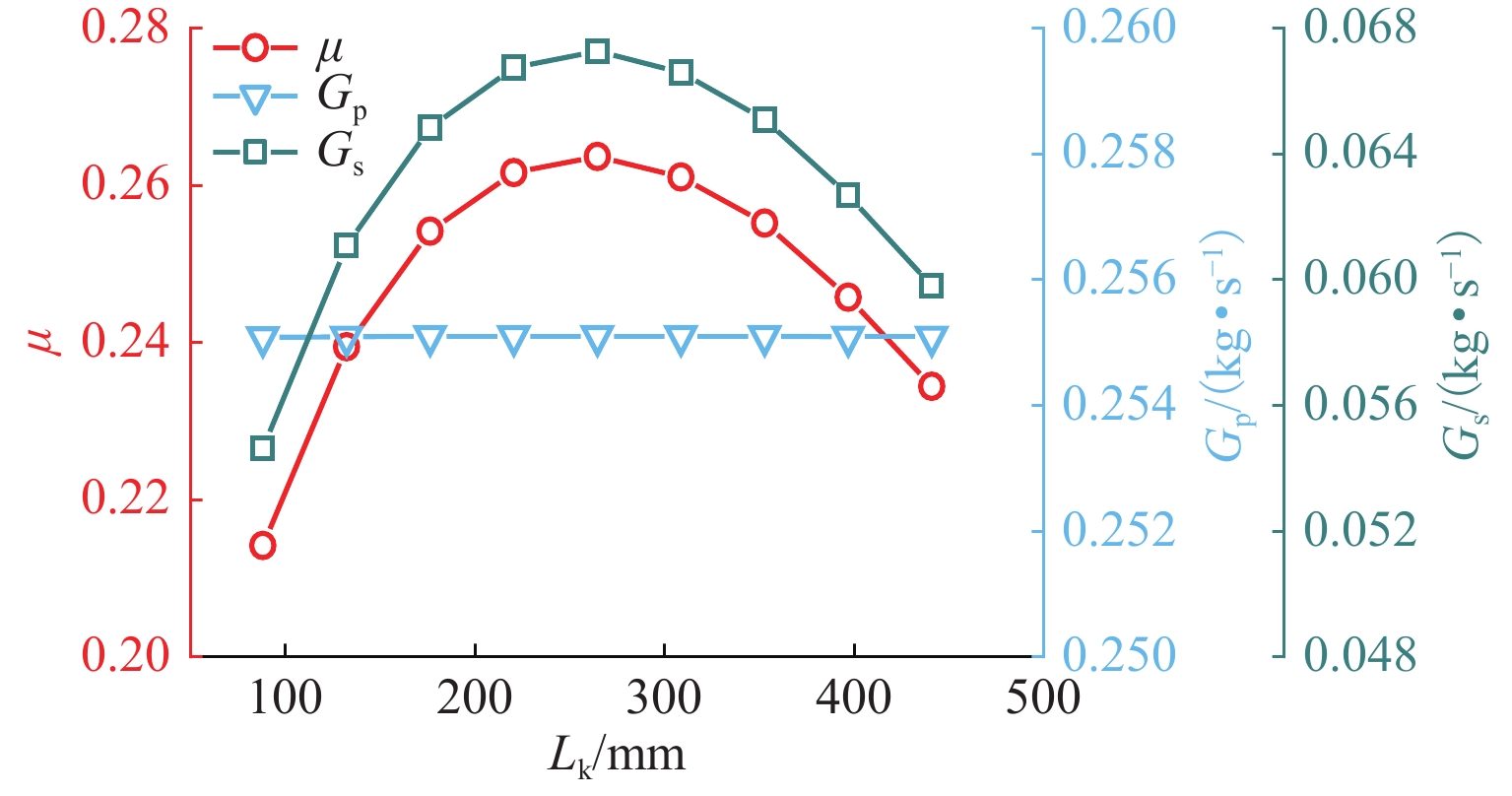
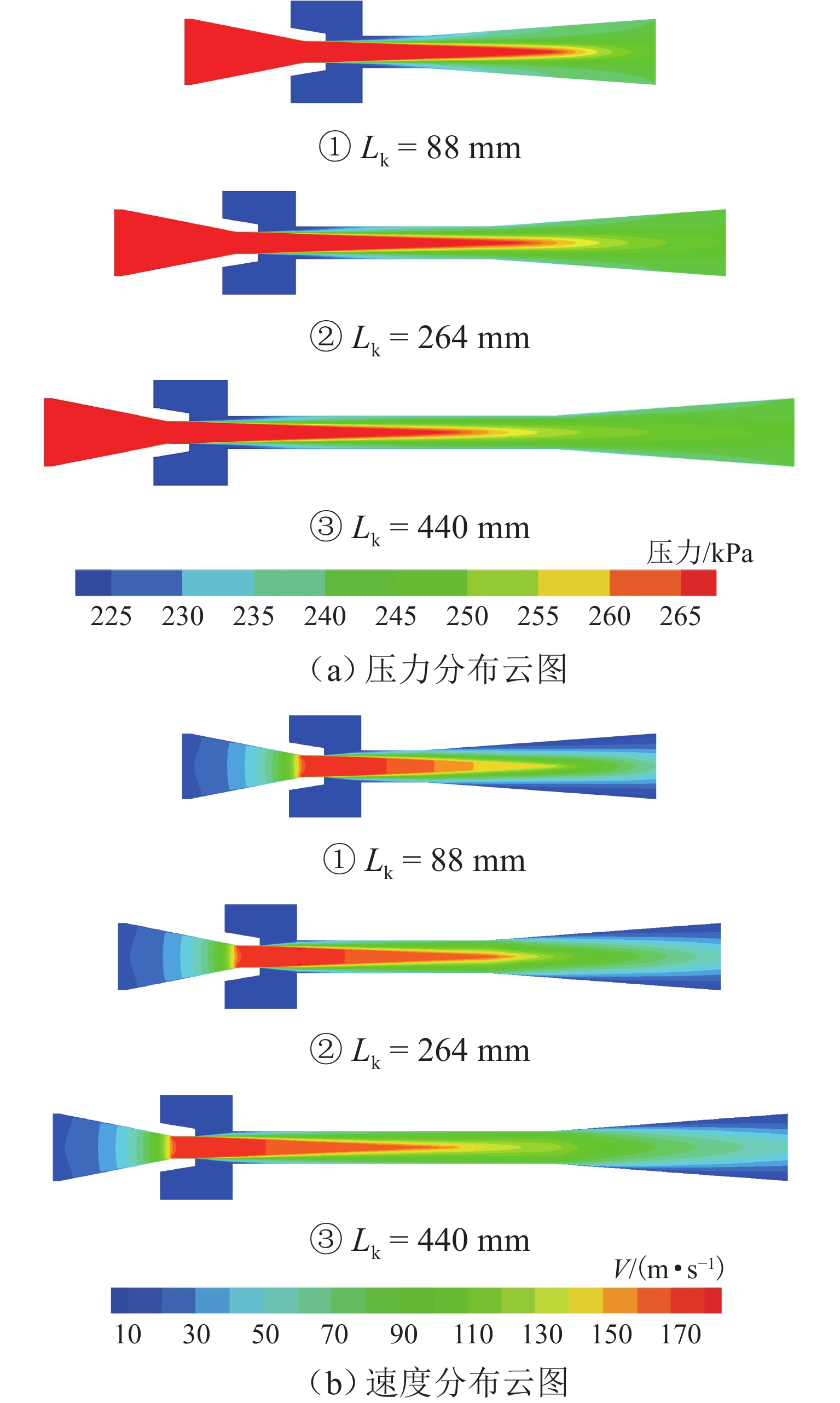
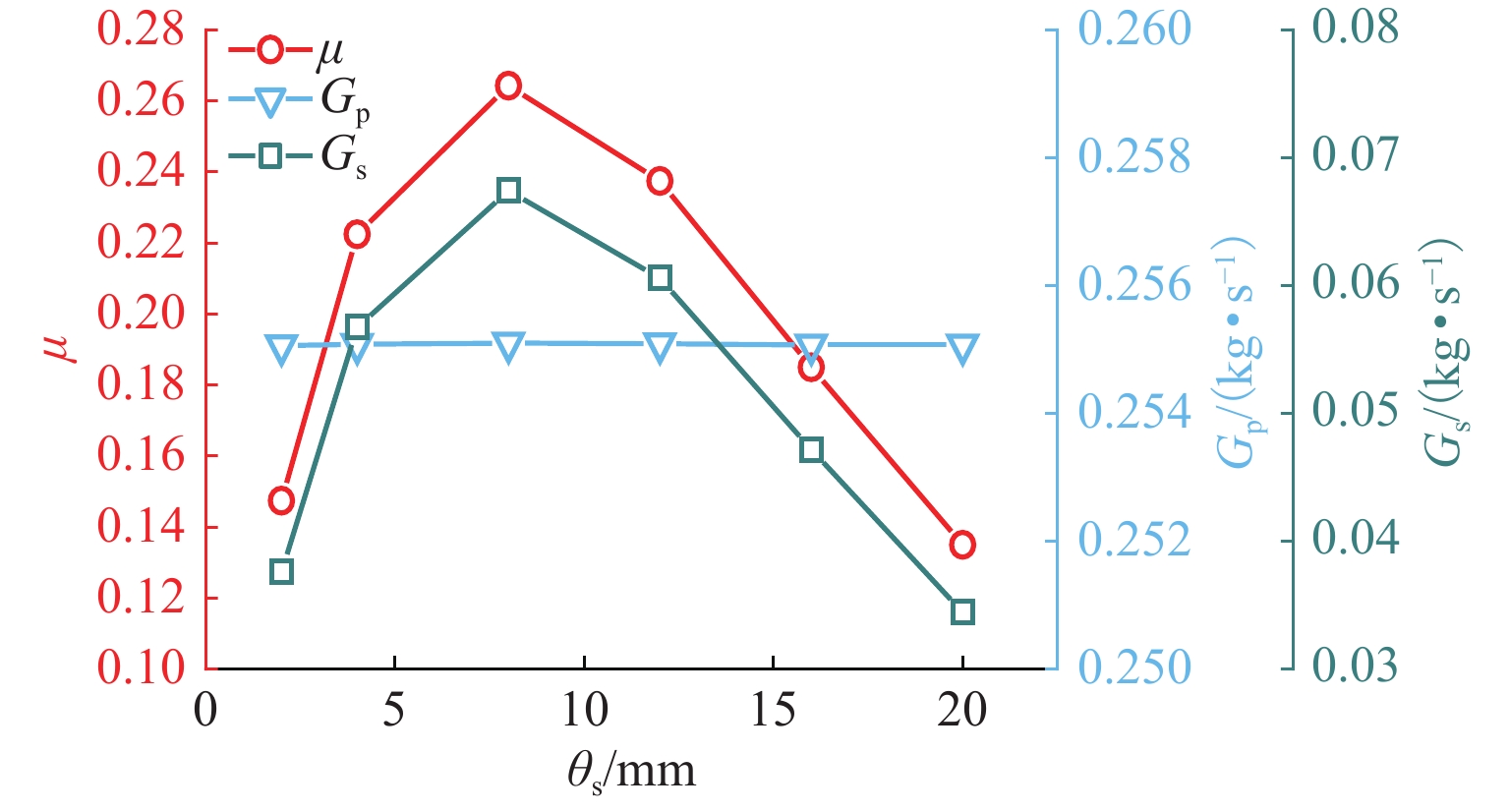
参数 基准值 变化范围 dk/ mm 44.1 40.1～48.1 Ls/ mm 315 265～365 Lk/ mm 175 85～265 θs/（°） 8 4～12 Lc/ mm 55 35～75
下载: 导出CSV
表 4 引射器计算参数及引射系数
Table 4. Calculation matrix and entrainment coefficient of ejector
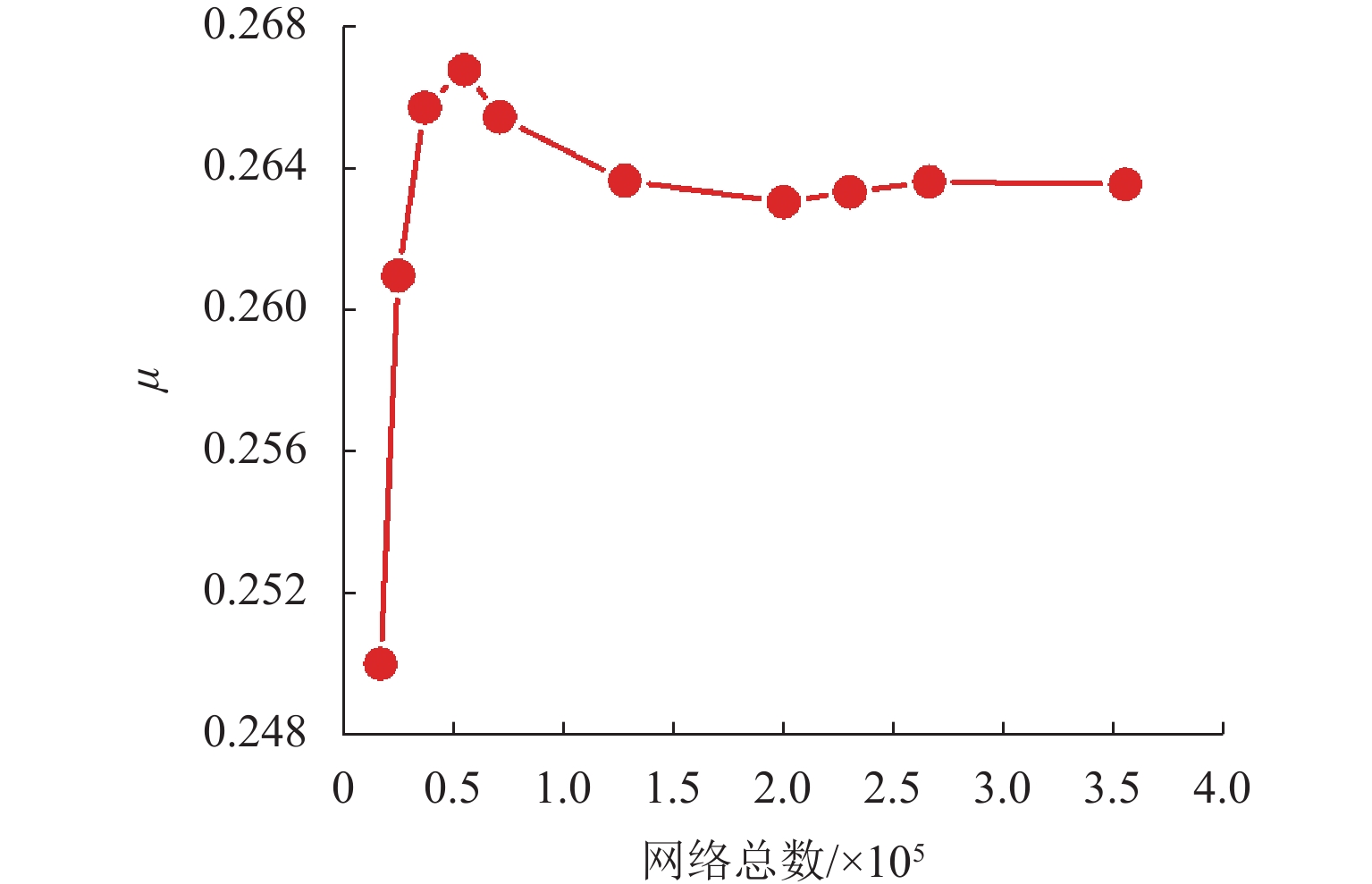
组别 dk/mm Ls/mm Lk/mm θs/（°） Lc/mm μ 1 40.1 265 85 4 35 0.189558 2 48.1 265 85 12 35 0.07164 3 44.1 315 85 4 35 0.209247 4 40.1 365 85 12 35 0.188561 5 48.1 365 85 8 35 0.146944 6 48.1 365 175 4 35 0.214265 7 40.1 265 265 12 35 0.186404 8 48.1 265 265 4 35 0.180986 9 40.1 365 265 4 35 0.231475 10 48.1 365 265 12 35 0.244793 11 40.1 265 85 12 55 0.172385 12 48.1 365 85 4 55 0.188328 13 44.1 265 175 4 55 0.206013 14 40.1 365 175 8 55 0.243177 15 40.1 315 265 4 55 0.199469 16 48.1 315 265 8 55 0.24531 17 40.1 265 85 8 75 0.190808 18 44.1 265 85 12 75 0.171817 19 48.1 265 85 4 75 0.161238 20 40.1 365 85 4 75 0.215495 21 48.1 365 85 12 75 0.15856 22 40.1 315 175 12 75 0.175558 23 48.1 315 175 8 75 0.235737 24 40.1 265 265 4 75 0.14897 25 48.1 265 265 12 75 0.230014 26 40.1 365 265 12 75 0.169519 27 44.1 365 265 8 75 0.261608 28 48.1 365 265 4 75 0.210122 29 48.1 365 265 12 75 0.244963 30 48.1 365 265 12 75 0.244963 31 48.1 365 265 12 75 0.244963
下载: 导出CSV
表 5 引射系数响应面模型的评价指标
Table 5. Evaluation index of response surface model of entrainment coefficient
组成项 P值 组成项 P值 dk 0.0554 dkLs 0.6644 Ls < 0.0001 dkLk < 0.0001 Lk < 0.0001 dkθs 0.1199 θs 0.0208 dkLc 0.0001 Lc 0.8256 LsLk 0.8086 $d_{\rm{k}}^2 $ 0.0008 Lsθs 0.2287 $L_{\rm{s}}^2 $ 0.3913 LsLc 0.0128 $L_{\rm{k}}^2 $ 0.0895 Lkθs 0.0002 $\theta_{\rm{s}}^2 $ 0.0033 LkLc 0.002 $L_{\rm{c}}^2 $ 0.0693 θsLc 0.2378
下载: 导出CSV
-
[1] FU W N, LIU Z L, LI Y X, et al. Numerical study for the influences of primary steam nozzle distance and mixing chamber throat diameter on steam ejector performance[J]. International Journal of Thermal Sciences, 2018, 132: 509-516. doi: 10.1016/j.ijthermalsci.2018.06.033 [2] SAMAKÉ O, GALANIS N, SORIN M. On the design and corresponding performance of steam jet ejectors[J]. Desalination, 2016, 381: 15-25. doi: 10.1016/j.desal.2015.11.027 [3] CHEN W X, CHONG D T, YAN J J, et al. The numerical analysis of the effect of geometrical factors on natural gas ejector performance[J]. Applied Thermal Engineering, 2013, 59(1/2): 21-29. [4] BANASIAK K, PALACZ M, HAFNER A, et al. A CFD-based investigation of the energy performance of two-phase R744 ejectors to recover the expansion work in refrigeration systems: an irreversibility analysis[J]. International Journal of Refrigeration, 2014, 40: 328-337. doi: 10.1016/j.ijrefrig.2013.12.002 [5] HAKKAKI-FARD A, AIDOUN Z, OUZZANE M. A computational methodology for ejector design and performance maximisation[J]. Energy Conversion and Management, 2015, 105: 1291-1302. doi: 10.1016/j.enconman.2015.08.070 [6] ZHU Y H, CAI W J, WEN C Y, et al. Numerical investigation of geometry parameters for design of high performance ejectors[J]. Applied Thermal Engineering, 2009, 29(5/6): 898-905. [7] CHONG D T, YAN J J, WU G S, et al. Structural optimization and experimental investigation of supersonic ejectors for boosting low pressure natural gas[J]. Applied Thermal Engineering, 2009, 29(14/15): 2799-2807. [8] NIKIFOROW K, KOSKI P, KARIMÄKI H, et al. Designing a hydrogen gas ejector for 5 kW stationary PEMFC system-CFD-modeling and experimental validation[J]. International Journal of Hydrogen Energy, 2016, 41(33): 14952-14970. doi: 10.1016/j.ijhydene.2016.06.122 [9] 王子瑞. 基于响应面法的贯流式水轮机多目标优化设计[D]. 西安: 西安理工大学, 2012. [10] OMIDVAR A, GHAZIKHANI M, MODARRES RAZAVI S M R. Entropy analysis of a solar-driven variable geometry ejector using computational fluid dynamics[J]. Energy Conversion and Management, 2016, 119: 435-443. doi: 10.1016/j.enconman.2016.03.090 [11] LI S Y, YAN J, LIU Z, et al. Optimization on crucial ejector geometries in a multi-evaporator refrigeration system for tropical region refrigerated trucks[J]. Energy, 2019, 189: 116347.1-116347.14. [12] BANASIAK K, HAFNER A, ANDRESEN T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump[J]. International Journal of Refrigeration, 2012, 35(6): 1617-1625. doi: 10.1016/j.ijrefrig.2012.04.012 [13] SOLMAZ H, ARDEBILI S M S, CALAM A, et al. Prediction of performance and exhaust emissions of a CI engine fueled with multi-wall carbon nanotube doped biodiesel-diesel blends using response surface method[J]. Energy, 2021, 227: 1205181.1-1205181.13. -
下载:
点击查看大图
计量
- 文章访问数: 72
- HTML全文浏览量: 54
- PDF下载量: 14
- 被引次数: 0