Rail Transit “Network-Source-Storage-Vehicle” Collaborative Energy Supply Technology System
-
摘要:
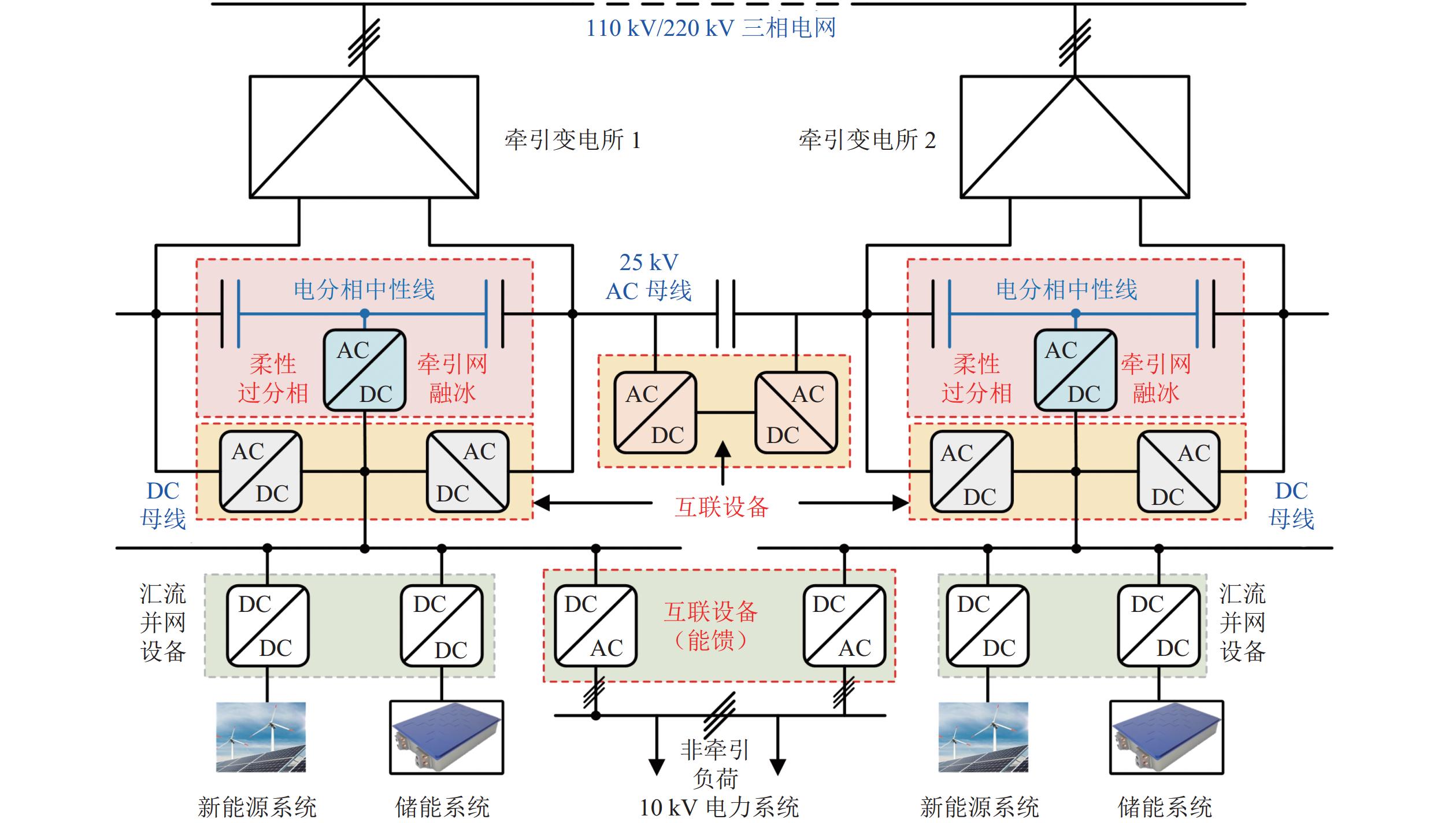
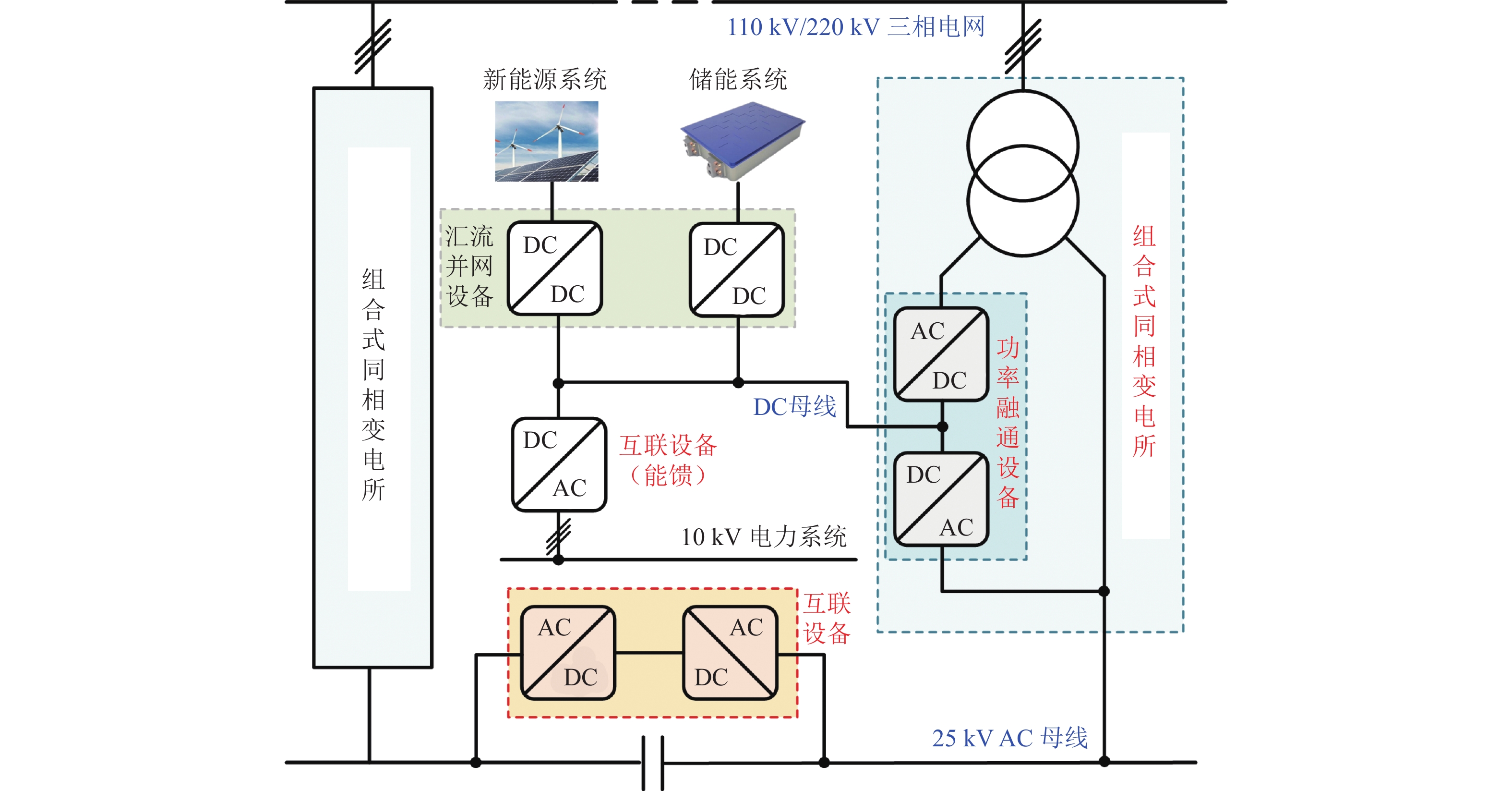
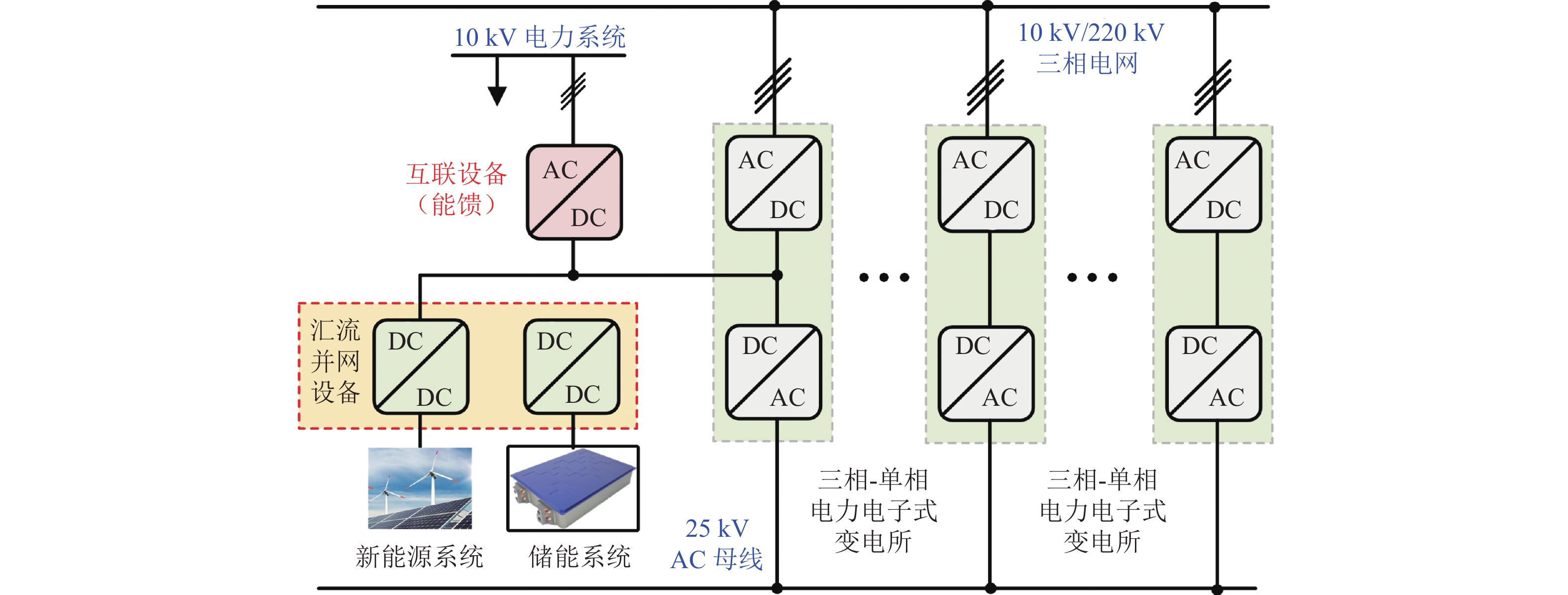
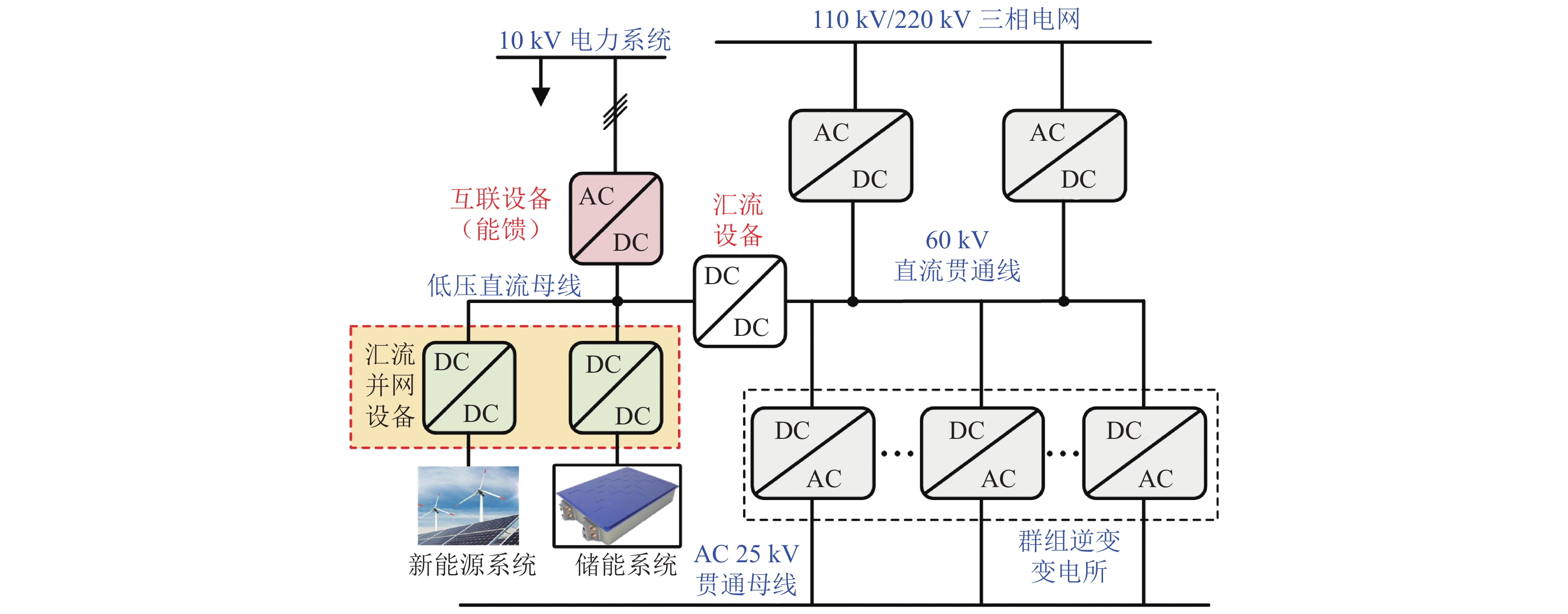
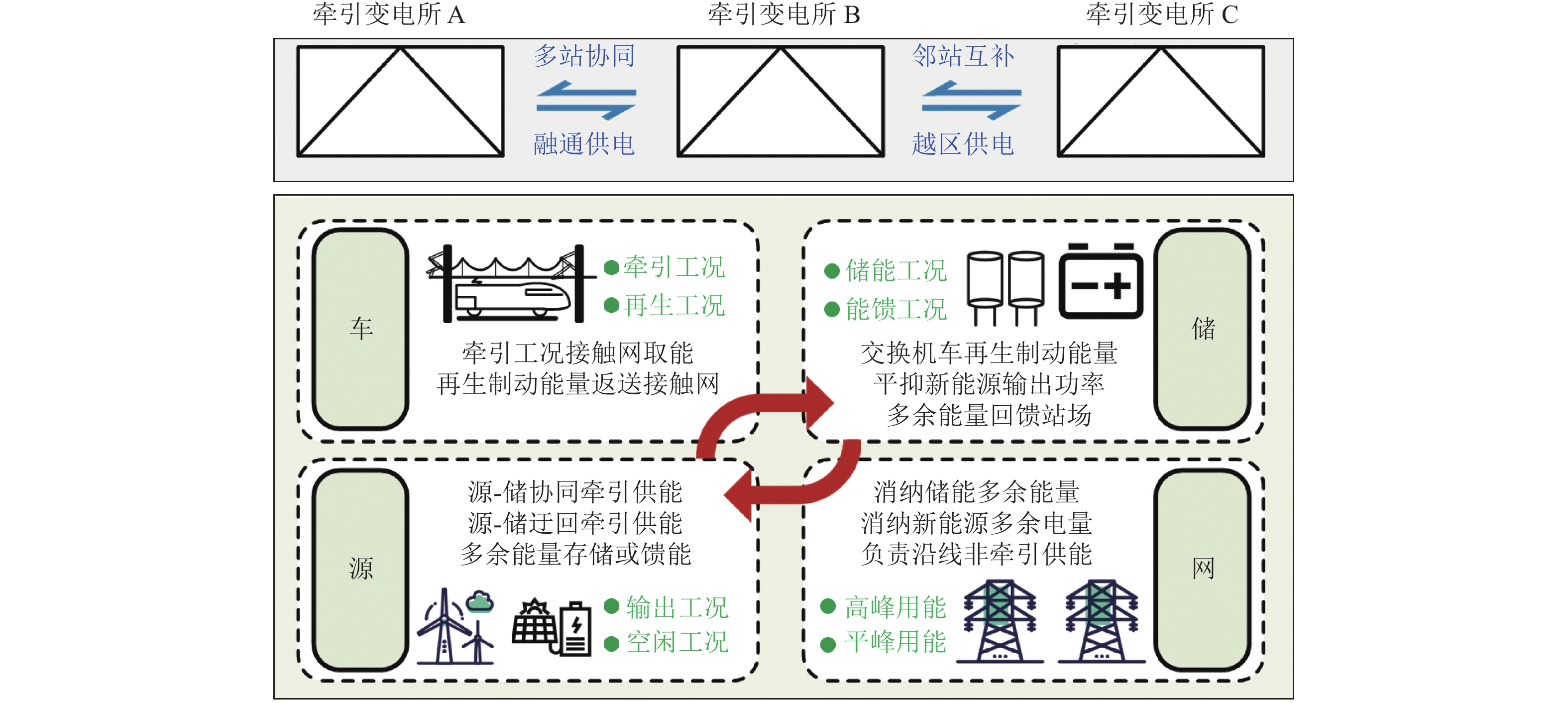
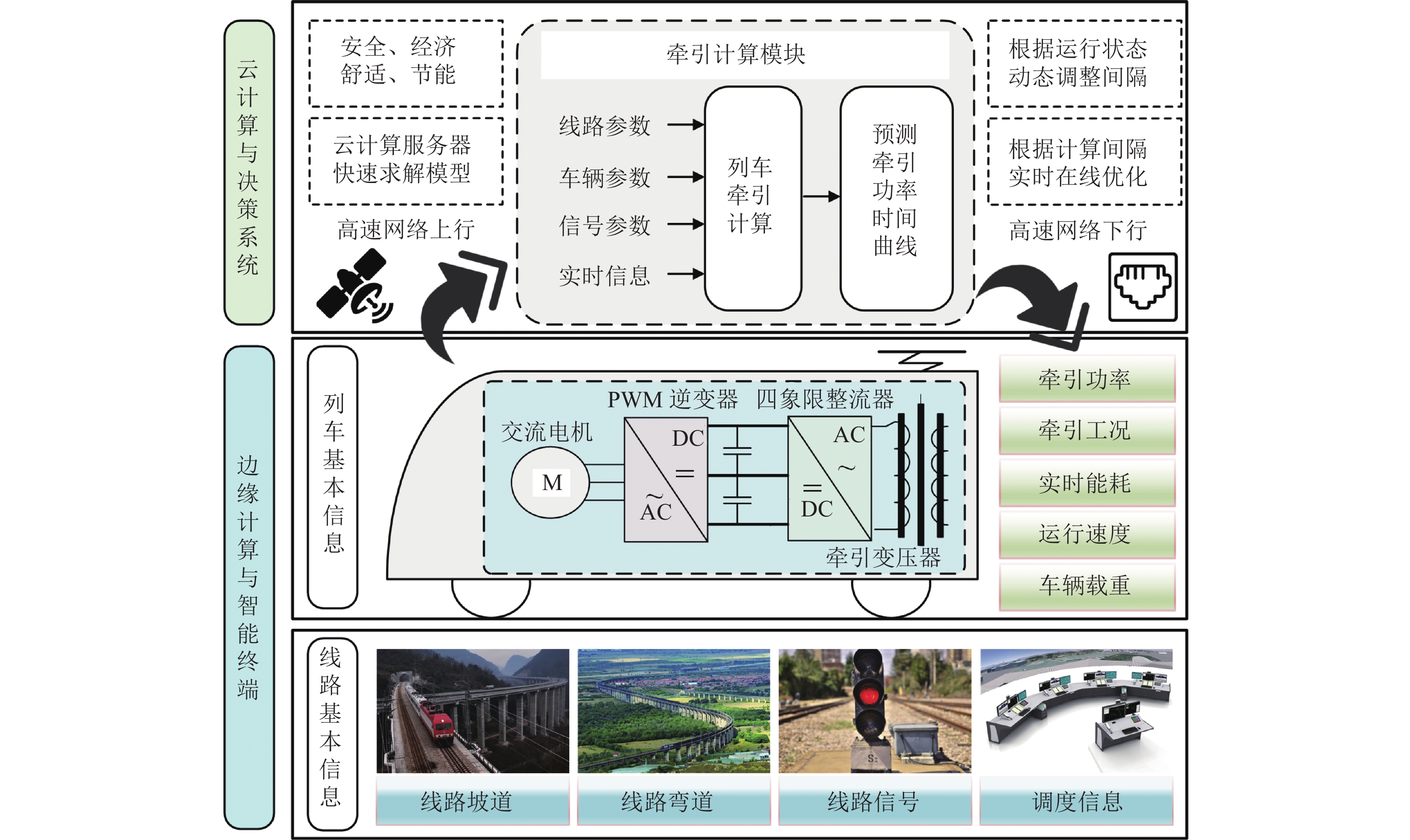
为降低轨道交通系统牵引能耗，轨道交通“网-源-储-车”协同供能技术通过可再生能源的就地消纳，构建新型协同供能技术体系，实现跨时空高效用能. 针对此新型供电系统结构，本文全面分析协同供能系统的物理架构、信息架构和社会架构的基本组成及类型特征；在此基础上，围绕资产能源化的基本概念，总结“荷-源”时空匹配评估方法与优化技术，并从系统角度阐述多源融合技术、保护重构、弹性评估等重要技术体系；重点分析“网-源-储-车”协同的高效能与高弹性的能源自洽技术，并基于人工智能和信息技术构建多层级能量管控系统，实现不同能量流的高效耦合，保障系统安全稳定经济运行. 本文系统性地总结了轨道交通“网-源-储-车”协同供能系统的架构特征、评估优化、安全运维及协同运行等关键技术，阐述协同供能系统的技术组成体系，为协同供能系统的工程实践提供相应参考.
Abstract:In order to minimize energy consumption in rail transit systems, the coordinated power supply technology of “network-source-storage-vehicle” integrates with renewable energy power generation systems along the line. This approach establishes a new coordinated power supply technology system that enables efficient energy utilization across time and space. This paper comprehensively analyzes the fundamental composition and characteristic types of physical, informational, and social architectures within the coordinated power supply system. Building upon this analysis, it introduces a temporal and spatial matching evaluation method for "load-source" based on the core concept of asset energization from a systemic comprehensive evaluation and operational perspective. Furthermore, it elaborates on important technological systems such as multi-source integration, protection reconstruction, and elastic evaluation. Emphasizing efficient energy-saving operations, it focuses on high-efficiency and high-resilience energy self-consistency technology through coordination among network, source, storage, and vehicle components. Additionally, leveraging artificial intelligence and information technology tools is proposed to construct multi-level energy management systems aimed at achieving effective coupling of diverse energy flows while ensuring safe, stable, and cost-effective operation of the system. The paper systematically summarizes key technologies related to the “network-source-storage-vehicle” coordinated energy supply system for rail transit including architectural characteristics; evaluation; optimization; safe operation; as well as coordinated operation of the system. It also outlines technical composition systems relevant to coordinated energy supply systems providing valuable references for engineering practices.
-
Key words:
- Rail transit /
- energy self-consistent /
- coordinated energy supply /
- elasticity assessment
-
图 1 轨道交通“网-源-储-车”协同供能系统结构
Figure 1. “Network-source-storage-vehicle”collaborative energy supply system structure of rail transit
图 2 基于功率融通设备的互联架构
Figure 2. Interconnection architecture based on power fusion equipment
图 3 基于组合式同相供电的互联架构
Figure 3. Interconnection architecture based on combined in-phase power supply
图 6 基于物联网的云边协同信息处理技术架构
Figure 6. Cloud-side collaborative information processing technology architecture based on the internet of things
图 7 牵引供电系统产消者运行模式
Figure 7. Operation mode of producer and consumer of traction power supply system
图 8 源-荷时空匹配度评估及优化方法
Figure 8. Source-load space-time matching degree evaluation method
图 9 “源-储”双层协同优化结构
Figure 9. “Source-storage” double-layer collaborative optimization structure
图 11 “网-源-车-储”协同能量管理系统
Figure 11. “network-source-vehicle-storage” collaborative energy management system
-
[1] 中国国家铁路集团有限公司. 中国国家铁路集团有限公司2023年统计公报[Z]. 北京: 中国国家铁路集团有限公司,2024. [2] 胡海涛,郑政,何正友,等. 交通能源互联网体系架构及关键技术[J]. 中国电机工程学报,2018,38(1): 12-24,339.HU Haitao, ZHENG Zheng, HE Zhengyou, et al. The framework and key technologies of traffic energy Internet[J]. Proceedings of the CSEE, 2018, 38(1): 12-24,339. [3] 何正友,向悦萍,廖凯,等. 能源-交通-信息三网融合发展的需求、形态及关键技术[J]. 电力系统自动化,2021,45(16): 73-86.HE Zhengyou, XIANG Yueping, LIAO Kai, et al. Demand, form and key technologies of integrated development of energy-transport-information networks[J]. Automation of Electric Power Systems, 2021, 45(16): 73-86. [4] 高仕斌,高凤华,刘一谷,等. 自感知能源互联网研究展望[J]. 电力系统自动化,2021,45(5): 1-17.GAO Shibin, GAO Fenghua, LIU Yigu, et al. Prospect of research on self-aware energy internet[J]. Automation of Electric Power Systems, 2021, 45(5): 1-17. [5] 孙秋野,滕菲,张化光. 能源互联网及其关键控制问题[J]. 自动化学报,2017,43(2): 176-194.SUN Qiuye, TENG Fei, ZHANG Huaguang. Energy internet and its key control issues[J]. Acta Automatica Sinica, 2017, 43(2): 176-194. [6] 韦晓广,高仕斌,臧天磊,等. 社会能源互联网:概念、架构和展望[J]. 中国电机工程学报,2018,38(17): 4969-4986,5295.WEI Xiaoguang, GAO Shibin, ZANG Tianlei, et al. Social energy internet: concept, architecture and outlook[J]. Proceedings of the CSEE, 2018, 38(17): 4969-4986,5295. [7] 韦晓广,高仕斌,李多,等. 基于连锁故障网络图和不同攻击方式的输电线路脆弱性分析[J]. 中国电机工程学报,2018,38(2): 465-474,677.WEI Xiaoguang, GAO Shibin, LI Duo, et al. Cascading fault graph for the analysis of transmission network vulnerability under different attacks[J]. Proceedings of the CSEE, 2018, 38(2): 465-474,677. [8] 胡海涛,葛银波,黄毅,等. 电气化铁路“源–网–车–储”一体化供电技术[J]. 中国电机工程学报,2022,42(12): 4374-4391.HU Haitao, GE Yinbo, HUANG Yi, et al. “source-network-train-storage” integrated power supply system for electric railways[J]. Proceedings of the CSEE, 2022, 42(12): 4374-4391. [9] 黄文龙,胡海涛,陈俊宇,等. 枢纽型牵引变电所再生制动能量利用系统能量管理及控制策略[J]. 电工技术学报,2021,36(3): 588-598.HUANG Wenlong, HU Haitao, CHEN Junyu, et al. Energy management and control strategy of regenerative braking energy utilization system in hub traction substation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 588-598. [10] 邓文丽,戴朝华,陈维荣. 光伏接入牵引供电系统的多元制约因素初探[J]. 太阳能学报,2020,41(8): 192-203.DENG Wenli, DAI Chaohua, CHEN Weirong. Preliminary research of multiple constriction for pv access traction power supply system[J]. Acta Energiae Solaris Sinica, 2020, 41(8): 192-203. [11] 邓文丽,戴朝华,陈维荣,等. 铁路功率调节器研究进展[J]. 中国电机工程学报,2020,40(14): 4640-4655,4742.DENG Wenli, DAI Chaohua, CHEN Weirong, et al. Research progress of railway power conditioner[J]. Proceedings of the CSEE, 2020, 40(14): 4640-4655,4742. [12] 黄小红,赵艺,李群湛,等. 电气化铁路同相储能供电技术[J]. 西南交通大学学报,2020,55(4): 856-864. doi: 10.3969/j.issn.0258-2724.20181083HUANG Xiaohong, ZHAO Yi, LI Qunzhan, et al. Co-phase traction power supply and energy storage technology for electrified railway[J]. Journal of Southwest Jiaotong University, 2020, 55(4): 856-864. doi: 10.3969/j.issn.0258-2724.20181083 [13] 何晓琼,韩鹏程,王怡,等. 基于级联-并联变换器的贯通式牵引变电所系统研究[J]. 铁道学报,2017,39(8): 52-61. doi: 10.3969/j.issn.1001-8360.2017.08.008HE Xiaoqiong, HAN Pengcheng, WANG Yi, et al. Study on advanced cophase traction power substation system based on cascade-parallel converter[J]. Journal of the China Railway Society, 2017, 39(8): 52-61. doi: 10.3969/j.issn.1001-8360.2017.08.008 [14] 魏文婧,胡海涛,王科,等. 基于铁路功率调节器的高速铁路牵引供电系统储能方案及控制策略[J]. 电工技术学报,2019,34(6): 1290-1299.WEI Wenjing, HU Haitao, WANG Ke, et al. Energy storage scheme and control strategies of high-speed railway based on railway power conditioner[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1290-1299. [15] 张秀峰,高仕斌,钱清泉,等. 基于阻抗匹配平衡变压器和AT供电方式的新型同相牵引供电系统[J]. 铁道学报,2006,28(4): 32-37. doi: 10.3321/j.issn:1001-8360.2006.04.007ZHANG Xiufeng, GAO Shibin, QIAN Qingquan, et al. A novel cophase traction power supply system based on impedance matching balance transformer and AT power supply mode[J]. Journal of the China Railway Society, 2006, 28(4): 32-37. doi: 10.3321/j.issn:1001-8360.2006.04.007 [16] 陈民武,蒋汶兵,王旭光,等. 高速铁路新型同相贯通供电方案及其仿真研究[J]. 铁道学报,2016,38(1): 28-34. doi: 10.3969/j.issn.1001-8360.2016.01.005CHEN Minwu, JIANG Wenbing, WANG Xuguang, et al. Study on scheme and simulation of new co-phase continuous traction power supply system for high-speed railway[J]. Journal of the China Railway Society, 2016, 38(1): 28-34. doi: 10.3969/j.issn.1001-8360.2016.01.005 [17] JIANG Y, LIU J Q, TIAN W, et al. Energy Harvesting for the Electrification of Railway Stations: getting a charge from the regenerative braking of trains[J]. IEEE Electrification Magazine, 2014, 2(3): 39-48. [18] 张丽艳,贾瑛,韩笃硕,等. 电气化铁路同相储能供电系统能量管理及容量配置策略[J]. 西南交通大学学报,2023,58(1): 22-29. doi: 10.3969/j.issn.0258-2724.20210247ZHANG Liyan, JIA Ying, HAN Dushuo, et al. Energy management and capacity allocation scheme for co-phase traction power supply and energy storage system in electrified railways[J]. Journal of Southwest Jiaotong University, 2023, 58(1): 22-29. doi: 10.3969/j.issn.0258-2724.20210247 [19] 王辉,李群湛,解绍锋,等. 基于vv-SVG的电气化铁路同相供电综合补偿方案及控制策略[J]. 铁道学报,2021,43(9): 46-55. doi: 10.3969/j.issn.1001-8360.2021.09.007WANG Hui, LI Qunzhan, XIE Shaofeng, et al. Comprehensive compensation scheme and control strategy of cophase power supply for electrified railway based on vv-SVG[J]. Journal of the China Railway Society, 2021, 43(9): 46-55. doi: 10.3969/j.issn.1001-8360.2021.09.007 [20] DAI N Y, WONG M C, LAO K W, et al. Modelling and control of a railway power conditioner in co-phase traction power system under partial compensation[J]. IET Power Electronics, 2014, 7(5): 1044-1054. [21] SHU Z L, XIE S F, LU K, et al. Digital detection, control, and distribution system for co-phase traction power supply application[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 1831-1839. [22] 李群湛,王辉,黄文勋,等. 电气化铁路牵引变电所群贯通供电系统及其关键技术[J]. 电工技术学报,2021,36(5): 1064-1074.LI Qunzhan, WANG Hui, HUANG Wenxun, et al. Interconnected power supply system of traction substation group and its key technologies for the electrified railway[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1064-1074. [23] 夏焰坤,李群湛,解绍锋,等. 电气化铁道贯通同相供电变电所控制策略研究[J]. 铁道学报,2014,36(8): 25-31. doi: 10.3969/j.issn.1001-8360.2014.08.005XIA Yankun, LI Qunzhan, XIE Shaofeng, et al. Study on control strategy of continuous co-phase power supply substions of electrical railways[J]. Journal of the China Railway Society, 2014, 36(8): 25-31. doi: 10.3969/j.issn.1001-8360.2014.08.005 [24] 王鑫,涂春鸣,郭祺,等. 电气化铁路贯通型供电系统综述[J]. 机车电传动,2022(3): 17-28.WANG Xin, TU Chunming, GUO Qi, et al. Review of through-type power supply system for electrified railways[J]. Electric Drive for Locomotives, 2022(3): 17-28. [25] GAZAFRUDI S M M, LANGERUDY A T, FUCHS E F, et al. Power quality issues in railway electrification: a comprehensive perspective[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3081-3090. [26] 孟令辉,周犹松,闫晗,等. 应用于贯通供电系统的两相–单相变换器直流电压纹波特性与功率均衡控制[J]. 中国电机工程学报,2022,42(17): 6449-6460.MENG Linghui, ZHOU Yousong, YAN Han, et al. DC-link voltage ripple analysis and power balanced control for two-phase to single-phase converter in advanced traction power supply system[J]. Proceedings of the CSEE, 2022, 42(17): 6449-6460. [27] 周志成. 基于树形双边供电的重载铁路贯通同相供电方案[J]. 铁道科学与工程学报,2020,17(3): 722-731.ZHOU Zhicheng. Cophase connected power supply scheme of heavy haul railway based on tree bilateral power supply[J]. Journal of Railway Science and Engineering, 2020, 17(3): 722-731. [28] 马建军,李平,马小宁,等. 铁路一体化信息集成平台总体架构及关键技术研究[J]. 中国铁道科学,2020,41(5): 153-161.MA Jianjun, LI Ping, MA Xiaoning, et al. Research on the overall framework and key technologies of railway integrated information platform[J]. China Railway Science, 2020, 41(5): 153-161. [29] 胡金磊,朱泽锋,林孝斌,等. 变电站无人机机巡边缘计算框架设计及资源调度方法[J]. 高电压技术,2021,47(2): 425-433.HU Jinlei, ZHU Zefeng, LIN Xiaobin, et al. Framework design and resource scheduling method for edge computing in substation UAV inspection[J]. High Voltage Engineering, 2021, 47(2): 425-433. [30] 白昱阳,黄彦浩,陈思远,等. 云边智能:电力系统运行控制的边缘计算方法及其应用现状与展望[J]. 自动化学报,2020,46(3): 397-410.BAI Yuyang, HUANG Yanhao, CHEN Siyuan, et al. Cloud-edge intelligence: status quo and future prospective of edge computing approaches and applications in power system operation and control[J]. Acta Automatica Sinica, 2020, 46(3): 397-410. [31] 邬明亮,郭爱,邓文丽,等. 铁路牵引用背靠背光伏发电系统及其消纳能力研究[J]. 太阳能学报,2019,40(12): 3444-3450.WU Mingliang, GUO Ai, DENG Wenli, et al. Research on back-to-back pv generation system for railway traction and its accommodation ability[J]. Acta Energiae Solaris Sinica, 2019, 40(12): 3444-3450. [32] 张磊,朱凌志,陈宁,等. 新能源发电模型统一化研究[J]. 电力系统自动化,2015,39(24): 129-138. doi: 10.7500/AEPS20150629010ZHANG Lei, ZHU Lingzhi, CHEN Ning, et al. Review on generic model for renewable energy generation[J]. Automation of Electric Power Systems, 2015, 39(24): 129-138. doi: 10.7500/AEPS20150629010 [33] 邓文丽,戴朝华,陈维荣. 轨道交通能源互联网背景下光伏在交/直流牵引供电系统中的应用及关键问题分析[J]. 中国电机工程学报,2019,39(19): 5692-5702,5897.DENG Wenli, DAI Chaohua, CHEN Weirong. Application of PV generation in AC/DC traction power supply system and the key problem analysis under the background of rail transit energy Internet[J]. Proceedings of the CSEE, 2019, 39(19): 5692-5702,5897. [34] 诸斐琴,杨中平,林飞,等. 城轨交通牵引供电系统参数与储能系统容量配置综合优化[J]. 电工技术学报,2019,34(3): 579-588.ZHU Feiqin, YANG Zhongping, LIN Fei, et al. Synthetic optimization of traction power parameters and energy storage systems in urban rail transit[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 579-588. [35] 邬明亮. 分时电价政策下电气化铁路储能的经济性[J]. 电力自动化设备,2020,40(6): 1-3,191-197.WU Mingliang. Economy of energy storage in electrified railway under time-of-use price policy[J]. Electric Power Automation Equipment, 2020, 40(6): 1-3,191-197. [36] 陈维荣,王璇,李奇,等. 光伏电站接入轨道交通牵引供电系统发展现状综述[J]. 电网技术,2019,43(10): 3663-3670.CHEN Weirong, WANG Xuan, LI Qi, et al. Review on the development status of PV power station accessing to traction power supply system for rail transit[J]. Power System Technology, 2019, 43(10): 3663-3670. [37] CUI G P, LUO L F, LIANG C G, et al. Supercapacitor integrated railway static power conditioner for regenerative braking energy recycling and power quality improvement of high-speed railway system[J]. IEEE Transactions on Transportation Electrification, 2019, 5(3): 702-714. [38] 魏波,胡海涛,王科,等. 基于实测数据和行车运行图的高铁牵引变电站负荷预测方法[J]. 电工技术学报,2020,35(1): 179-188.WEI Bo, HU Haitao, WANG Ke, et al. Research on traction load forecasting method for high-speed railway traction substation based on measured data and train timetable[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 179-188. [39] WU C X, LU S F, XUE F, et al. A two-step method for energy-efficient train operation, timetabling, and onboard energy storage device management[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 1822-1833. [40] 罗嘉明,韦晓广,高仕斌,等. 高速铁路储能系统容量配置与能量管理技术综述与展望[J]. 中国电机工程学报,2022,42(19): 7028-7051.LUO Jiaming, WEI Xiaoguang, GAO Shibin, et al. Summary and outlook of capacity configuration and energy management technology of high-speed railway energy storage system[J]. Proceedings of the CSEE, 2022, 42(19): 7028-7051. [41] DÍAZ-GONZÁLEZ F, SUMPER A, GOMIS-BELLMUNT O, et al. A review of energy storage technologies for wind power applications[J]. Renewable and Sustainable Energy Reviews, 2012, 16(4): 2154-2171. [42] 袁佳歆,曲锴,郑先锋,等. 高速铁路混合储能系统容量优化研究[J]. 电工技术学报,2021,36(19): 4161-4169,4182.YUAN Jiaxin, QU Kai, ZHENG Xianfeng, et al. Optimizing research on hybrid energy storage system of high speed railway[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4161-4169,4182. [43] 薛禹胜,雷兴,薛峰,等. 关于电力系统广域保护的评述[J]. 高电压技术,2012,38(3): 513-520.XUE Yusheng, LEI Xing, XUE Feng, et al. Review on wide area protection of electric power systems[J]. High Voltage Engineering, 2012, 38(3): 513-520. [44] 井友刚. 电气化铁路广域保护系统自愈重构功能研究与应用[J]. 电气化铁道,2020,31(3): 12-15,32.JING Yougang. Study on and application of self-healing reconfiguration function of wide area protection system for electrified railway[J]. Electric Railway, 2020, 31(3): 12-15,32. [45] 刘育权,华煌圣,李力,等. 多层次的广域保护控制体系架构研究与实践[J]. 电力系统保护与控制,2015,43(5): 112-122. doi: 10.7667/j.issn.1674-3415.2015.05.018LIU Yuquan, HUA Huangsheng, LI Li, et al. Research and application of multi-level wide-area protection system[J]. Power System Protection and Control, 2015, 43(5): 112-122. doi: 10.7667/j.issn.1674-3415.2015.05.018 [46] 王潘潘. 京张高铁智能牵引供电系统自愈重构方案研究[J]. 电气化铁道,2020,31(增2): 126-131.WANG Panpan. Research on self-healing reconstruction scheme of intelligent traction power supply system for Beijing—Zhangjiakou high-speed railway[J]. Electric Railway, 2020, 31(S2): 126-131. [47] 尹项根,李振兴,刘颖彤,等. 广域继电保护及其故障元件判别问题的探讨[J]. 电力系统保护与控制,2012,40(5): 1-9. doi: 10.3969/j.issn.1674-3415.2012.05.001YIN Xianggen, LI Zhenxing, LIU Yingtong, et al. Study on wide area relaying protection and fault element identification[J]. Power System Protection and Control, 2012, 40(5): 1-9. doi: 10.3969/j.issn.1674-3415.2012.05.001 [48] 李振坤,赵向阳,朱兰,等. 智能配电网故障后自愈能力评估[J]. 电网技术,2018,42(3): 789-796.LI Zhenkun, ZHAO Xiangyang, ZHU Lan, et al. Evaluation of self-healing ability for smart distribution network after failure[J]. Power System Technology, 2018, 42(3): 789-796. [49] 张小瑜,吴俊勇. 高速铁路牵引供电系统的供电可靠性评估方法[J]. 电网技术,2007,31(11): 27-32. doi: 10.3321/j.issn:1000-3673.2007.11.006ZHANG Xiaoyu, WU Junyong. Reliability estimation method of traction power supply system for high-speed railway[J]. Power System Technology, 2007, 31(11): 27-32. doi: 10.3321/j.issn:1000-3673.2007.11.006 [50] 周桂法,邵志和,曾嵘. 轨道交通RAMS工作的理解与实施[J]. 机车电传动,2014(2): 1-5,15.ZHOU Guifa, SHAO Zhihe, ZENG Rong. Comprehension and implementation of RAMS for rail transit[J]. Electric Drive for Locomotives, 2014(2): 1-5,15. [51] YANG X W, HU H T, GE Y B, et al. An improved droop control strategy for VSC-based MVDC traction power supply system[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5173-5186. [52] GOMEZ-EXPOSITO A, MAURICIO J M, MAZA-ORTEGA J M. VSC-based MVDC railway electrification system[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 422-431. [53] 程红,高巧梅,朱锦标,等. 基于双重移相控制的双向全桥DC-DC变换器动态建模与最小回流功率控制[J]. 电工技术学报,2014,29(3): 245-253. doi: 10.3969/j.issn.1000-6753.2014.03.031CHENG Hong, GAO Qiaomei, ZHU Jinbiao, et al. Dynamic modeling and minimum backflow power controlling of the bi-directional full-bridge DC-DC converters based on dual-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 245-253. doi: 10.3969/j.issn.1000-6753.2014.03.031 [54] 何晓琼,彭俊,韩鹏程,等. 电气化铁路综合补偿器控制策略研究[J]. 铁道学报,2020,42(9): 74-84. doi: 10.3969/j.issn.1001-8360.2020.09.010HE Xiaoqiong, PENG Jun, HAN Pengcheng, et al. Study on control strategy of comprehensive compensator for electrified railway[J]. Journal of the China Railway Society, 2020, 42(9): 74-84. doi: 10.3969/j.issn.1001-8360.2020.09.010 [55] 鲍冠南,陆超,袁志昌,等. 基于动态规划的电池储能系统削峰填谷实时优化[J]. 电力系统自动化,2012,36(12): 11-16.BAO Guannan, LU Chao, YUAN Zhichang, et al. Load shift real-time optimization strategy of battery energy storage system based on dynamic programming[J]. Automation of Electric Power Systems, 2012, 36(12): 11-16. [56] 邓文丽,戴朝华,张涵博,等. 复杂电气化铁路牵引用光伏发电系统综合优化控制方法研究[J]. 中国电机工程学报,2020,40(18): 5849-5865.DENG Wenli, DAI Chaohua, ZHANG Hanbo, et al. Research on comprehensive optimization control method for traction photovoltaic generation system of complex electrified railway[J]. Proceedings of the CSEE, 2020, 40(18): 5849-5865. [57] 申建建,曹瑞,苏承国,等. 水火风光多源发电调度系统大数据平台架构及关键技术[J]. 中国电机工程学报,2019,39(1): 43-55,319.SHEN Jianjian, CAO Rui, SU Chengguo, et al. Big data platform architecture and key techniques of power generation scheduling for hydro-thermal-wind-solar hybrid system[J]. Proceedings of the CSEE, 2019, 39(1): 43-55,319. [58] 胡威,张新燕,郭永辉,等. 基于游程检测法重构CEEMD的短时风功率预测[J]. 太阳能学报,2020,41(11): 317-325.HU Wei, ZHANG Xinyan, GUO Yonghui, et al. Short-time wind power prediction of ceemd reconstructed based on run-length detection method[J]. Acta Energiae Solaris Sinica, 2020, 41(11): 317-325. [59] HUANG J, THATCHER M. Assessing the value of simulated regional weather variability in solar forecasting using numerical weather prediction[J]. Solar Energy, 2017, 144: 529-539. [60] 肖雅君,吴汶麒. 用于轨道交通列车自动控制系统的通信技术[J]. 城市轨道交通研究,2002,5(2): 59-64,72. doi: 10.3969/j.issn.1007-869X.2002.02.013XIAO Yajun, WU Wenqi. Communication technology applied in ATC system of UMT[J]. Urban Mass Transit, 2002, 5(2): 59-64,72. doi: 10.3969/j.issn.1007-869X.2002.02.013 [61] 王凯,刘留,于蒙,等. 超高速列车车地无线通信系统性能分析[J]. 北京交通大学学报,2021,45(4): 117-126. doi: 10.11860/j.issn.1673-0291.20210074WANG Kai, LIU Liu, YU Meng, et al. System performance analysis on train-ground wireless communication for the ultra high-speed train[J]. Journal of Beijing Jiaotong University, 2021, 45(4): 117-126. doi: 10.11860/j.issn.1673-0291.20210074 [62] 王磊,何正友. 高速列车通信网络技术特点及其应用[J]. 城市轨道交通研究,2008,11(2): 57-61,64. doi: 10.3969/j.issn.1007-869X.2008.02.016WANG Lei, HE Zhengyou. Technological characteristics of high-speed train communication network and its application[J]. Urban Mass Transit, 2008, 11(2): 57-61,64. doi: 10.3969/j.issn.1007-869X.2008.02.016 [63] 上官伟,王韦舒,张路,等. 北斗导航RAIM技术在列车定位的应用研究[J]. 铁道学报,2018,40(2): 73-81. doi: 10.3969/j.issn.1001-8360.2018.02.011SHANGGUAN Wei, WANG Weishu, ZHANG Lu, et al. Application of BDS-based RAIM technology in train positioning[J]. Journal of the China Railway Society, 2018, 40(2): 73-81. doi: 10.3969/j.issn.1001-8360.2018.02.011 [64] 肖白,邢世亨,王茂春,等. 基于改进KDE法和GA-SVM的多风电场聚合后输出功率长期波动特性预测方法[J]. 电力自动化设备,2022,42(2): 77-84.XIAO Bai, XING Shiheng, WANG Maochun, et al. Prediction method of output power long-term fluctuation characteristic for multiple wind farms after aggregation based on improved KDE method and GA-SVM[J]. Electric Power Automation Equipment, 2022, 42(2): 77-84. [65] 易善军,王汉军,向勇,等. 基于集成多尺度LSTM的短时风功率预测[J]. 重庆大学学报,2021,44(7): 75-81. doi: 10.11835/j.issn.1000-582X.2021.07.008YI Shanjun, WANG Hanjun, XIANG Yong, et al. Short-term wind power forecasting based on integrated multi-scale LSTM[J]. Journal of Chongqing University, 2021, 44(7): 75-81. doi: 10.11835/j.issn.1000-582X.2021.07.008 [66] BREKKEN T K A, YOKOCHI A, VON JOUANNE A, et al. Optimal energy storage sizing and control for wind power applications[J]. IEEE Transactions on Sustainable Energy, 2010, 2(1): 69-77. [67] 琚垚,祁林,刘帅. 基于改进乌鸦算法和ESN神经网络的短期风电功率预测[J]. 电力系统保护与控制,2019,47(4): 58-64. doi: 10.7667/PSPC180251JU Yao, QI Lin, LIU Shuai. Short-term wind power forecasting based on improved crow search algorithm and ESN neural network[J]. Power System Protection and Control, 2019, 47(4): 58-64. doi: 10.7667/PSPC180251 [68] 徐诗鸿,张宏志,林湘宁,等. 近海海岛多态能源供需自洽系统日前优化调度策略[J]. 中国电机工程学报,2019,39(增1): 15-29.XU Shihong, ZHANG Hongzhi, LIN Xiangning, et al. Optimal dispatching strategy of self-consistent supply and demand system of polymorphic energy in offshore islands recently[J]. Proceedings of the CSEE, 2019, 39(S1): 15-29. [69] 张丽艳,李群湛,朱毅. 新建电气化铁路牵引负荷预测[J]. 西南交通大学学报,2016,51(4): 743-749. doi: 10.3969/j.issn.0258-2724.2016.04.020ZHANG Liyan, LI Qunzhan, ZHU Yi. Prediction of traction load for new electrified railway[J]. Journal of Southwest Jiaotong University, 2016, 51(4): 743-749. doi: 10.3969/j.issn.0258-2724.2016.04.020 [70] 杨丘帆,黄煜彬,石梦璇,等. 基于一致性算法的直流微电网多组光储单元分布式控制方法[J]. 中国电机工程学报,2020,40(12): 3919-3928.YANG Qiufan, HUANG Yubin, SHI Mengxuan, et al. Consensus based distributed control for multiple PV-battery storage units in DC microgrid[J]. Proceedings of the CSEE, 2020, 40(12): 3919-3928. [71] 金波,孙鹏飞,王青元,等. 基于混合整数规划的高速列车多区间节能优化研究[J]. 铁道学报,2020,42(2): 11-17.JIN Bo, SUN Pengfei, WANG Qingyuan, et al. Energy-saving optimization of multi-interstation high-speed train with mixed integer linear programming[J]. Journal of the China Railway Society, 2020, 42(2): 11-17. [72] 荀径,杨欣,宁滨,等. 列车节能操纵优化求解方法综述[J]. 铁道学报,2014,36(4): 14-20. doi: 10.3969/j.issn.1001-8360.2014.04.003XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14-20. doi: 10.3969/j.issn.1001-8360.2014.04.003 [73] 冷勇林,陈德旺,阴佳腾. 基于专家系统及在线调整的列车智能驾驶算法[J]. 铁道学报,2014,36(2): 62-68. doi: 10.3969/j.issn.1001-8360.2014.02.010LENG Yonglin, CHEN Dewang, YIN Jiateng. An intelligent train operation (ITO) algorithm based on expert system and online adjustment[J]. Journal of the China Railway Society, 2014, 36(2): 62-68. doi: 10.3969/j.issn.1001-8360.2014.02.010 [74] LU S F, WESTON P, HILLMANSEN S, et al. Increasing the regenerative braking energy for railway vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2506-2515. [75] 刘宏杰. 结合能量存储的城轨列车调度控制一体化节能优化方法研究[D]. 北京: 北京交通大学,2019. [76] 郑亚晶,李耀辉,李雨恒,等. 再生制动条件下地铁列车运行图的节能优化[J]. 华南理工大学学报(自然科学版),2021,49(7): 1-7. doi: 10.12141/j.issn.1000-565X.200552ZHENG Yajing, LI Yaohui, LI Yuheng, et al. Energy saving optimization of metro train working diagram under regenerative braking[J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(7): 1-7. doi: 10.12141/j.issn.1000-565X.200552 [77] 沈迪,王青元,夏菲,等. 高速列车应急自走行辅助驾驶研究[J]. 机车电传动,2021(1): 91-97.SHEN Di, WANG Qingyuan, XIA Fei, et al. Research on urgent operation assistant driving for high-speed train[J]. Electric Drive for Locomotives, 2021(1): 91-97. [78] 王青元,冯晓云,朱金陵,等. 考虑再生制动能量利用的高速列车节能最优控制仿真研究[J]. 中国铁道科学,2015,36(1): 96-103. doi: 10.3969/j.issn.1001-4632.2015.01.14WANG Qingyuan, FENG Xiaoyun, ZHU Jinling, et al. Simulation study on optimal energy-efficient control of high speed train considering regenerative brake energy[J]. China Railway Science, 2015, 36(1): 96-103. doi: 10.3969/j.issn.1001-4632.2015.01.14 -
下载:
点击查看大图
图(13)
计量
- 文章访问数: 277
- HTML全文浏览量: 171
- PDF下载量: 86
- 被引次数: 0