Maintenance Mechanism of Ballast Tamping and Stone-Blowing Using Discrete Element Method
-
摘要:
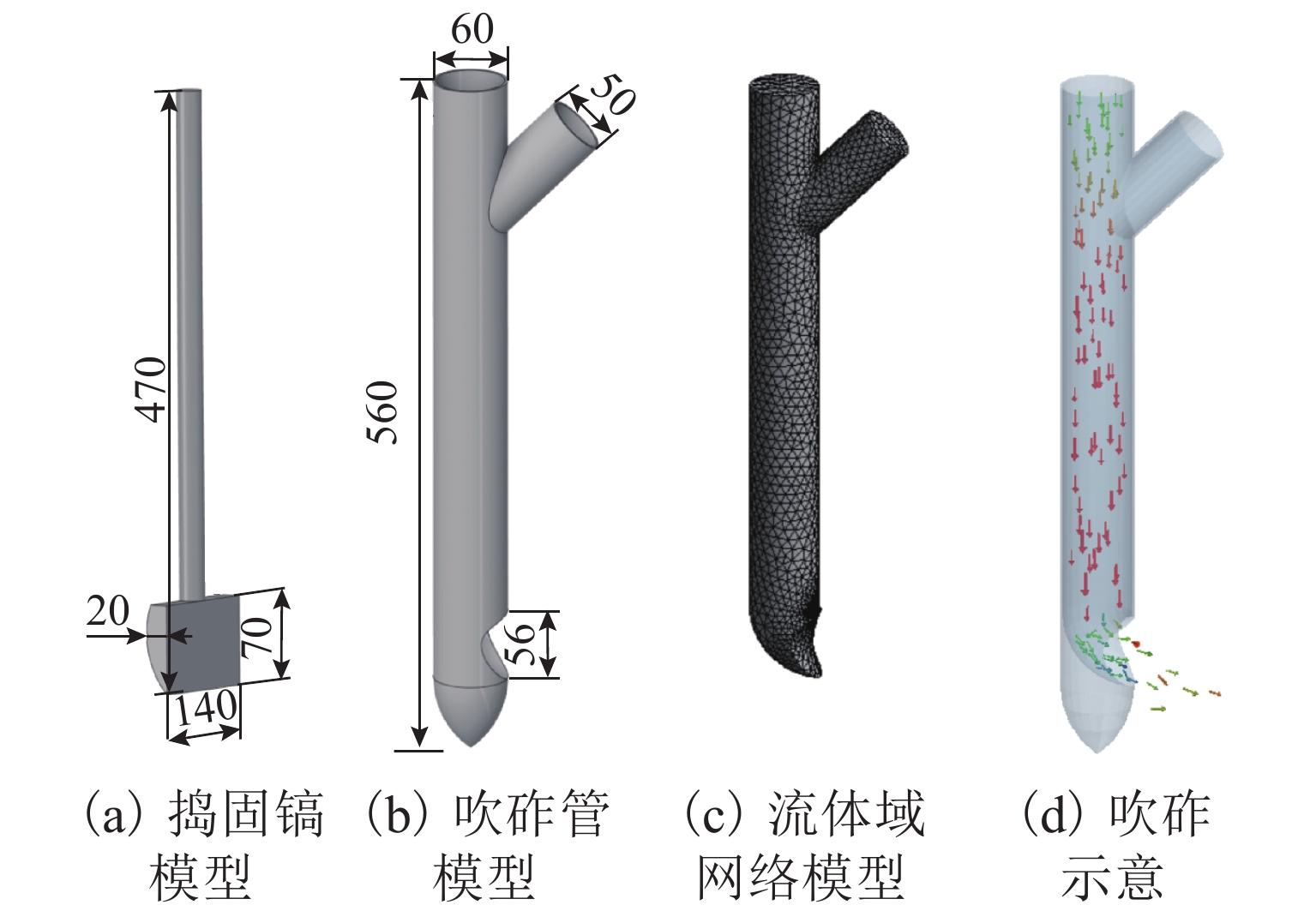
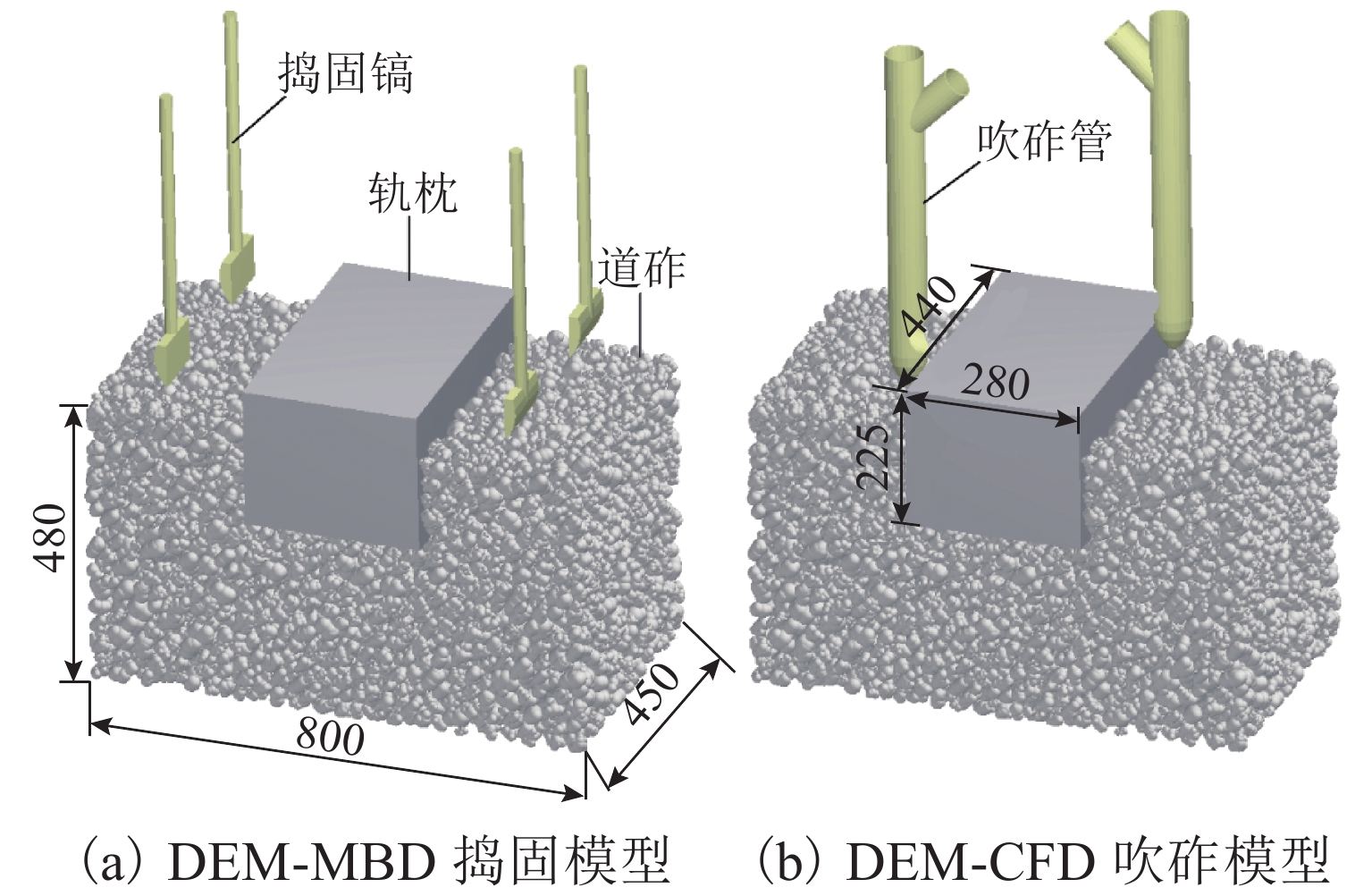
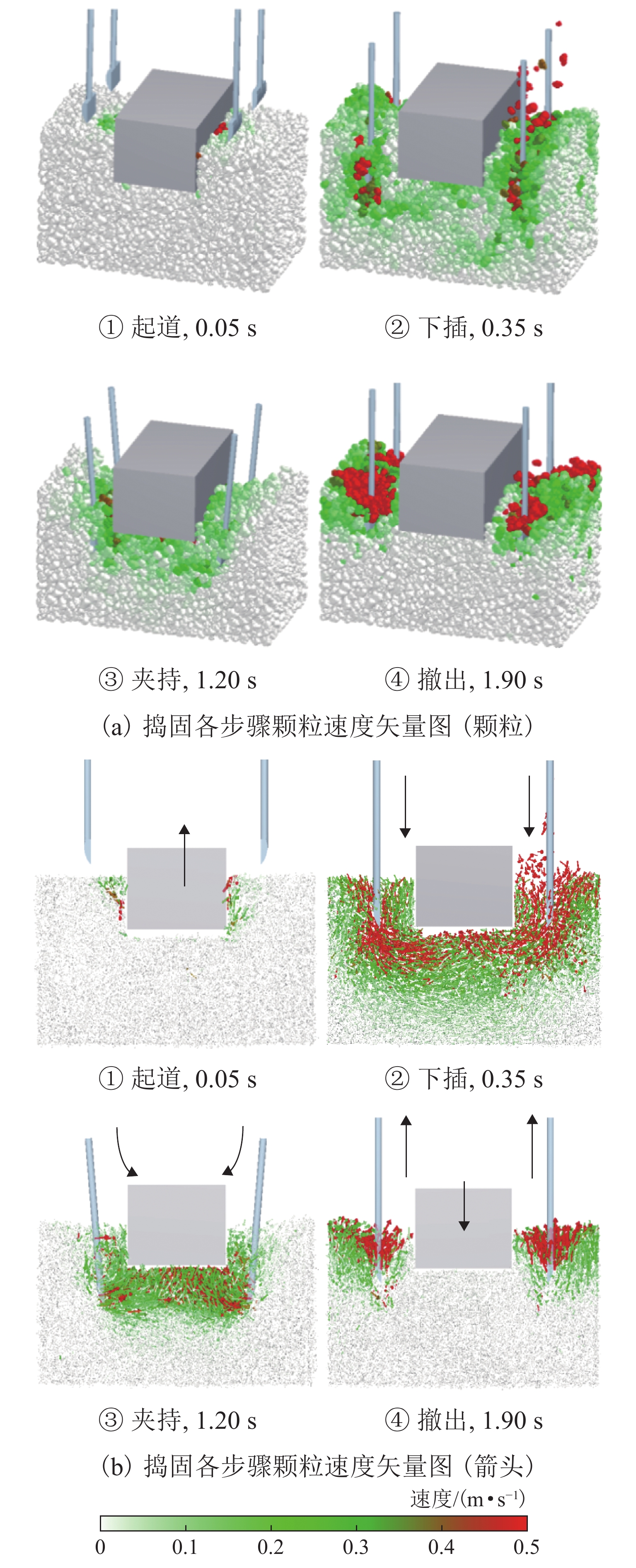
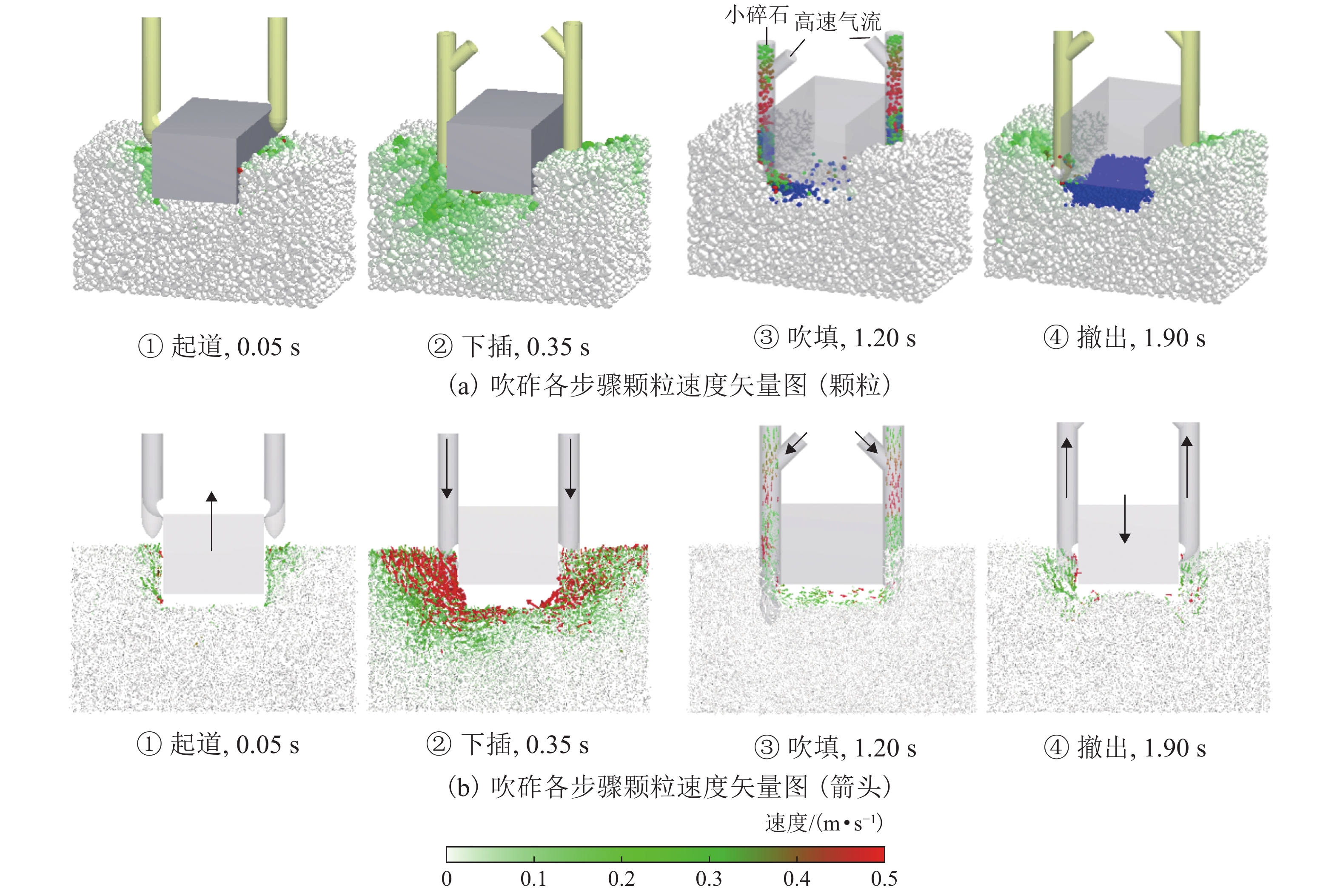
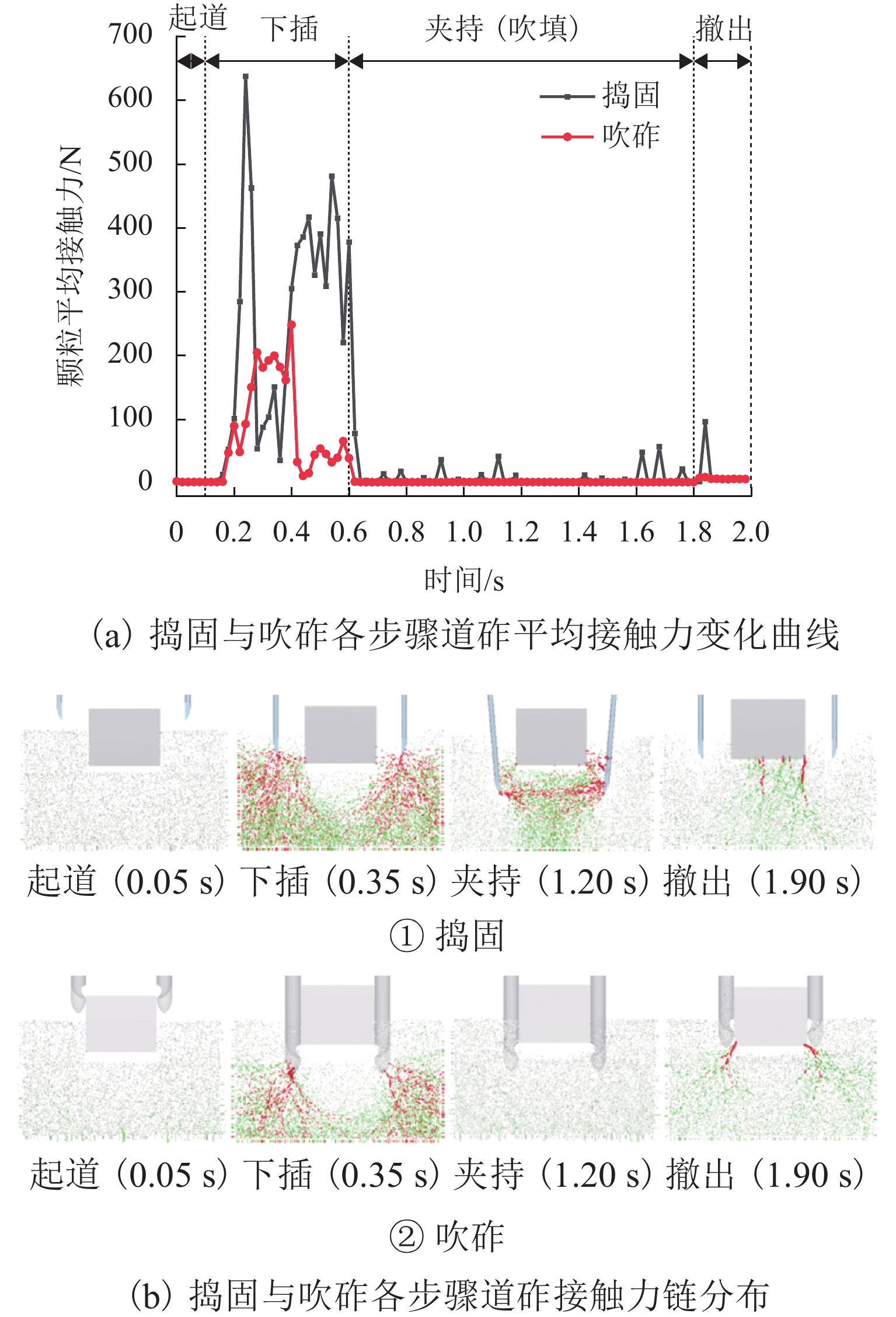
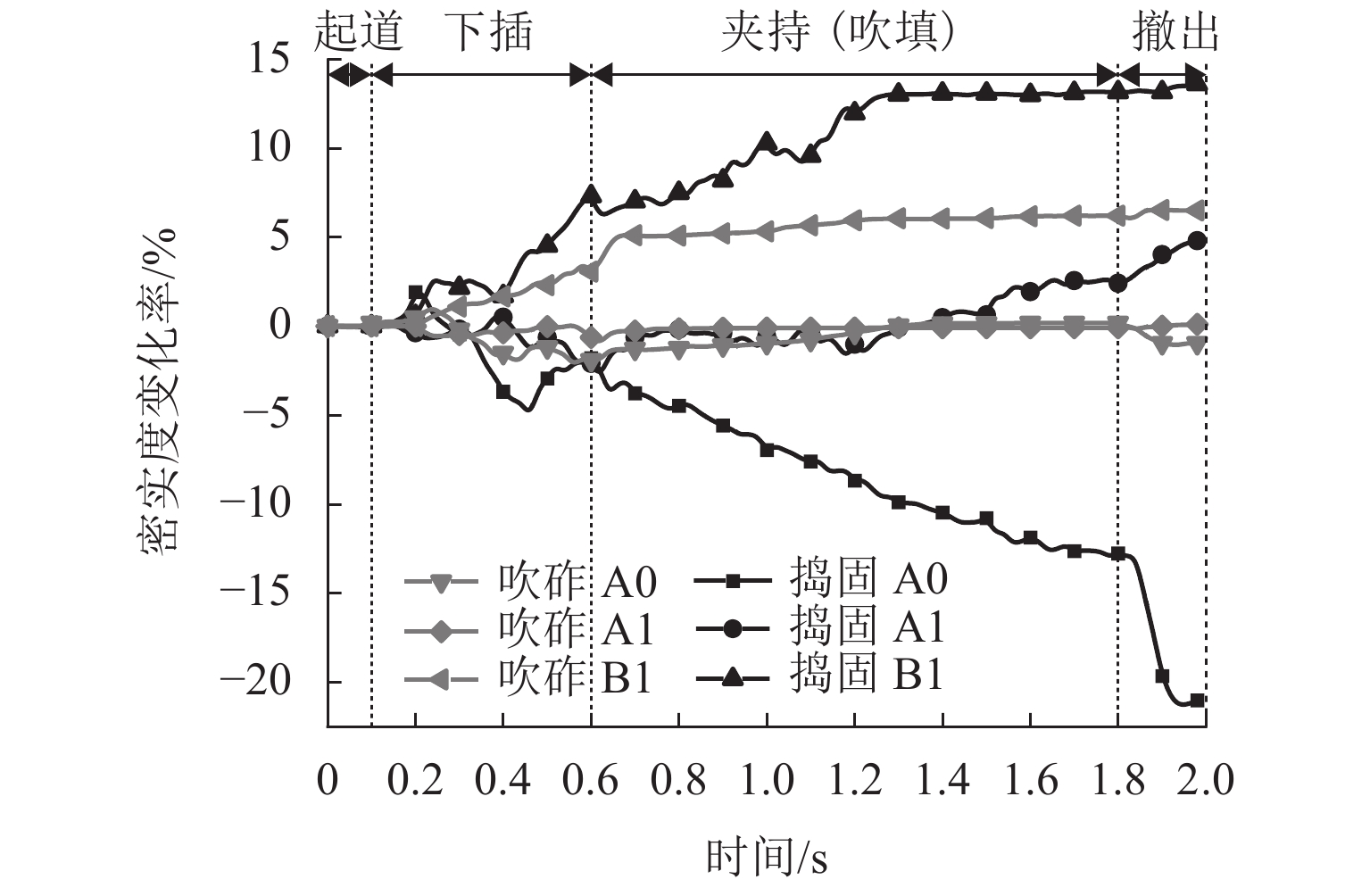
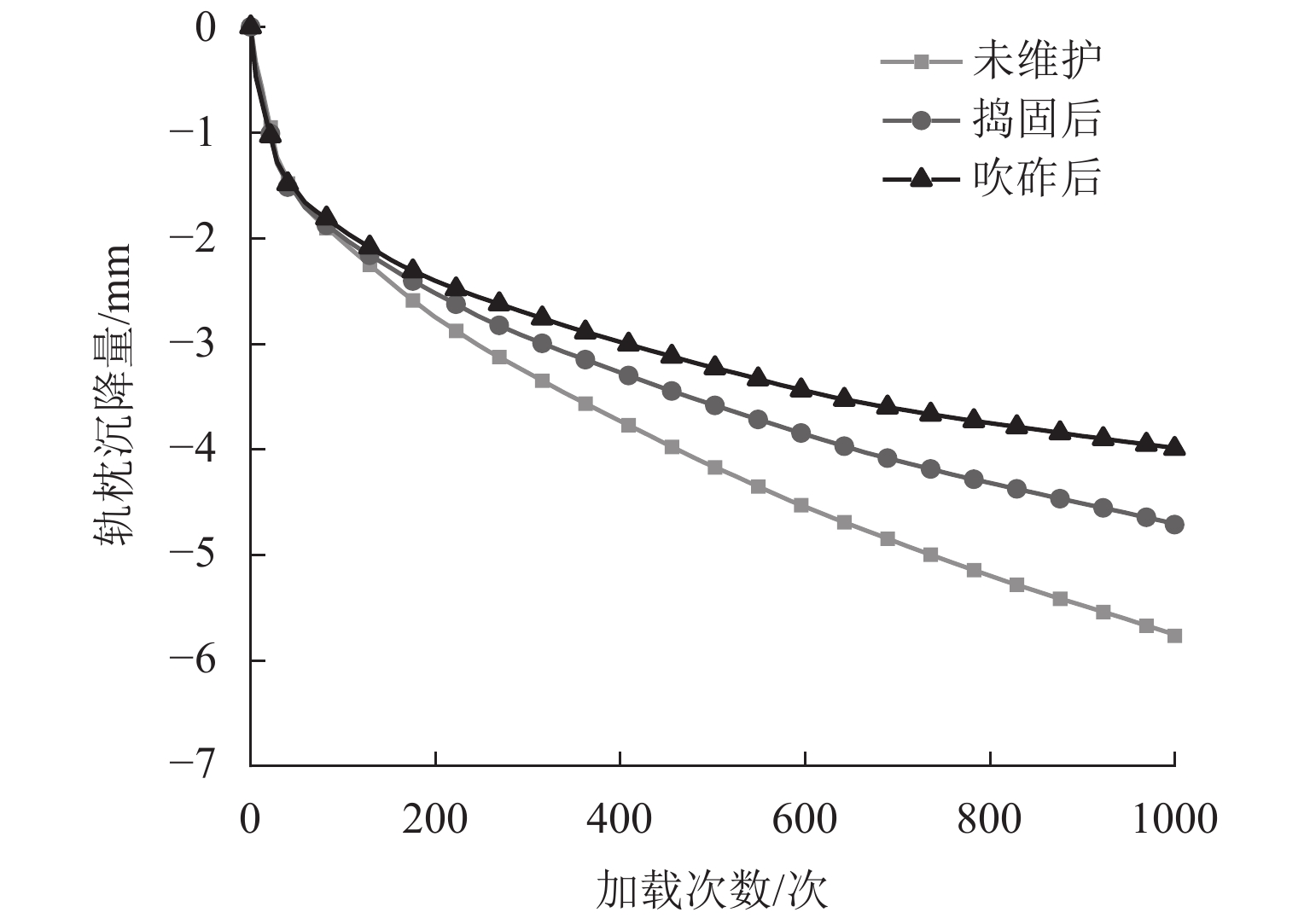
为从细观上研究捣固和吹砟的维护机理，建立了离散元道砟箱数值模型，并耦合多体动力学的捣固镐模型和计算流体力学的吹砟管模型，对捣固与吹砟的作业全过程进行可视化模拟，基于离散元耦合数值模拟，对比分析了2种道床维护方法对道床扰动及作业后轨枕沉降. 结果表明：吹砟作业各阶段对道床的扰动和道砟平均接触力均小于捣固，且扰动主要集中在下插阶段，吹砟作业过程中道砟颗粒速度峰值和接触应力峰值仅为捣固的37.5%和38.9%；捣固后，轨枕底部区域密实度提高了约13.6%，轨枕间上部和下部区域密实度分别降低了约21.0%和提高了约4.8%；吹砟后，轨枕底部区域密实度提高了约6.5%，轨枕间上部和下部区域密实度几乎无变化；在轨枕底部吹入碎石，吹砟作业极大地改善了轨枕底的接触状态和应力扩散，轨枕与道砟颗粒接触数增加了约243%，荷载传递更均匀；1 000次循环加载后，吹砟作业后的轨枕沉降相较捣固和未维护工况分别减少了约18.1%和44.4%.
Abstract:In order to study the maintenance mechanism of ballast tamping and stone-blowing from a micro view, a ballast box numerical model using the discrete element method was established, and the whole processes of ballast tamping and stone-blowing were visually simulated by coupling the tamping hammer model of multi-body dynamics and the blowing tube model of computational fluid dynamics. Based on the discrete element coupled numerical simulation, the effects of two ballast maintenance methods on ballast disturbance and sleeper settlement after operation were compared. The results show that the ballast disturbance and the average contact force of the ballast of the stone-blowing are less than those of the tamping, and the disturbance is mainly concentrated in the insertion stage. Moreover, the peak velocity and contact stress of ballast particles during the stone-blowing are only 37.5% and 38.9% of those during the tamping. After tamping, the compactness at the bottom of the sleeper is increased by about 13.6%, and the compactness of the upper and lower areas between sleepers is reduced by about 21% and increased by about 4.8%, respectively. After stone-blowing, the compactness at the bottom of the sleeper is increased by about 6.5%, and the compactness of the upper and lower areas between sleepers is almost unchanged. Due to the stone-blowing beneath the sleeper, the stone-blowing greatly improves the contact state and stress diffusion at the bottom of the sleeper. The contact number between the sleeper and the ballast particles increases by about 243%, which makes the load transfer more uniform. After 1 000 cycles of loading, the sleeper settlement after stone-blowing is reduced by about 18.1% and 44.4% respectively compared with tamping and unmaintained conditions.
-
Key words:
- ballast /
- discrete element method /
- tamping /
- stone-blowing /
- ballast maintenance
-
图 1 道砟与吹砟碎石颗粒建模与级配曲线
Figure 1. Modeling and gradation curves of ballast and crushed stone particles by stone-blowing
图 6 捣固与吹砟全过程中道砟平均速度变化曲线
Figure 6. Variation curves of ballast average velocity during tamping and stone-blowing operations
图 7 捣固与吹砟各步骤道砟接触力状况
Figure 7. Ballast contact force in each stage of tamping and stone-blowing
图 8 捣固与吹砟全过程道床密实度变化曲线
Figure 8. Compaction curves of ballast during whole tamping and stone-blowing processes
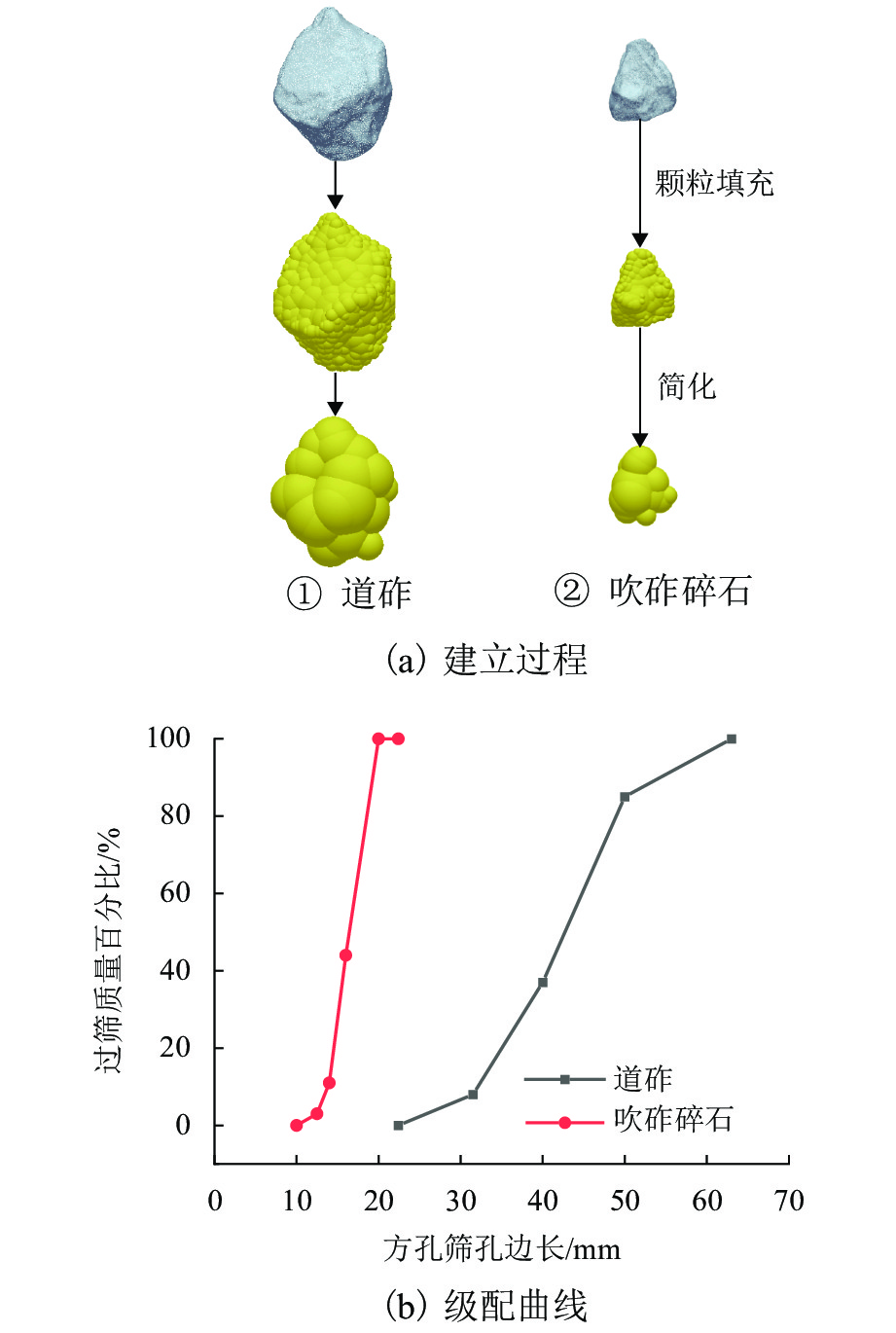
表 1 DEM耦合模拟的参数
Table 1. Parameters of DEM coupling simulation
模型结构 泊松比 剪切模量/GPa 密度/（kg·m−3） 摩擦系数 道砟 0.30 20 2 700 0.55 吹砟碎石 0.30 20 2 700 0.55 轨枕 0.23 15 2 800 0.85 捣固镐 0.29 80 7 800 0.40 吹砟管 0.29 80 7 800 0.40 
下载: 导出CSV
-
[1] 翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226.ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. [2] GUO Y L, MARKINE V L, JING G Q. Review of ballast track tamping: mechanism, challenges and solutions[J]. Construction and Building Materials, 2021, 300: 123940.1-123940.22. doi: 10.1016/j.conbuildmat.2021.123940 [3] FASTENRATH F. Railroad track theory and practice[M]. New York: Frederick Publishing, 2003: 175-178. [4] ESVELD C. Modern railway track[M]. 2nd ed. Zaltbommel: MRT-productions, 2001: 369-373. [5] MCMICHAEL P L. The economics of stoneblowing for the maintenance of way[C]//International Heavy Haul Railway Conference. Vancouver: International Heavy Haul Association, 1991: 98-104. [6] SOL-SÁNCHEZ M, MORENO-NAVARRO F, RUBIO-GÁMEZ M C. Analysis of ballast tamping and stone-blowing processes on railway track behaviour: the influence of using USPs[J]. Géotechnique, 2016, 66(6): 481-489. [7] ANDERSON W F, KEY A J. Model testing of two-layer railway track ballast[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 317-323. doi: 10.1061/(ASCE)1090-0241(2000)126:4(317) [8] AURSUDKIJ B. A laboratory study of railway ballast behaviour under traffic loading and tamping maintenance[D]. Nottingham: University of Nottingham, 2007. [9] BOLER H, MISHRA D, TUTUMLUER E, et al. Stone blowing as a remedial measure to mitigate differential movement problems at railroad bridge approaches[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019, 233(1): 63-72. doi: 10.1177/0954409718778654 [10] 王众保,许永贤,王红,等. 大型养路机械捣固作业参数对捣固效果影响规律的研究[J]. 铁道建筑,2020,60(1): 129-133. doi: 10.3969/j.issn.1003-1995.2020.01.30WANG Zhongbao, XU Yongxian, WANG Hong, et al. Study on influence laws of working parameters of heavy-duty maintenance machinery tamping on tamping effect[J]. Railway Engineering, 2020, 60(1): 129-133. doi: 10.3969/j.issn.1003-1995.2020.01.30 [11] SHI S W, GAO L, CAI X P, et al. Effect of tamping operation on mechanical qualities of ballast bed based on DEM-MBD coupling method[J]. Computers and Geotechnics, 2020, 124: 103574.1-103574.10. [12] SHI S W, DAO L, XIAO H, et al. Research on ballast breakage under tamping operation based on DEM-MBD coupling approach[J]. Construction and Building Materials, 2021, 272: 121810.1-121810.13. [13] LIU J X, WANG P, LIU G Z, et al. Influence of a tamping operation on the vibrational characteristics and resistance-evolution law of a ballast bed[J]. Construction and Building Materials, 2020, 239: 117879.1-117879.14. [14] 井国庆,高亮,邵磊. 吹砟车维修机理离散元仿真与应用[J]. 铁道工程学报,2011,28(11): 58-62. doi: 10.3969/j.issn.1006-2106.2011.11.011JING Guoqing, GAO Liang, SHAO Lei. Simulation and application of maintenance mechanism of ballast blowing car with DEM[J]. Journal of Railway Engineering Society, 2011, 28(11): 58-62. doi: 10.3969/j.issn.1006-2106.2011.11.011 [15] 陈成, 饶文锦, 朱思凡, 等. 多通道吹砟装置和方法: CN113494030B[P]. 2022-10-14. [16] INDRARATNA B, NGO N T, RUJIKIATKAMJORN C, et al. Behavior of fresh and fouled railway ballast subjected to direct shear testing: discrete element simulation[J]. International Journal of Geomechanics, 2014, 14(1): 34-44. doi: 10.1061/(ASCE)GM.1943-5622.0000264 [17] 李朋. 铁路碎石道床车致垂向振动特性分析[D]. 成都: 西南交通大学, 2020. [18] KIM D S, HWANG S H, KONO A, et al. Evaluation of ballast compactness during the tamping process by using an image-based 3D discrete element method[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(7): 1951-1964. doi: 10.1177/0954409718754927 [19] CHEN C, INDRARATNA B, MCDOWELL G, et al. Discrete element modelling of lateral displacement of a granular assembly under cyclic loading[J]. Computers and Geotechnics, 2015, 69: 474-484. doi: 10.1016/j.compgeo.2015.06.006 -
下载:
点击查看大图
计量
- 文章访问数: 151
- HTML全文浏览量: 41
- PDF下载量: 33
- 被引次数: 0