Experimental Study on Hydraulic Characteristics in Baffle-Drop Shaft During Gas Explosion
-
摘要:
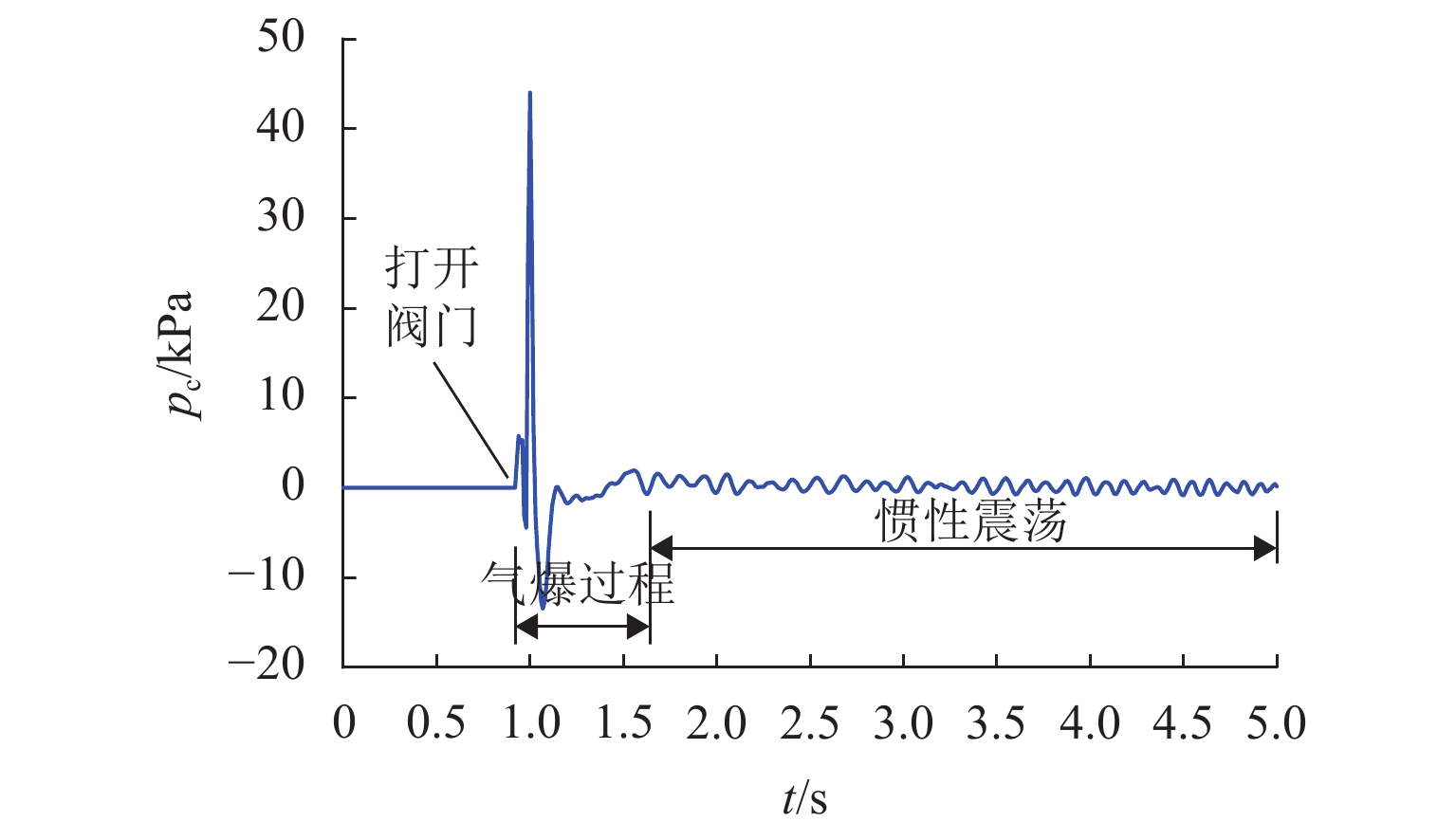
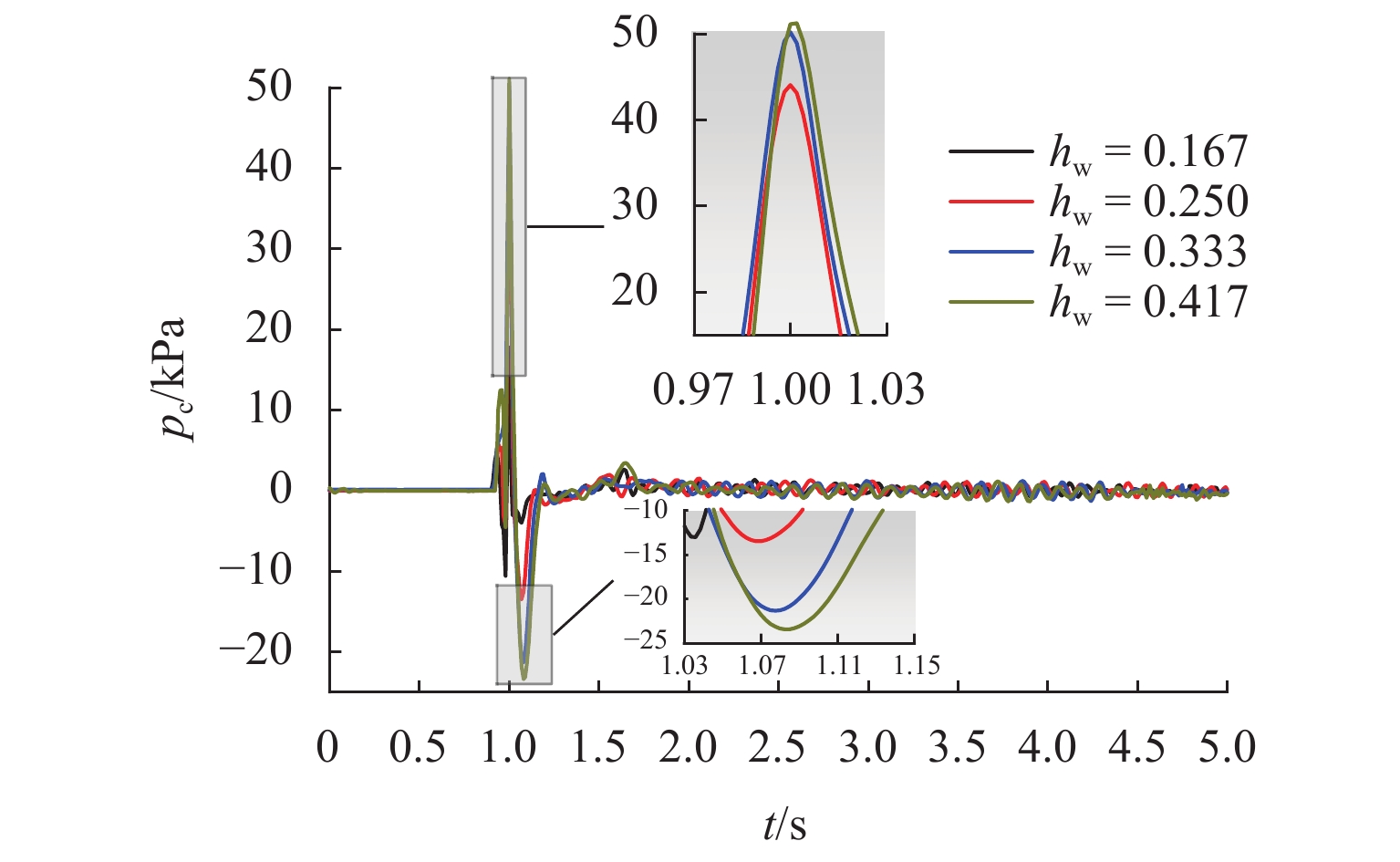
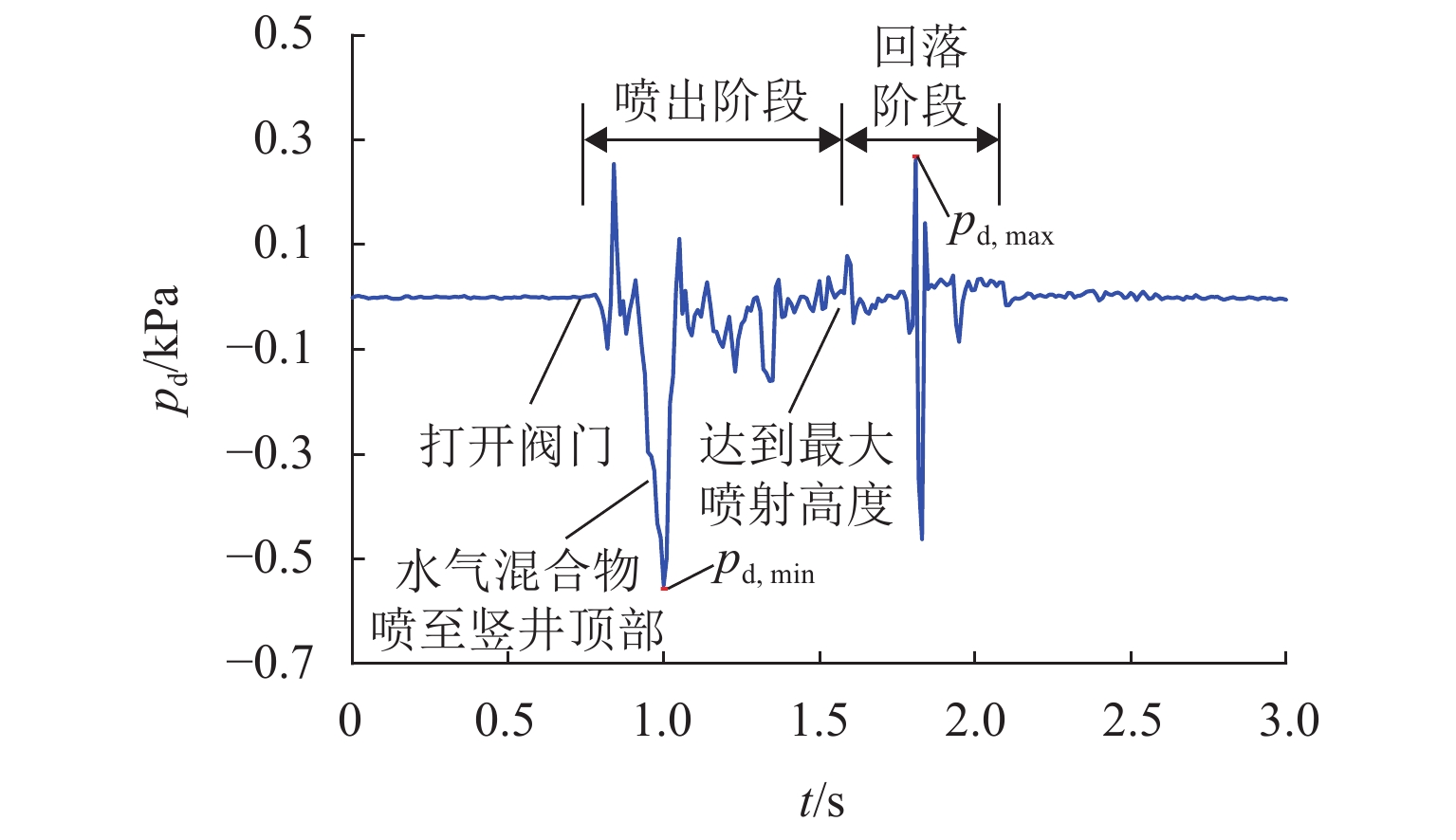
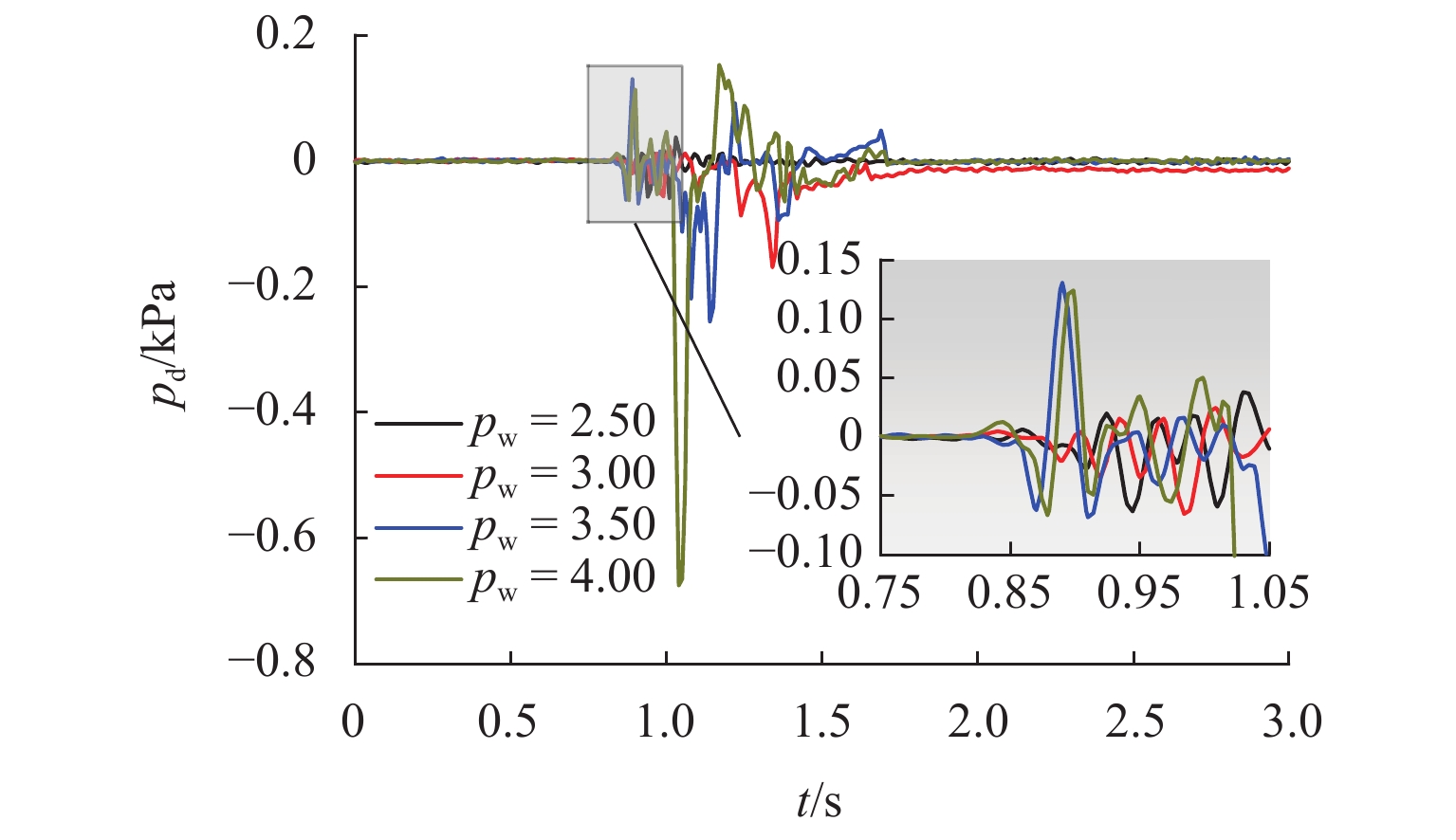
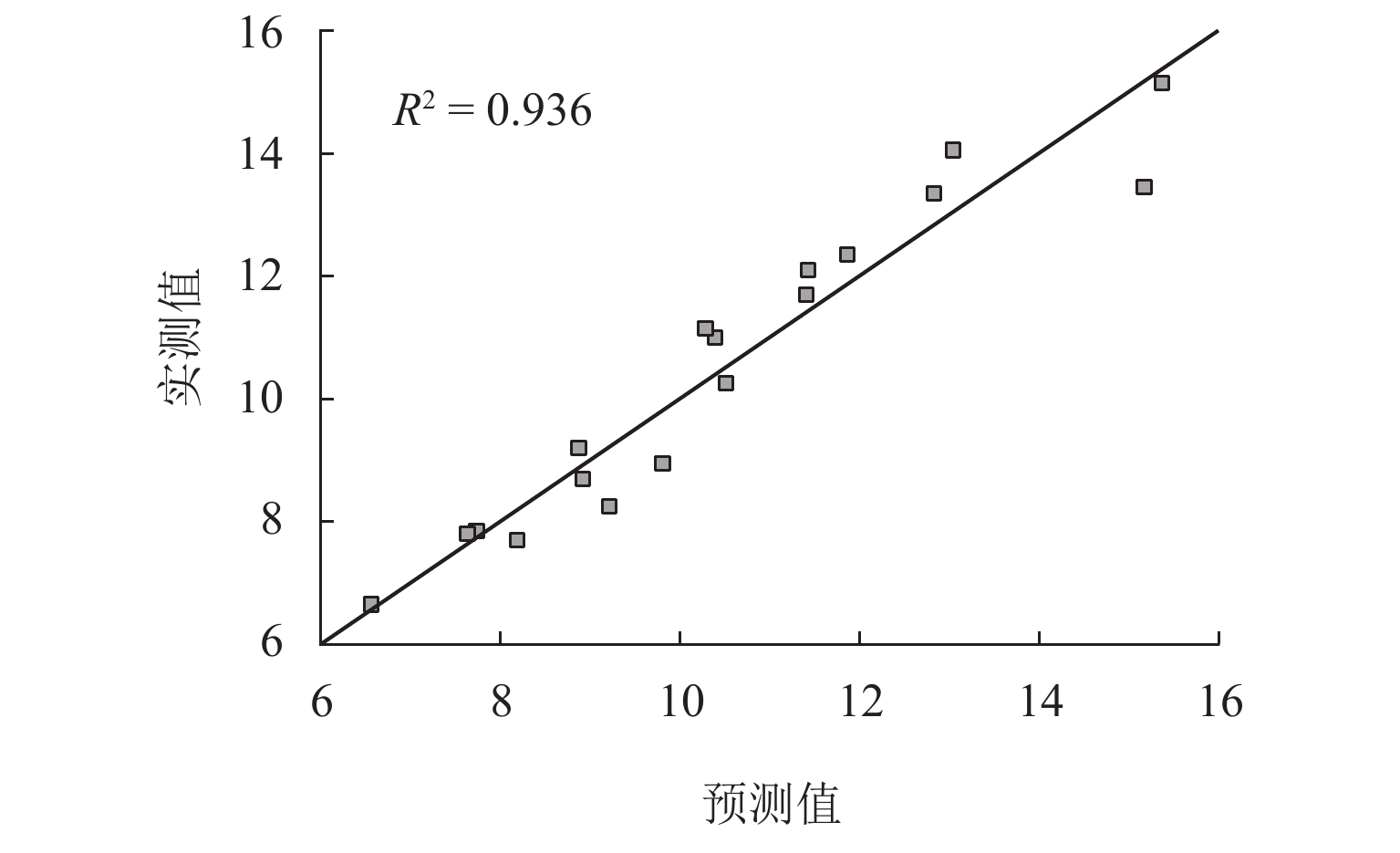
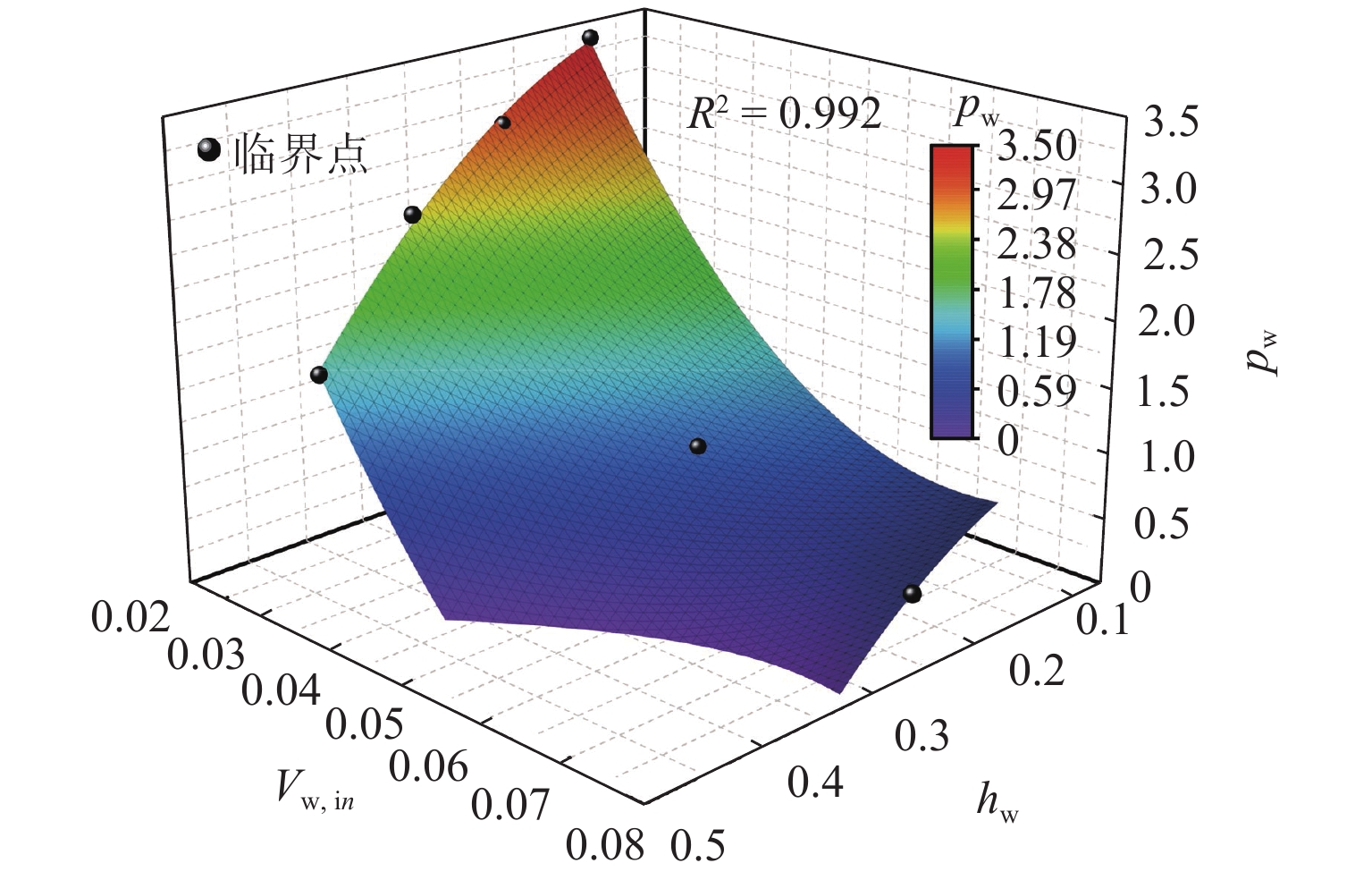
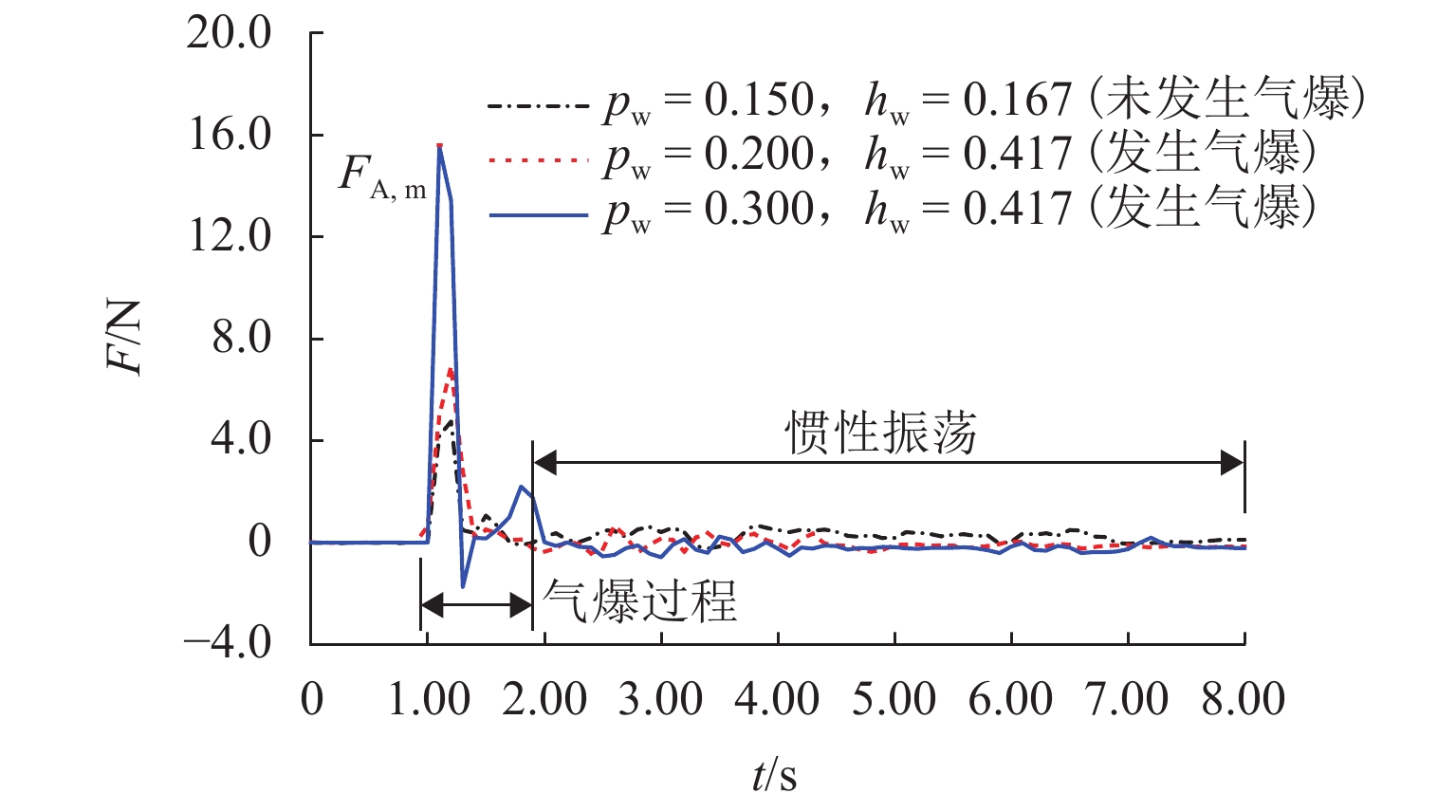
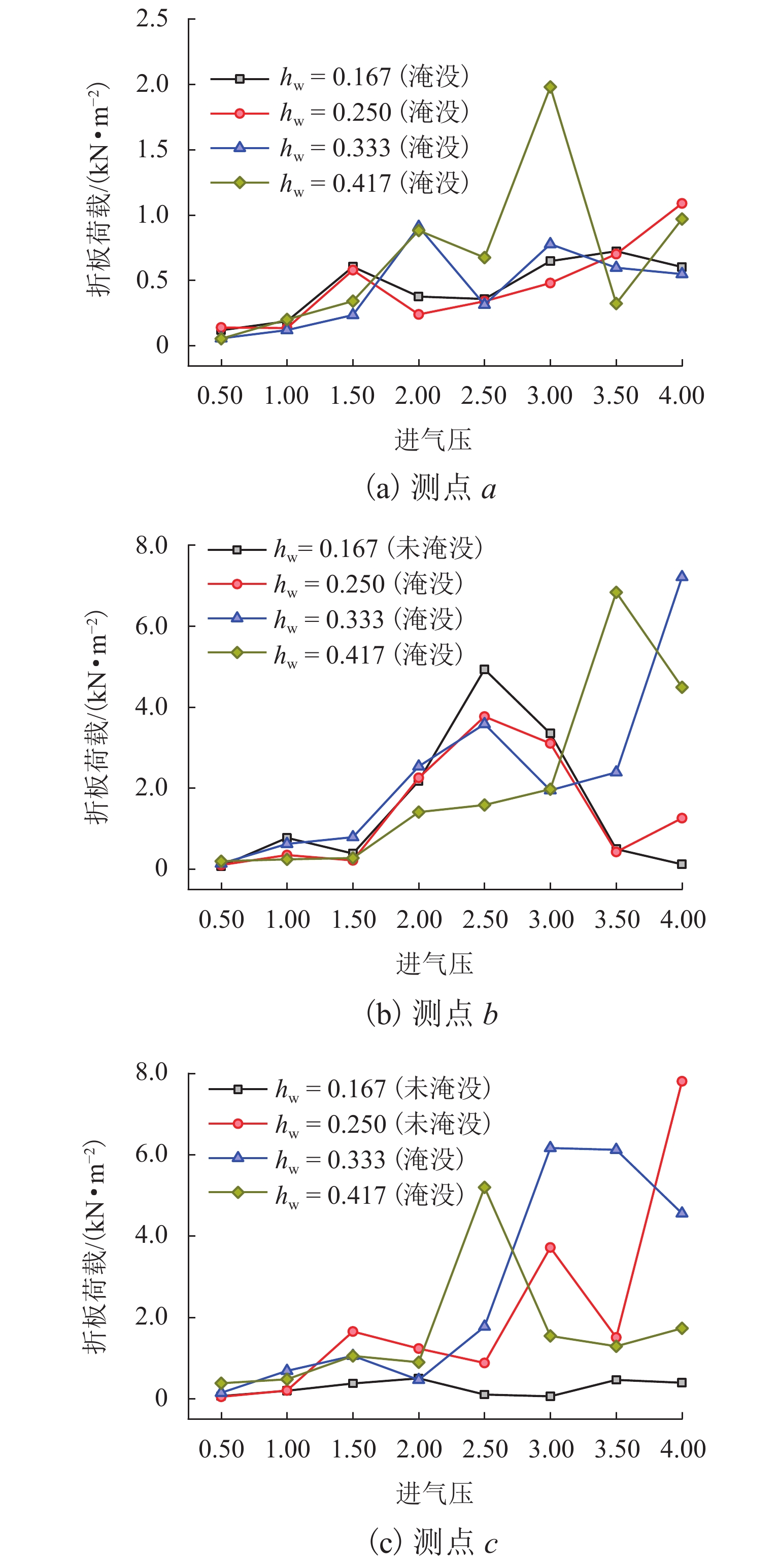
为研究水深、进气压、进气量和干/湿区连通面积等参数与气爆产生机制之间的响应关系，首先，构建了1∶50水力模型试验系统，观测气爆喷射过程并分析竖井内压强变化规律；其次，通过气爆定义建立了竖井最大喷射高度预测模型及产生气爆临界条件；最后，对比分析了多种变量对竖井底部不同折板冲击荷载的影响. 结果表明：气爆过程中折板型竖井内压强剧烈波动，一方面是由于高压气团的释放所导致，另一方面是因高速运动的水气混合物使得竖井内局部气压不平衡所形成；采用多元线性回归模型建立的经验公式可有效预测折板型竖井气爆最大喷射高度；结合不同变量与气爆强度之间响应关系提出的临界条件能够准确判断气爆是否发生；产生气爆时竖井底部折板的水冲击荷载除了与进气压、折板淹没状态、测点位置等因素有关以外，还与水气混合物喷射在折板底部时的随机性有关，气爆过程中折板下方最大水冲击荷载大于10倍正常泄流状态下折板表面的水动力荷载.
Abstract:In order to investigate the response relationship between the gas explosion mechanism and parameters such as water depth, inlet pressure, inlet volume, and connected area of dry/wet areas, a 1∶50 scale hydraulic model test system was first conducted to observe the gas explosion jetting process and analyze the variation law of pressure in the shaft. Secondly, a prediction model for the maximum jetting height of the shaft and the critical conditions of the gas explosion were established according to the definition of the gas explosion. Finally, the influences of different variables on the impact load of different baffles in the bottom of the shaft were compared. The results show that the pressure in the baffle-drop shaft fluctuates sharply during a gas explosion. On the one hand, it is caused by the release of high-pressure air mass; on the other hand, high-speed movement of the air-water mixture makes the local pressure in the shaft imbalanced, which contributes to strong fluctuation. The empirical formula established by the multiple linear regression model can effectively predict the maximum jetting height of the baffle-drop shaft. The critical condition established according to the response relationship between the gas explosion intensity and different variables can accurately determine whether a gas explosion occurs. Except for the inlet pressure, submerged state of the baffle, and measured point location, the hydrodynamic load on the baffle in the bottom of the shaft during the gas explosion is also related to the randomness of air-water mixture jetted on the baffle bottom. The maximum hydrodynamic load on the baffle bottom during a gas explosion is more than 10 times as much as the hydrodynamic load on the baffle surface under normal discharge conditions.
-
Key words:
- baffle-drop shaft /
- gas explosion /
- pressure /
- jetting height /
- impact load
-
图 2 气爆过程中不同时刻对应的几种典型状态
Figure 2. Typical states at different times during gas explosion
图 11 不同进气压下不同测点的最大荷载
Figure 11. Maximum load on measured points under different inlet pressures
表 1 气爆模型试验参数及取值
Table 1. Test parameters and values of gas explosion model
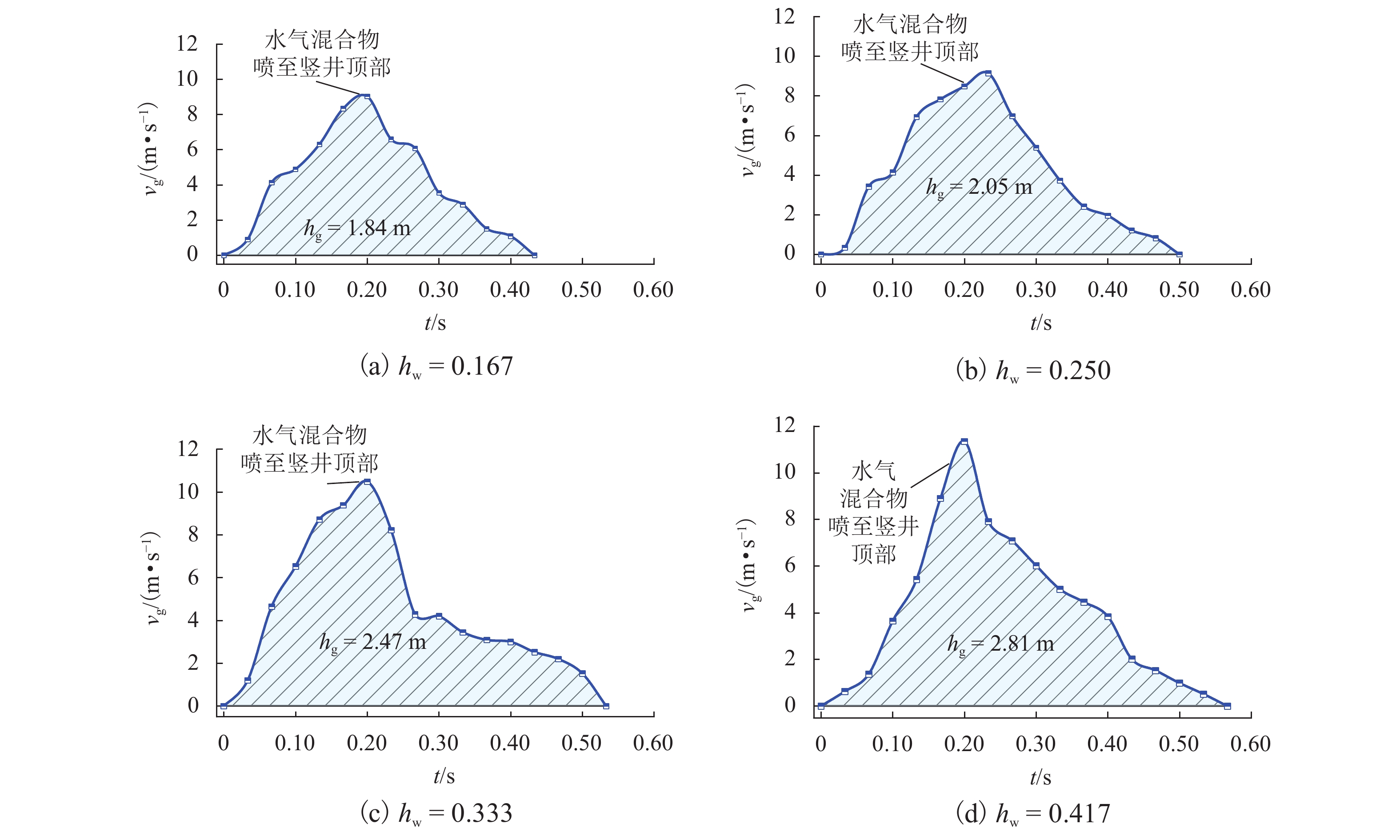
参数 取值 hw 0.167、0.250、0.333、0.417 pw 0.50、1.00、1.50、2.00、2.50、3.00、3.50、4.00 Vw,in 0.026、0.052、0.078 Sw,i 0、0.159、0.318、0.478 
下载: 导出CSV
表 2 不同工况下气爆喷射最大速度及最大高度
Table 2. Maximum jetting velocity and height under different conditions during gas explosion
工况 pw hw Vw,in vg/(m·s−1) hg/m 工况 pw hw Vw,in vg/(m·s−1) hg/m 1 4.00 0.167 0.026 9.023 1.84 13 2.00 0.250 0.052 9.886 2.23 2 3.50 0.250 0.026 8.534 1.65 14 2.50 0.250 0.052 10.807 2.67 3 4.00 0.250 0.026 9.146 2.05 15 3.00 0.250 0.052 11.574 3.03 4 3.00 0.333 0.026 8.703 1.74 16 1.00 0.250 0.078 8.369 1.56 5 3.50 0.333 0.026 9.839 2.20 17 1.50 0.250 0.078 10.117 2.34 6 4.00 0.333 0.026 10.487 2.47 18 2.00 0.250 0.078 10.958 2.69 7 2.00 0.417 0.026 7.535 1.33 19 3.50 0.167 0.026 临界条件 8 2.50 0.417 0.026 8.245 1.54 20 3.00 0.250 0.026 临界条件 9 3.00 0.417 0.026 8.827 1.79 21 2.50 0.333 0.026 临界条件 10 3.50 0.417 0.026 10.303 2.42 22 1.50 0.417 0.026 临界条件 11 4.00 0.417 0.026 11.347 2.81 23 1.00 0.250 0.052 临界条件 12 1.50 0.250 0.052 8.355 1.57 24 0.50 0.250 0.078 临界条件
下载: 导出CSV
-
[1] WRIGHT S J, LEWIS J W, VASCONCELOS J G. Geysering in rapidly filling storm-water tunnels[J]. Journal of Hydraulic Engineering, 2011, 137(1): 112-115. doi: 10.1061/(ASCE)HY.1943-7900.0000245 [2] POZOS-ESTRADA O, POTHOF I, FUENTES-MARILES O A, et al. Failure of a drainage tunnel caused by an entrapped air pocket[J]. Urban Water Journal, 2015, 12(6): 446-454. doi: 10.1080/1573062X.2015.1041990 [3] SONG C C S, GUO Q Z, ZHENG Y F. Hydraulic transient modeling of TARP systems[R]. Minneapolis: University of Minnesota, Minneapolis, 1988. [4] GUO Q Z, SONG C. Dropshaft hydrodynamics under transient conditions[J]. Journal of Hydraulic Engineering, 1991, 117(8): 1042-1055. doi: 10.1061/(ASCE)0733-9429(1991)117:8(1042) [5] LEON A S. Mechanisms that lead to violent geysers in vertical shafts[J]. Journal of Hydraulic Research, 2019, 57(3): 295-306. doi: 10.1080/00221686.2018.1459895 [6] LEON A S, ELAYEB I S, TANG Y. An experimental study on violent geysers in vertical pipes[J]. Journal of Hydraulic Research, 2019, 57(3): 283-294. doi: 10.1080/00221686.2018.1494052 [7] VASCONCELOS J G, WRIGHT S J. Geysering generated by large air pockets released through water-filled ventilation shafts[J]. Journal of Hydraulic Engineering, 2011, 137(5): 543-555. doi: 10.1061/(ASCE)HY.1943-7900.0000332 [8] LEWIS J, WRIGHT S J, VASCONCELOS J, et al. Mechanisms for surges in vertical shafts in stormwater tunnels[J]. Journal of Water Management Modeling, 2011: 41-55. [9] VASCONCELOS J G, WRIGHT S J. Investigation of rapid filling of poorly ventilated stormwater storage tunnels[J]. Journal of Hydraulic Research, 2009, 47(5): 547-558. doi: 10.3826/jhr.2009.3390 [10] SHAO Z Y, YOST S A. Using a multiphase flow numerical model to simulate geysers in stormwater systems[C]//World Environmental and Water Resources Congress 2013. Cincinnati: ASCE, 2013: 1827-1838. [11] ZHOU F, HICKS F E, STEFFLER P M. Transient flow in a rapidly filling horizontal pipe containing trapped air[J]. Journal of Hydraulic Engineering, 2002, 128(6): 625-634. doi: 10.1061/(ASCE)0733-9429(2002)128:6(625) [12] CHEGINI T, LEON A S. Numerical investigation of field-scale geysers in a vertical shaft[J]. Journal of Hydraulic Research, 2020, 58(3): 503-515. doi: 10.1080/00221686.2019.1625817 [13] LI X, ZHANG J, ZHU D Z, et al. Modeling geysers triggered by an air pocket migrating with running water in a pipeline[J]. Physics of Fluids, 2023, 35(4): 045126. doi: 10.1063/5.0138342 [14] 安瑞冬,游景皓,廖磊等. 深层隧道排水系统中井隧水力学特性研究[J]. 水利学报,2021,52(12): 1498-1507. doi: 10.13243/j.cnki.slxb.20210090AN Ruidong, YOU Jinghao, LIAO lei, et al. Study on the hydraulic characteristics of dropshaft and tunnel in the deep tunnel drainage system[J]. Journal of Hydraulic Engineering, 2021, 52(12): 1498-1507. doi: 10.13243/j.cnki.slxb.20210090 [15] BASHIRI-ATRABI H, HOSODA T. The motion of entrapped air cavities in inclined ducts[J]. Journal of Hydraulic Research, 2015, 53(6): 814-819. doi: 10.1080/00221686.2015.1060272 [16] HUANG B, WU S Q, ZHU D Z, et al. Experimental study of geysers through a vent pipe connected to flowing sewers[J]. Water Science and Technology: a Journal of the International Association on Water Pollution Research, 2017, 2017(1): 66-76. [17] LIU J C, ZHANG S Q, HUANG B, et al. Numerical study on effects of chamber design and multi-inlet on storm geyser[J]. Water Science and Technology: a Journal of the International Association on Water Pollution Research, 2021, 83(6): 1286-1299. doi: 10.2166/wst.2021.061 [18] DAVIES R M, TAYLOR G. The mechanics of large bubbles rising through extended liquids and through liquids in tubes[J]. Proceedings of the Royal Society A, 1950, 200(1062): 375-390. [19] WRIGHT S J, LEWIS J, VASCONCELOS J, et al. Mechanisms for stormwater surges in vertical shafts[J]. Journal of Water Management Modeling, 2007: 109-131. [20] YANG Q H, YANG Q. Experimental investigation of hydraulic characteristics and energy dissipation in a baffle-drop shaft[J]. Water Science and Technology: a Journal of the International Association on Water Pollution Research, 2020, 82(8): 1603-1613. doi: 10.2166/wst.2020.441 [21] 刘万海,王翔. 动能定理在物理问题教学中的应用: 以空气阻力上抛运动为例[J]. 绵阳师范学院学报,2020,39(5): 20-23,30.LIU Wanhai, WANG Xiang. The application of kinetic energy theorem in the teaching of practical physics: an example of up-throw motion in air[J]. Journal of Mianyang Teachers’ College, 2020, 39(5): 20-23,30. -
下载:
点击查看大图
计量
- 文章访问数: 195
- HTML全文浏览量: 60
- PDF下载量: 23
- 被引次数: 0